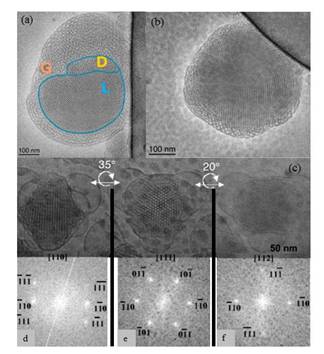
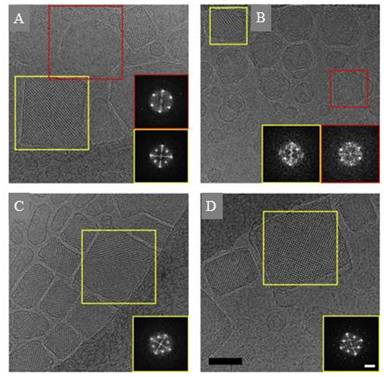
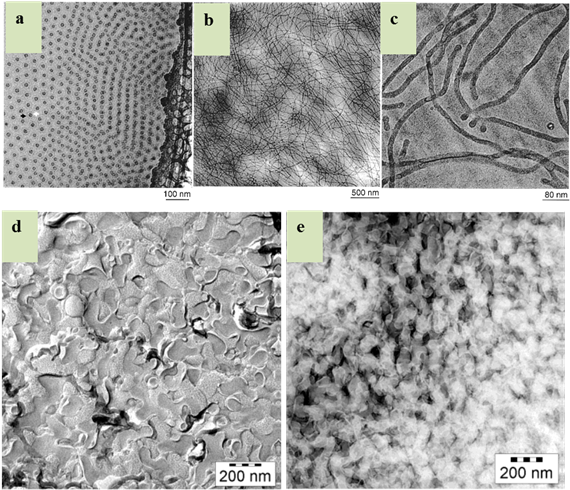
Cryo-transmission electron microscopy (Cryo-TEM), and its technological variations thereof, have become a powerful tool for detailed morphological characterization and 3D tomography of soft lipid and polymeric nanoparticles as well as biological materials such as viruses and DNA without chemical fixation. Here, we review and discuss recent advances in Cryo-TEM analysis of lipid-based drug nanocarriers with particular emphasis on morphological and internal nanostructure characterization of lyotropic liquid crystalline nanoparticles such as cubosomes and hexosomes.
1.
Introduction
Numerous investigations in applied and social sciences, including engineering, environmental studies, economics, and management, often deal with ambiguous and inaccurate data. Traditional methods struggle to address these complexities. Current frameworks like bipolar neutrosophic sets (BNSs) also face difficulties in managing the inherent uncertainty and vagueness of complex datasets, hindering accurate representation and analysis, especially in decision-making contexts.
A collection of contemporary theories effectively addresses ambiguities and uncertainties, including fuzzy set (FS) theories [1], interval-valued fuzzy set theories [2], and bipolar fuzzy sets [3]. Zhang [4] proposed an extension of fuzzy set theory by integrating bipolarity, leading to the development of bipolar-valued fuzzy sets. It is noted that bipolar fuzzy sets (BFS) are particularly suitable for representing information that encompasses both a property and its negation. Further exploration by Lee [3] delved into the fundamental operations associated with bipolar-valued fuzzy sets. Additionally, Lee et al. [5] conducted a comparative analysis of intuitionistic fuzzy sets, interval-valued sets, and BFSs. For instance, BFSs are characterized by positive and negative membership values within the range of $ [-1, 1] $. Elements with zero membership indicate a lack of alignment with the specified property, while the interval $ (0, 1] $ signifies varying degrees of membership satisfaction. Conversely, the interval $ [-1, 0) $ suggests an implicit acknowledgment of the counter property by the elements. Furthermore, the application of BFS-based information has been integrated into decision analysis [6,7]. This is exemplified by the work of Wei et al. [8] (2018), who proposed an expansion of the BFS framework to include the concept of interval-valued bipolar fuzzy sets (IVBFS) within a multi-attribute decision-making context. Jun et al. [9] introduced the abstraction of cubic sets, which extend both interval-valued fuzzy sets and fuzzy sets, allowing for the representation of vagueness through the simultaneous use of exact and interval values. Riaz and Tehrim [10,11] further developed a novel model known as the cubic bipolar fuzzy set (CBFS), which generalizes BFSs to accommodate two-sided opposing features, thereby enabling the representation of information through both bipolar fuzzy numbers and interval-valued bipolar fuzzy numbers.
The neutrosophic set is characterized by three distinct membership functions: the truth-membership function (T), the indeterminacy-membership function (I), and the falsity-membership function (F). Each of these functions is defined within the context of explicit quantification of indeterminacy. The values of T, I, and F are constrained to subsets of the real standard or nonstandard interval $]0, 1+[$. In their work, Wang et al. [12] proposed a single-valued neutrosophic set (SVNS) along with its associated operators, which serve as subclasses of neutrosophic sets. This innovation allows for the restriction of these sets to the real standard interval $[0, 1]$, thereby facilitating their application in scientific and engineering contexts. Additionally, the dual aspects of bipolarity are incorporated into decision-making processes, where positive information is utilized for favorable or appropriate descriptions, while negative information highlights aspects that are rejected or implausible. Building on this concept and the application of BFS, Deli et al. [13] introduced BNSs, exploring their properties, theorems, and aggregation operators, exemplified through a car purchasing scenario. As BNS emerged as a compelling field within neutrosophic theory, Deli et al. [14] further advanced the discourse by presenting the interval-valued bipolar neutrosophic set (IVBN-set), which serves as a broader generalization encompassing FSs, bipolar sets, neutrosophic sets, and bipolar neutrosophic sets. Nonetheless, the previously discussed models face challenges related to effective parameterization, stemming from the constraints of their parametric definitions, which hinder the precise representation of problem parameters.
Molodtsov [15] introduces an enhanced parameterization tool that offers a thorough and complete representation of problem parameters by utilizing soft set theory to address uncertainty and ambiguity. This innovative capability in parameterization, when compared to previous methodologies, has inspired numerous models in the literature, such as neutrosophic soft sets [16], bipolar neutrosophic soft sets [17], and bipolar neutrosophic graded soft sets [18]. Although bipolar neutrosophic sets demonstrate superior efficiency over neutrosophic sets in evaluating real-world problems characterized by inherent uncertainty-both positive and negative-this simplicity in bipolar neutrosophic sets is insufficient for adequately capturing the nuances of ratings or grades due to information constraints. Likewise, interval-valued bipolar neutrosophic sets fall short in conveying expert opinions based on the properties of alternatives. This research presents a novel framework termed cubic bipolar neutrosophic sets (CBNSs), which serves as a generalization of bipolar neutrosophic sets. This new model enhances accuracy and flexibility relative to prior approaches by encompassing a greater volume of information, thus rendering it more comprehensive and rational. Specifically, it integrates information in a more thorough and appropriate manner. To further enhance the parameterization tool, the study explores an additional model that improves the adequacy of final decisions and the quality of information provided. Crucially, the application of these proposed models in decision-making is illustrated, demonstrating their utility in addressing realistic uncertain problems.
Established models like BNSs and IVBN-sets have advanced uncertainty modeling but often fail to capture the complexities of real-world situations, especially with conflicting data or ambiguous membership levels. This study introduces CBNSs, a new framework that combines bipolar fuzzy numbers and interval-valued bipolar fuzzy numbers for a more nuanced representation of uncertainty. CBNSs enhance the accuracy of modeling complex systems, particularly in decision-making processes that involve both positive and negative information, such as evaluating investment alternatives by illustrating trade-offs between potential rewards and risks.
1.1. Comparative analysis
● Comparison with Conventional BNSs:
BNSs struggle with uncertainty due to their binary membership grades. In contrast, CBNSs offer a more advanced framework with cubic membership grades, allowing for a wider range of possibility, impossibility, and indeterminacy. This flexibility enables CBNSs to convey more information and adapt better to different contexts.
● Comparison with Other Related Theories:
CBNSs differ from FSs and interval-valued neutrosophic sets by incorporating bipolarity, allowing for the representation of both positive and negative information. Their cubic membership grades provide enhanced flexibility in expressing uncertainty, while an indeterminacy membership grade addresses ambiguous information. Overall, CBNSs offer a more nuanced framework than BNSs and are particularly useful for decision-making and information processing due to their ability to manage uncertainty, imprecision, and indeterminacy.
1.2. Traditional methods
To enhance our research, we expanded the background section to include a detailed analysis of conventional methods and their limitations. Before cubic bipolar neutrosophic soft sets CBNSSs, various strategies were used to address uncertainty and imprecision in decision-making, including:
● FSs: FSs introduced by Zadeh offer a mathematical framework for representing uncertainty and vagueness. However, they are limited to representing uncertainty within a single dimension.
● Interval-Valued Fuzzy Sets: To address the limitations of FSs, interval-valued fuzzy sets were proposed. These sets allow for the representation of uncertainty using intervals instead of single values.
● BFSs: BFSs extend FSs to incorporate both positive and negative membership grades, providing a more nuanced representation of information.
● Interval-Valued Bipolar Fuzzy Soft Sets: Combining the concepts of interval-valued fuzzy sets and BFSs, interval-valued bipolar fuzzy soft sets offer a framework for handling uncertainty and bipolarity in soft set theory.
- Limitations of Traditional Methods:
While these traditional methods have contributed to the field of decision-making, they often face challenges in handling complex real-world problems. Some limitations include:
● Restricted representation of uncertainty: FSs and interval-valued fuzzy sets may not adequately capture the full spectrum of uncertainty, especially in situations with conflicting or contradictory information.
● Lack of bipolarity: FSs and interval-valued fuzzy sets do not consider both positive and negative aspects of information, limiting their applicability in certain domains.
● Inflexibility: These methods may be less flexible in adapting to different decision-making scenarios, especially when dealing with highly uncertain or imprecise information.
- The Need for CBNSs:
This study introduces CBNSSs to address the limitations of conventional methods. CBNSSs offer a flexible framework for managing uncertainty, bipolarity, and imprecision in decision-making by combining cubic sets, BFSs, and neutrosophic sets for a more detailed representation of information.
This research is organized into five sections. Section 1 provides a foundational overview of the study, outlining the motivation and research objectives. Section 2 offers a concise review of essential concepts and notations related to cubic sets, BFSs, neutrosophic sets, and neutrosophic soft sets. Section 3 introduces the novel concept of CBNSs and elaborates on their fundamental operations, including complement, union, and intersection. Section 4 delves into the concept of CBNSSs, presenting their operational rules, definitions, and properties. Finally, Section 5 demonstrates the practical application of CBNSSs in addressing decision-making challenges within the cubic bipolar neutrosophic soft set domain.
2.
Preliminaries
2.1. Fuzzy set
Definition 1. [1] An FS $ \mathrm{A} $ in $ \omega = \{ \ddot{x}_1, \ddot{x}_2, \ldots, \ddot{x}_n \} $ is given by
where $ 0 \leq \mu_{\mathrm{A}}(\ddot{x}) \leq 1 $ is the grade of satisfaction of $ \ddot{x} \in \omega $ in the set $ \mathrm{A} $.
Definition 2. [2] Let $ \mathbb{I} = [0, 1] $ be a closed unit interval and $ ⓐ = [\ell, u] $ be a closed subinterval of $ \mathbb{I} $, where $ 0 \leq \ell \leq u \leq 1 $. Let $ [\mathbb{L}] $ be the family of all subintervals. The interval-valued fuzzy set (IVFS) defined on $ \omega $ is a function $ \mho: \omega \longrightarrow[\mathbb{L}] $. The set of all IVFSs is denoted by $ [\mathbb{L}]^\omega $ and $ ⓐ (\ddot{x}) = [\ell(\ddot{x}), u(\ddot{x})] $, for each $ ⓐ \in[\mathbb{L}]^\omega $ and $ \ddot{x} \in \omega $, is called degree of membership of $ \ddot{x} $ to $ ⓐ $, where $ \ell(\ddot{x}) $ and $ u(\ddot{x}) $ are called lower and upper FSs respectively.
Definition 3. [9] A cubic set on $ \omega = \left\{\ddot{x}_1, \ddot{x}_2, \ldots, \ddot{x}_n\right\} $ can be defined as
where $ ⓐ $ is an IVFS on $ \omega $ and $ \lambda $ is a FS in $ \omega $.
2.2. Bipolar valued FS
Definition 4. [4] A bipolar valued FS $ \mathbb{B} $ on $ \omega = \{ \ddot{x}_1, \ddot{x}_2, \ldots, \ddot{x}_n \} $ is defined by a positive membership function $ \chi_{\mathbb{B}}^+ $, that is $ \chi_{\mathbb{B}}^+: \omega \longrightarrow [0, 1] $, and a negative membership function $ \chi_{\mathbb{B}}^- $, that is $ \chi_{\mathbb{B}}^-: \omega \longrightarrow [-1, 0] $. Mathematically, a bipolar valued FS is represented by
Definition 5. [5] An IVBFS over the reference set $ \omega = \{ \ddot{x}_1, \ddot{x}_2, \ldots, \ddot{x}_n \} $ is defined as
where the positive membership degree $ \left[\mathbb{V}_{\ell}^+(\ddot{x}), \mathbb{V}_u^+(\ddot{x})\right] \subseteq [0, 1] $ depicts the satisfaction degree of an element $ \ddot{x} $ to the property corresponding to an IVBFS ($ \delta $) and the negative membership degree $ \left[\mathbb{V}_{\ell}^-(\ddot{x}), \mathbb{V}_u^-(\ddot{x})\right] \subseteq [-1, 0] $ depicts the satisfaction degree of an element $ \ddot{x} $ to some implicit counter property corresponding to the IVBFS ($ \delta $), respectively, for every $ \ddot{x} \in \omega $. An interval-valued bipolar fuzzy number (IVBFN) is written as $ \delta = \left\{ \left[\mathbb{V}_{\ell}^+, \mathbb{V}_u^+\right], \left[\mathbb{V}_{\ell}^-, \mathbb{V}_u^-\right] \right\} $.
Definition 6. [19] A CBFS over the reference set $ \omega = \{ \ddot{x}_1, \ddot{x}_2, \ldots, \ddot{x}_n \} $ is defined as
where $ \delta $ is an IVBFS on $ \omega $ and $ \mathbb{B} $ is a BFS on $ \omega $. Thus, CBFS can be rewritten as
where the interval $ \left[\mathbb{V}_{\ell A}^+(\ddot{x}), \mathbb{V}_{u A}^+(\ddot{x})\right] \subseteq [0, 1] $ and $ \left[\mathbb{V}_{\ell A}^-(\ddot{x}), \mathbb{V}_{u A}^-(\ddot{x})\right] \subseteq [-1, 0] $ represent the interval valued positive and negative membership degrees, respectively, and $ \chi_A^+(\ddot{x}) \subseteq [0, 1] $ and $ \chi_A^-(\ddot{x}) \subseteq [-1, 0] $ represent the positive and negative membership, respectively.
2.3. Neutrosophic set
Definition 7. [11] Assume that $ \omega = \{\ddot{x}_1, \ddot{x}_2, \ldots, \ddot{x}_n\} $ is a reference set $ \omega $. Then the neutrosophic set (NS) is formed as the following structure:
where $ \ddot{\partial}_{\hat{\mathbb{A}}}^t(\ddot{x}), \ddot{\partial}_{\hat{\mathbb{A}}}^i(\ddot{x}), \ddot{\partial}_{\hat{\mathbb{A}}}^f(\ddot{x}) $ refer to true membership, indeterminacy membership, and falsehood membership of object $ \ddot{x} $ in $ \omega $ and persist as a mapping:
Definition 8. [13] A bipolar neutrosophic set $ \mathbb{B}^{BNS} $ in the reference set $ \omega = \{\ddot{x}_1, \ddot{x}_2, \ldots, \ddot{x}_n\} $ is given by
where $ \mathbb{B}^{T^+}, \mathbb{B}^{I^+}, \mathbb{B}^{F^+} \rightarrow [0, 1] $ denote, respectively, the positive-Truth Membership(TM), positive-Indeterminacy Membership(IM), and positive-Falsity Membership (FM) degrees of an element $ \ddot{x} \in \omega $ to the property in line with a bipolar NS $ \mathrm{B}^{BNS} $, and $ \mathbb{B}^{T^-}, \mathbb{B}^{I^-}, \mathbb{B}^{F^-} \rightarrow [-1, 0] $ denote, respectively, the negative-TM, negative-IM, and negative-FM degrees of an object $ \ddot{x} \in \omega $.
Definition 9. [13] Let
and
be two BNSs on the reference set $ \omega = \{\ddot{x}_1, \ddot{x}_2, \ldots, \ddot{x}_n\} $. Then the fundamental operation on BNS is defined as follows:
1. Union
for all $ \ddot{x} \in \omega $.
2. Intersection
for all $ \ddot{x} \in \omega $.
3. Complement
4. Subset
and
for all $ \ddot{x} \in \omega $.
Definition 10. [14] An interval-valued bipolar neutrosophic set (IVBNS) $ \mathbb{V}^{IBNS}(\ddot{x}) $ in the reference set $ \omega = \left\{\ddot{x}_1, \ddot{x}_2, \ldots, \ddot{x}_n\right\} $ is given by
where $ \mathbb{V}_{N \ell}{}^{IT^+} $, $ \mathbb{V}_{N u}{}^{IT^+} $, $ \mathbb{V}_{N \ell}{}^{II^+} $, $ \mathbb{V}_{N u}{}^{II^+} $, $ \mathbb{V}_{N \ell}{}^{IF^+} $, $ \mathbb{V}_{N u}{}^{IF^+} $ $ \rightarrow [0, 1] $ and $ \mathbb{V}_{N \ell}{}^{IT^-} $, $ \mathbb{V}_{N u}{}^{IT^-} $, $ \mathbb{V}_{N \ell}{}^{II^-} $, $ \mathbb{V}_{N u}{}^{II^-} $, $ \mathbb{V}_{N \ell}{}^{IF^-} $, $ \mathbb{V}_{N u}{}^{IF^-} $ $ \rightarrow [-1, 0] $, such that the family of all IVBNS sets over $ \omega $ will be denoted by IVBNS$ { }^\omega $.
Definition 11. [14] For $ \mathrm{V}^{IBNS}_1, \mathrm{V}^{IBNS}_2 \in {IVBNS}^\omega $, some operations are defined as follows:
1. Union
for all $ \ddot{x} \in \omega $.
2. Intersection
for all $ \ddot{x} \in \omega $.
3. Complement
4. Subset
$ \mathbb{VIBNS}_1 \subseteq \mathbb{VIBNS}_2 $ if
5. Equality
$ \mathbb{VIBNS}_1 = \mathbb{VIBNS}_2 $ if
2.4. Soft set
Definition 12. [15] Let $ \omega = \{ \ddot{x}_1, \ddot{x}_2, \ldots, \ddot{x}_n \} $ and $ E = \{ \ddot{e}_1, \ddot{e}_2, \ldots, \ddot{e}_m \} $ be a reference set and attribute set, respectively. Then, a soft set (SS) over $ \omega $ is given by the structure:
where $ S $ is a mapping given by:
Here, $ \mathcal{P}(\omega) $ refers to the collection of subsets of the reference set $ \omega $.
Definition 13. [16] Let $ \omega = \{ \ddot{x}_1, \ddot{x}_2, \ldots, \ddot{x}_n \} $ and $ E = \{ \ddot{e}_1, \ddot{e}_2, \ldots, \ddot{e}_m \} $ be a reference set and attribute set, respectively. Then, a neutrosophic Soft Set over $ \omega $ is given by the structure:
where $ S_N $ is a mapping given by:
Here, $ \mathcal{P}_N(\omega) $ refers to the collection of subsets of the reference set $ \omega $.
Definition 14. [17] Let $ \omega = \left\{\ddot{x}_1, \ddot{x}_2, \ldots, \ddot{x}_n\right\} $ and $ E = \left\{\ddot{e}_1, \ddot{e}_2, \ldots, \ddot{e}_m\right\} $ be a reference set and attribute set, respectively. A bipolar neutrosophic SS $ \mathbb{F}^B $ in reference set $ \omega $ is given by
where $ \mathbb{B}_{N S}{ }^{T^{+}}, \mathbb{B}_{N S}{ }^{I^{+}}, \mathbb{B}_{N S}{ }^{F^{+}} \rightarrow [0, 1] $ denote, respectively the positive-TM, positive-IM, and positive-FM degrees of an element $ \ddot{x} \in \omega $ to the property in line with a $ \mathbb{F}^B $, and $ \mathbb{B}_{N S} {}^{T^{-}}, \mathbb{B}_{N}{}^{I^{-}}, \mathbb{B}_{N S} {}^{F^{-}} \rightarrow [-1, 0] $ denote, respectively the negative-TM, negative-IM and negative-FM degrees of an object $ \ddot{x} \in \omega $.
3.
CBNSs
3.1. CBNSs
In this part, we introduce the definition of CBNSs and their basic operations, derive their properties, and provide some examples.
Definition 15. Consider a universal set $ \omega $. A CBNS $ \mathrm{A}^{CBNS} $ defined over the universe set $ \omega $ is an ordered pair which is defined as follows:
where $ \mathbb{V}^{IBNS} = \left\{\mathbb{V}^{IT^+}(\ddot{x}), \mathbb{V}^{II^+}(\ddot{x}), \mathbb{V}^{IF^+}(\ddot{x}), \mathbb{V}^{IT^-}(\ddot{x}), \mathbb{V}^{II^-}(\ddot{x}), \mathbb{V}^{IF^-}(\ddot{x})\right\} $ is called IVBNS,
whereas $ \mathbb{B}^{BNS} = \left\{\mathbb{B}^{N^+}(\ddot{x}), \mathbb{B}^{N^-}(\ddot{x})\right\} $ is called BNS. Consider the interval $ \mathbb{I} = [-1, 1] $. Suppose that $ \left[\mathbb{I}_+\right] $ and $ \left[\mathbb{I}_-\right] $ are the collection of all subintervals of $ [0, 1] $ and $ [-1, 0] $, respectively. Then, we obtain the mappings:
and
Similarly, we get
Then, the CBNS $ \mathrm{A}^{C B N S} $ is represented as
Note that the set of all CBNSs over $ \omega $ will be denoted by $ \mathbb{C}_{B N}^\omega $.
Example 1. Let $ \omega = \left\{\ddot{x}_1, \ddot{x}_2, \ddot{x}_3\right\} $ be a universe set. Suppose an IVBNS $ \mathbb{V}^{I B N S} $ in $ \omega $ is defined by
and a BNS $ \mathrm{B}^{B N S} $ is a set of $ \omega $ and is defined by
Then, the CBNSs $ \mathrm{A}^{C B N S} = \langle\mathbb{V}^{I B N S}, \mathbb{B}^{B N S}\rangle $ will have the tabular representation as in Table 1.
Definition 16. Let $ \mathrm{A}_{1}^{{CBNS}} = \langle \mathbb{V}_1^{{IBNS}}, \mathbb{B}_1^{{BNS}} \rangle $ and $ \mathrm{A}_{2}^{{CBNS}} = \langle \mathbb{V}_2^{{IBNS}}, \mathbb{B}_2^{{BNS}} \rangle \in \mathcal{C}_\omega^{{BN}} $, where
and
1. Then, $ \mathrm{A}_{1}^{{CBNS}} \subseteq \mathrm{A}_{2}^{{CBNS}} $ if, and only if:
$ i. $ $ \mathbb{V}_1^{{IBNS}} \subseteq \mathbb{V}_2^{{IBNS}} $ for all $ \ddot{x} \in \omega $, and we have:
and
$ ii. $ $ \mathbb{B}_1^{{BNS}} \subseteq \mathbb{B}_2^{{BNS}} $ for all $ \ddot{x} \in \omega $, and we have:
2. Then, $ \mathrm{A}_{1}^{{CBNS}} = \mathrm{A}_{2}^{{CBNS}} $ if, and only if:
and
Definition 17. Let $ \mathrm{A}^{{CBNS}} = \langle \mathbb{V}^{{IBNS}}, \mathbb{B}^{{BNS}} \rangle \in \mathbb{C}^{\omega}_{{BN}} $, where
If
and
for all $ \ddot{x} \in \omega $, then $ \mathrm{A}^{{CBNS}} $ is called an internal cubic bipolar neutrosophic set (ICBNS).
Example 2. Let $ \mathrm{A}^{{CBNS}} = \langle \mathbb{V}^{{IBNS}}, \mathbb{B}^{{BNS}} \rangle \in \mathbb{C}^{\omega}_{\text{BN}}.If \mathbb{V}^{{IBNS}} $
and
for all $ \ddot{x} \in \omega, $ then $ \mathrm{A}^{{CBNS}} = \langle \mathbb{V}^{{IBNS}}, \mathbb{B}^{{BNS}} \rangle $ is an ICBNS.
Definition 18. Let $ \mathrm{A}^{{CBNS}} = \langle \mathbb{V}^{{IBNS}}, \mathbb{B}^{{BNS}} \rangle \in \mathbb{C}^{\omega}_{\text{BN}} $, where
If
and
for all $ \ddot{x} \in \omega $, then $ \mathrm{A}^{{CBNS}} $ is called an external cubic bipolar neutrosophic set (ECBNS).
Example 3. Let $ \mathrm{A}^{{CBNS}} = \langle \mathbb{V}^{{IBNS}}, \mathbb{B}^{{BNS}} \rangle \in \mathbb{C}^{\omega}_{\text{BN}} $. If $ \mathbb{V}^{{IBNS}} $
and
for all $ \ddot{x} \in \omega $, then $ \mathrm{A}^{{CBNS}} = \langle \mathbb{V}^{{IBNS}}, \mathbb{B}^{{BNS}} \rangle $ is an ECBNS.
Remark 1. Let $ \mathrm{A}^{{CBNS}} = \langle \mathbb{V}^{{IBNS}}, \mathbb{B}^{{BNS}} \rangle \in \mathbb{C}^{\omega}_{{BN}} $. Then, $ \mathrm{A}^{{CBNS}} $ is said to be neither ICBNS nor ECBNS if:
and
Example 4. Let $ \mathrm{A}^{{CBNS}} = \langle \mathbb{V}^{{IBNS}}, \mathbb{B}^{{BNS}} \rangle \in \mathbb{C}^{\omega}_{{BN}}. { If } \mathbb{V}^{{IBNS}} $
and
for all $ \ddot{x} \in \omega $, then $ \mathrm{A}^{{CBNS}} = \langle \mathbb{V}^{{IBNS}}, \mathbb{B}^{{BNS}} \rangle $ is not an ICBNS or an ECBNS.
Theorem 1. Let $ \mathrm{A}^{\mathit{\text{CBNS}}} = \langle \mathbb{V}^{\mathit{\text{IBNS}}}, \mathbb{B}^{\mathit{\text{BNS}}} \rangle \in \mathbb{C}^{\omega}_{\mathit{\text{BN}}} $, which is not an ECBNS. Then, there exists $ \ddot{x} \in \omega $ such that:
Proof. Suppose that $ \mathrm{A}^{\text{CBNS}} = \langle \mathbb{V}^{\text{IBNS}}, \mathbb{B}^{\text{BNS}} \rangle \in \mathbb{C}^{\omega}_{\text{BN}} $. Then, $ \mathrm{A}^{{CBNS}} $ is ECBNS. By using Definition 18, we get:
Since $ \mathrm{A}^{\text{CBNS}} $ is not an ECBNS in $ \omega $, we have:
That means:
□
Theorem 2. Let $ \mathrm{A}^{\mathit{\text{CBNS}}} = \langle \mathbb{V}^{\mathit{\text{IBNS}}}, \mathbb{B}^{\mathit{\text{BNS}}} \rangle \in \mathbb{C}^{\omega}_{\mathit{\text{BN}}} $. If $ \mathrm{A}^{\mathit{\text{CBNS}}} $ is both ICBNS and ECBNS, then:
for all $ \ddot{x} \in \omega $, where:
Proof. Suppose that $ \mathrm{A}^{\text{CBNS}} = \langle \mathbb{V}^{\text{IBNS}}, \mathbb{B}^{\text{BNS}} \rangle \in \mathbb{C}^{\omega}_{\text{BN}} $. Then, $ \mathrm{A}^{\text{CBNS}} $ is both ICBNS and ECBNS. By using Definitions 17 and 18, we get:
and
Thus,
Hence,
□
3.2. Basic operations on CBNSs
In this part, we introduce some basic operations with examples for CBNS.
Definition 19. Let $ \mathrm{A}^{{CBNS}} = \langle \mathbb{V}^{{IBNS}}, \mathbb{B}^{{BNS}} \rangle \in \mathbb{C}^{\omega}_{{BN}} $, where:
The complement of $ \mathrm{A}^{{CBNS}} $ is denoted by $ \mathrm{A}^{{cCBNS}} $ and is defined by:
and:
for all $ \ddot{x} \in \omega $.
Theorem 3. Let $ \mathrm{A}^{\mathit{\text{CBNS}}} = \langle \mathbb{V}^{\mathit{\text{IBNS}}}, \mathbb{B}^{\mathit{\text{BNS}}} \rangle \in \mathbb{C}^{\omega}_{\mathit{\text{BN}}} $. If $ \mathrm{A}^{\mathit{\text{CBNS}}} $ is an ICBNS, then $ \mathrm{A}^{\mathit{\text{cCBNS}}} $ is also an ICBNS.
Proof. Since $ \mathrm{A}^{\text{CBNS}} = \langle \mathbb{V}^{\text{IBNS}}, \mathbb{B}^{\text{BNS}} \rangle $ is an ICBNS in $ \omega $, we have:
which means:
and this means $ \mathrm{A}^{\text{cCBNS}} $ is also an ICBNS in $ \omega $. □
Theorem 4. Let $ \mathrm{A}^{\mathit{\text{CBNS}}} = \langle \mathbb{V}^{\mathit{\text{IBNS}}}, \mathbb{B}^{\mathit{\text{BNS}}} \rangle \in \mathbb{C}^{\omega}_{\mathit{\text{BN}}} $. If $ \mathrm{A}^{\mathit{\text{CBNS}}} $ is an ECBNS, then $ \mathrm{A}^{\mathit{\text{cCBNS}}} $ is also an ECBNS.
Proof. The proof can be easily stated according to Definitions 18 and 19. □
Definition 20. Let
and
be two CBNSs in $ \omega $.
Then, the union is defined as:
Definition 21. Let
and
be two CBNSs in $ \omega $. Then, their intersection is defined as:
Example 5. Let $ \omega = \{\ddot{x}_1, \ddot{x}_2\} $. Then,
and
are two CBNSs in $ \omega $.
1. Then, the complement of a cubic bipolar neutrosophic set (ACBNS)$ _1 $ is given as follows:
2. Then, their union is given as follows:
3. Then, their intersection is given as follows:
To facilitate the analysis, we define the parameters used throughout this study. A detailed overview of these parameters is provided in Table 2.
4.
CBNSSs
CBNSs are a novel framework introduced in this research to address the limitations of existing methods, particularly BNSs, in handling uncertainty and vagueness within data analysis.
Key Components of CBNSs:
Bipolarity: This refers to the ability to represent both positive and negative membership degrees simultaneously, allowing for a more nuanced representation of information. Cubic Sets: Cubic sets introduce an interval-valued membership grade, providing a more flexible and expressive representation of uncertainty. How CBNSs Work:
Representation: CBNSs represent information using a membership triplet, consisting of a truth membership grade, an indeterminacy membership grade, and a falsity membership grade. Each membership grade can take values within the interval [0, 1]. Operations: CBNSs support various operations, including union, intersection, complement, and scalar multiplication, allowing for mathematical manipulation and analysis. Decision-Making: CBNSs can be applied to decision-making problems by defining decision rules and calculating similarity measures between alternatives. Advantages of CBNSs:
Enhanced Representation: CBNSs provide a more comprehensive and accurate representation of information compared to BNSs, especially in dealing with complex and uncertain data. Flexibility: The interval-valued membership grades in CBNSs offer greater flexibility in modeling uncertainty and vagueness. Versatility: CBNSs can be applied to various domains, including decision-making, pattern recognition, and information fusion.
4.1. CBNSSs
In this part, we introduce the definition of a CBNSS and its basic operations, derive its properties and give some definitions.
Let $ \omega $ be a universe set, $ \hbar $ be a set of parameters and $ \mathcal{H} \subseteq \hbar $. $ \mathbb{C}_{B N S}^\omega \prec $ is the set of all $ C B N S S s $ on $ \omega $.
Definition 22. A pair $ (\mathbb{F}, \mathcal{H}) $ is called a CBNSSs on $ \omega $, where $ \mathbb{F} $ is a mapping given by
A CBNSS is a mapping from parameters to $ \mathbb{C}_{B N S}^\omega $. It is a parameterized family of CBNS-subsets of $ \omega $ and it can be written as:
where $ \mathbb{F}^V(e) = \left\{\mathbb{V}_{\mathcal{F}(e)}^{I T^{+}}(\ddot{x}), \mathbb{V}_{\mathcal{F}(e)}^{I I^{+}}(\ddot{x}), \mathbb{V}_{\mathcal{F}(e)}^{I F^{+}}(\ddot{x}), \mathbb{V}_{\mathcal{F}(e)}^{I T^{-}}(\ddot{x}), \mathbb{V}_{\mathcal{F}(e)}^{I I^{-}}(\ddot{x}), \mathbb{V}_{\mathcal{F}(e)}^{I F^{-}}(\ddot{x})\right\} $
is called intervalued bipolar neutrosophic soft set (IBNSS) whereas $ \mathbb{F}^B(e) = \left\{\mathbb{B}_{\mathcal{F}(e)}^{T^{+}}(\ddot{x}), \mathbb{B}_{\mathcal{F}(e)}^{I^{+}}(\ddot{x}), \mathbb{B}_{\mathcal{F}(e)}^{F^{+}}(\ddot{x}), \mathbb{B}_{\mathcal{F}(e)}^{T^{-}}(\ddot{x}), \mathbb{B}_{\mathcal{F}(e)}^{I^{-}}(\ddot{x}), \mathbb{B}_{\mathcal{F}(e)}^{F^{-}}(\ddot{x})\right\} $ is called bipolar neutrosophic soft set (BNSS).
Suppose that $ \left[\mathbb{I}_{+}\right] $and $ \left[\mathbb{I}_{-}\right] $ are the collection of all subintervals of $ [0, 1] $ and $ [-1, 0] $, respectively, where
and
To illustrate this notion, let us consider the following example.
Example 6. A set of two motorbikes in the universe $ \omega $ given by $ \omega = \left\{\ddot{x}_1, \ddot{x}_2\right\} $ and parameters $ \hbar = \left\{e_1 = \right. $ styling, $ e_2 = $ price, $ e_3 = $ stamina $ \} $.
For $ \mathcal{H} = \left\{e_1, e_3\right\} \subseteq \hbar $, the set $ (\mathbb{F}, \mathcal{H}) = \left\{\mathbb{F}\left(e_1\right), \mathbb{F}\left(e_3\right)\right\} $ is a CBNSS over $ \omega $ where
Then, the CBNSS $ (\mathbb{F}, \mathcal{H}) $ will have a tabular representation as shown in Table 3.
In the following, we introduce the concept of the subset of two CBNSSs and the equality of two CBNSSs.
Definition 23. Let $ (\mathbb{F}, \mathcal{H}) = \{\mathbb{F}(e) \mid e \in \mathcal{H}\} = \left\{\langle e, \mathbb{F}^V(e), \mathbb{F}^B(e)\rangle: e \in \mathcal{H}\right\} $ and $ (\mathbb{G}, \mathcal{T}) = \{\mathbb{G}(e) \mid e \in \mathcal{T}\} = \left\{\langle e, \mathbb{G}^V(e), \mathbb{G}^B(e)\rangle: e \in \mathcal{T}\right\} $ be two CBNSS over $ \omega, \mathcal{H} $, and $ \mathcal{T} \subseteq \hbar $ Then, define the following:
1. (Equality) $ (F, \mathcal{H}) = (\mathbb{G}, \mathcal{T}) $ if, and only if $ ($ iff $) $, the following conditions are satisfied:
$ i. $ $ \mathcal{H} = \mathcal{T} $,
$ ii. $ $ \mathbb{F}(e) = \mathbb{G}(e), \forall e \in \hbar \Leftrightarrow \mathbb{F}^V(e) = \mathbb{G}^V(e) $ and $ \mathbb{F}^B(e) = \mathbb{G}^B(e), \forall e \in \hbar $.
2. (P-Order) $ (\mathbb{F}, \mathcal{H}) \subseteq_P(\mathbb{G}, \mathcal{T}) $ if, and only if $ ($ iff $) $, the following conditions are satisfied:
$ i. $ $ \mathcal{H} \subseteq \mathcal{T}, $
$ ii. $ $ \mathbb{F}(e) \subseteq_P \mathbb{G}(e), \forall e \in \hbar \Leftrightarrow \mathbb{F}^V(e) \subseteq \mathbb{G}^V(e) $ and $ \mathbb{F}^B(e) \subseteq \mathbb{G}^B(e), \forall e \in \hbar $
3. (® - Order) $(F, H) \subseteq $ (G, T) if, and only if (iff), the following conditions are satisfied:
$ i. $ $ H \subseteq T, $
$ ii. $ $ F(e) \subseteq G(e), \forall e \in \omega $, which is equivalent to $ F_V(e) \subseteq G_V(e) $ and $ F_B(e) \supseteq G_B(e), \forall e \in \omega $.
Example 7. Refer to Example 6 and take a CBNSS $ (G, T) $ over $ \omega $, which is given in the following tabular form (see Table 4).
Then, it is clear that the CBNSS $ (F, H) $ in Example 6 is a P-Order of $ (G, T) $.
Example 8. Refer to Example 6 and take a CBNSS $ (G, T) $ over $ \omega $, which is given in the following tabular form (see Table 5).
Then, it is clear that the CBNSS $ (F, H) $ in Example 6 is an ®-Order of $ (G, T) $.
4.2. Basic operations on CBNSSs
In this part, we introduce some basic operations with examples for CBNSSs.
Definition 24. Let $ (\mathcal{F}, \mathcal{H}) $ be a CBNSSs over $ \omega $. The complement of $ (\mathbb{F}, \mathcal{H}) $ is denoted by $ (\mathbb{F}, \mathcal{H})^c $ and is defined by $ (\mathbb{F}, \mathcal{H})^c = \left(\mathbb{F}^c, \neg \mathcal{H}\right) $, where $ \mathbb{F}^c: \neg \mathcal{H} \rightarrow \mathbb{C}_{B N S}^\omega $ is a mapping given by
where
and
Example 9. Referring to Example 6, we can write
By using Definition 24, the complement of the $ \operatorname{CBNSS}(\mathbb{F}, \mathcal{H}) $ is
Theorem 5. If $ (\mathbb{F}, \mathcal{H}) $ is a CBNSSs over $ \omega $, then $ \left((\mathbb{F}, \mathcal{H})^c\right)^c = (\mathbb{F}, \mathcal{H}) $.
Proof. Suppose that $ (\mathbb{F}, \mathcal{H}) $ is a CBNSSs over $ \omega $. The complement $ (\mathbb{F}, \mathcal{H}) $, denoted by $ (\mathbb{F}, \mathcal{H})^c = \left(\mathbb{F}^c, \neg \mathcal{H}\right) $, is defined as:
Now let $ (\mathbb{F}, \mathcal{H})^c = (\mathcal{Q}, R) = \left(\mathbb{F}^c, \neg \mathcal{H}\right) $. Then, we obtain the following:
□
Definition 25. The union of two CBNSSs $ (\mathbb{F}, \mathcal{H}) = \{\mathbb{F}(e) \mid e \in \mathcal{H}\} = \left\{\langle e, \mathbb{F}^V(e), \mathbb{F}^B(e)\rangle: e \in \mathcal{H}\right\} $ and $ (\mathbb{G}, \mathcal{T}) = \{\mathbb{G}(e) \mid e \in \mathcal{T}\} = \left\{\langle e, \mathbb{G}^V(e), \mathbb{G}^B(e)\rangle: e \in \mathcal{T}\right\} $ over $ \omega $, denoted by $ (\mathbb{F}, \mathcal{H}) \tilde{\cup}(\mathbb{G}, \mathcal{T}) $, is a $ \operatorname{CBNSS}(\mathcal{U}, \mathcal{S}) $, where $ \mathcal{S} = \mathcal{H} \cup \mathcal{T} $,
and
$ \forall e \in \mathcal{S} $.
We write $ (\mathcal{U}, \mathcal{S}) = (\mathbb{F}, \mathcal{H}) \tilde{\cup}(\mathbb{G}, \mathcal{T}) $, where
Definition 26. The intersection of two CBNSSs
$ (\mathbb{G}, \mathcal{T}) = \{\mathbb{G}(e) \mid e \in \mathcal{T}\} = \left\{\langle e, \mathbb{G}^V(e), \mathbb{G}^B(e)\rangle: e \in \mathcal{T}\right\} $ over $ \omega $, denoted by $ (\mathbb{F}, \mathcal{H}) \tilde{\cap}(\mathbb{G}, \mathcal{T}) $, is a $ \operatorname{CBNSS}(\mathcal{U}, \mathcal{S}) $, where $ \mathcal{S} = \mathcal{H} \cup \mathcal{T} $,
and
$ \forall e \in \mathcal{S} $.
We write $ (\mathcal{U}, \mathcal{S}) = (\mathbb{F}, \mathcal{H}) \tilde{\cap}(\mathbb{G}, \mathcal{T}) $, where
Example 10. For $ \omega = \{\ddot{x}_1, \ddot{x}_2\} $ and parameters $ \{e_1, e_2, e_3\} $, let $ (\mathcal{F}, \mathcal{H}) $ and $ (\mathcal{G}, \mathcal{T}) $ be CBNSSs in $ \omega $ with the tabular representations in Tables 6 and 7, respectively.
Then, the union $ (\mathcal{U}, \mathcal{S}) = (\mathbb{F}, \mathcal{H}) \tilde{\cup}(\mathbb{G}, \mathcal{T}) $ and intersection $ (\mathcal{U}, \mathcal{S}) = (\mathbb{F}, \mathcal{H}) \mathfrak{\cap}(\mathbb{G}, \mathcal{T}) $ are given in Tables 8 and 9, respectively.
Theorem 6. Let $ [(\mathbb{F}, \mathcal{H}) = \{\mathbb{F}(e) \mid e \in \mathcal{H}\}, (\mathbb{G}, \mathcal{H}) = \{\mathbb{G}(e) \mid e \in \mathcal{H}\}] \in \mathbb{C}_{B N S}^\omega $. Then, the following are true.
1. $ (\mathbb{F}, \mathcal{H}) \subseteq (\mathbb{G}, \mathcal{H}) \iff (\mathbb{F}, \mathcal{H}) \tilde{\cap} (\mathbb{G}, \mathcal{H}) = (\mathbb{F}, \mathcal{H}), $
2. $ (\mathbb{F}, \mathcal{H}) \subseteq (\mathbb{G}, \mathcal{H}) \iff (\mathbb{F}, \mathcal{H}) \tilde{\cup} (\mathbb{G}, \mathcal{H}) = (\mathbb{G}, \mathcal{H}). $
Proof.
1. $ (\Longrightarrow) $ Suppose that $ (\mathbb{F}, \mathcal{H}) \subseteq(\mathbb{G}, \mathcal{H}) $, then we have $ \mathbb{F}(e) \subseteq \mathbb{G}(e) $ for all $ e \in \mathcal{H} $. Let $ (\mathbb{F}, \mathcal{H}) \cong(G G, \mathcal{H}) = (\mathcal{U}, \mathcal{H}) $. $ \quad $ Since $ \mathcal{U}(e) = \mathbb{F}(e) \cap \mathbb{G}(e) = \mathbb{F}(e) $ for all $ e \in \mathcal{H} $, then $ (\mathcal{U}, \mathcal{H}) = (\mathbb{F}, \mathcal{H}). $
$ (\Leftarrow) $ Suppose that $ (\mathbb{F}, \mathcal{H}) \tilde{\cap}(\mathbb{G}, \mathcal{H}) = (\mathbb{F}, \mathcal{H}) $ and let $ (\mathbb{F}, \mathcal{H}) \tilde{\cap}(\mathbb{G}, \mathcal{H}) = (\mathcal{U}, \mathcal{H}). \quad $ Since $ \mathcal{U}(e) = \mathbb{F}(e) \cap \mathbb{G}(e) $ for all $ e \in \mathcal{H} $, we know that $ \mathbb{F}(e) \subseteq \mathbb{G}(e) $ for all $ e \in \mathcal{H} $. Hence, $ (\mathbb{F}, \mathcal{H}) \subseteq(\mathbb{G}, \mathcal{H}) $.
2. $ (\Longrightarrow) $ Suppose that $ (\mathbb{F}, \mathcal{H}) \subseteq(\mathbb{G}, \mathcal{H}) $, then we have $ \mathbb{F}(e) \subseteq \mathbb{G}(e) $ for all $ e \in \mathcal{H} $. $ (\mathcal{U}, \mathcal{H}) = (\mathbb{G}, \mathcal{H}) $.
$ (\Leftarrow) $ Suppose that $ (\mathbb{F}, \mathcal{H}) \tilde{\cup}(\mathbb{G}, \mathcal{H}) = (\mathbb{G}, \mathcal{H}) $ and let $ (\mathbb{F}, \mathcal{H}) \tilde{\cup}(\mathbb{G}, \mathcal{H}) = (\mathcal{U}, \mathcal{H}) $. Since $ \mathcal{U}(e) = \mathbb{F}(e) \cup \mathbb{G}(e) $ for all $ e \in \mathcal{H} $, we know that $ \mathbb{F}(e) \subseteq \mathbb{G}(e) $ for all $ e \in \mathcal{H} $. Hence, $ (\mathbb{F}, \mathcal{H}) \subseteq(\mathbb{G}, \mathcal{H}) $.
□
5.
Application of CBNSSs in decision-making
5.1. Similarity measure between CBNSSs
Similarity measures are essential for pattern recognition and clustering analysis, particularly in fuzzy soft sets. This section will introduce similarity measures for two CBNSSs based on the axioms of fuzzy soft sets [20], which will be applied in a pattern recognition context.
Definition 27. Let $ \mathbb{S}_{C B N S S} $ be a mapping $ \mathbb{S}_{C B N S S}: \mathbb{C}_{B N S}^\omega \curlyeqprec \times \mathbb{C}_{B N S}^\omega \curlyeqprec \rightarrow [0, 1] $, then the degree of similarity between $ \left(\mathbb{F}_1, \mathcal{H}\right) \in \mathbb{C}_{B N S}^\omega \curlyeqprec $ and $ \left(\mathbb{F}_2, \mathcal{H}\right) \in \mathbb{C}_{B N S}^\omega \curlyeqprec $ is defined as $ \mathbb{S}_{C B N S S}\left[\left(\mathbb{F}_1, \mathcal{H}\right), \left(\mathbb{F}_2, \mathcal{H}\right)\right] $, which satisfies the following properties:
$ (\hat{P} 1) $ $ 0 \leq \mathbb{S}_{C B N S S}\left[\left(\mathbb{F}_1, \mathcal{H}\right), \left(\mathbb{F}_2, \mathcal{H}\right)\right] \leq 1 $,
$ (\hat{P} 2) $ $ \mathbb{S}_{C B N S S}\left[\left(\mathbb{F}_1, \mathcal{H}\right), \left(\mathbb{F}_2, \mathcal{H}\right)\right] = \mathbb{S}_{C B N S S}\left[\left(\mathbb{F}_2, \mathcal{H}\right), \left(\mathbb{F}_1, \mathcal{H}\right)\right], $
$ (\hat{P} 3) \mathbb{S}_{ {CBNSS }}\left[\left(\mathbb{F}_1, \mathcal{H}\right), \left(\mathbb{F}_2, \mathcal{H}\right)\right] = 1 \Longleftrightarrow\left(\mathbb{F}_1, \mathcal{H}\right) = \left(\mathbb{F}_2, \mathcal{H}\right) $,
$ (\hat{P} 4) \mathbb{S}_{ {CBNSS }}\left[\left(\mathbb{F}_1, \mathcal{H}\right), \left(\mathbb{F}_2, \mathcal{H}\right)\right] = 0 $ and $ \mathbb{S}_{ {CBNSS }}\left[\left(\mathbb{F}_1, \mathcal{H}\right), \left(\mathbb{F}_3, \mathcal{H}\right)\right] = 0 \quad\left(\mathbb{F}_3, \mathcal{H}\right) \in \mathbb{C}_{B N S}^\omega $ $ \curlyeqprec $, then $ \mathbb{S}_{C B N S S}\left[\left(\mathbb{F}_2, \mathcal{H}\right), \left(\mathbb{F}_3, \mathcal{H}\right)\right] = 0 $.
Now, we introduce the formula to calculate the similarity between two CBNSSs as follows:
Definition 28. Let $ \omega = \left\{\ddot{x}_1, \ddot{x}_2, \ldots, \ddot{x}_n\right\} $ be the universal set of elements and $ \hbar = $ $ \left\{e_1, e_2, \ldots, e_m\right\} $ be the universal set of parameters. $ \quad\left(\mathbb{F}_1, \mathcal{H}\right) = \left\{\mathbb{F}_1(e) \mid e \in \mathcal{H}\right\} = $ $ \left\{\langle e, \mathbb{F}_1^V(e), \mathbb{F}_1^B(e)\rangle: e \in \mathcal{H}\right\} $ and $ \left(\mathbb{F}_2, \mathcal{H}\right) = \left\{\mathbb{F}_2(e) \mid e \in \mathcal{H}\right\} = \left\{\langle e, \mathbb{F}_2^V(e), \mathbb{F}_2^B(e)\rangle: e \in \mathcal{H}\right\} $ are two families of CBNSSs in $ \omega $. We define $ \mathbb{S}_{ {CBNSS }}\left[\left(\mathbb{F}_1, \mathcal{H}\right), \left(\mathbb{F}_2, \mathcal{H}\right)\right] $ as follows:
where
and
Then, $ {S}^c_{{BNSS}}[(\mathbb{F}_1, \mathcal{H}), (\mathbb{F}_2, \mathcal{H})] $ is a similarity measure between two CBNSSs $ (\mathbb{F}_1, \mathcal{H}) $ and $ (\mathbb{F}_2, \mathcal{H}) $.
5.2. The applicability of the proposed similarity metrics in pattern identification
This section presents a methodology for assessing similarity measures between two CBNSSs in pattern recognition. For example, determining if a person with specific symptoms has a certain disease can be framed as a supervised pattern recognition task. We construct an ideal CBNSS for the disease and one for the symptomatic individual. If the similarity measure between these CBNSSs is 0.55 or higher, it suggests a potential diagnosis of the disease.
The algorithm of this method is as follows:
$ \bf{Step 1.} $ To start, we construct an ideal CBNSS $ (\mathbb{F}, \mathcal{H}) = \langle\mathbb{F}^V(e), \mathbb{F}^B(e)\rangle $ for illness, which can be done with the help of a medical expert.
$ \bf{Step 2.} $ Then, we construct CBNSSs $ \left(\mathbb{F}_l, \mathcal{H}\right) = \langle\mathbb{F}_l^V(e), \mathbb{F}_l^B(e)\rangle, l = 1, 2, \ldots, m $, on $ \omega $ for ill person(s).
$ \bf{Step 3.} $ The similarity measures between the ideal $ (\mathbb{F}, \mathcal{H}) = \langle\mathbb{F}^V(e), \mathbb{F}^B(e)\rangle $ for illness and the $ \left(\mathbb{F}_l, \mathcal{H}\right) = \langle\mathbb{F}_l^V(e), \mathbb{F}_l^B(e)\rangle, l = 1, 2, \ldots, m $, for ill the person are calculated using the formula given in Definition 28.
$ \bf{Step 4.} $ If $ \mathbb{S}_{CBNSS}\left[(\mathbb{F}, \mathcal{H}), \left(\mathbb{F}_l, \mathcal{H}\right)\right] \geq 0.55 $, then the ill person is possibly suffering from the diseases, and if $ \mathbb{S}_{CBNSS}\left[(\mathbb{F}, \mathcal{H}), \left(\mathbb{F}_l, \mathcal{H}\right)\right] < 0.55 $, then the ill person is possibly not suffering from the diseases.
Example 11. This section presents a hypothetical numerical example derived from the aforementioned decision-making methodology to demonstrate the potential use of the similarity measure of CBNSS in addressing a medical diagnostic issue. The aim of this problem is to ascertain whether an individual exhibiting certain visible symptoms is afflicted with diabetes or is not suffering from the condition.
Let $ \omega = \left\{\ddot{x}_1 = \right. $ Highdiabetes, $ \ddot{x}_2 = $ lowdiabetes $ \} $ be the reference set and $ \omega = \left\{e_1 = \right. $ sweating, $ e_2 = $ headache $ \} $ be a set of certain visible symptoms.
[Step 1] To construct an ideal $ \operatorname{CBNSS}(\mathbb{F}, \mathcal{H}) = \langle\mathbb{F}^V(e), \mathbb{F}^B(e)\rangle $ for illness (diabetes), one can seek the assistance of a medical expert, as demonstrated in Table 10.
[Step 2] Construct CBNSSs for ill persons (patients) X and Y, as illustrated in Tables 11 and 12.
[Step 3] By Definition 28, similarity measure between $ (\mathbb{F}, \mathcal{H}) $ and $ \left(\mathbb{F}_1, \mathcal{H}\right) $ is given by $ \mathbb{S}_{ {CBNSS }}\left[(\mathbb{F}, \mathcal{H}), \left(\mathbb{F}_1, \mathcal{H}\right)\right] = 0.507 $ and similarity measure between $ (\mathbb{F}, \mathcal{H}) $ and $ \left(\mathbb{F}_2, \mathcal{H}\right) $ is given by $ \mathbb{S}_{ {CBNSS }}\left[(\mathbb{F}, \mathcal{H}), \left(\mathbb{F}_2, \mathcal{H}\right)\right] = 0.6 $.
[Step 4] Since $ \mathbb{S}_{ {CBNSS }}\left[(\mathbb{F}, \mathcal{H}), \left(\mathbb{F}_2, \mathcal{H}\right)\right] = 0.6 > 0.55 $, therefore patient $ Y $ is possibly suffering from diseases. Again, since $ \mathbb{S}_{ {CBNSS }}\left[(\mathbb{F}, \mathcal{H}), \left(\mathbb{F}_1, \mathcal{H}\right)\right] = 0.507 < 0.55 $, therefore patient $ X $ is possibly not suffering from diseases.
6.
Conclusions
This research has introduced CBNSs, a novel framework that significantly advances the capabilities of BNSs in addressing uncertainty and vagueness within data analysis. By integrating bipolarity and cubic sets, CBNSs offer a more comprehensive and accurate representation of information, outperforming existing methods in terms of accuracy, flexibility, and applicability.
We have thoroughly investigated the structural properties of CBNSs and defined key operations related to them. Additionally, we have introduced CBNSSs as a flexible parameterization tool. To validate the practical utility of CBNSs, we conducted a case study in decision-making, demonstrating their effectiveness in handling complex scenarios with uncertainty and vagueness. While CBNSs offer significant advantages, it is important to acknowledge potential limitations. The applicability of CBNSs may be constrained by the availability and quality of data. Furthermore, the computational complexity of CBNS operations might be a consideration for large-scale applications.Future research could explore extending CBNSs (investigating potential extensions) or modifications of CBNSs to address specific domains or challenges, computational efficiency (developing more efficient algorithms for CBNS operations), and real-world applications (applying CBNSs to a wider range of real-world problems and domains).
Author contributions
Khulud Fahad Bin Muhaya: Conceptualization, methodology, investigation and writing-original draft; Kholood Alsager: Writing-review and editing. All authors have read and approved the final version of the manuscript for publication.
Acknowledgments
The researchers would like to thank the Deanship of Graduate Studies and Scientific Research at Qassim University for financial support (QU-APC-2024-9/1).
Conflict of interest
The authors declare that they have no competing interests.









 DownLoad:
DownLoad: