Bioprospecting Saccharomyces cerevisiae in fruits from Amazonian region for beer brewing

1.   Introduction

For real numbers $a, b, c$ with $-c \notin \mathbb{N}\cup \left\{0\right\}$, the Gaussian hypergeometric function is defined by

where $(a, 0) = 1$ for $a\neq0$ and $(a, n)$ is the shifted factorial function given by

for $n\in \mathbb{N}$. It is well known that the Gaussian hypergeometric function, $F(a, b; c; x)$, has a broad range of applications, including in geometric function theory, the theory of mean values, and numerous other areas within mathematics and related disciplines. Many elementary and special functions in mathematical physics are either particular cases or limiting cases. Specifically, $F(a, b;c; x)$ is said to be zero-balanced if $c = a+b$. For the case of $c = a+b$, as $x\to 1$, Ramanujan's asymptotic formula satisfies

where

is the classical beta function ^[1] and

here $\Psi(z) = \Gamma'(z)/\Gamma(z)$, $Re(x) > 0$ is the psi function, and $\gamma$ is the Euler–Mascheroni constant ^[1].

Throughout this paper, let $a\in \lbrack \frac{1}{2}, 1)$, and we denote $r' = \sqrt{1-r^2}$ for $r\in (0, 1)$. The generalized elliptic integrals of the first and second kind are defined on $(0, 1)$ as follows ^[2]:

and

Set $\mathcal{K}_a'(r) = \mathcal{K}_a(r'), \; \mathcal{E}_a'(r) = \mathcal{E}_a(r')$. Note that when $a = \frac{1}{2}$, $\mathcal{K}_a(r)$ and $\mathcal{E}_a(r)$ reduce to the classical complete elliptic integrals $\mathcal{K}(r)$ and $\mathcal{E}(r)$ of the first and second kind, respectively

It is well known that complete elliptic integrals play a crucial role in various areas of mathematics and physics. In particular, these integrals provide a foundation for investigating numerous special functions within conformal and quasiconformal mappings, including the Grötzsch ring function, Hübner's upper bound function, and the Hersch–Pfluger distortion function^[3,4]. In 2000, Anderson, et al. ^[5] reintroduced the generalized elliptic integrals in geometric function theory. They discovered that the generalized elliptic integral of the first kind, denoted as $\mathcal{K}_a$, originates from the Schwarz–Christoffel transformation ^[3] of the upper half–plane onto a parallelogram and established several monotonicity theorems for $\mathcal{K}_a$ and $\mathcal{E}_a$. The generalized Grötzsch ring function in generalized modular equations and the generalized Hübner upper bound function can also be expressed in terms of generalized elliptic integrals^[6]. Recently, generalized elliptic integrals have garnered significant attention from mathematicians. A wealth of properties and inequalities for these integrals can be found in the literature. Specifically, various properties of elliptic integrals and hypergeometric functions, including monotonicity, approximation, and discrete approximation, have been investigated in ^[7,8,9], with sharp inequalities derived for elliptic integrals. Additionally, studies in ^[10,11] primarily focus on inequalities between different means, such as the Toader mean, and Hölder mean, as well as their applications in elliptic integrals.

For $r\in(0, 1)$, $r' = \sqrt{1-r^2}$, it is known that the arc-length of an ellipse with semiaxes 1 and $r$, denoted as $L(1, r)$, is given by $L(1, r) = 4\mathcal{E}(r')$. Muir indicated that $L(1, r)$ can be approximated by $2\pi\{\left(\frac{1+r^{\frac{3}{2}}}{2}\right)^{\frac{2}{3}}$. Later, Vuorinen conjectured the following inequality for $r\in(0, 1)$:

which was subsequently proven by Barnard et al.^[12].

The Hölder mean of positive numbers $x, y > 0$ with order $s\in \mathbb{R}$, is defined as

It is easy to see $H_s(x, y)$ is strictly increasing with respect to $s$. Alzer and Qiu ^[13] established the following inequalities:

with the best constants $s_1 = 3/2$ and $s_2 = \log2/\log(\pi/2) = 1.5349\dots$, see ^[13,14] for details.

The generalized weighted Hölder mean of positive numbers $x, y$, with weight $\omega$ and order $s$, is defined as ^[14]:

Wang et al. ^[15] proved that for $r\in(0, 1)$, the following inequality holds:

and the best parameters $\alpha = \alpha(s)$, $\beta = \beta(s)$ satisfy

where $s_0 = \frac{\log2}{\log(2/\pi)} = 1.5349\dots$, $\eta = F_s(r_0) > \frac{1}{2}$, $F_s = \frac{1-[2\mathcal{E}(r)/\pi]^s}{1-r'^s}$, and $r_0 = r_0(s)\in(0, 1)$ is the value such that $F_s(r)$ is strictly increasing on $(0, r_0)$ and strictly decreasing on $(r_0, 1))$ for $s\in(\frac{3}{2}, 2)$.

The extension of the inequality (1.6) to the second kind of generalized elliptic integral $\mathcal{E}_a$, where $a\in \lbrack \frac{1}{2}, 1)$, is a natural inquiry. This paper aims to address this question. One might wonder why the parameter $a$ is restricted to the interval $\left[ \frac{1}{2}, 1 \right)$ rather than $(0, 1)$. For $a \in (0, \frac{1}{2})$, our analysis has revealed a lack of the expected monotonicity in the function $\mathcal{F}_{a, p}(x)$, as defined in Theorem 3.1. This monotonicity is crucial for establishing the desired inequalities.

To achieve our purpose, we require some more properties of generalized elliptic integrals of the first and second kind. Therefore, Section 2 will introduce several lemmas that establish these properties. Section 3 will present our main results along with their corresponding proofs. In Section 4, we establish several functional inequalities involving $\mathcal{E}_a$ as applications. Finally, we give the conclusion of this article.

2.   Lemmas

In this section, several key formulas and lemmas are presented to support the proof of the main results. The derivative formulas of the generalized elliptic integrals are given.

Lemma 2.1 (^[5]). For $a\in (0, 1)$ and $r\in (0, 1)$, we have

The following lemma provides the monotonicity of some generalized elliptic integrals with respect to $r$, which can be found in ^[16].

Lemma 2.2. Let $a\in (0, 1)$. Then the following function:

(1) $r \mapsto {\frac{\mathcal{E}_a-r'^2\mathcal{K}_a}{r^2}}$ is increasing from $(0, 1)$ to $(\frac{\pi a}{2}, \frac{\sin(\pi a)}{2(1-a)})$;

(2) $r \mapsto {\frac{\mathcal{E}_a-r'^2\mathcal{K}_a}{r^2\mathcal{K}_a}}$ is decreasing from $(0, 1)$ to $(0, a)$;

(3) $r \mapsto {\frac{r'^2(\mathcal{K}_a-\mathcal{E}_a)}{r^2\mathcal{E}_a}}$ is decreasing from $(0, 1)$ to $(0, 1-a)$;

(4) $r \mapsto {\frac{\mathcal{K}_a-\mathcal{E}_a)}{r^2\mathcal{K}_a}}$ is increasing from $(0, 1)$ to $(1-a, 1)$;

(5) $r \mapsto {\frac{r'^c(\mathcal{K}_a-\mathcal{E}_a)}{r^2}}$ is decreasing on $(0, 1)$ if and only if $c\geq a(2-a)$.

Lemmas 2.3 and 2.4 are important tools for proving the monotonicity of the related functions.

Lemma 2.3 (^[17]). Let $\alpha(x) = \sum_{n = 0}^{\infty}a_nx^n$ and $\beta(x) = \sum_{n = o}^{\infty}b_nx^n$ be real power series that converge on $(-r, r)(r > 0)$, and $b_n > 0$ for all $n$. If the sequence $\{\frac{a_n}{b_n}\}_{n\geq0}$ is increasing (or decreasing) on $(0, r)$, then so is $\frac{\alpha(x)}{\beta(x)}$.

Lemma 2.4 (^[3]). For $a, b \in (-\infty, \infty)$ and $a < b$, let $f, g:[a, b]$ be continuous on $[a, b]$ and be differentiable on $(a, b)$, and $g'(x) \neq 0$ for all $x\in (a, b)$. If $\frac{f'(x)}{g'(x)}$ is increasing (or decreasing) on $(a, b)$, then so are

In particular, if $f(a) = g(a) = 0(or\; f(b) = g(b) = 0)$, then the monotonicity of $\frac{f(x)}{g(x)}$ is the same as $\frac{f'(x)}{g'(x)}$.

However, $\frac{f'(x)}{g'(x)}$ is not always monotonic; it is sometimes piecewise monotonic. An auxiliary function $H_{f, g}$ ^[8] is defined as

where $f$ and $g$ are differentiable on $(a, b)$ and $g'\neq 0$ on $(a, b)$ for $-\infty < a < b < \infty$. If $f$ and $g$ are twice differentiable on $(a, b)$, the function $H_{f, g}$ satisfies the following identities:

Here, $H_{f, g}$ establishes a connection between $\frac{f}{g}$ and $\frac{f'}{g'}$.

Lemma 2.5. Define the function $f_1(x)$ on $\lbrack \frac{1}{2}, 1)$ by

Then $2-x < {f_1(x)} < 2$.

Proof. To establish the right-hand side of the inequality, it suffices to prove that

Denote

By differentiation, we obtain

Observe that $g''_1(\frac{1}{2}) = \pi^2-10 = -0.130... < 0$, and $\lim\limits_{x\to 1^-}g''_1(x) = +\infty$. This implies that there exists $x_0\in \lbrack\frac{1}{2}, 1)$ such that $g'_1(x)$ is decreasing on $\lbrack\frac{1}{2}, x_0)$ and increasing on $(x_0, 1)$. Since $g'_1(\frac{1}{2}) = \log2-1 = -0.306\dots,$ and $g'_1(1^-) = 0,$ it is clear that

which implies that $g_1(x)$ is decreasing on $\lbrack \frac{1}{2}, 1)$. Consequently,

In order to establish the left-hand side of the inequality, we define

Note

Differentiating $g_2(x)$ yields

Observe that

Based on these observations and the intermediate value theorem, there exists $x_2\in \lbrack \frac{1}{2}, 1)$ such that $g'_2(x_2) = 0$ and $g_2(x)$ is decreasing on $\lbrack\frac{1}{2}, x_2)$ and increasing on $(x_2, 1)$. Therefore, together with (2.4), we conclude that

This completes the proof. □

Lemma 2.6. For each $a\in \lbrack\frac{1}{2}, 1)$, the function

is decreasing from $(0, 1)$ to $\left(0, \frac{a}{2-a}\right)$.

Proof. Following from (1.2) and (1.3), we deduce that

To establish the desired monotonicity of $f_2(r)$, it suffices to prove that the function $f_3(x)$, defined on (0, 1) by

is decreasing on $(0, 1)$, where $p(a) = \frac{2-a(2-a)}{2}$. Using the power series expansion, the function can be expressed as

where the coefficients $U_n$ and $V_n$ satisfy the recursive relations, as detailed in ^[18]:

with

By Lemma 2.3, we aim to prove that the sequence $\left\{\frac{{U_n}}{{V_n}}\right\}_{n\geq0}$ is decreasing. Note that

and

Observe that

which implies

Assuming that $U_{k}-\frac{V_{k}}{V_{k-1}}{U_{k-1}} < 0$ for all $1 \leq k\leq n$, we prove by induction that $U_{n+1}-\frac{V_{n+1}}{V_{n}}{U_{n}} < 0$. According to (2.5), we have

Since $a\in \lbrack \frac{1}{2}, 1)$, it is easy to know that

and

is positive for $a\in \lbrack \frac{1}{2}, 1)$ when $n\geq 1$. For $a\in \lbrack \frac{1}{2}, 1)$ and $n\geq 1$, we have that

where

In fact, $\delta(n)$ is a quadratic function of $n$ and is decreasing on $(1, \infty)$, it follows that

which implies that

By induction, we conclude that $U_{n+1}-\frac{V_{n+1}}{V_{n}}{U_{n}} < 0$ for all $n\geq1$. Therefore, the sequence $\left\{\frac{{U_n}}{{V_n}}\right\}_{n\geq0}$ is decreasing. Consequently, the function $f_2(r)$ is decreasing on $(0, 1)$. Moreover,

This completes the proof. □

Lemma 2.7. For each $a\in \lbrack\frac{1}{2}, 1)$, we define the function $h(r)$ on $(0, 1)$ by

Then, $2-a < h(r) < 2$.

Proof. First of all, we prove the right-hand side inequality. To establish the desired result, we need to show the following inequality:

which is equivalent to

Denote that

By differentiation, we obtain

Therefore, $h_1(r)$ is decreasing on $(0, 1)$ and

which implies $h(r) < 2$.

Next, we prove $h(r) > 2-a$. This is equivalent to the following inequality.

Denote

The derivative of $F(r)$ yields

Note that $(\mathcal{E}_a-r'^2\mathcal{K}_a-ar^2\mathcal{E}_a)/r'^2$ is increasing from (0, 1) to $(0, \infty)$. In fact, by differentiation, we know

According to Lemma 2.2(1)(5) and Lemma 2.6, we have that $F'(r)$ is increasing on (0, 1) and $F'(r) > \lim\limits_{r\to0^+}F'(r) = 0$, which implies that $F(r)$ is increasing on $(0, 1)$. Moreover,

Thus, $h(r) > 2-a$. The proof is completed. □

For $a\in\left[\frac{1}{2}, 1\right)$, it is also found that $h(r)$ is strictly increasing on $(0, 1)$.

Lemma 2.8. For each $a\in \lbrack\frac{1}{2}, 1)$, $r\in(0, 1)$, we define the function $f_4(r)$ by

Then $f_4(r)$ is strictly decreasing from $(0, 1)$ to $\left(0, \frac{(1-a)\pi}{2a(2-a)}\right)$.

Proof. Let

With Lemma 2.4 and $f_{41}(0^+) = f_{42}(0^+) = 0$, we only prove the monotonicity of $f'_{41}(r)/f'_{42}(r)$. Then we have

By differentiation, we see

With Lemma 2.2(2), we obtain

Thus, $f_{43}(r)$ is strictly decreasing on $(0, 1)$, which shows $f_4(r)$ is strictly decreasing. And

The proof is completed. □

Lemma 2.9. For each $a\in \lbrack\frac{1}{2}, 1)$, $r\in(0, 1)$, we define the function $f_5(r)$ by

Then $f_5(r)$ is strictly increasing from $(0, 1)$ to $\left(\frac{\pi}{2}, +\infty\right)$.

Proof. Let

Taking the derivative, we have

where

In fact, we see

which demonstrates $f'_5(r) > 0$ for $r\in(0, 1)$ and $f_5(r)$ is increasing on $(0, 1)$. Moreover,

The proof is completed. □

Lemma 2.10. For each, $a\in \lbrack\frac{1}{2}, 1)$, $r\in(0, 1)$, $h(r)$ is given as in Lemma 2.7. Then, $h(r)$ is strictly increasing from $(0, 1)$ to $(2-a, 2)$.

Proof. Let

Clearly, $h(r) = \frac{h_2(r)}{h_3(r)}$ and $h_2(0^+) = h_3(0^+) = 0$. By differentiations,

Then,

With Lemmas 2.8 and 2.9, we obtain that $h(r)$ is strictly increasing on $(0, 1)$. Furthermore,

This completes the proof. □

3.   Main results

In this section, we present some of the main results of $\mathcal{E}_a(r)$.

Theorem 3.1. Let $a \in \left[\frac{1}{2}, 1\right)$, $p \in \mathbb{R} \setminus \left\{0\right\}$, and for $r \in (0, 1)$, define

The monotonicity of $\mathcal{F}_{a, p}(r)$ is as follows:

(1) $\mathcal{F}_{a, p}(r)$ is strictly increasing from $(0, 1)$ to $(1-a, 1-b)$ if and only if $p \geq 2$, where

(2) $\mathcal{F}_{a, p}(r)$ is strictly decreasing on $(0, 1)$ if and only if $p \leq 2-a$. Moreover, if $p\in(0, 2-a\rbrack$, the range of $\mathcal{F}_{a, p}(r)$ is $(1-b, 1-a)$, and the range is $(0, 1-a)$ if $p\in(-\infty, 0)$.

(3) If $p \in (2-a, 2)$, $\mathcal{F}_{a, p}(r)$ is piecewise monotonic. To be precise, there exsists $r_0 = r_0(a, p) \in (0, 1)$ such that $\mathcal{F}_{a, p}(r)$ is strictly increasing on $(0, r_0)$ and strictly decreasing on $(r_0, 1)$. Furthermore, for $r \in (0, 1)$, if $p \in (2-a, p_0)$, the range of $\mathcal{F}_{a, p}(r)$ satisifies

while

if $p \in \lbrack p_0, 2)$, where

Proof. For $r\in (0, 1)$,

Clearly, we have $\varphi_1(0) = \varphi_2(0) = 0$. By differentiation,

and

By differentiating $\log \varphi_3(r)$, we obtain

where $h(r)$ is defined as in Lemma 2.7. By Lemmas 2.2(2), 2.7, and 2.10, there are three cases to consider.

$(i)$ If $p\geq 2.$ It follows from (3.3) that $\varphi_3(r)$ is strictly increasing on $(0, 1)$, and so is $\mathcal{F}_{a, p}(r)$. Furthermore, in this case,

$(ii)$ If $p\leq 2-a$, as in the proof of case $(i)$, we know that $\varphi_3(r)$ is strictly decreasing on $(0, 1)$, and so is $\mathcal{F}_{a, p}(r)$. Also, $\mathcal{F}_{a, p}(0^+) = 1-a$, and

$(iii)$ If $2-a < p < 2$. According to Ramanujan's approximation (1.1), it shows that $r'^c\mathcal{K}_a \to 0$ ($r \to 1^{-}$) if $c\geq 0$. With Lemma 2.2(4) and the equation

we obtain

Together with (3.3), (3.4), Lemmas 2.7 and 2.10, and the formulas

which follows from (2.2) and (2.3), it shows that there exists $r_0\in(0, 1)$ such that $H_{\varphi_1, \varphi_2}(r) > 0$ for $r \in (0, r_0)$ and $H_{\varphi_1, \varphi_2}(r) < 0$ for $r \in (r_0, 1)$. Thus, $\mathcal{F}_{a, p}(r)$ is strictly increasing on $(0, r_0)$ and strictly decreasing on $(r_0, 1)$. Therefore, for all $r\in(0, 1)$, we get

In fact, $\mathcal{F}_{a, p}(r_0)\geq \mathcal{F}_{a, p}(r) > \text{max}{\left\{\mathcal{F}_{a, p}(0^+), \mathcal{F}_{a, p}(1^-)\right\}}$. It follows from Lemma 2.5 that

which makes $p_0$ the unique root of

on $(2-a, 2)$ and $p \mapsto 1-\left(\frac{\sin(\pi a)}{(1-a)\pi}\right)^{{\frac{p}{2(1-a)}}}$ is strictly increasing on $(-\infty, \infty)$. Hence we have $\mathcal{F}_{a, p}(0^+) \geq \mathcal{F}_{a, p}(1^-)$ if $p\in(2-a, p_0\rbrack$ and $\mathcal{F}_{a, p}(0^+) < \mathcal{F}_{a, p}(1^-)$ if $p \in (p_0, 2)$. Consequently, the range of $\mathcal{F}_{a, p}(r)$ in case 3 is valid. The proof is completed. □

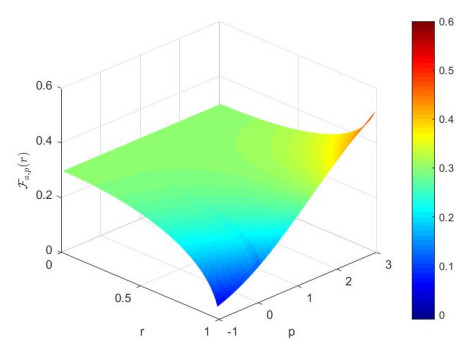
Figure 1 shows the monotonicity of $\mathcal{F}_{a, p}$ with $a = 0.7$ as an example.

Applying the property of $\mathcal{F}_{a, p}(r)$ from Theorem 3.1, we obtain our main result.

Theorem 3.2. For $a \in \lbrack \frac{1}{2}, 1)$, let $\mu, \nu \in [0, 1]$ and $p_0, \sigma_0$ be given as in Theorem 3.1. Then for any fixed $p\in \mathbb{R}$, the double inequality

holds for all $r\in (0, 1)$ with the equality only for certain values of $r$ if and only if $\mu \leq \mu(a, p)$ and $\nu \geq \nu(a, p)$, where $\mu(a, p)$ and $\nu(a, p)$ satisfy

where

Particularly, for $p = 0$, (3.5) holds if and only if $\mu \leq 1-2(1-a)^2$ and $\nu \geq 1$.

Proof. First we consider the case of $p \neq 0$, by (1.5), the inequality (3.5) is equivalent to

where $F_{a, p}(r)$ is defined as in Theorem 3.1. It follows from Theorem 3.1 that we immediately conclude the best possible constants $\mu = \mu(a, p)$ and $\nu = \nu(a, p)$ in (3.6).

For $p = 0$, we define the function $T(r)$ on (0, 1) by

Obviously, we see that $T_1(0^+) = T_2(0^+) = 0$. By differentiation, we have

Together with Lemma 2.2(3), this implies $\frac{T'_1(r)}{T'_2(r)}$ is strictly decreasing on (0, 1), and by Lemma 2.4, $T(r)$ shares the same monotonicity. Clearly, $T(1^-) = 0$ and

which indicates $1-2(1-a)^2 < 1-T(r) < 1$ for $r\in(0, 1)$. As a result, Eq (1.5) demonstrates that the inequality

holds for all $r\in(0, 1)$ if and only if $\mu\leq 1-2(1-a)^2$ and $\nu \geq 1$.

This completes the proof. □

Figure 2 shows the sharpness of the bound with $a = 0.7$ as an example.

Remark 3.1. For $a = \frac{1}{2}$, we see that (3.5) holds if the parameters satisfy the conditions given in Theorem 3.2. This conclusion has been proved in ^[15].

4.   Applications

In this section, by applying Theorem 3.2, we present several sharp bounds of weighted Hölder mean for $\mathcal{E}_a$.

Note that for the case of $\mu(a, p) = \nu(a, p) = a$, the best bounds of $\mathcal{E}_a$ are attained at $p = 2-a$ and $p = p_0$, which will be proved in the following corollary.

Corollary 4.1. Let $a\in \lbrack\frac{1}{2}, 1)$ and $p_1, p_2\in \mathbb{R}$. Then the inequality

holds for all $r\in (0, 1)$ with the best possible constants $p_1 = 2-a$ and $p_2 = p_0$, where $p_0$ is given as in Theorem 3.1.

Proof. For $a\in [\frac{1}{2}, 1)$, we consider $(\mu, p) = (a, 2-a)$ and $(\nu, p) = (a, p_0)$ satisfying (3.6), which yields (4.1) upon substitution into (3.5).

To establish that $a$ and $p_0$ are the best possible constants, we observe that the Hölder mean is monotonically increasing with respect to $p$. Consequently, it suffices to analyze the case of $2-a < p < p_0$.

According to Theorem 3.2, the inequality

holds for all $r\in (0, 1)$, where $1-\sigma_0$ and $b$ are sharp, with $b$ given as in Theorem 3.2. From Theorem 3.1, together with the monotonicity of $\omega \mapsto H_p(1, r';\omega)$, we have $1-\sigma_0 < a < b$ for $p\in(2-a, p_0)$, implying

Therefore, considering the sharpness of $1-\sigma_0$ and $b$ in inequality (4.2), we conclude that there exist two numbers $r_1, r_2 \in (0, 1)$ such that

Thus, the proof is completed. □

Figure 3 demonstrates that the sharp bounds of $\mathcal{E}_a$ are attained at $p_1 = 2-a$ and $p_2 = p_0$ with $a = 0.7$ as an example.

Furthermore, it is observed that computing the lower bound in (3.6) for the case $\mu(a, p) = 1-\sigma_0$ is challenging, while the case $\nu(a, p) = 1$ is trivial. Thus, we propose using $\mu(a, p) = b$ for $p\in [2, \infty)$ and $\nu(a, p) = b$ for $p\in (0, p_0)$ to establish new bounds. The specific inequality is as follows.

Corollary 4.2. Inequality

holds for $r\in (0, 1)$.

Lemma 4.3. Let $a\in\lbrack\frac{1}{2}, 1)$,

Then, the function $\Delta(p, r)$ with respect to $p$ is strictly decreasing on $(0, \infty)$ for $r\in (0, 1)$.

Proof. By differentiating $\log\Delta(p, r)$:

where

and

Differentiating $\tilde{\Delta}(p, x)$ with respect to $x$ yields

Give the observation that $\Delta_0(p, x)$ is strictly decreasing for $x\in(0, 1)$. In fact,

And

indicate that $\tilde{\Delta}(p, x)$ first strictly increases on $(0, x_0)$ and then strictly decreases on $(x_0, 1)$ for some $x_0\in (0, 1)$. Note that for $p > 0$, it is observed that

Hence, $\tilde{\Delta}(p, x) > 0$ for $x \in (0, 1)$.

Consequently, monotonicity of $\Delta(p, r)$ with respect to $p$ follows from (4.4). □

Remark 4.1. Following Lemma 4.3 and inequality (3.5), we observe that

where

According to the proof of (3.2), if $p\in(p_0, 2)$, it follows that

Therefore, it results in

by the monotonicity of $H^{2(1-a)}_p(1, r';\zeta)$ with respect to $\zeta$.Theorem 3.2 presents that, for $p\in(p_0, 2)$, $1-\sigma_0$ is sharp weight of $H^{2(1-a)}_p(1, r';\zeta)$ as the lower bound of $\mathcal{E}_a$, while $a$ is sharp weight as the upper bound of $\mathcal{E}_a$.

Hence, as a bound of $\mathcal{E}_a$, $H^{2(1-a)}_p(1, r';b)$ can attain the best upper bound at $p = p_0$ and the best lower bound at $p = 2$ by (4.6).

5.   Conclusions

In this article, we have proved the monotonicity of $\mathcal{F}_{a, p}(r)$, where $\mathcal{F}_{a, p}(r)$ is given as in Theorem 3.1. Moreover, we find the sharp weighted Hölder mean approximating $\mathcal{E}_a$:

holds for all $r\in (0, 1)$ if and only if $\mu \leq \mu(a, p)$ and $\nu \geq \nu(a, p)$, where $\mu(a, p)$ and $\nu(a, p)$ are given as in (3.6). Besides, we derive several bounds of $\mathcal{E}_a$ in terms of weights and power, which are given by Corollary 4.1, Corollary 4.2, and Remark 4.1. These conclusions provide an extension of the work of ^[15].

Author contributions

Zixuan Wang: Investigation, Writing – original draft. Chuanlong Sun: Validation. Tiren Huang: Writing – review & editing. All authors have read and approved the final version of the manuscript for publication.

Use of Generative-AI tools declaration

The authors declare that they have not used artificial intelligence (AI) tools in the creation of this article.

Conflict of interest

The authors declare no conflicts of interest regarding the publication for the paper.