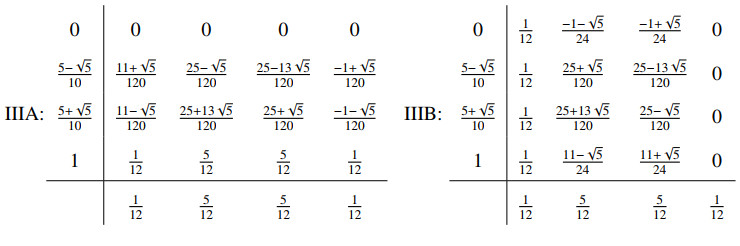1.
Introduction
In this paper, we consider numerically a class of nonlinear dispersive equations [18] as follows:
which models a variety of nonlinear dispersive phenomena depending on the parameters κ and γ. If κ≥0 and γ=1, it reduces to the Camassa-Holm (CH) equation:
which characterizes unidirectional shallow water waves [2,3], with u representing the height of the fluid's free surface above a flat bottom (or equivalently the fluid velocity in the x direction), and κ denoting the critical shallow water wave speed. The CH model possesses a bi-Hamiltonian structure, is completely integrable, and has global solutions. Moreover, it has solitary waves. Compared with the Korteweg-de Vries equation, the solitary waves become peaked in the limit of κ→0 (called "peakons"), which characterize in physical context "wave-breaking" [25]. It is worth noting that the dispersive Eq (1.1), by choosing different values of κ and γ [18], may turn into other physical models, such as the Dai equation and regularized long wave equation.
The system (1.1) can be rewritten in an infinite-dimensional Hamiltonian system
where D=(1−∂xx)−1∂x is a skew-adjoint operator, and H is the Hamiltonian energy functional
In this paper, we choose the periodic boundary condition
Besides the energy conservation law H(t)=H(0), the dispersive system (1.1) further satisfies the following mass and momentum conservation laws, respectively,
Over the past few decades, structure-preserving methods have come to the fore due to their superior capability for long-term computation over traditional numerical methods [12]. In Ref. [4], Cohen et al. first proposed multisymplectic finite difference schemes for the CH equation. Subsequently, their idea was generalized to solve generalized hyperelastic-rod wave equation [5]. In particular, the wavelet collocation method [30] and discontinuous Galerkin method [24] were further shown to be powerful tools for constructing multisymplectic schemes of the nonlinear system (1.1). In addition to the geometric structure, the nonlinear dispersive equation also satisfies three first integrals Eqs (1.3)–(1.6). It is well-known that the first integral plays a key role in the numerical analyses for conservative systems. In Ref. [18], Matsuo et al. first proposed an energy-preserving Galerkin scheme for the dispersive system (1.1), and some numerical experiments for the CH equation and Dai equation were also investigated. Moreover, numerical comparisons between the energy-preserving scheme and momentum-preserving scheme have been conducted for the CH equation [17]. Further discussions on energy-preserving Galerkin schemes can be found in Ref. [19]. Cohen et al. [5] then proposed a new energy-preserving scheme based on the discrete gradient approach. Later on, Gong et al. [9] combined the averaged vector field method and wavelet collocation method to design an energy-preserving wavelet collocation scheme, and some numerical comparisons with the multisymplectic wavelet collocation scheme [30] were also carried out. Recently, Brugnano et al. [1] developed an energy-conserving and space-time spectrally accurate method for Hamiltonian systems. However, almost all the mentioned schemes are fully implicit, which implies that the nonlinear iteration is inevitable at each time step, and thus it may be time consuming. In Ref. [8], Furihata and Matsuo first proposed a linearly implicit energy-preserving scheme for the CH model, in which only a linear system needs to be solved at each time step. Thus it is computationally much cheaper than that of the fully implicit counterparts. Another efficient strategy for constructing linearly implicit energy-preserving schemes of the nonlinear dispersive system (1.1) is based on the Kahan's method and the polarised discrete gradient method. For more details, please refer to Refs. [6,7]. Moreover, some linearly implicit momentum-preserving schemes can be founded in Refs. [13,16]. Nevertheless, to our best knowledge, the mentioned linearly implicit schemes are of only second-order accuracy in time at most.
It's worth noting that Yang et al. [27] coined the idea of invariant energy quadratization (IEQ) to develop energy stable schemes for solving the MBE model. Then Gong et al. [10] first generalized their idea to construct arbitrarily high-order energy stable algorithms for gradient flow models. Subsequently, the IEQ method [22] was further shown to be an efficient approach to design second-order and linearly implicit energy-preserving schemes for the CH model [14,15]. However, it is known that the issue with IEQ /EQ method is that it only preserves the modified energy. Recently, this has been partially addressed with a relaxation technique [29]. Moreover, for certain types of nonlinear systems, numerical schemes based on the IEQ idea have been shown to preserve the original energy law [28].
In this paper, we aim to develop a class of high-order, linearly implicit and energy-preserving schemes for the dispersive Eq (1.1). Based on the idea of the IEQ approach, the original model is firstly reformulated into an equivalent system with a quadratic energy by introducing an auxiliary variable. Inspired by the previous works [11,21], we further apply the prediction-correction strategy and the symplectic Partitioned Runge-Kutta (PRK) method [12,23] for temporal discretization, and the resulting semi-discrete system is linear, high-order accurate, and can preserve the quadratic energy of the reformulated system exactly. Finally, various numerical tests are addressed to verify the efficiency and accuracy of the proposed schemes.
2.
Model reformulation using the EQ approach
In this section, we utilize the EQ idea to recast the model Eq (1.1) into an equivalent system, which possesses a modified energy function of the new variable. The new system can provide an elegant platform for developing high-order, linearly implicit and energy-preserving schemes. Here, we consider the system (1.1) in a finite domain [0,L]×[0,T], and define the L2 inner product as (f,g)=∫L0fgdx,∀f,g∈L2([0,L]).
Inspired by the EQ approach [27], we first introduce an auxiliary variable
and the Hamiltonian energy Eq (1.3) can be reformulated in a quadratic form rewritten as
According to the energy variational principle, we further reformulate the system (1.2) to the following equivalent form
with consistent initial conditions
It is readily to verify the energy conservation law. The integration by parts, together with the periodic boundary condition and Eq (2.2), yields
where the skew-symmetry of the operator D was used.
3.
High-order, linearly implicit and energy-preserving scheme
In this section, we develop a class of high-precision, linearly implicit schemes for the reformulated system (2.2) by combing the prediction-correction approach and the PRK method, then show that the proposed schemes can exactly preserve the modified energy Eq (2.1). We here focus on temporal semi-discretization, and denote tn=nτ,n=0,1,2,⋯, where τ is the time step.
Inspired by the previous works in [11,21], we employ the prediction-correction strategy, together with the PRK method, to the system (2.2), and obtain the following prediction-correction method:
Scheme 3.1. Let bi,ˆbi,aij,ˆaij(i,j=1,⋯,s) be real numbers and let ci=∑sj=1aij,ˆci=∑sj=1ˆaij, we apply a s-stage PRK method to the system (2.2) in time, and first compute the predicted values un,∗i,i=1,⋯,s, as follows:
1. Prediction: for given (un,qn), we set un,0i=un,qn,0i=qn. Let M>0 be a given integer, for m=0 to M−1, we compute un,m+1i,qn,m+1i,kn,m+1i,ln,m+1i by using
Then, for the predicted value, we set un,∗i=un,Mi, followed by the following correction step:
2. Correction: we further compute the intermediate values kni,lni,uni,qni via
then (un+1,qn+1) is updated via
Theorem 3.1. If the coefficients of Scheme 3.1 satisfy
then it preserves the following semi-discrete energy conservation law
where En=(un,qn).
Proof. It follows from the last two equalities of Eq (3.1) that
where the skew-symmetry of D was used. This, together with the first two equalities of Eq (3.1) and the condition (3.2), derives that
which completes the proof.
Remark 3.1. If the coefficients of a partitioned Runge-Kutta method satisfy Eq (3.2), it conserves the quadratic invariant of the form Q(y,z)=y⊤Dz (see Ref. [12] for more details), thus the energy conservation law Eq (3.3) stands naturally. Moreover, the coefficients of PRK methods of order 4 and 6 are explicitly given in Tables 1 and 2 (please see [20]), respectively. Hereafter, the prediction-correction scheme 3.1, coupled with 4th- and 6th-order PRK methods, are denoted by 4th- and 6th-order LEQP1, respectively. Exchanging the order of Lobatto IIIA-IIIB pairs, we further derive 4th- and 6th-order LEQP2 methods.
Remark 3.2. In general, a numerical algorithm, which can preserve the corresponding energy exactly, is called an energy-preserving scheme. Thus, for the semi-discrete Scheme 3.1, it should be careful to choose a suitable spatial discretization, and we need to consider the following aspects: (i) It should preserve the skew-symmetry of the operator D; (ii) The accuracy of spatial discretization should be comparable to that of temporal counterpart. These, together with the periodic boundary condition (1.4), enlighten us to use the Fourier pseudo-spectral method for spatial discretization, which allows the application of FFT technique. In fact, the derived full discrete schemes also preserve the corresponding full discrete energy conservation law. The details are omitted here.
Remark 3.3. To our best knowledge, no theoretical result is found on the choice of iteration step M. From our numerical experience, the 4th-order LEQP methods can reach fourth-order accuracy by choosing M=3, while the 6th-order LEQP methods can reach sixth-order accuracy by choosing M=5.
4.
Numerical experiments
In this section, some numerical tests are carried out to investigate the accuracy, efficiency and invariants-preservation of the proposed schemes. For brevity, we only take the CH equation as a benchmark model for illustration purposes, and the corresponding prediction-correction schemes can be directly obtained by setting κ=0,γ=1 in Scheme 3.1. As shown above, the proposed scheme, which preserves the modified energy, could reach arbitrary high-order accuracy in time. Some comparisons would be made with the linearized Crank-Nicolson (IEQ-LCN) method [15] and energy-preserving Fourier pseudo-spectral (EPFP) method [9], where the wavelet collocation discretization in space is substituted by the standard Fourier pseudo-spectral method. In the following, the convergence rate in time is computed by the following formula
where τl,errorl (l=1,2) are time steps and errors with time step τl, respectively.
Example 4.1 We first consider the CH equation as follows
with the following conservation laws
where u0(x)= sin(x),Ω=[0,2π], and M,H denote the mass and Hamiltonian energy, respectively. Moreover, the numerical "exact" solution is obtained by 6th-order LEQP1 scheme with small time step τ=0.001 and mesh size h=2π/128. Numerical results involving accuracy test are shown in Table 3. As is observed that the 4th- and 6th-order LEQP methods arrive at fourth- and sixth-order convergence rates in time, respectively. What's more, they perform obviously more accurate than the other second-order schemes, while the LEQP1 schemes seem a bit more accurate than the corresponding LEQP2 schemes for both 4th- and 6th-order cases.
In Figure 1a, we show the L∞-norm solution error versus the execution time for different schemes, and it can be clearly seen that the proposed high-order methods perform more effective than other second-order counterparts. Subsequently, Figures 1b–d investigate the errors of invariants of different schemes in the long-time behaviour, where we choose τ=1/3000,N=1/128.
As illustrated in Figure 1b, all schemes conserve the mass exactly. Though the proposed schemes can not preserve the exact Hamiltonian energy theoretically, the corresponding numerical errors can be preserved up to machine errors as demonstrated in Figure 1c. Moreover, Figure 1d illustrates that the proposed schemes preserve the quadratic energy precisely, which confirms the preceding theoretical analysis.
Example 4.2 In this example, we further apply the proposed method to simulate the three-peakon interaction of the CH equation with the initial condition [26]
where
The corresponding parameters are taken as c1=2,c2=1,c3=0.8,x1=−5,x2=−3,x3=−1,L=30, and the computational domain is Ω=[0,L] with a periodic boundary condition.
In Figure 2a, we show the dynamics of three-peakon interaction computed by 4th-order LEQP1 scheme, and other LEQP schemes perform similarly. It is clearly seen that the moving peak interaction is resolved well. The taller wave overtakes the shorter counterparts, and afterwards they still keep their original shapes and velocities. Meanwhile, we study the invariants of the proposed schemes in long-time simulations. As demonstrated in Figures 2b–d, the proposed schemes preserve the mass and quadratic energy precisely, and perform more accurate than the IEQ-LCN method in terms of Hamiltonian energy.
5.
Concluding remarks
In this paper, we develop a class of high-order, linearly implicit numerical algorithms, which can preserve the modified energy exactly, for the nonlinear dispersive equation. The proposed schemes, which can reach arbitrarily high-order accuracy in time, are easy to implement and computationally efficient. The key strategy lies in the application of the prediction-correction technique and the PRK method. Compared with the second-order linearly implicit structure-preserving schemes, the proposed methods perform more accurate and more efficient in longtime computations, and they can be directly applied to some relevant background problems, such as the Dai equation and regularized long wave equation in high dimensions.
Acknowledgments
Jin Cui's work is partially supported by the High Level Talents Research Foundation Project of Nanjing Vocational College of Information Technology (Grant No. YB20200906), the "Qinglan" Project of Jiangsu Province. Yayun Fu's work is partially supported by the National Natural Science Foundation of Henan Province (No. 222300420280).
Conflict of interest
The authors declare there is no conflict of interest.
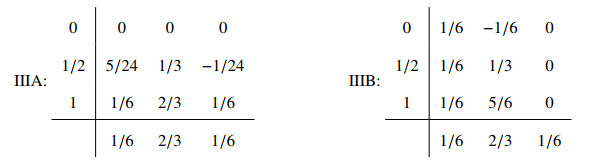









 DownLoad:
DownLoad: