The Influence of Sleep on the Consolidation of Positive Emotional Memories: Preliminary Evidence

Alexis M. Chambers; Jessica D. Payne; Alexis M. Chambers; Jessica D. Payne

doi:10.3934/Neuroscience.2014.1.39

AIMS Neuroscience

2014, Volume 1, Issue 1: 39-51. doi: 10.3934/Neuroscience.2014.1.39

Previous Article Next Article

Research article Special Issues

The Influence of Sleep on the Consolidation of Positive Emotional Memories: Preliminary Evidence

Alexis M. Chambers ^,,
Jessica D. Payne

Sleep, Stress, and Memory Laboratory, Department of Psychology, University of Notre Dame, 118 Haggar Hall, Notre Dame, IN 46556, USA

Received: 31 March 2014 Accepted: 12 May 2014 Published: 29 May 2014

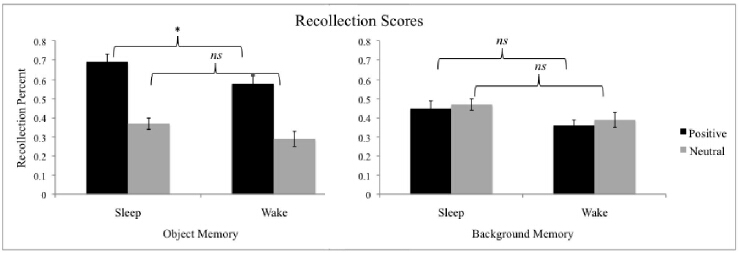
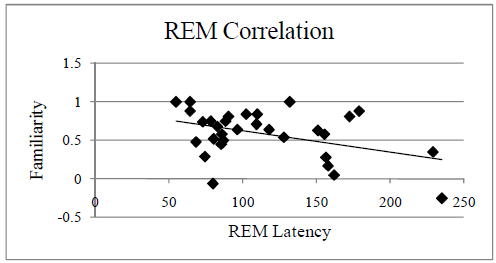
Studies have not only shown that a period of sleep following learning offers greater benefits to later memory than a period of wakefulness, but also that sleep actively promotes those components of memories that are emotionally salient. However, sleep's role in emotional memory consolidation has largely been investigated with memories that are specifically negative in content, such as memory for negative images or texts, leaving open the question of whether sleep influences positive memories in a similar manner. The current study investigated the emotional memory trade-off effect for positive versus neutral information. Scenes in which a positive or neutral object was placed on a neutral background were encoded prior to a period of polysomnographically-monitored nocturnal sleep or daytime wakefulness. Recognition memory was tested for the objects and backgrounds separately following the delay using the Remember/Know paradigm. Compared to wake participants, those who slept during the delay had increased recollection memory performance for positive objects, but not the neutral components of the studied scenes. Further, familiarity of positive objects was negatively correlated with REM latency. These results provide preliminary evidence that sleep contributes to the selective processing of positive memories, and point toward a role for REM sleep in positive memory formation.

Keywords:

Citation: Alexis M. Chambers, Jessica D. Payne. The Influence of Sleep on the Consolidation of Positive Emotional Memories: Preliminary Evidence[J]. AIMS Neuroscience, 2014, 1(1): 39-51. doi: 10.3934/Neuroscience.2014.1.39

Related Papers:

[1]	Luis Caffarelli, Antoine Mellet . Random homogenization of fractional obstacle problems. Networks and Heterogeneous Media, 2008, 3(3): 523-554. doi: 10.3934/nhm.2008.3.523
[2]	Joachim von Below, José A. Lubary . Isospectral infinite graphs and networks and infinite eigenvalue multiplicities. Networks and Heterogeneous Media, 2009, 4(3): 453-468. doi: 10.3934/nhm.2009.4.453
[3]	Delio Mugnolo . Gaussian estimates for a heat equation on a network. Networks and Heterogeneous Media, 2007, 2(1): 55-79. doi: 10.3934/nhm.2007.2.55
[4]	Caihong Gu, Yanbin Tang . Global solution to the Cauchy problem of fractional drift diffusion system with power-law nonlinearity. Networks and Heterogeneous Media, 2023, 18(1): 109-139. doi: 10.3934/nhm.2023005
[5]	Giuseppe Maria Coclite, Lorenzo di Ruvo . $ H^1 $ solutions for a modified Korteweg-de Vries-Burgers type equation. Networks and Heterogeneous Media, 2024, 19(2): 724-739. doi: 10.3934/nhm.2024032
[6]	Kota Kumazaki, Adrian Muntean . Local weak solvability of a moving boundary problem describing swelling along a halfline. Networks and Heterogeneous Media, 2019, 14(3): 445-469. doi: 10.3934/nhm.2019018
[7]	Hantaek Bae, Rafael Granero-Belinchón, Omar Lazar . On the local and global existence of solutions to 1d transport equations with nonlocal velocity. Networks and Heterogeneous Media, 2019, 14(3): 471-487. doi: 10.3934/nhm.2019019
[8]	Debora Amadori, Stefania Ferrari, Luca Formaggia . Derivation and analysis of a fluid-dynamical model in thin and long elastic vessels. Networks and Heterogeneous Media, 2007, 2(1): 99-125. doi: 10.3934/nhm.2007.2.99
[9]	Markus Musch, Ulrik Skre Fjordholm, Nils Henrik Risebro . Well-posedness theory for nonlinear scalar conservation laws on networks. Networks and Heterogeneous Media, 2022, 17(1): 101-128. doi: 10.3934/nhm.2021025
[10]	Steinar Evje, Kenneth H. Karlsen . Hyperbolic-elliptic models for well-reservoir flow. Networks and Heterogeneous Media, 2006, 1(4): 639-673. doi: 10.3934/nhm.2006.1.639

Abstract

1. Introduction

The 3D incompressible resistive Hall-Magnetohydrodynamics system (Hall-MHD in short) is the following system of PDEs for $ (u, p, B) $:

$\begin{align} &u_{t} +u\cdot \nabla u - B\cdot \nabla B+\nabla p-\mu\Delta u = 0, \end{align}$ $

(1a)

$\begin{align} &B_{t} + u\cdot \nabla B -B\cdot \nabla u +{\rm{curl}}\left(\left({\rm{curl}} \;B\right)\times B\right)- \nu\Delta B = 0, \end{align}$ $

(1b)

$\begin{align} &{\rm{div}}\; u = 0, \quad {\rm{div}}\; B = 0, \end{align}$ $

(1c)

where $ u = (u_{1}, u_{2}, u_{3}) $ is the plasma velocity field, $ p $ is the pressure, and $ B = (B_{1}, B_{2}, B_{3}) $ is the magnetic field. $ \mu $ and $ \nu $ are the viscosity and the resistivity constants, respectively. The Hall-MHD is important in describing many physical phenomena [2,17,19,23,26,27,33]. In particular, the Hall MHD explains magnetic reconnection on the Sun which is very important role in acceleration plasma by converting magnetic energy into bulk kinetic energy.

The Hall-MHD recently has been studied intensively. The Hall-MHD can be derived from either two fluids model or kinetic models in a mathematically rigorous way [1]. Global weak solution, local classical solution, global solution for small data, and decay rates are established in [4,5,6]. There have been many follow-up results of these papers; see [7,8,12,13,14,15,16,18,29,30,31,32,34,35] and references therein.

1.1. The Hall equation with fractional Laplacian

We note that the Hall term $ {\rm{curl}}\left(\left({\rm{curl}} \;B\right)\times B\right) $ is dominant in mathematical analysis of (1) and so we only consider the Hall equations ($ (u, p) = 0 $ in (1)). Also motivated by [7], we consider the Hall equation with fractional Laplacian:

$\begin{eqnarray} B_{t}+{\rm{curl}} \left(({\rm{curl}} \;B)\times B\right)+\Lambda^{\beta}B = 0, \quad {\rm{div}}\; B = 0, \end{eqnarray}$ $

(2)

where we take $ \nu = 1 $ for simplicity. (2) is locally well-posed [7] when $ \beta>1 $. But, we do not know whether (2) is locally well-posed when $ \beta = 1 $:

$\begin{eqnarray} B_{t}+{\rm{curl}} \left(({\rm{curl}} \;B)\times B\right)+\Lambda B = 0, \quad {\rm{div}}\; B = 0. \end{eqnarray}$ $

(3)

However, we can show the existence of solutions globally in time if initial data is sufficiently small.

Theorem 1.1. Let $ B_{0} \in H^{k} $ with $ k>\frac{5}{2} $ and $ {\rm{div}}\; B_{0} = 0 $. There exists a constant $ \epsilon_{0}>0 $ such that if $ \|B_{0}\|_{H^{k}} \leq \epsilon_{0} $, there exists a unique global-in-time solution of (3) satisfying

$ \left\|B(t)\right\|^{2}_{H^{k}}+(1-C\epsilon_{0})\int^{t}_{0}\left\|\Lambda^{\frac{1}{2}}B(s)\right\|^{2}_{H^{k}}ds\leq \left\|B_{0}\right\|^{2}_{H^{k}} \quad {{for\; all \; t > 0 .}} $

Moreover, $ B $ decays in time

$\begin{eqnarray} \left\|\Lambda^{l}B(t)\right\|_{L^{2}}\leq \frac{C_{0}}{(1+t)^{l}}, \quad 0 < l\leq k, \end{eqnarray}$ $

(4)

where $ C_{0} $ depends on $ \|B_{0}\|_{H^{k}} $ which is expressed in (27) explicitly.

Remark 1. The decay rate (4) is consistent with the decay rates of the linear part of (3).

Remark 2. After this work was completed, the referee pointed out that the same result is proved in [37,Theorem 1.1]. Compared to the proof in [37] where they use the Littlewood-Paley decomposition, we use the standard energy energy estimates and classical commutator estimates.

As one of a minimal modification of (3) to show the existence of unique local in time solutions, we now take a logarithmic correction of (3):

$\begin{eqnarray} B_{t}+{\rm{curl}} \left(({\rm{curl}} \;B)\times B\right)+\ln(2+\Lambda)\Lambda B = 0, \end{eqnarray}$ $

(5)

where the Fourier symbol of $ \ln(2+\Lambda)\Lambda $ is $ \ln(2+|\xi|)|\xi| $.

Theorem 1.2. Let $ B_{0} \in H^{k} $ with $ k>\frac{5}{2} $ and $ {\rm{div}}\; B_{0} = 0 $. There exists $ T_\ast = T_{\ast}(\|B_{0}\|_{H^{k}})>0 $ such that there exists a unique local-in-time solution of (5) satisfying

$\begin{eqnarray} \|B(t)\|_{H^{k}}\leq \ln \left(\frac{1}{e^{-\|B_{0}\|_{H^{k}}}-Ct}\right), \quad 0 < t < T^{\ast} = \frac{\exp\left(-\|B_{0}\|_{H^{k}}\right)}{C}. \end{eqnarray}$ $

(6)

1.2. 2D models

In this paper, we also deal with 2D models closely related to the $ 2\frac{1}{2} $ dimensional (3). If we take $ B $ of the form

$\begin{eqnarray} B(t, x, y) = \left(-\psi_{y}(t, x, y), \psi_{x}(t, x, y), Z(t, x, y)\right), \end{eqnarray}$ $

(7)

we can rewrite (3) as

$\begin{align} & \psi_{t}+\Lambda\psi = [\psi, Z], \end{align}$ $

(8a)

$\begin{align} & Z_{t}+\Lambda Z = [\Delta \psi, \psi], \end{align}$ $

(8b)

where $ [f, g] = \nabla f\cdot \nabla^{\perp}g = f_{x}g_{y}-f_{y}g_{x} $. (7) is used to show a finite-time collapse to a current sheet [3,20,21,24] and is used in [10] to study regularity of stationary weak solutions.

1.2.1. Case 1

Although (8) is defined in 2D and has nice cancellation properties (18), the local well-posedness seems unreachable. But, suppose that we redistribute the power of the fractional Laplacians in (8) in such a way that (8b) has the full Laplacian and (8a) is inviscid:

$\begin{eqnarray} \psi_{t} = [\psi, Z], \quad Z_{t}-\Delta Z = [\Delta \psi, \psi]. \end{eqnarray}$ $

(9)

(9) has no direct link to (2), but we may interpret (9) as the $ 2\frac{1}{2} $ dimensional model of the Hall equations where only $ B_{3} $ has the full Laplacian in (2). In this case, we can show that (9) is locally well-posed. Let

$\begin{eqnarray} \mathcal{E}(t) = \left\|\psi(t)\right\|^{2}_{H^{4}}+\left\|Z(t)\right\|^{2}_{H^{3}}, \quad \mathcal{E}_{0} = \left\|\psi_{0}\right\|^{2}_{H^{4}}+\left\|Z_{0}\right\|^{2}_{H^{3}}. \end{eqnarray}$ $

(10)

Theorem 1.3. There exists $ T_{\ast} = T_{\ast}(\mathcal{E}_{0})>0 $ such that there exists a unique solution of (9) satisfying

$ \mathcal{E}(t)\leq \frac{\mathcal{E}_{01}}{1-Ct\mathcal{E}_{0}} \quad {{for \;all}}\; \ 0 < t\leq T_{\ast} < \frac{1}{C \mathcal{E}_{0}}. $

Moreover, we have the following blow-up criterion:

$ \mathcal{E}(t)+ \int^{t}_{0}\left\|\nabla Z(s)\right\|^{2}_{H^{2}}ds < \infty\iff \int^{t}_{0}\left(\left\|\nabla^{2} Z(s)\right\|_{L^{\infty}} +\left\|\nabla^{2}\psi(s)\right\|^{2}_{L^{\infty}} \right)ds < \infty. $

Since there is no dissipative effect in the equation of $ \psi $ in (9), we only have the local in tim result in Theorem 1.3. Among the possible conditions for the global existence, we find that adding a damping term to the equation of $ \psi $ works. More precisely, we deal with the following

$\begin{eqnarray} \psi_{t}+\psi = [\psi, Z], \quad Z_{t}-\Delta Z = [\Delta \psi, \psi]. \end{eqnarray}$ $

(11)

In this case, we can show the existence of global in time solutions with small initial data having regularity one higher than the regularity in Theorem 1.3. Moreover, we can find decay rates of $ \psi $ by using the structure of equation of $ \psi $ which is a damped transport equation, and this is also the reason why the same method cannot be applied to $ Z $. Let

$\begin{split} &\mathcal{F}(t) = \left\|\psi(t)\right\|^{2}_{H^{5}}+\left\|Z(t)\right\|^{2}_{H^{4}}, \quad \mathcal{F}_{0} = \left\|\psi_{0}\right\|^{2}_{H^{5}}+\left\|Z_{0}\right\|^{2}_{H^{4}}, \\ & \mathcal{N}_{1}(t) = \left\|\nabla\psi(t)\right\|^{2}_{H^{4}}+\left\|\nabla Z(t)\right\|^{2}_{H^{4}}. \end{split}$ $

Theorem 1.4. There exists a constant $ \epsilon_{0}>0 $ such that if $ \mathcal{F}_{0} \leq \epsilon_{0} $, there exists a unique global-in-time solution of (11) satisfying

$ \mathcal{F}(t)+(1-C \epsilon_{0})\int^{t}_{0}\mathcal{N}_{1}(s)ds\leq \mathcal{F}_{0} \quad {{for\; all\; t > 0 .}} $

Moreover, $ \psi $ decays exponentially in time

$ \left\|\psi(t)\right\|_{L^{2}}\leq \left\|\psi_{0}\right\|_{L^{2}} e^{-t}, \quad \left\|\Lambda^{k}\psi(t)\right\|_{L^{2}}\leq \mathcal{F}^{\frac{k-1}{8}}_{0}\left\|\nabla \psi_{0}\right\|^{\frac{5-k}{4}}_{L^{2}} e^{-\frac{(5-k)(1-C\epsilon_{0})}{4}t} $

with $ 1\leq k<5. $

1.2.2. Case 2

As another way to redistribute the derivatives in (8), we also deal with

$\begin{eqnarray} \psi_{t}-\Delta \psi = [\psi, Z], \quad Z_{t} = [\Delta \psi, \psi]. \end{eqnarray}$ $

(12)

Let $ \mathcal{E}(t) $ and $ \mathcal{E}_{0} $ be defined as before (10).

Theorem 1.5. There exists $ T_{\ast}>0 $, which is depending on $ \mathcal{E}_{0} $, such that there exists a unique solution of (12) satisfying

$ \mathcal{E}(t)\leq \frac{\mathcal{E}_{0}}{1-Ct\mathcal{E}_{0}} \quad {{for \;all}}\; \ 0 < t\leq T_{\ast} < \frac{1}{C \mathcal{E}_{0}}. $

Moreover, we have the following blow-up criterion

$ \mathcal{E}(t)+\int^{t}_{0}\left\|\nabla \psi\right\|^{2}_{H^{4}}ds < \infty \iff \int^{t}_{0}\left\|\nabla^{2}\psi\right\|^{2}_{L^{\infty}}ds. $

We now add a damping term to the equation of $ Z $ in (12):

$\begin{eqnarray} \psi_{t}-\Delta \psi = [\psi, Z], \quad Z_{t} + Z = [\Delta \psi, \psi]. \end{eqnarray}$ $

(13)

In this case, we can use the same regularity used in Theorem 1.5 because the dissipative effect in $ \psi $ helps to control $ \Delta \psi $ in the equation of $ Z $. Let $ \mathcal{N}_{2}(t) = \left\|\nabla\psi(t)\right\|^{2}_{H^{5}}+\left\|Z(t)\right\|^{2}_{H^{3}} $.

Theorem 1.6. There exists a constant $ \epsilon_{0}>0 $ such that if $ \mathcal{E}_{0} \leq \epsilon_{0} $, there exists a unique global-in-time solution of (13) satisfying

$ \mathcal{E}(t)+(1-C \epsilon_{0})\int^{t}_{0}\mathcal{N}_{2}(s)ds\leq \mathcal{E}_{0} \quad {{for \;all \; t > 0 .}} $

Remark 3. Compared to Theorem 1.3, we only need one term in the blow-up criterion in Theorem 1.5 which is due to the dissipative effect in the equation of $ \psi $. Compared to Theorem 1.4, the proof of Theorem 1.6 is simpler, but we are not able to derive decay rates of $ \psi $ and $ Z $.

2. Preliminaries

All constants will be denoted by $ C $ and we follow the convention that such constants can vary from expression to expression and even between two occurrences within the same expression. And repeated indices are summed over.

The fractional Laplacian $ \Lambda^{\beta} = (\sqrt{-\Delta})^{\beta} $ has the Fourier transform representation

$ \widehat{\Lambda^{\beta} f}(\xi) = |\xi|^{\beta}\widehat{f}(\xi). $

For $ s>0 $, $ H^{s} $ is a energy space equipped with

$ \|f\|_{H^{s}} = \|f\|_{L^{2}}+\|f\|_{\dot{H}^{s}}, \quad \|f\|_{\dot{H}^{s}} = \left\|\Lambda^{s}f\right\|_{L^{2}}. $

In the energy spaces, we have the following interpolations: for $ s_{0}<s<s_{1} $

$\begin{eqnarray} \left\|f\right\|_{\dot{H}^{s}}\leq \left\|f\right\|^{\theta}_{\dot{H}^{s_{0}}}\left\|f\right\|^{1-\theta}_{\dot{H}^{s_{1}}}, \quad s = \theta s_{0}+(1-\theta)s_{1}. \end{eqnarray}$ $

(14)

2.1. Inequalities

We begin with two inequalities in 3D:

$\begin{align} & \left\|f\right\|_{L^{\infty}}\leq C\|f\|_{H^{s}}, \quad s > \frac{3}{2}, \end{align}$ $

(15a)

$\begin{align} & \left\|f\right\|_{L^{p}}\leq C\|f\|_{\dot{H}^{s}}, \quad \frac{1}{p} = \frac{1}{2}-\frac{s}{3}. \end{align}$ $

(15b)

We also provide the following inequalities in 2D

$ \left\|f\right\|_{L^{4}}\leq C\left\|f\right\|^{\frac{1}{2}}_{L^{2}}\left\|\nabla f\right\|^{\frac{1}{2}}_{L^{2}}, \quad \left\|f\right\|_{L^{\infty}} \leq C\left\|f\right\|^{\frac{1}{2}}_{L^{2}} \left\|\Delta f\right\|^{\frac{1}{2}}_{L^{2}} $

which will be used repeatedly in the proof of Theorem 1.3, Theorem 1.4, Theorem 1.5, and Theorem 1.6. We also recall

$ \left\|\nabla^{2}f\right\|_{L^{2}} = \left\|\Delta f\right\|_{L^{2}} $

which holds in any dimension.

We finally provide the Kato-Ponce commutator cstimate [22]

$\begin{eqnarray} \begin{split} \left\|\left[\Lambda^{k}, f\right]g\right\|_{L^{2}}& = \left\|\Lambda^{k}(fg)-f\Lambda^{k}g\right\|_{L^{2}}\\ &\leq C \left\|\nabla f\right\|_{L^{\infty}}\left\|\Lambda^{k-1}g\right\|_{L^{2}}+C \left\|g\right\|_{L^{\infty}}\left\|\Lambda^{k}f\right\|_{L^{2}} \end{split} \end{eqnarray}$ $

(16)

and the fractional Leibniz rule [11]: for $ 1\leq p<\infty $ and $ p_{i}, q_{i} \ne 1 $,

$\begin{eqnarray} \begin{split} &\left\|\Lambda^{s}(fg)\right\|_{L^{p}} \le C\left\|\Lambda^{s}f\right\|_{L^{p_{1}}} \|g\|_{L^{q_{1}}} +C\|f\|_{L^{p_{2}}} \left\|\Lambda^{s}g\right\|_{L^{q_{2}}}, \\ & \frac{1}{p} = \frac{1}{p_{1}}+\frac{1}{q_{1}} = \frac{1}{p_{2}}+\frac{1}{q_{2}}. \end{split} \end{eqnarray}$ $

(17)

2.2. Commutator

We recall the commutator $ [f, g] = \nabla f\cdot \nabla^{\perp}g = f_{x}g_{y}-f_{y}g_{x} $. Then, the commutator has the following properties:

$\begin{align} & \Delta [f, g] = [\Delta f, g] +[f, \Delta g] + 2[f_{x}, g_{x}] +2[f_{y}, g_{y}], \end{align}$ $

(18a)

$\begin{align} & \int f[f, g] = 0, \end{align}$ $

(18b)

$\begin{align} & \int f[g, h] = \int g [h, f]. \end{align}$ $

(18c)

3. Proof of Theorem 1.1 and Theorem 1.2

3.1. Proof of Theorem 1.1

We recall (3):

$\begin{eqnarray} B_{t}+{\rm{curl}} (\left({\rm{curl}} \;B)\times B\right)+\Lambda B = 0. \end{eqnarray}$ $

(19)

3.1.1. Approximation

We first approximate (19) by putting $ \epsilon \Delta B $ to the right-hand side of (19):

$\begin{eqnarray} B_{t}+{\rm{curl}} (\left({\rm{curl}} \;B\right)\times B)+\Lambda B = \epsilon \Delta B. \end{eqnarray}$ $

(20)

We then mollify (20) as follows

$\begin{eqnarray} \begin{split} &\partial_{t} B^{(\epsilon)}+{\rm{curl}} \left(\mathcal{J}_{\epsilon}\left({\rm{curl}} \mathcal{J}_{\epsilon} B^{(\epsilon)}\right)\times \mathcal{J}_{\epsilon} B^{(\epsilon)}\right)+\Lambda \mathcal{J}^{2}_{\epsilon} B^{(\epsilon)} = \epsilon \mathcal{J}^{2}_{\epsilon}\Delta B^{(\epsilon)}, \\ & B^{(\epsilon)}_{0} = \mathcal{J}_{\epsilon} B_{0}, \end{split} \end{eqnarray}$ $

(21)

where $ \mathcal{J}_{\epsilon} $ is the standard mollifier described in [25,Chapter 3.2]. Then, as proved in [4,Proposition 3.1], there exists a unique global-in-time solution $ \left\{B^{(\epsilon)}\right\} $ of (21). Since the bounds in Section 3.1.2 are independent of $ \epsilon>0 $, we can pass to the limit in a subsequence and show the existence of smooth solutions globally in time when $ B_{0}\in H^{k} $, $ k>\frac{5}{2} $, is sufficiently small as in [37,Section 3.2].

3.1.2. A priori estimates

We begin with the $ L^{2} $ bound:

$\begin{eqnarray} \frac{1}{2}\frac{d}{dt}\left\|B\right\|^{2}_{L^{2}}+\left\|\Lambda^{\frac{1}{2}}B\right\|^{2}_{L^{2}} = 0. \end{eqnarray}$ $

(22)

We now take $ \Lambda^{k} $ to (19) and take the inner product of the resulting equation with $ \Lambda^{k}B $. Then,

$\begin{split} &\frac{1}{2}\frac{d}{dt}\left\|\Lambda^{k}B\right\|^{2}_{L^{2}}+\left\|\Lambda^{\frac{1}{2}+k}B\right\|^{2}_{L^{2}} = -\int\Lambda^{k}{\rm{curl}} (\left({\rm{curl}} \;B)\times B\right) \cdot \Lambda^{k}B\\ & = \int \left(\left[\Lambda^{\frac{1}{2}+k}, B\right]\times {\rm{curl}} \;B\right)\cdot \Lambda^{k-\frac{1}{2}}{\rm{curl}} \;B\leq \left\|\left[\Lambda^{\frac{1}{2}+k}, B\right]\times {\rm{curl}} \;B\right\|_{L^{2}}\left\|\Lambda^{\frac{1}{2}+k}B\right\|_{L^{2}}. \end{split}$ $

By (16) and (15a) with $ k>\frac{5}{2} $,

$\begin{eqnarray} \begin{split} \left\|\left[\Lambda^{\frac{1}{2}+k}, B\right]\times {\rm{curl}} \;B\right\|_{L^{2}}&\leq C \left\|\nabla B\right\|_{L^{\infty}}\left\|\Lambda^{k-\frac{1}{2}}{\rm{curl}} \;B\right\|_{L^{2}}\\ &\leq C \left\|B\right\|_{H^{k}}\left\|\Lambda^{\frac{1}{2}+k}B\right\|^{2}_{L^{2}}. \end{split} \end{eqnarray}$ $

(23)

So, we obtain

$\begin{eqnarray} \frac{d}{dt}\left\|\Lambda^{k}B\right\|^{2}_{L^{2}}+\left\|\Lambda^{\frac{1}{2}+k}B\right\|^{2}_{L^{2}}\leq C \left\|B\right\|_{H^{k}}\left\|\Lambda^{\frac{1}{2}+k}B\right\|^{2}_{L^{2}}. \end{eqnarray}$ $

(24)

By (22) and (24),

$ \frac{d}{dt}\left\|B\right\|^{2}_{H^{k}}+\left\|\Lambda^{\frac{1}{2}}B\right\|^{2}_{H^{k}}\leq C \left\|B\right\|_{H^{k}}\left\|\Lambda^{\frac{1}{2}+k}B\right\|^{2}_{L^{2}}. $

If $ \left\|B_{0}\right\|_{H^{k}} = \epsilon_{0} $ is sufficiently small, we can derive a uniform bound

$\begin{eqnarray} \left\|B(t)\right\|^{2}_{H^{k}}+(1-C\epsilon_{0})\int^{t}_{0}\left\|\Lambda^{\frac{1}{2}}B(s)\right\|^{2}_{H^{k}}ds\leq \left\|B_{0}\right\|^{2}_{H^{k}} \quad {{\rm{for}} \;{\rm{all}} \;t > 0 .} \end{eqnarray}$ $

(25)

3.1.3. Uniqueness

Let $ B_{1} $ and $ B_{2} $ be two solutions of (19). Then, $ B = B_{1}-B_{2} $ satisfies

$\begin{eqnarray} B_{t}+\Lambda B+{\rm{curl}} \left(\left({\rm{curl}} \;B_{1}\right)\times B\right) - {\rm{curl}} \left(\left({\rm{curl}} \;B\right)\times B_{2}\right) = 0 \end{eqnarray}$ $

(26)

with $ B_{0} = 0 $. We take the inner product of (26) with $ B $. By (17) with $ k>\frac{5}{2} $,

$\begin{equation*} \begin{split} \frac{1}{2}\frac{d}{dt}\|B\|^{2}_{L^{2}}+\left\|\Lambda^{\frac{1}{2}} B\right\|^{2}_{L^{2}}& = -\int \left({\rm{curl}}\left(\left({\rm{curl}} \;B_{1}\right)\times B\right)\right) \cdot B\\ & = -\int \Lambda^{\frac{1}{2}}\left(\left(\left({\rm{curl}} \;B_{1}\right)\times B\right)\right) \cdot \Lambda^{-\frac{1}{2}}{\rm{curl}} \;B\\ &\leq C\left\|\nabla B_{1}\right\|_{L^{\infty}}\left\|\Lambda^{\frac{1}{2}} B\right\|^{2}_{L^{2}} +C\left\|\nabla \Lambda^{\frac{1}{2}}B_{1}\right\|_{L^{6}}\|B\|_{L^{3}}\left\|\Lambda^{\frac{1}{2}} B\right\|_{L^{2}}\\ &\leq C\left\|\nabla B_{1}\right\|_{L^{\infty}}\left\|\Lambda^{\frac{1}{2}} B\right\|^{2}_{L^{2}} +C\left\|\Lambda^{\frac{5}{2}}B_{1}\right\|_{L^{2}}\left\|\Lambda^{\frac{1}{2}} B\right\|^{2}_{L^{2}} \\ &\leq C\left\|B_{1}\right\|_{H^{k}} \left\|\Lambda^{\frac{1}{2}} B\right\|^{2}_{L^{2}}, \end{split} \end{equation*}$ $

where we use (15b) to control $ L^{6} $ and $ L^{3} $ terms. If $ C\epsilon_{0}<1 $, (25) implies $ B = 0 $ in $ L^{2} $ which gives the uniqueness of a solution.

3.1.4. Decay rates

By (14), it is enough to derive the decay rate with $ k = l $ to show (4). Since

$ \left\|\Lambda^{k}B\right\|^{\frac{2k+1}{k}}_{L^{2}}\leq \left\|B\right\|^{\frac{1}{k}}_{L^{2}}\left\|\Lambda^{\frac{1}{2}+k}B\right\|^{2}_{L^{2}} \leq \left\|B_{0}\right\|^{\frac{1}{k}}_{L^{2}}\left\|\Lambda^{\frac{1}{2}+k}B\right\|^{2}_{L^{2}} $

by (14) and (22), we create the following ODE from (24)

$ \frac{d}{dt}\left\|\Lambda^{k}B\right\|^{2}_{L^{2}}+\frac{1-C\epsilon_{0}}{\left\|B_{0}\right\|^{\frac{1}{k}}_{L^{2}}}\left\|\Lambda^{k}B\right\|^{\frac{2k+1}{k}}_{L^{2}}\leq 0. $

By solving this ODE, we find the following decay rate

$\begin{eqnarray} \left\|\Lambda^{k}B(t)\right\|_{L^{2}}\leq \frac{\left((2k)^k \left\|B_{0}\right\|_{L^{2}}\left\|\Lambda^{k}B_{0}\right\|_{L^{2}}\right)}{\left(2k \left\|B_{0}\right\|^{\frac{1}{k}}_{L^{2}} +(1-C\epsilon_{0})\left\|\Lambda^{k}B_{0}\right\|^{\frac{1}{k}}_{L^{2}}t\right)^k}. \end{eqnarray}$ $

(27)

3.2. Proof of Theorem 1.2

We recall (5):

$ B_{t}+{\rm{curl}} \left(({\rm{curl}} \;B)\times B\right)+\ln(2+\Lambda)\Lambda B = 0, $

The the uniqueness part of Theorem 1.2 is the same as that of Theorem 1.1 and we only derive a priori bounds. Let

$ \left\|\sqrt{\ln(2+\Lambda)}\Lambda^{s}f\right\|^{2}_{L^{2}} = \int \left(\ln(2+|\xi|)\right)|\xi|^{2s}\left|\widehat{f}(\xi)\right|^{2}d\xi. $

We begin with the $ L^{2} $ bound:

$\begin{eqnarray} \frac{1}{2}\frac{d}{dt}\left\|B\right\|^{2}_{L^{2}}+\left\|\sqrt{\ln(2+\Lambda)}\Lambda^{\frac{1}{2}}B\right\|^{2}_{L^{2}} = 0. \end{eqnarray}$ $

(28)

Following the computations in the proof of Theorem 1.1, we also have

$\begin{eqnarray} \frac{d}{dt}\left\|\Lambda^{k}B\right\|^{2}_{L^{2}}+\left\|\sqrt{\ln(2+\Lambda)}\Lambda^{\frac{1}{2}+k}B\right\|^{2}_{L^{2}}\leq C \left\|B\right\|_{H^{k}}\left\|\Lambda^{\frac{1}{2}+k}B\right\|^{2}_{L^{2}}. \end{eqnarray}$ $

(29)

For each $ N\in \mathbb{N} $, we have

$\begin{equation*} \begin{split} &\left\|\Lambda^{\frac{1}{2}+k}B\right\|^{2}_{L^{2}} = \int_{|\xi|\leq 2^{N}} |\xi|^{2k+1}\left|\widehat{B}(\xi)\right|^{2}d\xi+\int_{|\xi|\ge 2^{N}} |\xi|^{2k+1}\left|\widehat{B}(\xi)\right|^{2}d\xi\\ &\leq 2^{N}\int_{|\xi|\leq 2^{N}} |\xi|^{2k}\left|\widehat{B}(\xi)\right|^{2}d\xi+\frac{1}{\ln(2+2^{N})}\int_{|\xi|\ge 2^{N}} \ln(2+|\xi|)|\xi|^{2k+1}\left|\widehat{B}(\xi)\right|^{2}d\xi\\ &\leq 2^{N}\left\|\Lambda^{k}B\right\|^{2}_{L^{2}} +\frac{1}{\ln(2+2^{N})}\left\|\sqrt{\ln(2+\Lambda)}\Lambda^{\frac{1}{2}+k}B\right\|^{2}_{L^{2}}. \end{split} \end{equation*}$ $

So, (29) is replaced by

$\begin{split} &\frac{d}{dt}\left\|\Lambda^{k}B\right\|^{2}_{L^{2}}+\left\|\sqrt{\ln(2+\Lambda)}\Lambda^{\frac{1}{2}+k}B\right\|^{2}_{L^{2}} \\ &\leq C 2^{N}\left\|\Lambda^{k}B\right\|^{2}_{L^{2}}\|B\|_{H^{k}} + \frac{C\|B\|_{H^{k}}}{\ln(2+2^{N})}\left\|\sqrt{\ln(2+\Lambda)}\Lambda^{\frac{1}{2}+k}B\right\|^{2}_{L^{2}}. \end{split}$ $

We now choose $ N>0 $ such that

$ \frac{1}{2}\ln(2+2^{N}) < C\left\|B\right\|_{H^{k}} < \ln(2+2^{N}) $

and so $ N \sim \|B\|_{H^{k}} $. Then, (29) is reduced to

$\begin{eqnarray} \frac{d}{dt}\left\|\Lambda^{k}B\right\|^{2}_{L^{2}} \leq C \exp\left(\|B\|_{H^{k}}\right)\|B\|_{H^{k}} \left\|\Lambda^{k}B\right\|_{L^{2}}. \end{eqnarray}$ $

(30)

By (28) and (30), we obtain

$ \frac{d}{dt}\left\|B\right\|^{2}_{H^{k}}\leq C \exp\left(\|B\|_{H^{k}}\right)\|B\|^{2}_{H^{k}} $

and so we have

$ \frac{d}{dt}\left\|B\right\|_{H^{k}}\leq C \exp\left(\|B\|_{H^{k}}\right)\|B\|_{H^{k}} \leq C \exp\left(\|B\|_{H^{k}}\right). $

By solving this ODE, we can derive (6).

4. Proof of Theorem 1.3 and Theorem 1.4

4.1. Proof of Theorem 1.3

We recall (9):

$\begin{align} & \psi_{t} = [\psi, Z], \end{align}$ $

(31a)

$\begin{align} & Z_{t}-\Delta Z = [\Delta \psi, \psi]. \end{align}$ $

(31b)

4.1.1. Approximation

We first approximate (31a) by putting $ \epsilon \Delta \psi $ to the right-hand side and mollify the resulting equations as (21). Then, we have

$\begin{eqnarray} \begin{split} &\partial_{t}\psi^{(\epsilon)} = \mathcal{J}_{\epsilon}[\mathcal{J}_{\epsilon}\psi^{(\epsilon)}, \mathcal{J}_{\epsilon}Z^{(\epsilon)}]+\epsilon \mathcal{J}^{2}_{\epsilon}\Delta \psi^{(\epsilon)}, \\ & \partial_{t}Z^{(\epsilon)}-\Delta \mathcal{J}^{2}_{\epsilon}Z^{(\epsilon)} = \mathcal{J}_{\epsilon}[\Delta \mathcal{J}_{\epsilon}\psi^{(\epsilon)}, \mathcal{J}_{\epsilon}\psi^{(\epsilon)}] \end{split} \end{eqnarray}$ $

(32)

with $ \psi^{(\epsilon)}_{0} = \mathcal{J}_{\epsilon}\psi_{0} $ and $ Z^{(\epsilon)}_{0} = \mathcal{J}_{\epsilon}Z_{0} $. Since (32) is defined in $ \mathbb{R}^{2} $, the proof of the existence of a unique global-in-time solution of (32) is relatively easier than the one to (21). Moreover, the bounds in Section 4.1.2 are independent of $ \epsilon>0 $ and so we can pass to the limit in a subsequence and show the existence of smooth solutions locally in time when $ \psi_{0}\in H^{4} $ and $ Z_{0}\in H^{3} $.

4.1.2. A priori estimates

We first note that

$\begin{eqnarray} \frac{1}{2}\frac{d}{dt}\left\|\psi\right\|^{2}_{L^{2}} = \int \psi[\psi, Z] = 0. \end{eqnarray}$ $

(33)

We next multiply (31a) by $ -\Delta \psi $, (31b) by $ Z $, and integrate over $ \mathbb{R}^{2} $. By (18c),

$\begin{eqnarray} \frac{1}{2}\frac{d}{dt} \left(\left\|\nabla \psi\right\|^{2}_{L^{2}}+\left\|Z\right\|^{2}_{L^{2}}\right) + \left\|\nabla Z\right\|^{2}_{L^{2}} = \int \left(-\Delta \psi[\psi, Z]+Z[\Delta \psi, \psi]\right) = 0. \end{eqnarray}$ $

(34)

We also multiply (31a) by $ \Delta^{4} \psi $, (31b) by $ -\Delta^{3} Z $ and integrate over $ \mathbb{R}^{2} $. Then,

$\begin{eqnarray} \begin{split} \frac{1}{2}\frac{d}{dt} \left(\left\|\Delta^{2}\psi\right\|^{2}_{L^{2}}+\left\|\nabla\Delta Z\right\|^{2}_{L^{2}} \right) +\left\|\Delta^{2} Z\right\|^{2}_{L^{2}} & = \int \Delta^{4} \psi [\psi, Z] -\int\Delta^{3} Z[\Delta \psi, \psi]\\ & = \mathcal{R}. \end{split} \end{eqnarray}$ $

(35)

We now compute the right-hand side of (35). By (18a), (18b), and (18c),

$\begin{equation} \begin{split} \mathcal{R}& = 2\int\Delta^{2}\psi[\Delta \psi, \Delta Z]+4\int \Delta^{2} \psi[\psi_{x}, \Delta Z_{x}]+4\int \Delta^{2} \psi[\psi_{y}, \Delta Z_{y}]\\ & +4\int \Delta^{2} \psi[\Delta\psi_{x}, Z_{x}]+4\int \Delta^{2} \psi[\Delta \psi_{y}, Z_{y}]+4\int \Delta^{2} \psi[\psi_{xx}, Z_{xx}]\\ &+8\int \Delta^{2} \psi[\psi_{xy}, Z_{xy}]+4\int \Delta^{2} \psi[\psi_{yy}, Z_{yy}]-2\int\Delta^{2}Z[\Delta \psi_{x}, \psi_{x}]\\ &-2\int\Delta^{2}Z[\Delta \psi_{y}, \psi_{y}]. \end{split} \end{equation}$ $

(36)

So, we find that the number of derivatives acting on $ (\psi, \psi, Z) $ are $ (4, 4, 2) $, $ (3, 4, 3) $, and $ (4, 2, 4) $ up to multiplicative constants. Hence,

$\begin{equation*} \begin{split} & \frac{d}{dt} \left(\left\|\Delta^{2}\psi\right\|^{2}_{L^{2}}+\left\|\nabla\Delta Z\right\|^{2}_{L^{2}} \right) +\left\|\Delta^{2} Z\right\|^{2}_{L^{2}}\\ & \leq C\int \left|\nabla^{4}\psi\right| \left|\nabla^{4}\psi\right| \left|\nabla^{2} Z\right|+ C\int \left|\nabla^{3}\psi\right| \left|\nabla^{4}\psi\right| \left|\nabla^{3} Z\right|+ C\int \left|\nabla^{4}\psi\right| \left|\nabla^{2}\psi\right| \left|\nabla^{4} Z\right|\\ & \leq C\left\|\Delta^{2}\psi\right\|^{2}_{L^{2}} \left\|\nabla^{2} Z\right\|_{L^{\infty}}+ C\left\|\nabla^{3}\psi\right\|_{L^{4}} \left\|\Delta^{2}\psi\right\|_{L^{2}} \left\|\nabla^{3} Z\right\|_{L^{4}}\\ &+ C\left\|\Delta^{2}\psi\right\|_{L^{2}} \left\|\nabla^{2}\psi\right\|_{L^{\infty}} \left\|\Delta^{2} Z\right\|_{L^{2}}\\ & \leq C\left\|\Delta^{2}\psi\right\|^{2}_{L^{2}} \left\|\nabla^{2} Z\right\|_{L^{\infty}}+ C\left\|\Delta^{2}\psi\right\|^{\frac{3}{2}}_{L^{2}} \left\|\nabla\Delta\psi\right\|^{\frac{1}{2}}_{L^{2}} \left\|\Delta^{2} Z\right\|_{L^{2}}\\ &+C\left\|\Delta^{2}\psi\right\|_{L^{2}} \left\|\nabla^{2}\psi\right\|_{L^{\infty}} \left\|\Delta^{2} Z\right\|_{L^{2}}\\ &\leq C \mathcal{E}^{2}+\frac{1}{4}\left\|\Delta^{2} Z\right\|^{2}_{L^{2}}+\delta \left\|\nabla^{2} Z\right\|^{2}_{L^{\infty}} \leq C \mathcal{E}^{2}+\frac{1}{2}\left\|\Delta^{2} Z\right\|^{2}_{L^{2}}+\frac{1}{4}\left\|\nabla Z\right\|^{2}_{L^{2}}, \end{split} \end{equation*}$ $

where we use

$\begin{split} \left\|\nabla^{2} Z\right\|^{2}_{L^{\infty}}&\leq C \left\|\Delta Z\right\|_{L^{2}}\left\|\Delta^{2} Z\right\|_{L^{2}}\leq C \left\|\nabla Z\right\|^{\frac{2}{3}}_{L^{2}}\left\|\Delta^{2} Z\right\|^{\frac{4}{3}}_{L^{2}}\\&\leq C \left\|\nabla Z\right\|^{2}_{L^{2}}+C\left\|\Delta^{2} Z\right\|^{2}_{L^{2}} \end{split}$ $

with $ \delta $ satisfying $ 4C\delta = 1 $. So, we have

$\begin{eqnarray} \frac{d}{dt} \left(\left\|\Delta^{2}\psi\right\|^{2}_{L^{2}}+\left\|\nabla\Delta Z\right\|^{2}_{L^{2}} \right) +\left\|\Delta^{2} Z\right\|^{2}_{L^{2}} \leq C \mathcal{E}^{2}+\frac{1}{2}\left\|\nabla Z\right\|^{2}_{L^{2}}. \end{eqnarray}$ $

(37)

By (33), (34), and (37), we derive $ \mathcal{E}' \leq C \mathcal{E}^{2} $ from which we deduce

$\begin{eqnarray} \mathcal{E}(t)\leq \frac{\mathcal{E}_{0}}{1-Ct\mathcal{E}_{0}} \quad {{\rm{for}}\; {\rm{all}}} \;\ 0 < t\leq T_{\ast} < \frac{1}{C \mathcal{E}_{0}}. \end{eqnarray}$ $

(38)

4.1.3. Uniqueness

Let $ (\psi_{1}, Z_{1}) $ and $ (\psi_{2}, Z_{2}) $ be two solutions of (31) and let $ \psi = \psi_{1}-\psi_{2} $ and $ Z = Z_{1}-Z_{2} $. Then, $ (\psi, Z) $ satisfies the following equations:

$ \psi_{t} = [\psi, Z_{1}]+[\psi_{2}, Z], \quad Z_{t}-\Delta Z = [\Delta\psi, \psi_{1}]+[\Delta\psi_{2}, \psi] $

with $ \psi(0, x) = Z(0, x) = 0 $. For these equations, we have

$\begin{equation*} \begin{split} &\frac{1}{2}\frac{d}{dt}\left(\left\|\nabla \psi\right\|^{2}_{L^{2}}+ \|Z\|^{2}_{L^{2}}\right)+ \left\|\nabla Z\right\|^{2}_{L^{2}}\\ & = -\int \Delta \psi [\psi, Z_{1}]-\int \Delta \psi [\psi_{2}, Z]+\int Z [\Delta\psi, \psi_{1}]+\int Z[\Delta\psi_{2}, \psi]\\ & = \text{(I)+(II)+(III)+(IV)}. \end{split} \end{equation*}$ $

The first term is bounded using the definition of $ [f, g] $ and $ {\rm{div}}\; \nabla^{\perp}Z_{1} = 0 $:

$ \text{(I)} = \int \left(\nabla^{\perp}Z_{1}\cdot \nabla \psi\right) \Delta \psi = -\int \left(\nabla^{\perp}\partial_{l}Z_{1}\cdot \nabla \psi\right) \partial_{l} \psi\leq C \left\|\nabla^{2}Z_{1}\right\|_{L^{\infty}}\left\|\nabla \psi\right\|^{2}_{L^{2}}. $

We next bound $ \text{(II)+(III)} $ as

$\begin{split} \text{(II)+(III)}& = -\int Z[\Delta \psi, \psi]\leq C \left\|\nabla^{2}\psi\right\|_{L^{\infty}}\left\|\nabla \psi\right\|_{L^{2}}\left\|\nabla Z\right\|_{L^{2}} \\ &\leq C \left(\left\|\nabla^{2}\psi_{1}\right\|^{2}_{L^{\infty}}+\left\|\nabla^{2}\psi_{2}\right\|^{2}_{L^{\infty}}\right)\left\|\nabla \psi\right\|^{2}_{L^{2}}+\frac{1}{4}\left\|\nabla Z\right\|^{2}_{L^{2}}. \end{split}$ $

The last term is bounded as

$ \text{(IV)}\leq C \left\|\nabla^{2}\psi_{2}\right\|_{L^{\infty}}\left\|\nabla \psi\right\|_{L^{2}}\left\|\nabla Z\right\|_{L^{2}} \leq C \left\|\nabla^{2}\psi_{2}\right\|^{2}_{L^{\infty}}\left\|\nabla \psi\right\|^{2}_{L^{2}}+\frac{1}{4}\left\|\nabla Z\right\|^{2}_{L^{2}}. $

So, we have

$\begin{eqnarray} \begin{split} &\frac{d}{dt}\left(\left\|\nabla \psi\right\|^{2}_{L^{2}}+ \|Z\|^{2}_{L^{2}}\right)\\ &\leq C\left( \left\|\nabla^{2}Z_{1}\right\|_{L^{\infty}}+\left\|\nabla^{2}\psi_{1}\right\|^{2}_{L^{\infty}}+\left\|\nabla^{2}\psi_{2}\right\|^{2}_{L^{\infty}}\right)\left(\left\|\nabla \psi\right\|^{2}_{L^{2}}+ \|Z\|^{2}_{L^{2}} \right). \end{split} \end{eqnarray}$ $

(39)

By (38), $ \left\|\nabla^{2}\psi_{1}\right\|^{2}_{L^{\infty}}+\left\|\nabla^{2}\psi_{2}\right\|^{2}_{L^{\infty}} $ is integrable in time. Integrating (34) and (35) in time, we have

$ \int^{t}_{0}\left(\left\|\nabla Z(s)\right\|^{2}_{L^{2}}+\left\|\Delta^{2} Z(s)\right\|^{2}_{L^{2}}\right)ds < \infty \quad {{\rm{for}}} \; 0 < t\leq \frac{T_{\ast}}{2} $

which gives the integrability of the first term in the parentheses on the right-hand side of (39). By repeating the same argument one more time, we have the uniqueness up to $ T_{\ast} $.

4.1.4. Blow-up criterion

Let

$ \mathcal{B}(s) = \left\|\nabla^{2}Z(s)\right\|_{L^{\infty}} +\left\|\nabla^{2}\psi(s)\right\|^{2}_{L^{\infty}} . $

We first deal with

$\begin{split} &\frac{1}{2}\frac{d}{dt} \left(\left\|\Delta\psi\right\|^{2}_{L^{2}}+\left\|\nabla Z\right\|^{2}_{L^{2}} \right) +\left\| \Delta Z\right\|^{2}_{L^{2}} = \int \Delta^{2} \psi [\psi, Z] -\int\Delta Z[\Delta \psi, \psi]\\ & = 2\int \Delta \psi[\psi_{x}, Z_{x}]+2\int \Delta \psi[\psi_{y}, Z_{y}]\leq C \left\|\nabla^{2}Z\right\|_{L^{\infty}}\left\| \Delta \psi\right\|^{2}_{L^{2}} \end{split}$ $

and so we have

$ \frac{d}{dt} \left(\left\|\Delta\psi\right\|^{2}_{L^{2}}+\left\|\nabla Z\right\|^{2}_{L^{2}} \right) +\left\| \Delta Z\right\|^{2}_{L^{2}} \leq C \left\|\nabla^{2}Z\right\|_{L^{\infty}}\left\| \Delta \psi\right\|^{2}_{L^{2}}. $

This implies

$\begin{eqnarray} \begin{split} &\left\|\Delta \psi(t)\right\|^{2}_{L^{}}+ \left\|\nabla Z(t)\right\|^{2}_{L^{2}}+\int^{t}_{0}\left\| \Delta Z(s)\right\|^{2}_{L^{2}} ds < \infty \\ &\iff \int^{t}_{0}\left\|\nabla^{2}Z(s)\right\|_{L^{\infty}}ds < \infty. \end{split} \end{eqnarray}$ $

(40)

We also deal with

$\begin{split} &\frac{1}{2}\frac{d}{dt} \left(\left\|\nabla \Delta\psi\right\|^{2}_{L^{2}}+\left\|\Delta Z\right\|^{2}_{L^{2}} \right) +\left\| \nabla \Delta Z\right\|^{2}_{L^{2}} = -\int \Delta^{3} \psi [\psi, Z] +\int\Delta^{2} Z[\Delta \psi, \psi]\\ & = -\int \Delta^{2}\psi [\Delta \psi, Z] -2\int \Delta^{2}\psi \left([\psi_{x}, Z_{x}]+[\psi_{y}, Z_{y}]\right) \\ &- 2\int \Delta\psi \left([\psi_{x}, \Delta Z_{x}]+[\psi_{y}, \Delta Z_{y}]\right) = \text{(I)+(II)+(III)}. \end{split}$ $

As in Section 4.1.3,

$\begin{eqnarray} \text{(I)} = \int \left(\nabla \nabla^{\perp}Z\cdot \nabla \Delta \psi\right)\cdot \nabla \Delta\psi \leq C\left\|\nabla^{2}Z\right\|_{L^{\infty}} \left\|\nabla\Delta \psi \right\|^{2}_{L^{2}}. \end{eqnarray}$ $

(41)

We next estimate $ \text{(II)}+\text{(III)} $:

$\begin{equation} \begin{split} &\text{(II)}+\text{(III)} = -4\int \Delta\psi \left([\Delta \psi_{y}, Z_{y}]+[\psi_{y}, \Delta Z_{y}]+[\psi_{xy}, Z_{xy}]+ [\psi_{yy}, Z_{yy}]\right)\\ &\leq C\int \left|\nabla^{2}Z\right| \left|\nabla^{3}\psi \right|^{2}+C\int \left|\nabla^{2}\psi \right| \left|\nabla^{3}\psi \right|\left|\nabla^{3}Z\right|\\ &\leq C\left\|\nabla^{2}Z\right\|_{L^{\infty}} \left\|\nabla\Delta \psi \right\|^{2}_{L^{2}}+C\left\|\nabla^{2}\psi\right\|^{2}_{L^{\infty}} \left\|\nabla \Delta \psi \right\|^{2}_{L^{2}}+\frac{1}{2}\left\|\nabla \Delta Z \right\|^{2}_{L^{2}}. \end{split} \end{equation}$ $

(42)

By (41) and (42), we have

$ \frac{d}{dt}\left(\left\|\nabla \Delta \psi\right\|^{2}_{L^{2}}+\left\|\Delta Z\right\|^{2}_{L^{2}}\right) +\left\|\nabla \Delta Z\right\|^{2}_{L^{2}}\leq C\left(\left\|\nabla^{2} Z\right\|_{L^{\infty}} +\left\|\nabla^{2}\psi\right\|^{2}_{L^{\infty}} \right)\left\|\nabla\Delta \psi \right\|^{2}_{L^{2}} $

which implies

$\begin{eqnarray} \left\|\nabla \Delta \psi(t)\right\|^{2}_{L^{2}}+\left\|\Delta Z(t)\right\|^{2}_{L^{2}}+\int^{t}_{0} \left\|\nabla \Delta Z(s)\right\|^{2}_{L^{2}}ds < \infty \iff \int^{t}_{0}\mathcal{B}(s)ds < \infty. \end{eqnarray}$ $

(43)

We finally deal with

$ \frac{1}{2}\frac{d}{dt} \left(\left\|\Delta^{2}\psi\right\|^{2}_{L^{2}}+\left\|\nabla\Delta Z\right\|^{2}_{L^{2}} \right) +\left\|\Delta^{2}Z\right\|^{2}_{L^{2}} = \int \Delta^{4} \psi [\psi, Z] -\int\Delta^{3} Z[\Delta \psi, \psi] = \mathcal{R} $

with the same $ \mathcal{R} $ in (36). So, we have

$\begin{equation*} \begin{split} &\frac{1}{2} \frac{d}{dt} \left(\left\|\Delta^{2}\psi\right\|^{2}_{L^{2}}+\left\|\nabla\Delta Z\right\|^{2}_{L^{2}} \right) +\left\|\Delta^{2} Z\right\|^{2}_{L^{2}}\\ & \leq C\left\|\nabla^{2} Z\right\|_{L^{\infty}}\left\|\Delta^{2}\psi\right\|^{2}_{L^{2}}+ C\left\|\nabla^{2}\psi\right\|_{L^{\infty}}\left\|\Delta^{2} Z\right\|_{L^{2}} \left\|\Delta^{2}\psi\right\|_{L^{2}} \\ &+C\left\|\nabla\Delta Z\right\|_{L^{4}}\left\|\nabla\Delta \psi\right\|_{L^{4}}\left\|\Delta^{2}\psi\right\|_{L^{2}}\\ &\leq C\left(\left\|\nabla^{2}Z\right\|_{L^{\infty}} +\left\|\nabla^{2}\psi\right\|^{2}_{L^{\infty}} +\left\|\nabla \Delta Z\right\|^{\frac{3}{2}}_{L^{2}}\left\|\nabla \Delta \psi\right\|^{\frac{3}{2}}_{L^{2}}\right)\left\|\Delta^{2} \psi \right\|^{2}_{L^{2}}+\frac{1}{2}\left\|\Delta^{2} Z\right\|^{2}_{L^{2}} \end{split} \end{equation*}$ $

which gives

$\begin{eqnarray} \begin{split} &\frac{d}{dt} \left(\left\|\Delta^{2}\psi\right\|^{2}_{L^{2}}+\left\|\nabla\Delta Z\right\|^{2}_{L^{2}} \right) +\left\|\Delta^{2} Z\right\|^{2}_{L^{2}}\\ &\leq C\left(\mathcal{B}(s)+\left\|\nabla \Delta Z\right\|^{\frac{3}{2}}_{L^{2}}\left\|\nabla \Delta \psi\right\|^{\frac{3}{2}}_{L^{2}}\right)\left\|\Delta^{2} \psi \right\|^{2}_{L^{2}}. \end{split} \end{eqnarray}$ $

(44)

By (40) and (43), (44) implies

$ \left\|\Delta^{2} \psi(t)\right\|^{2}_{L^{2}}+\left\|\nabla \Delta Z(t)\right\|^{2}_{L^{2}}+\int^{t}_{0} \left\|\Delta ^{2}Z(s)\right\|^{2}_{L^{2}}ds < \infty \iff \int^{t}_{0}\mathcal{B}(s)ds < \infty. $

4.2. Proof of Theorem 1.4

We recall (11):

$ \psi_{t}+\psi = [\psi, Z], \quad Z_{t}-\Delta Z = [\Delta \psi, \psi] $

Since the uniqueness is already proved in Section 4.1.3 even without the damping term, we only focus on the a priori bounds and the decay rates.

4.2.1. A priori estimates

We first have

$\begin{equation} \begin{split} &\frac{1}{2}\frac{d}{dt}\left\|\psi\right\|^{2}_{L^{2}}+\left\|\psi\right\|^{2}_{L^{2}} = 0, \\ &\frac{1}{2}\frac{d}{dt} \left(\left\|\nabla \psi\right\|^{2}_{L^{2}}+\left\|Z\right\|^{2}_{L^{2}}\right) +\left\|\nabla \psi\right\|^{2}_{L^{2}}+ \left\|\nabla Z\right\|^{2}_{L^{2}} = 0. \end{split} \end{equation}$ $

(45)

We now consider the highest order part:

$\begin{split} &\frac{1}{2}\frac{d}{dt} \left(\left\|\nabla \Delta^{2}\psi\right\|^{2}_{L^{2}}+\left\|\Delta^{2} Z\right\|^{2}_{L^{2}} \right)+\left\|\nabla\Delta^{2}\psi\right\|^{2}_{L^{2}} +\left\|\nabla\Delta^{2} Z\right\|^{2}_{L^{2}} \\ & = -\int \Delta^{5} \psi [\psi, Z] +\int\Delta^{4} Z[\Delta \psi, \psi]. \end{split}$ $

We compute the right-hand side of this. By (18a), (18b), and (18c),

$\begin{equation} \begin{split} &-\int \Delta^{5} \psi [\psi, Z] +\int\Delta^{4} Z[\Delta \psi, \psi]\\ & = 2\int \Delta^{3}Z\left[\Delta \psi_{x}, \psi_{x}\right]+2\int \Delta^{3}Z\left[\Delta \psi_{y}, \psi_{y}\right]+2\int \Delta^{2}Z\left[\Delta^{2} \psi_{x}, \psi_{x}\right]\\ &+2\int \Delta^{2}Z\left[\Delta^{2} \psi_{y}, \psi_{y}\right] +2\int \Delta Z\left[\Delta^{2} \psi_{x}, \Delta\psi_{x}\right]+2\int \Delta Z\left[\Delta^{2} \psi_{y}, \Delta\psi_{y}\right] \\ &-\int \Delta^{3}\psi[\Delta\psi, \Delta Z]-2\int\Delta^{3}\psi[\Delta \psi_{x}, Z_{x}] -2\int\Delta^{3}\psi[\Delta \psi_{y}, Z_{y}] -2\int\Delta^{3}\psi[ \psi_{x}, \Delta Z_{x}] \\ &-2\int\Delta^{3}\psi[ \psi_{y}, \Delta Z_{y}] -2\int\Delta^{4}\psi[ \psi_{x}, Z_{x}] -2\int\Delta^{4}\psi[ \psi_{y}, Z_{y}] -\int \Delta^{3}\psi[\Delta^{2}\psi, Z]. \end{split} \end{equation}$ $

(46)

We now count the number of derivatives hitting on $ (Z, \psi, \psi) $ using the integration by parts and (18b) and (18c) up to multiplicative constants. Except for the last integral, we have

$\begin{split} &(6, 2, 4) \mapsto (5, 2, 5), \ (5, 3, 4)\, \quad (4, 2, 6) \mapsto (5, 5, 2), \ (4, 3, 5)\\ &(2, 2, 8) \mapsto (3, 2, 7) \mapsto (4, 2, 6), \ (3, 3, 6) \mapsto (5, 5, 2), \ (4, 3, 5)\\ & (2, 4, 6) \mapsto (2, 5, 5), \ (3, 4, 5). \end{split}$ $

The last integral is

$ \int \left(\nabla^{\perp}Z\cdot \nabla \Delta^{2}\psi\right)\Delta^{3}\psi = -\int \left(\nabla^{\perp}\partial_{l}Z\cdot \nabla \Delta^{2}\psi\right)\partial_{l}\Delta^{2}\psi $

and so this gives $ (2, 5, 5) $. So, the combinations of the numbers of derivatives taken on $ (Z, \psi, \psi) $ are

$ (2, 5, 5), \ (3, 4, 5), \ (4, 3, 5), \ (5, 2, 5), \ (5, 3, 4). $

The first and the fourth cases are bounded by

$\begin{split} &C\left\|\nabla^{2}Z\right\|_{L^{\infty}}\left\|\nabla \Delta^{2}\psi\right\|^{2}_{L^{2}}\leq C\left\|\nabla^{2}Z\right\|^{2}_{L^{\infty}}\left\|\nabla \Delta^{2}\psi\right\|^{2}_{L^{2}}+\frac{1}{6}\left\|\nabla \Delta^{2}\psi\right\|^{2}_{L^{2}}, \\ & C\left\|\nabla^{2}\psi\right\|_{L^{\infty}}\left\|\nabla \Delta^{2}Z\right\|^{2}_{L^{2}}\leq C\left\|\nabla^{2}\psi\right\|_{L^{\infty}}\left\|\nabla \Delta^{2}Z\right\|^{2}_{L^{2}}+\frac{1}{4}\left\|\nabla \Delta^{2}Z\right\|^{2}_{L^{2}}. \end{split}$ $

The second case is bounded by

$\begin{split} &C\left\|\nabla^{3}Z\right\|_{L^{4}}\left\|\nabla^{4}\psi\right\|_{L^{4}}\left\|\nabla\Delta^{2}\psi\right\|_{L^{2}}\leq C\left\|\Delta Z\right\|^{\frac{1}{2}}_{L^{2}}\left\|\nabla\Delta^{2}Z\right\|^{\frac{1}{2}}_{L^{2}} \left\|\Delta^{2}\psi\right\|^{\frac{1}{2}}_{L^{2}}\left\|\nabla\Delta^{2}\psi\right\|^{\frac{3}{2}}_{L^{2}}\\ & \leq C\left\|\Delta Z\right\|^{2}_{L^{2}}\left\|\Delta^{2}\psi\right\|^{2}_{L^{2}}\left\|\nabla\Delta^{2}Z\right\|^{2}_{L^{2}} +\frac{1}{6}\left\|\nabla\Delta^{2}\psi\right\|^{2}_{L^{2}}. \end{split}$ $

The third case is bounded by

$\begin{split} &C\left\|\nabla^{4}Z\right\|_{L^{4}}\left\|\nabla^{3}\psi\right\|_{L^{4}}\left\|\nabla\Delta^{2}\psi\right\|_{L^{2}}\leq C\left\|\Delta^{2}Z\right\|^{\frac{1}{2}}_{L^{2}}\left\|\nabla\Delta^{2}Z\right\|^{\frac{1}{2}}_{L^{2}} \left\|\Delta \psi\right\|^{\frac{1}{2}}_{L^{2}}\left\|\nabla\Delta^{2}\psi\right\|^{\frac{3}{2}}_{L^{2}}\\ & \leq C\left\|\Delta \psi\right\|^{2}_{L^{2}}\left\|\Delta^{2}Z\right\|^{2}_{L^{2}}\left\|\nabla\Delta^{2}Z\right\|^{2}_{L^{2}} +\frac{1}{6}\left\|\nabla\Delta^{2}\psi\right\|^{2}_{L^{2}}. \end{split}$ $

The last one is bounded by

$\begin{split} &C\left\|\nabla^{3}\psi\right\|_{L^{4}}\left\|\nabla^{4}\psi\right\|_{L^{4}}\left\|\nabla\Delta^{2}Z\right\|_{L^{2}}\leq C\left\|\nabla\Delta \psi\right\|^{\frac{1}{2}}_{L^{2}}\left\|\Delta^{2}\psi\right\|_{L^{2}}\left\|\nabla\Delta^{2}\psi\right\|^{\frac{1}{2}}_{L^{2}}\left\|\nabla\Delta^{2}Z\right\|_{L^{2}}\\ & \leq C\left\|\nabla \Delta \psi\right\|_{L^{2}}\left\|\nabla \Delta^{2}\psi\right\|_{L^{2}}\left\|\nabla\Delta^{2}Z\right\|_{L^{2}} \leq C\left\|\nabla \Delta \psi\right\|^{2}_{L^{2}}\left\|\nabla \Delta^{2}\psi\right\|^{2}_{L^{2}} +\frac{1}{4}\left\|\nabla\Delta^{2}Z\right\|^{2}_{L^{2}}. \end{split}$ $

So, we obtain

$\begin{equation} \begin{split} &\frac{d}{dt} \left(\left\|\nabla \Delta^{2}\psi\right\|^{2}_{L^{2}}+\left\|\Delta^{2} Z\right\|^{2}_{L^{2}} \right)+\left\|\nabla\Delta^{2}\psi\right\|^{2}_{L^{2}} +\left\|\nabla\Delta^{2} Z\right\|^{2}_{L^{2}}\\ & \leq C\left\|\nabla^{2}Z\right\|^{2}_{L^{\infty}}\left\|\nabla \Delta^{2}\psi\right\|^{2}_{L^{2}}+ C\left\|\nabla^{2}\psi\right\|^{2}_{L^{\infty}}\left\|\nabla \Delta^{2}Z\right\|^{2}_{L^{2}}+C\left\|\nabla \Delta \psi\right\|^{2}_{L^{2}}\left\|\nabla \Delta^{2}\psi\right\|^{2}_{L^{2}}\\ &+C\left\|\Delta Z\right\|^{2}_{L^{2}}\left\|\Delta^{2}\psi\right\|^{2}_{L^{2}}\left\|\nabla\Delta^{2}Z\right\|^{2}_{L^{2}}+C\left\|\Delta \psi\right\|^{2}_{L^{2}}\left\|\Delta^{2}Z\right\|^{2}_{L^{2}}\left\|\nabla\Delta^{2}Z\right\|^{2}_{L^{2}} \end{split} \end{equation}$ $

(47)

By (45) and (47),

$ \mathcal{F}'(t)+\mathcal{N}_{1}(t)\leq C \left(\mathcal{F}(t)+\mathcal{F}^{2}(t)\right)\mathcal{N}_{1}(t). $

So, if $ \mathcal{F}_{0} = \epsilon_{0} $ is sufficiently small, we obtain

$ \label{A priori damping dd} \mathcal{F}(t)+(1-C \epsilon_{0})\int^{t}_{0}\mathcal{N}_{1}(s)ds\leq \mathcal{F}_{0} \quad {{\rm{for}} \;{\rm{all}} \;t > 0 .} $

4.2.2. Decay rates

From (45), $ \left\|\psi(t)\right\|_{L^{2}}\leq \left\|\psi_{0}\right\|_{L^{2}} e^{-t} $. Since

$\begin{split} \frac{1}{2}\frac{d}{dt}\left\|\nabla \psi\right\|^{2}_{L^{2}}+\left\|\nabla \psi\right\|^{2}_{L^{2}}& = -\int \Delta \psi[\psi, Z] = \int \left(\nabla^{\perp}Z\cdot \nabla \psi\right)\Delta \psi\\ & = -\int \left(\partial_{l}\nabla^{\perp}Z\cdot \nabla \psi\right)\partial_{l} \psi\\ &\leq \left\|\nabla^{2}Z\right\|_{L^{\infty}}\left\|\nabla \psi\right\|^{2}_{L^{2}} \leq C\epsilon_{0}\left\|\nabla \psi\right\|^{2}_{L^{2}}, \end{split}$ $

we have

$ \left\|\nabla \psi(t)\right\|_{L^{2}}\leq \left\|\nabla \psi_{0}\right\|_{L^{2}} e^{-(1-C\epsilon_{0})t}. $

By using (14), we also obtain

$ \left\|\Lambda^{k}\psi(t)\right\|_{L^{2}}\leq \mathcal{F}^{\frac{k-1}{8}}_{0}\left\|\nabla \psi_{0}\right\|^{\frac{5-k}{4}}_{L^{2}} e^{-\frac{(5-k)(1-C\epsilon_{0})}{4}t}, \quad 1\leq k < 5. $

5. Proof of Theorem 1.5 and Theorem 1.6

5.1. Proof of Theorem 1.5

We recall (12):

$ \psi_{t}-\Delta \psi = [\psi, Z], \quad Z_{t} = [\Delta \psi, \psi]. $

By applying the same approximation and mollification methods in Section 4.1.1, we can show the existence of smooth solutions locally in time when $ \psi_{0}\in H^{4} $ and $ Z_{0}\in H^{3} $.

5.1.1. A priori estimates

We first have

$\begin{equation} \begin{split} &\frac{1}{2}\frac{d}{dt}\left\|\psi\right\|^{2}_{L^{2}}+\left\|\nabla \psi\right\|^{2}_{L^{2}} = 0, \\ & \frac{1}{2}\frac{d}{dt} \left(\left\|\nabla \psi\right\|^{2}_{L^{2}}+\left\|Z\right\|^{2}_{L^{2}}\right) + \left\|\Delta \psi\right\|^{2}_{L^{2}} = 0. \end{split} \end{equation}$ $

(48)

We next deal with

$ \frac{1}{2}\frac{d}{dt} \left(\left\|\Delta^{2}\psi\right\|^{2}_{L^{2}}+\left\|\nabla\Delta Z\right\|^{2}_{L^{2}} \right) +\left\|\nabla \Delta^{2} \psi\right\|^{2}_{L^{2}} = \int \Delta^{4} \psi [\psi, Z] -\int\Delta^{3} Z[\Delta \psi, \psi] = \mathcal{R} $

with the same $ \mathcal{R} $ in (36). In this case, we choose the the number of derivatives acting on $ (\psi, \psi, Z) $ different from Section 4.1.2, which are given by $ (3, 5, 2) $, $ (2, 5, 3) $, and $ (4, 4, 2) $ after several integration by parts. Hence, we have

and so we have the following bound

$\begin{eqnarray} \frac{d}{dt} \left(\left\|\Delta^{2}\psi\right\|^{2}_{L^{2}}+\left\|\nabla\Delta Z\right\|^{2}_{L^{2}} \right) +\left\|\nabla \Delta^{2} \psi\right\|^{2}_{L^{2}} \leq C \mathcal{E}^{2}. \end{eqnarray}$ $

(49)

By (48) and (49), we derive $ \mathcal{E}' \leq C \mathcal{E}^{2} $ from which we deduce

$\begin{eqnarray} \mathcal{E}(t)\leq \frac{\mathcal{E}_{0}}{1-Ct\mathcal{E}_{0}} \quad {{\rm{for}}\; {\rm{all}}} \;\ 0 < t\leq T_{\ast} < \frac{1}{C \mathcal{E}_{0}}. \end{eqnarray}$ $

(50)

5.1.2. Uniqueness

Let $ (\psi_{1}, Z_{1}) $ and $ (\psi_{2}, Z_{2}) $ be two solutions and let $ \psi = \psi_{1}-\psi_{2} $ and $ Z = Z_{1}-Z_{2} $. As in Section 4.1.3

$\begin{equation*} \begin{split} &\frac{1}{2}\frac{d}{dt}\left(\left\|\nabla \psi\right\|^{2}_{L^{2}}+ \|Z\|^{2}_{L^{2}}\right)+ \left\|\Delta \psi\right\|^{2}_{L^{2}}\\ & = -\int \Delta \psi [\psi, Z_{1}]-\int \Delta \psi [\psi_{2}, Z]+\int Z [\Delta\psi, \psi_{1}]+\int Z[\Delta\psi_{2}, \psi]\\ & = \text{(I)+(II)+(III)+(IV)}. \end{split} \end{equation*}$ $

The first term three terms are bounded as

$\begin{split} \text{(I)}&\leq \left\|\nabla Z_{1}\right\|_{L^{\infty}}\left\|\nabla \psi\right\|_{L^{2}}\left\|\Delta \psi\right\|_{L^{2}} \leq C\left\|\nabla Z_{1}\right\|^{2}_{L^{\infty}}\left\|\nabla \psi\right\|^{2}_{L^{2}}+\frac{1}{3}\left\|\Delta \psi\right\|^{2}_{L^{2}}, \\ \text{(II)+(III)}& = -\int Z[\Delta \psi, \psi]\leq C \left\|\nabla Z\right\|_{L^{\infty}}\left\|\nabla \psi\right\|_{L^{2}}\left\|\Delta \psi\right\|_{L^{2}} \\ &\leq C \left(\left\|\nabla Z_{1}\right\|^{2}_{L^{\infty}}+\left\|\nabla Z_{2}\right\|^{2}_{L^{\infty}}\right)\left\|\nabla \psi\right\|^{2}_{L^{2}}+\frac{1}{3}\left\|\Delta \psi\right\|^{2}_{L^{2}} \end{split}$ $

The last term is bounded as

$\begin{split} \text{(IV)}&\leq C \left\|\nabla^{3}\psi_{2}\right\|_{L^{4}}\left\|\nabla \psi\right\|_{L^{4}}\left\|Z\right\|_{L^{2}} \leq C \left\|\nabla^{3}\psi_{2}\right\|_{L^{4}}\left\|\nabla \psi\right\|^{\frac{1}{2}}_{L^{2}}\left\|\Delta \psi\right\|^{\frac{1}{2}}_{L^{2}}\left\|Z\right\|_{L^{2}} \\ & \leq C \left\|\nabla^{3}\psi_{2}\right\|^{\frac{4}{3}}_{L^{4}}\left\|\nabla \psi\right\|^{\frac{2}{3}}_{L^{2}}\left\|Z\right\|^{\frac{4}{3}}_{L^{2}} +\frac{1}{3}\left\|\Delta \psi\right\|^{2}_{L^{2}} \leq C \left\|\nabla^{3}\psi_{2}\right\|^{4}_{L^{4}}\left\|\nabla \psi\right\|^{2}_{L^{2}}\\ &+ C \left\|Z\right\|^{2}_{L^{2}} +\frac{1}{3}\left\|\Delta \psi\right\|^{2}_{L^{2}}\\ & \leq C \left\|\nabla\Delta \psi_{2}\right\|^{2}_{L^{2}}\left\|\Delta^{2}\psi_{2}\right\|^{2}_{L^{2}} \left\|\nabla \psi\right\|^{2}_{L^{2}}+ C \left\|Z\right\|^{2}_{L^{2}} +\frac{1}{3}\left\|\Delta \psi\right\|^{2}_{L^{2}}. \end{split}$ $

So, we have

$\begin{split} &\frac{d}{dt}\left(\left\|\nabla \psi\right\|^{2}_{L^{2}}+ \|Z\|^{2}_{L^{2}}\right)\\&\leq C\left(\left\|\nabla Z_{1}\right\|^{2}_{L^{\infty}}+\left\|\nabla Z_{2}\right\|^{2}_{L^{\infty}} +\left\|\nabla\Delta \psi_{2}\right\|^{2}_{L^{2}}\left\|\Delta^{2}\psi_{2}\right\|^{2}_{L^{2}}\right)\left(\left\|\nabla \psi\right\|^{2}_{L^{2}}+ \|Z\|^{2}_{L^{2}}\right). \end{split}$ $

By (50), the terms in the parentheses are integrable up to $ \frac{T_{\ast}}{2} $. By repeating the same argument one more time, we have the uniqueness up to $ T_{\ast} $.

5.1.3. Blow-up criterion

To derive the blow-up criterion, we first bound

$\begin{split} &\frac{1}{2}\frac{d}{dt} \left(\left\|\Delta\psi\right\|^{2}_{L^{2}}+\left\|\nabla Z\right\|^{2}_{L^{2}} \right) +\left\| \nabla \Delta \psi\right\|^{2}_{L^{2}} = \int \Delta^{2} \psi [\psi, Z] -\int\Delta Z[\Delta \psi, \psi]\\ & = 2\int \Delta \psi[\psi_{x}, Z_{x}]+2\int \Delta \psi[\psi_{y}, Z_{y}]\leq C \left\|\nabla^{2}\psi\right\|_{L^{\infty}}\left\|\nabla Z\right\|_{L^{2}}\left\|\nabla \Delta \psi\right\|_{L^{2}}\\ &\leq C \left\|\nabla^{2}\psi\right\|^{2}_{L^{\infty}}\left\|\nabla Z\right\|^{2}_{L^{2}}+\frac{1}{2}\left\|\nabla \Delta \psi\right\|^{2}_{L^{2}} \end{split}$ $

and so we have

$ \frac{d}{dt} \left(\left\|\Delta\psi\right\|^{2}_{L^{2}}+\left\|\nabla Z\right\|^{2}_{L^{2}} \right) +\left\| \nabla \Delta \psi\right\|^{2}_{L^{2}} \leq C \left\|\nabla^{2}\psi\right\|^{2}_{L^{\infty}}\left\|\nabla Z\right\|^{2}_{L^{2}}. $

This implies

$\begin{eqnarray} \begin{split} &\left\|\Delta \psi(t)\right\|^{2}_{L^{}}+ \left\|\nabla Z(t)\right\|^{2}_{L^{2}}+\int^{t}_{0}\left\| \nabla \Delta \psi(s)\right\|^{2}_{L^{2}} ds < \infty\\& \iff \int^{t}_{0}\left\|\nabla^{2}\psi(s)\right\|^{2}_{L^{\infty}}ds < \infty \end{split} \end{eqnarray}$ $

(51)

We also take

$\begin{split} &\frac{1}{2}\frac{d}{dt} \left(\left\|\nabla \Delta\psi\right\|^{2}_{L^{2}}+\left\|\Delta Z\right\|^{2}_{L^{2}} \right) +\left\| \Delta^{2} \psi\right\|^{2}_{L^{2}} = -\int \Delta^{3} \psi [\psi, Z] +\int\Delta^{2} Z[\Delta \psi, \psi]\\ & = -\int \Delta^{2}\psi [\Delta \psi, Z] -2\int \Delta^{2}\psi \left([\psi_{x}, Z_{x}]+[\psi_{y}, Z_{y}]\right) \\&\qquad- 2\int \Delta\psi \left([\psi_{x}, \Delta Z_{x}]+[\psi_{y}, \Delta Z_{y}]\right)\\ & = \text{(I)+(II)+(III)}. \end{split}$ $

By using the computation in (41),

$\begin{split} \text{(I)}& = \int \left(\nabla \nabla^{\perp}Z\cdot \nabla \Delta \psi\right)\cdot \nabla \Delta\psi \leq C\left\|\nabla^{2}Z\right\|_{L^{2}} \left\|\nabla^{3}\psi \right\|^{2}_{L^{4}} \\ &\leq C\left\|\nabla^{2}Z\right\|^{2}_{L^{2}} \left\|\nabla\Delta \psi \right\|^{2}_{L^{2}}+\frac{1}{6}\left\|\Delta^{2}\psi \right\|^{2}_{L^{2}}. \end{split}$ $

We next estimate $ \text{(II)}+\text{(III)} $ using (42):

$\begin{equation*} \begin{split} \text{(II)}+\text{(III)}&\leq C\int \left|\nabla^{2}Z\right| \left|\nabla^{3}\psi \right|^{2}+C\int \left|\nabla^{2}\psi \right| \left|\nabla^{4}\psi \right|\left|\nabla^{2}Z\right|\\ &\leq C\left\|\Delta Z\right\|^{2}_{L^{2}} \left\|\nabla\Delta \psi \right\|^{2}_{L^{2}}+C\left\|\nabla^{2}\psi\right\|^{2}_{L^{\infty}} \left\|\Delta Z \right\|^{2}_{L^{2}}+\frac{1}{3}\left\|\Delta^{2}\psi \right\|^{2}_{L^{2}} \end{split} \end{equation*}$ $

So, we have

$\begin{eqnarray} \begin{split} &\frac{d}{dt}\left(\left\|\nabla \Delta \psi\right\|^{2}_{L^{2}}+\left\|\Delta Z\right\|^{2}_{L^{2}}\right) +\left\|\Delta^{2} \psi\right\|^{2}_{L^{2}}\\&\leq C\left(\left\|\nabla\Delta \psi \right\|^{2}_{L^{2}}+\left\|\nabla^{2}\psi\right\|^{2}_{L^{\infty}}\right)\left\|\Delta Z\right\|^{2}_{L^{2}}. \end{split} \end{eqnarray}$ $

(52)

By (51), (52) implies

$\begin{eqnarray} \begin{split} &\left\|\nabla \Delta \psi(t)\right\|^{2}_{L^{2}}+\left\|\Delta Z(t)\right\|^{2}_{L^{2}}+\int \left\|\Delta^{2} \psi(s)\right\|^{2}_{L^{2}}ds < \infty \\ &\iff \int^{t}_{0}\left\|\nabla^{2}\psi(s)\right\|^{2}_{L^{\infty}}ds < \infty. \end{split} \end{eqnarray}$ $

(53)

We finally deal with

where we count the number of derivatives acting on $ (\psi, \psi, Z) $ in (46) as $ (3, 5, 2) $, $ (2, 5, 3) $, and $ (4, 4, 2) $. Then, we obtain

$\begin{equation*} \begin{split} &\frac{1}{2} \frac{d}{dt} \left(\left\|\Delta^{2}\psi\right\|^{2}_{L^{2}}+\left\|\nabla\Delta Z\right\|^{2}_{L^{2}} \right) +\left\|\nabla\Delta^{2} \psi\right\|^{2}_{L^{2}}\\ & \leq C\left\|\Delta Z\right\|^{2}_{L^{2}}\left\|\Delta^{2}\psi\right\|^{2}_{L^{2}}\\&\qquad+ C\left\|\nabla^{2}\psi\right\|^{2}_{L^{\infty}}\left\|\nabla \Delta Z\right\|^{2}_{L^{2}} +C\left\|\Delta Z\right\|^{2}_{L^{4}}\left\|\nabla^{3}\psi\right\|^{2}_{L^{4}}+\frac{1}{2}\left\|\nabla \Delta^{2} \psi\right\|^{2}_{L^{2}}\\ &\leq C\left\|\Delta Z\right\|^{2}_{L^{2}}\left\|\Delta^{2}\psi\right\|^{2}_{L^{2}}+ C\left\|\nabla^{2}\psi\right\|^{2}_{L^{\infty}}\left\|\nabla \Delta Z\right\|^{2}_{L^{2}} +C\left\|\Delta Z\right\|^{2}_{L^{2}}\left\|\nabla\Delta Z\right\|^{2}_{L^{2}}\\ &+C\left\|\nabla \Delta \psi\right\|^{2}_{L^{2}}\left\|\Delta^{2}\psi\right\|^{2}_{L^{2}}+\frac{1}{2}\left\|\nabla \Delta^{2} \psi\right\|^{2}_{L^{2}} \end{split} \end{equation*}$ $

and so we have

$\begin{equation} \begin{split} &\frac{d}{dt} \left(\left\|\Delta^{2}\psi\right\|^{2}_{L^{2}}+\left\|\nabla\Delta Z\right\|^{2}_{L^{2}} \right) +\left\|\nabla\Delta^{2} \psi\right\|^{2}_{L^{2}}\\ &\leq C\left(\left\|\nabla^{2}\psi\right\|^{2}_{L^{\infty}}+\left\|\Delta Z\right\|^{2}_{L^{2}}\right)\left\|\nabla \Delta Z\right\|^{2}_{L^{2}} +C\left(\left\|\nabla \Delta \psi\right\|^{2}_{L^{2}}+\left\|\Delta Z\right\|^{2}_{L^{2}}\right)\left\|\Delta^{2}\psi\right\|^{2}_{L^{2}} \end{split} \end{equation}$ $

(54)

By (51) and (53), (54) implies

$ \label{BW 5}

$\begin{split} &\left\|\Delta^{2} \psi(t)\right\|^{2}_{L^{2}}+\left\|\nabla \Delta Z(t)\right\|^{2}_{L^{2}}+\int^{t}_{0} \left\|\nabla\Delta^{2} \psi(s)\right\|^{2}_{L^{2}}ds < \infty\\& \iff \int^{t}_{0}\left\|\nabla^{2}\psi(s)\right\|^{2}_{L^{\infty}}ds < \infty. \end{split}$ $

5.2. Proof of Theorem 1.6

We recall (13):

$ \psi_{t}-\Delta \psi = [\psi, Z], \quad Z_{t}+Z = [\Delta \psi, \psi]. $

Since the uniqueness is already proved in Section 5.1.2 even without the damping term, we only focus on the a priori bounds.

We first have

(55)

We also have

$\begin{split} \frac{1}{2}\frac{d}{dt} \left(\left\|\Delta^{2}\psi\right\|^{2}_{L^{2}}+\left\|\nabla\Delta Z\right\|^{2}_{L^{2}} \right) &+\left\|\nabla \Delta^{2} \psi\right\|^{2}_{L^{2}}+\left\|\nabla\Delta Z\right\|^{2}_{L^{2}} \\ & = \int \Delta^{4} \psi [\psi, Z] -\int\Delta^{3} Z[\Delta \psi, \psi] = \mathcal{R} \end{split}$ $

with the same $ \mathcal{R} $ in (36). In this case, we also choose the the number of derivatives acting on $ (\psi, \psi, Z) $ as $ (3, 5, 2) $, $ (2, 5, 3) $, and $ (4, 4, 2) $. Hence,

$\begin{equation*} \begin{split} & \frac{d}{dt} \left(\left\|\Delta^{2}\psi\right\|^{2}_{L^{2}}+\left\|\nabla\Delta Z\right\|^{2}_{L^{2}} \right) +\left\|\nabla\Delta^{2} \psi\right\|^{2}_{L^{2}} +\left\|\nabla\Delta Z\right\|^{2}_{L^{2}}\\ & \leq C \left\|\nabla^{2} Z\right\|_{L^{2}}\left\|\Delta^{2}\psi\right\|^{2}_{L^{4}} + C\left\|\nabla \Delta Z\right\|_{L^{2}} \left\|\nabla^{2}\psi\right\|_{L^{\infty}} \left\|\nabla \Delta^{2} \psi\right\|_{L^{2}}\\ &+ C\left\|\Delta Z\right\|_{L^{4}}\left\|\nabla^{3}\psi\right\|_{L^{4}} \left\|\nabla \Delta^{2}\psi\right\|_{L^{2}} \\ & \leq C \left\|\nabla Z\right\|^{\frac{1}{2}}_{L^{2}}\left\|\nabla\Delta Z\right\|^{\frac{1}{2}}_{L^{2}} \left\|\nabla \Delta\psi\right\|^{\frac{1}{2}}_{L^{2}}\left\|\nabla \Delta^{2}\psi\right\|^{\frac{3}{2}}_{L^{2}}+C\left\|\nabla \Delta Z\right\|_{L^{2}} \left\|\nabla^{2}\psi\right\|_{L^{\infty}} \left\|\nabla \Delta^{2} \psi\right\|_{L^{2}}\\ &+ C\left\|\Delta Z\right\|^{\frac{1}{2}}_{L^{2}}\left\|\nabla\Delta Z\right\|^{\frac{1}{2}}_{L^{2}} \left\|\Delta\psi\right\|^{\frac{1}{2}}_{L^{2}} \left\|\nabla \Delta^{2}\psi\right\|^{\frac{3}{2}}_{L^{2}}\\ & \leq C\left(\left\|\nabla Z\right\|^{2}_{L^{2}}\left\|\nabla \Delta\psi\right\|^{2}_{L^{2}}+\left\|\Delta Z\right\|^{2}_{L^{2}}\left\|\Delta\psi\right\|^{2}_{L^{2}}+\left\|\nabla^{2}\psi\right\|^{2}_{L^{\infty}}\right)\left\|\nabla\Delta Z\right\|^{2}_{L^{2}}\\&\qquad +\frac{1}{2} \left\|\nabla \Delta^{2} \psi\right\|_{L^{2}}. \end{split} \end{equation*}$ $

So, we obtain

$\begin{equation} \begin{split} &\frac{d}{dt} \left(\left\|\Delta^{2}\psi\right\|^{2}_{L^{2}}+\left\|\nabla\Delta Z\right\|^{2}_{L^{2}} \right) +\left\|\nabla\Delta^{2} \psi\right\|^{2}_{L^{2}} +\left\|\nabla\Delta Z\right\|^{2}_{L^{2}}\\ & \leq C\left(\left\|\nabla Z\right\|^{2}_{L^{2}}\left\|\nabla \Delta\psi\right\|^{2}_{L^{2}}+\left\|\Delta Z\right\|^{2}_{L^{2}}\left\|\Delta\psi\right\|^{2}_{L^{2}}+\left\|\nabla^{2}\psi\right\|^{2}_{L^{\infty}}\right)\left\|\nabla\Delta Z\right\|^{2}_{L^{2}} \end{split} \end{equation}$ $

(56)

By (55) and (56),

$ \mathcal{E}'(t)+\mathcal{N}_{2}(t)\leq C \left(\mathcal{E}(t)+\mathcal{E}^{2}(t)\right)\mathcal{N}_{2}(t). $

So, if $ \mathcal{E}_{0} = \epsilon_{0} $ is sufficiently small, we obtain

$ \mathcal{E}(t)+(1-C \epsilon_{0})\int^{t}_{0}\mathcal{N}_{2}(s)ds\leq \mathcal{E}_{0} \quad {\rm{for}}\; {\rm{all}}\; t > 0 . $

Acknowledgments

H.B. was supported by NRF-2018R1D1A1B07049015. H. B. acknowledges the Referee for his/her valuable comments that highly improve the manuscript.

References

[1]	Wagner U, Gais S, Born J. (2001) Emotional memory formation is enhanced across sleep intervals with high amounts of rapid eye movement sleep. Learn Memory 8: 112-119. doi: 10.1101/lm.36801
[2]	Hu P, Stylos-Allan M, Walker MP. (2006) Sleep facilitates consolidation of emotional declarative memory. Psychol Sci 17: 891-898. doi: 10.1111/j.1467-9280.2006.01799.x
[3]	Nishida M, Pearsall J, Buckner RL, Walker MP. (2009) REM sleep, prefrontal theta, and the consolidation of human emotional memory. Cereb Cortex 19:1158-1166. doi: 10.1093/cercor/bhn155
[4]	Payne JD, Stickgold R, Swanberg K, Kensinger EA. (2008) Sleep preferentially enhances memory for emotional components of scenes. Psychol Sci 19: 781-788. doi: 10.1111/j.1467-9280.2008.02157.x
[5]	Payne JD, Chambers AM, Kensinger EA. (2012) Sleep promotes lasting changes in selective memory for emotional scenes. Front Integrative Neurosci 6(108): DOI:10. 3389/fnint. 2012. 00108.
[6]	Braun AR, Balkin TJ, Wesenten NJ, Carson RE, Varga M, Baldwin P, et al. (1997) Regional cerebral blood flow throughout the sleep-wake cycle: An H215O PET study. Brain 120:1173-1197. doi: 10.1093/brain/120.7.1173
[7]	Stickgold R, Hobson JA, Fosse R, Fosse M. (2001). Sleep, learning, and dreams: Off-line memory reprocessing. Science 294: 1052-1057. doi: 10.1126/science.1063530
[8]	Plihal W, Born J. (1999) Memory consolidation in human sleep depends on inhibition of glucocorticoid release. NeuroReport 10: 2741-2747. doi: 10.1097/00001756-199909090-00009
[9]	Gais S, Born J. (2004) Low acetylcholine during slow-wave sleep is critical for declarative memory consolidation. P Natl Acad Sci USA 101: 2140–2144.
[10]	Wagner U, Hallschmid M, Rasch B, Born J. (2006) Brief sleep after learning keeps emotional memories alive for years. Biol Psychiat 60: 788-790. doi: 10.1016/j.biopsych.2006.03.061
[11]	Heller AS, Johnstone T, Shackman AJ, et al. (2009) Reduced capacity to sustain positive emotion in major depression reflects diminished maintenance of fronto-striatal brain activation. P Natl Acad Sci USA 106: 22445-22450. doi: 10.1073/pnas.0910651106
[12]	Gruber J, Oveis C, Keltner D, Johnson SL. (2011) A discrete emotions approach to positive emotion disturbance in depression. Cognition Emotion 25: 40-52. doi: 10.1080/02699931003615984
[13]	Tsuno N, Besset A, Ritchie K. (2005) Sleep and depression. J Clin Psychiat 66: 1254-1269. doi: 10.4088/JCP.v66n1008
[14]	Lang A, Dhillon K, Dong Q. (1995) The effects of emotional arousal and valence on television viewers' cognitive capacity and memory. J Broadcast Electron 39: 313-327. doi: 10.1080/08838159509364309
[15]	Hamann SB, Ely TD, Grafton ST, Kilts CD. (1999) Amygdala activity related to enhanced memory for pleasant and aversive stimuli. Nat Neurosci 2: 289-293. doi: 10.1038/6404
[16]	Libkumen TM, Stabler CL, Otani H. (2004) Arousal, valence, and memory for detail. Memory 12:237-247. doi: 10.1080/09658210244000630
[17]	Hamann S. (2001) Cognitive and neural mechanisms of emotional memory. Trends Cogn Sci 5:394-400. doi: 10.1016/S1364-6613(00)01707-1
[18]	Hamann SB, Ely TD, Hoffman JM, Kilts CD. (2002) Ecstasy and agony: Activation of human amygdala in positive and negative emotion. Psychol Sci 13: 135-141. doi: 10.1111/1467-9280.00425
[19]	Waring JD, Kensinger EA. (2009) Effects of emotional valence and arousal upon memory trade-offs with aging. Psychol Aging 24: 412-422. doi: 10.1037/a0015526
[20]	Waring JD, Kensinger EA. (2011) How emotion leads to selective memory: Neuroimaging evidence. Neuropsychologia 49: 1831-1842. doi: 10.1016/j.neuropsychologia.2011.03.007
[21]	Payne JD, Kensinger EA. (2011) Sleep leads to changes in the emotional memory trace: Evidence from fMRI. J Cogn Neurosci 23: 1285-1297. doi: 10.1162/jocn.2010.21526
[22]	Payne JD, Kensinger EA. (2010) Sleep's role in the consolidation of emotional episodic memories. Curr Dir Psychol Sci 19: 290-295
[23]	Iber C, Ancoli-Israel S, Chesson AL, Quan SF, eds. (2007) The AASM Manual for the Scoring of Sleep and Associated Events: Rules, Terminology, and Technical Specifications. 1 Eds. , Westchester, Illinois: American Academy of Sleep Medicine.
[24]	Yonelinas AP. (2002) The nature of recollection and familiarity: A review of 30 years of research. J Mem Lang 46: 441-517. doi: 10.1006/jmla.2002.2864
[25]	Yonelinas AP, Jacoby LL. (1995) The relation between remembering and knowing as bases for recognition: Effects of size congruency. J Mem Lang 34: 622–643.

Reader Comments

Your name:*

Email:*
© 2014 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

AIMS Neuroscience

3.1 4.2

Metrics

Article views(7580) PDF downloads(991) Cited by(9)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

AIMS Neuroscience

The Influence of Sleep on the Consolidation of Positive Emotional Memories: Preliminary Evidence

Related Papers:

Abstract

1. Introduction

1.1. The Hall equation with fractional Laplacian

1.2. 2D models

1.2.1. Case 1

1.2.2. Case 2

2. Preliminaries

2.1. Inequalities

2.2. Commutator

3. Proof of Theorem 1.1 and Theorem 1.2

3.1. Proof of Theorem 1.1

3.1.1. Approximation

3.1.2. A priori estimates

3.1.3. Uniqueness

3.1.4. Decay rates

3.2. Proof of Theorem 1.2

4. Proof of Theorem 1.3 and Theorem 1.4

4.1. Proof of Theorem 1.3

4.1.1. Approximation

4.1.2. A priori estimates

4.1.3. Uniqueness

4.1.4. Blow-up criterion

4.2. Proof of Theorem 1.4

4.2.1. A priori estimates

4.2.2. Decay rates

5. Proof of Theorem 1.5 and Theorem 1.6

5.1. Proof of Theorem 1.5

5.1.1. A priori estimates

5.1.2. Uniqueness

5.1.3. Blow-up criterion

5.2. Proof of Theorem 1.6

Acknowledgments

References

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog

Abstract

1. Introduction

1.1. The Hall equation with fractional Laplacian

1.2. 2D models

1.2.1. Case 1

1.2.2. Case 2

2. Preliminaries

2.1. Inequalities

2.2. Commutator

3. Proof of Theorem 1.1 and Theorem 1.2

3.1. Proof of Theorem 1.1

3.1.1. Approximation

3.1.2. A priori estimates

3.1.3. Uniqueness

3.1.4. Decay rates

3.2. Proof of Theorem 1.2

4. Proof of Theorem 1.3 and Theorem 1.4

4.1. Proof of Theorem 1.3

4.1.1. Approximation

4.1.2. A priori estimates

4.1.3. Uniqueness

4.1.4. Blow-up criterion

4.2. Proof of Theorem 1.4

4.2.1. A priori estimates

4.2.2. Decay rates

5. Proof of Theorem 1.5 and Theorem 1.6

5.1. Proof of Theorem 1.5

5.1.1. A priori estimates

5.1.2. Uniqueness

5.1.3. Blow-up criterion

5.2. Proof of Theorem 1.6

Acknowledgments