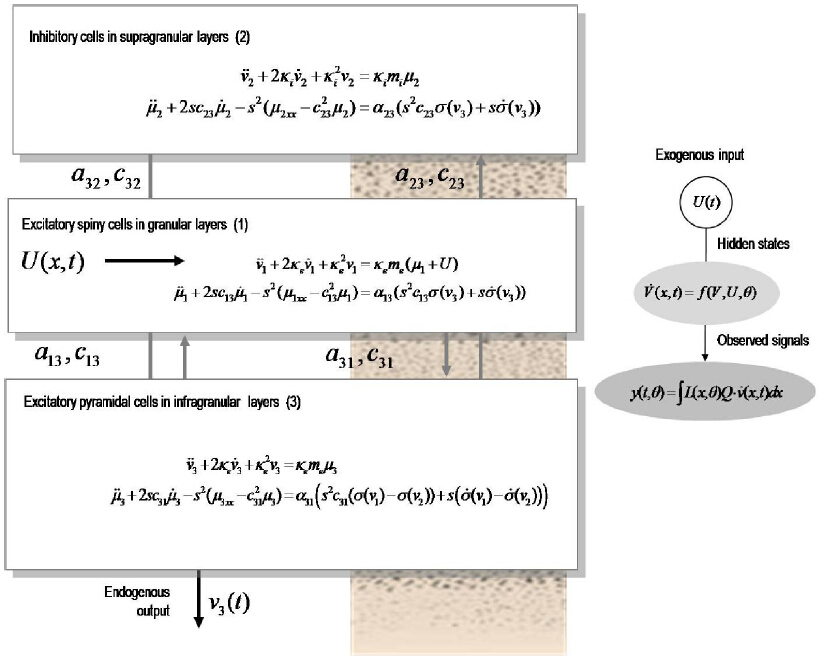
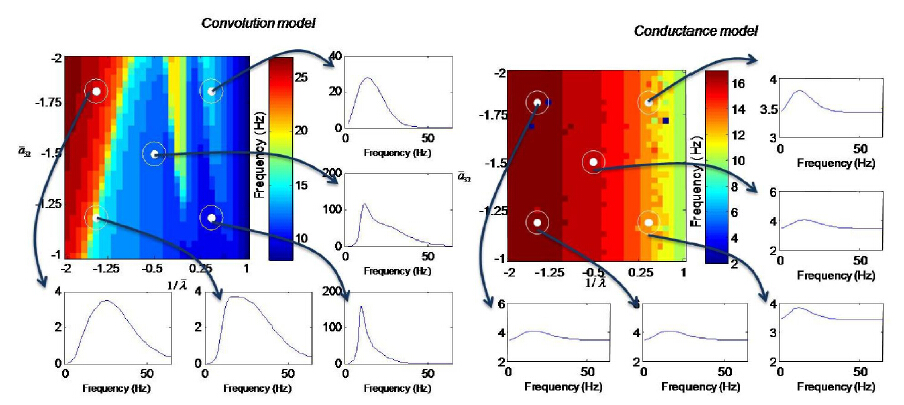
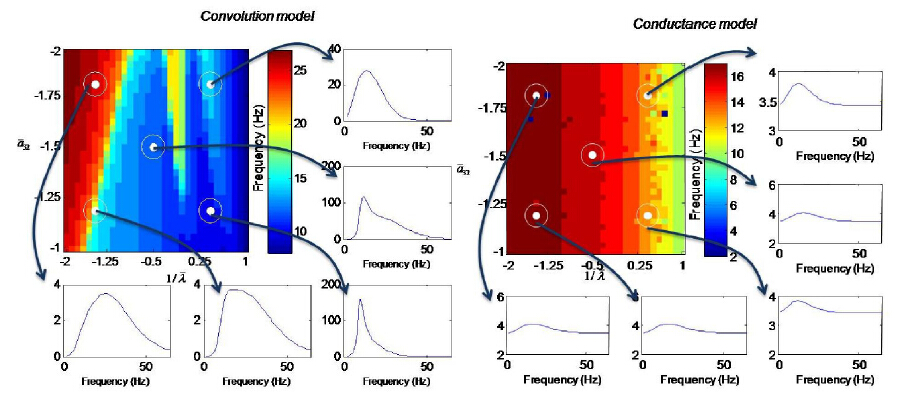
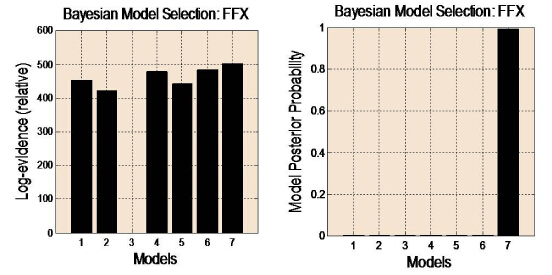
This paper shows how gamma oscillations can be combined with neural population models and dynamic causal modeling (DCM) to distinguish among alternative hypotheses regarding cortical excitability and microstructure. This approach exploits inter-subject variability and trial-specific effects associated with modulations in the peak frequency of gamma oscillations. Neural field models are used to evaluate model evidence and obtain parameter estimates using invasive and non-invasive gamma recordings. Our overview comprises two parts: in the first part, we use neural fields to simulate neural activity and distinguish the effects of post synaptic filtering on predicted responses in terms of synaptic rate constants that correspond to different timescales and distinct neurotransmitters. We focus on model predictions of conductance and convolution based field models and show that these can yield spectral responses that are sensitive to biophysical properties of local cortical circuits like synaptic kinetics and filtering; we also consider two different mechanisms for this filtering: a nonlinear mechanism involving specific conductances and a linear convolution of afferent firing rates producing post synaptic potentials. In the second part of this paper, we use neural fields quantitatively—to fit empirical data recorded during visual stimulation. We present two studies of spectral responses obtained from the visual cortex during visual perception experiments: in the first study, MEG data were acquired during a task designed to show how activity in the gamma band is related to visual perception, while in the second study, we exploited high density electrocorticographic (ECoG) data to study the effect of varying stimulus contrast on cortical excitability and gamma peak frequency.
1.
Introduction
Robotic manipulators have been widely used in various fields such as electronics industries, automobile industries, military affairs, space exploration, and mining. Furthermore, the application fields of manipulators continue to expand, such as riot control, health industries, catering industries, construction industries, and explosion prevention. Trajectory planning, as one of the most imperative topics on manipulators, has been investigated since the manipulators appeared. A considerable number of approaches have been proposed to solve the robot planning problem, such as artificial potential field (APF) [1,2], probabilistic roadmap [3], rapidly-exploring random tree (RRT) [4], configuration space method [5], optimization algorithm [6,7], reinforcement learning [8,9], metaheuristics [10,11,12,13], and Tau theory [14,15,16,17,18,19,20,21]. The goal of trajectory planning is to make robots move fast, accurately, and stably. Besides, researchers also dedicate to make robots safer to the circumstances, more intelligent, and more compliant. In recent years, Tau theory has been utilized on robots to plan trajectories due to the compliant feature [17,18,19,20,21].
Since many objectives need to be achieved in robot planning, the optimization algorithms provide a promising way to solve the challenging issue. For example, the improved sparrow search algorithm was proposed to plan the shortest path for mobile robots [22]. The modified particle swarm optimization and the Tabu search algorithm were used to handle inverse kinematics and obstacle avoidance problems [23]. A novel multi-group particle swarm optimization was proposed to achieve motion planning [24]. The ant colony optimization algorithm was applied on unmanned air vehicles trajectory planning tasks [25]. Huang et al. [26] employed the elitist non-dominated sorting genetic algorithm — version Ⅱ (NSGA-Ⅱ) to optimize the 5th-order B-spline trajectory for an industrial robot manipulator. NSGA-Ⅱ was also adopted to tune the proportional-integral-derivative (PID) controller of the robotic manipulator [27]. A hybrid differential evolution-based method was presented to address the 6-degree of freedom (DOF) manipulator trajectory planning problem [28]. Most optimization algorithms are imitated from the practical long-tested-by-nature behaviors of creatures. This inspired the design philosophy of the algorithms, which are also called bio-inspired optimization algorithms. Among the bio-inspired optimization algorithms, bacteria foraging optimization algorithm (BFOA) was successfully applied on liquid level control [29], which indicates the effectiveness of being employed on robot planning.
In this paper, a novel bio-inspired trajectory planning method is proposed for robotic systems based on the improved BFOA (IBFOA) and Tau-J*. The main contributions can be described as follows.
(1) The trajectory planning of the manipulator is considered as a multi-objective optimization problem. Then, the multi-objective optimization algorithm IBFOA is proposed to generate a set of optimal control points in the trajectory planning. Compared with the original BFOA, the IBFOA is presented with decreased reproduction size, decreased elimination & dispersal probability, and the elite-preservation strategy. In this way, the IBFOA can achieve better performance and more stable optimization in comparison to the original BFOA. Besides, the IBFOA performance improvement can be measured as the mean fitness change which is $ 6\% $. Similarly, the stability improvement can be measured as the fitness standard deviation change which is $ 7\% $. The improvement requires nearly no extra computation.
(2) A bio-inspired trajectory generation algorithm Tau-J* is proposed to interpolate the waypoints between the control points, enabling the calculation burden to be alleviated and the collision-free compliant trajectory of the manipulator to be obtained. Compared with other Tau-based guidance strategies, Tau-J* has the benefits of zero initial and final jerk due to the usage of the high-order Tau function. Next, a more compliant trajectory can be acquired using the proposed Tau-J* guidance strategy. Hence, a novel IBFOA-Tau-J* algorithm is designed to facilitate robotic manipulator planning.
The rest of the paper is structured as follows. In Section 2, the related work is introduced. In Section 3, the original BFOA, IBFOA, and the trajectory generation based on IBFOA are described. In Section 4, the interpolation algorithm Tau-J* is presented. Afterward, the simulation tests on a 6-DOF manipulator are conducted based on the proposed algorithm, and the test results are discussed in Section 5. and the discussion is also given. Finally, the conclusions and our future work are drawn in Section 6.
2.
Related work
BFOA, as a bio-inspired optimization algorithm, was proposed to imitate the foraging behaviors of Escherichia coli, including chemotaxis, swarming, reproduction, and elimination & dispersal. Subsequently, the BFOA and its improved algorithms were presented to address the optimization problem. For instance, an adaptive BFOA was presented by adding a constant parameter in the denominator of the step size formula [30]. Similarly, Chen et al. [31] modified the chemotaxis behavior by introducing population diversity of the bacterial colony, universal iterations, mean fitness in two chemotaxis processes. Different from the above adaptive BFOAs, the nonlinear decreasing methods, the roulette gambling mechanism, and the linear decreasing adaptive regulation mechanism were introduced to chemotaxis behavior, reproduction behavior, and elimination & dispersal behavior, respectively [32]. BFOA was applied to optimize the controller parameters [33], and the better results were obtained compared to the conventional proportional-integral (PI) controller and genetic algorithm-based controller. Abd-Elazim et al. [34] built the hybrid particle swarm optimization-BFOA (BSO) to optimize the design of power system stabilizers and demonstrated the superiority of the proposed method to BFOA and PSO. Additionally, BFOA was used to optimize the nonlinear load frequency controller parameters [35]. Panda et al. [36] introduced the principle of swarming to hybrid BFOA and PSO, which was tested in automatic generation control. The BFOA was applied to real-time pose adjustment of the Hexa robot [37]. Besides, the multi-subpopulation bacterial foraging optimization algorithm [38] was proposed to facilitate unmanned surface vehicle path planning by constructing a new strategy that protects the elite member in the subpopulation. The above investigations suggest that the BFOA and its improved algorithms possess good performances in parameters optimization and searching extremum value. However, the application of BFOA for trajectory planning of robotic manipulators needs to be further investigated because it may fail to find the global optimum, and the current solution may become worse during iteration. Thus, the reproduction behavior and the elimination & dispersal behavior are modified by introducing the elite-preservation strategy and a decay factor $ d_k $ on the two behaviors. In this way, a novel improved BFOA (IBFOA) can be conducted to facilitate the trajectory planning of robotic manipulators.
Notably, the unexpected calculation burden and unsmooth trajectories would occur provided that the IBFOA (or BFOA) is implemented alone on the trajectory planning of robotic manipulators. One feasible way is to establish smoothness evaluation criteria in the cost function to obtain the smooth trajectories. However, the calculation burden problem would be further aggravated since more terms were introduced in the cost function. With the purpose of alleviating the above deficiencies, IBFOA is adopted to generate a small set of control points, and the interpolation algorithms (such as polynomial interpolation [39], cubic spline [40], linear segment with parabolic blend [41], and Tau theory) are then performed to generate the waypoints between the control points. In this way, both fast calculation and smooth trajectories can be achieved.
Tau theory, as a bio-inspired interpolation method, was applied to generate the trajectory of robotic systems in recent years owing to its fast calculation and smooth trajectory generation. In the early stage, researchers focused on the physical meaning of Tau [14,15]. Then, Tau theory was employed to describe the law of creatures approaching objects [16]. A so-called intrinsic Tau jerk (Tau-J) guidance strategy was proposed and applied to quadrotors [17]. Then, Tau-J also implemented on manipulators [18], and the performance was thoroughly discussed [21]. Besides, Tau harmonic (Tau-H) was proposed by introducing harmonic movement into Tau theory and used on unmanned aerial vehicles based on PSO to overcome the shortages of Tau-J [19]. Moreover, Lee modified the work of [16], making it possible to guide a movement to a departing destination [20]. However, Tau theory cannot be used to handle the global multi-objective trajectory planning of robotic manipulators.
3.
Improved bacteria foraging optimization algorithm
In this section, the fundamentals of the bacteria foraging optimization algorithm (BFOA) are first presented. Then a novel improved bacteria foraging optimization algorithm (IBFOA) is proposed. Different from the existed BFOAs, the decay factors are used in the reproduction behavior and elimination & dispersal behavior. Furthermore, the elite-preservation strategy is introduced in the proposed algorithm. Moreover, the trajectory generation for the robotic manipulator is described based on the proposed IBFOA.
3.1. Fundamentals of BFOA
BFOA [29] is a bio-inspired optimization algorithm that imitates the foraging behavior of Escherichia coli. The E. coli will survive and breed in nutrient-rich places and will die in a food-lacking or noxious circumstance. As a result, E. coli tend to move and stay in a comfort zone. In BFOA, all the bacteria only need to chase the global minimum (or maximum) of the fitness function by taking the following four kinds of behaviors.
(a) Chemotaxis: It consists of tumbling and swimming. In short, the bacteria tumble to change direction and swim forward.
(b) Swarming: Each bacterium attracts and repels other bacteria to approach while all the bacteria cannot be too close.
(c) Reproduction: The bacteria in better places will live and reproduce asexually, and others will die. The population remains unchanged.
(d) Elimination & dispersal: Every bacterium will be eliminated and dispersed to another random place stochastically with a constant probability.
At the early stage of the BFOA optimization process, the potential optimal domain can be obtained by searching the whole domain field. As the optimization process proceeds, the step size remains fixed and has to be selected carefully in advance to determine a compromise between efficiency and optimal solutions. Given the drawback, different kinds of adaptive-step BFOA were proposed [30,31,32]. Moreover, the best bacteria may be eliminated and dispersed to another random place, resulting in a worse current solution.
3.2. Improved BFOA
A decay factor $ d_k $ is defined and multiplied by the reproduction size $ S_r $ and the elimination & dispersal probability $ P_{ed} $. $ S_r $ and $ P_{ed} $ will decrease over time by the decay factor. Consequently, the reproduction and elimination & dispersal behaviors are improved. The advantage is that the bacteria will focus on exploring the searching space and then pay increasing attention to find better solutions around the current optimal solution, contributing to a quick achievement of the optimal solutions. Generally, the decay variables are linearly reduced or exponentially reduced. In this paper, the decay factor $ d_k $ is defined as,
where $ N = {N_c} \cdot {N_{re}} \cdot {N_{ed}} $ is the total iteration number, $ N_c $ denotes the number of the chemotaxis steps, $ N_{re} $ refers to the number of reproduction steps, $ N_{ed} $ represents the number of elimination & dispersal steps, and $ n $ is the current iteration number (starts at 1). A decay variable can be obtained by multiplying $ d_k $ by a nonzero constant.
Different from the previous research [30,31,32], a novel IBFOA is proposed with decreased reproduction size $ S_r $, decreased elimination & dispersal probability $ P_{ed} $, and the elite-preservation strategy. By introducing the elite-preservation strategy to the elimination & dispersal behavior, the bacterium in the best place will always survive, protecting the current optimum. In this study, $ \Theta $ is defined as the search agents and stores all the bacterium positions. Define the bacteria $ \Theta(j, k, l) = [\theta^{1}(j, k, l), \ldots, \theta^{S}(j, k, l)] $, where $ S $ indicates the number of bacteria, $ \theta^{i}(j, k, l) $ represents a $ p $-dimensional position vector with $ i = 1, \cdots, S; j = 1, \cdots, N_c; k = 1, \cdots, N_{re} $; and $ l = 1, \cdots, N_{ed} $ that stores the $ i $-th bacterium position at the $ j $-th chemotactic step, the $ k $-th reproduction step, and the $ l $-th elimination & dispersal step. The IBFOA (compared with BFOA) can be described as Algorithm 1.
Define a fitness function $ J(i, j, k, l) $ as,
where $ J_c(i, j, k, l) $ represents the cost function that will be defined later, and $ J_{ar}(i, j, k, l) $ denotes the combined attraction and repelling effect, defined as,
where $ {{\theta _m}} $ represents the $ m $-th dimension of the bacterium position, $ {{\theta _m^i}} $ is the $ m $-th dimension of the $ i $-th bacterium position, $ d_{attract} $ denotes the depth of the attractant, $ w_{ {attract}} $ strands for the width of the attractant, $ h_{ {repellant}} $ indicates the height of the repellant, and $ w_{ {repellant}} $ refer to the width of the repellant.
The objective of IBFOA is to minimize the fitness function $ J(i, j, k, l) $ so as to to determine the optimal solution stored by $ J_{last} $ according to Algorithm 1. Besides, the health function $ J^i_{health} $ is defined as follows to evaluate the health of the bacteria:
The objective of the health function $ J^i_{health} $ is to examine whether the i-th bacterium obtains enough nutrients during its lifetime of foraging evaluate "healthy"[29].
3.3. Trajectory planning based on IBFOA
First, it is assumed that the trajectory planning for an $ n $-DOF robotic manipulator is conducted in an environment with $ N_{obs} $ obstacles using the proposed IBFOA. Additionally, the obstacles are set to be spheres randomly in the workspace to simplify the calculations. The initial and final joint angles are also set to be random values if no collision happens.
Second, trajectory planning is regarded as a multi-objective optimization problem. Then, the proposed IBFOA can be employed to obtain the optimal trajectory. With the purpose of avoiding the unstable and cumbersome inverse kinematics, all control points and waypoints are calculated in the joint space of the robotic manipulator, and forward kinematics is applied in collision detection. The robot links are modeled as the cylinders with hemispheres for each joint, and the obstacles are modeled as the spheres. Afterward, a collision model composed of the cylinders with hemispheres and the spheres is established. In the collision model, the cylinder with hemispheres is abstracted as the line segment, while the radius of the cylinder, the modeling error compensation, and the safe stopping distance are all modeled in the spheres. In this way, only the distance between the line segment and the center of the sphere needs to be calculated in the collision model for collision detection. The cost function is defined as,
where $ {\omega _{1}} $, $ {\omega _{2}} $, and $ {\omega _{3}} $ are weights, $ L $ denotes the path length of the end effector, $ L_q $ represents the sum of angles of all joints, $ C $ refers to the collision flag (0 and 1 indicates no collision and collision, respectively), and $ P $ suggests the penalty that will increase when the manipulator approaches and collides the obstacles. The path length $ L $ can be defined as,
where $ N_w $ denotes the overall number of waypoints, $ k $ is the number of current waypoint, $ x_k $, $ y_k $, and $ z_k $ describe the current position of the end effector. The sum of angles $ L_q $ is expressed as,
where $ N_{DOF} $ indicates the degree of freedom of the manipulator, and $ q^i $ denotes the $ i $-th joint of the manipulator. The penalty $ P $ can be defined as,
where $ N_{obs} $ is the number of obstacles, $ r_{ {obs}}^{j} $ denotes the radius of the $ j $-th obstacle, $ r_{ {expansion }}^{j} $ denotes the expansion radius of the $ j $-th obstacle, and
represents the distance between the $ j $-th obstacle and all links of the manipulator at $ k $-th waypoint, where $ l^i $ indicates the $ i $-th link, and $ obs^j $ represents the $ j $-th obstacle, respectively.
Generally, the weight parameters $ {\omega _{1}} $, $ {\omega _{2}} $, and $ {\omega _{3}} $ can be manually selected to minimize the moving path of the manipulator in both Cartesian space and joint space. Notably, $ {\omega _{3}} $ is chosen to be large, allowing the fitness to be significantly increased provided that the manipulator collides with obstacles.
Then, the planned trajectory can be obtained by using the proposed IBFOA. However, it is inefficient to obtain every single waypoint of a trajectory through IBFOA since the calculation burden will be aggravated and the unsmooth trajectories will be generated. One feasible way to handle these problems is that a small set of control points can be planned using IBFOA, and then the plenty of waypoints between two adjacent control points can be generated by an interpolation algorithm. It suggests that only the positions of control points for all the joints of the manipulator need to be optimized using the proposed IBFOA. In this way, the calculation burden and the unsmooth trajectories will be reduced since the interpolation algorithms can generate the trajectories between the two adjacent control points as smoothly as possible with simple computation.
4.
Tau-J*: an interpolation algorithm
Several interpolation algorithms are used to generate the trajectories of industrial robotic manipulators, so as to improve the implementation efficiency. However, the common interpolation algorithms generally suffer from the nonzero initial jerk and final jerk, which would damage the actuators. Thus, a bio-inspired interpolation algorithm, Tau theory, is utilized to generate a smooth trajectory and achieve the compliant motion. Based on the Tau theory, an improved Tau-J (Tau-J*) is presented in this section to generate the trajectory with zero initial and final jerk, contributing to achieving the compliant trajectory.
4.1. Tau theory
Lee [14] investigated how creatures utilize visual information when approaching objects and then proposed the Tau theory in 1976. Lee et al. [15] explicitly described the Tau function $ \tau(x) $ as,
where $ x(t) $ denotes the gap between the current position and the object, and $ \dot{x}(t) $ indicates the approaching velocity.
If there are two movements reaching the object simultaneously, the relationship of the two movements can be described as,
where $ k_{A} $ represents the coupling coefficient [16], and $ x_A(t) $ refers to the gap of the intrinsic guidance movement (IGM), which represents a virtual movement guiding the actual gap $ x(t) $. Given the IGM, one can obtain the IGM-guided actual movement by Eq (4.2).
Intrinsic Tau jerk (Tau-J) guidance strategy [19] was proposed by applying constant jerk movement as IGM $ x_A(t) = \frac{1}{6}j\left({{T^3} - {t^3}} \right) $. By solving Eq (4.2), the actual movement can be obtained as,
where $ x_0 $ denotes the initial motion gap, $ T $ indicates the reach time, and $ k $ represents the coupling coefficient. Tau-J can guide a movement with zero initial acceleration and zero final acceleration. The IGM of Tau-J is a cubic polynomial, causing the second derivative of gap (acceleration) to start and end at zero. However, the initial jerk and final jerk are nonzero, resulting in uncompliant movement, even damage to the actuators.
4.2. Improved Tau-J (Tau-J*)
To make the movement more complaint, we propose an improved intrinsic Tau jerk (Tau-J*) guidance strategy. With a quartic polynomial as the IGM, $ x_A(t) = \frac{1}{24}j^*\left({{T^4} - {t^4}} \right) $, the third derivative of gap (jerk) will start and end at zero. It can be obtained that,
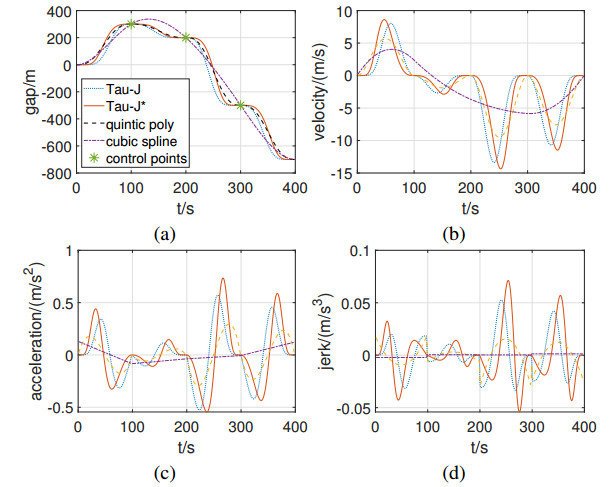
Since the higher-order IGM is used, Eq (4.4) can guide the movement with zero initial jerk and zero final jerk. Tau-J, Tau-J*, quintic polynomial, and cubic spline algorithms are compared to demonstrate the performances of the interpolation algorithms. It is assumed that the gaps are $ 0 $, $ 300 $ m, $ 200 $ m, $ -300 $ m, $ -700 $ m at $ 0 $, $ 100 $ s, $ 200 $ s, $ 300 $ s, $ 400 $ s, respectively, which can be considered one start point, three control points, and one endpoint. Then, the four interpolation algorithms are used to generate trajectories, respectively. Figure 1 illustrates the interpolation results of the gap, velocity, acceleration, and jerk curves, with the parameters $ k = 0.1 $, and $ T = 100 $ chosen for Tau-J and Tau-J*, respectively. The results demonstrate that the Tau-J, Tau-J*, and quintic polynomial can stop at every control point while the cubic spline algorithm can generate a nonstop trajectory. As revealed from Figure 1(c), the accelerations of the cubic spline are nonzero values at the start and end of the movement, and this would cause instability or damage the actuators. Figure 1(d) indicates that the jerks of Tau-J, quintic polynomial, and cubic spline are discontinuous and nonzero at the start and end of the movement, while the jerk of the proposed Tau-J* is continuous and zero at the start and end of the movement. It indicates that Tau-J* can guide more compliant movements.
5.
Simulation
In this section, the simulation tests are conducted for a robotic manipulator on the robot simulator CoppeliaSim (also known as V-REP) to validate the performances of the proposed bio-inspired trajectory planning method.
5.1. Simulation Procedure
We set up a 6-DOF robotic manipulator in the CoppeliaSim, where three obstacles are assumed to exist in the workspace. The initial and final joint angles of the robotic manipulator are set to be random, and the positions of the obstacles are randomly chosen in the workspace. The multi-objective collision-free compliant trajectories are obtained with the proposed bio-inspired trajectory planning method. The control points are updated every iteration through IBFOA in the joint space, and the waypoints between the control points are generated by Tau-J*. Within such an algorithm design, the joint angle, velocity, acceleration, jerk, and torque are reasonable values, and there is no need to evaluate kinematical and dynamical constraints. Particularly, a larger number of waypoints is desired since collision detection is used for every waypoint. Nonetheless, more waypoints would lead to more computational consumption. Therefore, one can make a trade-off between optimality and computational efficiency by choosing an adequate number of waypoints. Following the analyses of Section 3.3 and above, the numbers of the control points and waypoints are both selected by the trial-and-error method.
The whole procedure is described in Algorithm 2, where the function $ CptF(i, j, k, l) $ that computes the fitness is invoked as Algorithm 3.
5.2. Simulation results
Two cases are conducted under the same condition to compare the proposed method with other similar methods. For simulation, it is assumed that there are $ 3 $ obstacles in the circumstance. By the trial-and-error method, $ 3 $ control points, $ 1 $ initial point and $ 1 $ endpoint can be chosen, followed by 120 waypoints between the adjacent control points. Case 1 is implemented to compare the performances of IBFOA, BFOA, and BSO; Case 2 is conducted to demonstrate the convergence of the solutions by using IBFOA BFOA, and BSO, respectively. Notably, IBFOA, BFOA, and BSO are implemented with Tau-J*. The parameters of the two cases are exhibited in Table 1, where some parameters are selected according to the literature [29,35] and the others are tuned by the trial-and-error method. BFOA and BSO share the same parameters. The tests are performed on the desktop with a 3.4 GHz central processing unit (CPU) and 16 GB DDR4 memory.
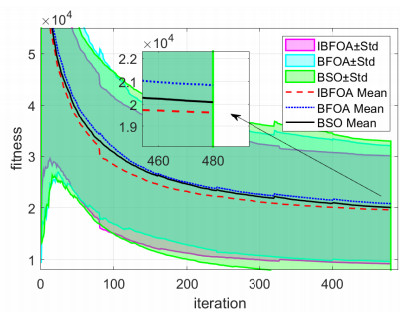
Case 1: Three hundred results of IBFOA and BFOA are collected respectively, with each result containing 480 iterations. Figure 2 illustrates the mean fitness and standard deviation, where $ \pm $std denotes the standard deviation. As indicated in Figure 2, IBFOA has faster convergence with lower fitness compared to BFOA and BSO. This demonstrates that IBFOA can achieve better solutions and be more stable.
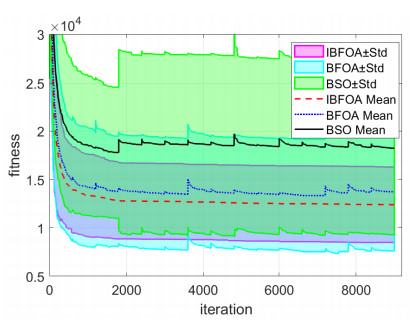
Case 2: Twenty results of IBFOA, BFOA, and BSO are collected respectively, with each result containing 9000 iterations. Figure 3 shows the mean fitness and standard deviation, revealing that IBFOA is superior to BFOA and BSO in the stability, speed of convergence, and quality of solutions with the larger iteration numbers.
Table 2 provides the final fitness (mean $ \pm $ std) of Case 1 and Case 2, suggesting that IBFOA can achieve smaller final fitness. Specifically, the smaller mean value generally indicates the better solution, and the smaller standard deviation value reflects the more stable optimization algorithm.
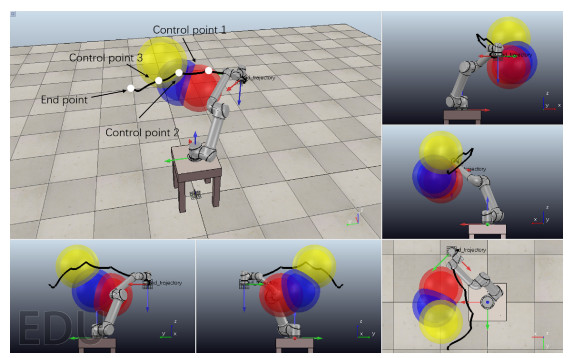
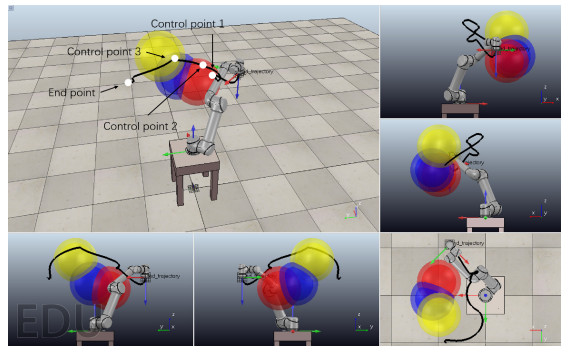
Besides, a set of optimal solutions of IBFOA (with Tau-J*) and BFOA (with Tau-J) is chosen respectively to be visualized on CoppeliaSim, so as to further intuitively demonstrate the performances of the proposed trajectory planning method. Figures 4 and 5 present the visualized scenes with the same positions of the obstacles and initial and final joint angles obtained using IBFOA-Tau-J* and BFOA-Tau-J, respectively. The three obstacles are colored in yellow, blue, and red, respectively; the path of the end-effector is drawn as black lines; the coordinates at the bottom right in each subfigure indicate the angle of view; the endpoint and control points of the end-effector in Cartesian space are exhibited with white dots.
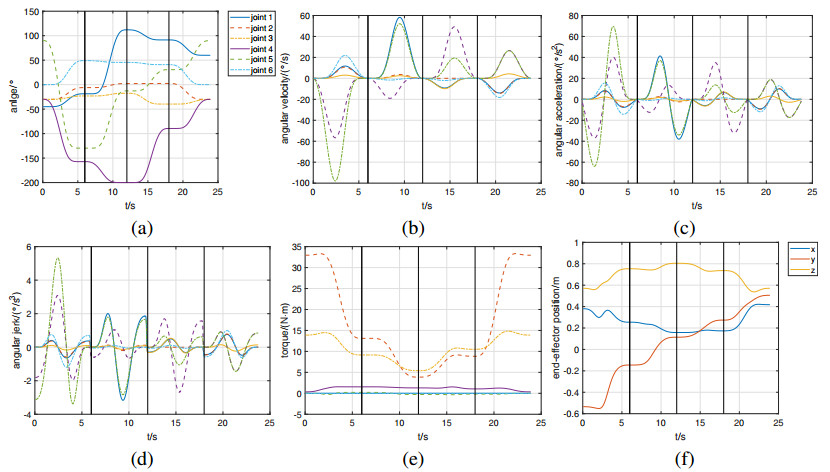
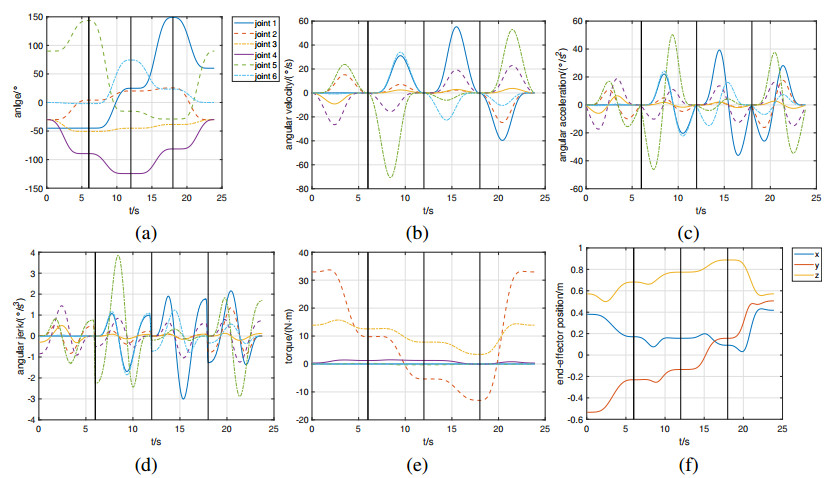
Figures 6 and 7 exhibit the angle, angular velocity, angular acceleration, angular jerk, torque, and end-effector position obtained by IBFOA and BFOA, respectively. The control points at $ 6 $s, $ 12 $s and $ 18 $s of planned trajectories are indicated by the black vertical lines.
5.3. Discussion
As illustrated in Figures 2 and 3, the faster the fitness decreases, the smaller the mean and standard deviation of the observable fitness. This implies that the proposed IBFOA can achieve faster converges, better solutions, and more stable performance compared to BFOA and BSO. Moreover, there are the stepped increases in the mean BFOA and BSO fitness (Figure 3), which worsen the optimization process. The reason is that the elimination & dispersal behavior forces several bacteria "rebirth" in a random place, making the best bacterium "rebirth" in a bad place. According to the parameters in Table 1, there are $ N_c \times N_{re} = 30 \times 20 = 600 $ iterations in the chemotaxis and reproduction behaviors, and the stepped increases would occur every $ 600 $ iterations. In Figure 2, the stepped mean fitness increase would also appear every $ N_c \times N_{re} = 10 \times 8 = 80 $ iterations. The mean fitness of IBFOA does not increase in Figures 2 and 3 because of the elite-preservation strategy.
Multiple parameters should be tuned in IBFOA to achieve good solutions. Larger $ S $ and $ N_c $ boost the chance to find global optimal while raising the computational burden. $ N_t $ can be considered the search step length. If $ N_t $ is too large the bacteria may swim through local optimal; if $ N_t $ is too small the bacteria may take too many steps to find local minimal and be unable to jump out. In Case 1 and Case 2, $ N_t $ is adequately chosen under the consideration of the manipulator joint limit and the desired solution coarseness. The swimming behavior is controlled by $ N_s $ to determine how long the bacteria should swim to the better solution. This behavior leads to the random evaluation times of the cost function and causes inconvenience when IBFOA is compared with other optimization algorithms. $ N_s $ and $ S_r $ control the "rebirth" in good places; $ N_{ed} $ and $ P_{ed} $ control the "rebirth" in random places. Since the "rebirth" behaviors are improved by $ d_k $, large values can be selected and will decay in the optimization progress.
In Figures 4 and 5, both of the algorithms can avoid obstacles. However, the end-effector position curve of BOFA is intuitively longer than that of IBFOA, reflecting the smaller $ L $ in the cost function obtained by IBFOA.
By comparing Figure 6 with Figure 7, the subfigures (a), (b), and (c) in both figures demonstrate that the compliant angle, velocity, and acceleration curves can be generated by both IBFOA and BFOA. However, in subfigures (d), the jerk of IBFOA is zero at every control point while the jerk of BFOA may suddenly change at control points leading to uncompliant movements. Meanwhile, more compliant trajectories can be obtained by using Tau-J*. In subfigures (f), the end-effector position of IBFOA is quite more steady than that of BFOA at $ 6\sim18 $ s.
Case 1 takes 54.924 seconds on average for 480 iterations to generate a feasible trajectory according to 300 tests. Case 2, which is used for testing the performance of IBFOA in a long-running process, takes 2520.544 seconds on average for 9000 iterations to test the converge performance of IBFOA according to 20 tests. Moreover, the number of iterations can be chosen adequately. The feasible trajectory can be obtained as shown in Figures 4 and 5 in Case 1. Based on the average runtime of Case 1, the computation time is acceptable for the trajectory planning task since the robotic manipulator moves in a static circumstance. According to the experimental tests, $ 93\% $ runtime is used to calculate the cost function as the collision detection has to be calculated at all the waypoints and control points to guarantee a collision-free trajectory; $ 2\% $ runtime and $ 3\% $ runtime are consumed by IBFOA and Tau-J*, respectively; the remaining $ 2\% $ runtime is occupied by other codes.
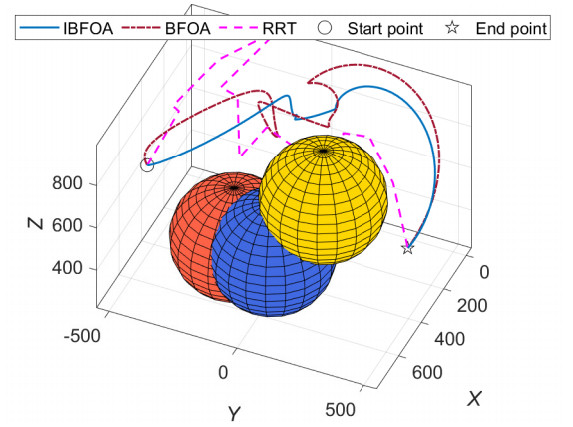
Additionally, the experimental tests are conducted for the end-effector trajectory planning using IBFOA-Tau-J*, BFOA-Tau-J, and RRT methods to demonstrate the effective performance of the proposed method. The experimental results are presented in Figure 8, where the results of each method are obtained for running around $ 60 $ seconds. Compared with BFOA-Tau-J and IBFOA-Tau-J* methods, RRT can be used to discover feasible solutions by sampling the domain field in high-dimensional spaces without prior knowledge. However, the RRT method may be inefficient considering that there are no potential optimal areas in the whole domain field for finding the solutions due to the absence of priori knowledge. As suggested in Figure 8, all the planned trajectories are achieved to be collision-free with the above methods. Nevertheless, the shortest and most compliant collision-free trajectory can be achieved by the proposed IBFOA-Tau-J* method compared with BFOA-Tau-J and RRT methods.
6.
Conclusions
In this study, an IBFOA has been proposed for the trajectory planning of robotic manipulators by introducing adaptive factor and elite-preservation strategy. A, bio-inspired interpolation algorithm Tau-J* with high-order IGM has been designed to generate trajectories between the control points obtained by IBFOA. The advantages of the proposed method can be concluded that the calculation burden would be alleviated, facilitating the compliant collision-free trajectory planning to be obtained. The simulation results demonstrate that the proposed bio-inspired trajectory planning method has superiority in stability, speed of convergence, and quality of solutions. However, it possesses some disadvantages. First, some parameters in the proposed method should be manually chosen. Second, the computation time is too long for trajectory planning in a dynamic environment. Regarding the future work, a criterion will be developed to determine the best number of control points, the fast collision detection algorithm will be designed to promote the cost function calculation using the MoveIt collision checking module, the other behaviors of BFOA will be further improved, and the effectiveness will be analyzed by performing statistical tests [42,43,44,45].
Acknowledgments
This work was supported by the National Natural Science Foundation of China (Grant No. 61773351), and the Program for Science & Technology Innovation Talents in Universities of Henan Province (Grant No. 20HASTIT031).
Conflict of interest
The authors declare that they have no conflict of interest.










 DownLoad:
DownLoad: