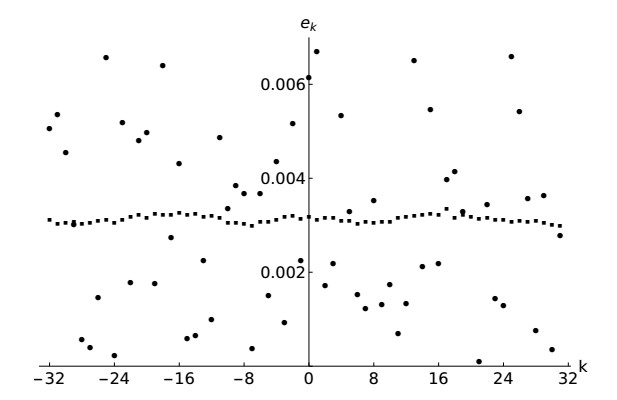
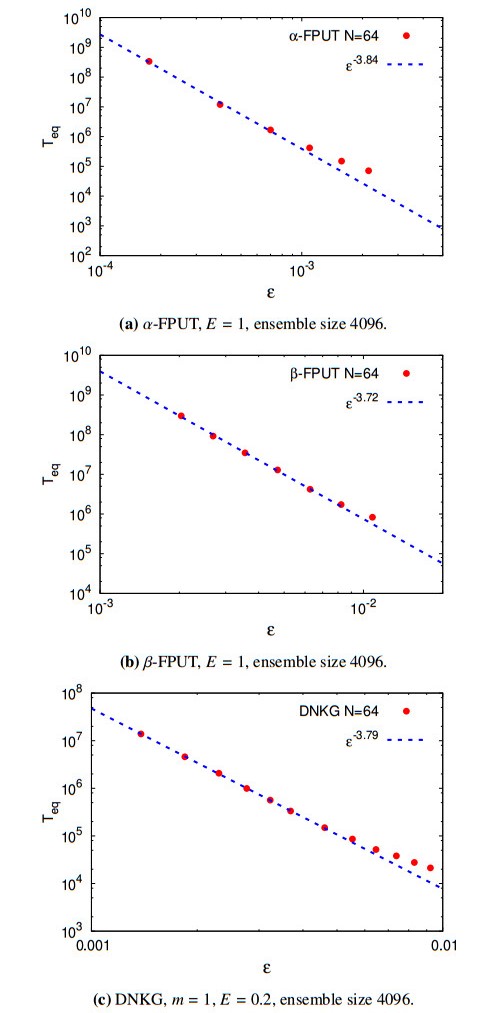
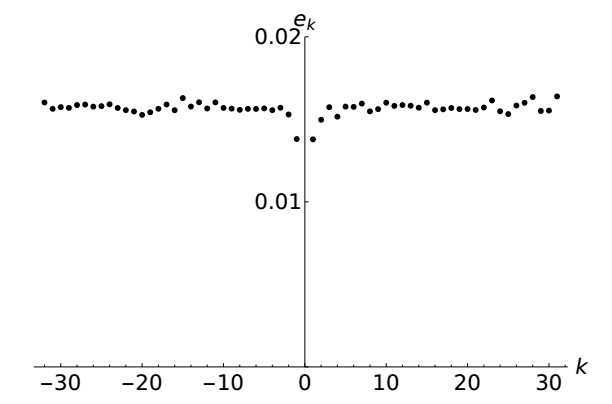
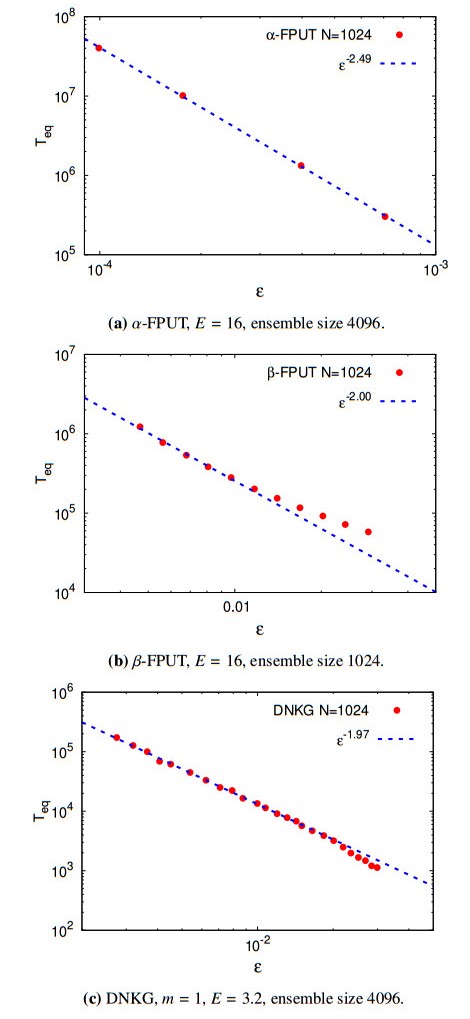
Assuming that resonances play a major role in the transfer of energy among the Fourier modes, we apply the Wave Turbulence theory to describe the dynamics on nonlinear one-dimensional chains. We consider α and β Fermi-Pasta-Ulam-Tsingou (FPUT) systems, and the discrete nonlinear Klein-Gordon chain. We consider both the thermodynamic limit and the discrete regime and we conjecture that all the systems thermalize for large times, and that the equipartition time scales as a power-law of the strength of the nonlinearity, at least for a range of values of the nonlinear parameter. We perform state of the art numerical simulations and show that the results are mostly consistent with theoretical predictions. Some observed discrepancies are discussed. We suggest that the route to thermalization, based on the presence of exact resonance, has universal features. Moreover, a by-product of our analysis is the asymptotic integrability, up to four wave interactions, of the discrete nonlinear Klein-Gordon chain.
1.
Introduction
An increase of the mean surface air temperature (SAT) presents the most prominent evidence of the present-day climate change (climate warming) both on global and local scales [1,2,3,4]. However, climate changes manifest themselves not only in the evolution of mean climate characteristics, but also in the changes of the climate variability and in the occurrence of climate extremes. Potential intensification of the anthropogenic forcing influences thus not only the climate state but becomes involved in the variability and instability of weather and climate. The precise knowledge of the air temperature variability and of the frequency of the occurrences of temperature extremes may be to some degree even more crucial than the proper impact of the gradual increase of the mean air temperature [5,6,7]. Especially the sudden temperature extremes can trigger subsequent climatic and natural events that consequently endanger various sectors of life (e.g. strongly variable precipitation, floods, rising sea level, warmer water temperatures, effect on plant development, etc.). All these events have serious consequences on human every-day-life and on the difficulty of the society adaptation to the unexpected intense weather changes [8].
In the last dozen years numerous investigations focused on the ongoing changes in air temperature variability on different time scales [9,10,11]. Previously such studies were based on the global gridded SAT data sets. However, in the last two or three decades the warming trend and the related climatic changes have become so strong that they become detectable in many local weather stations. The climate change studies at the regional level provide more detailed picture as they facilitate the possibility to understand and compare the local specific manifestations [12,13,14,15]. While the regionally detected warming trends are generally similar, the temperature variability exhibits a more diverse pattern with extensive regions with either positive and/or negative climate variability trends. E.g. Xu et al. [15] analyzed the variability of different daily climatic indices (including air temperatures) using ~50-years long high spatial resolution data set in China and found that the daily variability of climate was higher in North China than in South China. On the other hand, Huntingford et al. [16] argued for no increase in global temperature variability even if annual temperature variations show noticeable geographical variations. Scale differences (annual, seasonal, daily) and especially methodological differences between various studies represent additional problem because some of the obtained results are difficult to be compared. Some researchers perform the detection of variability by generally simple statistics like comparing the mean values and their variance [14,17,18], while others prefer more advanced statistical methods, like the N-point change method [19,20,21] or the fractal dimensional analysis [15]. Geographical complexity of the variability pattern and the methodological differences in its detection have produced ongoing serious debates in the interpretation of the results [22] but have inspired numerical research attempts for a broader variability assessment all over the world.
In the present work we have tried to investigate the SAT variability in the temperature-time series data obtained at the observation station Prague-Sporilov (the Czech Republic) in years 2003–2016. We continue the initial similar studies which focused on temperature record 1994–2001. We described that climate systems are variable on all time scales and that their evolution could be better understood when the insight was aimed not only on the changes in mean characteristics, but the climate variability and climate extremes were considered [20]. The interpretation of the Sporilov data were completed and compared with the results of the long-term observation of the Prague Klementinum station to confirm the Prague-Sporilov results.
2.
Data
2.1. Sporilov data
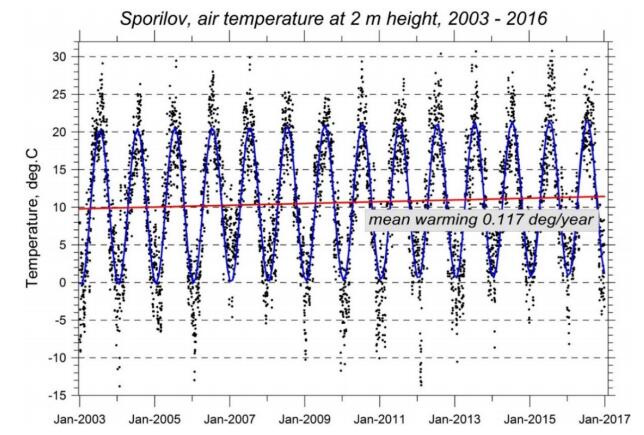
Daily Average Temperatures (DAT) were calculated from the recorded SAT series measured at 2 m height at the Geothermal Climate Change Observatory (GCCO) Sporilov, Prague (50°02.43' N, 14°28.54x E, 275 m a.s.l.). The experiment started in 1992 when the GCCO was built as a part of the long-term paleoclimate project to understand the mechanism of the downward propagation of the ground surface temperature signal into shallow subsurface [23,24,25]. The DAT used here are a part of observational material covering the time interval 2003–2016 (Figure 1) and the present interpretation continues the previous similar studies [20]. Original data were recorded by a 16-channel data logger M4016 [26]; the proper temperature sensor (platinum Pt1000, four-wire mode) located in a waterproof tube is placed on the top of the 2 m long rod. The 5-minutes original input data were stored and hourly means computed to interpret daily variations and further computed daily means when describing the inter-annual variation patterns. Battery failures, occasional sensor failures, and unstable voltage inputs in the data logger unfortunately disrupted the compactness of the registration record. General data coverage over the whole registration period varied between 96 and 97%. No serious attempt can be made to statistically improve the observed 5-min data series by infilling the existing gaps. However, the entire duration of the whole 14-year-long observational interval and its 96% data coverage is a certain guarantee to identify the obtained variability results. In contrast to the previous work [20], when the variability was investigated in the temperature time series measured between 1994–2001 and the calculation was performed for surface (z = 0 m) air temperatures data averaged for 6-hour and for 24-hour intervals, now we preferred air temperature at 2 m height and have focused on daily means, to be able to compare the GCCO-Sporilov results with the data from the Prague-Klementinum record (see further). The GCCO-site, situated at the campus of the Institute of Geophysics, is located on the top of the local gentle crest framing the southern periphery of Prague. The area can be characterized as a surviving island of typical suburban houses, with a plenty of greenery, on the outskirts of the quickly expanding robust development of the growing city.
2.2. Klementinum data
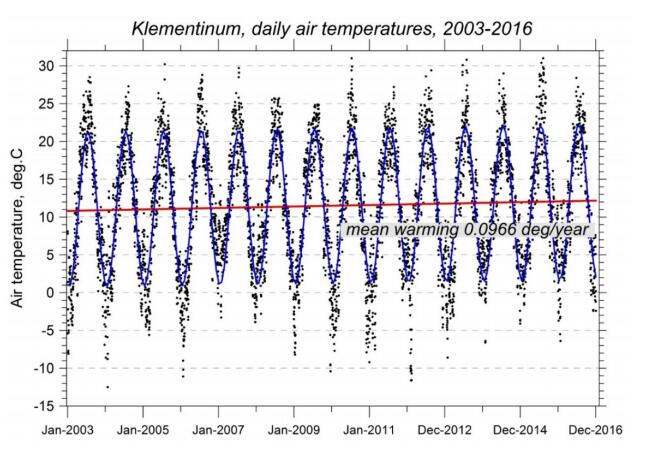
The Klementinum station (50°05.20' N, 14°24.98' E, 191 m a.s.l.) is the oldest Czech meteorological observatory, with the systematic air temperature measurements started in 1775 [27]. Contrary to Sporilov site, the station is located in the very downtown of Prague and may serve to demonstrate the influence of the urban environment. Even when in the past its instrumentation underwent several modifications, the almost 250-year-long observational record presents valuable scientific material. Here for practical purpose we have analyzed only the comparable time interval as provided the Sporilov station, namely years 2003–2016 (Figure 2), and added few more findings analyzing longer time spans 1900–2016 and 1970–2016. In addition to the daily averaged temperatures (DAT) the results include also the daily maximum Tmax and daily minimum Tmin temperatures.
3.
Results
3.1. Warming trends
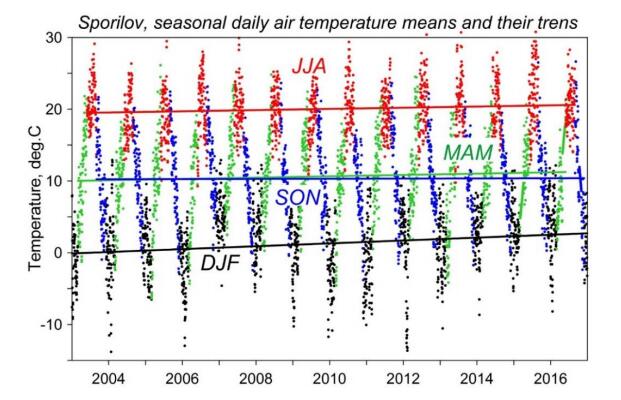
Numerous observations have shown that during the second half of the 20th century the mean SAT has been increasing on daily, monthly and annual scales overall in Europe [1,28,29] and that since the late 1970s the mean temperature increase has been substantially accelerated. This phenomenon is observable not only in the SAT series themselves but on the seasonal scales and is especially evident in the summer temperatures [30]. Figure 3 shows seasonal linear trends calculated for the Prague-Sporilov temperature series, similar calculations were done for the Klementinum station. It is interesting to mention that the most intensive warming always corresponds to the winter season. The spring and summer warming are approx. two-three times lower and the lowest warming rate for Sporilov corresponds to the fall season (more than an order lower than the winter). The difference between summer and winter temperatures reduces the decrease of climate variability on the annual scale and produces a shift in the duration of the individual seasons (spring comes earlier and cold weather/frosts are arriving later in the fall). Table 1 summarizes the parameters of the linear trends calculated for the interval 2003–2016 of both investigated stations. As seen, Klementinum daily air temperature averages are by about 0.5 to 1 K higher that Sporilov averages (the fact that can be attributed to the urban heat island effect, UHI), but the Sporilov warming rate is slightly higher.
The UHI can noticeably affect the measured air temperatures (both their trends and fluctuations) and its intensity need not be constant, but depends on various factors related to town development dynamics, such as population and building growth, increasing heat production, energy consumption, etc. Detailed investigations of the UHI effect for the Prague-Klementinum station were performed [31,32]. The former work analyzed daily mean temperatures measured between 1921–1995 at 17 rural stations located within 40 km range from Prague-Klementinum. The later work was based on the daily minimum temperatures measured during 1961–1990 at 3 stations situated in the 50 km neighbourhood of the Klementinum station. The Prague UHI intensity has shown progressive intensification since 1922 (especially from mid 40's to mid 60's), and certain stagnation after 60s. The trend was practically zero between 1980–1995. The highest daily mean temperature increase was observed in winter and spring (0.06 K/decade) and the smallest, practically insignificant (0.01 K/decade) in summer. The annual warming was ~0.05 K/decade. The UHI increase is thus 20–25 times lower than the air temperature warming trends presented in Table 1 and do not exceed the uncertainty of warming trend. The elimination of the UHI effect from the warming trends will not markedly change the observed linear trends. This is clearly visible in Figure 5 [32]), where measured temperatures and temperatures reduced by the intensification of the UHI according to the linear trend in 1922–1995 practically coincide. The UHI intensification trend for the daily minimum temperatures is somewhat higher than calculated for daily mean temperatures (0.12 K/decade within 1961–1990 period [31]). However, it is still an order of magnitude lower than that presented in Table 1 and is smaller than the uncertainty of calculated warming trend.
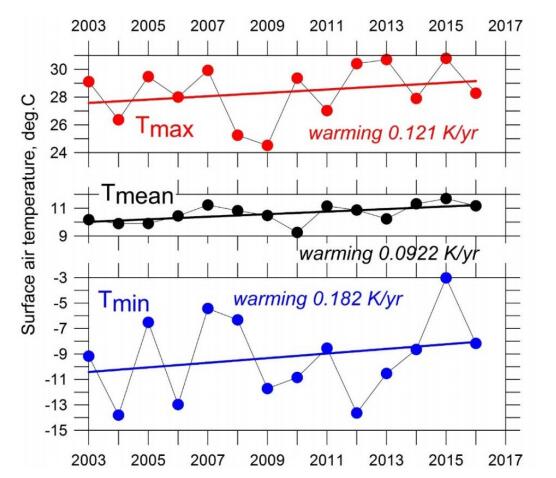
The temperature trends exhibit similar patterns on the annual scale. Figure 4 shows annual mean temperatures as well as maximum (hottest day) and minimum (coldest day) daily temperatures for the period 2003–2016 at the Sporilov station. The range of annual daily temperature variations fluctuates between 32.3–44.0 K. Positive/warming trends are characteristic for all three variables. However, an increase of annual coldest day temperature is ~1.5 times faster than the temperature of the annual hottest day. It hints that the climate faster becomes less cold rather than getting warmer. Similar conclusion is presented in the work by Alexander et al. [33].
Table 2 presents similar results related to several longer periods calculated for the Klementinum station. Warming trends and average daily temperatures are growing with time and this growth increased sharply in the last few decades. The present mean temperature has increased by 3.2 K compared with year 1900, when one third of this increase occurred since year 2000. It may be interesting to mention that according to the National Climate Assessment (NCA) the average temperature on the USA territory has increased by 1.3–1.9 K since 1895 and most of this increase is also due to the last couple decades [34]. The observed Klementinum temperature increase is thus 1.7 times greater. Such increase is in a good agreement with similar studies in Western Europe where last few decades have been getting warmer faster than the global average and far stronger than predicted by the standard models based on the anthropogenic greenhouse gas increases [12,35,36].
Both daily minimum and daily maximum temperatures have been increasing with time as well. The calculated trends are generally similar for mean, maximum and minimum temperatures and exhibit an increase on both monthly and annual scales. The magnitudes of both trends are comparable with the rate of the daily average temperature warming. Noticeable feature is that minimum daily temperatures (Tmin) increase approx. 30% faster than daily maxima (Tmax). This result in a progressive decrease of the diurnal temperature range (DTR), and decrease in the intra-day variability and daily temperatures have been getting warmer. The observed evidence, namely a faster increase in the diurnal minimum temperature compared with the diurnal maximum temperature in the last 50 years leading to a decrease in the DTR is consistent with the mean global trend of the DTR reducing [37,38,39]. It should be stressed, however, that the DTR trend course is not stable, but to some degree variable and may incorporate temporally rate variation (slowdown) or even reversals to the negative trend in recent decades [40].
The processes responsible for the DTR decrease are still poorly apparent as well as the role of the potential anthropogenic forcing. Some authors have argued that shortwave radiation could have a strong and sufficiently homogeneous effect to change DTR on a global scale [41,42]. Anyhow, as shown above, the decreasing DTR trend represents an exact and easily identifiable characteristic of the recent climate change, and its detection in the forcing mechanisms of the present-day climate change (in particular in its potential anthropogenic component) may be important.
3.2. Variability
Variability indicates the degree of fluctuation and uncertainty of the temperature change process. One of the remarkable aspects of the global warming is the fact that the global mean temperature (SAT) increase may be accompanied by certain temperature variability decrease. Climate simulations studies predict not only climate warming, but also a general decrease in climate variability [19,43,44]. It was recognized that the variability decreases on average, it was also pointed out that these trends are roughly constant or linear in time. The variability trend may be likewise frequency dependent [20].
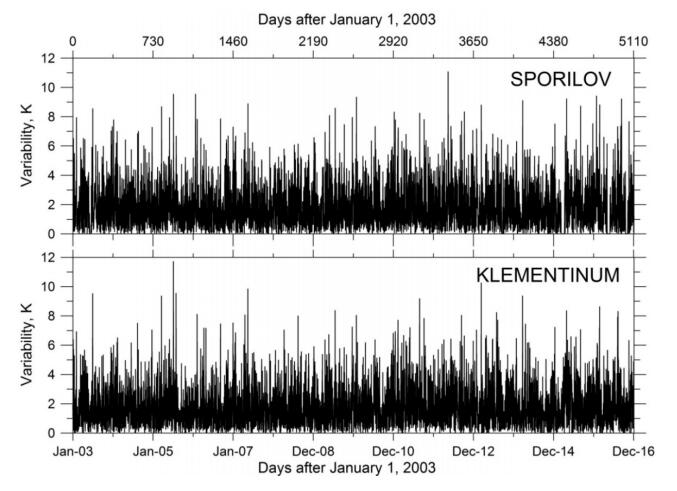
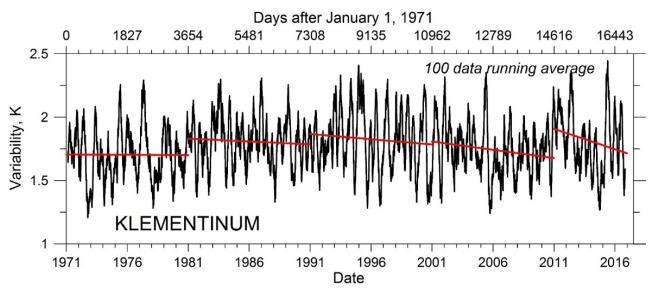
There are several ways to detect variability changes. Here we used so-called N-point change method introduced in detail earlier [20,21]. The measured data series were converted into temperature anomalies by means of detrending and removing the annual wave. Figure 5 presents variability patterns calculated for the daily temperature averages for both Prague-Sporilov site and Klementinum station for the 2003–2016 period. The variability shows an insignificant decreasing trend of −0.003 K/yr that is by an order of magnitude lower than the value −0.038 ± 0.002 K/yr obtained earlier for this site for the 1994–2001 period [20]. The above Sporilov variability trends are quite similar to the variability trends for the Prague-Klementinum data, namely −0.019 K/yr and/or −0.005 K/yr for the 1994–2001 and 2003–2016 period, respectively. Figure 6 and Table 3 summarizes the variability trends calculated from the Prague-Klementinum data for the 10-years intervals within 1971–2016 period. As seen, all trends are negative (variability decreases) and this decrease accelerates with time. This decrease was practically negligible in the beginning of the studied period and has grown by more than two orders of magnitude within last about 5 decades.
The detected decreasing trend exists only on an average. Its persistency often breaks off both in the value as well as in the sign of the variability change. On the shorter time scales the calculated slope value strongly depends on the length and the beginning of an investigated time interval. The positive slope values were obtained for the Prague-Sporilov data for the spring-summer time intervals in year 2003 and above all in year 2015. Noticeable changes in the variability generally coincided with more pronounced temperature extremes. E.g., two reversals in the variability change mentioned above can be attributed to the warming occurred due to record-breaking European heat waves [36,45].
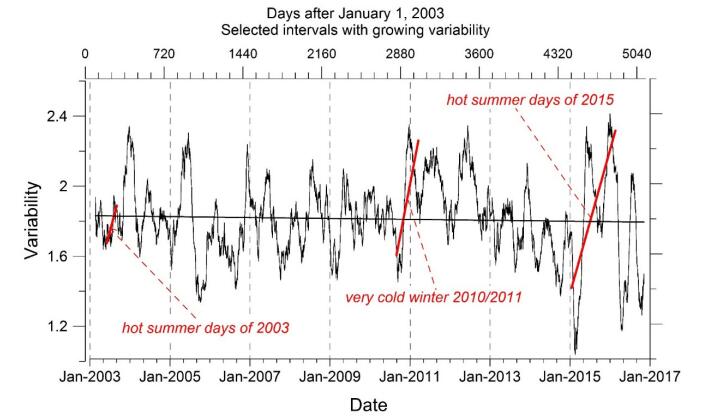
3.3. Changing variability trends
The variability trends calculated for data measured at both Sporilov and Klementinum sites exhibit an insignificant decrease within the 2003–2016 time interval. However, it should be emphasized, that such trend corresponds to the calculated value only when calculated for the whole interval as entirety. This fact may lose its validity when calculation is applied to another time section (Figure 7). On a shorter time scale the calculated slope value may strongly depend on the length and the beginning of the selected time interval. In our case, positive slope values were obtained for the 2003 spring-summer time interval and especially for the 2015 summer. Such noticeable changes in the variability generally coincide with pronounced temperature extremes. For example, the two above mentioned reversals in the variability change can be undoubtedly attributed to the periods of a sequence of exceptionally hot days (European heat waves) [36,45].
1. The record breaking European temperature heat wave occurred in the summer of 2003 (approx. from June to mid-August), when temperatures were about 20–30 percent above average. It has affected much of Western Europe, but was generally concentrated in England, France and Spain. Temperatures were as high as 47 ℃ in the south of Portugal and the heat wave had extremely hard human consequences [46,47].
2. An unusually strong and prolonged heat waves occurred across Europe from late June to mid-September 2015 [48]. The record temperatures above 40 ℃ have been recorded in several locations (the Mediterranean coast, south-western, central and south-eastern Europe; see e.g. [49]). The maximum daily temperatures approached to about 37 ℃ during both 2003 and 2015 heat waves in Prague.
3.4. Temperature extremes
The past 2–3 decades of the 20th Century and the beginning of the 21st Century have been characterized not only by the global temperature increase, but also by an increased frequency of extreme events such as heat/cold waves, heavy rainfall and floods, droughts, etc. Numerous climatic models predict more frequent occurrence of extreme events [50]. An increased occurrence of weather extremes has acquired a high social resonance that initiated an intensive research activity to quantify the variability, frequency and possible evolution of observed extreme events. For example, Nicholls [51] reported, that extreme weather values may work as good indicators of coming climate changes. Weather extremes are relatively rare; a proper assessing of their occurrence creates certain problems. The most frequently used methods are based on probability characteristics and the counts of days exceeding a certain specified threshold value. To not engage only with a few individual events, a list of indices for extreme temperature phenomena has been worked out in the frames by the CLIVAR project of the World Climate Research Program [52]. The guidelines for the recommended temperature-based CLIVAR indices were presented by Klein Tank [53].
Numerous evidences support that most global land areas have experienced significant warming of both maximum and minimum temperature extremes during at least the second half of the 20th Century. Changes in the occurrence of cold and warm days are not unambiguous. On the whole, rapid warming observed in the last decades was accompanied by increases in summer temperature extremes over Western Europe while the number of unusually cold days has generally decreased [54]. The IPCC AR4 Climate Model calculations have shown that since the middle of the 20th Century the indices of cold extremes had likely decreased and indices of warm extremes increased at the most of global land areas [55]. Similar conclusions were presented in the review work by Meehl et al.[9]. Number of days with unusually cold winter temperatures (particularly extremely cold nights) became less common. This phenomenon is consistent with the general climate warming. In the first approximation the observed trends in the SAT extremes are often interpreted as a simple shift of the total temperature distribution towards higher temperatures [56].
On the other hand, the trends of the extreme indices based on 60 European weather stations located within the 40–70°N zone stretching from Great Britain to Russia have very local character [57,58]. It was also shown that in spite of the fact that the individual extremely cold months (ECM) represent a frequent phenomenon in Europe, the winter ECMs were observed only at 10 of all investigated weather stations within the 1951–2000 yr period and only at 25 and 27 stations during 2001–2006 and 2007–2011 periods, respectively. The lowest number of ECMs occurred in the 1991–2000 decade, but their frequency and the territorial extent has started to increase since the beginning of the 21th century [57].
Europe experienced almost similar number of severe winters and the heat waves in the last decades. There were 11 extremely cold winters (ECW) during 1951/52–1979/80 period and another 7 ECWs during 1980/81–2009/2010 interval (the number of ECWs somewhat diminished, but not significantly [58]. At the same periods, the numbers of heat waves occurring in Europe were 5 and 9, respectively [59]. The most recent European heat wave occurred on summer 2015, in Central Europe it started at the end of July and continued during the first ten days of August.
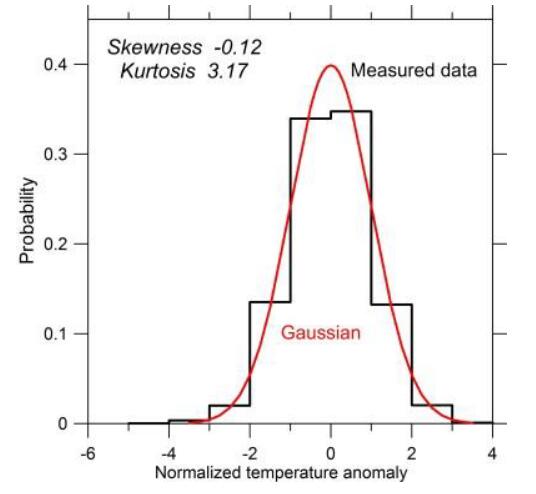
As Prague belongs to the temperate climate zone, unusually warm as well as unusually cold days are rare. Changes in climate variability and extremes can be visualized in relation to changes in the probability distribution. Figure 8 shows the probability distribution of the temperature excess values (i.e. the differences between detrended observed temperature data and the Fourier sinusoidal representation applied on Sporilov 2003–2016 record). While the previously investigated 1994–2001 data exhibited a right skewed distribution and a more heavy right tail [20], the 2003–2016 probability distribution is close to the normal (Gaussian) distribution. A prominent feature of the 1994–2001 temperature record was the prevalence of extremes in warm seasons, while the number of cold season extremes was practically insignificant. The present disappearance of the right skewness and the shift to the normal distribution can be explained by the increase of cold extremes. The minimal temperature anomaly was a little less than −10 K during 1994–2001 period and the anomaly values lower or equal to −10 K occurred only once for the investigated 8 years. During 2003–2016 period the minimal anomaly equals already to −15.6 K and the number of days with the values equal or lower than −10 K occurred already 29 times. Similar tendency can be observed at the Prague-Klementinum station (Table 4), the number of both warm and cold extremes increases with time; however the number of cold extremes is growing faster. While the A2/A1 relation in seventh years was ~ 6, in the last decade it fell to ~3.
While the increase of number and the growth of the intensity of warm extremes is a general European phenomenon and can be attributed to the global warming trend and the corresponding increase of the hot days (>25 ℃), the reasons for the growth of cold extremes are so far not clear and need further explanation. The evolution of the number of cold extremes has a local character; Spinoni et al. [60] have investigated the heat and the cold waves in the Carpathian Region and have described different spatial patterns of heat and cold waves. While heat wave events exhibit a general increase in all investigated parameters, cold wave events show a decrease in the area west to the Carpathians and an increase in the area north–east to the Carpathians. In the south Italian high-altitude region Capozzi and Budillon [61] revealed a strong and significant positive trend in the last 40 years in heat waves frequency, intensity and duration, while cold wave events have exhibited a significant and positive trend only in their intensity.
For further investigations we have used the CLIVAR-recommended percentile-based and the absolute temperature indices. The four temperature percentile indices consider the coldest and warmest deciles for both maximum and minimum temperatures to evaluate the degree of extremes changing. Absolute indices represent maximum or minimum values within the season or within the year and reflect the longer time scale processes. Table 5 represents the CLIVAR-recommended indices based on the 10th and 90th percentiles of maximum and minimum daily temperatures recorded at Prague-Klementinum station. The 10th percentile is a temperature value such that at least 10% of the observations is less or equal to this value, while the rest of observations is greater than or equal to this value. Below we used the following abbreviations: Tmin 10p–Tmin below 10th percentile, Tmax 10p–Tmax below 10th percentile, Tmin 90p–Tmin above 90th percentile, Tmax 90p–Tmax above 90th percentile. The values lower than Tmin10p and/or Tmax10p usually arise at cold nights and cold days, while the values surpassing Tmin90p and Tmax90p are characteristic for the warm nights and warm days, respectively [33,60].
As seen, all calculated percentiles exhibit significant warming since at least the mid of the 20th century. The permanent warming is characteristic for both cold nights and cold days. The warming characteristic for warm nights and warm days has slowed down or practically stopped in the first two decades of the 21th century. Similar phenomenon is characteristic for the daily maximum temperatures. The maximum temperature observed in the 1971–1980 interval was 34.7 ℃, while in the last two intervals it equals to 37.3 and 37.6 º C, respectively. It is of interest, that at the present time such heat and/or cold extremes are short and rare in the temperate climate zone and can be regarded as synoptic rather than climatic events, unlikely they can seriously distort the characteristic pattern.
Absolute indices represent maximum or minimum values within a given time interval. They include maximum daily maximum temperature (TXx), maximum daily minimum temperature (TNx), minimum daily maximum temperature (TXn), minimum daily minimum temperature (TNn). The index TXx can be generally attributed to extremely warm day and TXn to the coldest day, while the TNn index corresponds to extremely cold night and TNx to the warmest night [62,63]. In the present work we calculated the absolute indices from maximum and minimum daily temperatures measured at the Klementinum Observatory. Table 6 summarizes the indices calculated for the 10-years long intervals.
The absolute temperature indices exhibit a similar growing pattern as other investigated indices. The maximum daily maximum temperature (TXx) increased by nearly 3 K (the hottest days became hotter) which represents the greatest change in the absolute temperature indices. Similar increase was obtained for the most of investigated regions on the global scale [62,64]. An interesting local feature is that the most of the temperature increase occurred after 1980 and further has significantly slowed down. Similar, but somewhat weaker, warming are found for coldest days (TXn) and warmest nights (TNx), the process which is characteristic over the most of Europe [64].
The TNn index variations exhibit certain unusual regional detail. Donat et al. [64] have investigated the behavior of the absolute indices on the global scale and found that the warming trends are generally stronger for the coldest night temperatures than for indices calculated for warmest days. Significant increase of the TNn values was detected at the 70% of the grid boxes from 1951 to 2010, while significant decrease was found only in 3% of investigated data. The TNn increase was particularly strong over large parts of Asia. Globally averaged TNn temperature has increased by about 3 K in the last 1951–2010 period. According to Alexander et al. [33] the minimum daily minimum temperature (TNn) increased by ~ 5 K between 1951 and 2003 that represents the greatest change in the absolute temperature indices. However above authors have noted that this growth is dominated by the very large negative anomalies in the 1950s when there was increased sampling uncertainty. Our TNn indices show up to ~ 3–5 K differences between neighboring decadal values, but do not exhibit any significant warming/cooling trend.
4.
Concluding remarks
In the present work we have revealed some important features describing the daily average air temperature (DAT) changes, variability and their temporal evolution at the Prague-Sporilov site. The variability and trends in daily near-surface air temperatures recorded during the 2003–2016 period were analyzed. The results were compared with the findings of our previous work covering the earlier 1994–2001 period [20,21]. We compared above data with the longer DAT, Tmax and Tmin series measured at the Prague-Klementinum Station. The results of both stations have shown very similar changes in the investigated statistical parameters as well as in the temporal trends. Such similarity increases the reliability of the obtained results.
The following principal conclusions can be drawn:
(1) The results demonstrated increasing warming trends for all investigated temperature series as well as decreasing trends in the diurnal temperature range (DTR) that hints a decrease of intra-daily temperature variability.
(2) The results revealed the generally reducing temperature variability. However, the velocity of the variability decrease has slowed down by approx. an order of magnitude in comparison with the previously investigated 1994–2001 period. It was also recognized that the persistence of detected processes exists on average, e.g. in the annual scales, and may break down during shorter periods. The pattern of the variability changes during the 2003–2016 period is found to be more diverse than in our earlier studies [20].
(3) The study reveals that the occurrence of both hottest and coldest extremes have increased during the investigated period at both stations. While an increase of the hot extremes represents a generally global feature, an increase of cold extremes is a local phenomenon. However, as the frequency of extreme days is low, they have no significant influence on most of detected trends.
Acknowledgement
This work was supported by the research infrastructure RINGEN co-funded by the Operational Program "Research, Development and Education" (CZ.02.1.01/0.0/0.0/16_013/0001792) and by the Project LM2015079 CzechGeo/EPOS, both provided by the Ministry of Education, Youth and Sports of the Czech Republic. Special thanks are due to an anonymous reviewer who read the original text and offered valuable comments.
Conflict of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: