Climate-mediated activity of the Javan Slow Loris, Nycticebus javanicus

1.   Introduction

Labour and delivery is routinely monitored electronically with sensors that measure and record maternal uterine pressure

(UP) and fetal heart rate (FHR), a procedure referred to as cardiotocography (CTG). The objective of this monitoring is to detect the fetus at substantial risk of hypoxic injury so that intervention can prevent its occurrence.

Clinicians' interpretation of intra-partum CTG signals relies on the temporary decreases in FHR (FHR decelerations) in response to uterine contractions. FHR decelerations are due mainly to two contraction-induced events: (1) umbilical-cord compression and (2) a decrease in oxygen delivery through an impaired utero-placental unit. There is general consensus that deceleration depth, frequency and timing with respect to contractions are indicators of both the insult and the ability of the fetus to withstand it. In particular, later timing of decelerations, referred to as "late decelerations" are generally less reassuring to clinicians than the more innocuous (and rare) "early decelerations".

Assessing synchronization of the cardiotocography (CTG) signals uterine pressure (UP) and fetal heart rate (FHR) is a challenge both because of signal non-stationarity and noise in the form of signal discontinuities and maternal heart rate interference. As labour progress the maternal and fetal states evolve: contractions get more frequent and the cumulative effect of reduced oxygen transfer means that the fetus can experience increasing levels of hypoxia, progressing from respiratory to metabolic acidosis and finally to direct myocardial depression. Measurements under these conditions show that pH levels lower and base deficit increases: the buffer stores of the fetus which allow it to combat the increased acidosis become depleted ^[1]. Under such conditions, the state of the fetus as indicated by the FHR is quite non-stationary during labour and delivery.

We have characterized the stimulus-response system of UP and FHR using system identification (SI)^[2]. However, obtaining delay estimates from SI involved lengthy and iterative modelling with a sweep of candidate delays. It would be helpful to have a better mechanism to estimate the delay before estimating the SI models. It would also be helpful to compare SI models with other synchronization estimates. In this study we used the model-free approaches of mutual information and transfer entropy to estimate synchronization and delays using both FHR and UP signals.

While there have been numerous studies examining differences in entropy measures in fetal heart rate variability (e.g., the use of approximate entropy in ^[3]), few fetal studies have applied mutual entropy or transfer entropy to this domain. Authors in ^[4] computed the transfer entropy of maternal and fetal heart rates using single lag analysis.

They calculated TE on maternal and fetal heart rates (derived from ECG) during gestation from 31 weeks onward. They observed a decrease in TE from fetus to mother over time and an increase in TE from mother to fetus over time. Delays in the M $ \rightarrow $ F direction were estimated by TE analysis to be on the order of 5$ \, $s. We used mutual entropy in ^[5] to examine CTG synchronization and extend that analysis to more robust mutual information estimates and to transfer entropy in this paper.

2.   Data

We used CTG from singleton, term pregnancies having no known congenital malformations, with $ \ge $ 3 hours of tracing just prior to delivery. The CTG records for this study consisted of 42 pathological (P), 104 metabolic acidotic (MA) and 110 normal (N) fetuses. The pathological fetuses were severe enough to have confirmed evidence of hypoxic ischemic encephalopathy ($ < 1^{st} $ percentile of fetuses). The metabolic acidotic fetuses were defined by base deficit $ \ge $ 12 mmol/L and with no apparent neurological injury (5$ ^{th} $ percentile of fetuses). It would be advantageous to identify these MA fetuses because they can be considered "close calls", where appropriate intervention can occur prior to the onset of injury. The cesarean section rates for the N and MA cases were 19.2% and 30% respectively, while the rate for the P cases was not consistently reported in our database. Data were provided from two US hospitals in compliance with institutional regulations.

3.   Methods

3.1.   Preprocessing

The CTG data was recorded in a clinical setting, so it was subject to specific types of noise. The loss of sensor contact can temporarily interrupt the UP or FHR signals, and interference from the (much lower) maternal heart rate can corrupt the FHR. These both appeared in the signal as a sharp drop to much lower amplitude followed by a sharp signal restoration. As described in ^[6], we preprocessed the data to bridge interruptions less than 15$ \, $s with linear interpolation. UP and FHR with signal loss greater than 15$ \, $s were not included in the processed epochs and were removed from consideration.

As in ^[2], we detrended the signals by a high-pass FIR filter with sufficient extent (1991 filter coefficients) to pass a long contraction or deceleration without incurring excessive filter delay (there were 1991 coefficients). We chose a filter with a cutoff frequency of $ \frac{1}{220 s} = 4.5\times10^{-3}\, $ Hz as a compromise between these competing demands. Finally, we decimated the UP and FHR signals to 0.25 Hz using an anti-aliasing low-pass filter with a cutoff frequency of 0.125$ \, $Hz, before downsampling by 16. This was done to reduce the computational load of the entropy estimates described below.

Longer epochs generally result in superior numerical estimates while being more subject to the effects of non-stationarity. Following ^[2], we endeavoured to balance these competing effects by extracted 20-min epochs with 10-min overlap between successive epochs. This epoch length typically spanned several UP contraction-FHR deceleration pairs.

To address the issue of non-stationarity we extracted 20-min epochs with 10-min overlap between successive epochs. This epoch length typically spanned several UP contraction-FHR deceleration pairs. Epochs with insufficient valid signal were discarded.

3.2.   Mutual Information

The mutual information $ MI(X; Y) $ of random variables $ X $ and $ Y $ is defined as

where $ H(X) $ is the entropy of $ X $ and $ H(X|Y) = H(X, Y) - H(Y) $ is the conditional entropy of $ X $ given $ Y $. Mutual information is therefore the amount of uncertainty (i.e., entropy) about $ Y $ that is resolved by observing $ X $. Reduction of uncertainty is equivalent to information ^[7]. Mutual information is symmetrical: $ MI(X; Y) = MI(Y; X) $. In this work we use the natural logarithm, giving units of nats.

In a time-series context, following the notation of ^[8], the mutual information can be reformulated as

Here $ X $ and $ Y $ refer to the mutual information between $ Y $ at time instant $ t $, $ Y_t $ and the state $ \mathbf{X_{t- \tau }^{d_X}} $, encapsulates the recent past of $ X $, where $ \tau > 0 $ is a time lag in the information transfer and the dimension $ \mathbf{d_X} $ is the number of the lags in the state influencing $ Y_t $. The dimension $ \mathbf{d_X} $ is data dependent and limited in size only by candidate set of time lags $ C $.

We calculated $ MI $ for the preprocessed UP and FHR signal pair $ u(t) $ and $ f(t) $. In previous work ^[5], we used binned estimates of the probability densities $ p(u) $, $ p(f) $ and $ p(u, f) $ in Eq 3.1. This binned approach restricted the delay search to a single lag, i.e., $ \mathbf{d_X} = 1 $, from the source signal $ u(t) $ that maximized $ MI(u(t-\tau), f) $. We repeated this calculation in this work, observing the time lag and value of the maximum $ MI $ over a range of possible UP-FHR alignments for each 20 min epoch. The candidate set $ C $ was the range of lags from -20 to 90 s (the negative lags are explained in the following paragraphs).

We chose these alignments to capture the widest range of reasonable physiological delays, empirically confirmed in ^[2]. We note also that UP is measured by tocography, which places a belt with a strain-gauge pressure sensor on the maternal abdomen. Because this pressure sensor is an indirect measure of intrauterine pressure ^[9], it may have an inherent mechanical delay, and the measured UP may reflect this with delays in onset and termination of contractions ^[2]. For this reason, we admitted negative alignments (i.e., -20 to 0 s).

In this work, we used a technique that admits multiple source lags to contribute to the $ MI $; that is, where $ \mathbf{d_X}\ge1 $. We computed this estimate using the Information Dynamics Toolkit (IDTxl) ^[10]. In accordance with the possible negative delay noted previously, we shifted the UP earlier by 20 s before estimating $ MI $. We subsequently adjusted the lags analysis to account for this shift. Additionally, given the non-Gaussian nature of the UP and FHR distributions, we used the IDTxl implementation of the more robust $ k $-nearest-neighbour algorithm ^[11] for the density estimates of Eq 3.1, with $ k $ set to the default value of 4. Finally, we tested the $ MI $ estimates for significance using 200 realizations of surrogate target data (i.e., FHR), that were generated by IDTxl by random permutations of the epoch samples ($ p < 0.05 $ was considered significant). That is, if the MI with the UP corresponding to the measured FHR is greater than the value of MI of at least 190 other FHR permutations, it is significant. The surrogate testing ensures that spurious interactions in the data have a low probability (i.e., 5%) of being considered significant.

IDTxl chooses an embedding set $ Z $ of $ \mathbf{d_X} $ delays in a greedy fashion, following ^[12]. At each step, the delay from a candidate set $ C $ generating the highest MI and satisfying statistical significance is added to set $ Z $ (and removed from $ C $). The search is repeated using the reduced set $ C $ to add additional delays to $ Z $ that increase the estimated MI, subject to significance testing. This continues until adding more delays to the set fails to significantly increase the MI.

3.3.   Transfer Entropy

Schreiber introduced the concept of conditional mutual information, also known as transfer entropy $ TE $) to address the question "What information does the past of X provide about the future of Y, that the past of Y did not already provide?" ^[13]. The transfer entropy from random variable $ X $ to $ Y $ is denoted $ TE(X \rightarrow Y) $ and is not symmetrical, but directed: In general, $ TE(X \rightarrow Y) \neq TE(Y \rightarrow X) $. In the time-series context, it is defined as:

Like mutual information, transfer entropy measures the amount of uncertainty about $ Y $ that is resolved by observing the state $ \mathbf{X_{t- \tau }^{d_X}} $, but it also removes the influence of the redundancy of the state $ \mathbf{Y_{t-1}^{d_Y}} $ on $ Y $. This can decode influences of $ X $ on $ Y $ that are masked in the $ MI $ calculation. While this formulation of $ TE $ allows a variable transfer delay of $ \tau $ in the source $ X $ (as in Eq 3.2 for $ MI $), it fixes the target lag to 1 to fulfill what is referred to as $ TE $ self prediction optimality ^[14], that is, all the recent past of $ Y $ is considered in the state $ \mathbf{Y_{t-1}^{d_Y}} $. For $ TE $, source and target have variable state dimensions, $ \mathbf{d_X} $ and $ \mathbf{d_Y} $, respectively.

Wibral offers a formal proof that the $ TE $ is maximized when $ \tau = \delta $, the true interaction delay ^[14]. This proof of identifiability of the true delay in the information transfer holds strictly for the case of zero observation noise. However, with numerous numerical simulations with nonlinear dynamical systems, they demonstrate that the $ TE $ precision degrades gracefully under conditions of decreasing SNR.

3.4.   Statistical analysis

For each 20-min epoch of each CTG recording, we calculated the binned version of MI and the nearest-neighbour versions of $ MI $ and $ TE $ and their associated lag(s). We assessed the differences of the $ MI $, $ TE $ and their associated delays for the three fetal classes N, MA and P at each epoch over the last three hours of labour and delivery. We found that a single lag often dominated contributions to $ MI $ and $ TE $ and so we summarized lag reporting with these single values. The Kolgomorov-Smirnov (KS) test was used to test the null hypothesis that the distributions of pairwise-selected classes were the same, using the significance threshold $ p < 0.05 $.

In addition to the full-epoch estimates, we observed "local" (i.e., "instantaneous") $ MI $ and $ TE $ estimates $ mi(t) $ and $ te(t) $ provided by IdTxl that indicate the relative coupling of individual samples within the epoch. As discussed in ^[15], with sufficient data, overall MI and TE values are non-negative, but these local estimates can be negative and are referred to as "misinformation”, corresponding to the opposite of coupling (i.e., indicating an element of surprise between input and output).

In the results below, we refer to the binned estimates of $ MI $ as $ MI_b $ and the Kraskov estimates of $ MI $ as $ MI_k $. We refer to the single delay with the maximal contribution to $ MI_k $, that is, $ \text{arg}\ \text{max}_\tau\ MI_k(\tau) $ as $ \tau_{MI_k\_max} $. We refer to the overall TE with contributions from all significant lags as TE. We refer to the single delay with the maximal contribution to TE, that is $ \text{arg}\ \text{max}_\tau\ TE(\tau) $ as $ \tau_{TE\_max} $ and the $ TE $ contribution of that lag as $ TE_{max} $.

While all analysis was done using lag delays with the time unit of a 0.25 Hz sample, for clarity we convert these values to seconds in the subsequent time plots.

4.   Results

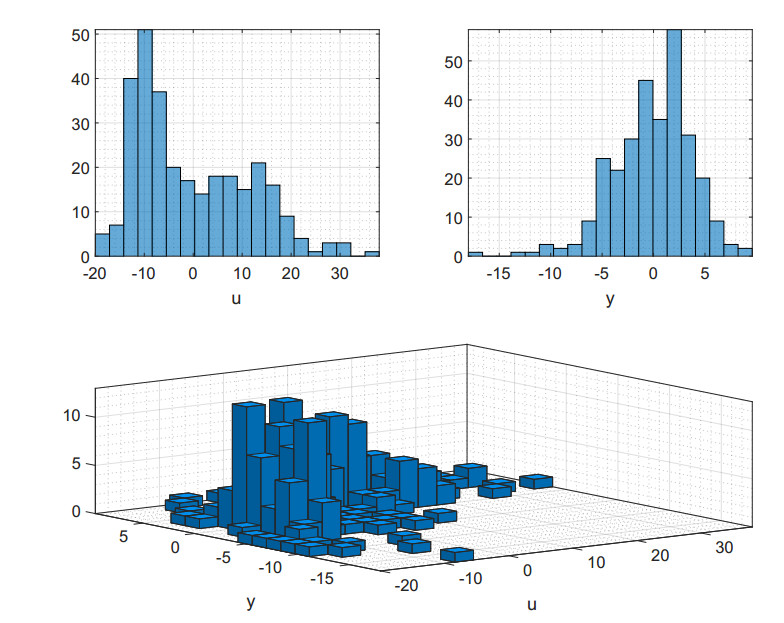
Figure 1 shows typical histograms of UP and FHR for a 20 min epoch. These approximations indicate that the univariate and joint densities are non-Gaussian, supporting the motivation to use the Kraskov density estimator.

Figure 1.  Histogram approximations to the univariate and joint densities of a typical UP (u) and FHR (y) CTG pair for a 20 minutes epoch.

DownLoad: Full-Size Img PowerPoint

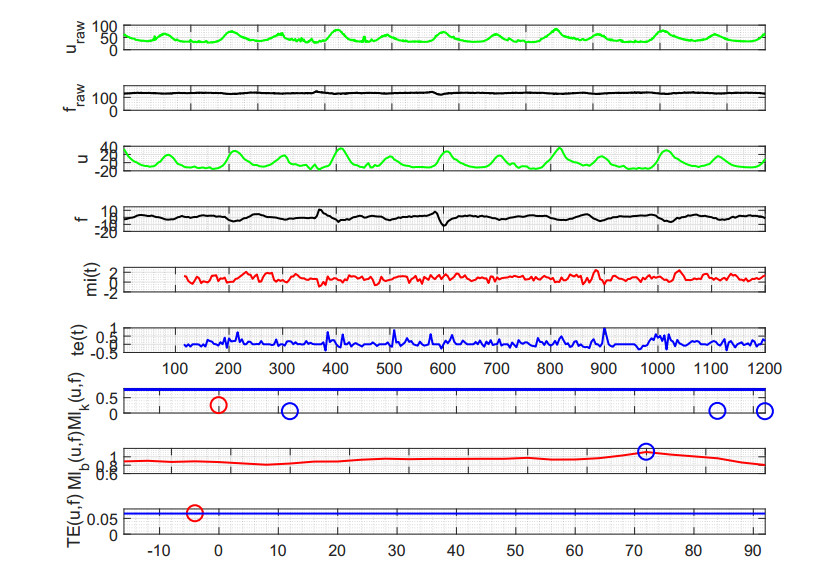
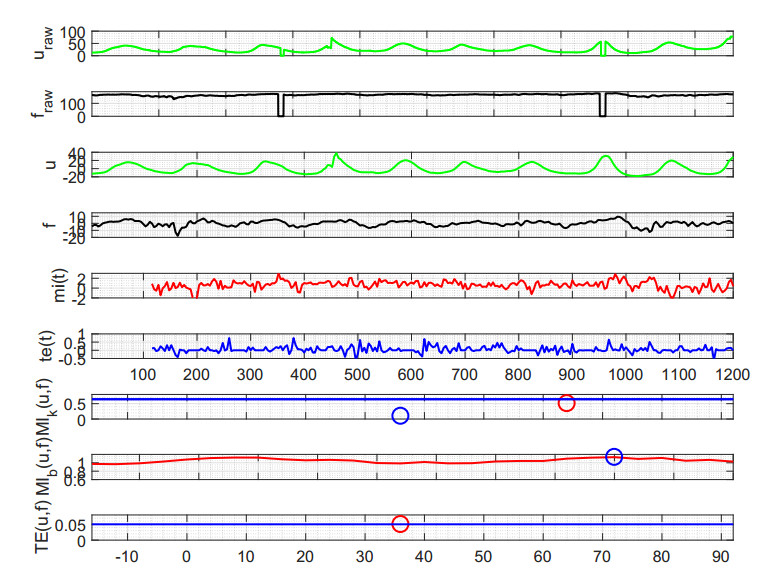
Figures 2 and 3 show calculations of the binned and Kraskov MIs and the Kraskov TE for typical normal and pathological fetuses, demonstrating for these two cases the longer delay of the pathological case.

Figure 2.  Typical 1200s epoch of a normal (N) case case showing (from top to bottom) raw UP $ u_{raw}(t) $, raw FHR $ f_{raw}(t) $, UP $ u(t) $, FHR $ f(t) $; local mutual information and transfer entropy $ mi(t) $ and $ te(t) $, respectively, starting at the maximum lag 90 $ + $ 20 s $ = $ 110 s; Kraskov UP-FHR mutual information $ MI_k $ (maximum and secondary MI delays and values indicated by red and blue circles, respectively) and overall $ MI_k $ value (blue line) with allowable lags -20 to 90s and lag resolution $ \tau $ $ = $ 4 s; binned mutual information $ MI_b(u, f) $ as a function of shifting $ u $ and $ f $ with respect to each other from -20 to 90 s; Kraskov UP$ \rightarrow $FHR transfer entropy $ TE $ delay (red circle) and overall $ TE $ value (blue line) with allowable lags and $ \tau $ as with $ MI_k(u, f) $. The horizonal axes of the top 6 plots and lower 3 plots are the epoch time from 0 to 1200 s and the lag times from -20 to 90 s, respectively. The UP and FHR plots have units of mmHb and beats per minute, respectively. The lower 6 entropy plots have units of nats.

DownLoad: Full-Size Img PowerPoint

Figure 3.  Typical 1200s epoch of a pathological (P) case showing (from top to bottom) raw UP $ u_{raw}(t) $, raw FHR $ f_{raw}(t) $, UP $ u(t) $, FHR $ f(t) $; local mutual information and transfer entropy $ mi(t) $ and $ te(t) $, respectively, starting at the maximum lag 90 $ + $ 20 s $ = $ 110 s; Kraskov UP-FHR mutual information $ MI_k $ (maximum and secondary MI delays and values indicated by red and blue circles, respectively) and overall $ MI_k $ value (blue line) with allowable lags -20 to 90 s and lag resolution $ \tau $ $ = $ 4 s; binned mutual information $ MI_b(u, f) $ as a function of shifting $ u $ and $ f $ with respect to each other from -20 to 90 s; Kraskov UP$ \rightarrow $FHR transfer entropy $ TE $ delay (red circle) and overall $ TE $ value (blue line) with allowable lags and $ \tau $ as with $ MI_k(u, f) $. The horizonal axes of the top 6 plots and lower 3 plots are the epoch time from 0 to 1200 s and the lag times from -20 to 90 s, respectively. The UP and FHR plots have units of mmHb and beats per minute, respectively. The lower 6 entropy plots have units of nats.

DownLoad: Full-Size Img PowerPoint

The normal case has a maximal Kraskov MI delay at 0 s with secondary delays at 12, 84 and 90 s. The TE is maximal at a sole delay of -4s. Visual inspection of the delay between UP contraction and FHR deceleration onsets in this epoch indicate that a near-zero delay is plausible. On the other hand, the binned MI value has an erroneous peak at 70 s.

The pathological case has a maximal Kraskov MI delay at 64 s and a secondary delay at 36 s. Visual inspection of the delay in this epoch indicates that these two delays are plausible. The TE is maximal at the shorter delay of 36s only. The binned MI value peaks at 70 s, closer to the longer delay.

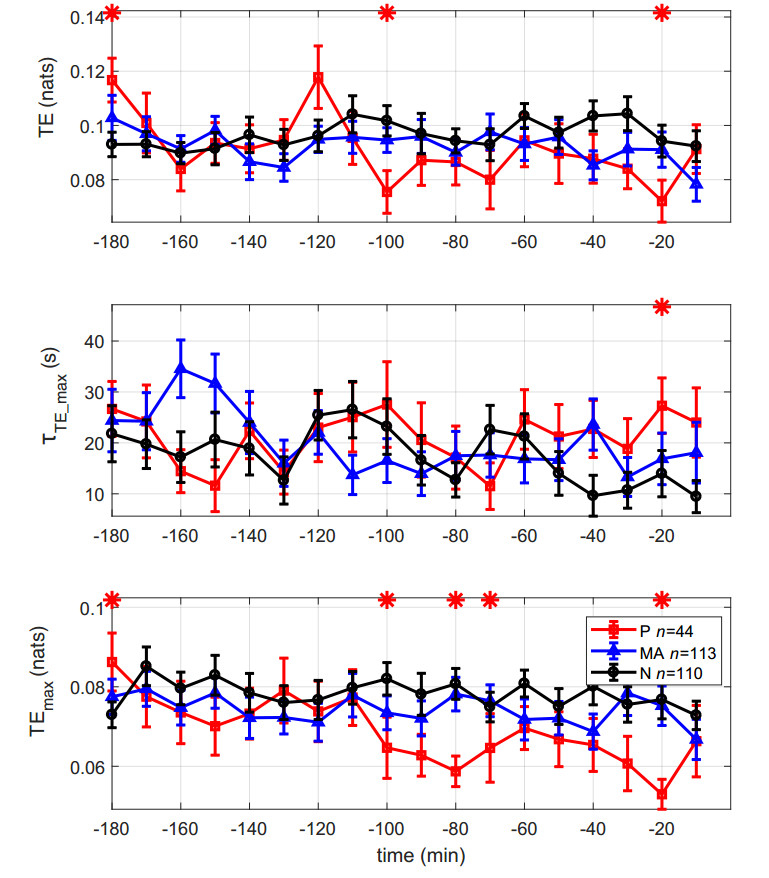
Table 1 summarizes the processing of MI and TE. MI or TE estimates were obtained when at least one significant delay was estimated. Estimates can be missing when no significant delays are found during the search. This can be the result of the absence of coupling from either signal loss and/or noise as discussed in the Preprocessing section. We obtained ME estimates for P, MA and N fetuses in 62.4%, 68.2% and 72.6% of the epochs, respectively. For TE these numbers were lower at 43.5%, 36.6% and 35.2%, respectively. The ratio of TE/MI estimates was higher for P cases: 69.7%, vs 53.6% and 48.5% for MA and N, respectively.

Table 1.  Processing summary.

Fetal class	P	MA	N
Number of recordings	42	104	110
Total epochs	756	1872	1980
MI: epochs estimated	472	1277	1437
TE: epochs estimated	329	685	697
MI: epochs estimated (%)	62.4%	68.2%	72.6%
TE: epochs estimated (%)	43.5%	36.6%	35.2%
Ratio TE/MI estimated	69.7%	53.6%	48.5%

---

 | Show Table

DownLoad: CSV

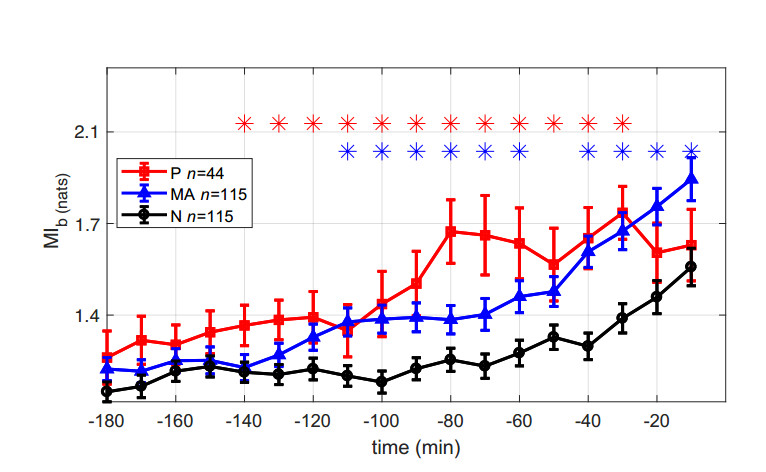
Figure 4 shows per-class binned MI estimates $ MI_b $ during the final 3 hours of delivery. The difference between N and P is statistically significant between 140 and 30 minutes before delivery. N-MA differences are significant slightly later, between 110 and 10 minutes before delivery. There is a tendency from N to MA to P fetuses to have higher MI. The delay at maximal MI (not shown) was not discriminating.

Figure 4.  Group mean $ \pm $ standard error of binned mutual information $ MI_b $ in the last 3 hours of labour and delivery. Epochs with statistically significant differences between N-P and N-MA groups are indicated by red and blue asterisks, respectively (KS test with $ p < 0.05 $).

DownLoad: Full-Size Img PowerPoint

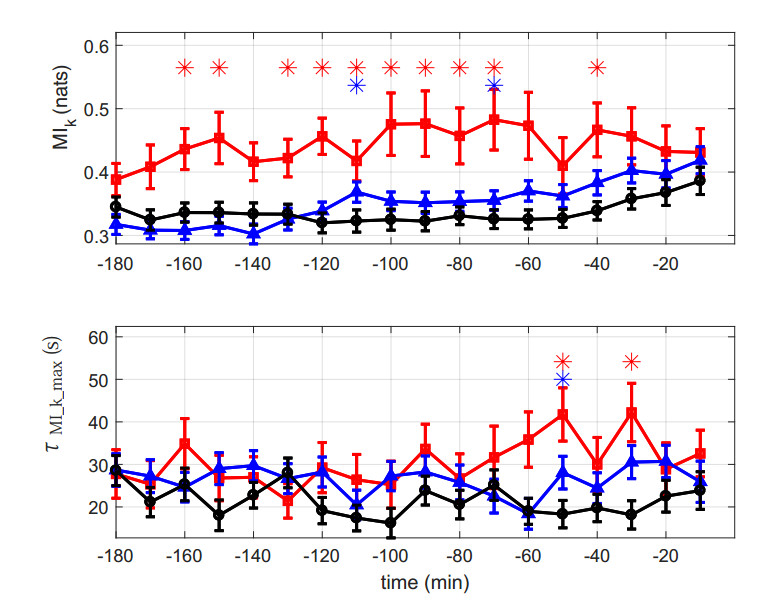
Figure 5 shows per-class Kraskov MI estimates $ MI_{K} $ during the final 3 hours of delivery. The difference between N and P is statistically significant between 160 and 40 minutes before delivery. N-MA differences are significant in two of these epochs, at 110 minutes and 70 minutes. There is a tendency from N to MA to P fetuses to have higher MI. Furthermore, two epochs in the final 50 minutes of delivery show longer P delays $ \tau_{{MI_k}_{max}} $ with statistical significance, while one epoch did so at 50 minutes for N-MA comparisons. There is a tendency from N to MA to P fetuses to have longer delays.

Figure 5.  Group mean $ \pm $ standard error of a Kraskov 4-nearest neighbour estimate of mutual information in the last 3 hours of labour and delivery, showing overall MI $ MI_{k} $, and the lag at maximum MI $ \tau_{{MI_k}_{max}} $. Epochs with statistically significant differences between N-P and N-MA groups are indicated by red and blue asterisks, respectively (KS test with $ p < 0.05 $).

DownLoad: Full-Size Img PowerPoint

Figure 6 shows per-class Kraskov TE estimates during the final 3 hours of delivery. The delay with the maximal contribution to TE, $ \tau_{TE\_max} $ shows differences between N and P that are statistically significant in 4 epochs between 100 and 20 minutes before delivery. There is a tendency from N to MA to P fetuses towards lower TE. Furthermore, one epoch in the final 20 minutes of delivery shows longer P delays with statistical significance. The overall TE value $ TE $ shows a similar pattern but with few epochs having significant differences. The delay where the contribution to TE is greatest, $ TE_{max} $, shows differences in the final 50 minutes of delivery, but only 1 epoch was statistically significant (at 20 minutes before delivery). Again there is a tendency form N to MA to P fetuses to have longer delays in these final epochs, although N-MA comparisons never reached statistical significance.

Figure 6.  Group mean$ \pm $ standard error of UP-FHR synchronization in the last 3 hours of labour and delivery using a Kraskov 4-nearest neighbour estimate of transfer entropy, showing overall TE $ TE $, and the lag and TE values at maximum TE $ \tau_{TE\_max} $ and $ TE_{max} $. Epochs with statistically significant differences between N and P fetus are indicated by a red asterisk (KS test with $ p < 0.05 $).

DownLoad: Full-Size Img PowerPoint

5.   Discussion

The delay estimates in the typical epochs shown were plausible and in accordance with the clinical expectation that pathology tends to be associated with longer delays between the mother and the fetus. These results are borne out at the larger scale of per-class comparisons over time, with statistically significant differences occurring early for both N-P cases but crucially for clinical significance, for N-MA comparisons. Detecting MA cases early, before injury, allows time for appropriate cesarian section to occur. It was also the case that $ MI $ and $ TE $ estimates were dominated by a single delay, and this was the rationale for displaying the argmax plots of Figures 5 and 6.

The typical epochs also illustrate that even with restricting the epoch length to 20 minutes, non-stationarity is present within the epoch, with delays occurring at at least two lags in the examples shown. This clearly introduces noise into the per-class comparisons that consider a single lag, and this noise diminishes discrimination.

Furthermore, we did not explicitly compare the degree of signal artefacts in this study among groups, but the previous study ^[2] shared the same pathological cases and the figure of 42% artifact for pathologicals vs. 8% for normal reported there is a valid comparison for this study. This can be a source of bias in our analysis, but the fact that we excluded very long artefacts from consideration diminishes this bias.

But despite these effects of non-stationarity and noise, the estimates do succeed about two-thirds of the time for MI and less so for TE, suggesting the degradation effect shown in ^[14]. The robust nearest neighbour Kraskov density estimator and the surrogate tests give confidence that the results are indeed significant. The significance of the generally lower TE success rates and the higher TE/MI ratio of epochs processed for P cases is interesting and merits further investigation, especially since TE values tended to be lower for these fetuses.

The increasing MI with fetal pathology was expected from our previous study ^[5]. This is plausibly explained by the fact that the fetus in distress reacts strongly, with deeper decelerations, to the onslaught of maternal contractions. But the decreasing TE with pathology was an unforeseen and novel result and cannot be explained merely by the fact that decelerations increase as labour progresses. This seems to indicate that the balance between MI and TE tips in the direction of more and more signal properties being (information-theoretically) redundant between source UP and target FHR. In contrast, more complex, FHR target-state dependent processing seems to vanish, possible indicating some regulatory mechanisms may be compromised. It is consistent with a view of a fetus in distress having difficulty compensating neurologically to the effects of labour, especially persistent contractions.

6.   Conclusions

We have demonstrated the utility of two new measures of perinatal fetal state, mutual entropy and transfer entropy, that may have complementary information for estimating the nature and timing of the fetal response to labour. The observed statistically significant differences indicate that these indices may be useful in future work for the development of a fetal state classifier.

Following from this study, we would like to assess and compare transfer entropy during specific baseline, acceleration and deceleration time intervals of FHR. We also hope to include maternal heart rate to obtain multivariate estimates of TE, which are currently supported by IDTxl. Further, we hope to compare fetus $ \rightarrow $ maternal TE, both for its inherent interest and also to aid in significance testing. We have assumed in this study that maternal $ \rightarrow $ fetal causality likely predominates, but this may be a matter of degree that is informative.

Finally, Wibral refers to "anticipative synchronization" occurring when a slave system ($ Y $) can anticipate the dynamics of a master system $ X $ when $ X $ is subject to a long feedback loop ^[14]. By testing TE (X$ \rightarrow $X) it is possible to tests for "feedback" in the source signal. This may be a way to overcome the challenges of detecting phase with signals like CTG with their inherent periodicity and under conditions of small sample sizes. This could benefit TE analysis with UP as a source in particular, especially at the end of labour when contractions become more frequent.

Acknowledgements

This research was supported by PeriGen Inc. The authors would like to thank Patricia Wollstadt and Michael Wibral for providing the open-source IDTxl package and for kindly assisting in the setup of the experiments and interpretation of the results.

Conflict of interest

PeriGen Inc. develops clinical decision support tools for cardiotocography.