Changes in soft coral Sarcophyton sp. abundance and cytotoxicity at volcanic CO₂ seeps in Indonesia

1.   Introduction

The objective of smart cities is to efficiently and effectively manage factors such as increasing urbanization, power usage, preservation of natural resources, and the well-being of the civilian economy. A population is capable of utilizing and embracing modern Information and Communication Technologies (ICT) ^[1]. In the notion of smart cities, ICT plays a crucial part in policy creation, decision, implementation, and ultimate productive services ^[1]. According to the United Nations Population Fund, around 3.3 billion people—or 54% of the world's population—lived in urban areas in 2014; this figure is expected to rise to 5 billion (i.e., 66%) by 2030 ^[2]. If urbanization continues at this rate, it will have a severe impact on city management, security, and the environment. In order to effectively manage data analysis, data communications, and the successful execution of complicated strategies to maintain the smooth and secure functioning of a smart city, the efficient use of ICTs is very important [3−5].

Research has mostly concentrated on investigating potential applications and their effects on smart citizens and smart cities ^[6,7]. Before the recent, unexpected and widespread distributed denial of services (DDoS) attacks and ransomware threats ^[8,9], security and privacy in smart city systems were not considered to be critical factors. For instance, in the case of smart vehicles, a Jeep Cherokee was hacked on a highway, which prompted Chrysler to issue a recall for 1.4 million vehicles. Examples of such assaults have been mentioned in ^[10,11]. Complex cyberattack vectors that might affect cloud services including infrastructure, applications, and platforms continue to be a severe danger. Cyberattacks such as DDoS attacks, ransomware, and botnet attacks are frequent attempts to access cloud services and interfere with their processing resources ^[12].

These modifications have sparked a new wave of research into cybersecurity and data privacy in cloud computing, the Internet of Things (IoT), and intelligent city communities. Businesses have started marketing safe smart city goods ^[6]. The IoT can gain from improved efficiency, performance, and payload in cloud infrastructure. The development of an industrial electronic business also benefitted from Cloud Computing. Hence, IoT and cloud are extremely connected to upcoming internet technologies that are compatible with IoT systems ^[13]. The most accurate and effective course of action might be difficult to determine in the midst of large and complicated volumes of data.

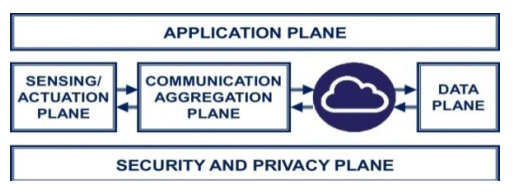
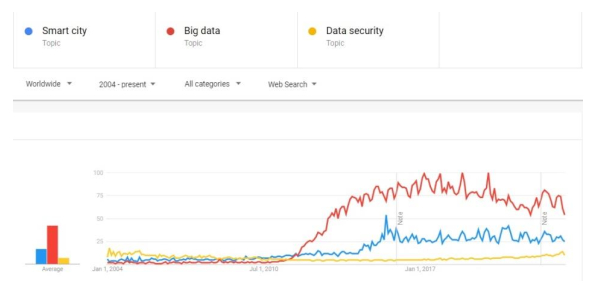
To make the best judgment possible, modern techniques such as Artificial Intelligence (AI) and Machine Learning (ML) may be used to analyze large amounts of data ^[14,15]. As seen in Figure 1, the concepts of "smart cities", "big data", "data security", and the usage of AI and ML in many contexts are still in the early phases of development and will likely bring more opportunities in the future. Each element in Figure 2, which shows the architecture of a smart city application, requests security and privacy assurance procedures to address consumers' increased awareness of smart city cybersecurity ^[16].

Figure 1.  The popularity of big data, data security, and smart cities (Google Trends).

DownLoad: Full-Size Img PowerPoint

Figure 2.  A high-level illustration of the architecture of smart city applications ^[16].

DownLoad: Full-Size Img PowerPoint

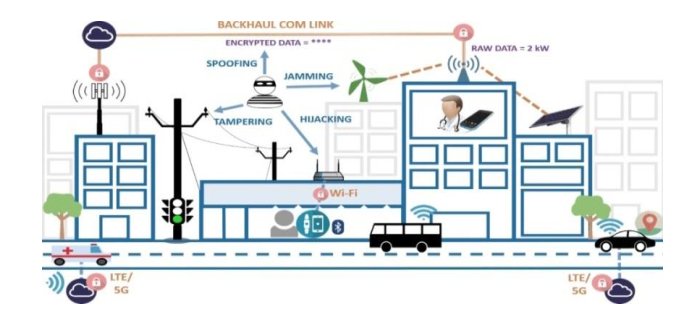
The IoT is a new communication paradigm that has emerged as a result of the tremendous increase in connectedness between people, devices, and services during the past ten years. In the upcoming generation of sustainable smart cities, this paradigm is anticipated to play a large role on the internet- and service-centric computing inside the networks of the current generation (4G/5G) and the future generation (6G and beyond) ^[17]. Recently, wireless technologies have emerged as a significant enabler, linking people to physical items through phones, tablets, and personal computer interfaces, which have contributed to this astonishing expansion of linked things ^[18]. We expect wireless transmissions to represent 2/3 of all internet traffic until 2020, with cellular/Wi-Fi connections contributing 66% of all internet protocol (IP) data ^[19]. As the Cloud network for data exchange grows, there is a significant risk of misusing cloud services when focusing on wireless edge devices, where sensitive and frequently semi-critical data can be fraudulently acquired, as depicted in Figure 3. By exploiting the weaknesses of wireless networks, a significant number of attackers or offenders attempted to either steal the personal information of target users or seek to obtain unauthorized access to the target's resources or applications ^[17].

Figure 3.  The complexity, scale, and extent of smart services provide more opportunities for the adversary ^[6].

DownLoad: Full-Size Img PowerPoint

A cybersecurity system often consists of both networks and computer security technologies. To intercept cyberattacks, several elements (such as firewalls) and cryptographic techniques are installed, and an IDS is employed to stop external intrusions, respectively ^[20]. Additionally, IDS is used to define, assess, and identify unauthorized system actions, such as unauthorized access, modifications, and damage ^[21,22].

In order to preserve the cloud network of smart cities, IDS is a security protection technique that is used to find suspicious activity in the system and quickly intercept the attacking source ^[23]. Depending on the types of cyber data that are accessible, IDS can be separated into host- and network-based detection. Host-based detection refers to monitoring internal resources such as logs, disc resources, and file systems on electronic devices like smartphones and laptops ^[21]. Antiviruses are a prime example of host-based detection. Network-based detection occurs by examining the network traffic between electronic devices and the internet ^[24]. In this study, we concentrate on network-based IDS for tracking fraudulent activity in the cloud network of connected device-based smart cities ^[24]. An effective network-based IDS should be able to identify a variety of intrusions on a cloud network of smart cities, including injection, flooding, and impersonation attacks that can originate from both internal and external attackers ^[25].

A smart city should include linked sensors, actuators, and relays that are safe, secure, and dependable for gathering, processing, and transmitting data in order to guarantee reliable and effective digital services; additionally, it is necessary to address the cybersecurity challenges posed by the interconnection of various devices ^[26]. The majority of the data is produced by IoT devices that are cloud-based and play a key part in many smart city applications ^[27]. IDS is frequently implemented using a centralized design, in which a single central unit is entirely in charge of evaluating all network traffic data and detecting if attacks have occurred ^[28]. The dependence on a single processing unit makes this strategy insecure due to a single point of failure ^[17].

The choice of features is crucial for creating ML models and is one of the essential steps in creating efficient IDS. The process of choosing the most key features that go into creating a strong model is known as Feature Selection (FS) ^[29]. FS can be performed either manually or with the aid of several methods and algorithms. Eliminating features that raise false alerts and decrease system accuracy is a crucial step in developing strong IDS ^[30]. As mentioned by ^[31], significant features convey crucial information that considerably aids in the classification process. The fact that IDS's FS decreases storage requirements, lowers processing costs, and improves test data comprehension is an important consideration. Since FS is a machine-learning topic, several different techniques are used to accomplish it. It is noted that several methods, such as the employment of intelligence patterns, swarm intelligence, Artificial Neural Networks (ANNs), deterministic algorithms, and fuzzy and rough sets, can be used to determine features ^[32]. Due to their high degree of accuracy, metaheuristic algorithms are frequently utilized for FS in IDSs ^[33]. In this area, swarm intelligence is a key method employed in the construction and classification of metaheuristic algorithms. The AI known as "swarm intelligence" is modeled after the collective behavior of insects and swarms. It is employed to resolve challenging issues. For this research, PIO ^[34] and PSO ^[35] are two methods utilized in swarm intelligence.

A dataset that keeps expanding to the point that it is challenging to handle using traditional database concepts and technologies is referred to as big data. The data do not suit the structures of traditional database systems, are too big, move too quickly, or a combination of all three. To be beneficial, there is a need to select an alternative method of processing this data ^[36]. Big data is extremely challenging to store and process ^[37]. Hadoop is mostly used to process huge data. Hadoop uses the MapReduce framework to process the data and Hadoop Distributed File System (HDFS) to store it efficiently ^[38]. Spark is a framework distinguished for its responsiveness. It tries to speed up batch workloads by performing the entire calculation in memory and processing optimization ^[39]. Additionally, spark is effective at performing iterative calculations, making it a good choice for the creation of large-scale machine-learning systems ^[40]. Nowadays, organizations are placing more emphasis on big data systems to manage such data and to use them for commercial expansion. The top seven data drivers include instances of big data from the financial, Internet, mobile, Smart cities-based data, science, sensor, and streaming industries.

The use of ML approaches to enhance IDS performance has been the subject of many studies ^[41,42]. However, these systems are limited because they use only one classifier, which prevents them from identifying and thwarting serious threats. In order to address this problem, Hansen and Salamon ^[43] have created several ensemble algorithms that outperform single classifiers. In this context, Pham et al. ^[44] and Rashid et al. ^[45] highlight numerous factors that might affect IDS performance, including feature selection, base classifiers, and ensemble techniques. This suggests the value of investigating ensemble-based IDS from diverse angles. Tree-based ML techniques have demonstrated promising results in predictive analytics ^[46]. Additionally, compared to many other kinds of ML models, tree-based classifiers may be trained significantly more quickly ^[47]. In this paper, we provide a tree-based SEM for enhancing IDS performance after taking their applicability into account.

1.1.   Motivation

To provide connected solutions for the general public, smart cities combine the IoT with a range of software, user interfaces, and communication networks. The most likely security threats to the networks of smart cities include various malicious attacks like DDoS, ransomware, remote recording, routing attacks, and data leakage attacks ^[6]. A DDoS attack is when many compromised machines launch a denial of service (DoS) attack on the smart cities network. With this attack, the attacker floods the server with erroneous request packets to block it, thereby depriving users of the resources and lengthening response times. Hence, it is important to make sure that smart cities are protected from cyberattacks, hacking, and data theft. The network of smart cities is protected by several security measures, including access control algorithms, public key-based security methods, and IDSs. However, there are no effective security options. An efficient IDS is necessary to provide integrated solutions that meet the fundamental security goals of availability, integrity, confidentiality, and accountability of the smart city network.

Currently, intrusion detection in smart cities has drawn increased interest in the cybersecurity field. Numerous FS and intrusion detection algorithms have been studied during the last few decades. Due to limitations, in many cases, these algorithms could no longer address the difficulties in real-time and distributed a nature of applications. The application of population-based metaheuristic algorithms in optimization, including feature selection, has recently increased. In order to handle the cloud network data from smart cities, the IDS must be scalable and dispersed. The use of only one classifier makes it impossible to detect and neutralize severe threats. Tree-based ML techniques have demonstrated promising outcomes in predictive analytics. In order to reduce potential future security attacks against the cloud network data of smart cities, the motivation is to propose an IDS using tree-based SEM ML classifiers. Additionally, we adopt the HDFS and Spark framework in our proposed work because the data generated from the cloud network of smart cities is enormous and can only be stored and processed in a cloud environment.

1.2.   Contribution

IDSs are crucial in preventing intrusions into the cloud network of smart cities, which contains private data and information. This research lists the most recent developments in FS and classification techniques for IDSs using cloud network data from smart cities. The following tasks are included: using a wrapper-based FS approach that uses PIO and PSO, storing the data in the HDFS, processing cloud network data for smart cities using WEKA's Knowledge flow ^[48], and classifying the cloud network traffic of smart cities using a tree-based SEM approach that uses J48 ^[49], RF ^[50], and XGBoost ^[51]. The UNSW-NB15 ^[52] and NSL-KDD ^[53] datasets were used to assess the system's performance. HDFS is used for storing and processing massive datasets. WEKA is used to train ML for massive data mining and analysis. The "DistributedWekaSpark" package allows us to configure Spark and WEKA together.

This effort's core contribution consists of examining the breadth and scope of the effects of cyberattacks, and the results are frequently utilized as the foundation for new legislation and regulations. Computer scientists and researchers make up the second branch. They examine the technological tools to ensure they adhere to the security and privacy standards set out by smart city rules. The research community has recognized that the technological implementation of smart city security is also a complicated issue, with the system's total security being determined by the most delicate link in the network. This insight is the source of vulnerabilities in existing smart city systems since developers erroneously think they can boost their products' security by protecting one aspect of the system while ignoring others.

The main contributions are pointed out as follows:

(1) The suggested IDS has been modified to ensure that secure communication with service providers only happens when it is performed between people of smart cities, trustworthy third-party organizations, and service providers.

(2) This research effort proposes a unique approach for automatically identifying intruder attacks by classifying both legal and malicious data.

(3) The hybrid monitoring system that makes up the intrusion detection mechanism combines data preprocessing methods, PIO and PSO for data dimensionality reduction, HDFS for data storage, and a tree-based SEM technique that employs J48, RF, and XGBoost for attacks classification using WEKA's Knowledge flow and Spark framework.

(4) A model built on the Spark platform to divide the processing of cloud network data for smart cities in order to save computation time.

(5) With reference to benchmark datasets, the suggested model is assessed to demonstrate how it outperforms standard baseline methods.

1.3.   Paper structure

The structure of the article is as follows. The related work is discussed in Section 2. Prerequisites for the proposed methodology, which include dataset enumerations, FS tools (PSO and PIO), classification approaches (J48, RF and XGBoost), and WEKA and Spark frameworks are discussed in Section 3. In Section 4, the suggested tree-based SEM ML algorithms implementation on Spark and WEKA are used to evaluate cloud network data from smart cities. In Section 4, a performance assessment, model performance, implementation, and comparison of the proposed model are included. Finally, Section 5 concludes the paper and lays out the research agenda for the future.

2.   Related work

In this section, we review related research and present the most pertinent related work to address barriers that need to be considered in this study. Without question, the emergence of smart cities will improve many aspects of urban life, while significantly increasing vulnerability. We research these concerns on a variety of levels. The associated works are divided into many categories, including secure Cloud/Edge/Fog/IoT ecosystems for smart cities, IDSs for smart cities, and FS techniques. The following subsections explain these categories in more depth.

2.1.   Secure Cloud/Edge/Fog/IoT ecosystem for smart cities

The architecture called Hybrid IoT was proposed by Qian et al. ^[54] to enable the well-organized transmission, caching, and computation of massive data produced by widely scattered and substantial IoT devices that are installed in smart cities. A paradigm for monitoring in the transportation sector was proposed by Garg et al. ^[55]. They used real-time analytics and apps at several levels to solve the issue of security risks in aerial vehicles. To discover cyber-threats in smart cars, they applied the probabilistic data structure method. By gathering data from moving objects and passing the load to edge devices through aggregators, extreme aerial vehicles serve as data providers. The real-time security of the odd vehicle movements was assured by the creators. In order to describe the function of cloud computing in providing storage, computation, databases, and a variety of application services for access through the internet, Dener ^[56] reviewed many research publications. These cloud-based services facilitate information sharing and integration amongst various smart city systems.

Applications based on reinforcement learning have produced successful outcomes in mobile edge computing (MEC), vehicular edge computing (VEC), and other areas. Reinforcement learning (RL) has emerged as an important class of algorithms in AI. The AI discipline of RL contributes to the further optimization of energy usage and the performance of MEC ^[57]. In a network, MEC provides execution resources, such as storage and calculations, which are close to the users and can be used to process and store content, as well as deliver services. Two sub-problems are created from the energy consumption optimization problem: computation optimization (data segmentation) and transmission optimization (time division). The authors ^[57] have suggested DDQNL-IST, an intelligent game method that combines distributed LSTM (Long Short-Term Memory) and DDQN (Double Deep Q-Network) with an intermediate state transition (IST). The results of the experiments demonstrate that the suggested DDQNL-IST can perform better in terms of average latency and energy cost. Due to the restricted processing resources available to the VEC servers, the authors of the research ^[58] suggest a resource management strategy based on Deep-RL (DRL) to motivate the VEC servers.

An innovative framework known as VCoT, presented by Khattak et al. ^[59], merges IoT and vehicular-networking clouds. The purpose of IoT-VC (VCoT) for numerous real-world applications, including smart traffic signals, home automation, and smart cities, is thoroughly explained in the article, along with the challenges that must be overcome. For the progress of smart cities, Kaur et al. ^[60] suggested an architecture that relies on cloud computing and IoT. The author concentrated on the various cloud characteristics and utilized IoT to deploy them to improve smart cities. The author used the smart city of Dubai as a case study and suggested a scenario-based design for healthcare in a smart city. A big-data analysis based on a smart city employing cloud computing infrastructure was described by Massobrio et al. ^[61]. The Hadoop framework was used to implement the map reduced parallel model. In essence, they concentrated on two cases: the estimate of the origin-to-destination matrix and public transportation services. The first case uses information about prior sites, whereas the latter case uses information about ticket sales. The actual outcome demonstrates how well the model supports a large volume of data.

PROTeCt (Privacy aRchitecture for IntegratiOn of Internet of Things and Cloud computing), is a device-based security system that enhances user privacy through a cryptography-based system in which only interested users may access their data, which is stored on a cloud in encrypted form to guard against unauthorized access ^[62]. The gateway was authenticated in this operation. Users must repeatedly register and accept invitations to join the network, which raises the cost of communication. A framework for effective IDS that is more suitable for IoT-based applications was provided by the authors in ^[63]. To deal with security anomalies for IoT networks, the suggested framework uses machine learning-based methodologies. The link measurement required to choose the best routing option is missing from the research. These limitations increase the percentage of route breakages and the rate of packet loss.

The authors in ^[6] investigated the deployments of cyber-physical systems in smart cities. They focused on the security issues associated with smart infrastructure and the impact that ransomware causes on governmental organizations, the healthcare system, and transportation. Moreover, the solutions include game theory, IDS, and cryptography. It is important to note that the writers also focused on human error. The authors in ^[17] introduced an IDS based on ML in a semi-distributed and distributed mode for the resource-constrained IoT. This IDS is based on different FS strategies, and each technique is investigated independently.

The authors of ^[64] focused on the security of IoT devices in the smart city and presented an architecture dubbed the Anomaly Detection-IoT (AD-IoT) system that was built on RF ML. The authors of ^[65] presented a novel DRL-based architecture to protect a smart city's digital infrastructure from any kind of cyber incursion and for early detection of intrusions based on data behavior. To reduce latency and energy use, the authors of ^[66] introduced a neuro-fuzzy-based secure PSO computational offloading system for the Fog-Cloud-IoT context. The authors of ^[67] envisioned an ML-based secure cloud service for connected automobiles that would identify cyberattacks and satisfy user QoS and Quality of Experience (QoE) requirements.

The aforementioned papers offer the first step towards the ecosystem of smart cities. As the number of connected devices grows due to technological innovation, it becomes impractical to individually connect many low-end 'things' to management or analytics systems. In general, some end-system devices produce so much data that the core communication channel may become saturated. An array of crucial tasks, including data filtering and processing, and security are carried out by the Cloud/Edge/Fog/IoT ecosystem for smart cities. Security concerns in smart cities are application-based. For instance, the security flaw in smart meters might result in energy disruptions and ineffective Smart Grids. Therefore, more sophisticated and cutting-edge techniques based on big data analytics are required to guarantee the cyber safety and security of smart city applications. However, the aforementioned cryptographic and technical approach is viewed as insufficient due to the increasingly sophisticated and varied cyber-attacks. This drives the creation of an IDS with built-in intelligence to move away from "one-shot" security protection and to include a sophisticated method of continuous learning from changing network data. The discussion and summary of existing works are included in Table 1.

Table 1.  Brief literature Survey for implementing secure Cloud/Edge/Fog/IoT ecosystem for smart cities.

Reference	Year	Method Employed	Summary
[60]	2016	Cloud and IoT	The integration of any smart city application requires cloud computing and IoT.
[65]	2017	Restricted Boltzmann Machine	Generalized method to spot and stop DoS in smart cities.
[63]	2017	ML based IDS	A cutting-edge intrusion detection technology that recognizes security irregularities in IoT networks using ML algorithms
[61]	2018	Hadoop	Smart city Big Data analysis paradigm utilizing cloud computing infrastructures.
[62]	2018	PROTeCt	User privacy is increased through the privacy architecture for the IoT and CC integration.
[55]	2018	Triple Bloom filter PDS	A data-driven transportation optimization model that uses a PDS-based method to identify cyber threats in smart cars.
[54]	2019	UDN and MEC	Lower the energy use and end-to-end latency of computing data from large IoT devices installed in a smart city.
[56]	2019	Cloud Computing	Cloud-based services facilitate information sharing and integration amongst various smart city systems.
[59]	2019	VCoT	A new framework for architectural and communication design that successfully integrates IoT and cloud-based vehicular networking.
[6]	2019	Reviews for Security for Smart cities	A multi-level structure, including a "security level", can be used to conceptualize smart cities. All other levels' weaknesses are caused by the security level.
[64]	2019	RF-based binary classification	AD-IoT system is suggested as a solution to deal with the cybersecurity concerns posed by IoT in smart cities.
[66]	2019	Neuro-Fuzzy Model and PSO	SecOFF-FCIoT
[67]	2019	Deep belief and DT	IDS offers services that satisfy users' QoS and QoE needs.
[17]	2020	SAE and MLP	IDS is based on semi-distributed and fully-distributed approaches.
[57]	2021	Energy consumption optimization in MEC.	RL-based performance enhancement of MEC by energy consumption optimization.
[58]	2022	DRL and Stackelberg game-based resource management for VEC.	A DRL-based resource management plan is suggested to boost vehicle and VEC server revenues.
UDN- Ultra-Dense Networking, PDS- probabilistic data structure, VCoT- vehicular networking clouds with IoT, SAE- Stacked Auto-Encoder, MLP- Multi-layer perceptron, SecOFF-FCIoT- Secure offloading in a Fog-Cloud-IoT.

---

 | Show Table

DownLoad: CSV

2.2.   IDS for smart cities

IDSs have long been a topic of study in the field of communication networks; however, the practical need for such networks has only recently led to a shift in emphasis to IDS for smart city-based networks. IDSs are divided into host-based ^[68,69] and network-based ^[70,71] subcategories. Due to several factors, host-based IDSs are considerably less effective in identifying corrupted IoT devices. First, the development of detection algorithms uses the energy and computing of smart IoT devices. Second, certain IoT devices have restrictions on what software may be installed on them. Third, deploying detection techniques on many diverse IoT devices linked to smart networks in smart cities is extremely difficult. Lastly, IoT device makers rarely incorporate detection techniques into their designs ^[72].

DeepCoin is an innovative Deep Learning (DL) and blockchain-based energy framework for smart grids ^[73]. The blockchain-based system is divided into five stages: setup, agreement, block creation and consensus, view modification, and conclusion. It provides a high throughput methodology and contains a revolutionary, trustworthy peer-to-peer energy system based on the useful Byzantine fault tolerance algorithm ^[73]. The suggested system generates blocks using hash functions and short signatures to guard against smart grid attacks. It is suggested to use the statistical correlation between measurements for unsupervised anomaly identification with the objective to create a scalable anomaly detection engine that is appropriate for large-scale smart grids that can distinguish between a genuine malfunction and either a disturbance or sophisticated cyber-attack ^[74] The suggested approach uses feature extraction while learning about the causal relationships between the subsystems using symbolic dynamic filtering (SDF), which also helps to lighten the computing load.

The authors in ^[75] presented an intrusion detection/prevention system (IDPS) with fog-assisted software-defined networking (SDN) using an enhanced decentralized computing structure known as fog-computing as an IoT framework. To address an IoT scalability issue, they suggested a useful technique for allocating fog resources. Additionally, they examined four classifiers to identify intrusions and provided design recommendations to control cybersecurity threats at the edge of the IoT network and to spot anomalies. An online Sequential Extreme Learning Machine (OS-ELM) was used by the authors of ^[76] to construct a fog-oriented IDS, which summarizes the identified intrusion. First, fog-nodes will identify the malicious traffic from the IoT environment, and the information of the identified intrusion is further transferred to the cloud server. Since the suggested approach is a distributed IDS, it can offer scalability, interoperability, and flexibility. However, it is unable to summarize the data without a cloud server and will become problematic once the cloud server goes down.

A supervised IDS was suggested by the authors of ^[77] for an IoT network in a smart house. The three-layered model of the proposed IDS architecture worked to identify malicious packets. Three experiments were tested over the layers using nine classifiers. Consequently, the J48 classifier produced F-measure values of 96.2%, 90%, and 98% for each of the three experiments, respectively, to obtain the best performance. The system's drawback is that it must integrate the three levels in order to detect malicious communications. The entire system will have problems if one of the layers fails. To assist managers of smart cities in defining the most sensitive threats, researchers in ^[78] suggested an intrusion detection framework and an attack categorization scheme. Additionally, this paper demonstrates how a One-Class Support Vector machine (OC-SVM) and rule-based detection may be used together to dramatically enhance detection results.

In ^[79], the authors investigated the viability of using single model classifiers in an ensemble learning setting to identify cyberattacks in IoT-based smart city applications. The tests using the most recent IoT attack the database, stacking a component of the ensemble technique outperforms single models in distinguishing attacks from benign samples. In terms of various performance emetrics, information gain (IG) is employed for FS and classification outcomes outperform either single or other ensemble models. Diro and Chilamkurti suggested a DL model to detect distributed intrusions in a social IoT network using the NSL-KDD open-source dataset, which logs attack data in both distributed and centralized systems; their model achieved 99.2% and 98.27% accuracy for binary-class and multi-class identification, respectively ^[78].

Due to the negative effects of low-frequency threats, such as user to-root (U2R) and remote-to-local (R2L) attacks, Pajouh et al. introduced a two-stage dimension reduction and classification approach to identify anomalies in IoT backbone networks ^[18]. After reducing the dataset's features using principal component analysis (PCA) and linear discriminate analysis (LDA), they employed naive bayes and K-Nearest Neighbor (KNN) to find anomalies. This method resulted in an identification rate of 84.82% ^[18]. However, this method is centralized and was only tested for DoS, remote-to-local, user-to-root, and Probe attacks. In ^[80], Kozik et al. presented an attack detection system that used the Apache Spark cloud architecture and the ELM method. The accuracy levels of this investigation, which focused on the three key IoT system, used cases of scanning, command and control, and infected host were 99%, 76%, and 95%, respectively.

The Gain Ratio (GR) FS approach, based on ANN and Bayesian networks, was suggested ^[81] and the performance was assessed on the KDD'99 and NSL-KDD datasets, with ensemble techniques achieving 99.42 and 98.07% accuracy, respectively. An ensemble technique that incorporates Naive Bayes, Bayesian Net, and DT classifier was put out by Haq et al. ^[82], while using FS methods such as Best First Search, Genetic, and Rank Search, where they were able to extract the common features. The ensemble methodology generated a 98% true positive rate when examined using the 10-fold cross-validation approach. A reduced error pruning tree (REPTree) was utilized as the basis classifier in the bagging ensemble approach that Gaikwad et al. ^[83] developed on the NSL-KDD dataset; their model had an accuracy rate of 81.29%. Jabbar et al. ^[84] suggested an ensemble approach that combined an Alternating DT (ADTree) with KNN, and the performance evaluation showed that the proposed ensemble outperformed the current strategies in terms of the Detection Rate (DR) (99.8%).

Zhou et al. proposed a FS and ensemble method-based IDS model in ^[47], where an optimal FS was achieved using a combination of Correlation-based FS (CFS) and Bat algorithm, followed by an ensemble method made up of the Decision Tree (DT), RF, and Forest by Penalizing Attributes (Forest PA) algorithms. A hybrid IDS that combined the C5 classifier and OC-SVM was introduced in ^[85]. Using DT and RF trees as the basic classifiers, the authors of ^[44] developed bagging and boosting ensemble approaches. Experiments were conducted on the NSL-KDD dataset, where it was discovered that bagging with DT produces superior outcomes.

The aforementioned models were created for IoT networks; however, because they primarily focused on the network structure, they did not take the resource limits and limitations that exist within IoT networks into account. The models' findings indicated that impersonation attacks appear to have a less favorable outcome or detection rate. However, these security measures come at a high performance cost and are inappropriate for the accepted smart city context. The discussion and summary of existing works are comprised in Table 2.

Table 2.  Brief of literature Survey for implementing IDS which are suitable smart cities.

Reference	Year	Method Employed	Summary
[81]	2014	Ensemble-based Multi classification	GR FS approach combined with ANN and Bayesian Net classifiers for an IDS.
[82]	2015	Ensemble-based Multi classification	J48, Bayesian Network, and NB classification model ensemble utilizing a hybrid FS technique.
[78]	2017	OC-SVM	Rule-based detection using OC-SVM is employed to increase performance.
[84]	2017	Ensemble-based Multi classification	The ADTree and KNN oriented cluster- based ensemble classifier is constructed.
[75]	2018	RNN, MLP, and ADT	IoT Network Anomaly Detection Using a Fog-Assisted SDN
[76]	2018	OS-ELM	The testing findings indicate that the fog nodes identify attacks 25% more quickly than cloud-based implementations while maintaining a low false alarm rate.
[86]	2018	Neural Network based Multi classification	A novel method of cybersecurity called DL makes it possible to identify threats in the social IoT.
[80]	2018	ELM based Multi classification	Sharing the traffic load between edge and cloud for effective traffic classification using ELM.
[44]	2018	Ensemble-based Binary classification	Bagging ensemble model with J48 as the basic classifier.
[85]	2019	Multi-classification by C5 classifier and One class-SVM	Ensemble of C5 classifier with the OC-SVM classifier, to identify both known intrusions and zero-day attacks with high detection accuracy and low false-alarm rates.
[18]	2019	NB and kNN	Two-tier classification module to spot unusual R2L and U2R attack behaviors.
[77]	2019	J48	A three-layered IDS to identify several common network-based cyberattacks on IoT networks.
[74]	2019	Symbolic Dynamic Filtering (SDF) and Boltzmann Machine	This technique identifies unobservable intrusions in smart grids.
[47]	2020	Ensemble-based Multi classification	Combination of the C4.5, RF, and Forest by Penalizing Attributes (Forest PA) algorithms for attack identification through the voting process.
[79]	2020	ANN, SVM LR, DT, RF, and KNN	Examine a machine learning-based attack and anomaly detection strategy to counter and reduce IoT cybersecurity vulnerabilities in a smart city.
[73]	2020	RNN, Blockchain, and Byzantine fault tolerance algorithm.	IDS to identify network attacks and fraudulent energy network transactions.
[83]	2021	Ensemble-based Binary classification	Utilizing REPTree as the foundation class, the ensemble's bagging method is utilized to construct an IDS.

---

 | Show Table

DownLoad: CSV

2.3.   Feature selection procedures

The important step in intrusion detection in cloud Internet traffic data of smart cities is feature selection. It is difficult to categorize and detect anomalous and unknown classes without feature extraction and selection. Thus, for the field of network traffic identification, a comprehension of FS and extraction is very essential. There are many intrusion detection techniques [87−94] employed to provide security for communication networks while employing the NSL-KDD and UNSW-NB15 datasets.

In ^[95], Tama et al. introduced an ensemble-based IDS, which combined a two-stage classifier with a hybrid FS technique including PSO, ant colony algorithm (ACO), and genetic algorithm (GA), applied on UNSW-NB15 and NSL-KDD datasets. By altering the value of the parameter n, which stands for the number of particles, population size, and ants in PSO, GA, and ACO, respectively, experiments were conducted to ascertain the ideal configuration for feature selection. With an accuracy of 99.5570 ± 0.134%, PSO with n = 2 clearly revealed the best classification result. This case produced a collection of 37 features. The feature set of 19 was produced using PSO with n = 5, which yield the highest classification accuracy of 97.0550 ± 0.125% for UNSW-NB15.

An IDS that is based on stacking ensembles was proposed by Smitha et al. ^[96]. Experiments were conducted on the heterogeneous datasets UNSW-NB15 and UGR'16. Only the best features were retrieved after the most important traits were provided weights in order to prioritize them. The IG-based hashing approach was used to minimize the dimension of the features; only 11 characteristics from the UNSW NB-15 dataset were chosen ^[96]. Alternatively, five characteristics of the UGR'16 dataset's were taken into consideration. In order to create a hybrid IDS, Salo et al. ^[97] combined an ensemble approach with two FS techniques IG-PCA. The IG-PCA ensemble approach selected seven features out of 20 features of the ISC2012 dataset and achieved the highest accuracy of 99.011. For the NSL-KDD dataset, 12 features out of 41 features were selected by the IG-PCA ensemble approach to gain the highest accuracy (98.24%). Twelve out of 24 features were selected by the IG-PCA ensemble approach using the Kyoto 2006+ dataset to obtain the highest accuracy of 98.95.

Zhou et al. introduced an ensemble-based, feature-selected IDS in ^[47]. They coupled the Bat algorithm with CFS (CFS-BA) to choose features. After choosing the features, they conducted the experiment using the NSL-KDD, AWID, and CICIDS2017 datasets. The CFS-BA approach selected 10 out of 41 features of the NSL-KDD dataset. For the AWID dataset, eight out of 155 features were selected. Alternatively, 13 out of 80 features were selected by the CFA-BA approach using the CICIDS2017 dataset. In ^[79], Rashid et al. examined several ML techniques to identify cyber-attacks from IoT-based smart city applications using an FS approach. For UNSW-NB15 and CICIDS2017, the authors employed the information-gain model and chose 25 features. To improve the suggested ensemble approach, they added FS algorithms to select the most pertinent features. The top 20 out of 41 features from the NSL-KDD dataset were chosen using the proposed model and the SelectKbest FS algorithm ^[45]. The results of FS utilizing CFS as the feature evaluator and PSO as the search strategy (CFS+PSO) were presented in this work ^[98]. For PSO, we assume that there are 50 particles, that the inertia weight constant is 0.33, and that the values of c₁ and c₂ are equal at 0.34. After utilizing CFS+PSO to execute FS on the NSL-KDD dataset, 11 important features are effectively acquired.

To select the best subset of attributes for IDS, a unique combination technique based on the Iterative Dichotomiser 3 (ID3) algorithm and the bee algorithm (BA) was proposed ^[97]. The BA was used to offer a subset of features, while the ID3 approach acted as a classifier. When applied to the KDD Cup 99 dataset, the results showed that the proposed model performed better for DR and Arrival Rate (AR) when the number of features was less than 30. An IDS based on FS and a clustering utilizing filter and wrapper approaches were proposed in study ^[31]; this featured grouping based on a linear correlation coefficient (FGLCC) algorithm and a cuttlefish algorithm (CFA), which are the names of the filter and wrapper approaches, respectively. The suggested technique used a DT as the classifier. Using the KDD Cup 99 dataset, FGLCC and FGLCC-CFA FS techniques choose 15 and 10 features, respectively ^[31].

Acharya and Singh ^[99] developed a unique method for choosing IDS features that used the Intelligence Water Drops (IWD) algorithm. IWD is also recognized as a metaheuristic-based swarm intelligence optimization technique. With the help of the KDD CUP99 dataset, this strategy was assessed. The suggested wrapper model obtained a minimum of nine features out of a total of 41. The suggested study used a filter and wrapper-based technique using the firefly algorithm in the wrapper to choose the features from the KDD-CUP99 dataset since FS affects how quickly the analysis is completed ^[100]. Ten features are considered. This method employs the selection process by means of an optimizer that was inspired by pigeons. The conventional approach for binarizing continuous swarm intelligence algorithms is contrasted with a novel approach for a continuous PIO ^[101]. The UNSW-NB15 dataset has 49 features, whereas the KDDCUP 99 and NSL-KDD datasets each have 41. However, not all of these features are crucial for creating IDS. Both the Sigmoid PIO (SPIO) and the Cosine PIO (CPIO) binarized versions of PIO for FS chose 10 and 7 features from the KDD-Cup99 dataset, respectively. From the NSL-KDD dataset, the PIO for FS (SPIO and CPIO) chose 18 and 5 features, respectively. From the UNSW-NB15 dataset, the PIO for FS (SPIO and CPIO) chose 14 and 5 features, respectively.

It is crucial to note that while most of the described methods have been evaluated using the most recent KDD dataset (i.e., NSL- KDD and UNSW-NB15), a small number have also been tested using the extremely old KDD'99 dataset (1999). In this research, we used both datasets to evaluate the proposed framework. In conclusion, it should be noted that the research does not agree on a specific number of features or subset of features, and that the proposed FS algorithms deal with a tradeoff between the accuracy and FPR. The brief of existing works is comprised in Table 3.

Table 3.  Brief of literature survey for implementing feature selection.

Reference	Year	Method		Dataset	Total Features	Feature Selected
[102]	2015	ID3-BA		KDD CUP 99	41	< 30
[98]	2017	CFS-PSO		NSL-KDD	41	11
[99]	2018	IWD		KDD CUP 99	41	9
[100]	2019	Firefly		KDD CUP 99	41	10
[31]	2019	FGLCC		KDD CUP 99	41	15
		FGLCC-CFA		KDD CUP 99	41	10
[97]	2019	IG-PCA		NSL-KDD	41	12
				Kyoto 2006+	24	12
[95]	2019	PSO		NSL-KDD	41	37
				UNSW-NB15	49	19
[96]	2020	IG-Hashing		UNSW-NB15	49	11
				UGR'16	12	5
[47]	2020	CFS-BA		NSL-KDD	41	10
				AWID	155	8
				CIC-IDS-2017	80	13
[79]	2020	IG		UNSW-NB15	49	25
				CIC-IDS-2017	80	25
[101]	2020	PIO	SPIO	NSL-KDD	41	18
				UNSW-NB15	49	14
			CPIO	NSL-KDD	41	5
				UNSW-NB15	49	5
[45]	2022	SelectKbest		NSL-KDD	41	20

---

 | Show Table

DownLoad: CSV

3.   Prerequisites

3.1.   Dataset enumeration

3.1.1.   NSL-KDD

The KDD Cup 99 dataset has been revised to become NSL-KDD. The dataset is comprised of 41 attributes that are divided into 5 classes—4 attack groups and 1 normal class—that are explained in more detail in Table 4. The 42nd attribute, aka class attribute, gives details about these groups and has either positive or negative examples. Here, we outline the most common forms of malicious behavior, which are divided into 4 categories of attacks.

Table 4.  NSL-KDD dataset with feature number, name, and type.

Feat. No.	Name	Type	Feat. No.	Name	Type
42	Class	Nominal	21	Is host login	Discrete
41	Destination host service rerror rate	Discrete	20	Number of outbound cmds	Discrete
40	Destination host rerror rate	Discrete	19	Number of access files	Discrete
39	Destination host service serror rate	Discrete	18	Number of shells	Discrete
38	Destination host serror rate	Discrete	17	Number of file creations	Discrete
37	Destination host service different host rate	Discrete	16	Number of root	Discrete
36	Destination host same source port rate	Discrete	15	Su attempted	Discrete
35	Destination host different service rate	Discrete	14	Root shell	Discrete
34	Destination host same service rate	Discrete	13	Number of compromised	Discrete
33	Destination host service count	Discrete	12	Logged in	Discrete
32	Destination host count	Discrete	11	Number of failed logins	Discrete
31	Service different host rate	Discrete	10	Hot	Discrete
30	Different service rate	Discrete	9	Urgent	Discrete
29	Same service rate	Discrete	8	Wrong fragment	Continuous
28	Service rerror rate	Discrete	7	Land	Discrete
27	Rerror rate	Discrete	6	Destination byte	Continuous
26	Service serror rate	Discrete	5	Source byte	Continuous
25	Serror rate	Discrete	4	Flag	Discrete
24	Service count	Continuous	3	Service	Discrete
23	Count	Discrete	2	Protocol type	Discrete
22	Is guest login	Discrete	1	Duration	Continuous

---

 | Show Table

DownLoad: CSV

● DoS attacks- Attacks that restrict the services of legitimate users fall under the term DoS. A few examples include Smurf, teardrop, SYN flooding, and Neptune.

● The term "User to Root" (U2R) refers to situations in which an attacker takes control of local machines by abusing flaws within them. U2R is a type of exploit in which the attacker first gains access to a regular user account on the system, and then uses that account to exploit a security hole to take control of it ^[103]. A few examples include rootkit, espionage, buffer overflow, and SQL attacks.

● R2L (Root to Local)- R2L occurs when an attacker, who can send packets to a system across a network but who lacks an account on that machine, uses a vulnerability to acquire local access as a user of that machine ^[103]. A few examples include Warezmaster, Imap, multihope, and spy.

● A computer network is probed to learn more about it with the apparent goal of getting beyond security measures. An example of a probe attack is when the attacker uses a traffic analysis to learn more about the network. Examples include nmap, satan, ping-sweep, and port-scan.

The training part of the NSL-KDD dataset (KDDTrain+) is a dataset of 125,973 records, of which 67,343 records are normal and the remaining 58,630 records are anomalous. The test part of the dataset (KDDTest+) is comprised of 22,544 records. of which 9711 records are normal and the 12,833 records are anomalous.

3.1.2.   UNSW-NB15

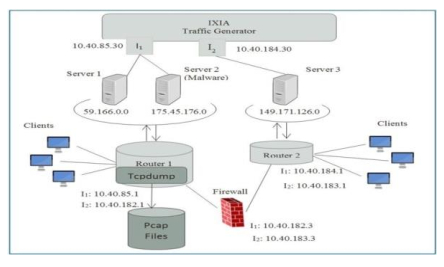
The dataset is critical for evaluating and measuring the performance of IDS. During the past few decades, IDS datasets have been introduced. Moustafa et al. ^[52] generated the UNSW-NB15 dataset lately. The UNSW-NB15 testbed is shown in Figure 4. The UNSW-NB15 dataset is a combination of a real-world network operation and a synthetically modified attack. In this study, the UNSW-NB15 dataset is used. IXIA PerfectStorm, which is an attack creation tool, was used to produce the UNSW-NB15 dataset. It includes both modified and actual attacks from nine different families. Different servers are targeted in these attacks. At the beginning of 2015, the authors acquired tcpdump traces of the network traffic for a total of 31 hours. In addition, the dataset consists of 12 methods that are utilized to provide 49 features for the class label ^[96]. For each network flow, these network records were utilized to create a dataset containing 49 features. Some of the features are numerical, while others are statistical. Other qualities refer to the values of time stamps.

Figure 4.  The Testbed Visualization for UNSW-NB15 ^[52].

DownLoad: Full-Size Img PowerPoint

There are 175,341 records in the training set and 82,332 records in the testing dataset, which include all types of attacks, as well as typical traffic samples. There are 45 features in the testing and training datasets. These features are listed in Table 5. The UNSW-NB15 dataset has been subjected to nine different types of attacks.

Table 5.  Enumeration of the employed dataset.

Feat. No.	Feat. Name	Feat. No.	Feat. Name	Feat. No.	Feat. Name
45	label	30	transdepth	15	sloss
44	attack_cat	29	dmean	14	dload
43	issmipsports	28	smean	13	sload
42	ctsrvdst	27	ackdat	12	dttl
41	ctsrcltm	26	synack	11	sttl
40	ctflwhttpmthd	25	tcprtt	10	rate
39	ctftpcmd	24	dwin	9	dbytes
38	isftplogin	23	dtcpb	8	sbytes
37	ctdstsrcltm	22	stcpb	7	dpkts
36	ctdstsportltm	21	swin	6	spkts
35	ctsrcdportltm	20	dit	5	state
34	ctdstltm	19	sjit	4	service
33	ctstatettl	18	dinpkt	3	proto
32	ctsrvsrc	17	sinpkt	2	dur
31	responsebodylen	16	dloss	1	id

---

 | Show Table

DownLoad: CSV

The training section of the UNSW-NB15 dataset consists of 175,341 records, of which 56,000 are normal and 119,341 are attacks. The test part of the dataset is comprised of 82,332 records, of which 37,000 records are normal and 45,332 records are anomalous.

3.2.   Feature selection tools

3.2.1.   Pigeon Inspired Optimization (PIO)

One of the recently created bio-inspired swarm intelligence algorithms is the PIO ^[104]. Pigeons' homing behavior was influenced by two primary operators: landmark operators and map and compass operators. According to the research on pigeon homing abilities, the pigeon's capacity to find its way home is caused by small magnetic particles that are found in its beak (i.e., through the trigeminal nerve). These particles communicate with the brain of the species, and Pigeons can feel the earth's magnetic field using their magneto-reception abilities. Additionally, they can utilize the sun's height as a compass to change their orientation ^[101]. The pigeons grow less dependent on the map and compass operator as they approach their objective ^[104]. Guilford and others in ^[105] devised the PIO algorithm, which is based on the two primary operators employed by pigeons and is meant to match their behavior.

By changing the position X_i and velocity V_i of pigeon i throughout each iteration, this operator may be mathematically stated in a more straightforward manner. Based on the value of the current iteration t in Eqs (1) and (2), the values of X_i and V_i are changed for the following (t + 1)^th iteration, as stated in ^[104]:

where X_g is the global best solution, X_i(t)stands for the current position of a pigeon at iteration t, and V_i(t) stands for its current at iteration t. R stands for the map and compass factor. "random" is a uniform random number in the range [0, 1]. Equation (1) is used to calculate each pigeon's velocity in the traditional manner, and Eq (3) uses a sigmoidal function to convert the velocity into binary form:

where r is an evenly distributed random number and $ {V}_{i}\left(t\right) $ is the pigeon velocity in iteration t.

In this research, we apply the PIO's new binary version to an IDS FS method. The features selected by CPIO generate efficient results compared to SPIO and traditional PIO in terms of accuracy, TPR, and FPR ^[101]. The outcome demonstrates that the proposed CPIO, which used the cosine similarity to binarized the solution velocities rather than the sigmoid function, had a faster convergence ^[101]. Hence, we adopted the Cosine version of PIO for FS purposes. The cosine similarity was employed by CPIO to determine the pigeons' velocity. Initial binary values of either zero or one were chosen at random to set the value of the solution. The cosine similarity formula is used to calculate the velocity and to determine how similar the local and global pigeons, X_p and X_g, are to one another. The pigeon velocity calculation is shown in Eq (5). The position of the pigeon will be updated in accordance with Eq (6) based on the probability that it is similar to the overall global solution ^[101]:

where r is a constant random number in this case. According to Eq (6), the probability of the solution updating its position in the direction of the global solution is higher if it is not a neighbor of the global solution when compared to if it is.

3.2.2.   Particle Swarm Optimization (PSO)

BPSO, or binary PSO ^[106], is based on the fighting strategies used by flocks of birds. Each particle follows the leader particle (global best) and the nearby particles (local best). The particle best solution (pb) refers to the particle's own optimal position. The global best solution (gb) refers to the solution that best fits the swarm as a whole. d is the dimension of the particle. The values of the variables c₁ and c₂ are both set to 1. r₁ and r₂ represents a random number between 0 and 1. The number of particles and the number of iterations are both set to 50. The position (Eq (8)) and velocity (Eq (7)) in case of PSO is calculated as follows:

Equation (7) is replaced by Eq (9) for BPSO so that $ {X}_{i}^{d}\left(t\right) $ can only be either 0 or 1. Here, the sigmoidal function, Eq (10), is used. For BPSO, the position in the binary search space is converted using a sigmoidal function (using Eq (10)), and Eq (8) is replaced by Eq (11). In the case of the BPSO algorithm, the position and velocity of the i^th particle are calculated by the following:

Additionally, the inertial weight w has a value of 1. rand is a random number selected in the interim [0, 1]. $ Sig\left({v}_{i}^{d}\right) $ denotes a sigmoidal function, and $ {X}_{i}^{d} $ represents the position of the i^th particle in dimension d.

3.3.   Classification approaches

3.3.1.   J48

To create the DT, a modified version of the c4.5 and ID3 algorithms, called J48, is employed ^[49]. The estimate criteria are used for each node of the DT to choose pertinent input variables for prediction. The estimate criteria are based on IG and entropy reduction to determine input variables ^[107]. Equation (12), where pP and pN represent the fraction of positive and negative (training) instances, yields the entropy (E).

There are many different DT algorithms, though one of the most often used ones is probably J48, which is an improved version of the C4.5 tree method and constructs a DT by employing the idea of information entropy ^[108]. J48 has been extensively used in earlier network security efforts ^[24,108,109] since it is an integrable component for the machine learning-based security architecture. Therefore, it is a supervised learning model.

3.3.2.   Random Forest

The RF method is based on ensemble learning. In the paradigm of "ensemble learning", a learning algorithm may be used repeatedly to improve upon itself.

Since a RF is created by repeatedly running the DT algorithm, it is important to fully comprehend the DT technique before attempting to create one ^[110]. When cloud network data from smart cities are provided as the input, the DT algorithm's job in the suggested technique is to forecast if class labels are either normal or anomalous. Each tree in the "forest" is created by resampling using the bootstrap methodology. Additionally, a subset of attributes is randomly chosen on each node split, and this subset is used to pick the split variable. For classification, the projected value is the decision of the majority vote. Breiman ^[50] developed the strategy, which was based on the principles presented by Amit and Geman ^[111].

One of the most effective techniques used in ML for classification issues is RF. The supervised classification category includes the RF technique. Rather than relying on the result of a single DT, learning is carried out based on the outcomes of many DT ^[110].

3.3.3.   XGBoost

XGBoost is a more recent tree classifier that can scale to large-scale data ^[112] and is gaining popularity for its outstanding performance across a variety of applications, including cybersecurity (e.g., ^[24,51,113]). In a nutshell, the classification and regression tree (CART) results are accumulated by Gradient Boosting DT (GBDT) to reach the conclusion. At each iteration, the GBDT must repeatedly traverse the full data collection. The size of the data can only be as much as what can fit in the memory; otherwise, time-consuming read-and-write operations must be performed repeatedly. Therefore, GBDT is unable to satisfy its needs when presented with huge and high-dimensional data. XGBoost was created to address GBDT's problem in handling big samples and high-dimensional data. Tianqi Chen et al. ^[51] advocated for the creation of XGBoost. In order to achieve high efficiency, versatility, and portability, it is an improved distributed gradient improvement library that applies ML methods within the gradient boosting framework.

Decision trees are generated sequentially by the XGBoost system, an efficient gradient tree-boosting method ^[51]. It can somewhat perform pertinent calculations in all computer environments more quickly. Because of its effectiveness in modeling newer features and label classification, XGBoost is widely employed. With the implementation of the XGBoost method in structured and tabular datasets, the use of the technique has greatly increased. The DT-based technique, which involved computing graphical representations of potential decision answers based on specific conditions, served as the foundation for the growth of the XGBoost algorithm. Then, "bagging", which is an ensemble Meta algorithm that aggregates forecasts from several DT using the majoritarian voting technique, was developed. This bagging strategy was further developed to create a forest, or an accumulation of DT, by randomly choosing attributes. The models' performance was improved by lowering the errors that occurred throughout the sequential model generation process. The gradient descent approach was used as an additional improvement to lower the mistakes in the sequential model. Finally, it was determined that the XGBoost algorithm was a useful method for improving the gradient boosting algorithm by removing missing data and eradicating overfitting problems through parallel processing. By utilizing parallelization, tree pruning, and hardware optimization, the XGBoost method optimizes the system.

3.4.   WEKA and sark famework

WEKA ^[48] is a well-known and comprehensive workbench for data mining with an easy-to-use interface. Only a sequential single-node execution is supported. As a result, the size of the datasets and processing jobs that WEKA can manage in its current context is constrained by both sequential execution and the quantity of RAM in a single node. The DistributedWekaSpark may be utilized to circumvent this. It serves as WEKA's distributed framework and preserves the latter's current user interface. The framework is built on top of Spark, a distributed framework linked to Hadoop with quick in-memory processing and support for iterative calculations. WEKA's usability and Spark's processing power are combined to create DistributedWekaSpark, a useable prototype distributed big data mining workbench that executes a variety of real-world scale tasks with an average weak scaling efficiency of 91.4% and an average speed up to 4x quicker than Hadoop ^[114].

The processing engine Apache Spark is incredibly reliable and scalable. It makes use of a resilient distributed dataset (RDD) ^[115], which is a group of fault-tolerant components that may be used concurrently. When processing huge datasets in memory, Apache Spark is noted for being quicker than Apache Hadoop MapReduce. Hadoop processes data from the disc, making it ineffective for applications that frequently use repetition in data mining. A more contemporary distributed framework called Spark ^[40] integrates with Hadoop and offers in-memory computation, which speeds up the processing of iterative jobs, making it a better foundation for data mining. By extending the current WEKA framework, DistributedWekaSpark eliminates the need to completely re-implement algorithms. As a result, existing systems may be more quickly ported, and users can continue to utilize the same interface for both local and remote data processing. In a MapReduce paradigm, it explains a unified framework for representing WEKA's algorithms. As a result, there is no need to examine algorithms to find their parallel components and reimplement them using MapReduce ^[114]. WEKA developer Mark Hall suggested a trio of additional packages that would give WEKA the ability to perform distributed processing. The first new package, DistributedWekaBase, independently performs fundamental map-reduce functions of any other distributed processing platform. The second one is DistributedWekaHadoop, which offers tasks and wrappers based on the Hadoop platform. The third one is DistributedWekaSpark, which performs tasks based on the Spark platform ^[116]. The DistributedWekaSpark includes the Spark core classes that are required and sufficient for local Spark execution on a workstation, communicating with the station's local file system, without the need for a cluster Spark. Additionally, it is possible to run many workers in independent worker threads, taking advantage of all the processors on the computer to maximize power from the project ^[116].

4.   Implementation

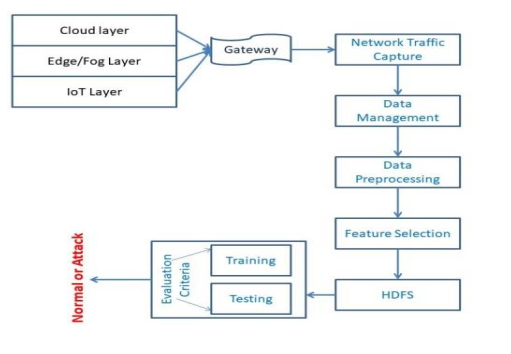
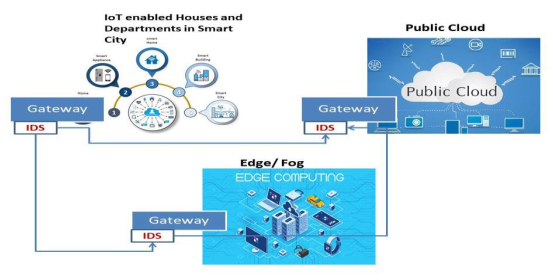
As shown in Figure 5, we suggest an architecture that demonstrates the links between IoT-enabled homes and departments, Edge/Fog, and the Cloud, as well as the deployment of IDS at network gateways.

Figure 5.  Proposed Methodology with Cloud, Edge/Fog, and IoT layer.

DownLoad: Full-Size Img PowerPoint

The Edge/Fog and Cloud layers interact with devices and sensors in homes and departments to subscribe to and broadcast telemetry data over network systems. There are several sensors in smart homes and offices, including sensors for the garage, door, smart light, temperature, humidity, and pressure. In Edge/Fog networks, the suggested IDS system would also be installed at gateways, such as routers and switches. It can be used to defend against zero-day attacks on these networks.

The distributed IDS system that is being proposed is used to keep an eye on the endpoints that connect the Edge/Fog, Cloud, and layers of IoT of residences and departments in a smart city, as depicted in Figure 6. The system gathers key network characteristics from these endpoints, logs them in the HDFS, and then adapts its methodology to train and test either normal or attack network vectors.

Figure 6.  IDS placement in a smart city scenario.

DownLoad: Full-Size Img PowerPoint

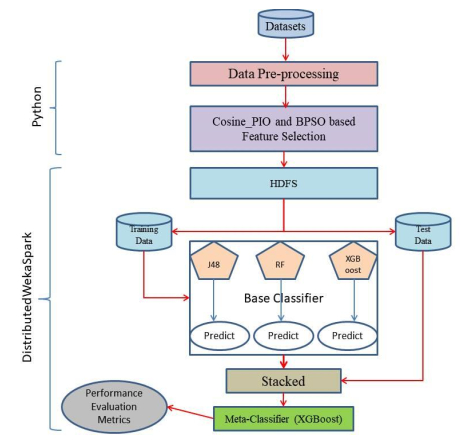
This section delves into the methods for detecting intrusions. DistributedWekaSpark is used to evaluate the dataset, which is stored in an HDFS. Following the FS technique, we built models using three different classifiers as base classifiers, and one meta-classifier, as shown in Figure 7. These stages are outlined in the sections below.

Figure 7.  Proposed methods.

DownLoad: Full-Size Img PowerPoint

4.1.   Data preprocessing

Data preprocessing is an important step that may speed up the experiment and enhance the output. Feature normalization and encoding depending on the intrusion dataset's features are part of data pre-processing.

4.1.1.   Feature normalization

The range of features is normalized by feature scaling, which guarantees that distinct features have different values. Furthermore, training high-dimensional datasets require high computational power. Data is frequently scaled using methods such as Z-score standardization, decimal scaling, Max normalization, and Min–Max scaling to address these difficulties ^[117]. The approach to utilize is frequently determined by the application. Moreover, we have incorporated Min–Max scaling (Eq 13):

where X_min and X_max are the minimum and maximum values of feature X, respectively.

4.1.2.   Feature encoding

For efficient model training, all categorical features will be encoded into vectors. There are several methods for converting categorical data into vectors. 'Label encoding', 'One Hot Encoding', and 'scikit-learn feature mapping' are the most utilized approaches. We adopted the first approach since the number of feature dimensions in the later techniques significantly rises ^[118]. It took a straightforward approach to convert feature values to numeric numbers; for example, the values of instances like "icmp, http, tcp" in the dataset will turn into vectors 0, 1, 2, respectively.

4.1.3.   Feature removal

Two features (attack_cat and label) are the class labels out of the 45 features in the UNSW-NB15 dataset. The last feature in the NSL-KDD dataset is the class label. Since the objective is to reduce the number of features, it is imperative to get rid of them.

4.2.   Feature selection

An adopted metaheuristic based on CPIO and BPSO is used in this article to handle the FS process. In this section, CPIO and BPSO FS techniques were assessed using the NSL-KDD and UNSW-NB15 datasets. The CPIO approach's chosen collection of features from the NSL-KDD and UNSW-NB15 datasets is shown in Table 6. All the aforementioned FS approaches are carried out using Python, on a workstation using a 64-bit Windows operating system and a 2.40 GHz Intel Xeon processor and 16 GB of RAM.

Table 6.  Selected features.

Dataset	Approach	No. of features Selected	Feature Number
NSL-KDD	CPIO	5	27, 22, 10, 6, 2
	BPSO	9	39, 37, 30, 29, 26, 12, 6, 5, 4
UNSW-NB15	CPIO	5	29, 12, 8, 4, 3
	BPSO	16	43, 33, 29, 27, 26, 25, 24, 21, 17, 16, 12, 11, 7, 5, 2, 1

---

 | Show Table

DownLoad: CSV

We investigate only five and nine of the 41 features in the NSL-KDD dataset based on CPIO and BPSO, respectively, and only five and 16 of the 43 features in the UNSW-NB15 dataset based on CPIO and BPSO, respectively. By reducing the number of features, the smaller subset of features may assist us in designing a simpler model. Additionally, the model's detection skills are improved by removing redundant features. Once the FS procedure has been completed using the FS algorithms, the collection of features is trained using an SEM for classification.

4.3.   Stacking Ensemble Method (SEM)

Ensemble approaches are a type of ML methodology in which numerous base classifiers are combined to generate a single, effective prediction model ^[43,119]. The final model will overcome each learner's flaws, yielding a strong model that will improve prediction results. Algorithm 1 explains the procedures necessary for training our proposed SEM.

The SEM is a general architecture made up of two types of classifiers: base and meta-classifiers. The training dataset is used to train the base (initial) classifiers, while a new dataset is created for the meta-classifier. Then, this new dataset is used to train the meta-classifier. Finally, the test dataset is predicted using the trained meta-classifier. We provide a model based on the SEM of ML algorithms, in which J48, RF, and XGBoost serve as base classifiers, and XGBoost serves as a meta-classifier. This research supports all of the proposed classifiers, particularly because their findings are simply interpretable, and their training is robust against outliers.

4.4.   Performance assessment

The most popular performance metrics, including sensitivity, specificity, precision, FPR, accuracy, F1 Score, and MCC, were utilized to assess the performance. Table 7 represents the confusion matrix, which displays how well a classification system performs. The undermentioned metrics in Table 8 are widely used to assess models. The following are the performance metrics. True Positive (TP) refers to an attack sample that has been correctly identified as an attack. A specimen that is correctly identified as normal is represented by the True Negative (TN) code. False Positive (FP) refers to the misidentification of an attack in a normal specimen. An attack sample that has been incorrectly classified as normal is known as a False Negative (FN).

Table 7.  Confusion matrix.

		Actual
		Benign	Malware
Predicted	Benign	TP	FP
	Malware	FN	TN

---

 | Show Table

DownLoad: CSV

Table 8.  Metrics generated from the confusion matrix for performance evaluation.

Metrics	Formula
MCC	"(TP*TN-FP*FN)/sqrt((TP+FP)*(TP+FN)*(TN+FP)*(TN+FN))"
Accuracy	"(TP+TN)/(FP+TP+FN+TN)"
Precision	"TP/(TP+FP)"
Sensitivity	"TP/(TP+FN)"
F1-Score	"2TP/(2TP+FP+FN)"
FPR	"FP/(FP+TN)"
Specificity	"TN/(FP+TN)"

---

 | Show Table

DownLoad: CSV

4.5.   Model performance

Using the features chosen by CPIO and BPSO for the NSL-KDD and UNSW-NB15 datasets, Figures 8 and 9 and Tables 9−12 show the outcomes of the proposed methodology by distinguishing between classes that are either attack or normal for the supplied dataset. By training the model with only the chosen features, each FS strategy or method was tested using the base classifiers and SEM. Then, the model was examined using the testing set. An average of 20 runs was used to calculate the results. However, our analysis considered a more trustworthy metric (such as MCC) that was discovered to produce more accurate estimates for the suggested model. Therefore, our study argues for the use of the MCC metric as an evaluation criterion in future work, particularly in anomaly-based IDS.

Figure 8.  Results for both FS methods on the NSL-KDD dataset.

DownLoad: Full-Size Img PowerPoint

Figure 9.  Results for both FS methods on the UNSW-NB15 dataset.

DownLoad: Full-Size Img PowerPoint

Table 9.  Finding for NSL-KDD dataset using CPIO selected features.

Classifier	Sensitivity	Specificity	Precision	FPR	Accuracy	F1-Score	MCC
J48	0.9289	0.9406	0.9405	0.0594	0.9347	0.9346	0.8695
RF	0.9377	0.9495	0.9494	0.0505	0.9436	0.9435	0.8872
XGBoost	0.9553	0.9674	0.9673	0.0326	0.9613	0.9613	0.9227
Stacking	0.9730	0.9852	0.9852	0.0148	0.9791	0.9790	0.9582

---

 | Show Table

DownLoad: CSV

Table 10.  Finding for NSL-KDD dataset using BPSO selected features.

Classifier	Sensitivity	Specificity	Precision	FPR	Accuracy	F1-Score	MCC
J48	0.9359	0.9477	0.9476	0.0523	0.9418	0.9417	0.8837
RF	0.9474	0.9593	0.9592	0.0407	0.9533	0.9533	0.9067
XGBoost	0.9580	0.9700	0.9700	0.0300	0.9640	0.9639	0.9280
Stacking	0.9801	0.9923	0.9923	0.0077	0.9862	0.9861	0.9724

---

 | Show Table

DownLoad: CSV

Table 11.  Finding for UNSW-NB15 dataset using CPIO selected features.

Classifier	Sensitivity	Specificity	Precision	FPR	Accuracy	F1-Score	MCC
J48	0.9404	0.9395	0.9394	0.0605	0.9400	0.9399	0.8799
RF	0.9441	0.9431	0.9431	0.0569	0.9436	0.9436	0.8872
XGBoost	0.9489	0.9480	0.9479	0.0520	0.9485	0.9484	0.8969
Stacking	0.9562	0.9553	0.9552	0.0337	0.9558	0.9557	0.9115

---

 | Show Table

DownLoad: CSV

Table 12.  Finding for UNSW-NB15 dataset using BPSO selected features.

Classifier	Sensitivity	Specificity	Precision	FPR	Accuracy	F1-Score	MCC
J48	0.9429	0.9419	0.9419	0.0581	0.9424	0.9424	0.8848
RF	0.9477	0.9468	0.9467	0.0532	0.9473	0.9472	0.8945
XGBoost	0.9526	0.9516	0.9516	0.0484	0.9521	0.9521	0.9042
Stacking	0.9587	0.9577	0.9577	0.0323	0.9582	0.9582	0.9164

---

 | Show Table

DownLoad: CSV

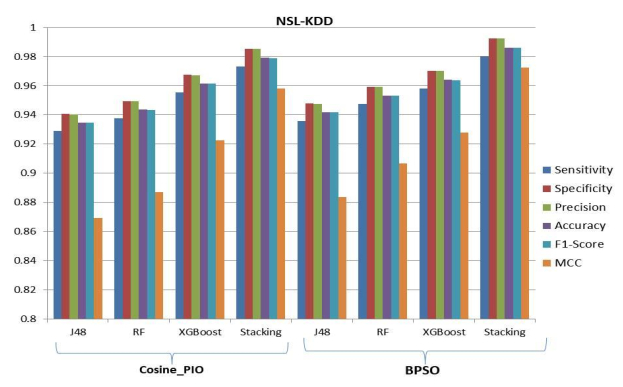
In the case of NSL-KDD, the results of stacking-based classification appear promising for identifying intrusions in the Cloud network data coming from smart cities when using the feature chosen by CPIO and BPSO. The best classification result for the features selected by CPIO, sensitivity (0.9730), specificity and precision (0.9852), accuracy (0.9791), F1-Score (0.9790), MCC (0.9582), and FPR (0.0148), is for SEM, as depicted in Table 9 and Figure 8. The best classification result for the features selected by BPSO, sensitivity (0.9810), specificity and precision (0.9923), accuracy (0.9862), F1-Score (0.9861), MCC (0.9724), and FPR (0.0077), is for SEM, as depicted in Table 10 and Figure 8.

For NSL-KDD, the results of SEM-based classification appear promising for identifying intrusion. A difference of about 0.8188% in sensitivity when the feature selected by BPSO is considered. BPSO selected features generate better classification results, since there is a difference of 0.7225% in accuracy. When CPIO selected features are considered for classification, a higher FPR is obtained; when compared to the consideration of features selected by BPSO, the percentage difference is 63.11% in the FPR.

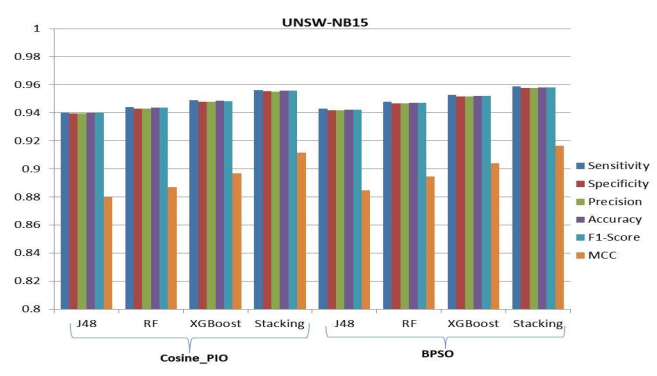
In the case of UNSW-NB15, the results of stacking-based classification appear promising for identifying intrusions in the cloud network data coming from smart cities when using the feature chosen by CPIO and BPSO. The best classification result for the features selected by CPIO, sensitivity (0.9562), specificity (0.9553), precision (0.9552), accuracy (0.9558), F1-Score (0.9557), MCC (0.9115), and FPR (0.0337), is for SEM, as depicted in Table 11 and Figure 9. The best classification result for the features selected by BPSO, sensitivity (0.9587), specificity (0.9577), precision (0.9577), accuracy (0.9582), F1-Score (0.9582), MCC (0.9164), and FPR (0.0323), is for SEM, as depicted in Table 12 and Figure 9.

For UNSW-NB15, a difference of about 0.2611% in sensitivity when the feature selected by BPSO is considered. BPSO selected features generates better classification results as there is a difference of 0.2507% in accuracy. When CPIO selected features are considered for classification, a higher FPR is received; when compared to the consideration of features selected by BPSO, the difference is 4.24% in the FPR.

The stacking approach requires more processing time, since it combines several base classifiers, each of which requires development time. The amount of time it takes classifiers to forecast intrusions for the test dataset is shown in Table 13. In terms of model building and testing time, we found that the best classifiers in our setting are J48 and RF, and J48 obtains the lowest computation time even if the complexity of the stacking model has risen; as a result, the time requirements increased, which beats conventional IDS, as noted in the previous result, and is a significant consideration. If computationally expensive, high-performing classification strategies have significant implications for IoT-based smart cities applications. The cost of missing an intrusion in such a system can be quite expensive. As an outcome, the cost of a little extra time, which is reported in seconds for the datasets examined and therefore potentially well scalable in comparison to earlier approaches, is justified. The capacity to quickly identify odd activity in the network is crucial for the sustainability of services in commercial sectors such as smart cities and financial institutions. Attacks that go unnoticed in these places can be expensive, though manually identifying the attacks can be exceedingly challenging. The focus is on a precise intrusion detection in such systems, which frequently use considerable computational resources for automatically identifying intrusions. As a result, the suggested model has significant practical usefulness. Table 13 shows the model construction time for the given dataset. J48 takes the least amount of time among the classifiers, whereas stacking takes the most time to create models for both datasets.

Table 13.  for the base and stacking ensembles, model construction, and testing time.

Methodologies	NSL-KDD		UNSW-NB15
	Model Building Time (s)	Testing Time (μs)	Model Building Time (s)	Testing Time (μs)
J48	0.458	0.187	0.97	0.436
RF	0.593	0.287	1.30	0.487
XGBoost	1.21	0.79	2.01	1.14
Stacking	6.34	3.09	10.54	5.74

---

 | Show Table

DownLoad: CSV

4.6.   Performance comparison with current methodologies

Using the NSL-KDD and UNSW-NB15 datasets, Table 14 compares the performance of the stacking model with other methodologies. The proposed model outperforms earlier similar ensemble classifiers described in ^[97], which, according to the table, use 10-fold cross validation and consider intrusion detection as a classification issue. In terms of accuracy, our spark-based SEM-oriented ensemble model exceeds several current approaches. A "-" in the table denotes a value that is either inapplicable or unavailable.

Table 14.  Performance comparison with current methodologies.

NSL-KDD
Author & Reference	Year	Methodologies	FS Approach	No. of Features Selected	Accuracy	FPR
Alazzam et al. [101]	2021	DT	SPIO	18	0.869	0.064
			CPIO	5	0.883	0.088
Khraisat et al. [87]	2020	C5-DT/OC-SVM	-	-	0.8324	-
Tama et al. [95]	2019	REPT	PSO	37	0.8579	11.7
Louk and Tama [88]	2023	Bagging-GBM	-	-	0.9157	1.3
Krishnaveli et al. [89]	2022	Weighted majority voting	-	-	0.8523	12.8
Zhang et al. [90]	2021	MFFSEM	-	-	0.8433	24.82
Tama et al. [91]	2020	Stacking	-	-	0.9217	2.52
Prabavathy et al. [76]	2018	OS-ELM	-	-	0.9736	0.37
Shrivas et al. [81]	2014	ANN-Bayesian	GR	29	0.9778	-
Zhou et al. [47]	2020	Voting Ensemble	CFS-BA	10	0.8737	3.19
Salo et al. [97]	2019	Ensemble	IG-PCA	12	0.9824	0.017
Alghanam et al. [92]	2021	LS-PIO	iForest	10	0.947	-
Proposed Work	-	SEM (HDFS and DistributedWekaSpark)	CPIO	5	0.9791	0.0148
			BPSO	9	0.9862	0.0077
UNSW-NB15
Alazzam et al. [101]	2021	DT	SPIO	14	0.913	0.052
			CPIO	5	0.917	0.034
Rashid et al. [45]	2022	Ensemble	SelectKbest	20	0.94	0.06
Smitha et al. [96]	2020	Stacking Ensemble	-	42	0.9400	5.2
Tama et al. [95]	2019	REPT	PSO	19	0.9127	8.90
Alghanam et al. [92]	2021	LS-PIO	iForest	10	0.9445	-
Zehong et al. [93]	2022	EFS-DNN	Light-GBM	15	0.8834	12.46
Nazir et al. [95]	2021	TS-RF	TS	16	0.8312	3.7
Proposed Work	-	SEM (HDFS and DistributedWekaSpark)	CPIO	5	0.9558	0.0337
			BPSO	16	0.9582	0.0323

---

 | Show Table

DownLoad: CSV

For comparing the outcomes, we primarily employ the accuracy and FPR variables. This is a tried-and-true method that has been applied to a variety of practical machine-learning projects. We have compared the achieved rates with those presented in undermentioned work because accuracy rates are a crucial component of any IDS performance evaluation. Since our method uses a nature-inspired FS approach and classifiers that are HDFS and Spark-based, which is not the case with the other models, it outperforms the other models' accuracy rates. FPR is a term used to explain the inability to recognize normal behavior. In other words, there is a warning. The table below compares the FPR of our methodology to the works described in the citations. Compared to the current state-of-the-art, our method yields the lowest FPR: 0.0077% for NSL-KDD and 0.0323% for UNSW-NB15.

Our approach is distributed in nature with the aid of HDFS and DistributedWekaSpark, thereby ensuring high availability and fault tolerance of our IDS and making it appropriate to handle big Cloud network data of smart cities, which is another crucial point that sets it apart from all the works cited. Our presented methodology outperforms ^[101] in terms of accuracy and the number of selected features, while using the same number of features. Additionally, the comparative results demonstrate that our work surpasses many other works in terms of accuracy and FPR when using the NSL-KDD and UNSW-NB15 datasets, as shown in Table 14. In comparison to ^[95], we can see that our research is able to identify fewer features for the NSL-KDD and UNSW-NB15 datasets, with the latter displays a superior accuracy. Summarizing the results, we can see that our approach outperformed all other methods in terms of accuracy. The suggested model makes it abundantly evident that the presented approach outperforms earlier reported approaches in terms of results.

5.   Conclusions

In this study, we developed a distributed and potent IDS that enables the processing of large amounts of Cloud data from Smart Cities and improves accuracy while utilizing the fewest features possible. It uses Spark and ML approaches to effectively manage massive amounts of data in vast networks of smart cities. We used the Python-based FS methods CPIO and BPSO to create this system. The IDS used in this study for Cloud network data from smart cities used Spark and WEKA. Due to the connection between WEKA and Spark (DistributedWekaSpark package), it is distributed and scalable. Using the capabilities of distributed systems while maintaining the familiar WEKA interface, DistributedWekaSpark is a scalable Big Data Mining toolkit. Built on top of Spark, DistributedWekaSpark offers quick in-memory iterative processing using both parallel and distributed execution, making it the perfect platform for data mining techniques. Using WEKA's Knowledge flow, this combination enables the analysis of Cloud network data for smart cities and the storage of HDFS data. In order to build parallelized learning models for cyber-data analytics, we used machine-learning approaches for feature extraction and selection. For NSL-KKD and UNSW-NB15, the CPIO FS technique reduced the number of selected features from 41 to five and from 43 to five features, respectively. For NSL-KKD and UNSW-NB15, the BPSO FS technique reduced the number of selected features from 41 to nine and from 43 to 16 features, respectively. For classifying the cloud network traffic of smart cities, the tree-based SEM of J48, RF, and XGBoost was applied. The best results were obtained for sensitivity (0.9810), specificity and precision (0.9923), accuracy (0.9862), F1-Score (0.9861), MCC (0.9724), and FPR (0.0077) in the NSL-KDD dataset, while in case of UNSW-NB15 dataset, the best results were obtained for sensitivity (0.9587), specificity (0.9577), precision (0.9577), accuracy (0.9582), F1-Score (0.9582), MCC (0.9164), and FPR (0.0323). The results demonstrate that CPIO and BPSO contribute to a greater accuracy and better outcomes fitting. Since Spark functionality has been implemented, our methodology has been discovered to be scalable and dispersed, making it suitable for the IoT context of smart cities. Compared to contemporary systems, our suggested system experimentally exhibits a higher accuracy and lower FPR.

As a result, research in the future must take a larger range of intrusion data sets in diverse settings, environments and with wider range of threats into account. More evaluation metrics will be used in upcoming studies. Using upgraded and latest nature-inspired algorithms for FS and several deep neural network algorithms, including Auto-Encoder, Gated Recurrent Units and LSTM, will be used to implement the strategy. We intend to use explainable AI for IDS ML/DL-based algorithms for the detection and classification of cyberattacks in networks of smart cities.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgements

The first author would like to thank the Department of Science & Technology (DST), Ministry of Science and Technology, GOI, for financial support in terms of research fellowship (DST-INSPIRE).

Conflict of interest

The authors declare that they do not have any known competing interests.

Appendix

This section provides instructions for setting up Weka-Spark to work with a Hadoop cluster in order to continue managing data for the intrusion detection issue in cloud networks for smart cities. Weka's ability to be used as a data mining tool is one of its benefits. Since it was created in Java, it can function on any OS as long as JVM is installed (Java Virtual Machine). Applications written for Spark can operate on any OS, albeit Windows requires some specialized libraries for execution whereas Linux does not. To use the Spark utilities in Weka, in addition to these prerequisites, a number of basic setups must be completed. First, the environment variables for Java and Hadoop must be established. Second, the Hadoop environment variable's path must contain both the hadoop.dll and the winutils library, and at last DistributedWekaBase and DistributedWekaSpark dependencies need to be installed on the Weka. With all of the prior Weka Knowledge Flow settings, a result similar to that in Figure A.1 is shown.

Figure A.1.  Spark elements in the Weka's knowledge flow palette.

DownLoad: Full-Size Img PowerPoint

The tool WekaClassifierEvaluationSparkJob is used for J48, RF, and XGBoost training and evaluation. It allows assessing a classifier using cross-validation, a distinct dataset, or training data. In our case, for training, the training dataset is used while for testing the data, a distinct test dataset is employed. The data for training is passed through the ArffHeaderSparkJob, so some of the most crucial variables must be indicated, including the path (Copy the datasets' CSV files to HDFS and point the inputFile setting of the ArffHeaderSparkJob to the HDFS location) to the data to execute the evaluation and the chosen classifier, stacking. Three base classifiers are added to the stacking section's classifier field, and XGBoost is selected as the meta-classifier. The fields that contain the route in HDFS to a different test suite that includes the path detail to the test dataset are some of the most crucial fields.

Weka's KnowledgeFlow is an alternative to Weka Explorer with a graphical environment. It is well known for its simplicity of use because it is a fairly intuitive work system with a graphical interface that allows you to drag the objects from a palette to the workspace and create connections between them in various types to obtain the results and information.

All of the filters, classifiers, regressors, and other tools that are present in the version of Weka that is being used can be used in KnowledgeFlow ^[117]. Additionally, some additional tools can be used, such as in the case presented in this work, which is the distributed processing capability of Hadoop and Spark. While Explorer only handles batch data, KnowledgeFlow can process data incrementally or in large batches ^[117]. Once the libraries are installed and configured, one can find the many Spark jobs that can be carried out in the Weka component palette. The TextViewer is the last visualization tool that is suggested; it enables the data to be obtained in text form for subsequent analysis and storage. Once the runs are completed, getting the results is quite easy because they are stored in the output configuration folder, 'OutputDir', as well as in the TextViewer, which allows you to view the results of the tests.

In addition to Weka's KnowledgeFlow, a Web service offered by Spark that is active on the computer where the application driver is running allows for more detailed monitoring of the applications and their progress. With access through a Web browser to the website where the cluster jobs are monitored through its URL and its web access port, by default this is 8080, you can check if the program is discovered running, as well as the resources it has, in addition to other extensive capabilities.