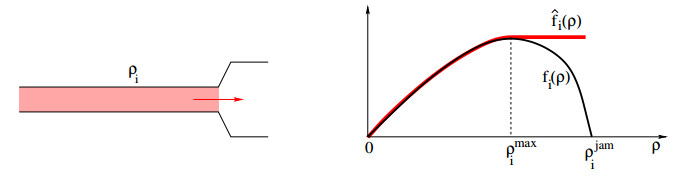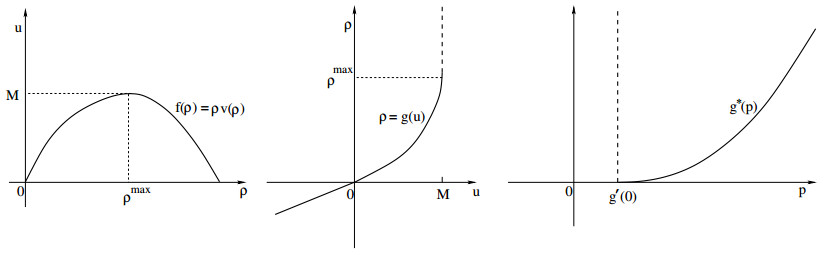Globally optimal departure rates for several groups of drivers

1.   Introduction

Macroscopic models of traffic flow, first introduced in ^[26,28], have now become a topic of extensive research. On a single road, the evolution of the traffic density can be described by a scalar conservation law. In order to extend the model to a whole network of roads, additional boundary conditions must be inserted, describing traffic flow at each intersection; see ^{[10,16,20,21,23,24]} or the survey ^[4]. A major eventual goal of these models is to understand traffic patterns, determined by the behavior of a large number of drivers with different origins and destinations.

In a basic setting, one can consider $N$ groups of drivers, say ${\cal G}_1, \ldots, {\cal G}_N$. Drivers from each group have the same origin and destination, and a cost which depends on their departure and arrival time. For such a model, two kind of solutions are of interest:

$-$ The Nash equilibrium solution, where each driver chooses his own departure time and route to destination, in order to minimize his own cost.

$-$ The global optimization problem, where a central planner seeks to schedule all departures in order to minimize the sum of all costs.

In general, these criteria determine very different traffic patterns. To fix the ideas, let $t\mapsto u_i(t)$, $i = 1, \ldots, N$, be the departure rate of drivers of the $i$-th group, so that

yields the total number of these drivers who depart before time $t$. We recall that the support of $u_i$, denoted by Supp$(u_i)$, is the closure of set of times $t$ where $u_i(t) > 0$.

Roughly speaking, the two above solutions can be characterized as follows.

(Ⅰ) In a Nash equilibrium, all drivers within the same group pay the same cost. Namely, there exists constants $K_1, \ldots, K_N$ such that

● every driver of the $i$-th group, departing at a time $t\in Supp(u_i)$ bears the cost $K_i$.

● if a driver of the $i$-th group were to depart at any time $t\in I\!\!R$ (possibly outside the support of $u_i$), he would incur in a cost $\geq K_i$.

(Ⅱ) For a global optima, there exist constants $C_1, \ldots, C_n$ (where $C_i$ is the marginal cost for adding one more driver of the $i$-th group) such that

● If one additional driver of the $i$-th group is added at any time $t\in \hbox{Supp}(u_i)$, then the total cost increases by $C_i$.

● If one additional driver of the $i$-th group is added at any time $t\in I\!\!R$ (possibly outside the support of $u_i$), then the increase in the total cost is greater or equal to $C_i$.

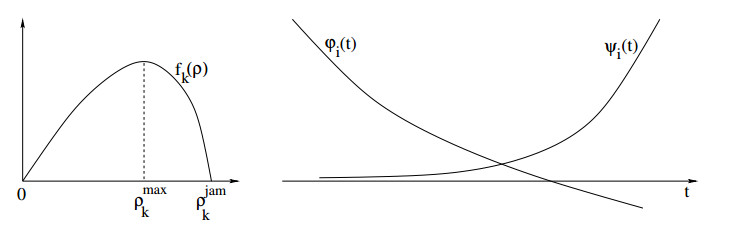
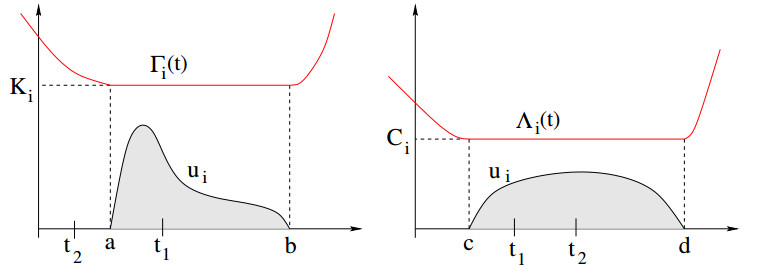
At an intuitive level, these conditions are easy to explain. In Figure 1(left), the function $\Gamma_i(t)$ denotes the cost to an $i$-driver departing at time $t$. If $\Gamma_i$ did not attain its global minimum simultaneously at all points $t\in [a, b] = \hbox{Supp}(u_i)$, then we could find times $t_1\in [a, b]$ and $t_2\in I\!\!R$ such that $\Gamma_i(t_2) < \Gamma_i(t_1)$. In this case, the driver departing at time $t_1$ could lower his own cost choosing to depart at time $t_2$ instead. This contradicts the definition of equilibrium.

In Figure 1(right), the function $\Lambda_i(t)$ denotes the marginal cost for inserting one additional driver of the $i$-th family, departing at time $t$. This accounts for the additional cost to the new driver, and also for the increase in the cost to all other drivers who are slowed down by the presence of one more car on the road. If $\Lambda_i$ did not attain its global minimum at all points in $[c, d] = \hbox{Supp}(u_i)$, then we could find times $t_1\in [c, d]$ and $t_2\in I\!\!R$ such that $\Lambda_i(t_2) < \Lambda_i(t_1)$. In this case we could consider a new traffic pattern, with one less driver departing at time $t_1$ and one more departing at time $t_2$. This would achieve a smaller total cost, contradicting the assumption of optimality.

While the criterion (Ⅰ) for an equilibrium solution is easy to justify, a rigorous proof of the necessary condition (Ⅱ) for a global optimum faces considerable difficulties. Indeed, to compute the ``marginal cost" for adding one more driver, one should differentiate the solution of a conservation law w.r.t. the initial data (or the boundary data). As it is well known, in general one does not have enough regularity to carry out such a differentiation. To cope with this difficulty one can introduce a ``shift differential", describing how the shock locations change, depending on parameters. See ^{[8,9,13,27,30]} for results in this direction.

The first part of this paper contains an introduction to macroscopic models of traffic flow on a network of roads. Section 2 starts by reviewing the classical LWR model for traffic flow on a single road, in terms of a scalar conservation law for the traffic density. We then discuss various boundary conditions, modeling traffic flow at an intersection. Finally, given a cost function depending on the departure and arrival times of each driver, we review the concepts of globally optimal solution and of Nash equilibrium solution.

The second part of paper contains original results. We consider here $N$ groups of drivers traveling along the same road, but with different departure and arrival costs. We seek departure rates $u_1(\cdot), \ldots, u_N(\cdot)$ which are globally optimal. Namely, they minimize the sum of all costs to all drivers. A set of necessary conditions for optimality is derived, thus extending the result in ^[5] to the case where several groups of drivers are present. Relying on these conditions, in the last section we introduce an algorithm that numerically computes such globally optimal solutions.

For an introduction to the general theory of conservation laws we refer to ^[3,19,29]. A more comprehensive discussion of various models of traffic flow can be found in ^[1,2,18,20].

2.   Conservation law models for traffic flow

2.1.   Traffic flow on a single road

According to the classical LWR model ^[26,28], traffic density on a single road can be described in terms of a scalar conservation law

Here $t$ is the time, while $x\in I\!\!R$ is the space variable along the road. Moreover

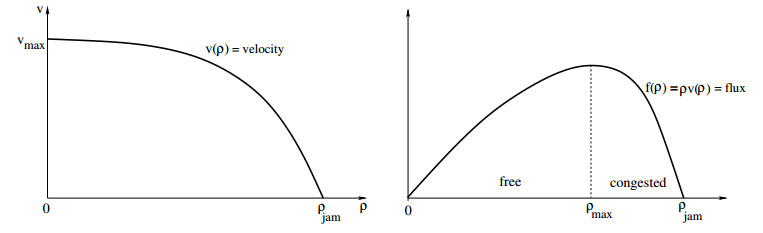
● $\rho$ is the traffic density, i.e., the number of cars per unit length of the road.

● $v = v(\rho)$ is the velocity of cars, which we assume depends only on the traffic density.

● $f = f(\rho)$ is the flux, i.e., the number of cars crossing a point $x$ along the road, per unit time. We have the identity

As shown in Figure 2, the velocity should be a decreasing function of the car density. Concerning the flux function, a natural set of assumptions is

Here $\rho_{jam}$ is the maximum density of cars allowed on the $k$-th road. This corresponds to bumper-to-bumper packing, where no car can move.

Smooth solutions of the conservation law (2.1) can be computed by the classical method of characteristics. By the chain rule, one obtains

Hence, if $t\mapsto x(t)$ is a curve such that

then the equation (2.3) yields

In other words, the density is constant along each characteristic curve satisfying (2.4). Notice that the assumptions (2.2) imply the inequality

With reference to Figure 2, let $\rho_{max}$ be the density at which the flux is maximum. We say that a state $\rho$ is

● free, if $\rho < \rho_{max}$, hence the characteristic speed $f'(\rho)$ is positive,

● congested, if $\rho > \rho_{max}$, hence the characteristic speed $f'(\rho)$ is negative.

Due to the non-linearity of the flux function $f$, it is well known that solutions can develop shocks in finite time. The conservation law (2.1) must thus be interpreted in distributional sense. For the general theory of entropy weak solutions to conservation laws, we refer to ^[3,29].

2.2.   Traffic flow at road intersections

To model vehicular traffic on an entire network of roads, the conservation laws describing traffic flow on each road must be supplemented with boundary conditions, describing the behavior at road intersections.

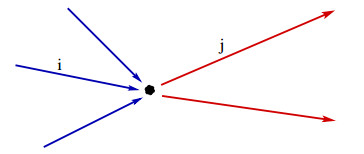
Consider an intersection, say with $m$ incoming roads $i\in \{1, \ldots, m\} = {\cal I}$ and $n$ outgoing roads $j\in \{m+1, \ldots, m+n\} = {\cal O}$, see Figure 3. We shall use the space variable $x\in \, ]-\infty, \, 0]$ for incoming roads and $x\in [0, +\infty[\,$ for outgoing roads. Throughout the following we assume that the density of traffic on each road is governed by a conservation law

where the flux function $f_k$ satisfies (2.2), for every $k = 1, \ldots, m+n$.

An appropriate model must depend on various parameters, namely

● $c_i$ = relative priority of drivers arriving from road $i$.

● $\theta_{ij}$ = fraction of drivers from road $i$ that turn into road $j$.

For example, if the intersection is regulated by a crosslight, $c_i$ could measure the fraction of time when drivers from road $i$ get green light, on average. It is natural to assume

Boundary conditions should determine the limit values of the traffic density on each of the $m+n$ roads meeting at the intersection:

At first sight, one might guess that $m+n$ conditions will be required. However, this is not so, because on some roads the characteristics move toward the intersection. For these roads, the limits in (2.7) are already determined by integrating along characteristics. Boundary conditions are required only for those roads where the characteristics move away from the origin. Recalling the definition of free and congested states, we thus have

It now becomes apparent that, to assign a meaningful set of boundary conditions, several different cases must be considered.

To circumvent these difficulties, an alternative approach developed by Coclite, Garavello, and Piccoli ^[16,21,22] relies on the construction of a Riemann Solver. Instead of assigning a variable number of boundary conditions, here the idea is to introduce a rule for solving all Riemann problems (i.e., the initial-value problems where at time $t = 0$ the densities $\rho_k$ and turning preferences $\theta_{ij}$ are constant along each road). Relying on front-tracking approximations, under suitable conditions one can prove that the solutions with general initial data are also uniquely determined.

We briefly review the main steps of this construction, for the constant initial data

Step 1. Determine the maximum flux $f_i^{max}$ that can exit from each incoming road $i\in{\cal I}$.

As shown in Figure 4, this is computed by

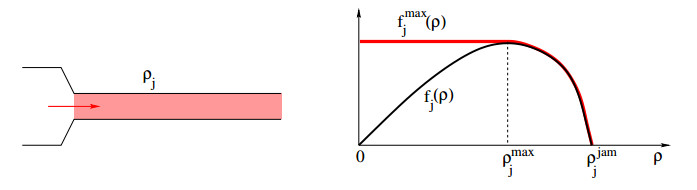
Step 2: Determine the maximum flux $f_j^{max}$ that can enter each outgoing road $j\in{\cal O}$.

As shown in Figure 5, this is computed by

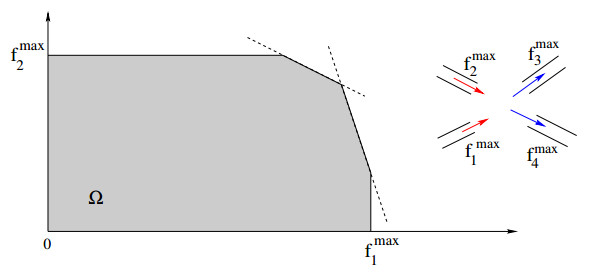
Step 3: Given the maximum incoming and outgoing fluxes $f_i^{max}$, $f_j^{max}$, and the turning preferences $\theta_{ij}$, determine the region of admissible incoming fluxes (see Figure 6)

Step 4. To construct a Riemann solver, it now suffices to give a rule for selecting a point $\bar \omega = (f_1, \ldots, f_m)$ in the feasible region $\Omega$. In general, this rule will depend on the priority coefficients $c_1, \ldots, c_m$ assigned to incoming roads. Observe that, as soon as the incoming fluxes $f_i$, $i\in{\cal I}$, are given, the outgoing fluxes are uniquely determined by the identities

Various ways to define a Riemann Solver are illustrated by the following examples.

Example 1: Given priority coefficients $c_1, \ldots, c_m$, following ^[16] one can choose the vector of incoming fluxes

In particular, if $c_1 = \cdots = c_m = {1\over m}$, this means we are maximizing the total flux through the intersection (see Figure 7(left)).

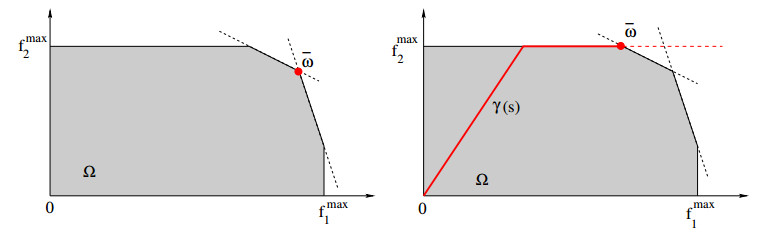
Since in (2.10) we are maximizing a linear function over a polytope, in some cases the maximum can be attained at multiple points. This somewhat restricts the applicability of this model. An alternative model, with better continuity properties, is considered below.

Example 2: Given positive coefficients $c_1, \ldots, c_m$ as in (2.6), consider the one-parameter curve

where

As shown in Figure 7(right), we then choose the vector of incoming fluxes

where

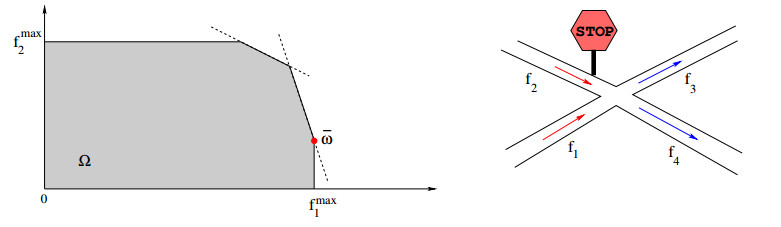
Example 3 : To model an intersection with two incoming and two outgoing roads, where road 2 has a stop sign, we choose the point $\overline\omega = (f_1, f_2)$ according to the following rules (see Figure 8).

According to (2.13), as many cars as possible are allowed to arrive from road 1. According to (2.14), if any available space is left, cars arriving from road 2 are allowed through the intersection.

2.3.   Intersection models with buffers

Having defined a way to solve each Riemann problem, a major issue is whether the Cauchy problem with general initial data is well posed. Assuming that the turning preferences $\theta_{ij}$ remain constant in time, some results in this direction can be found in ^[16].

We remark, however, that in general these turning preferences may well vary in time. One should thus regard $\theta_{ij} = \theta_{ij}(t, x)$ as variables. Assuming that drivers know in advance their itinerary, the conservation of the number of drivers on road $i$ that will eventually turn into road $j$ is expressed by the additional conservation law

Combining (2.15) with the conservation law

one obtains a linear transport equation for each of the quantities $\theta_{ij}$, namely

A surprising counterexample constructed in ^[14] shows that, for a very general class of Riemann Solvers, one can construct measurable initial data $\rho_i(0, \cdot)$, $\rho_j(0, \cdot)$, and $\theta_{ij}(0, \cdot)$, so that the Cauchy problem has two distinct entropy-admissible solutions.

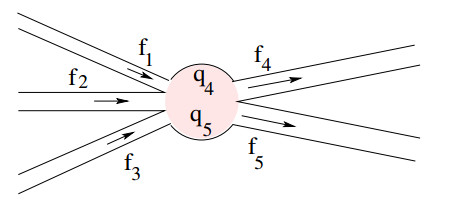
The ill-posedness of these model equations represents a serious obstruction, toward the existence of globally optimal traffic patterns, or Nash equilibria, on a general network of roads. To cope with this difficulty, in ^[10] an alternative model was proposed, for traffic flow at an intersection. Namely, it is assumed that the junction contains a buffer (say, a traffic circle), as shown in Figure 9. Incoming cars are admitted at a rate depending of the amount of free space left in the buffer, regardless of their destination. Once they have entered the intersection, cars flow out at the maximum rate allowed by the outgoing road of their choice.

More precisely, consider a constant $M > 0$, describing the maximum number of cars that can occupy the intersection at any given time, and constants $c_i > 0$, $i\in {\cal I}$, accounting for priorities given to different incoming roads. For $j\in {\cal O}$, at any time $t$ we denote by $q_j(t)\in [0, M]$ the number of cars, already within the buffer, that seek to turn into road $j$.

As before, let $f_i^{max}$ and $f_j^{max}$ the maximum fluxes that can exit from road $i\in{\cal I}$, or can enter into road $j\in{\cal O}$. We then require that the incoming fluxes $f_i$ satisfy

In addition, the outgoing fluxes $f_j$ should satisfy

Having determined the incoming and outgoing fluxes $f_i$, $f_j$, the time derivatives of the queues $q_j$ are then computed by

The well-posedness of the intersection model with buffers, for general ${\bf L}^\infty$ data, was proved in ^[10].

It is interesting to understand the relation between the intersection model with buffer, and the models based on a Riemann Solver. The analysis in ^[12] shows that, letting the size of the buffer $M\to 0$, the solution of the problem with buffers converges to the solution determined by the Riemann Solver at (2.11) and (2.12), described in Example 2.

2.4.   Optima and equilibria on a network of roads

Consider a network of roads, with several intersections. We call $\gamma_k$, $k = 1, \ldots, \bar k$ the arcs corresponding to the various roads, and $A_1, \ldots, A_\nu$ the nodes corresponding to intersections. It is assumed that, on the $k$-th road, the flux function has the form $f_k(\rho) = \rho\, v_k(\rho)$, with $v_k$ a decreasing function of the density. As in the previous sections, traffic flow at each intersection can be modeled in terms of a Riemann Solver, or by means of a buffer.

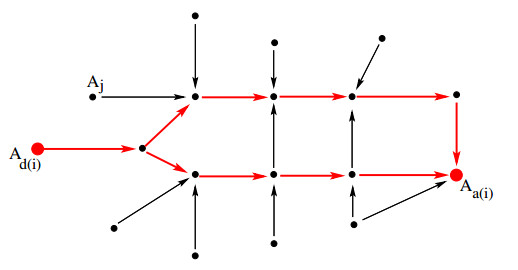
We consider $N$ groups of drivers with different origins and destinations, and possibly different departure and arrival costs. As shown in Figure 10:

● Drivers in the $i$-th group depart from the node $A_{d(i)}$ and arrive at the node $A_{a(i)}$.

● Their cost for departing at time $t$ is $\varphi_i(t)$, while their arrival cost is $\psi_i(t)$.

● They can use different paths $\Gamma_1, \Gamma_2, \ldots$ to reach destination.

In the following, $\bar u_{i, p}(\cdot)$ will denote the departure rate of drivers of the $i$-th group, who choose the path $\Gamma_p$ to reach destination. Calling $G_i$ the total number of drivers in the $i$-th group, we say that the departure rates $\bar u_{i, p}$ are admissible if, for every $i = 1, \ldots, N$ they satisfy the obvious constraints

Given the departure rates, in principle one can then solve the equation of traffic flow on the whole network and determine the arrival times of the various drivers. We call

In practice, we always expect $\tau_p(t) < +\infty$. However, it is possible to envision a situation where traffic becomes completely stuck, and $\tau_p$ becomes infinite. See ^[15] for a discussion of this issue.

With the above notations, we can introduce

Definition 2.1. An admissible family $\{ \bar u_{i, p}\}$ of departure rates is globally optimal if it minimizes the sum of the total costs of all drivers

Definition 2.2. An admissible family $\{ \bar u_{k, p}\}$ of departure rates is a Nash equilibrium if no driver of any group can lower his own total cost by changing departure time or switching to a different path to reach destination.

From the above definition it follows the existence of constants $C_1, \ldots, C_N$ such that

As remarked in the Introduction, a similar characterization for the globally optimal solution is much harder to justify.

In the above setting, a natural set of assumptions is (see Figure 11)

${\bf (A1)}$ On each road $k = 1, \ldots, \bar k$, the flux function $f_k$ satisfies

${\bf (A2)}$ For each group of drivers $i = 1, \ldots, N$, the cost functions $\varphi_i$, $\psi_i$ satisfy

When all intersections are modeled in terms of a buffer as in (2.17)–(2.19), under the assumptions (A1), (A2) the existence of a globally optimal solution was proved in ^[11]. Moreover, if an upper bound on the travel time $\tau_p(t)-t$ can be given, then a Nash equilibrium solution also exists.

3.   Optimal solutions: A single road, several groups of drivers

Consider a single road, where the traffic density is governed by the conservation law

We assume that $N$ groups of drivers are present, of sizes $G_1, \ldots, G_N$, with departure and arrival costs $\varphi_i$, $\psi_i$, $i = 1, \ldots, N$. The flux function will be denoted by

Here

is the flux of drivers of the $i$-th group. As in (2.6), we always assume that

For each $i\in \{1, \ldots, N\}$, the conservation of the number of drivers of the $i$-th family yields the additional conservation law

By (3.1), one obtains the linear equations

The incoming flux at the beginning of the road is

The global optimization problem can be formulated as follows.

${\bf (OP)}$ Given the constants $G_i > 0$, $i = 1, \ldots, N$, find departure rates $\bar u_i(t) = \bar\theta_i(t)\bar u(t)$ which provide an optimal solution to the problem

and satisfy the constraints

We recall that $u_i(t, L) = \theta_i(t, L) u(t, L)$ is the rate at which the drivers of the $i$-th group arrive at the end of the road.

Since no intersections are present, the existence of a globally optimal solution follows as a special case of the result in ^[11]. Here we briefly recall the main argument in the proof.

1. Let $(\bar u_1^{(n)}, \ldots, \bar u_N^{(n)})_{n\geq 1}$ be a minimizing sequence of admissible departure rates. Namely

for every $n\geq 1$, and moreover

2. By the assumption (A2), as $t\to \pm\infty$ the cost functions $\varphi_i, \psi_i$ become very large. By possibly modifying the functions $\bar u_i$, we can thus obtain a minimizing sequence where all departure rates vanish outside a fixed time interval $[a, b]$.

3. By taking a subsequence, we obtain a weak limit $(\bar u_1^{(n)}, \ldots, \bar u_N^{(n)})\rightharpoonup (\bar u_1, \ldots, \bar u_N)$.

The boundedness of the supports guarantees that these limit departure rates are still admissible (i.e., no mass leaks at infinity).

4. Call $u_i^{(n)}(t, x)$, $u_i(t, x)$ the corresponding solutions. By the genuine nonlinearity of the conservation law (3.1), after taking a subsequence, one obtains the strong convergence $u^{(n)}(\cdot, L)\to u(\cdot, L)$ in ${\bf L}^1 ( I\!\!R)$, and the weak convergence of the departure and arrival rates

Since the cost functional in (3.7) is linear w.r.t. these departure and arrival rates, it is continuous w.r.t. weak convergence. This yields the optimality of the departure rates $(\bar u_1, \ldots, \bar u_N)$.

3.1.   Optimality conditions

In the remainder of this section, we seek necessary conditions for a solution to be optimal. As a first step, we derive an explicit representation of the solution.

Following ^[5,6], it is convenient to switch the roles of the variables $t, x$, and write the density $\rho$ as a function of the flux $u$. The boundary value problem (3.1)–(3.6) thus becomes a Cauchy problem for the conservation law describing the flux $u = \rho v(\rho)$, namely

As shown in Figure 12, the function $u\mapsto g(u) = \rho$ is defined as a partial inverse of the function $\rho\mapsto \rho\, v(\rho) = u$, assuming that

To justify this assumption, consider any solution $\rho = \rho(t, x)$ of (2.1), where the initial data satisfy

Then, since all cars that reach the end of the road at $x = L$ can exit immediately, we have

For convenience, we extend $g$ to the entire real line by setting

The solution to (3.10) and (3.11) can now be expressed by means of the Lax formula ^[19,25]. Namely, call

the Legendre transform of $g$. Notice that

On the other hand, for $p \geq g'(0)$ the strict convexity of $g$ implies that there exists a unique value $u = \gamma(p)\geq 0$ where the maximum in (3.13) is attained, so that

This function $\gamma: [g'(0), +\infty[\, \mapsto [0, M[\,$ is implicitly defined by the relation

Consider the integrated function

which measures the number of drivers that have crossed the point $x$ along the road before time $t$. The conservation law (3.10) can be equivalently written as a Hamilton-Jacobi equation

with data at $x = 0$

The solution to (3.10) and (3.11) is now provided by the Lax formula

We observe that the function $U = U(t, x)$ is globally Lipschitz continuous. Its values satisfy

Car trajectories $t\mapsto y(t)$ are defined to be the solutions to the ODE

In the region where $\rho > 0$, and hence $u = \rho v(\rho) > 0$ as well, these trajectories coincide with the level curves of the integral function $U$. Indeed, observing that $v = u/\rho$, when $\rho = g(u) > 0$ we can write

By (3.15) one has

More generally, consider a car departing at time $t_0$. The solution to the Cauchy problem

can be determined by the formula

The arrival time of a driver departing at time $t_0$ is

By (3.5), the functions $\theta_i$ are constant along car trajectories. With the notation introduced in (3.24), in connection with the boundary data (3.6) we thus have the identities

In order to compute the arrival rates $u_i = \theta_iu$ at the terminal point of the road $x = L$, we first observe that the map

in (3.16) is nondecreasing. Hence we can define an inverse by setting

We then introduce the functions

By (3.5), the functions $\theta_i = \theta_i(t, x)$ are constant along car trajectories. The general solution to (3.5) and (3.6) can thus be written as

We shall be mostly interested in the terminal values $u(t, L)$, describing the rate at which cars arrive at the end of the road. Denoting the arrival distribution as $U^a (t)\doteq U(t, L)$, the total cost can now be written as

Theorem 3.1. Let the flux function $f$ satisfy the standard assumptions (2.2). Assume that all drivers have the same departure cost $\varphi_i = \varphi$ and possibly different arrival costs $\psi_1, \ldots, \psi_N$, satisfying (2.22). Let $(\bar u_1, \ldots, \bar u_N)$ an optimal departure rate, minimizing the total cost to all drivers.

Then the corresponding solution does not contain shocks. Moreover, there exists constants $C_1, \ldots, C_N$ such that, setting

the following holds:

(i) For any $t\in I\!\!R$, let $T(t)$ be the unique time such that

Then, for every point $(t', x')$ along the segment with endpoints $(t, 0)$ and $(T(t), L)$, one has

(ii) Calling $u_i(\cdot, L)$ the arrival rate of drivers of the $i$-th group, one has

A proof of Theorem 3.1 will be given in the next section.

Remark 3.2. The above theorem can be regarded as a first step in the analysis of optimality conditions for traffic flow on a general network. A natural further step would be to look at optimality conditions for (ⅰ) two groups of drivers, starting their journey on the same road and then bifurcating on two distinct roads, or (ⅱ) two groups of drivers starting on two distinct roads that merge into a single one.

We remark that the optimal solution constructed in Theorem 3.1 does not change if the cost functions $\varphi_i, \psi_i$, $i = 1, \ldots, N$, are replaced by $\varphi_i+c_i, \psi_i+c_i$ respectively, for any constants $c_1, \ldots, c_N$. Therefore, the result remains valid if one only assumes that any two departure costs $\varphi_i, \varphi_j$ differ by a constant.

4.   Proof of the necessary conditions

As a preliminary, we review the basic theory of scalar conservation laws with convex flux ^[3,19,29]. Notice that in (3.10) the usual role of the variables $t, x$ is reversed, because of the particular meaning of the equations.

Let $u = u(t, x)$ be a weak solution to (3.10), taking values within the interval $[0, M]$. This solution is entropy admissible if it contains only downward jumps, namely

By a generalized characteristic we mean a function $x\mapsto t(x)$ which provides a solution to the differential inclusion

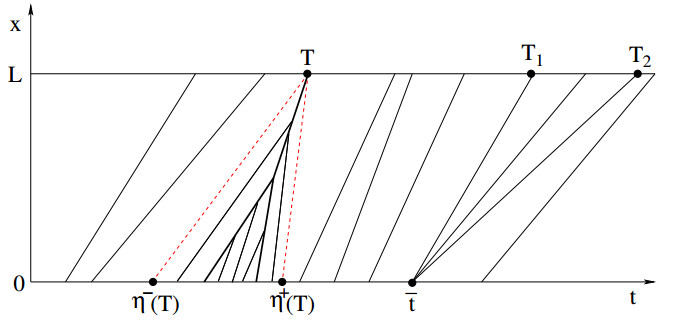
For any given point $(T, L)$, there exists a minimal and a maximal backward characteristic. As shown in Figure 13, we denote by $(\eta^-(T), 0)$ and $(\eta^+(T), 0)$ the initial points of these characteristics. Calling $\overline U$ the integral function in (3.16), the points $\eta^-(T)$ and $\eta^+(T)$ are respectively the minimum and the maximum elements within the set

where the function $\Lambda(t)\; \doteq\; L g^*\left({T-t\over L}\right) + \overline U(t)$ attains its global minimum.

Two cases can occur:

(ⅰ) The global minimum in (4.2) is attained at a single point $t^* = \eta^-(T) = \eta^+(T)$.

The function $u(\cdot, L)$ is then continuous at the point $T$, and

(ⅱ) The global minimum in (4.2) is attained at multiple points, hence $\eta^-(T) < \eta^+(T)$.

In this case the solution contains a shock through the point $(T, L)$. Recalling (3.14), the left and right values across the shock are determined by

We observe that characteristics do not cross each other. Indeed, one has the implication

From (4.3) it immediately follows that

(ⅰ) The profile $u(\cdot, L)$ can contain at most countably many shocks. Namely, there can be at most countably many points $T_i$ such that $\eta^-(T_i) < \eta^+(T_i)$.

(ⅱ) There can be at most countably many points $t_i$ such that

for two distinct points $T_1 < T_2$.

We recall that, given any function $\phi\in {\bf L}^1_{loc}( I\!\!R)$, almost every point $t\in I\!\!R$ is a Lebesgue point of $\phi$. By definition, this means

As proved in ^[5], if $t$ is a Lebesgue point of the initial datum $\bar u(\cdot)$, then there exists a unique forward characteristic starting at $t$. In particular, $t$ cannot be the center of a rarefaction wave, and there exists a unique point $T$ such that

The next lemma is concerned with the stability of the map $T\mapsto \eta^\pm(T)$, w.r.t. small perturbations in the initial datum $\bar u$.

Lemma 4.1. Let $u = u(t, x)$ be the unique entropy weak solution of (3.10) and (3.11). Assume that $t$ is a Lebesgue point for the initial datum $\bar u$, and let $T$ be the unique point such that (4.6) holds. Then, for any $\varepsilon > 0$, one can find $\delta, \delta' > 0$ such that the following holds.

Let $\bar u^\dagger$ be a second initial datum, with

If we call $u^\dagger$ the corresponding solution, and define the maps $(\eta^\dagger)^\pm$ accordingly, then

Proof. 1. Let $\varepsilon > 0$ be given. By the uniqueness assumption, for the solution $u$ the backward characteristics through the points $T-\varepsilon$ and $T+\varepsilon$ satisfy

Hence we can find $\delta' > 0$ such that

2. If the conclusion of the lemma does not hold, we could find a sequence of initial data $\bar u_n$ with $\|\bar u_n-\bar u\|_{{\bf L}^1}\to 0$, such that the corresponding maps $\eta_n^\pm$ satisfy

To fix the ideas, assume that the first case holds. Namely, for every $n\geq 1$, there exists $t_n\geq t-\delta'$ such that

By possibly taking a subsequence we can assume $t_n\to t^*\geq t-\delta'$. The uniform convergence $\overline U_n\to \overline U$ now yields

This implies $\eta^+(T-\varepsilon)\geq t-\delta'$, reaching a contradiction.

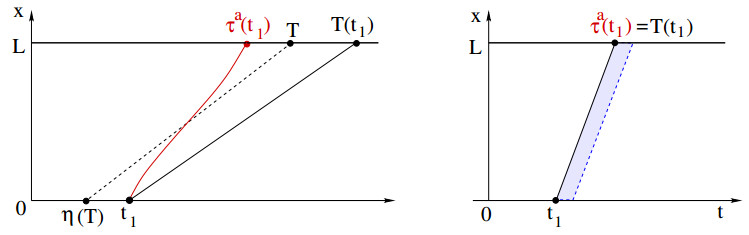
Remark 4.2. As shown in Figure 13, consider a solution $u = u(t, x)$ containing a shock through the point $(T, L)$. Then we can modify the initial data at $x = 0$ inside the interval $[\eta^-(T), \eta^+(T)]$ so that the solution perturbed solution $u^\dagger$ contains a centered compression wave which breaks exactly at $(T, L)$. In view of (3.14), This is achieved by taking

This ensures that all characteristics starting at a point $(t, 0)$ with $t\in [\eta^-(T), \eta^+(T)]$ join together at the point $(T, L)$.

Consider the constant

Then the corresponding integrated function $\overline U^\dagger$ satisfies

By (4.2), this implies

while the corresponding solutions coincide at $x = L$, namely

The next lemma, analyzing various perturbations to an optimal solution $u$, provides the key step toward the proof of Theorem 3.1.

Lemma 4.3. Let $(\bar u_1, \ldots, \bar u_N) = (\bar\theta_1 \bar u, \ldots, \bar\theta_N \bar u)$ be optimal departure rates. Assume that $t_1, t_2$ are Lebesgue points for all functions $\bar u, \bar\theta_1, \ldots, \bar\theta_N$, and

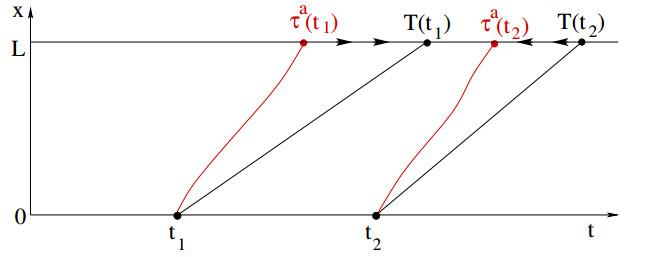
Call $\tau^a(t_1), \tau^a(t_2)$ the arrival times of a driver departing at times $t_1, t_2$, respectively. Moreover, let $T(t_1), T(t_2)$ be the times where the (unique) generalized forward characteristic starting from $t_1, t_2$ reaches the point $L$. Then

Remark 4.4. The left hand side of (4.16) can be interpreted as the cost for inserting an additional $i$-driver, departing at time $t_1$. In this case, an additional driver arrives at time $T(t_1)$, but this is not the same one! Indeed, the new driver arrives at time $\tau^a(t_1)$. However, the presence of this additional car slows down all the other cars whose arrival time is $T\in [\tau^a(t_1), \, T(t_1)]$. The delay in the arrival time of all these cars causes a further increase in the total cost, accounted by the integral term on the left hand side of (4.16). Similarly, the right hand side is the amount which can be saved by removing an $i$-driver departing at time $t_2$.

Proof of Lemma 4.3.  1. Since $t_1, t_2$ are Lebesgue points of $\bar u$, they cannot be the center of a rarefaction wave. Hence there exist unique points $T_1 = T(t_1)$ and $T_2 = T(t_2)$ such that

Assuming that (4.16) fails, we shall derive a contradiction. Indeed, we will construct a new initial data $\bar u_i^\dagger$ which is slightly smaller than $\bar u_i$ in a neighborhood of $t_1$ and slightly larger than $\bar u_i$ in a neighborhood of $t_2$, yielding a lower total cost. Various cases can arise, depending on the relative position of $\tau^a(t_i)$ and $T(t_i)$. To fix the ideas, in the following we assume that

as shown in Figure 14. The other cases are handled in a similar way.

We observe that the above strict inequalities imply that $u(\cdot, L)$ is strictly positive on the intervals $[\tau^a(t_1), T(t_1)]$ and $[\tau^a(t_2), T(t_2)]$. Indeed, the car speed is always $\leq v(0) = {1\over g'(0)}$. As shown in Figure 15, if

then the car speed would be identically equal to the maximum speed $v(0)$. In this case the car trajectory coincides with a characteristic line, and hence $T(t_1) = \tau^a(t_1)$, against the assumption (4.18). Therefore, we must have

Since characteristics do not cross each other, for every $T\in \, ]\tau^a(t_1), T(t_1)[\,$ the initial point of a characteristic through $(T, L)$ must satisfy

Hence

Since $g'$ is an increasing function, this yields a lower bound on $u(T, L)$.

2. Consider a perturbed set of initial data of the form $(\bar u_1, \ldots, \bar u_i^\dagger, \ldots, \bar u_N)$, where only the component $\bar u_i$ is modified. The new departure rate for drivers of the $i$-th group is chosen so that

Given $\varepsilon > 0$, according to Lemma 4.1, we can choose $\delta, \delta' > 0$ small enough so that the perturbation in the initial datum

affects the values of $u(\cdot, L)$ only in a small neighborhood of the points $T(t_1), T(t_2)$, namely

3. We now consider a sequence of perturbations of the form (4.20) and (4.21), with $\varepsilon_n, \delta_n, \delta'_n\to 0$. Calling $\tau^a_n(t)$ the corresponding arrival times, we claim that the following holds.

${\bf(C)}$ Let $t$ be a Lebesgue point for $\bar u$, with $\bar u(t) > 0$, and let $\tau^a(t)$ be a Lebesgue point for $u(\cdot, L)$. Then $u(\tau^a(t), L) > 0$ and the following implications hold.

In first approximation, the above limits show that:

● For those drivers who were reaching destination at a time $T\in \, ]\tau^a(t_1), T_1[\,$, the arrival time is delayed by $\delta_n/u(\tau^a(t), L)$.

● For those drivers who were reaching destination at a time $T\in \, ]\tau^a(t_2), T_2[\,$, the arrival time is anticipated by $\delta_n/u(\tau^a(t), L)$.

● For all other drivers, the arrival time does not change.

To prove the above claim we first observe that, if $u(\tau^a(t), L) = 0$, then $u(t', x') = 0$ along the backward characteristic

but in this case, this characteristic coincides with a car trajectory. Hence $\bar u(t) = u(0, t) = 0$ as well, contradicting our first assumption.

To prove (4.23), assume $\tau^a(t_1) < \tau^a(t) < T_1$. Then, for all $n$ large enough, the arrival time $\tau^a_n(t)$ is uniquely determined by the identity

Observing that the partial derivative is

from (4.26) one obtains (4.23). Notice that here the denominator is uniformly positive, as a consequence of (4.19).

The proof of (4.24) is entirely similar, replacing (4.26) with the identity

Finally, if the condition on the left hand side of (4.25) holds, then for all $n\geq 1$ sufficiently large one has $\tau_n^a(t) = \tau^a(t)$, and the implication is trivial.

4. By the properties (4.23) it follows

An entirely similar computation can be performed on the interval $]\tau^a(t_2), T_2[\,$. Combining these estimates, we thus conclude

If the inequality (4.16) does not hold, then the right hand side of (4.28) is negative. This yields a contradiction with the optimality of the departure rates $(\bar u_1, \ldots, \bar u_i, \ldots, \bar u_N)$.

5. The above analysis proves the lemma in the case where (4.18) holds. On the other hand, if $T(t_1) = \tau^a(t_1)$, then a small perturbation of the departure rate on the interval $[t_1, t_1+\delta_n]$ will modify the arrival rate only in a small neighborhood of $\tau^a(t_1)$ (see Figure 15(right)). In this case, one directly proves that the limit (4.28) remains valid, since the integral over the interval $[\tau^a(t_1), \, T(t_1)]$ trivially vanishes.

4.1.   Proof of Theorem 3.1

Let $u_i(t, 0) = \bar\theta_i(t)\bar u(t)$ be optimal departure rates, and let $u$, $\theta_i$ be the corresponding solutions to

The proof will be worked out in several steps.

1. We begin by showing that an optimal solution cannot contain any shock in the interior of the domain, i.e., for $0\leq x < L$.

Indeed, assume on the contrary that a shock is present, and let $(T, L)$ be the terminal position of this shock. According to Remark 4.2, we can change the initial datum so that the new solution $u^\dagger$ contains a centered compression wave focusing at $(T, L)$. More precisely, define $\overline U^\dagger$, $\bar u^\dagger$ as in Remark 4.2. Assuming that the functions $\Theta_i(s)$ are defined by

define the components $(\overline U^\dagger_1, \ldots, \overline U^\dagger_N)$ by setting

Notice that these definition imply

hence the arrival costs remain the same. On the other hand, we have

for all $i, t$. Observing that there exists some $i$ and some $t\in [\eta^-(T), \, \eta^+(T)]$ where (4.32) is satisfied as a strict inequality, we claim that the total departure cost for the perturbed solution is strictly smaller.

To see this, introduce a variable $\xi\in [0, G_i]$ labeling drivers of the $i$-th group. Define the departure times

By the previous definitions it follows

with strict inequality holding at least for some index $i$ and some values of $\xi\in [0, G_i]$. We now compute

proving our claim.

2. Next, we claim that an optimal departure rate satisfies

Indeed, since the characteristic speed satisfies $g'(u)\to +\infty$ as $u\to M$, if $\bar u(\tau) = M$ at some point $\tau$ then the solution $u(\cdot, x)$ would immediately contain a shock, for every $x > 0$. By the previous step, this contradicts the optimality assumption.

3. According to Lemma 4.3, by (4.34), the quantity

is equal to some constant $C_i$ for all $t\in {\rm Supp}(\bar u_i)$, and is greater or equal to $C_i$ for all $t\in I\!\!R$. In other words, for each $i = 1, \ldots, N$ we have

This implies

for all $t\in \hbox{Supp}(\bar u_i)$. We now observe that, for a.e. $s\in [\tau^a(t), T(t)]$ and $j\in \{1, \ldots, N\}$, one has the implication

Moreover, for every $j, k$ and a.e. $s$ in the set

one has $\psi_j'(s) = \psi_k'(s)$. Therefore, defining $\psi$ as in (3.31) and recalling that $\sum_j\theta_j = 1$, we obtain

In turn, this implies

According to (4.41), each characteristic where the solution $u$ is positive must connect two points $(t, 0)$ with $(T(t), L)$ with $\varphi(t)+\psi(T(t)) = 0$. This proves part (ⅰ) of Theorem 3.1. Finally, part (ⅱ) follows from (4.39).

5.   An algorithm to construct optimal solutions

Here we illustrate how these necessary conditions can be used to construct optimal solutions. For simplicity, we shall assume that the cost functions $\psi_i$ are ${\cal C}^2$ and satisfy the assumption

${\bf (A3)}$ For any $i\not = j$ one has the implication

Notice that, by (5.1), for any given constants $C_1, \ldots, C_N$, the set of times

consists only of isolated points, hence it has measure zero.

We remark that the assumption (A3) is generically valid in the space of twice continuously differentiable functions. Indeed, given $\varepsilon > 0$ and any $N$-tuple of twice continuously differentiable functions $(\widehat \psi_1, \ldots, \widehat \psi_N)$, by a small perturbation one can construct functions $\psi_1, \ldots, \psi_N$ which satisfy (A3) together with

Let now $G_1, \ldots, G_N$ be the sizes of the $N$ groups of drivers. In order to construct a globally optimal family of departure rates $u_1(\cdot), \ldots, u_N(\cdot)$, we introduce the following algorithm.

(ⅰ) Start by guessing $N$ constants $C_1, \ldots, C_N$, and define the cost function $\psi$ as in (3.31).

(ⅱ) Let $u = u(t, x)$ be the solution of (3.10) constructed according to (3.32) and (3.33).

(ⅲ) Define the sets

Notice that, by (A3), for a.e. $t\in I\!\!R$ the minimum in (5.2) is attained by a unique index $k\in \{1, \ldots, N\}$.

(ⅳ) Consider the map $\Lambda: I\!\!R^N\mapsto I\!\!R^N$, $\Lambda (C_1, \ldots, C_N) = (\kappa_1, \ldots, \kappa_N)$, where $\kappa_i$ is the total number of drivers of the $i$-th group, defined by

Determine values $\widehat C_1, \ldots, \widehat C_N$ such that

(ⅴ) Set

And let $u = u (t, x)$ be the solution of (3.10) whose characteristics satisfy (3.32).

(ⅶ) Finally, for $T\in A_i$, call $\eta(T)$ the departure time of the driver that arrives at time $T$. This is obtained by solving the ODE

with terminal condition

The solution $t\mapsto x(t, T)$ of (3.22) and (5.6) yields the trajectory of a car arriving at the end of the road time $T$. Its departure time $\eta(T)$ is defined by the equality $x(\eta(T)) = 0$.

We now consider the sets of departure times

The departure distribution

then satisfies all the necessary conditions for optimality.

We remark that these conditions are only necessary, not sufficient for optimality. Since an optimal solution exists, and can obtained by the above method, the previous analysis implies that, if the $N$-tuple $(\widehat C_1, \ldots, \widehat C_N)$ which satisfies (5.4) is unique, then this must yield the optimal solution.

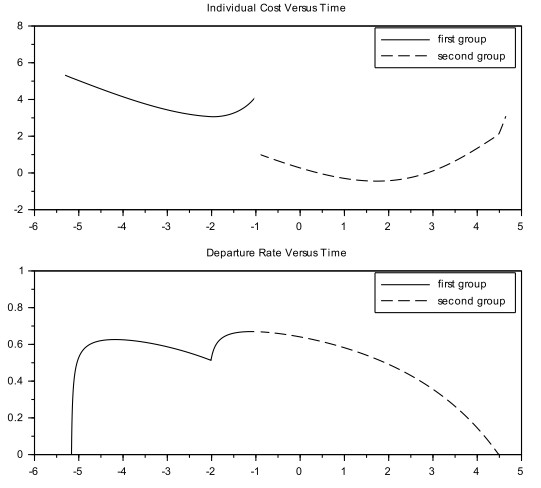
Example 4. We seek a globally optimal departure rate for two groups of drivers, with sizes $G_1 = G_2 = 2.51$ on a road with length $L = 10$. The conservation law governing traffic density is

The departure and arrival costs for drivers of the two groups are

The optimal solution, found by the algorithm described above, is shown in Figure 16. The marginal costs for adding one more driver of the first group or of the second group are found to be $\widehat C_1 = 5.18$ and $\widehat C_2 = 2.10$, respectively.

Acknowledgment

This research was partially supported by NSF, with grant DMS-1411786: "Hyperbolic Conservation Laws and Applications".

Conflict of interest

The authors declare no conflict of interest.