Global dynamics of tick-borne diseases

1.   Introduction

Tick-borne diseases are a serious health problem throughout the world, and demand an attention, since they have rapidly increased over last few years ^[1]. According to Centers Disease Control and Prevention, the number of tick-borne disease cases in the US was 22527 in 2004, while by 2017, it significantly increased up to 59349. In 1920 there was one case per million and in 2015 there were 13 cases per million ^[2]. One of the examples of the tick-borne disease is Crimean-Congo hemorrhagic fever, that occurs in Central Asia, China, Eastern Europe, Africa, and the Middle East. Omsk Hemorrhagic Fever (OHF) is another tickborne disease found in Omsk, Tyumen, and Novosibirsk.

The most prevalent tick-borne disease in the United States is Rocky Mountain Spotted Fever. It occurs mostly in Oklahoma, Missouri, Arkansas, Tennessee, and North Carolina. 5–10% of Rocky Mountain spotted fever cases are fatal if treatment is not taken on time ^[2]. The agent that cause Rocky Mountain spotted fever is known as Rickettsia rickettsi. It is transmitted by three species of ticks: brown dog tick (Rhipicephalus sanguineus), Rocky Mountain wood tick (Dermacentor andersoni), and American dog tick (Dermacentor variabilis).

One of the dangerous tick-borne disease in Africa, Middle East and Central Asia including Kazakhstan is Crimean-Congo Hemorrhagic Fever (CCHF). CCHF virus among people is transmitted by ixodid ticks and mostly occur among agricultural workers which can be fatal. For instance, 704 cases of CCHF were reported in Kazakhstan between 1948 and 2013 with mortality rate of 14.8% ^[3]. From 5% to 30% of hospitalized individuals can ended up with death ^[4]. In Kazakhstan at most 10 CCHF cases occur annually ^[4].

Due to its mathematical tractability the continuous epidemic models are more frequently used than the discrete models ^[5]. However, there is an increasing interest for the discrete models since clinical data is given in discrete time. One of the advantages of the current study is that we consider epidemic models with piecewise constant arguments of generalized type which have features of both discrete and continuous time dynamics. On the other hand, differential equations with piecewise constant arguments (DEPCA) are used to approximate numerically delay differential equations ^[6,7,8]. Thus, the need for DEPCA or sometimes called as differential equations with deviated arguments come from the real world application problems. These equations take their origin from the article of Busenberg and Cooke published in 1982 where authors studied vertically transmitted diseases ^[9]. Shortly after publication of this paper, theoretical analysis of DEPCA was investigated by many authors such as Cook and Wiener ^[10] and Shah and Wiener ^[11]. Since then, it has gained a lot of attention because of many practical applications in population dynamics, neural networks, and many biological models ^{[12,13,14,15,16]}. To the best of our knowledge, there is no study modeling epidemic dynamics by means of DEPCA except the paper by Busenberg and Cooke ^[9]. In their study, the authors used the simplest piecewise constant function, the greatest integer functions, to model transmission of a disease. The present study generalizes this idea by considering so-called $\beta -$type argument functions. That is, we consider epidemic models with piecewise constant arguments of generalized type which have features of both discrete and continuous time dynamics. Furthermore, this article will contribute to the recent studies of epidemic models using hybrid systems ^[17].

1.1.   Disease epidemiology

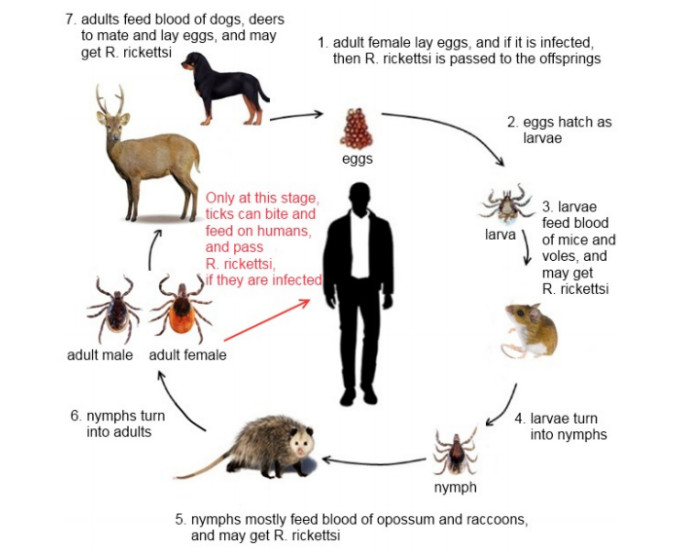
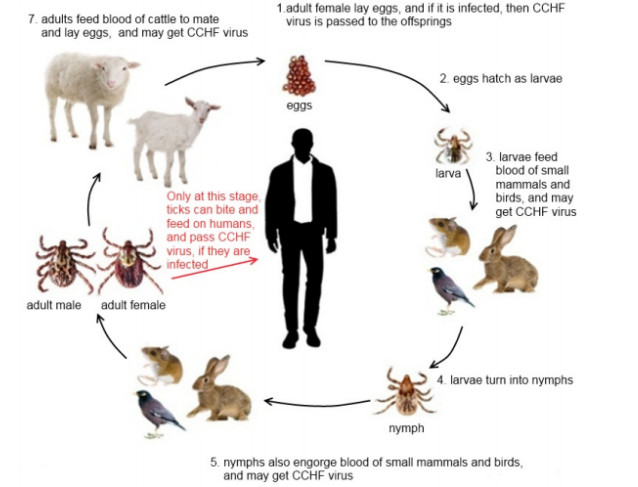
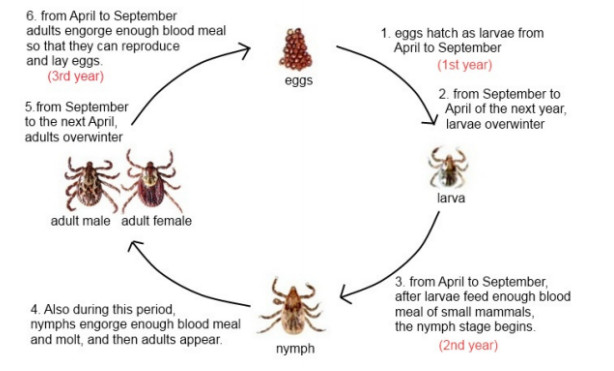
Ticks pass through four stages of the life cycle: Eggs, larvae, nymphs, and adults. To pass from one stage to the next, it need to feed blood meal of the host. As we can see from the Figure 1, usually ticks feed blood meal of host from April to September and the rest of the time they overwinter. For instance, brown dog tick usually engorge blood meal of the same host during all its life stages. At the stage of nymphs and adults, they can even bite and feed on humans, and transmit Rickettsia rickettsi, if they are infected. As a result, a contact with infected ticks may cause a Rocky Mountain spotted fever among people ^[9]. However, unlike brown dog ticks, American dog ticks engorge different hosts at their different life stages (See Figure 2). Usually, larvae prefer blood of mice and voles, nymphs prefer opossum and raccoons, and adults prefer dogs and deers ^[18]. Only at this stage, ticks can also bite and engorge blood of humans, and transmit Rickettsia rickettsi, if they are infected. Whereas, larvae and nymphs of ixodid tick species require blood meal of birds, mice and hares, and adult ticks engorge livestock such as goats and sheep ^[19]. Similarly as American dog ticks, only infected adult ticks can bite and feed humans, and may transmit CCHF virus (See Figure 3).

1.2.   Preliminaries

Throughout the paper we use the following notations: $\mathbb{N}, \mathbb{R}^{+}$ and $\mathbb{R}^{n}$ are the sets of natural, nonnegative real numbers, and $n$ -dimensional real space, respectively. Further, $\left\lVert. \right\rVert$ is the Euclidean norm in $\mathbb{R} ^{n}$.

Let us briefly introduce DEPCA and refer the interested readers to ^[20,21]. Consider the following DEPCA of the generalized type.

where $x \in B(h), \enspace B(h) = \{x \in \mathbb{R} ^{n}: \left\lVert x \right\rVert < h \}, \enspace t \in \mathbb{R}^{+}, \enspace \beta(t) = \theta_{i} \;$ for $t \in [\theta_{i}, \theta_{i+1}), \; i \in \mathbb{N},$ and $\theta_{i}, \; i \in \mathbb{N},$ is a fixed real-valued increasing sequence such that ${\theta_{i}\to\infty}$ as ${i\to\infty}$. We assume that there exists a positive number $\theta$ such that $\theta_{i+1} - \theta_{i} \leq \theta, \; i \in \mathbb{N}.$ It worth nothing to mentioning that the greatest integer function, $[t]$, is a particular case of the the delay argument function $\beta(t)$ if $\theta_i = i, \, i\in \mathbb{Z}.$ Similarly, one can easily see that if $\theta_i = 3i, \, i\in \mathbb{Z},$ then $\beta(t) = 3[t/3]$. Thus, it is possible to obtain more general constant argument functions than the greatest integer function by considering different $\theta_i$ sequences.

Definition 1.1. A function $x(t)$ is a solution of (1.1) on $\mathbb{R}^{n}$ if

ⅰ. $x(t)$ is continuous on $\mathbb{R}^{n}$;

ⅱ. the derivative $x'(t)$ exists for $t \in \mathbb{R}^{n}$ with the possible exception of the points $\theta_{i}, \; i \in \mathbb{N},$ where one-sided derivatives exist;

ⅲ. (1.1) is satisfied by $x(t)$ on each interval $(\theta_{i}, \theta_{i+1}), \; i \in \mathbb{N}$ and it holds for the right derivative of $x(t)$ at the points $\theta_{i}, \; i \in \mathbb{N}$.

1.3.   Mathematical modeling

As it can be seen from the Figures 2 and 3 it takes time for ticks grow up as adults to pass an infection to humans. Different species of ticks need different time period to complete their life cycle. For example, in Nova Scotia it occurs for two years; whereas, in Virginia it would be one year ^[9]. To model Rocky Mountain spotted fever and to make a computation easier, Busenberg and Cooke normalized the time variable so that each generation is considered for one unit of time. They used the greatest integer functions to represent a time delay as $[t]$ to denote that an infection is handed down with discrete generations ^[9]. The present study generalizes this idea by considering so-called $\beta -$type argument functions where $\beta(t) = \theta_i$ for $t\in [\theta_i, \theta_{i+1}), \; i \in \mathbb{N},$ and $\theta_{i}, \; i \in \mathbb{N},$ is a fixed real-valued increasing sequence such that ${\theta_{i}\to\infty}$ as ${i\to\infty}$. Another advantages of the current study is that we do not normalize the time variable as life cycles of ticks are different and can take up to three years to complete the cycle.

The dynamics of a tick-borne disease depend on the number of infected adult ticks. Thus, it is of utmost importance to predict the number of infected ticks during an agricultural period. From Figures 2 and 3 it is clear that ticks need a host to grow. Although tick-borne diseases can be transmitted to a new generation of ticks through female adult thicks, we do not take these ticks into account since only small portion of these can find a host to feed. Therefore, for the sake of simplicity we neglect the number of infected ticks from offspring of parentage and assume that susceptible ticks pick up the disease through contact of infected ticks. In general, this happens if they feed from the same host. Let $i(t)$ and $s(t)$ be the number of the infected and susceptible ticks at time $t$, respectively. In most of the existing compartmental models in the literature population size is considered to be constant. That is possible if deaths are balanced by births or a disease spreads rapidly. However, in the reality these are merely the case. Thus, the population size, $N(t) = s(t) + i(t),$ is not constant for the model. These assumptions lead us to consider SI (susceptible-infected) model that takes the following form.

where, $\alpha$ is the recruitment rate, $\kappa$ is the natural death rate, and the nonlinear function $f(s, i)$ is used to model an incidence rate. We impose the following conditions on this function.

(C1) $f(s, 0) = f(0, i) = 0$;

(C2) $f(s, i)$ is a positive, continuous, differentiable and monotonically increasing function, i.e.,

(C3) $f(s, i)$ is concave with respect to $i$, i.e.,

It can be easily seen that all incidence rate functions such as

where $\gamma$ is the per capita infection rate of an average susceptible and $N$ is the total number of population. One can easily check that these incidence rate functions satisfy the conditions (C1)–(C3) ^{[23,22,24,25]}. Thus, the models (1.2) with the nonlinear function $f(s, i)$ are the generalizations of the existing models in the literature.

By means of the condition (C1) one can easily show that the system (1.2) has an equilibrium state $E_{0} = (s_{0}, i_{0})$, where $s_{0} = \alpha / \kappa$ and $i_{0} = 0$. This equilibrium is called as a disease-free equilibrium since the infected population is zero. Moreover, the models (1.2) may have a positive equilibrium state $E^{*} = (s^{*}, i^{*})$, called as an endemic equilibrium, where for (1.2) its coordinates satisfy:

To ensure the uniqueness of the endemic equilibrium which satisfy the above equations and for the further analysis we should need the following conditions:

(C4)

(C5)

In what follows, asymptotic behavior of the compartmental models considered in this paper essentially depend on a threshold value, $\mathcal{R}_0$, so-called the basic reproduction number. It is important to compute this value as it gives the expected number of secondary cases produced by an infective individual in a completely susceptible population. To this end, we follow the next generation matrix technique ^[26] to compute $\mathcal{R}_0$ for the model (1.2). Van den Driessche and Watmough in ^[26] consider a heterogeneous population that can be grouped into $m$ homogeneous compartments, $x_1, \cdots, x_m$, which satisfy the following equations.

where $x = (x_1, \cdots, x_m)^T,$ $\mathcal{F}_i(x)$ is the rate of appearance of new infections in compartment $i$ and $\mathcal{V}_i(x)$ is the rate of transfer of individuals out of compartment $i$. Let $x_0$ be the disease-free equilibrium state of the above system. Since we do not distinguish the infected population by behavior, spatial position and/or stage of disease we have $m = 1$. Thus, $\mathcal{R}_0$ is given by the spectral radius of the next generation matrix $FV^{-1}$ where $F = \dfrac{\partial \mathcal{F}}{\partial x}(x_0)$ and $V = \dfrac{\partial \mathcal{V}}{\partial x}(x_0)$. For the model (1.2) one has $\mathcal{F}(x) = f(s, i)$ and $\mathcal{V}(x) = \kappa i$. Therefore we compute $F = \dfrac{\partial f(s_0, 0)}{\partial i}$ and $V = \kappa$ which yield that the spectral radius of the matrix $FV^{-1}$ is given as follows.

The following lemma ^[27] ensures the uniqueness of the positive equilibrium $E^{*} (s^{*}, i^{*})$ if $\mathcal{R}_0 > 1$.

Lemma 1.2. ^[27] If the conditions $(C2)-(C4)$ hold, and if $\mathcal{R}_0 > 1,$ then in addition to the disease-free equilibrium state, systems (1.2) has a unique positive endemic equilibrium state $E^{*} (s^{*}, i^{*})$. If $\mathcal{R}_0 \leq 1,$ then the disease-free equilibrium $E_{0}(s_{0}, i_{0})$ is the only nonnegative equilibrium state of system (1.2).

2.   Global dynamics

Considering the system (1.2), it is sufficient to consider only the first two equations of (1.2), since the last variable does not appear in the equations for $s(t)$ and $i(t)$. We notice that

The last inequality implies that $\limsup\limits_{t\to\infty} \big[s(t) + i(t) \big] \leq \alpha / \kappa$. Thus, we study the system (1.2) in a biologically feasible region

One can easily show that $\Omega$ is positively invariant with respect to the model (1.2), i.e., every solution which starts in $\Omega$ will remain in $\Omega$ for $t\ge0$. Further, with the help of Lemma 1.2 we know that (1.2) has two steady states: disease-free positive equilibrium state $E_{0}(s_{0}, i_{0})$ and endemic positive equilibrium state $E^{*} (s^{*}, i^{*})$. In what follows, we analyze global stability of these equilibrium points by constructing appropriate Lyapunov functions.

Theorem 2.1.

$i.$If $(C1) - (C3)$ hold, and if $\mathcal{R}_0 \leq 1$, then the disease-free positive equilibrium state $E_{0}(s_{0}, i_{0})$ is globally asymptotically stable.

$ii.$If $(C2) - (C5)$ hold, and if $\mathcal{R}_0 > 1$, then the endemic positive equilibrium state $E^{*} (s^{*}, i^{*})$ is globally asymptotically stable.

Proof. To prove the fist part of the theorem we define Lyapunov function as follows.

It is easy to see that $V_1(s_0, i_0) = 0$. Let us show that $V_1(s, i) \ge 0$ for all $s, i\in \Omega.$ Note that $i(t) + \kappa \int_{\theta_i}^{t}i(u)du \ge 0$ since $i\ge0.$ On the other hand, $s(t)\le \alpha/\kappa = s_0$ for all $s\in \Omega$. Thus, by the condition (C4) we have $s(t)-s_0 - \int_{s_0}^{s(t)} \lim_{i\to 0} \frac{f(s_0, i)}{f(u, i)} du = s(t)-s_0 + \int_{s(t)}^{s_0} \lim_{i\to 0} \frac{f(s_0, i)}{f(u, i)} du > s(t)-s_0 + \int_{s(t)}^{s_0}1du = 0$. Thus, it follows that $V_1(s, i) \ge 0$ for all $s, i\in \Omega.$ Next, differentiating $V_1(s, i)$ along the trajectories of (1.2) for $t\in[\theta_i, \theta_{i+1})$ yields:

By theorem hypotheses, and from the monotonicity of $f(s, i)$ with respect to $s$, we have

The concavity of $f(s, i)$ with respect to $i$ leads to $f(s, i) \leq i \frac{\partial f(s, 0)}{\partial i}$, and hence we have

Therefore,

Hence, $\frac{dV_1}{dt} \leq 0$ for all $s, i > 0$. This proves that $E_{0}(s_{0}, i_{0})$ is stable. On the other hand, the equality $\frac{dV_1}{dt} = 0$ holds if and only if $s(t) = s_0$ and $i(t) = 0.$ Thus, $E_{0}(s_{0}, i_{0})$ is the largest invariant set in $\Lambda_1 = \Big\{(s, i)| \ \ \frac{dV_1}{dt} = 0\Big\}$. Therefore, we conclude by Lyapunov-Lasalle theorem ^[28,29] that the disease-free equilibrium $E_{0}(s_{0}, i_{0})$ is globally asymptotically stable.

To prove the second part of the theorem we define another Lyapunov function as:

One can easily see that $V_2(s^*, i^*) = 0$. Let us show $V_2(s, i)\ge0$ for all $s, i\ge0.$ Due to the monotonicity condition (C2) we have $f(\rho, i^{*}) > f(s^{*}, i^{*})$ for all $s^{*} < \rho < s(t)$ and $f(\rho, i^{*}) < f(s^{*}, i^{*})$ for all $s(t) < \rho < s^{*}$. Hence, in either case one has $s(t) - s^{*} - \int_{s^{*}}^{s(t)} \frac{f(s^{*}, i^{*})}{f(\rho, i^{*})} d\rho > s(t) - s^{*} - \int_{s^{*}}^{s(t)} d\rho = 0$. Let $h(i) = i - i^{*} - i^{*}\ln \frac{i}{i^{*}}$. Note that $h'(i) = 1-i^{*}/i$ yields that $h(i)$ is increasing for $i > i^{*}$, i.e., $h(i) > h(i^{*}) = 0,$ and $h(i)$ is decreasing for $0 < i < i^{*}$, i.e., $h(i) > h(i^{*}) = 0$. Thus, $h(i) > 0$ for all positive $i\ne i^{*}$. This proves that $V_2(s, i)$ is a Lyapunov function. Next, differentiating $V_2(s, i)$ along the trajectories of (1.2) for $t\in[\theta_i, \theta_{i+1})$ we have

From the monotonicity of $f(s, i)$ with respect to $s$, we have

Further, by theorem hypotheses (C5) it yields

Moreover,

for $\forall s, i > 0$, since the geometric mean is less than or equal to the arithmetic mean. Hence, $\frac{dV_2}{dt} \leq 0$ holds for $\forall s, i > 0$. The equality holds if and only if $s(t) = s^*$ and $i(t) = i^*.$ Thus, $E^{*} (s^{*}, i^{*})$ is the largest invariant set in $\Lambda_2 = \Big\{(s, i)| \ \ \frac{dV_2}{dt} = 0\Big\}$. This asserts that the endemic equilibrium $E^{*} (s^{*}, i^{*})$ is indeed globally asymptotically stable by Lyapunov-LaSalle theorem ^[28,29].

3.   Numerical simulations

Since we take into account susceptible ticks that can be infected only through sticking to an infected host, the transmission of a disease among susceptible population will start to 'saturate' after some period of time. That is, even if initially the number of infected ticks sticked to the host will increase, but eventually levels off at a constant regardless of increases in infected density. Thus, as an incidence rate for the model (1.2) we use Holling type II response function, $f(s, i) = \frac{\gamma si }{1 + i},$ where $\gamma$ is the per capita transmission rate for ticks. It is easy to verify that this functions satisfies the conditions (C1)–(C3). Although originally designed for predator-pray models, Holling type response functions have been successfully implemented by many authors in different models ^[30,31].

We estimate the parameters of the model (1.2) based on the studies of Wu et al. ^[32] and Hartemink et al. ^[33], where the authors considered Lyme disease Ixodes scapularis. In ^[32], the authors analyze the basic reproduction number under different climatic conditions by studying different stages of I scapularis. Since we take into account disease transmission only through a host, we estimate intake rate $\alpha$ by considering tick population that can attach a host. In the study ^[32], the authors calculated host-attaching rate from the mean monthly normal temperature data to be between $0.2$ day$^{-1}$ and $0.4$ day$^{-1}$ for adult ticks during the March-May and September-November periods and between $0.001$ day$^{-1}$ and $0.015$ day$^{-1}$ for immature ticks during the April-October period. Since host-attaching rates for immature ticks are very small compared to adult ticks $\alpha$ is taken to be equal to the host-attaching rate of adult ticks. For mortality rate we consider only feeding ticks which is approximated to vary from $0.5$ day$^{-1}$ to $0.65$ day$^{-1}$ from density-dependent mortality rates of feeding ticks ^[32]. The transmission rate $\gamma$ is estimated from the study of Hartemink et al. ^[33] where the authors estimate transmission efficiencies from ticks to competent hosts to vary from $0.5$ day$^{-1}$ to $0.8$ day$^{-1}$. The summary of parameter values are given in Table 1.

3.1.   Basic reproduction number and sensitivity analysis

By means of the next generation matrix technique and the choice of the incidence rate function we compute

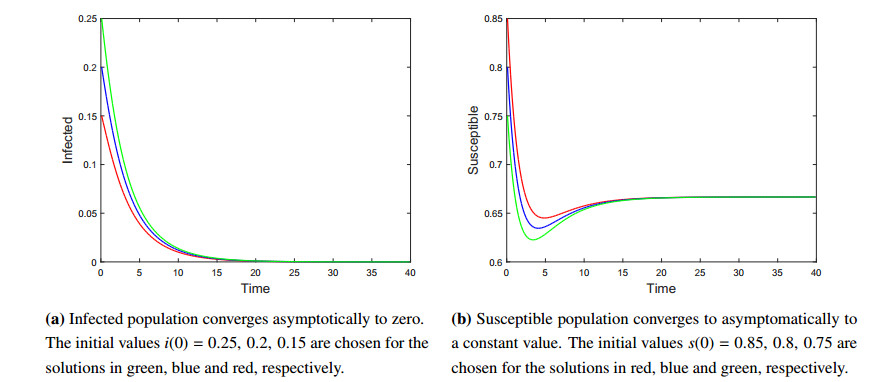
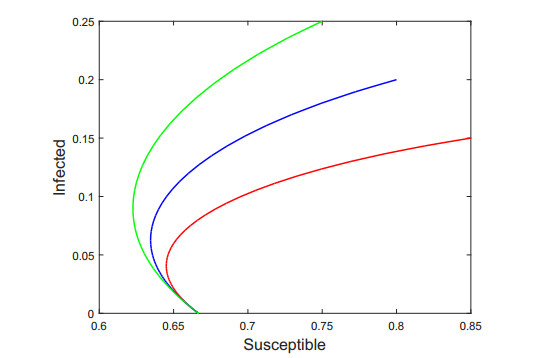
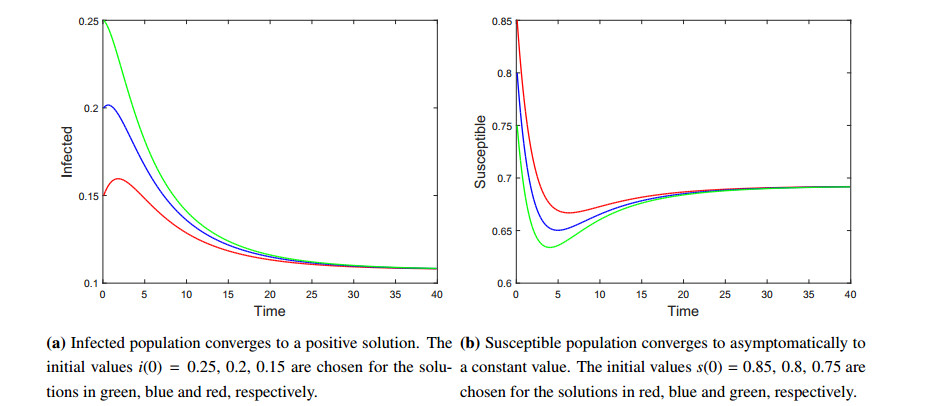
Since $\mathcal{R}_0$ depends on the choices of the parameters we choose different set of values from Table 1 to have two different scenarios. For the set of parameters $\alpha = 0.4$ day$^{-1}$, $\kappa = 0.6$ day$^{-1}$ and $\gamma = 0.5$ day$^{-1}$ we have $\mathcal{R}_0 \simeq 0.56 < 1$. By Theorem 2.1, the disease eventually dies out. A numerical simulation illustrates this result (see Figure 4). In this case from the phase portrait we observe that all solutions converge to the disease-free equilibrium state (see Figure 5). On the other hand, for the set of parameters $\alpha = 0.4$ day$^{-1}$, $\kappa = 0.5$ day$^{-1}$, and $\gamma = 0.8$ day$^{-1}$ one can compute that $\mathcal{R}_0 = 1.28 > 1$. Thus by Theorem 2.1 the endemic equilibrium state is globally asymptotically stable, i.e., the disease remains persistent. A numerical simulations illustrate the theoretical findings (see Figure 6). From the phase portrait we observe that all solutions converge to the positive endemic equilibrium state (see Figure 7). Moreover, from the Figures 4 and 6 we observe that susceptible population levels off to a constant value. That is, the result shows that Holling type II response.

Finally we carry out sensitivity analysis for the basic reproduction number. Since we can find explicitly expression for $\mathcal{R}_0 = \dfrac{\alpha\gamma}{\kappa^2}$, we see that $\mathcal{R}_0$ depends linearly on the parameters $\alpha$ and $\gamma$. Thus, we consider two cases with either $\alpha$ or $\gamma$ values fixed. One can see that for a fixed $\alpha$ the larger values of $\kappa$ and $\gamma$ the larger the basic reproduction number. However, one can show that if $\alpha = 0.2$ day$^{-1}$ then $\mathcal{R}_0 < 1$ for all values of $\gamma$ and $\kappa$ which can be justified due to low host-attaching rate. For the second case we fix $\gamma$ and observe that the basic reproduction number becomes larger for the larger values of $\alpha$ and $\kappa$. If $\gamma = 0.5$ day$^{-1}$ then $\mathcal{R}_0 < 1$ all values of $\alpha$ and $\kappa$ which can be justified due to low transmission efficiencies between cofeeding ticks.

4.   Discussions

In this article, we considered the dynamics of tick-borne diseases. These are diseases that transmits through adult ticks and in discrete generations of ticks. For this purpose, we developed SI (susceptible-infected) model with nonlinear incidence rate and piecewise constant delay, where the total population is varied with time elapse. We computed the basic reproduction number, using the next generation matrix technique ^[26], and showed that if $\mathcal{R}_0 < 1$, then there is only one equilibrium state, which is disease-free equilibrium and it is globally asymptotically stable, and if $\mathcal{R}_0 > 1$, then in addition to the disease-free equilibrium which is unstable, the model has also an endemic equilibrium that is globally asymptotically stable. By constructing suitable Lyapunov functions and using Lyapunov–LaSalle technique we showed that the basic reproduction number, $\mathcal{R}_0$, serves as the threshold value for the analysis of global dynamics. In the numerical simulations we have considered the dynamics of Lyme disease. The set of solutions with different initial values were simulated by considering different range of parameters obtained from Wu et al. ^[32] and Hartemink et al. ^[33].

4.1.   Limitations

This study is an attempt to understand the dynamics of tick-borne disease. In the model (1.2) we neglect ticks that were infected through offspring of parentage. That is, the model does not include vertical transmission. Although infected female ticks lay eggs only small portion of larva hatched from these eggs find a host. Nonetheless, if these larva find next feeding and grow up to an adult tick the dynamics of the disease will change accordingly. Moreover, we do not consider different life stages of ticks in the set of equations. Another shortage of this study is that we assume a constant, $\alpha$, intake rate for susceptible population. However, the logistic growth would be more realistic for the intake rate. Finally, there is a lack of data to check the theoretical finding of this study. However, it is possible (if data is available) to carry out parameter estimation to fit data and analyze the dynamics of a disease.

Acknowledgments

The first author was supported in part by Nazarbayev University Faculty Development Competitive Research Grants N 090118FD5353. The authors would like to thank the anonymous referees for helpful comments which significantly improved the quality of the paper.

Conflict of interest

No potential conflict of interest was reported by the authors.