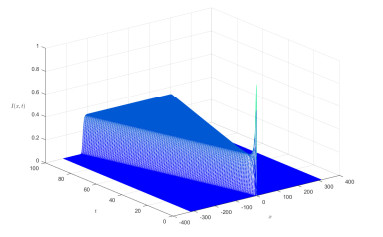
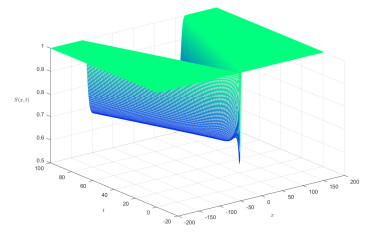
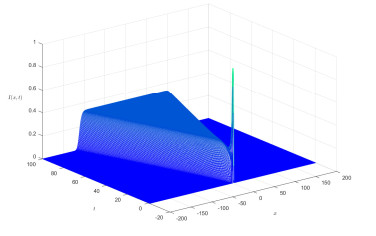
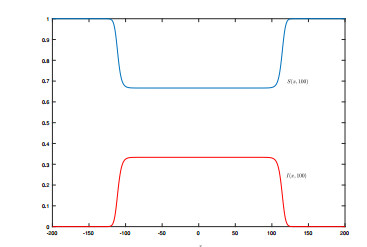
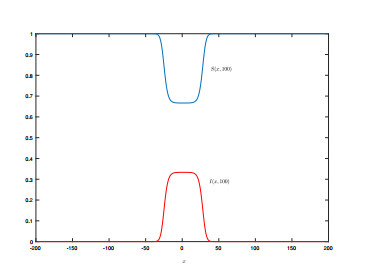
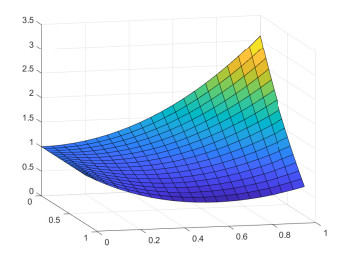
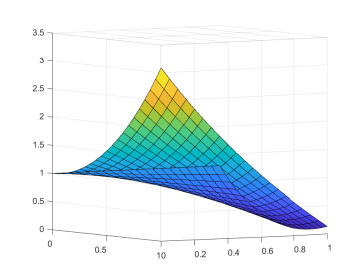
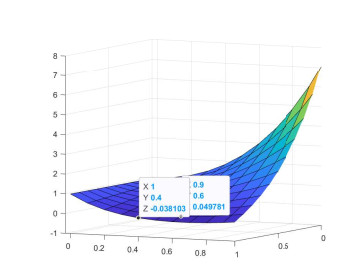
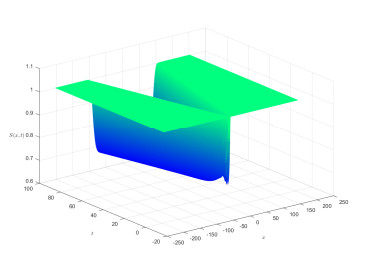
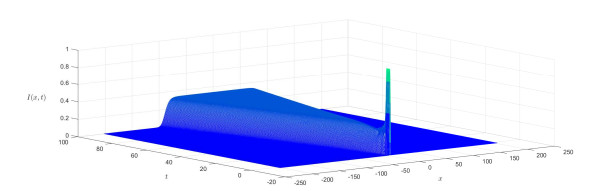
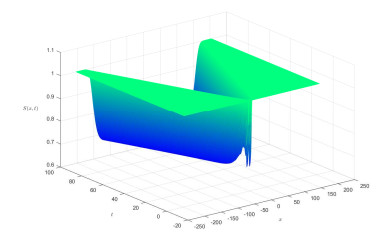
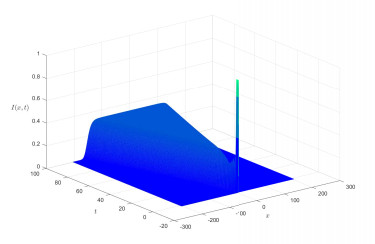
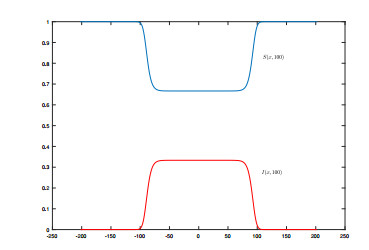
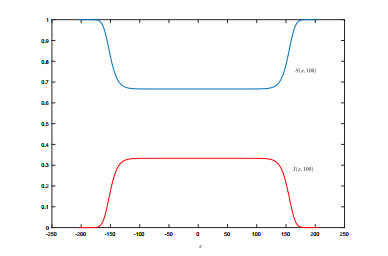
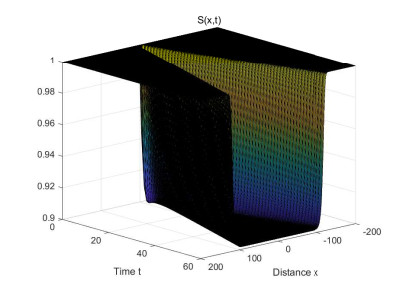
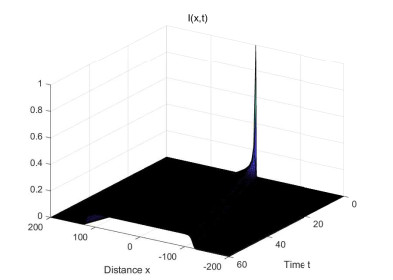
We estimate the spreading speeds in diffusive epidemic models with nonlocal delays, nonlinear incidence rate and constant recruitment rate. The purpose is to model the process that the infective invades the habitat of the susceptible, and they coexist eventually. In order to focus on our idea, a system with a nonlinear incidence rate is firstly studied, which implies a saturation level of the infective individuals and monotone incidence rate. When the initial value of the infective has nonempty compact support, we prove the rough spreading speed that equals the minimal wave speed of traveling wave solutions in the known results. Then for a general (nonmonotone) incidence rate, we obtain the spreading speeds by constructing auxiliary systems admitting a monotone incidence rate, and prove the convergence of solutions on any compact spatial interval. Furthermore, some numerical examples are given to estimate the invasion speed and show the nontrivial effect of time delay and spatial nonlocality, which implies that the stronger spatial nonlocality leads to larger spreading speeds.
1.
Introduction
IoT devices are an essential part of intelligent applications, such as the Healthcare system that plays an indispensable role between the user and the application providing assistance and personalized services [1,2,3]. Devices send real-time health data to cloud systems for analysis and update healthcare staff to revise or maintain patient care [4,5,6,7]. Modern 5G cellular networks support high data rates for portable devices such as smartphones and IoT machines for real-time communication [8]. A wireless communication environment supported by applications contains various cluster-based areas of operations [9]. The machines connect and authenticate with local base stations spread throughout a space [10]. Base stations regularly broadcast network information as messages to nearby devices searching for an access point, providing the strongest signal strength. A handover process occurs when a device moves between different base stations and connects with others to maintain good signal strength [11,12,13].
An attacker sets up a rogue base station or an access point to behave as a legitimate base station [14]. An SSID generated by the network administrator for uniquely identifying each access point is used by rogue nodes to disguise themselves as valid network members. The rogue base station attacks are easily performed using laptops, smartphones, and specialized software [15]. A broadcast message sent by a base station provides information about the network's signal strength data, which lacks security and data confidentiality. A rogue access point broadcasts a similar message during handover requests and attempts to collect private user data. A device analyzes multiple broadcasts from several base stations during the cell selection phase to select the one with the strongest signal strength. A device then establishes a connection and connects with a rogue base station [16]. An attacker steals confidential user data such as financial records, hospital patient data, and personal records to sell them to third-party entities, thus affecting user privacy. Additionally, data intercepted using man-in-the-middle attack results in a high probability of sensitive user data being tampered affecting data integrity.
A critical vulnerability and problem identified in telecommunication networks between a base station and device authentication are when malicious nodes behave as valid access nodes to steal user data [17,18]. A device focuses on connecting to new access points that provide superior signal strength, thus ensuring stable data rate flow. Users are unaware whether the access node is a legitimate part of the network or an attacker with a laptop/smartphone spoofing as an access node to steal and manipulate user data. A device connecting with a rogue base station is sent attack messages directly, bypassing security measures provided by the network. Various fake messages spoofing as official bank messages result in victims sharing confidential user data such as bank passwords and ATM pins. Devices are further vulnerable to Denial of Service-based attacks, resulting in them being unable to connect with existing networks and being forced to communicate with less secure 2G/3G systems. Attackers launch eavesdropping attacks to listen to user calls exploiting weak ciphers on devices connected on 2G networks [19,20]. Vulnerabilities caused by rogue base stations are a security issue in 2G and 3G networks. Public key encryption of the Subscriber Permanent Identifier (SUPI) in 5G networks prevents an attacker from obtaining the SUPI key, ensuring network-side security. However, the encryption of SUPI does not prevent rogue base station attacks on devices due to the lack of protection from broadcast messages received from unauthorized base stations.
The motivation for conducting this research is to address the vulnerability of unsecured broadcast messages of base stations used by attackers to spoof users into joining unauthorized nodes and compromise user data and user privacy. Base station IDs are unprotected and exposed, allowing attackers to disguise them as any access point in the network. A device on the network is unaware of a previously identified rogue node is now spoofing as a different access point. A handover process in an environment such as a hospital requires quick and seamless authentication between devices and base stations. Both base stations and devices should be aware of existing registered entities for immediate authentication. Maintenance of authorized and valid base stations and device profiles results in high data storage. Limited memories in IoT devices prevent them from maintaining an extensive database of all official base stations. A lightweight profile is necessary for both device and base stations to diminish data storage concerns and reduce data communication overhead during the authentication process.
In this paper, the proposed scheme presents a decentralized network for securing base station data from external data. The main contributions of this research include,
1) Base station IDs are generated using mined data and hashed using SHA256 to prevent an attacker from observing and learning the ID generation process. An authentication certificate is issued that lists IDs of all authorized base stations for future handover processes.
2) Each device joining the network for the first time is assigned a unique ID that is hashed using SHA256 and stored in the network database. A certificate of all devices is stored in the base station.
3) Each hashed device and Base station ID undergo a modulo operation that reduces the size of the certificate stored in devices where memory is limited. The reduced authentication certificate size reduces the overall storage overhead and communication overhead, enabling a quick and seamless handover authentication.
4) The proposed scheme is compared with existing studies based on Computation overhead and Storage overhead.
This paper is organized as follows: Section 2 discusses related work discussing recent research to secure devices from Rogue Base Stations (RBS) and includes the key considerations for securing devices against rogue base station attacks. In Section 3, we propose an overview of the proposed scheme and the detailed workflow of the proposed scheme. Section 4 analyzes the proposed scheme compared to existing studies and includes a comparative analysis of the proposed scheme with existing research based on identified key considerations. Finally, Section 5 concludes this paper.
2.
Related work
Existing studies address the identification of rogue base stations using three methods, location-based approach, captured signal strength, and key-based agreement methods. This section discusses related works and highlights their remaining open challenges. To mitigate these challenges, key considerations are highlighted that are required for a secure and robust lightweight authentication scheme for identifying rogue base stations.
A location-based approach-based study presented in [21] proposed two location-based awareness-based fake base station resistance schemes to combat spoofing attacks where signal strength is monitored based on the location of the device. The scheme relies on the authorized base stations and devices' location information, the path loss, shadowing effect, and small-scale fading, which confirm the Average Received Signal Strength synchronization (ARSSS) of the authorized base station is within an adequate range.
The following two studies approached the detection of RBS using the captured signal strength of base stations and compared it with the honest base station. The first study discussed in [22] presented a Density-based spatial clustering of applications with noise (DBSCAN) method to defend smart meters from cyberattacks connected in houses. The meters are installed as part of the Advanced Metering Infrastructure (AMI), which uses General Packet Radio Service (GPRS) to communicate with local base stations, resulting in devices vulnerable to rogue base stations' attacks. The DBSCAN method separates false base stations from authorized base stations based on observable variations in signal strengths. The profile benefits from both meters and base stations' stationary existence and requires less computational resources on meters to distinguish between an attacker and a rogue base station. The second study in [23] proposed an approach to safeguard IoT open meters systems such as power, water, and meter collectors in Open Metering Systems (OMS) from malicious cyberattacks by rogue femtocells. Fake femtocells are identified by observing the variations of the signal strength. The distance between the meter and the base station is measured using the Euclidean distance, and a 24-hour time window is used to identify a rogue femtocell. Analysis of the proposed approach shows a rogue base station connecting at 11:15 pm has the maximum signal strength by 01:00 am, but its signal begins to fade over time. The authors identify a limitation in the proposed approach where an attacker may remain consistently connected and static for over 24 hours rendering the solution infeasible.
The next three studies detect RBS using a handover authentication scheme based on key agreement schemes. The first study in[24] presented a secure handover authentication scheme non-reliant on certificates for the LTE network environment. The scheme is based on a key agreement method that consists of two phases, the initial authentication phase and the handover phase. First, devices generate a partial key and acquire another from the Home Subscriber Server. Secondly, during a handover scenario, the device proceeds with a key agreement method, and a shared session key are generated. Thus, three handshakes are required for the proposed mutual key agreement method to succeed. The second study in [25] based on key agreement proposed an Elliptic Curve Cryptography-based Proxy signature for the handover authentication scheme that includes both Edge-node base stations and Home edge-node base stations. The scheme is based on two phases, attach phase and the handover phase. The first phase is responsible for the authentication when a device registers with the network for the first time. The second phase manages the authentication of devices when they perform the handover process between different base stations. The scheme focuses on reducing the computational cost compared to other methods. The third study in [26] based on handover authentication relies on a proxy signature for secure authentication. The scheme focuses on handover validation between different home-edge node base stations and edge node base stations. An initial attach phase in the scheme requires every new UE joining the network to register and authenticate with the Home Subscriber Server and the MME. Mutual authentication between a device is required when it moves in proximity to the new base station, and a new session key is generated. The proxy signature algorithm generates new long-term secret keys during the handover authentication.
The final two studies implement Blockchain technology for authenticating IoT devices joining the network. The first study in [27] presents a Blockchain based Authentication and Key Agreement for 5G networks against Rogue Base Station attacks. A one-time hashing function designs the device's secret key preventing attackers from learning key data to impersonate as authorized devices. Keys are stored in a decentralized storage which are Denial of Service resilient, preventing attackers from obtaining authentication data. The second study in [28] proposes a lightweight authentication scheme for the IoT devices connecting with a decentralized network. The study focuses on maintaining the privacy of connected users and the security of their data using a modular square root technique. Smart Contracts register devices on the network to prevent malicious devices form transmitting data to the network. There are open research challenges in the above existing studies. The dependence on signal strength reception by [20,21] requires a device to record the base station's signal strength accurately. Environmental factors such as thick walls, physical obstructions, and other wireless devices in proximity prevent accurate reception of signal strength. The research conducted in [23] is dependent on static IoT meter devices and thus is unsuitable for portable IoT devices. Key-based authentication schemes in [24,25,26]—incur high computation and storage overheads during their evaluation. A lightweight scheme is required that is not dependent on an inaccurate recording of signal strength and is suitable for devices and base stations to authenticate mutually. Blockchain based authentication research presented in [27,28] do not focus on reducing the size of encryption keys resulting in high storage overheads and communication costs. Thus, they are not suitable for real-time operations in time critical environments such as Smart Healthcare and the Internet of Vehicles.
In order to maintain a secure and lightweight handover operation between IoT devices and base stations, the following key considerations are essential to the proposed scheme,
1) Access control – Base stations serve as access points for IoT devices to connect with the network and provide real-time services to users and other entities part of the intelligent cloud operations. Therefore, ownership of access control by network owners such as telecommunication organizations is essential to ensure that only it has the sole authority to assign base stations in the network. As a result, malicious entities are prevented from disguising themselves as a valid part of the network.
2) Data integrity – Information collected and transmitted from IoT devices for sensitive applications such as Smart Healthcare requires an analysis based on accurate data for precise diagnosis for patients. Man-in-the-middle attacks threaten the quality of data provided by devices by manipulation resulting in the reliability of the computation results.
3) Data Privacy – A significant challenge when transmitting data over untrusted access points and base stations is user identification and data confidentiality violation. Malicious users intercept data between the network and the device and collect and store data to sell it for economically profitable benefits. In addition, marketing organizations and fraudulent individuals promote promotional offers using data that users did not consent to release in the public domain.
4) Communication overhead – Handover authentication between devices and base stations relies on the presented access point to prove that it is a valid part of the network. Therefore, the exchange of IDs results in high communication overhead. Minimizing network costs enables a seamless handover operation and improves overall network performance.
5) Storage overhead – IoT devices are subject to low memory and computation capabilities, resulting in them unable to store large amounts of base station identification data for secure handover authentication. Devices are subject to rely on the truthfulness of access points that they are a valid part of the network. A low storage cost certificate that stores IDs of all nearby base stations must secure device data transmission and reduce the memory footprint on devices.
The novelty of the proposed scheme is based on the design of a lightweight Blockchain based secure mutual authentication system. Proof of Authority ensures only a single validator is responsible for mining blocks, thus removing the need for a solving cryptographic puzzle. Furthermore, authentication keys are designed to reduce the communication and storage overhead in both memory resource strained IoT devices and Blockchain networks with small block sizes. The authentication scheme depends on requiring both the destination Base Station and the device to prove their authenticity mutually. The handover destination base station must prove it is part of the Private Blockchain network by transmitting its ID to the original base station which is only possible if they both belong to the same Blockchain network. Only Blockchain members are aware of each other IDs which are not shared or communicated with any other entity. The device stores only its own ID and in the event, it is stolen or taken control by a botnet attack, the attacker cannot learn the Base Station ID to launch RBS attacks. The storage of Base Station and Device ID in a hashed form reduces the storage and communication costs in the network, essential for healthcare-based environments where latency is a major cause of concern in network performance.
3.
System model
We consider a healthcare environment consisting of a multi-departmental hospital and focus on the mutual authentication between the base station nodes and devices to prevent sensors from connecting with rogue base stations. The environment consists of several clusters of base stations connected using the Blockchain network. Each cluster consists of several medical devices that are free to move around within the boundaries of the hospital and connect with other base stations due to increased signal strength provided by the nearest base station. Devices assume that each base station is not malicious and is a pre-validated access point belonging to the telecommunication network. Each device regularly receives network information along with signal strength shared by various base stations in plaintext. Exposure of sensitive network information during a broadcast by the base station presents a challenge for network security leaving sensitive base station identity information exposed to attackers. Base stations attract devices based on their superior signal strength to ensure Quality of Service, essential for low delay-tolerant medical devices.
3.1. Problem definition
A critical vulnerability in the handover process is identified when an IoT device, referred to as User Equipment (UE), moves within a hospital cluster, such as from the general ward to the surgery center, and requires connecting to a different BS. The increasing distance from BS1 and the fading signal strength requires UE to connect to a closer base station. UE monitors all base stations in proximity and sends a connection request to the router with the strongest and reliable signal strength. BS2 requests the UE to send an ID, the UE responds by sending its International Mobile Subscriber Identity in plain text to the BS2, and a connection is established. It serves as a 64-bit unique identifier number of each user connected with the network. Base Stations collect information of all connected users, that include International Mobile Subscriber Identity numbers to distinguish between home base users of the telecommunication network and non-local users that are roaming and are part of an external region. In an attack scenario, UE shares its International Mobile Subscriber Identity (IMSI) in plaintext to the base station that exposes all data exchanged on the network to an attacker under the control of a rogue base station. UE is unaware of the base station it is connected to transmit an invalid BS identity code giving the impression it is an authorized network entity. Private medical data is accessible to an attacker affecting data privacy and integrity.
3.2. Scheme overview
In this sub-section, the overview of the proposed scheme describes the environment and the components used to authenticate both base stations and IoT devices. The environment consists of a hospital with multiple clusters, with each containing a group of base stations. Several IoT devices connect with local base stations and perform handover operations when moving further from their original base station. An authentication certificate issued by base stations contains unique IDs of both devices and all base stations in the local cluster. Devices and new base stations exchange certificates to enable a seamless and secure authentication with a low communication overhead.
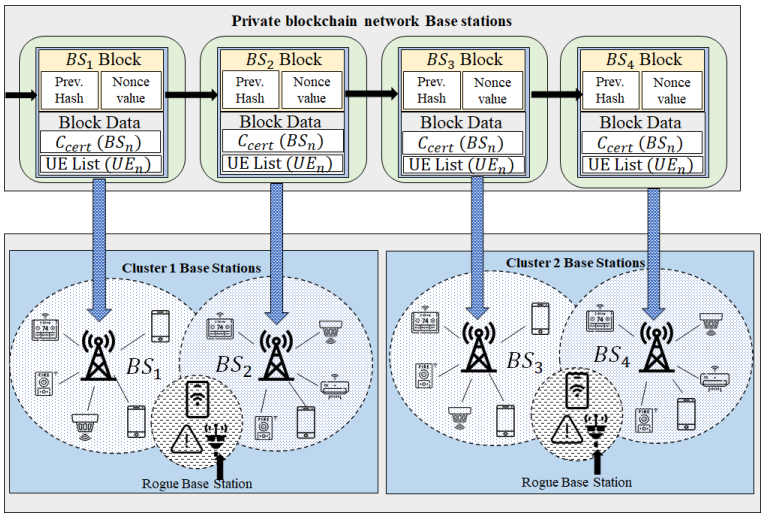
As shown in Figure 1, the network environment is based on blockchain-based nodes where each block represents a base station (BS) node. In this paper, we take the scenario of a hospital with several departments. Each section within the hospital consists of several wireless routers that are identified as BS. Several BS comprise a group cluster responsible for connecting and performing handover operations for all IoT devices in a specific geographical area. Different departments within the hospital, such as the emergency response unit, surgery, and general wards, comprise a separate cluster. Pediatrics, Birthing center, and its respective intensive care unit constitute a second cluster example. Each group consists of several IoT devices such as pacemakers, glucose monitors, heart-rate monitors, and drug effectiveness monitors for individual patients. Patients move between different departments based on their medical requirements and require a quick and seamless handover process to monitor patient health continuously.
4.
Proposed scheme
The proposed scheme implements a blockchain network to secure UEs from rogue base stations. A private blockchain provides the cellular network the privileged access to add blocks to the network system and speeds up handover requests. In this paper, we assume that blocks are pre-mined by the network where each Block is pre-mined by the network using proof-of-work for block mining. The Blockchain-based Base Station network ensures the security of data stored in immutable ledgers, prevents single point of failure vulnerabilities, and prevents unauthorized entities from accessing or modifying stored data in blocks. Each newly mined block by the network is connected with the previous block using a hash value making it impossible to modify or tamper with data. Transactions are validated using the Proof of Authority consensus ensuring the validity of the data stored. New blocks are added when new Base Stations join the network by the cellular network. Proof of Authority enables the network to behave as the validator and is resistant to 51% attacks and Denial of Service attacks. A successful attack is challenging as it requires the network system itself to be first compromised. Furthermore, the computationally and energy consuming task of solving cryptographic puzzles are removed by selecting the network as the sole authority to approve new blocks mined for adding new base stations. The reduced number of validators increases the transaction finality in the network, thus increasing the efficiency of the Private Blockchain. The consensus algorithm is suitable for Private Blockchain enables privacy of data storage and ensuring data ownership is retained by the network.
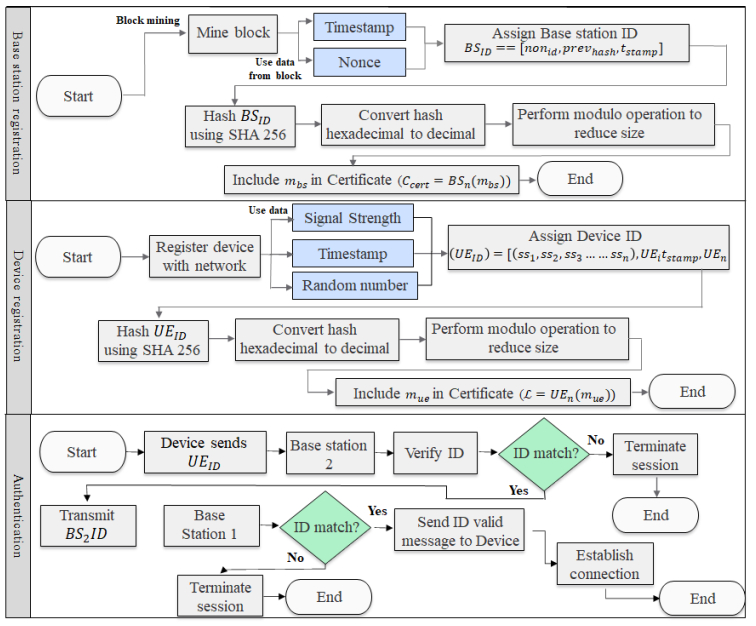
Blocks added to the network represent BSs authorized by the core network and establish a blockchain neighborhood to ensure all BSs are valid nodes and UEs are connected securely. The secure authentication process of the proposed scheme as shown in Figure 2 is as follows,
Step 1: BS are pre-mined nodes by the network. The telecommunication network does not require solving a complex cryptographic puzzle in a private blockchain as it is the only authorized entity to mine a block.
Step 2: A unique BS identity (ID) is generated that relies on the timestamp of the block creation, the nonce value to mine the block, and the hash of the previous block. The network owns the genesis block.
Step 3: The BSID is hashed using SHA-256 to prevent an attacker from learning the ID and pretend to be a valid node belonging to the network.
Step 4: BSID of all BS belonging to various clusters are generated using SHA-256. The BSID is required to be shared with the UEs; however, due to low available memory, UE cannot store multiple authentication certificates belonging to various clusters existing in a hospital.
Step 5: BSID hash is converted into a decimal number, and a modulo operation is performed to reduce the ID size. The modulo result is included as an identifier of each BS in the certificate and shared with other BSs in the cluster.
Step 6: Each UE registers with the network to support a seamless handover scenario. Each BS is aware of the UE's existence and its history with the network during a handover process. Therefore, a profile for each device is saved across all BSs in the cluster.
Step 7: UE registration initiates with collecting the signal strength profile, which is unique to each device, a timestamp, and a random number. The timestamp and the random number are not reliant on a specific order and are included to increase the randomness of the UEID generation.
Step 8: A similar BSID generation process follows for UEID, where an SHA-256 hash process hides the UEID generated. The hash is converted into a decimal number, and the modulo operation resultant is included in the UE profile that is safely stored in the network. A copy of the individual UE profile is shared with each BS in the existing cluster where it is registered.
Step 9: The authentication process during a handover scenario requires only the UE to share its UEID and initiate the authentication process. Preventing the base station from sharing its ID protects the network from a malicious device from learning the BSID.
Step 10: BS2 checks the validity of the UEID ensuring it is a valid part of the network. In the event, the UEID is invalid or blacklisted by the network due to the device being stolen, the authentication process fails. If the device is a valid part of the network, the next authentication step proceeds.
Step 11: The Private Blockchain network requires only pre-mined base station nodes to connect and communicate amongst each other. Therefore, BS2 sends its BS2ID to BS1. BS1 is the base station node with which the UE is currently connected. BS1 checks the validity of BS2ID from the list of stored valid base stations.
Step 12: If BS2 is a valid part of the network and not an RBS, then BS1 transmits a valid message directly to the UE attempting handover.
Step 13: Successful authentication between the BS2 and UE results in a successful handover operation.
The proposed scheme is dependent on pre-selected IoT devices that exist within the hospital environment to monitor patients. The BSID is a unique fingerprint for each authorized BS in the network and is issued only by the network system. The registered BSID is announced by each BS to other BSs within the cluster. The network maintains global knowledge of each BS in cluster and a new BS added is shared across all clusters in the hospital. The UEID, issued by the BS, is randomized using a timestamp and a random number and hashed using the SHA256, preventing an attacker from learning the ID. Usage of weak number generators or vulnerable software allows repeated nonce value usage to sign various keys [29]. Thus, each UE has a uniquely different ID based on changing signal strength, random number, and timestamp. A UEID generated is shared among all BS in a cluster. The network maintains the profile of all UEs added and shares it across all other BSs in different cluster.
The proposed scheme operates in three phases, as shown in Figure 2, Phase 1, Base station registration, and Phase 2, UE registration, which occur before the handover scenario. Phase 3, Authentication, represents the handover scenario where UE requests the BS to authenticate itself before establishing data communication among them. We assume two honest BSs, identified as BS1 and BS2 one UE, and one RBS. Phases 1 and 2 describe the key generation process, and Phase 3 represents the handover process.
4.1. Phase 1: Base station registration
In phase 1, Base station registration, requires the initial set of information to identify each BS and prevent an RBS from behaving as authorized by the network. Initially, we begin with BS1registration. A block is mined by the network for each BS and block parameters such as nonce ID (nonid), previous block hash (prevhash), and the block creation timestamp (tstamp) are recorded. These parameters are hashed using the SHA2 hashing function f(h) with a output of 256 bits. The hash serves as a secure key. The key generation and storage process is as follows,
Step 1: Each BS is assigned a pre-mined node in the Blockchain network and registered in the private Blockchain network using a BSID. The unique ID refers to its own BS and is inaccessible to entities external to the Blockchain.
Step 2: The BSID includes three parameters available after the block is mined, nonid, prevhash, and tstamp. The BSID is represented as follows,
Step 3: Using the SHA2 function, a 256-bit hash is generated to secure the BSID. The key is now represented as,
Step 4: The resulting hash in hexadecimal format serves as input when it is converted into a decimal number (dbs) using the function,
Step 5: A modulo (mod) operation is performed to reduce the size of the resultant decimal number.
Here mod is represented by (mbs). A unique and random number (ubs) is selected between 0 to 256 to perform the mod operation and prevent an attacker from learning the BSID. The limitation on the random number selection is to control the size of the resultant mbs and therefore reduce the storage overhead on resource constrained IoT devices. The final mod is included in the Cluster Certificate (Ccert) and is part of a single BS that is included in a certificate. Further BSs registered by the network are included in the Ccert as Ccert=(BS1(mbs),BS2(mbs),……BSn(mbs)). The network stores the certificate for quick validation of all included Cluster BS's.
4.2. Phase 2: UE registration
In the second phase, UE registration, a unique identity for each connecting device is generated. The UE joining the first local BS is registered as the source BS in the blockchain network. The registration process is as follows,
Step 1: We assume BS1 as the first source BS that collects details from the UE that includes a set of SS collected. A random nonce number (UEn) and timestamp (UEitstamp) are included in the device registration to increase randomness in the final UEID generation. These values form a unique UEID that ensures that the device is registered with the network and helps in future authentication with other BSs.
Step 2: A new UEID is generated serving as a fingerprint for the device. Three parameters are used, ss1,ss2,ss3……ssn, UEitstamp, and UEn.
Here, (ss1,ss2,ss3……ssn) represents a set of SS collected from the device when it registered with BS1 to form a unique profile based on user movement. Environmental factors impacting real SS are not considered as the primary goal. SS is not used to establish a unique device fingerprint but to collect the UE's movement pattern that is difficult for an attacker to imitate and determine. A timestamp (UEitstamp) is generated which is random and not dependent upon the device being registered. A secondary random number (UEn) is used to increase the randomness of the UE fingerprint.
Step 3: Storing the UEID on the UE risks exposure to being exposed to attackers. A cyberattack on an IoT device such as botnet reveals the UE and so the ID is hashed using SHA2 function (h).
Step 4: Similar to equation (3), the hexadecimal output of the hash is transformed into a decimal number (due) for further modulo operation. The objective is to reduce the size of the key for less communication overhead during final authentication process.
Step 5: A mod function operation (m) similar to equation (4) is as follows,
Here mue is the result of the mod operation and is stored in the UE to be used during the final authentication process.
Note: Equation (8) and its parameters due and uue and the UEID hash are stored as a list L=(UE1(mue),UE2(mue),……,UEn(mue)) in BS1 and shared with all other BSs (BS2,BS3,……,BSn) in the cluster.
Here mue is the result of the mod operation and is stored in the UE to be used during the final authentication process. Equation (8) and its parameters due and uue and the UEID hash are stored as a list L=(UE1(mue),UE2(mue),……,UEn(mue)) in BS1 and shared with all other BSs (BS2,BS3,……,BSn) in the cluster.
4.3. Phase 3: Authentication
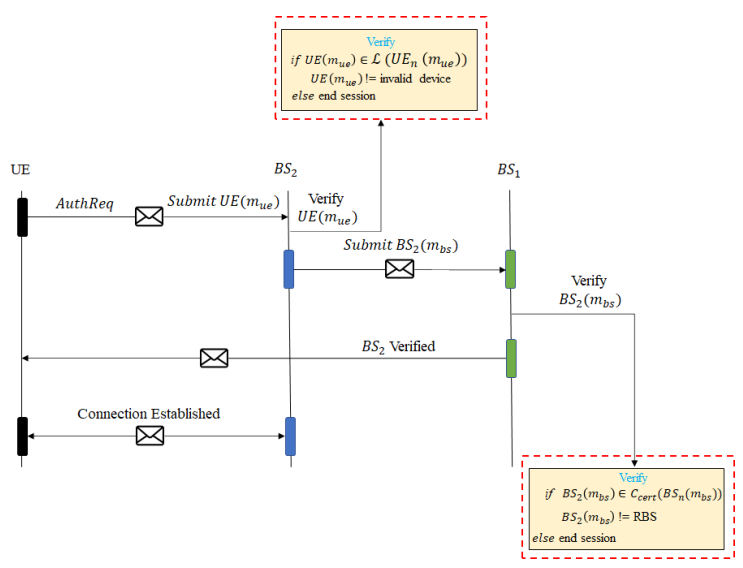
In this third phase, the UE moves from source BS1 to the destination BS2 for handover because of its stronger signal strength compared with other BS in the cluster BS1,BS3,BS4….BSn. The final phase mutually authenticates UE and BS2 to prevent an RBS from validating itself as part of the network and a malicious device from connecting with the network. The authentication process as shown in Figure 3 is as follows,
Step 1: UE sends a request to BS2 to initiate the handover process by sharing its 𝑈𝐸 (mue) and current BS(BS1) name with BS2 and waits for a response.
Step 2: BS2 verifies the identity of UE to ensure it is not a malicious device by searching UEID(mue)∈ L where L=(UE1(mue),UE2(mue),……,UEn(mue)).
Step 3: Upon successful device authentication, BS2 forwards its mod to BS1 for verification. Only members of the network service provider's private Blockchain network are allowed to communicate with other base stations.
Step 4: Each base station has access to the Ccert generated during the Phase 1: Base Station generation. BS1 checks if BS2(mbs) ∈ Ccert where Ccert=(BS1(mbs),BS2(mbs),……BSn(mbs)).
Step 5: BS1 verifies the identity of BS2 and that it is not malicious. BS1 then forwards authentication verification message directly to the UE.
An attack scenario in the authentication scheme is possible under two scenarios, the attacker steals the device or listens as an eavesdropper during the device and Base Station authentication communication. In the first scenario, if the device is stolen and leaves its cluster, the device is deregistered from the network and listed in a blacklist. The device remains blacklisted till it is recovered and re-registered with the network. The system administrator is additionally required to enable the registration and ensure the device is now controlled and managed by the healthcare facility.
In the second attack scenario, the attacker eavesdrops the authentication between the device and the Base Station. The data exchanged between the device and the Base Station includes only the 𝑈𝐸 (mue) and does not reveal any details of the BSID. An attacker is unaware of the BSID and therefore cannot perform the RBS attack. In the event, the attacker learns the BSID, the authentication process requires the RBS to be part of the Private Blockchain network and authenticate the RBS with another valid Base Station to enable devices to share their private data. The RBS being external to the Private Blockchain network results in an authentication failure as other Blockchain nodes return authentication failure message to the device.
5.
Evaluation
The analysis of the proposed scheme's performance is based on communication overhead and storage overhead. A scheme protecting UEs from RBS attacks is required to satisfy the following requirements and present a secure and reliable scheme for base station and UE security. We observe the proposed scheme requires fewer bytes during communication between the UE and BS2 resulting in reduced communication overhead compared with existing studies. The storage overhead incurred by the storing of Ccert and the L by the base station is less due to the modulo operation requiring a smaller amount of data storage in bytes.
5.1. Experimental setup
The performance evaluation of the Lightweight IoT Authentication scheme is evaluated using a desktop running Intel i7 based CPU with 16 GB RAM running Ubuntu 18.0.04 and Python 3.6. Key generation and authentication are determined using a custom python script, and Open SSL secures inter-node communication. Nodes are designed using Network Simulator 2. SHA256 computation is achieved using Crypto.js library. We examine the operation time of the scheme as shown in Table 1 by analyzing the SHA256 hashing operation f(h)[nonid,prevhash,tstamp], and the modulo operation to generate the modulo key using mbs=dbs%ubs. Next, the computation of the (UEID)=[(ss1,ss2,ss3……ssn),UEitstamp,UEn, the hashing process using SHA2, (UEID)=f(h)[(ss1,ss2,ss3……ssn),UEitstamp,UEn and the modulo operation, mue=due%uueare analyzed. Finally, the handover authentication process between BS2 and the UE are analyzed.
As presented in Table 1, the total computation overhead measures the time taken by the proposed method to complete the operation to calculate the BSID, UEID, and the final authentication BS1 validates if BS2(mbs)∈Ccert and BS2 completes verifying if UEID(mue)∈L.
5.2. Communication overhead
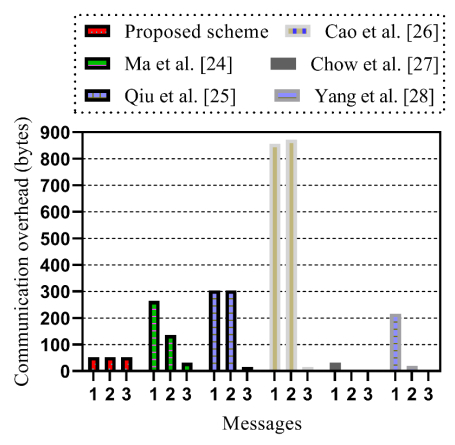
In the proposed scheme, a total of 3 messages are shared between BS2 and the UE. The first message is a request from the UE to BS2 for its mbs to verify if it is part of the valid network and is included in the Ccert. In our evaluation of the communication overhead, packets shared on the network in bytes for the authentication process are measured and compared with the works by Chow et al. [27], Yang et al. [28], Ma et al. [24], Qiu et al. [25], andCao et al. [26]. Three messages are required to complete the authentication process in the proposed scheme and the related research. Message 1 (M1), Message 2 (M2), Message 3 (M3) are the three messages exchanged. M1 represents the handover request for UE ̶˃BS2 and includes mue. M2 represents the reply from BS2 to BS1 with mbs. M3 is the final communication with BS1 transmitting establishing the final connection as authorized with UE. All M1, M2, and M3 are measured considering IP header, TCP header, source MAC, and destination MAC when measuring the packet size.
The proposed scheme compared with existing methods, as shown in Figure 4 and Table 2, requires fewer bytes of data transferred for the authentication process to succeed. The inclusion of the hashing process in the proposed scheme increases the individual UE and BSID size to nearly 32 bytes each. However, the modulo operation reduces the size of the authentication certificate mue=due%uue ensures that overall communication overhead compared to existing studies is at the minimum. Table 2 presents the communication overhead incurred by the proposed scheme without the default packet overhead incurred during communication between the BS2 and UE.
5.3. Storage overhead
Storage overhead in the proposed scheme is measured by considering a minimum of 10 UEID stored in one base station as part of one Ccert. As there are multiple access points set up nearby across departments in a hospital and devices with patients and the healthcare staff frequently request handover requests. Therefore, a minimum of 3 Ccert for 3 base stations each are considered allowing a single BS to seamlessly authenticate with a minimum of 10 devices in the hospital. The total storage overhead resulted in 30 bytes. Ma et al. [24] scheme performed the best among other existing studies with 288 bytes of device storage overhead. The scheme stores a partial public key, the private key, and the public parameters in the UE. In Qiu et al. [25] scheme, the UE stores public parameters and the proxy signature information and results in 296 byes of storage overhead. The UE stores long-term secret keys and public parameters in Cao et al. [26] scheme requiring 1616 bytes and thus results in the highest storage overhead. Chow et al. [27] highlights their proposal incurs higher energy costs during half open connections during DDoS attacks. The scheme proposed by Yang et al. [28] incurs a high storage overhead of 92 bytes, which includes storing the device identity, timestamp, random number, and a hash function. Figure 5 illustrates the comparison of incurred storage costs in a device with existing research. We observe the proposed scheme, compared to other existing techniques, is especially suitable for storing BSID on IoT devices that have low memory. The proposed study implements Proof of Authority consensus model preventing external entities from block data modification as there is only a single validator, the cellular network.
5.4. Discussion
In this section, we analyze the security of the proposed scheme and discuss comparison results with other existing studies. The four key areas of consideration, Access control, Data integrity, Data Privacy, Communication overhead, and Storage overhead, with current research are compared to determine a secure and lightweight authentication handover scheme against RBS attacks.
We observe from the Comparative Analysis given in Table 3 that existing researches do not fully satisfy all key areas of consideration. None of the current studies propose means to prevent an attacker from obfuscating as part of the network. Valid base stations are vulnerable to sharing private network data with the attacker. The network environments do not prevent an attacker from manipulating data by sending false information to other base stations. The proposed scheme adopts a cluster system where base stations are grouped belonging to a geographical area. The cluster is responsible for serving devices that include in the same area boundary. Each base station is aware of the other's existence due to the network assigning an ID and shares it with other BSs within the cluster. The ID serves as a unique fingerprint and prevents a rogue base station from replicating it. Only the network managing the private Blockchain generates the nonid,prevhash,tstamp. A rogue node unable to replicate a valid Base station ID is rejected by other nodes in the Blockchain and the network.
We observe from the Comparative Analysis given in Table 3 that existing researches do not fully satisfy all key areas of consideration. None of the current studies propose means to prevent an attacker from obfuscating as part of the network. Valid base stations are vulnerable to sharing private network data with the attacker. The network environments do not prevent an attacker from manipulating data by sending false information to other base stations. The proposed scheme adopts a cluster system where base stations are grouped belonging to a geographical area. The cluster is responsible for serving devices that include in the same area boundary. Each base station is aware of the other's existence due to the network assigning an ID and shares it with other BSs within the cluster. The ID serves as a unique fingerprint and prevents a rogue base station from replicating it. Only the network managing the private Blockchain generates the nonid,prevhash,tstamp. A rogue node unable to replicate a valid Base station ID is rejected by other nodes in the Blockchain and the network.
Data integrity concerns are addressed by existing research. However, user data privacy is an open vulnerability in Qiu et al. [25] and Cao et al. [26] proposed schemes where IMSI information is shared as part of the initial authentication process. As a result, user location privacy and data transmitted, such as calls and messages, are exposed to the attackers with the knowledge of the UE's IMSI. Recent studies by Chow et al. [27] and Yang et al. [28] do not provide privacy to secure the authentication protocols allowing attackers to learn user and device identity. The proposed scheme, UE's connecting the first time with the BS register with the local cluster BS and a unique UEID where (UEID)=[(ss1,ss2,ss3……ssn),UEitstamp,UEn] is generated. The ID uses the device's signal strength information which does not directly correlate to the device's identity. Furthermore, a timestamp and a random number are included to increase the randomness of the data gathered for ID generation. Finally, SHA256 produces a hash with a non-reversible property preventing an attacker from learning the user's identity.
Communication overhead and Storage overhead are vital components of the final analysis with existing studies. A large number of devices require mutual authentication and the handover process to be seamless with reduced latency. Significant bytes of data shared during the final authentication increase the communication overhead, resulting in slower authentication and inferior quality of service, especially in sensitive environments such as healthcare institutions. Large storage overheads are not feasible for IoT devices with low memory storage availability, thus affecting their overall operational capacity. All existing researches incur higher communication and storage overhead than the proposed scheme, which implements the modulo operation to decrease the size of the mbs stored in the Ccert. IoT devices are required to store fewer data in bytes for storing BS identifying data resulting in less storage overhead. Similarly, mue data stored in L reduces the data size stored in base stations. Communication overhead is decreased directly due to the reduced sizes of both mbs and mue.
In comparison with existing studies, the proposed framework outperforms them on Communication and Storage overhead and provides complete data integrity and privacy along with network access controls. The proposed scheme is suitable for handover authentication in hospitals with a pre-approved IoT device and a private blockchain network with mined nodes representing base stations.
6.
Conclusion
This paper presented a scheme to protect the cellular network and its connected devices from Rogue Base Stations. Private blockchain-based network with Proof of Authority consensus algorithm ensures all base stations are network approved, and each possesses a unique, encrypted ID. In addition, devices registered with the network have a unique ID designed based on captured signal strength data. Both IDs for base stations and devices are hashed using SHA256, and a modulo operation is performed to reduce the storage overhead of both IDs. The proposed scheme is evaluated and compared with existing research based on two parameters, communication overhead, and storage overhead. The proposed scheme, requires fewer bytes of data transmitted during final authentication. Additionally, the storage overhead for IoT devices with low memory is less in our scheme.
Lack of measures of physical device security for pre-registered IoT devices presents a vulnerability where an attacker joins the network as an authorized user and transmit malicious scripts to base stations. This limitation comprises the network security and enables an attacker to disrupt telecommunication services. In our future research, we aim to present a novel method for the physical security of devices to prevent attackers from accessing confidential data stored in IoT devices. The research will include intrusion detection systems along with access control measures to prevent unauthorized access of data.
Acknowledgments
This study was supported by the Research Program funded by the SeoulTech (Seoul National University of Science and Technology).
Conflict of interest
The authors declare there is no conflict of interest.









 DownLoad:
DownLoad: