Free vibration of summation resonance of suspended-cable-stayed beam is investigated in the article. A 3-DOF model of the coupled structure is built, with the main cable and sling (vertical cable) considered to be geometrically nonlinear, and the beam is taken as linear Euler beam. Hamilton's principle is used to derive the dynamic equilibrium equations of the coupled structure. Then, the dynamic equilibrium equations are solved by means of multiple scales method, the second order approximation solutions of single-modal motion of the coupled structure are obtained. Numerical examples are presented to discuss time history of free vibration of the summation resonance, with and without damping. Additionally, fourth-order Runge-Kutta method is directly used for the dynamic equilibrium equations to complement and verify the analytical solutions. The results show that the coupled structure performs strongly nonlinear and coupled characteristics, which is useful for engineering design.
1.
Introduction
The sling or the vertical cable is widely used in suspension bridge. By connecting the main cable with the beam, the sling plays a decisive role in transmitting force. However, in recent years as the span of the suspension bridge increases, length of the sling also increases, which directly leads to protruding nonlinear characteristics of overall structures. Furthermore, the coupling among the sling, the main cable and the beam results in new mechanisms of the internal resonance. Therefore, the study of nonlinear characteristics of the sling, especially the coupled characteristics with other structural members, is of considerable importance to mechanical and structural engineers. In recent years, cable structures have been intensive study by many researchers all over the world. Among the known solutions of them, there are harmonic balance method [1,2], multiple scales method [3] (including discretization approach and direct approach), finite element method [4,5], finite difference method [6], numerical integration method [7] and experimental method [8].
Since the beginning research of cable, some articles only forced on a single cable [9,10,11,12], which can not reveal the totally nonlinear characteristics of the whole structure.
From the perspective of the overall structure, Sun and Wang [13] established a 2-DOF cable-beam coupled model by simplifying the cable to a taut string and reducing the beam to a mass-spring system; he proved the displacement curves of the cable and beam have the characteristic of "beat". Fujino and Warnitchai [14] established another kind of 3-DOF cable-beam coupled model; in this model, the beam was considered to be linear Euler beam, with one end point fixed and another end point connected to the cable, the cable was taken as string with sag. Based on the same model, Xia and Fujino [15] further studied the behavior of the system under a random excitation. Then, Xia et al. [16] established a cable finite element to analyze the nonlinear vibration of cables in cable-stayed bridge; by comparing with the available analytical solutions, they demonstrate that the cable finite element can capture nonlinear vibration, in particular auto-parametric vibration of stay cables under harmonic and random loadings. Gattulli [17,18] established the similar kind of cable-beam coupled model and studied linear and nonlinear behave of the system. Gattulli and Lepidi [19] set up a finite element model and verified the results of theoretical analysis and finite element model through experiments. By considering the nonlinearity of the beam, Wang et al. [20] researched the nonlinear behavior of the coupled system. Wei et al. [21] investigated the nonlinear dynamics of a cable-stayed beam driven by the sub-harmonic resonance of the beam and the principal parametric resonance of the cable. For the first time, Wang and Li [22] researched the nonlinearity of cable-beam coupled structure under the thermal loads. Kang et al. [23] discussed the effects of some key parameters of the stay cable, such as initial tension force, damping and inclination angle, and the excitation frequency and amplitude on the nonlinear behavior of the combination structure. With the method of transfer matrix, Zhao and Kang [24,25] investigated the free vibration of the cable-stayed arch bridge.
Though many papers had studied the nonlinear vibration of cable-beam coupled structure and got some available conclusions of coupled characteristics of cable and beam, they mainly forced on the cable-stayed bridge, in which the stay cable is only under one kind of excitation on one end point and the coupled model is 2-DOF. However, in suspension bridge, the sling or the vertical cable is under two kinds of excitation on two end points. To well understand the coupling among the sling, the main cable and the beam, the coupled model will be 3-DOF. There exists new kind of internal resonance, such as summation resonance. This will be new and interesting topic for us.
About summation resonance, Nayfeh and Mook [26] introduced the fundamental theory of it, which can be used in many areas, such as ship engineering, civil engineering and so on. Zhao et al. [27] studied the summation resonance of a classic Spar platform under long periodic regular wave. Chen et al. [28] investigated the steady-state transverse vibration of a parametrically excited axially moving string with geometric nonlinearity and obtained the steady-state response of the summation resonance. There are also many other papers of summation resonance, which well guide us to introduce the theory of summation resonance into the suspension bridges.
In the paper, free vibration of summation resonance of the coupled structure is investigated with and without damping respectively. Firstly, a 3-DOF model is built, which treated the main cable and the sling as nonlinear taut string and the beam as Euler beam; secondly, Hamilton's principle and multiple scales method are used to derive and solve the dynamic equilibrium equations; thirdly, numerical integration method is used to discuss the nonlinear characteristics of the coupled structure. The conclusions show the three degrees of freedom strongly couple with each other and have the typical characteristics of "beat".
2.
Derivation of governing equation
In order to simplify the problem, some assumptions are made in this paper, as follows:
The material nonlinearity of the coupled structure is not considered;
The sag curve of the main cable under gravity is approximately parabolic;
The flexural rigidity, torsional stiffness and shear stiffness of the main cable and sling are not considered;
The cable force of the main cable and sling are constant along the longitudinal direction;
The main cable and sling keep linear elastic during vibration.
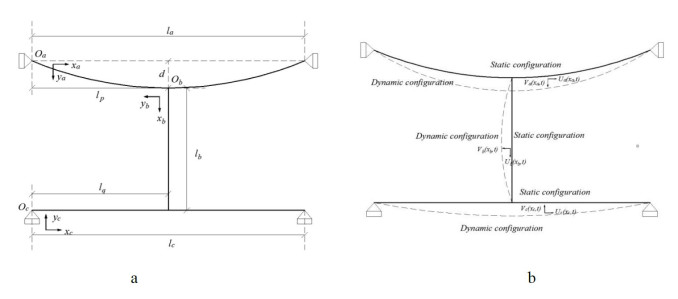
In Figure 1, the Cartesian coordinate system is established, with the main cable descripted in the system of oa – xaya, the sling descripted in the system of ob – xbyb, the beam descripted in the system of oc – xcyc; la, lb and lc donate the span of the main cable, sling and beam, respectively; lp is the distance between the installation position of sling on the main cable and the left end of the main cable; lq is the distance between the installation position of sling on the beam and the left end of the beam.
In particular, due to self-weight, the static configurations of the main cable, sling and beam exist. For simplicity, we neglect the contribution of static configurations of the sling and beam to the motion equations [29,30,31]. The static configuration of the main cable can be written as [32,33]:
where d is the sag of the main cable, Ha is the axial component of the initial cable force of the main cable.
The Lagrangian strain of the main cable and sling can be written as [30]:
According to Hamilton's principle and ignoring the movement of axial direction, the differential equation of lateral vibration of the coupled structure can be written as [18]:
where ma, mb, mc are the mass of the main cable, sling and beam per unit length; ca, cb, cc are the damping coefficients of the main cable, sling and beam; va, vb, vc are the main cable, sling and beam displacement components in the lateral direction respectively; Hb is the axial component of the static cable force of the main cable and sling; Ec, Ic are the Young's modulus and moment of inertia of the cross section of the beam.
ha and hb are the increment in the axial component of cable force of the main cable and sling, which can be written as [30]:
where Aa, Ab are the areas of the cross section of the main cable and sling.
F(t) is dynamic cable force of the sling, which can be written as:
For convenience, Eqs 4–6 is nondimensionalized by defining the following variables:
Substituting Eq 7 into Eqs 4–6 yields
The boundary conditions of the coupled structure can be written as:
In the procedure of Galerkin, basis functions that satisfy boundary conditions are used. In order to investigate the coupling among the main cable, sling and beam, this paper only deals with single-modal lateral vibration of the coupled structure. Then the displacements are assumed as
where qi(t) and ϕ(xi) are the generalized coordinate and mode shape of the linearized problem of the coupled structure respectively.
Substituting Eq 10 into Eq 8 yields
The coefficients presented in Eq 11 are interpreted in the Appendix A.
In Eq 11, quadratic and cubic nonlinear terms simultaneously exist, showing strong nonlinearity. By square nonlinear term, the main cable and beam couple with the sling and provide parametric excitation for the sling, which produces many kinds of internal resonance. The summation resonance is one of them and will be discussed in the following sections.
3.
Solution procedure
Both quadratic and cubic nonlinear terms are included in Eq 11, so the method of multiple scales can be used to solve the dynamic equilibrium equations. A small parameter ε should be introduced so that the damping and constant terms appear in the same perturbation equation. Eq 11 is then rewritten as
Introducing the time scales
an approximate solution can be given by
Substituting Eq 14 into Eq 12, and equating the coefficients of ε1, ε2 and ε3 in both sides of the equation, we obtain
Order ε1
Order ε2
Order ε3
where Di=∂/∂Ti
The complex solution of Eq 15 can be written as
where A1(T1, T2), A2(T1, T2), A3(T1, T2) are unknown complex functions, and cc is the complex conjugate part to the preceding terms.
Substituting Eq 18 into Eq 16 yields
When the resonance does not occur, for the elimination of secular terms, we obtain
Solving Eq 19, we can get
Substituting Eqs 18 and 21 into Eq 17 yields
The coefficients presented in Eq 22 are interpreted in the Appendix B.
From Eq 22, we can know that there are many kinds of internal resonance when the frequencies of the main cable, sling and beam satisfy some special relationship, such as 1:1 (ωa ≈ ωc) and 1:2 (ωa ≈ 2ωb, ωc ≈ 2ωb) internal resonance. This paper only deals with the situation when the sum of ωa and ωc approaches two times of ωb (ωa + ωc ≈ 2ωb).
Introducing a detuning parameter σ and supposing
Substituting Eq 23 into Eq 22 and eliminating the secular terms yields
The complex functions can be expressed as
where ai, θi are real functions with respect to T2.
Substituting Eq 25 into Eq 24, and setting the real and imaginary parts to be zero, respectively, we then get
where
From Eq 26, if not considering the damping of the system, then we can obtain
where E is a constant of integration proportional to the initial energy of the system. If f3/e5 and f4/m5 have the same sign and E is positive definite, Eq 28 shows that a1, a2 and a3 are always bounded. In the paper, we assume that the system does not contain regenerative elements [34], so that f3/e5 and f4/m5 have the same sign.
When considering the damping coefficients of the coupled structure, a1, a2 and a3 are also bounded, but E will decrease with time, which will show in the following section.
4.
Numerical results and discussion
In the following numerical investigations, the basis functions used here are [35,36,37]
which satisfy the boundary conditions in Eq 9.
4.1. Frequency of the sling
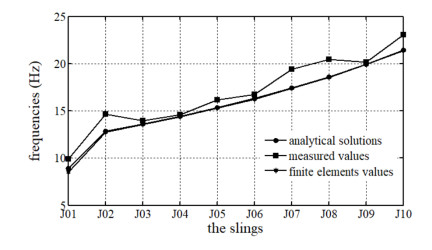
In the section, ten slings of Aizhai suspension bridge are taking as an example, the fundamental parameters of which are listed in Table 1. And then, a full bridge model with MIDAS CIVIL and a single sling model with ABAQUS are made to obtain the finite element values of the frequencies of the slings. Furthermore, we have measured the slings at the bridge construction site to get the measured values of the frequencies of the slings. At last, the frequencies of the slings obtained by Eq A9 are compared with those are measured and got by finite element models.
The calculation process of the finite element value of the frequency of the sling is: at first, a full bridge model is built with MIDAS CIVIL and from the model, we can get the cable force of the sling at the service stage of the bridge; then the cable force of one sling is used in the single cable model, which is built with ABAQUS, and from the model, we can get the frequency of the sling. In the full bridge model, the suspension and the sling are simulated with tension-only truss element, the beam and the tower are built with beam element. In the single cable model, the sling is simulated with the type of T3D2 of truss element. The screenshot of the finite element model of Aizhai suspension bridge is shown as follows, and the ten slings have been marked in red, the NO. is J01 to J10 from left to right.
Figure 3 shows the validity of the reduced models in Eq 10 for deriving formulas of this paper. A good agreement can be obtained. The frequency differences of analytical solutions with measured values and finite element values are in an allowance range of 5%.
4.2. Time history of amplitude
The initial parameters of the coupled structure are shown in Table 2.
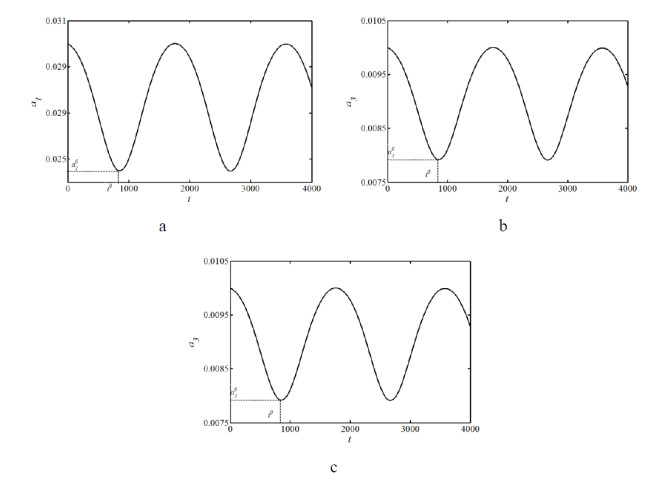
Time history of amplitude of the summation resonance of the coupled structure is analyzed. According to the parameters given above, the frequencies of the main cable, sling and beam will be ωa = 4.456, ωb = 8.911, ωc = 13.367 (Example A), which satisfies the condition of summation resonance of Eq 23 and ξ2σ = 0. Then, via Eq 26, time history of amplitude can be obtained and shown in Figures 4–5. Figure 4 does not consider the damping coefficients of the coupled structure, while Figure 5 considers four kinds of damping coefficient of the sling. Furthermore, a10, a20, a30 and t0 in Figure 4 stand for the first peaks of the amplitudes of the main cable, sling, beam; t0 stands for the time when a1, a2, a3 reach the first peaks, which we call it triggering time in the following sections.
From Figure 4 the following can be observed: Without damping, the summation resonance of the coupled structure is periodical, stable and bounded; total energy of the coupled structure is conserved and transferring among the main cable, sling and beam, which has typical characteristic of "beat"; the main cable and beam are energy provider while the sling is energy recipient in the first half cycle of each cycle.
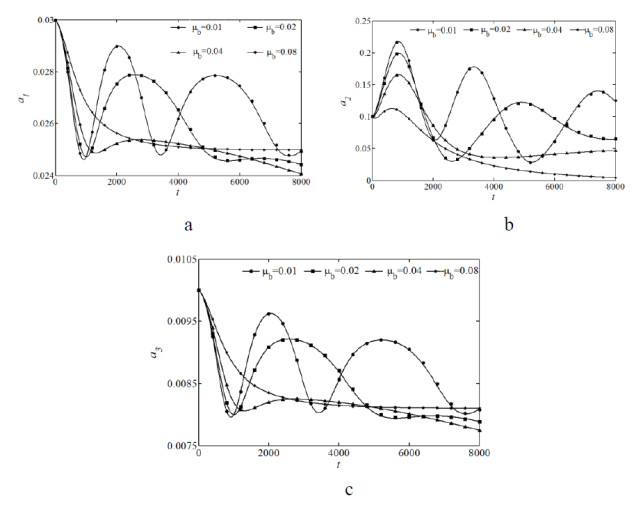
Figure 5 shows with damping, the summation resonance of the coupled structure still has the characteristic of "beat", but total energy of the coupled structure is gradually consumed with time going on. For any kind of damping, though we only take the damping coefficient of the sling into account, the peaks of the amplitudes of the main cable and beam also change. Therefore, we can conclude that due to the internal resonance, we can adjust the attenuation law of one degree by changing the damping coefficient of another degree. As the damping coefficient of the sling increases, the first peaks of the amplitudes of the main cable, sling, beam decrease and the triggering time becomes larger. It shows the inhibitory effect of the damping on the coupled structure increases. Thus, we can get that the increasing damping not only gradually decreases the amplitude of the coupled structure, but also makes the energy exchange become slower.
4.3. Time history of displacement
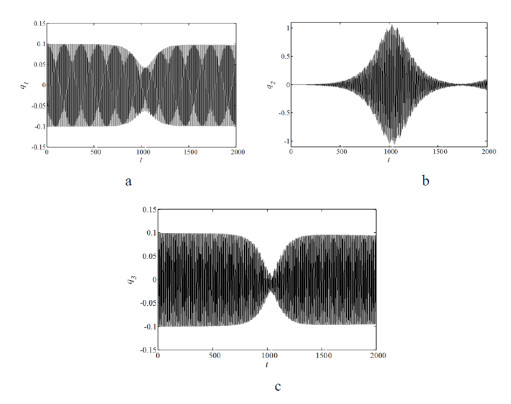
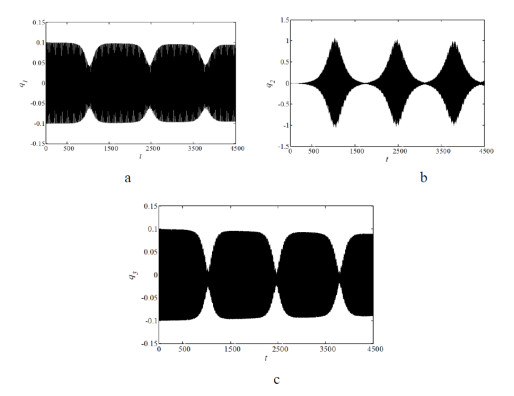
In the section, numerical investigations are used directly for the dynamic equilibrium equations to complement and verify the analytical solutions above. The initial solutions are set to Dqa = 0, Dqb = 0, Dqc = 0, qa = 0.001, qb = 0.1, qc = 0.1, where D indicates differentiation with respect to time t. By fourth-order Runge-Kutta method, time history of displacement of summation resonance with damping and without damping can be obtained and as shown in Figures 6–7.
From Figures 6–7, it can be observed that with and without damping, the displacement curves of the main cable, sling and beam have the characteristics of "beat"; the main cable and beam are energy provider and the sling is energy recipient in the first half cycle of each cycle of amplitude; total energy of the coupled structure is transferring among the main cable, sling and beam; total energy of the coupled structure is conserved, while with damping, total energy decreases with time.
The conclusions obtained above well verify the results got in Section 4.2, and further demonstrate the correctness of theoretical analysis obtained by multiple scales method.
4.4. Amplitude-frequency response
4.4.1. (a10, a20, a30, t0) – σ
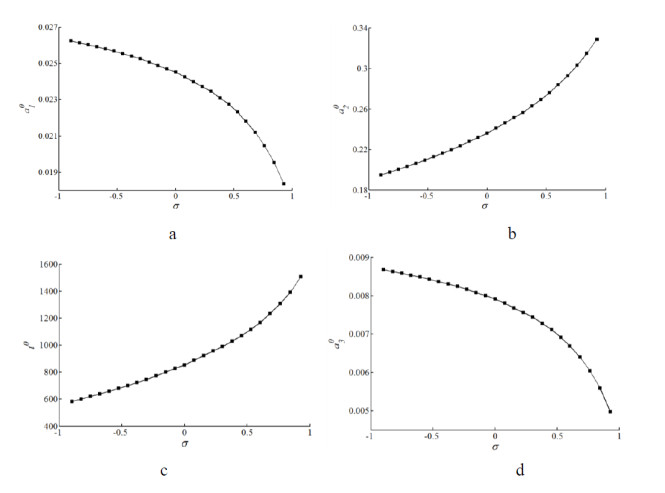
Given that some parameters of the coupled structure always vary, the sum of the frequencies of the main cable and beam is not always just two times of that of the sling. Therefore, based on the previous section, we slightly change the initial parameters of the coupled structure to make ωa + ωc slightly deviate from 2ωb. Then, the first peaks of the amplitudes of the coupled structure as functions of frequency (a10, a20, a30 – σ) and triggering time as function of frequency (t0 – σ) can be obtained and shown in Figure 8.
From Figure 8, it can be observed that all the curves are single-valued and nonlinear. With the increase of σ, the first peaks of amplitudes of the main cable and beam decrease, while the first peak of the sling and triggering time increases. It means as σ increases, the main cable and beam provide more energy and the sling receive more energy, but the energy exchange becomes slower.
4.2.2. (a10, a20, a30, t0) – (ωc – ωa)
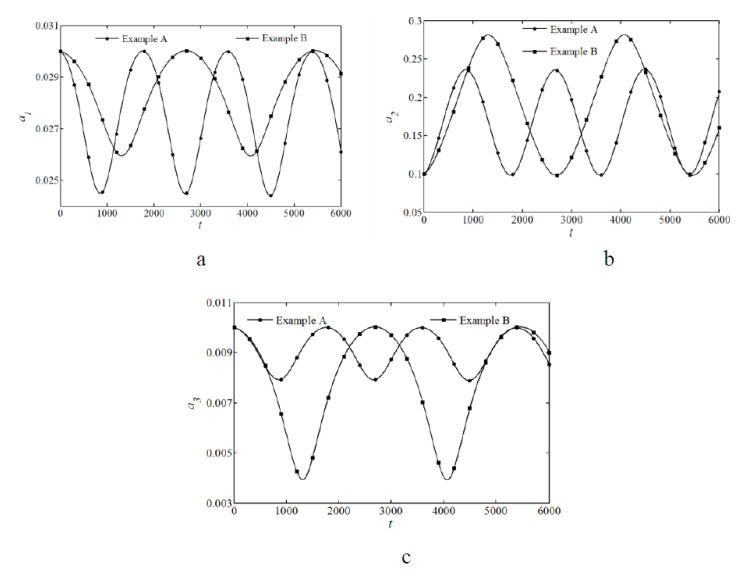
Changing the initial parameters of the coupled structure to make the frequencies of the main cable and beam to ωa = 8.911, ωc = 8.911 (Example B) and comparing the numerical results with that of Section 4.2 (without damping).
Figure 9 shows under the condition of summation resonance, different frequency combinations of the main cable (ωa) and beam (ωc) get different peaks (a10, a20, a30) and triggering time (t0). The following section will discuss the effect of the frequency combination of the main cable and beam on a10, a20, a30 and t0.
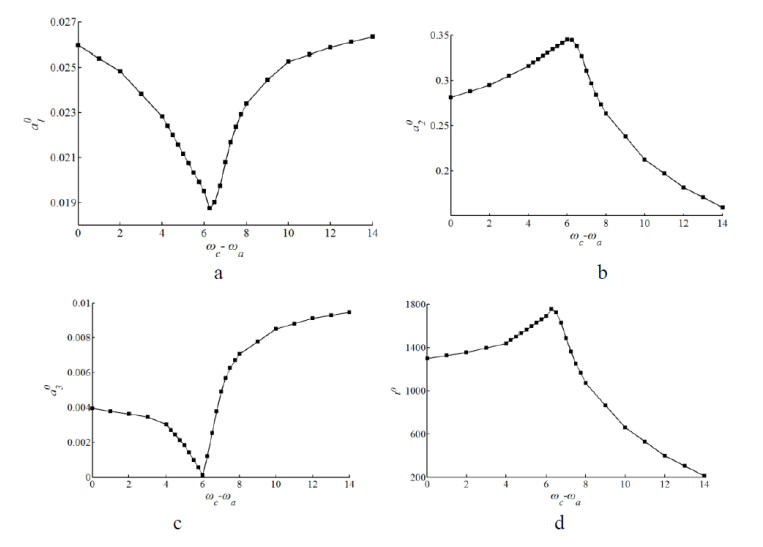
Many kinds of frequency combinations of the coupled structure are analyzed. Due to space limitations, only some of them are shown in Table 3. The influence curves of the frequency combination on a10, a20, a30 and t0 are obtained and shown in Figure 10 (without damping).
Figure 10 shows with the increase of ωc – ωa, a10 and a30 decrease first and then increase, while a20 and t0 increase first and then decrease, there exists inflection point when ωc – ωa gets the value of about 6.2. Thus, it indicates as ωc – ωa increases, the main cable and beam provide more energy with the sling until the inflection point and after then less energy will be provided. In the inflection point, the sling receives the most energy, having the biggest amplitude and the coupled structure has the longest triggering time, showing the energy exchange is the slowest.
5.
Conclusions
The paper investigates free vibration of summation resonance of the suspended–cable–stayed beam. At first, a 3-DOF model is built, which treated the main cable and the sling as nonlinear taut string and the beam as Euler beam; then, Hamilton's principle and multiple scales method are used to derive and solve the dynamic equilibrium equations; at last, numerical integration method is used to discuss the nonlinear characteristics of the coupled structure. We can yield the following conclusions:
1. Without damping, the free vibration of summation resonance of the coupled structure will be periodical, stable and bounded; total energy of the coupled structure is conserved and transferring among the main cable, sling and beam, which has typical characteristic of "beat"; the main cable and beam are energy provider and the sling is energy recipient in the first half cycle of each cycle.
2. With damping, total energy of the coupled structure is gradually consumed; due to the internal resonance, we can adjust the attenuation law of one degree by changing the damping coefficient of another degree; as the damping of the coupled structure increases, the peaks of the amplitudes decrease and the energy exchange becomes slower.
3. As σ increases, the main cable and beam provide more energy and the sling receive more energy, but the energy exchange becomes slower.
4. As the difference of the frequency of the beam and main cable (ωc – ωa) increases, the main cable and beam provide more energy with the sling until the inflection point and after then less energy will be provided. In the inflection point, the sling receives the most energy and the energy exchange is the slowest.
Acknowledgments
All the authors gratefully acknowledge the support of the National Natural Science of Foundation of China (No.51678247), Natural Science Foundation of Hebei Province (E2019210311) and the ‘Cooperative Innovation Center of Disaster Prevention and Mitigation for Large Infrastructure in Hebei province (Shijiazhuang Tiedao University)’.
Conflict of interest
The authors declare that they have no conflict of interest in this paper.









 DownLoad:
DownLoad: