1. Introduction
Nowadays, identity authentication is needed on many occasions such as door access control system, registration system and online payment. Traditional identity authentication, like passwords can not meet our requirements any more. In recent years, bio-metric authentication technology has become more and more popular, such as fingerprint authentication, face recognition and iris recognition. However fingerprints are easy to forge and the system always fails to recognize the right person when the fingers are wet or injured. The same problem happens to face recognition if glasses or masks are worn. Iris recognition is safe enough but many people feel embarrassed when they are in front of cameras. Therefore, some researchers proposed vein authentication to solve these problems. In 1992, researchers of Hokkaido University demonstrated that the vein pattern of human body was unique to a specific individual and even twins also had different vein patterns [8]. Therefore vein pattern can be used for authentication. Moreover, vein recognition has many advantages over other biometric authentication technologies. Since veins are hidden inside the body, they are difficult to forge. They aren't affected by race or skin discolorations. What's more, veins don't change followed by age [11,4]. Finger vein [3], hand vein [7] and hand-dorsa vein [16] have already been utilized for identity authentication. This paper proposes a wrist vein recognition system due to its unique advantages. With the development of portable and wearable devices, wearable vein authentication device is preferred. The wrist is a convenient part of our body to wear the device and wrist vein is easy to be acquired. Thus, it is of great significance to study the wrist vein recognition. Wrist vein is not so clear as finger and hand vein. Therefore, features selection and the way to ex-tract features are very important. Many different features are adopted in finger and hand vein recognition system. Sugandhi [13] chose center line of the vein as features. Kumar [9] extracted bifurcation and endings as features while Cross [2] considered every vascular segment as a vector that had position and angle. However, all of the features mentioned above need image segmentation. Image segmentation is a complex and time-consuming process. In addition, some vein information may be lost during image segmentation. Global features of vein image represent the images well and they can be extracted without image segmentation. Li [10] used modified invariant moments as characteristic features. Hsu [5] used modified 2-directional 2-demensional principal component analysis to obtain eigenvalues, which was a low dimensional representation of vein pattern features. Global features of vein image can be extracted without image segment and thinning. For this reason, the wrist vein recognition is simpler and faster. Moreover, the system which selects the global features has good robustness. In this paper, the principal component analysis is adopted to extract wrist vein global features. Which algorithm should be chosen to classify the features? Matching method is the most common recognition algorithm in vein recognition system. Yang [18] adopted nearest center classifier. Wu [17] used minimum directional code matching method and nearest neighbor classifier was adopted by Yang [19]. Whereas, intelligent classification algorithms are seldom used in the vein recognition system, mainly because the speed of the intelligent classification algorithms is far slower than required. Recently, a new classification algorithm namely Two-hidden-layer Extreme Learning Machine (TELM) was proposed by Qu [12]. The algorithm can achieve high accuracy at a fast speed. In this paper, TELM is adopted to classify the wrist vein images. The flow chat of the proposed system is shown in Figure 1.
The rest of this paper is organized as follows. Wrist vein images obtaining method is introduced in Section Ⅱ. Section Ⅲ presents image preprocessing and features extraction. Image classification and recognition are introduced in Section Ⅳ. Experiment results and discussions are shown in Section Ⅴ. Finally, conclusion and prospect are given in Section Ⅵ.
2. Wrist vein images obtaining
Since vein patterns are hidden inside the body, they can't be seen under visible light. However, they can be captured with a camera which is sensitive to infrared light. Wang [15] described that veins absorb almost all the near infrared light while tissues reflect the near infrared light. Under infrared light, the vein regions become dimmer than tissue regions. Therefore, wrist vein pattern can be obtained under infrared light.
Infrared light source is adopted by many researchers. However, if the infrared light source illuminates skin directly, there are many bright spots in the obtained images. The quality of obtained images is so poor that it is difficult to extract vein patterns in these images. In contrast, natural light is uniform. There are no bright spots in the images which are obtained under natural light. Moreover, natural light also contains infrared light. Only infrared light is left if natural light is filtered by infrared filter. From this point, natural light and infrared filter are equivalent to infrared light. This situation is shown in Figure 2.
2.1. Image acquisition devices
To obtain a high quality wrist vein image, the web camera and infrared filter are used. The camera used in this work is a simple charge coupled device (CCD). The number of its pixels is 30M. The original web camera is not able to obtain the wrist vein patterns because only visible lights can transform the lens of the camera. It should be reformed with an infrared filter. A circular infrared filter is selected in this paper. Its diameter and thickness are 18mm and 2mm respectively. If the natural light is filtered by it, only 800-1000nm wavelength infrared light is left. Nature light is turned into infrared light by the infrared filter. The details to reform the camera are described as follows:
• The original filter of the web camera is removed. There is a filter in the original web camera. Only visible light can pass through this filter. The original filter should be removed to allow infrared light in so that clear vein images can be obtained.
• The lens of the web camera is covered with the infrared filter mentioned above. All natural light can transmit through the camera lens after the original filter is removed. However, only infrared light is needed. Therefore, the lens is covered with an infrared filter. The reformed camera is able to obtain vein patterns.
2.2. Introduction of the obtained database
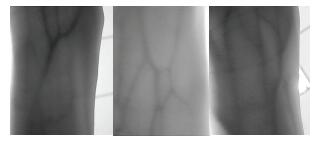
A small wrist vein images database is established in this paper. A total of 500 wrist vein images are collected from 10 persons. Fifty images are taken from each person. Different images are obtained under different illumination environment conditions, so the database can test the robustness of the system in some degree. The size of each image is 640×480 and the gray scale values range from 0 to 255. Figure 3 shows three of the obtained wrist vein images. Wrist vein patterns of different persons are quite different from each other.
3. Image preprocessing and features extraction
3.1. Image preprocessing
The obtained vein images contain not only vein regions but also background, tissue regions and other noises. These noises interfere with features extraction and classification. Therefore, it is necessary to preprocess the original images. In this paper, image preprocessing process includes occupation of the region of interest, gray normalization and contrast enhancement.
1) Occupation of the region of interest
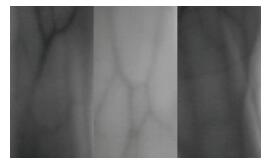
Only the vein pattern region is needed. Background and tissue regions should be cut off. The region of interest is obtained by cutting off the edges of the image. The obtained regions of interest are shown in Figure 4.
2) Gray normalization
The images of the same wrist are different under different light intensities, since their gray value ranges are different. The gray values of images under strong light are higher than gray values of images under weak light. Different images of the same wrist may be classified into different categories. The gray scale values are normalized to address this issue.
The gray scale values of original images range from 0 to 255. The values are normalized according to
where Imax is the largest gray value of original image; I(i,j) is the gray scale value of the pixel point (i,j) in original image; I′(i,j) denotes the gray scale value of pixel point (i,j) in normalized image. After gray normalization, the gray scale values of all images range from 0 to 1.
3) Contrast enhancement
The gray scale values of muscle tissue are enlarged while the gray scale values of vessels are reduced, thus increasing the contrast between vessels and muscle. In this paper, Histogram stretching method is adopted to enhance image contrast. The gray values of transformed image can be calculated according to the following equation:
|
I′(i,j)={0,0≤I(i,j)<a0.5b−a[I(i,j)−a],a≤I(i,j)<b0.5c−b[I(i,j)−b]+0.5,b≤I(i,j)<c1,I(i,j)≥c
|
(2)
|
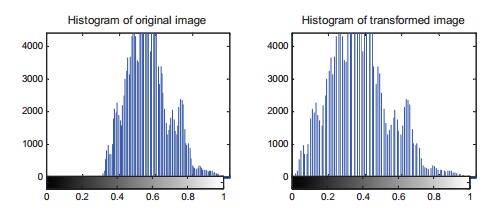
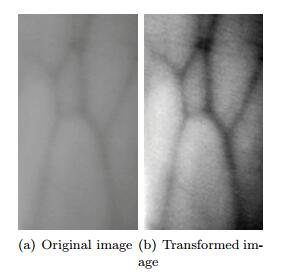
where a is the minimum gray scale value of original image; c is the maximum gray value of original image; b is equal to the average of a and c (b=(a+c)/2). Figure 5 shows the histogram comparison between original and transformed images. The comparison between original and transformed images is shown in Figure 6. The vein pattern in the transformed image is sharper than that in the original image. The preprocessing lays a good foundation for the features extraction.
3.2. Features extraction
The features selection is an important step. It highly affects the accuracy of the recognition system. In this paper, global features are selected to enhance the accuracy and robustness of the system. In addition, the global features can be obtained without image segmentation and thinning.
The PCA is an excellent technique to reduce the dimensionality of the feature space. It finds the linear subspaces which best represent the input data and extracts representative features by projecting the data into orthogonal subspaces. In this work, the input data are wrist vein images. The PCA extracts features which contain the most relevant information of wrist vein images.
Given an image data matrix A∈RN×D where N is the number of images and D is the dimensionality of the image, PCA derives a set of orthonormal basis images BD×D. The columns of B are the principal component directions. The principal components which account for more than 95% of the variance are chosen in this paper. In this paper, B is truncated and only the first d columns of it are kept. Thus, a matrix ˜B∈RD×d is obtained. The feature matrix is obtained according to
where X∈RN×d. Feature space dimensionality reduces from D to d. The feature matrix X acts as the input data of TELM to classify the images.
4. TELM based registration and recognition
4.1. Introduction of TELM
The selection of classification algorithm is extremely important for the wrist vein recognition system. Both high accuracy and speed are necessary. Extreme Learning Machine (ELM) [17] is a single-hidden layer feedforward neural network and it has been widely used due to its good generalization performance and fast learning speed [18,19]. Based on the ELM, TELM was proposed by Qu [15]. TELM has two hidden layers, which is obviously different from the original ELM. It inherits the advantages of the original ELM. As a kind of feedforward neural network, TELM is able to approximate model artificial phenomena and complex nonlinear mappings directly from the input data, which are difficult to deal with using classical techniques. Given a certain number of training data, TELM is able to provide models for the problem with fast speed. Unlike traditional learning algorithms, TELM avoids a time-consuming iterative training procedure by randomly choosing hidden nodes and analytically determining the output weights. What's more, it can achieve higher accuracy than original ELM. In the next section, TELM is adopted to classify wrist vein images.
4.2. Registration and recognition
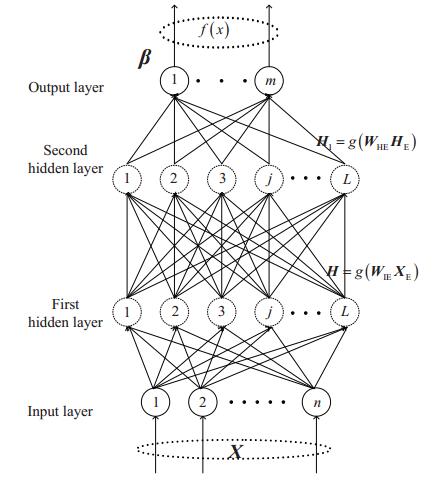
This system includes two stages: registration and recognition. The new users should input their wrist vein data into the system, namely registration stage. After learning from the input data, the system is able to recognize images of the same user, namely recognition stage. These two stages correspond to training and testing stage in TELM. The workflow and network structure of TELM are shown in Figure 7 and Figure 8 respectively. These two stages are described as follows.
1) Registration
Input: Features of N training images X=[x1,x2,…,xN]T, the labels of the features T=[t1,t2,…,tN]T, and 2L hidden neurons in total with activation function g(x).
• The connection weight matrix between the input layer and the first hidden layer W and the bias matrix of the first hidden layer B are randomly initialized. For simplicity, WIE is defined as [BW] and XE is defined as [1X] similarly.
• Estimate weight matrix between the second hidden layer and the output layer βe=H+T, where H+ is the Moore-Penrose (MP) generalized inverse of matrix H.
• Estimate the expected output of the second hidden layer He1=Tβ+e.
• Determine the parameters of the second hidden layer WHE=g−1(He1)H+E.
• Obtain the actual output of the second hidden layer H1=g(HWHE).
• Calculate the weight matrix between the second hidden layer and the output layer β=H+1T.
Output: WIE,WHE,β.
2) Recognition
Input: Features of M testing images S=[s1,s2,...,sM], 2L hidden neurons and activation function sig(S) in total with the output data of registration WIE,WHE,β. SE is defined as [S1].
Calculate the recognition result R=g(g(SEWIE)WHE)β
Output: R.
It can be concluded that this system works according to the following procedures. Firstly, train the TELM with features of training vein images. Secondly, save the parameters of the TELM. Thirdly, input features of testing vein images and calculate the recognition results.
5. Experimental Results and Analysis
The performance of the proposed system is evaluated on the wrist vein image database established in Section 2. The size of image is 640*480. 33 images of per person are chosen as training samples, and the other 17 images of per person act as testing samples. In this paper, the proposed system is compared with Extreme Learning Machine (ELM), Support Vector Machine (SVM) and Naive Bayes (NB). The performances of them are evaluated by testing accuracy, recognition time (per image), false reject rate (FRR) and false accept rate (FAR).
In TELM and ELM, sigmoid is chosen as the activation function. All the experiments are carried out in MATLAB R2014a computational environments running on a computer with a 2.81 GHZ AMD Athlon(tm)II 2 240 processor. Three different experiments have been carried out to verify the effectiveness of the proposed wrist vein image recognition method.
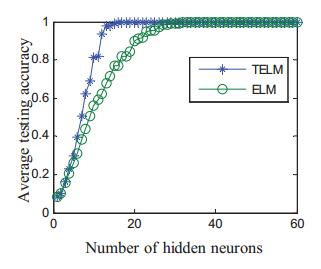
First, the performance of TELM and ELM with different number of hidden neurons is compared. The number of hidden neurons ranges from 1 to 60, and 50 trials are carried out on each number of hidden neuron. The average testing accuracies of TELM and ELM are shown in Figure 9. The average testing accuracies of TELM are higher than ELM from 3 to 60. In addition, the testing accuracy of TELM reaches 1 when the number of hidden neurons is more than 20.
Second, the effectiveness of gray normalization is verified. In this part, the number of hidden neurons of TELM and ELM is set to 19. TELM with and without gray normalization are tested 50 times and the mean accuracies are shown in Table 1. As shown, TELM with gray normalization achieves higher accuracy than TELM without gray normalization, which demonstrates that gray normalization is helpful for wrist vein image recognition.
Table 1. The performance of TELM with and without gray normalization.
| TELM with gray normalization |
TELM without gray normalization |
| 99.58±0.0671% |
94.39±0.4271% |
Third, TELM is compared with four other popular classifiers. The number of hidden neurons of TELM and ELM is still set to 19 in this part. The performances of the four algorithms are shown in Table 2. All the values in Table 1 are the mean values of 50 trials. It can be concluded that TELM achieves the highest testing accuracy. Besides, FRR and FAR of TELM are the lowest. Therefore the proposed system is accurate and reliable. Though the recognition time of TELM is not the shortest, it is comparable with the other three algorithms. The testing accuracy of ELM is lower than TELM, while ELM is faster than TELM. The reason is TELM has one more hidden layer. Just for this reason, TELM is able to deal with bigger data than ELM. What's more, we can conclude from Table 1 that SVM is the fastest but not accurate enough. SVM is fast because it need not train many parameters iteratively. Compared with SVM, NB achieves higher testing accuracy, while its recognition time is much longer.
Table 2. Performances of different algorithms.
| Algorithm name |
Accuracy (%) |
Ttraining(ms) |
Ttesting(ms) |
FRR |
FAR |
| TELM | 99.58±0.0671 | 8.1555 | 0.0177 | 0.42% | 0.74% |
| ELM | 96.35±0.0595 | 2.9158 | 0.0156 | 3.65% | 1.57% |
| SVM | 91.40±0.0592 | 0.0109 | 0.0097 | 8.60% | 10.25% |
| NB | 96.21±0.1005 | 0.0139 | 0.1548 | 3.79% | 2.54% |
6. Conclusions and prospect
A wrist vein recognition system is designed in this paper. It contains image obtaining, image pre-processing, features extraction and image classification. Firstly, a special camera is reformed to obtain wrist vein images. Unlike common vein acquisition devices, it can obtain clear vein patterns without infrared light source. Secondly, the obtained images are simply preprocessed. Image segmentation and thinning are avoided in this paper. Thirdly, global features are extracted with PCA. Most redundant information of vein images is eliminated in this step, so it takes little time to recognize the image. Finally, a fast and accurate learning algorithm TELM is adopted as a classifier. TELM and other three algorithms are tested on the obtained dataset. Experiment results show that TELM is the most accurate. Though, it is not the fastest, its recognition time is satisfactory. In conclusion, the proposed system can be applied in real time identity authentication system.
The proposed wrist vein recognition system will be tested on other database and it will be used in wearable recognition devices in the future. Since these devices are portable, they can be used to recognize and locate the user at the same time. Therefore, wrist vein recognition will have promising application prospect.
Acknowledgments
We acknowledge financial support by National Natural Science Foundation of China (61473266,61673404,61305080, and U1304602), China Postdoctoral Science Foundation (No.2014M552013), Project supported by the Research Award Fund for Outstanding Young Teachers in Henan Provincial Institutions of Higher Education of China (2014GGJS-004) and Program for Science and Technology Innovation Talents in Universities of Henan Province in China (16HASTIT041).










 DownLoad:
DownLoad: