1. Introduction
With the ever increasing amounts of data becoming available, strategic data analysis and decision-making will become more pervasive as a necessary ingredient for societal infrastructures. In many network engineering games, the performance metrics depend on some few aggregates of the parameters/choices. A typical example is the congestion field in traffic engineering where classical cars and smart autonomous driverless cars create traffic congestion levels on the roads. The congestion field can be learned, for example by means of crowdsensing, and can be used for efficient and accurate prediction of the end-to-end delays of commuters. Another example is the interference field where it is the aggregate-received signal of the other users that matters rather than their individual input signal. In such games, in order for a transmitter-receiver pair to determine his best-replies, it is unnecessary that the pair is informed about the other users' strategies. If a user is informed about the aggregative terms given her own strategy, she will be able to efficiently exploit such information to perform better. In these situations the outcome is influenced not only by the state-action profile but also by the distribution of it. The interaction can be captured by a game with distribution-dependent payoffs called mean-field-type games (MFTG). An MFTG is basically a game in which the instantaneous payoffs and/or the state dynamics functions involve not only the state and the action profile of the agents but also the joint distributions of state-action pairs.
The main contributions of this article can be summarized as follows. The first contribution of this article is the review of some relevant engineering applications of MFTG. Considering Liouville type systems with drift, diffusion and jumps, that are dependent on time-delays, state mean-field and action mean-field terms. Proposition 7 establishes an equilibrium equation for non-convex action spaces. Proposition 9 provides a stochastic maximum principle that covers decentralized information and partial observation systems which are crucial in engineering systems. Various engineering applications in discrete or continuous variables (state, action or time) are provided. Explicit solutions are provided in propositions 6 and 8 which are mean-field type game problems with non-quadratic costs.
The article is structured as follows. The next section overviews earlier works on static mean-field games, followed by discrete time mean-field games with measure-dependent transition kernels. Then, a basic MFTG with finite number of agents is presented. After that, the discussion is divided into two illustrations in each of the following areas of engineering (Figure 1) : Civil Engineering (CE), Electrical Engineering (EE), Computer Engineering (CompE), Mechanical Engineering (ME), General Engineering (GE).
• CE: road traffic networks with random incident states and multi-level building evacuation
• EE: Millimeter wave wireless communications and distributed power networks
• CompE: Virus spread over networks and virtual machine resource management in cloud networks
• ME: Synchronization of oscillators, consensus, alignment and energy-efficient buildings
• GE: Online meeting: strategic arrivals and starting time and mobile crowdsensing as a public good.
The article proceeds by presenting the effect of time delays of coupled mean-field dynamical systems and decentralized information structure. Then, a discussion on the drawbacks, limitations, and challenges of MFTGs is highlighted. Lastly, a summary of the article and concluding remarks are presented.
1.1. Mean-Field Games: Static Setup
A static mean-field game is one in which all users make choices (or select a strategy) simultaneously, without knowledge of the strategies that are being chosen by other users and the game is played once. Any mean-field game with sequential moves is a dynamic mean-field game. In this work, games which are played more than once will be considered as dynamic game. This subsection overviews static mean-field games and games in which the underlying processes are in stationary regime (time-independent). Mean-field games have been around for quite some time in one form or another, especially in transportation networks and in competitive economy. In the context of competitive market with large number of agents, a 1936 article [1] captures the assumption made in mean-field games with large number of agents, in which the author states:
"Each of the participants has the opinion that its own actions do not influence the prevailing price".
Another comment on the impact on the population mean-field term was given in [2] page 13:
" When the number of participants becomes large, some hope emerges that of the influence of every particular participant will become negligible..."
The population interaction involves many agents for each type or class and location, a common approach is to replace the individual agents' variables and to use continuous variables to represent the aggregate average of type-location-actions. In the large population regime, the mean field limit is then modeled by state-action and location-dependent time process (Figure 2). This type of aggregate models are also known as non-atomic or population games. It is closely related to the mass-action interpretation in [3], Equation (4) in page 287.
In the context of transportation networks, the mean-field game framework, underlying the key foundation, goes back to the pioneering works of [4] in the 1950s. Therein, the basic idea is to describe and understand interacting traffic flows among a large population of agents moving from multiple sources to destinations, and interacting with each other. The congestion created on the road and at the intersection are subject to capacity and flow constraints. This corresponds to a constrained mean-field game problem as noted in [5]. A common behavioral assumption in the study of transportation and communication networks is that travelers or packets, respectively, choose routes that they perceive as being the shortest under the prevailing traffic conditions. As noted in [6], collection of individual decisions may result to a situation which drivers cannot reduce their journey times by unilaterally choosing another route. The work in [6] such a resulting traffic pattern as an equilibrium. Nowadays, it is indeed known as the Wardrop equilibrium [4,7], and it is thought of as a steady state obtained after a transient phase in which travelers successively adjust their route choices until a situation with stable route travel costs and route flows has been reached [8,9]. In the seminal contribution [4], page 345 the author stated two principles that formalize this notion of equilibrium and the alternative postulates of the minimization of the total travel costs. His first principle reads:
"The journey times on all the routes actually used are equal, and less than those which would be experienced by a single vehicle on any unused route."
Wardrop's first principle of route choice, which is identical to the notion postulated in [6,10], became widely used as a sound and simple behavioral principle to describe the spreading of trips over alternate routes due to congested conditions. Since its introduction in the context of transportation networks in 1952 and its mathematical formalization by [5,11] transportation planners have been using Wardrop equilibrium models to predict commuters decisions in real-life networks.
The key congestion factor is the flow or the fraction of travelers per edge on the roads (Application 1). The above Wardrop problem is indeed a mean-field on a discrete space. The exact mean-field term here corresponds to a mean-field of actions (a choice of a route). Putting this in the context of infinite number of commuters results to end-to-end travel times that are function of own choice of a route and the mean-field distribution of travelers across the graph (network).
In a population context, the equilibrium concept of [4] corresponds to a Nash equilibrium of the mean-field game with infinite number of agents. The works [7,12] provide a variational formulation of the (static) mean-field equilibrium.
The game theoretic models such as evolutionary games [13,14,15], global games [16,17], anonymous games, aggregative games [18], population games [19,20,21], and large games, share several common features. Static mean-field games with large number of agents were widely investigated ([22,23,24,25,26,27] and the references therein).
1.2. Mean-Field Games: Dynamic Setup
This section overviews mean-field games which are dynamic (time-varying and played more than once) and their applications in engineering.
Definition 1 (Mean-Field Game: Infinite Regime). A (homogeneous population) mean-field game (MFG) is a game in which the instantaneous payoff of a generic agent (say 1) and/or the state dynamics coefficient functions involve an individual state-action pair x1t,u1t and the distribution of state-action pairs of the other decision-makers, mt at time t. The individual state and action spaces are identical across the homogeneous population denoted by Xi=X1,Uj=U1 for all i. The state transition to the next state follows P(.|x1t,u1t,mt). Thus, the instant payoff function of a generic agent (say j) has the following structure:
|
ri=r1=r: X1×U1×P(X1×U1)→R,
|
with r(x1t,u1t,mt).
The mean-field game model has been extended to include several other features such as incomplete information, common noise, heterogeneous population, finite population or a mixture between finite number of clusters and infinite population regimes.
The key ingredients of dynamic mean-field games appeared in [28,29] in the early 1980s. The work in [28] proposes a game-theoretic model that explains why smaller firms grow faster and are more likely to fail than larger firms in large economies. The game is played over a discrete time space. Therein, the mean-field is the aggregate demand/supply which generates a price dynamics. The price moves forwardly, and the agents react to the price and generate a demand and the firm produces a supply with associated cost, which regenerates the next price and so on. The author introduced a backward-forward system to find equilibria (for example Section 4, equations D.1 and D.2 in [28]). The backward equation is obtained as an optimality to the individual response, i.e., the value function associated with the best response to price, and the forward equation for the evolution of price. Therein, the consistency check is about the mean-field of equilibrium actions (population or mass of actions), that is, the equilibrium price solves a fixed-point system: the price regenerated after the reaction of the agents through their individual best-responses should be consistent with the price they responded to.
Following that analogy, a more general framework was developed in [29], where the mean-field equilibrium is introduced in the context of dynamic games with large number of decision-makers. A mean-field equilibrium is defined in [29], page 80 by two conditions: (1) each generic agent's action is best-response to the mean-field, and (2) the mean-field is consistent and is exactly reproduced from the reactions of the agents. This matching argument was widely used in the literature as it can be interpreted as a generic agent reacting to an evolving mean-field object and at the same time the meanfield is formed from the contributions of all the agents. The authors of [30] show how common noise can be introduced into the mean-field game model (the mean-field distribution evolves stochastically) and extend the Jovanovic-Rosenthal existence theorem [29].
Continuous time version of the works [28,29] can be found in [31,32,33,34]. The reader is referred to [36,37,38,39,40,41,42] for recent development of mean-field game theory. The authors [33,43,44,45,46,47] have developed a powerful tool for modelling strategic behavior of large population of agents, each of them having a negligible impact on the population mean-field term. Weak solutions of mean-field games are analyzed in [48], Markov jumps processes [49,50], and leader-followers models in [51]. Finite state mean-field game models were analyzed in [52,53,54,55,56,57,58,59]. Team and social optimum solutions can be found in [51,60,61,62,63]. The work in [64,65,66] provide mean-field convergence of a class of McKean-Vlasov dynamics. Numerical methods for mean-field games can be found in [67,68,69,70].
Table 1 summarizes some engineering applications of mean-field-type game models.
Table 1. Some applications of MFTGs in Engineering. HVAC stands for (heating, ventilation and air conditioning) systems. D2D stands for Device-to-Device (D2D).
| Area |
Works |
| planning |
[72] |
| state estimation and filtering |
[73,74] |
| synchronization |
[75,76,77,78] |
| opinion formation |
[79] |
| network security |
[80,81,82,83,84] |
| power control |
[85,86,87] |
| medium access control |
[88,89] |
| cognitive radio networks |
[90,91] |
| electrical vehicles |
[92,93] |
| scheduling |
[94] |
| cloud networks |
[95,96,97] |
| wireless networks |
[98] |
| auction |
[99,100] |
| cyber-physical systems |
[101,102] |
| airline networks |
[103] |
| sensor networks |
[104] |
| traffic networks |
[105,106,107,108] |
| big data |
[109] |
| D2D networks |
[110,111,112] |
| multilevel building evacuation |
[140,141,142,143] |
| power networks |
[113,114,115,116,117,174,179] |
|
[93,118,119,120,121] |
|
[122,123,124] |
| HVAC |
[125,126,127,128,129,130] |
1.2.1. Limitations of the existing mean-field game models
Most of the existing mean-field game models share the following assumptions:
Big size: A typical assumption is to consider an infinite number decision-makers, sometimes, a continuum of decision-makers. The idea of a continuum of decision-makers may seem outlandish to the reader. Actually, it is no stranger than a continuum of particles used in fluid mechanics, in water distribution, or in petroleum engineering. In terms of practice and experiment however, decision-making problems with continuum of decision-makers is rarely observed in engineering. There is a huge difference between a fluid with a continuum of particles and a decision-making problem with a continuum of agents. Agents may physically occupy a space (think of agents inside a building or a stadium) or a resource, and the size or number of agents that most of engineering systems can handle can be relatively large or growing but remain currently finite [71]. It is in part due to the limited resource per shot or limited number of servers at a time. In all the examples and applications provided below, we still have a finite number of interacting agents. Thus, this assumption appears to be very restrictive in terms of engineering applications.
Anonymity: The index of the decision-maker does not affect the utility. The agents are assumed to be indistinguishable within the same class or type. The drawback of this assumption is that most individual decision-makers in engineering are in fact not necessarily anonymous (think of Google, Microsoft, Twitter, Facebook, Tesla), the classical mean-field game model is inappropriate, and does not apply to such situations. In mean-field games with several types (or multi-population mean-field games), it is still assumed that there is large number of agents per type/class/population, which is not realistic in most of the engineering applications considered in this work.
NonAtomicity: A single decision-maker has a negligible effect on the mean-field-term and on the global utility. One typical example where this assumption is not satisfied is a situation of targeting a room comfort temperature, in which the air conditioning controller adjusts the heating/cooling depending on the temperature in the room, the temperatures of the other connecting zones and the ambient temperature. It is clear that the decision of the controller to heat or to cool affect the variance of the temperature inside the room. Thus, the effect of the individual action of that controller on the temperature distribution (mean-field) inside the room cannot be neglected.
To summarize, the above conditions appear to be very restrictive in terms of engineering applications, and to overcome this issue a more flexible MFTG framework has been proposed.
1.2.2. What MFTGs can bring to the existing decision-making models?
MFTGs not only relax of the above assumptions but also incorporate the behavior of the agents as well as their effects in the mean-field terms and in the outcomes (Table 2).
Table 2. Key limitations and differences between the game models.
| Area |
Anonymity |
Infinity |
Atom |
| population games [4,5] |
yes |
yes |
no |
| evolutionary games [131] |
yes |
yes |
no |
| non-atomic games [29] |
yes |
yes |
no |
| aggregative games [18] |
|
relaxed |
|
| global games [16,17] |
yes |
yes |
no |
| large games [22] |
yes |
yes |
no |
| anonymous games [29] |
yes |
yes |
no |
| mean-field games |
yes |
yes |
no |
| nonasymptotic mean-field games |
nearly |
no |
yes |
| MFTG |
relaxed |
relaxed |
relaxed |
(1) In MFTGs, the number of users can be finite or infinite.
(2) The indistinguishability property (invariance in law by permutation of index of the users) is not assumed in MFTGs.
(3) A single user may have a non-negligible impact of the mean-field terms, specially in the distribution of own-states and own mixed strategies.
These properties (1)-(3) make strong differences between mean-field games and MFTGs ([132] and the references therein).
MFTG seems to be more appropriate in such engineering situations because it does not assume indistinguishability, it captures the effect of each agent in the distribution and the number of agents is arbitrary as we will see below. Table 3 summarizes the notations used in the manuscript.
Table 3. Table of Notations.
| I |
≜ |
set of decision-makers |
| T |
≜ |
Length of the horizon |
| [0,T] |
≜ |
horizon of the mean-field-type game |
| t |
≜ |
time index |
| X |
≜ |
state space |
| W |
≜ |
Brownian motion |
| σ |
≜ |
Diffusion coefiicient |
| N |
≜ |
Poisson jump process |
| γ |
≜ |
Jump rate coefiicient |
| Ui |
≜ |
control action space of agent i∈I |
| Ui |
≜ |
admissible strategy space |
| ui |
≜ |
state space |
| ri |
≜ |
instantaneous payoff |
| D(x,u) |
≜ |
distribution of state-action |
| Ri |
≜ |
Long-term payoff functional |
1.3. Background on MFTGs
This section presents a background on MFTGs.
Definition 2 (Mean-Field-Type Game). A mean-field-type game (MFTG) is a game in which the instantaneous payoffs and/or the state dynamics coefficient functions involve not only the state and the action profile but also the joint distributions of state-action pairs (or its marginal distributions, i.e., the distributions of states or the distribution of actions). Let I be the set of agents, Xi the state space of agent i and X:=∏i∈IXi=X1×X2×… the state profiles space of all agents. Ui is the action space of agent i and U=∏jUj is the action profile space of all agents. A typical example of payoff function of agent j has the following structure:
with ri(x,u,D(x,u)) where (x,u) is the state-action profile of the agents and D(x,u) is the distribution of the state-action pair (x,u). X is the state space, U is the action profile space of all agents and P(X×U) is the set of probability measures over X×U.
From Definition 2, a mean-field-type game can be static or dynamic in time. One may think that MFTG is a small and particular class of games. However, this class includes the classical games in strategic form because any payoff function ri(x,u) can be written as ri(x,u,D).
When randomized/mixed strategies are used in the von Neumann-type payoff, the resulting payoff can be written as E[ri(x,u)]=∫ri(x,u)D(x,u)(dx,du)=ˆri(D). Thus, the form ri(x,u,D) is more general and includes non-von Neumann payoff functions.
Example 1 (Mean-variance payoff). The payoff function of agent i is E[ri(x,u)]−λ√var[ri(x,u)],λ∈R which can be written as a function of ri(x,u,D(x,u)). For any number of interacting agents, the term D(xi,ui) plays a non-negligible role in the standard deviation √var[ri(x,u)]. Therefore, the impact of agent i in the individual mean-field term D(xi,ui) cannot be neglected.
Example 2 (Aggregative games). The payoff function of each agent depends on its own action and an aggregative term of the other actions. Example of payoff functions include ri(ui,∑j≠iuαj), α>0 and ri(xiui,∑j≠ixjuj).
In the non-atomic setting, the influence of an individual state xi and individual action ui of any agent i will have a negligible impact on mean-field term ˆD(x,u)=limn→+∞ 1n−1∑j≠iδ{xj,uj}. In that case, one gets to the so-called mean-field game.
Example 3 (Population games). Consider a large population of agents. Each agent has a certain state/type x∈X and can choose a control action u∈U(x). Let the proportion of type-action of the population as m. The payoff of the agent with type/state x, control action u when the population profile m is r(x,u,m).
Global games with continuum of agents were studied in [16] based on the Bayesian games of [17], which uses the proportion of actions.
In the case where both non-atomic and atomic terms are involved in the payoff, one can write the payoff as ri(x,u,D,ˆD) where ˆD is the population state-action measure. Agent i may influence Di (distribution of its own state-action pairs) but its influence on ˆD may be limited.
The main goals of static mean-field-type games are: (1) identify solution concepts [35] such as Nash equilibrium, Bayesian equilibrium, correlated equilibrium, Stackelberg solution etc. (2) Computation of solution concepts. (3) Development of algorithms and learning procedures to reach and select efficient equilibria, (4) Mechanism design for incentivizing agents. The next section presents a class of dynamic MFTGs which are played over several stages.
2. A Basic Dynamic MFTG: Finite Regime
Consider a basic MFTG with n≥2 agents interacting over horizon [0,T], T>0. The individual state dynamics of agent i is given by
|
dxi=bi(xi,ui,D(xi,ui),∑k≠iδ(xk,uk)n−1)dt+σi(xi,ui,D(xi,ui),∑k≠iδ(xk,uk)n−1)dWi,xi(0)∼Di,0
|
(1)
|
and the payoff functional of agent i is
|
Ri(u)=gi(xi(T),Dxi(T),∑k≠iδxk(T)n−1)+∫T0ri(xi,ui,D(xi,ui),∑k≠iδ(xk,uk)n−1)dt,
|
(2)
|
where the strategy profile is u=(u1,…,un), which also denoted as (ui,u−i). The functions bi,σi,gi,ri are measurable functions. xi(t):=xi(t)[u] is the state of agents i under of the strategy profile u, Dxi(t)=L(xi(t)) is the probability distribution (law) of xi(t). D(xi(t),ui(t))=L(xi(t),ui(t)) is the probability distribution of the state-control action pair (xi(t),ui(t)) of agent i at time t. δy is the δ−Dirac measure concentrated at y, and Wi is a standard Brownian motion defined over the filtration (Ω,P,(Ft)t≤T).
The novelty in the modelling of (1)-(2) is that each individual agent i influences its own mean-field terms Dxi(t), and D(xi(t),ui(t)) independently on the total number of interacting agents. In particular, the influence of agent i on those mean-field terms remain non-negligible even when there is a continuum of agents. The distributions Dxi and D(xi,ui) represent two important terms in the modeling of MFTGs. These terms are referred to as individual mean-field terms. In the finite regime, the other agents are captured by the empirical measures ∑k≠iδxkn−1 and ∑k≠iδ(xk,uk)n−1. We refer these terms to as population mean-field terms.
Similarly, a basic discrete time (discrete or continuous state) MFTG is given by
|
xi,t+1∼qi(.|xi,t,ui,t,D(xi,t,ui,t),∑k≠iδ(xk,t,uk,t)n−1),xi0∼Di,0Ri(u)=gi(xi,T,Dxi,T,∑k≠iδxk,Tn−1)+T−1∑t=0ri(xi,t,ui,t,D(xi,t,ui,t),∑k≠iδ(xk,t,uk,t)n−1),
|
(3)
|
where qi(.|.) is the transition kernel of agent i to next states.
Mean-field-type control and global optimization can be found in [36,133,134,172,173,175]. The models (1) and (3) are easily adapted to bargaining solution, cooperative and coalitional MFTGs and can be found in [135,176,177]. Psychological MFTG was recently introduced in [111,178] where spitefulness, altruism, selfishness, reciprocity of the agents are examined by means empathy, otherregarding behavior and psychological factors.
Definition 3. An admissible control strategy of agent i is an Fi−adapted and square integrable process with values in a non-empty subset Ui. Denote by Ui=L2Fi([0,T], Ui) the class of admissible control strategies of agent i.
Definition 4 (Best response). Given a strategy profile of the other agents (u1,…,ui−1,ui+1,…,un), with uj, j≠i that are admissible and the mean-field terms D, the best response problem of agent i is:
|
{supui∈UiE[Ri(u)],subject to
|
(4)
|
The first goal is to find and characterize the best response strategies of each user. For user i it consists to solve problem (4). In problem (4), the information structure that is available to user plays in important role. We will distinguish three type of strategies: (1) open-loop strategies that are only measurable function of t, (2) state-feedback strategies that are measurable functions of state and time, (3) state-and-mean-field feedback strategies that measurable functions of state, mean-field and time. To solve problem (4), four different methods have been developed:
• Direct approach which consists to write the payoff functional in a form such that the optimal value and optimizers are trivially obtained, and a verification and validation procedure follows.
• A stochastic maximum principle (Pontryagin's approach) which provides necessary conditions for optimality.
• A dynamic programming principle (Bellman's approach) which consists to write the value of the problem (per agent) in (backward) recursion form, or as solution to a dynamical system.
• Uncertainty quantification approach by means of Wiener chaos expansion of all the stochastic terms and the use of Kosambi-Karhunen-Loeve expansion which is a representation of a stochastic process as an infinite linear combination of orthogonal functions, analogous to a Fourier series representation of a function over a bounded domain.
If every user solves its best-response problem, the resulting system will be a Nash equilibrium system defined below.
Definition 5. A (Nash) equilibrium of the game is a strategy profile (u∗1,…,u∗n) such that for every agent i,
|
E[Ri(u∗)]≥E[Ri(u∗1,…,u∗i−1,ui,u∗i+1,…,u∗n)],
|
for all ui∈Ui.
The second goal is to find and characterize Nash equilibria of the mean-field-type game. We provide below a basic example in which the Nash equilibrium problem can be solved semi-explicitly using Riccati system.
Example 4 (Network Security Investment [80]). A graph is connected if there is a path that joins any point to any other point in the graph. Consider n≥2 decision-makers over a connected graph. Thus, the security of a node is influenced by the others through possibly multiple hops. The effort of user i in security investment is ui. The associated cost may include money (e.g., for purchasing antivirus software), time and energy (e.g., for system scanning, patching). Let x(t) be the security level of the network at time t and
|
Ri(u)= −12[x(T)−Ex(T)]2+∫T0qi(t)x(t)(1−ϵi(t)x(t))−ρi(t)ui(t)−ri(t)2u2i(t)dt.
|
(5)
|
The best-response of user i to (u−i,E[x]):=(u1,…,ui−1,ui+1,…,un,E[x]), solves the following linear-quadratic mean-field-type control problem
|
{supui∈UiE[Ri(u1,…,un)], subject to dx={−ax−ˉaE[x]+n∑i=1biui}dt+cxdW,x(0)∈R,
|
(6)
|
where, qi(t)≥0,ϵi(t)≥0,ρi(t)≥0, ri(t)>0 and a,ˉa,bi,c are real numbers and where E[x(t)] is the expected value of network security level created by all users under the control action profile (u1,…,un). Note that the expected value of the terminal term in Ri can be seen as a weighted variance of the state [130] since E[(x(t)−E[x(t)])2]=var(x(t)). The optimal control action is in state-and-mean-field feedback form:
|
u∗i(t)=−biri(t)[βi(t)x(t)+η1i(t)E[x(t)]+η2i(t)]−ρi(t)ri(t),0=˙βi+(−2a+c2)βi−βin∑j=1b2jrjβj+2qiϵi,βi(T)=1,˙η1i−2(a+ˉa)η1i−2ˉaβi−βin∑j=1b2jrjη1j−η1in∑j=1b2jrj(βj+η1j)=0,η1i(T)=−1,˙η2i−(a+ˉa)η2i−βin∑j=1bjrj(bjη2j+ρj)−η1in∑j=1bjrj(bjη2j+ρj)−qi=0,η2i(T)=0.
|
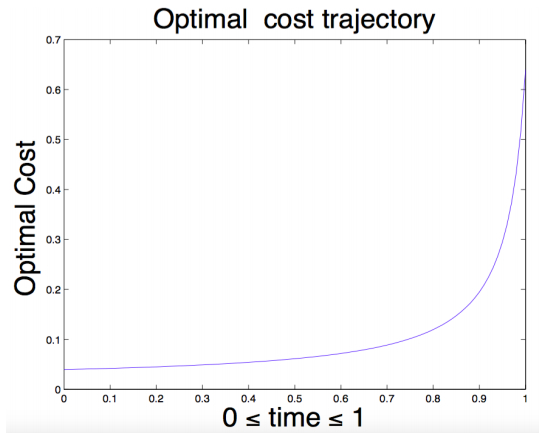
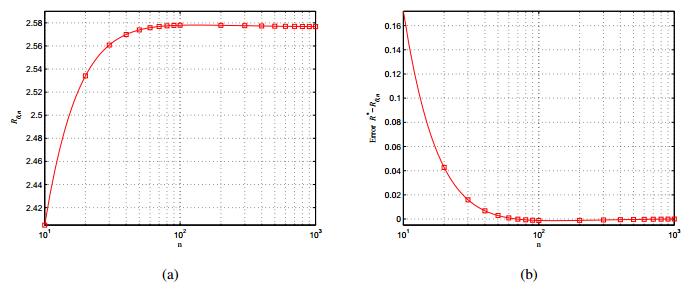
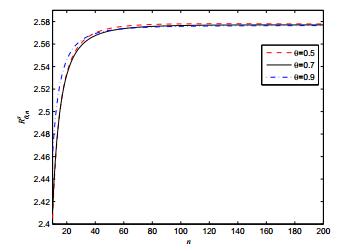
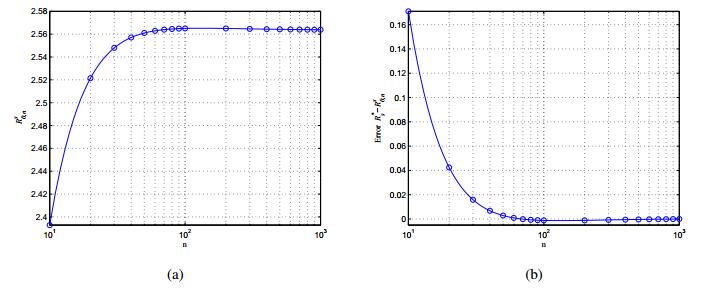
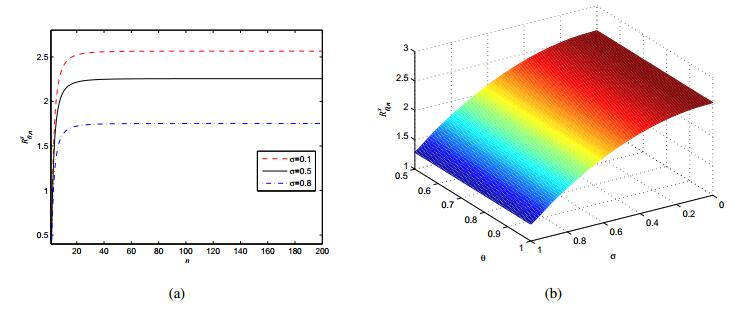
Figure 3 plots the optimal cost trajectory with the step size 2−8, the horizon is [0,1], the other parameters are b=5,r=1,q=1,ρ=0.0001,ϵ=0.1.
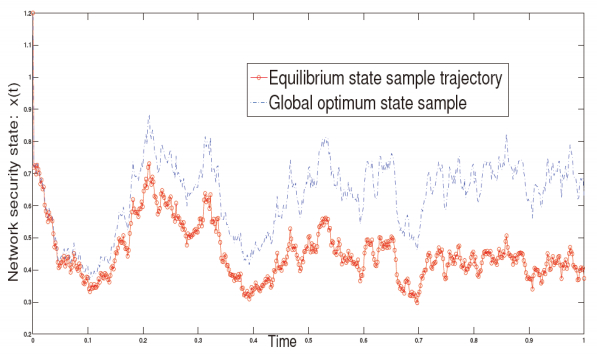
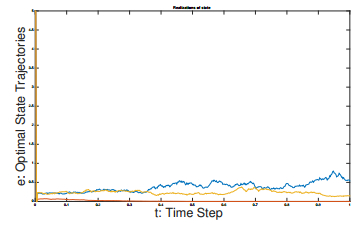
Figure 4 plots the optimal state vs the equilibrium state. As noted in [136], the security state is higher when there is a cooperation between the users and when the coalition formation cost is small enough. The inefficiency of Nash equilibria behavior is widely known in game theory in which the Nash equilibrium can be inefficient compared to the global optimum of the system. The relative payoff difference between the worse Nash equilibrium payoff and global optimum payoff have been proposed in the literature [180,183] as measure of inefficiency. Another measure of inefficiency is the Price of anarchy, which has been proposed in [181,182]. It measures the ratio between the worse Nash equilibrium payoff and global optimum payoff. Note however that, one needs to be careful by taking a ratio here, because the denominator may vanish in our context. Note that restricting the analysis to the set of symmetric strategies may lead to performance degradation [173] as symmetric Nash equilibria may not be performant even in symmetric games. Thus, looking at ϵ−Nash equilibria via mean-field limiting behavior does not help in improving the efficiency of Nash equilibria.
Example 4 can be used in the discrete-time mean-field-type game problem (4) associated with (3). It corresponds to a variance reduction problem which is widely used in risk quantification. The following example solves a distributed variance reduction problem in discrete time using MFTG.
Example 5 (Distributed Mean-Variance Paradigm, [137]). The best response problem of agent i is
|
{infui∈Ui{qiTvar(xT)+(qiT+ˉqiT)(E[xT])2+T−1∑t=0qitvar(xt)+(qit+ˉqit)(E[xt])2+T−1∑t=0ritvar(uit)+rit(Euit)2} subject to xt+1={axt+ˉaExt+n∑i=1biuit}+σW(t), x0∼L(X0), E[X0]=m0,
|
(7)
|
given the strategies (uj)j≠i of the other agents than i.
Under the assumption that for t∈{0,…,T−1}, and qjt≥0, (qjt+ˉqjt)≥0, rjt>0, there exists a unique best-response of agent i and it is given by
|
{ui,t=ηit(xt−Ext)+ˉηitExt,ηit=−[abiβi,t+1+biβi,t+1∑j≠ibjηjt]rit+b2iβi,t+1,ˉηit=−biγi,t+1(a+ˉa+∑j≠ibjˉηj,t)rit+b2iγi,t+1,βit=qit+βi,t+1{a2+2a∑j≠ibjηjt+[∑j≠ibjηjt]2}−[abiβi,t+1+biβi,t+1∑j≠ibjηjt]2rit+b2iβi,t+1,βiT=qiT≥0γit=(qit+ˉqit)+γi,t+1(a+ˉa+∑j≠ibjˉηj,t)2−(biγi,t+1(a+ˉa+∑j≠ibjˉηj,t))2rit+b2iγi,t+1,γiT=qiT+ˉqiT≥0
|
(8)
|
and the best response cost of agent i is
|
E[Li(u)]=Eβi0(x0−Ex0)2+γi0(Ex0)2+T−1∑t=0βi,t+1σ2.
|
In both examples 4 and 5 the optimal strategy of agent i is a feedback function of the state and the expected value of the state. This structure is different than the one obtained in classical stochastic optimal control which are mean-field-free. The methodology used in standard stochastic game problems do not apply directly to the mean-field-type game problems. These techniques need to be extended. This leads new optimality systems [36,179].
3. Engineering Applications
3.1. Civil Engineering
This subsection discusses two applications of MFTG in civil engineering.
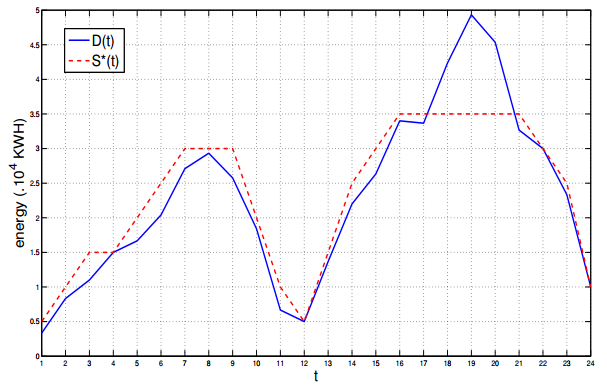
Application 1 (Road Traffic over Networks). The example below concerns transportation networks under dynamic flow and possible stochastic incidents on the lanes. Consider a network (V,L), where V is a finite set of nodes and L⊆V×V is a set of directed links. n users share the network (V,L). Let R be the set of possible routes in the network. A user with a given source-destination pair arrives in the system at source node s and leaves it at the destination node d after visiting a series of nodes and links, which we refer to as a route or path. Denote by cwi(xt,uit,mt) the average w−weighted cost for the path uit when mt fraction of users choose that path at time t and xt is the incident state on the route. The weight w simply depicts that the effective cost is the weighted sum of several costs depending on certain objectives. These metrics could be the delayed costs, queueing times, memory costs, etc and can be weighted by w in the multi-objective case. We define two regimes for the traffic game: a finite regime game with n drivers denoted by Gn and an infinite regime game denoted by G∞. The basic components of these games are (N,X,R,I={x},ci(x,.)). A pure strategy of driver i is a mapping from the information set I to a choice of a route that belongs to R. The set of pure strategies of a user is RX.
An action profile (route selection) (u1,…,un)∈Rn is an equilibrium of the finite mean-field-type game if for every user i the following holds:
|
ci(x,ui,m(x,ui))≤ci(x,u′i,m(x,u′i)+1n),∀u′i∈R,
|
for the realized state x.
The term +1n is the contribution of the deviating user to the new route. When n is sufficiently large the state-dependent equilibrium notion becomes a population profile m(x)=(m(x,u))u∈R such that for every user i
|
m(x,u)>0⟹ci(x,u,m(x,u))≤ci(x,u′,m(x,u′)),
|
for the realized state x and for all u′∈R. We refer to the equilibrium defined above as 0−Nash equilibrium. Note that the equilibrium profile depends on the realized state x.
We now discuss the existence conditions.
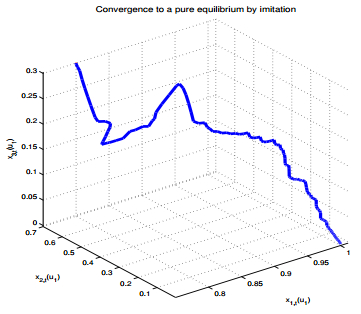
The equilibrium conditions can be rewritten in the form of variational inequalities: for each state x, (∗) ∑u∈R[m(x,u)−y(x,u)]c(x,u,m(x,u))≤0, for all y. Hence, the existence of an equilibrium is reduced to the existence of a solution to the variational inequality (*). By the standard fixed-point arguments, we know from [138] that for each single state, such a population game has an equilibrium if the cost functions are continuous in the second variable m. Moreover, the equilibrium is unique under strict monotonicity conditions of the cost function ci(x,u,.). Note that uniqueness in m does not mean uniqueness of the action profile u since one can permute some of the commuters. We use imitative learning in an information-theoretic view point. We introduce the cost of learning from strategy mi,t−1 to mi,t as the relative entropy dKL(mi,t−1,mi,t).
Then, each user reacts by taking a myopic conjecture given by
|
minmi,t ⟨ˆci,t,mi,t⟩+1βi,tdKL(mi,t−1,mi,t)
|
where ˆci,t is the estimated cost vector, βi,t is a positive parameter,
dKL is the relative entropy from mi,t−1 to mi,t.
dKL is not a distance (because it is not symmetric) but it is positive and can be seen as a cost to move from mi,t−1 to mi,t. We use the convexity property of the relative entropy to compute the strategy that minimizes the perturbed expected cost.
Proposition 1. Let βi,t=log(1+νi,t) for νi,t>0. Then, the imitative Boltzmann-Gibbs strategy is the minimizer of the above problem which becomes a multiplicative weighted imitative strategy:
|
mi,t(u):=mi,t−1(u)(1+νi,t)−ˆci,t−1(u)∑u′∈Rmi,t−1(u′)(1+νi,t)−ˆci,t−1(u′).
|
The advantage of the imitative strategy is that it makes sense not only in small learning rate but also in high learning rate. When the learning rate is large, the trajectory gets closer to the best reply dynamics and for small learning it leads to the replicator dynamics [139]. One useful interpretation of the imitative strategy is the following: Consider a bounded rationality setup where the parameter νi,t is the rationality level of user i. Then, a large value of νi,t means a very high rationality level for user i, hence user i will use an almost "best reply'' strategy. Small value of νi,t means that user i is of a low rationality level and is described by the replicator equation. It is interesting to see that both behaviors can be captured by the same imitative mean-field learning. Note that the logit (or Boltzmann-Gibbs) learning does not cover the low rationality level case.
Proposition 2. As νi,t goes to zero, the trajectory of the multiplicative weighted imitative strategy is approximated by the replicator equation of the estimated delays
|
˙mi,t(u)=mi,t(u)[−ˆci,t(u)+∑u′mi,t(u′)ˆci,t(u′)].
|
For one commuter case, the solution of the replicator equation yields
|
mi,t(u)=mi,0(u)e−t.1t∫t0ˆci,t′(u) dt′∑u′mi,0(u′)e−t.1t∫t0ˆci,t′(u′) dt′
|
The solution is
|
mi,t(u)=mi,0(u)e−tˉci(u)∑u′mi,0(u′)e−tˉci(u′).
|
Clearly the time-average trajectory based on average payoff and smooth best reply dynamics are closely related with parameter βi,t=t. Each driver knows the current state and employs the learning pattern. Each driver tries to exploit the information on the current state and build a strategy based on the observation of the vector of realized delays over all the routes at the previous steps. Then the Folk theorem for evolutionary game dynamics states:
• When starting from an interior mixed strategy, the replicator equation converges to one of the equilibria.
• All the faces of the multi-simplex are forward invariant. In particular, the pure strategies are steady states of the imitative dynamics.
• The set of global optima belongs to the set of steady states of the imitative dynamics.
The strategy-learning of user i is given by
|
L1i(xt): mi,t(xt,u):=mi,t−1(xt,u)(1+νi,t)−ci,t−1(xt,u)∑u′∈Rmi,t−1(xt,u′)(1+νi,t)−ci,t−1(xt,u′)
|
(9)
|
|
L2i(xt): mi,t(xt,u):=mi,t−1(xt,u)(1+νi,t)−ˉci,t−1(xt,u)∑u′mi,t−1(xt,u′)(1+νi,t)−ˉci,t−1(xt,u′),
|
(10)
|
where ˉci,t(x,u) is the time-average delay (up to t) in route u and state x.
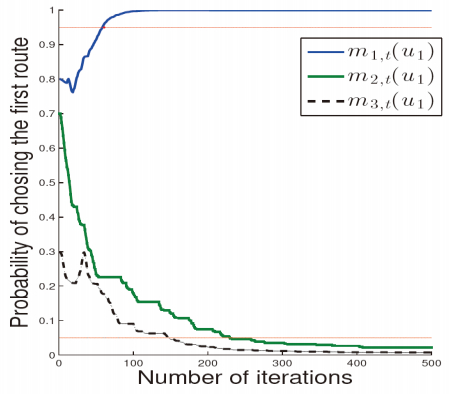
The imitative mean-field learning above can be used to solve a long-term mean-field game problem. We observe in Figures 6-6 that the imitative learning converges to one of the global optima. However, the exploration space grows in complexity. We explain how to overcome to this issue using mean-field learning based on particle swarm optimization (PSO). In it each user has a population of particles (multi-swarm). The particles within the same population (coalition) may pool their effort to learn faster and exploit better the available information.
The next example concerns multi-level building evacuation [140,141,142,143] using constrained mean-field games.
Application 2 (Multi-level building evacuation). A typical mean-field game model assumes that agents have unconstrained state dynamics. This has been, for example, the case with most of the existing mean-field models developed in the last three decades. Such models may not however be useful in practice, for example in a context of building evacuation. Evacuation strategies and values are designed using constrained mean-field-type game theory.
Particle-based pedestrian models have been studied in [144,145]. Continuum approximation of theoretical models have been proposed in [144,145,146,147,148,149]. Recent mean-field studies on crowd and pedestrian flows include [150,151,152,153,154]. Below a mean-field game for multi-level building evacuation is presented. Consider a building with multiple floors and resolutions represented by a compact domain D in the m−dimensional Euclidean space Rm. The number of floors is K. The domain at floor k is denoted as Dk. For 1<k<K, the floor k is connected to the higher floor k+1 using the intermediary domain I+k but also the lower floor k−1 using I−k. The sets Ik can be elevator zones or stairs.
n≥2 agents are distributed in a multi-level multi-resolution building with stairs, exit doors, sky-bridges. Each agent knows her current location in the building. The state/location xi of an agent i changes depending on her control action ui. The agent is interested in a safe evacuation from the building. This means that she is interested in the minimal exit time that avoid huge crowd around her. The problem of the agent i is equivalent to
|
{infui c3(xi(T),Gn(xi(T)))+∫T0c1(Gn(xi(t)))‖ui(t)‖2+c2(Gn(xi(t))) dt,˙xi=ui∈R3, 0<t<Txi(t)∈D⊂R3,Boundary constraints:ui| ∂D=0, ui| ExitDoor=k≠0∈R3
|
where ci is a positive increasing function, with c2(0)=0. T>0 is the exit time at one of the exits. The final exit cost is represented by c3 which can be written as ˜c3+˜h(x) where ˜c3>0 captures the initial response time of an agent (without congestion around),
|
Gn(xi(t))=1vol(B(xi(t),ϵ)) ∑j≠i1{d(xj(t),xi(t))≤ϵ}n−1,
|
represents the number of the agents around the position xi except i within a distance less than ϵ>0, vol(B) is the m-dimensional volume of the ball B(xi(t),ϵ) which does not depend on xi(t), due to translation invariance of the volume measure. When the number of agents grows, one obtains a mean-field game with several interacting agents. The state dynamics must satisfy the constraint xi(t)∈D at any time t before the exit. The non-optimized Hamiltonian in macroscopic setting as
|
H0(x,u,G,p)=−c1(G(x))‖u‖2−c2(G(x))+p.u,
|
where p is the adjoint variable. The Pontryagin maximum principle yields
|
˙p=−H0x,p(T)=−gx(x(T)),˙x=p2c1(G(x)), 0<t≤Tx(0)∈D.
|
The Hamiltonian H0(.,.,G,p(t)) is concave in (x,u) for almost everywhere (a.e.) t∈[0,T]. Then, for convex function c3, u∗ is an optimal response if H0(x∗(t),u∗,G∗,p∗(t))=maxuH0(x∗(t),u,G∗,p∗(t)). The (optimized) Hamiltonian as
|
H(x,p,G)=supu{−c1(G(x))‖u‖2−c2(G(x))+pu}.
|
The Hamiltonian can be computed as H(x,p,G)=‖p‖24c1(G(x))−c2(G(x)), and the optimal strategy is in (own)state-and-mean-field feedback form: u∗=p2c1(G(x))=Hp(x,p,G(x)), to be projected to the tangent space. The dynamic programming principle leads to the following optimality system:
|
{vt+H(x,vx,G(x))=0, on (0,T)×Dv(T,x)=−g(x), on Dρt+divx(ρHp)=0, ρ0(.) on D⊂R3u=0, y=0 on ∂Du=k, at exits
|
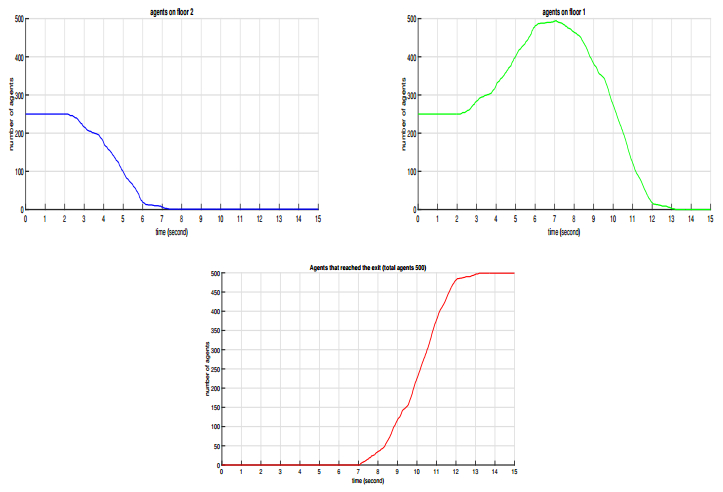
The development of numerical result, simulation and a validation framework can be found in [140,141,142,143]. Figures 7 and 8 show the application to a two floors building where 500 agents are spatially distributed.
Next, two applications of MFTGs in electrical engineering are presented.
3.2. Electrical Engineering
Application 3 (Millimeter Wave Wireless Communication). Millimeter wave (mmWave) frequencies, roughly between 30 and 300 GHz, offer a new frontier for wireless networks. The vast available bandwidths in these frequencies combined with large numbers of spatial degrees of freedom offer the potential for orders of magnitude increases in capacity relative to current networks and have thus attracted considerable attention for next generation 5G communication systems. However, sharing of the spectrum and the available infrastructure will be essential for fully achieving the potential of these bands. Unfortunately, rapidly changing network dynamics make it difficult to optimize resource sharing mechanisms for mmWave networks. MIMO mmWave wireless networks will rely extensively on highly directional transmissions, where both users, relays and base stations transmit in narrow, high-gain beams through electronically steerable antennas. While directional transmissions can improve signal range and provide greater degrees of freedom through spatial multiplexing, they also significantly complicate spectrum sharing. Nodes that share the spectrum must not only detect one another, but also search over a potentially large angular space to properly steer the beams and reduce interference. Power allocation, angle optimization and channel selection algorithms should consider the possible interference field and reduce it by adjusting the angles. This can facilitate rapid directional discovery in a dynamic and mobile environment as in Figure 9. Sometimes jammers and malicious are involved in the interactions. Beams adjustment and Interference coordination are central problem for users within the same network, or between users in different networks sharing the same spectrum. When multiple operators own separate core network and radio access network (RAN) nodes such as base stations and relays, but only loosely coordinate via wireless signaling, it is essential to use incentive mechanisms for better coordination to exploit the available resources. Cost sharing and pricing mechanisms capture some of the fundamental properties that arise when sharing resources among multiple operators. It can also be used in the uplink case, where users can select their preferred services and network provides and have to find tradeoffs between quality-of-experience (QoE) and cost (price).
As an illustrative example, a particle swarm learning mechanism, which is mean-field dynamics, in which the particles adapt the parameters such as angle and power is used to improve users' quality-of-experience. Here the key mean-field terms are the distributions of remaining energy, distribution of transmitter-receiver pairs and the sectorized interference field (per angle). Since users are carrying smartphones with limited power consumption, it is crucial to examine the remaining energy level. As in [91] the energy dynamic can be written as
subject to e(t)≥0, e(0)=e0, and u(.)≥0 is the transmission power and v(.) is the energy harvesting rate (for example, with distributed renewable energy sources).
Proposition 3. The marginal distribution me(t,e) of remaining energy solves the Fokker-Planck-Kolmogorov equation:
|
∂tme+∂e[(−u+v)me]−σ22∂eeme=0,
|
in a distribution sense. The first moment dynamics yields ddtˉe=−ˉu+ˉv, where ˉe(t)=E[e(t)],ˉu(t)=E[u(t)],ˉv(t)=E[v(t)] denotes the expected value of e(t), u(t),v(t) respectively.
Users move according to a mobility dynamics (which may not be stationary). The channel state can be modeled, for example using a matrix valued Ornstein-Uhlenbeck process dHj=Γj[ˆHj−Hj]dt+dWj where Γj,ˆHj are matrices with compatible dimensions of antennas at source and destination.
Proposition 4. The marginal distribution mHj(t,Hj) of channel state of user j solves the Fokker-Planck-Kolmogorov equation:
|
∂tmHj+divHj[(Γj(ˆHj−Hj))mHj]−12trace[∂HjHjmHj]=0,
|
in a weak sense. The first moment dynamics of user j yields
which decays exponentially to ˆHj as t increases.
The (unnormalized) distribution of the triplet (position, energy, channel) of the population at time (or period) t is ν(t,e,x,H)=∑nj=1δ{ej(t),xj(t),Hj(t)}, and the one within a beam A(s,d) with direction s−d is
|
˜ν(t,e,x,H,s,d)=n∑j=1δ{ej(t),xj(t),Hj(t)}1xj(t)∈A(s,d).
|
The sectorized interference field is I(t,x(t),d)=∫(ˉx,ˉH,ˉu)ϕ(ˉx−x(t),ˉH,ˉu))˜ν(t,E,ˉx,ˉH,x(t),d). Compared to other wireless technologies, mmWave may generate less interference because of reduced and optimized angles. However, interference may still occur when several users and blocking objects fall within the same angle as depicted in Figure 9. The success probability P(SINRi≥βi) from position xi(t) to destination di for both LoS and non-LoS can then be derived. The quality-of-experience of users can be termed as function of the sectorized interference field, satisfaction level and user-centric subjective measures such as MOS (mean opinion score) values.
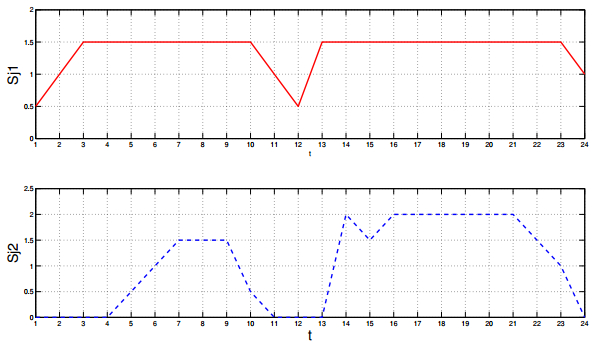
Application 4 (Distributed Power Networks (DIPONET)). Distributed power is a power generated at or near the point of use. This includes technologies that supply both electric power and mechanical power. The rise of distributed power is also being driven by the ability of distributed power systems to overcome the energy need constraints, and transmission and distribution lines. Mean-field game theoretic applications to power grid can be found in [93,113,114,115,116,117,118,119,120,121,122,123,124]. A prosumer (producer-consumer) is a user that not only consumes electricity, but can also produce and store electricity. Based on forecasted demand, each operator determines its production quantity, its mismatch cost, and engages an auction mechanism to the prosumer market. The performance index is Lj(sj,ej)=ljT(e(T))+∫T0lj(Dj(t)−Sj(t))+ρ2∑ks2jk(t) dt. Each producer aims to find the optimal production strategies:
|
{ infsj,ejLj(sj,ej,T)ddtejk(t)=cjk(t)−sjk(t)cjk(t)≥0, sjk(t)∈[0,ˉsjk], ∀j,k,tsjk(w)=0 ifwis a starting time of a maintenance period. ej,k(0) given.
|
where Dj(t) is a demand at time t, lj(Dj(t)−S(t)) denotes the instant loss where S(t)=Sproducer(t)+Sprosumer(t), Sproducer(t)=∑nj=1sj(t)=∑nj=1∑Kjk=1sj,k(t) where sj,k(t) is the production rate of plant/generator k of j at time t. Kj total number of power plants of j. The loss lj is assumed to be strictly convex. The stock of energy at time t is given by the classical motion ddtejk where cjk(t) is the maintenance cost of plant/generator k of j when it is in the maintenance phase. The optimality equation of the problem is given by Hamilton-Jacobi-Bellman:
|
{∂tvj(t,ej)+Hj(Dj(t),∂ejvj(t,ej))=0,t<Tvj(T,ej)=ljT(ej),
|
(11)
|
where Hj is the Hamiltonian function is
|
Hj(Dj,yj)=infsj[lj(Dj−Sj)+ρ2∑ks2jk+∑k(cjk−sjk)yjk]
|
(12)
|
The first order interior optimality condition yields −l′j(Dj−Sj)−yjk+ρsjk=0. By summing over k one gets an equation for the total production quantity S∗j solves −Kjl′j(Dj−Sj)−∑Kjk=1yjk+ρSj=0. The optimal supply of power plant k is s∗jk=min(ˉsjk,l′j(Dj−S∗j)+yjkρ). The solution of partial differential equation (11) can be explicitly obtained and it is given by the Hopf-Lax formula:
|
vj(t,ej)=infy∈RKj{ljT(y)+(T−t)H∗j(Dj,ej−yT−t)},
|
(13)
|
where H∗j is the Legendre transformation of Hj, and is given by
|
H∗j(Dj,a)=lj(Dj−1ρ∑kajk−l′j(Dj−S∗j)ρ)
|
Note that (13) provides an explicit solution to the Demand-Supply matching problem between power plants of prosumer j and this holds for arbitrary number of prosumers and power stations.
The mean-field equilibrium is obtained as fixed-point equation involving S∗ and D∗. When l′j is continuous and preserves the production domain [0,ˉs] one can guarantee the existence of such a solution by using Brouwer fixed-point theorem. One can use higher order fast mean-field learning to learn and compute of such a mean-field equilibrium.
Figure 10 illustrates the optimal supply based on an estimated demand curve. Figure 11 represents an allocation of the producer with two power stations.
3.3. Computer Engineering
This section provides applications of MFTG in computer engineering. It starts with an application of MFTG with number finite state-actions and then focuses on continuous state-action spaces.
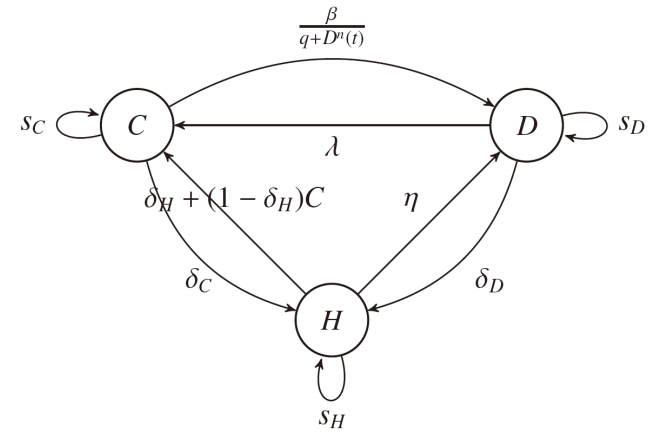
Application 5 (Virus Spread over Networks). We study a malware propagation over computer networks where the nodes interact through network-based opportunistic meetings (Figure 12 and Table 4). The security level of network is measured as a function of some key control parameters: acceptance/rejection of a meeting, opening/not opening a suspicious e-mail, file or packet. We model the propagation of the virus in network as a sort of epidemic process on a random graph of opportunistic connections [155]. A computer/node can randomly get online an infected or non infected data from other computers.
Table 4. Probabilities, effects (D,C,H), actions and loss function.
| Case | Transition proba. (θ,θ′∈{1,2}). | Mnθ(t+1)−Mnθ(t) | Actions | Propagation |
|
DδD→H | Dnθ(t)δD | (−1,0,1)/n | singleton set | −1/n |
|
2Dλ→2C | Dnθ(t)δ2mλ(Dnθ(t)−1n) | (−2,2,0)/n | {m,ˉm} | 0 |
|
%2' | Pnθ(t)δ2mλ(Pnθ′(t)−1n1{θ=θ′})1{θ=θ′} | (−2,2,0)/n | {m,ˉm} | 0 |
|
CδC→H | Cnθ(t)δC | (0,−1,1)/n | singleton set | −1/n |
|
Cβqθ+Dnθ(t)→D | Cnθ(t)βDnθ(t)qθ+Dnθ(t) | (−1,1,0)/n | singleton set | 0 |
|
HδH+(1−δH)Cn→C | Hn(t)[δH+(1−δH)Cn(t)] | (0,1,−1)/n | singleton set | 1/n |
|
Hη→D | Hn(t)(δeδSm+δmηDn(t)) | (1,0,−1)/n | {o,ˉo,m,ˉm} | 1/n |
An infected computer can be in two states: dormant or fully infected. The non-infected computers are susceptible to be approached by virus coming from infected ones. The possible states are therefore denoted as Dormant (D), Infected/Corrupt(C) and Susceptible/Honest (H). The set of types is 1 or 2, also denoted generically as θ,θ′. For each type the state may be different except for honest state where it is considered as honest in both regimes of the network. The network size is n≥1. The repartition of the nodes at time step t is denoted as n=Dθ(t)+Dθ′(t)+Cθ(t)+Cθ′(t)+H(t).
The frequency of the states θ is called occupancy measure of the population and is denoted as Mn(t)=(Dθ(t)/n,Dθ′(t)/n,Cθ(t)/n,Cθ′(t)/n,H(t)/n)=:(Dnθ(t),Dnθ′(t),Cnθ(t),Cnθ′(t),Hn(t)). Mn(.) is a random process and its limit measure corresponds to the mean field term. The goal is understand the impact of the control action on combatting virus spread, which is the minimization of proportion On(t):=1−Hn(t)). The interaction is simulated using the following rules:
Changes from Dormant states: A node in dormant state (transient) with type θ may become honest with probability δD∈(0,1). A dormant with type θ may opportunistically meet another dormant of type θ′, and both become active. This occurs with probability proportional to the frequency of other dormant agent at time t. For type θ, the probability is λ(Dnθ′(t)−1n1{θ=θ′}). Note that the dormant can decide to contact the other dormant or not, so there are two possible actions: {m,ˉm} (to meet or not to meet). Those events will be modeled with a Bernoulli random variable with success (meeting) probability δm, which represents u(m|D,θ).
Changes from Corrupt States: A corrupt node may become honest with probability δC. A corrupt node of type θ may become dormant with probability βDnθ(t)qθ+Dnθ(t) at time t. Here is assumed that, at high concentrations of dormants, each corrupt node infects at most a certain maximum number of dormant nodes per time step. This reflects the fact a corrupt has a limitation in terms its power, domination and capabilities. The parameter 0≤β≤1 can be interpreted as a maximum contamination rate. The parameter 0≤qθ≤1 is the dormant node density at which the infection spread proceeds.
Changes from Susceptible/Honest states: An honest node may become infected with probability δH+(1−δH)Cn(t). An honest node may become dormant via two ways. First, δSm is the probability of getting corrupt by the network representative node. In this case, the honest node can decide share or not, so there are two possible actions: {o,ˉo}. This case will be modeled using a coin toss with probability δe∈(0,1). Second, η(Dnθ(t)+Dnθ′(t)) models the probability of meeting a dormant node. Here η∈(0,1). In this case, the dormant node can decide to contact the honest node or not, and it is modeled analogously to the other two cases.
The payoff function is the opposite of the infection level. Each transition described above has a certain contribution to be infection level of the society, which could be 0 if no corrupt or dormant node become honest, −1/n if there is a node which become honest and +1/n if one node is corrupt (D or C). In Table 4 are the transition probabilities, the contribution to Mn(t+1)−Mn(t), the set of actions, and the contribution to information spread in the network.
The drift, that is, the expected change of Mn in one time step, given the current state of the system is fn(m)=nE(Mn(t+1)−Mn(t)|Mn(t)=m) which can be expressed as:
|
fn(m)=(−dθδD−2dθδ2mλndθ−1n−cθβdθqθ+dθ+h(δeδSm+δmηd)−dθ′δD−2dθ′δ2mλndθ′−1n−cθ′βdθ′qθ′+dθ′+h(δeδSm+δmηd)2dθδ2mλndθ−1n−cθδC+cθβdθqθ+dθ+h(δH+(1−δH)c)2dθ′δ2mλndθ′−1n−cθ′δC+cθ′βdθ′qθ′+dθ′+h(δH+(1−δH)c)dδD+cδC−2h(δH+(1−δH)c)−2h(δeδSm+δmηd))
|
where m=(dθ,dθ′,cθ,cθ′,h), d=dθ+dθ′ and c=cθ+cθ′. Then the limit of fn(m) is
|
f(m)=(−dθδD−2λd2θδ2m−cθβdθqθ+dθ+h(δeδSm+δmηd)−dθ′δD−2λd2θ′δ2m−cθ′βdθ′qθ′+dθ′+h(δeδSm+δmηd)2λd2θδ2m−cθδC+cθβdθqθ+dθ+h(δH+(1−δH)c)2λd2θ′δ2m−cθ′δC+cθ′βdθ′qθ′+dθ′+h(δH+(1−δH)c)dδD+cδC−2h(δH+(1−δH)c)−2h(δeδSm+δmηd))
|
Notice that the sum of the all the components of f(m) is zero. Furthermore, if one of the components mj of m=(dθ,dθ′,cθ,cθ′,h) is zero then the corresponding drift function fj(m)≥0. As a consequence, in the absence of birth and death process, the 4−dimensional simplex is forward invariant, meaning that if initially m(0) is in the simplex, then for any time greater than 0 the trajectory of m(t) stays in the simplex domain.
3.3.1. Centralized control design
We minimize the proportion of node with states C or D by means of controlling u(.|), i.e., by adjusting (δm,δe)∈[0,1]2. Since o(t)=c1+c2+d1+d2=1−h(t), minimizing o(t) is equivalent to maximize the proportion of susceptible node in the population. Therefore the optimization problem becomes
|
{sup δe,δm h(T)+∫T0h(t) dt˙m=f(m), m(0)=m0where, m=(c1,c2,d1,d2,h).
|
ˆH=h+f1p1+f2p2+f3p3+f4p4+f5p5. This is a twice continuously differentiable function in m, and ∂mjˆH=∑5i=1[∂mjfi]pi for j≤4. The optimum control strategies at time t are the ones that maximize ˆH.
|
{argmax δe,δmˆH˙m=f(m), m(0)=m0˙pj=−5∑i=1[∂mjfi]pi, j≤4, t<T˙p5=−1−5∑i=1[∂hfi]pi, t<T p(T)=<sup>[<xrefref−type="bibr"rid="b0">0</xref>,<xrefref−type="bibr"rid="b0">0</xref>,<xrefref−type="bibr"rid="b0">0</xref>,<xrefref−type="bibr"rid="b0">0</xref>,<xrefref−type="bibr"rid="b1">1</xref>]</sup>.
|
3.3.2. Combatting Virus Propagation by Means of Individual Action
Let S(t) be the random variable describing the individual state at time t of a generic individual and assume that a generic individual is in a state s at time t. Then S(t+1n) is independent of previous values (S(t′):t′≤t) and as n goes to infinity for all state s′. The reward of a generic individual payoff is defined as follows:
pθ(s,u,m)=0 if the individual state s is different than H, and equals 1 if the state s=H. By doing so, each individual tries to adjust its own trajectory. People in honest state will accept less meeting and will set their meeting rate δm to be minimal, and the other individual with state different than H will try to enter to H as soon as possible. As in a classical communicating Markov chain, this is the entry time to state H.
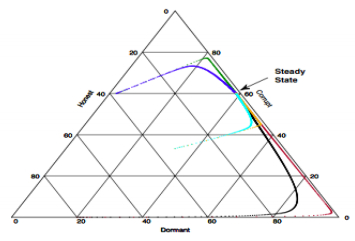
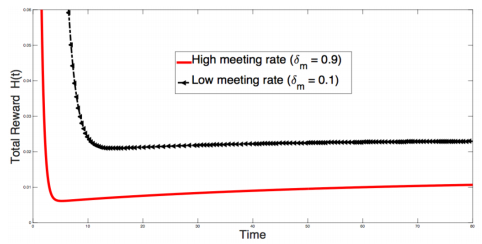
Figure 13 reports the result of the simulation with the following 3 starting points: (d,c)=(0.2,0.6), (d,c)=(1/3,1/3) and (d,c)=(0.2,0). In the three cases, the system converges to the same steady state which is around (d,c)=(0.38,0.6). Figure 14 plots the reward (honest people) as a function of time for two different control parameters δm=0.9 and δm=0.1. We observe that the reward is greater for δm=0.1 than the one for δm=0.9.
3.3.3. Network effect
The primary advantage of network models is their ability to capture complex individual-level structure in a simple framework. To specify all the connections within a network, we can form a matrix from all the interaction strengths which we expect to be sparse with the majority of values being zero. Usually, for simplicity, two individuals (or populations) are either assumed to be connected with a fixed interaction strength or unconnected. In such cases, the network of contacts is specified by a graph matrix G, where Gij is 1 if individuals i and j are connected, or 0 otherwise. A connection could be a relationship between the two nodes. It may be represent an internet, social network or physical connection. They may not be close in terms of location. The status of an node will be influenced by the status of its connection following the rules specified above. The resulting graph-based mean-field dynamics is illustrated in Figure 15.
Application 6 (Cloud Networks). Resource sharing solutions are very important for data centers as it is required and implemented at different layers of cloud networks [95,96,97]. The resource sharing problem can be formulated as a strategic decision-making problem. Lot of resources may be wasted if the cloud user consider an economic renting. Therefore a careful system design is required when a several clients interact. Price design can significantly improve the resource usage efficiency of large cloud networks. We denote such a game by Gn, where n is the number of clients. The action space of every user is U=R+ which is a convex set, i.e., each user i chooses an action ui that belongs to the set U. An action may represent a certain demand. All the actions together determine an outcome. Let pn be the unit price of cloud resource usage by the clients. Then, the payoff of user j is given by
|
ri(x,u1,…,un)=cn(x)h(ui)n∑j=1h(uj)−pn(x)ui,
|
(14)
|
if ∑nj=1h(uj)>0 and zero otherwise. The structure of the payoff function ri(x,u1,…,un) for user i shows that it is a percentage of allocated capacity minus the cost for using that capacity. Here, cn(x) represents the value of the available resources, h is a positive and nondecreasing function with h(0)=0. We fix the function h to be xα where α>0 denotes a certain return index. x is the state of cloud networks which is a random variable on the availability of the servers. The cloud game Gn is given by the collection (X,N,U,(ri)i∈I) where I={1,…,n}, n≥2, is the number of potential users. The next Proposition provides closed-form expression of the Nash equilibrium of the one-shot game Gn for a fixed state x such that cn(x)>0,pn(x)>0, and for some range of parameter α. It also provides the optimal price p∗n such that no resource is wasted in equilibrium.
Proposition 5. By direct computation, the following results:
(1) The resource sharing game Gn is a symmetric game. All the clients have symmetric strategies in equilibrium whenever it exists.
(2) For 0≤α≤1, and x∈X, the payoff ri is concave (outside the origin) with respect to own-action ui. The best response BRi(u−i) is strictly positive and is given by the root of
|
z(α−1)/2(αcn(x)npn(x)G)1/2−zαn−G=0, G≜1n∑j≠iuαj
|
where z≜ui and there is a unique equilibrium (hence a symmetric one) given by (zα−1αcn(x)npn(x)n−1nzα)12−zαn−n−1nzα=0, i.e.,
|
u∗NE(x)=α(n−1)cn(x)n2pn(x).
|
It follows that the total demand na∗NE(x) at equilibrium is less than cn(x)pn(x) which means that some resources are wasted.
The equilibrium payoff is ri(x,a∗NE)=uipn(x)[G+uαinαG−1] which is positive for α≤1.
(3) For α>1, the activity (participation) of user i depends mainly of the aggregate of the others. u∗i>0 only if G≤G∗ and the number of active clients should be less than αα−1. If n>αα−1 then BRi=0.
(4) With a participation constraint, the payoff at equilibrium (whenever it exists) is at least 0.
(5) By choosing the price p∗n=α(n−1)n<α one gets that the total demand at equilibrium is exactly the available capacity of the cloud. Thus, pricing design can improve resource sharing efficiency in the cloud. Interestingly, as n grows, the optimal pricing converges to α.
We say that the cloud renting game is efficient if no resource is wasted, i.e., the equilibrium demand is exactly cn(x). Hence, the efficiency ratio is na∗NEcn(x). As we can see from (ⅱ) of Proposition 5, the efficiency ratio goes to 1 by setting the price to p∗n. This type of efficiency loss is due to selfishness and have been widely used in the literature of mechanism design and auction theory. Note that the equilibrium demand increases with α, decreases with the charged price and increases with the capacity per user. The equilibrium payoff is positive and if α≤1 each user will participate in an equilibrium. In the Nash equilibrium the optimal pricing p∗n depends on the number of active clients in the cloud and value of α. When the active number of clients varies (for example, due to new entry or exit in the cloud), a new price needs to be setup which is not convenient.
3.4. Mechanical Engineering
Application 7 (Synchronization and Consensus). Consider a coupled oscillator dynamics with a control parameter per agent.
|
dθi=[ωi+n∑j=1Kij(θ)sin(θj−θi)+ui]dt+σdWi(t),
|
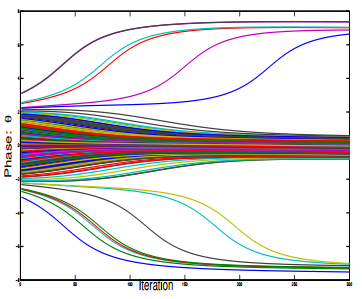
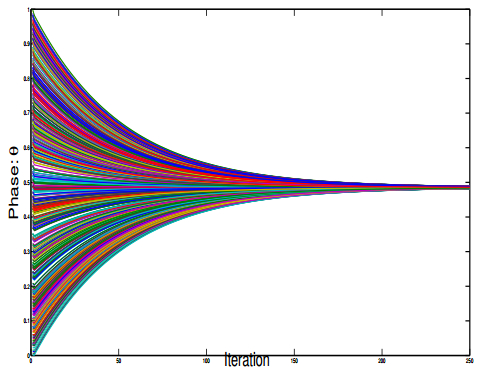
where θi is the phase of oscillator i, ωi is the natural frequency of oscillator i, n is the total number of oscillators in the system and K is a coupling interaction term. The objective here is to explore phase transition and self organization in large population dynamic systems. We explore the mean-field regime of the dynamical mean-field systems and explain how consensus and collective motion emerge from local interactions. These dynamics have interesting applications in multi-robot coordination. Figure 16 presents a Kuramoto-based synchronization scheme [156]. The uncontrolled Kuramoto model can lead to multiple clusters of alignment. Using mean-field control law, one can drive the trajectories (phases) towards a consensus as illustrated in Figure 17 which represents the behaviors for ui=−ωi+ηisin(1n∑nj=1θj−θi). This type of behavior is useful in mobile robot rendezvous problems in which each agent needs to move towards a common point (where the rendezvous will take place).
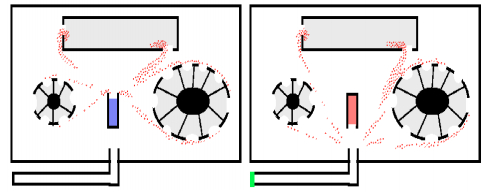
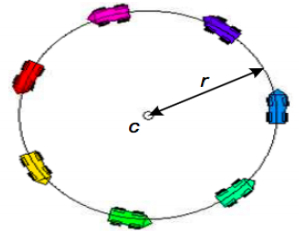
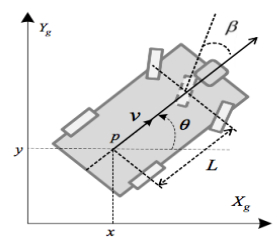
We now provide another relevant application of the Kuramoto model in convoy protection scenario with mobile car-like robots. The goal of the robots is to keep protecting the convoy by occupying the space as the convoy moves. The mean-field-type control helps to balance between energy, placement error and risk. The authors in [157] have shown that the Kuramoto model modified with phase shift of π2 radians can be used in convoy protection scenario given in Figure 18. In this scenario, we want the agents to follow the movement of the convoy while spreading out along a circular perimeter. The mean-field-type control law allow the agents to be positioned equally on a circle and self-organizing the distribution pattern once new agents are added into the network for protecting the convoy and occupying the space. Note that re-configuration of the multi-robot team will be done in a distributed way over the circle with center c and with radius r. The protecting convoy is a rear-wheel drive, front-wheel steerable car-like mobile robot. The car-like robot to be controlled is given in Figure 19. The kinematic parameters of the mobile robot i are given by (pi(t),vi(t),θi(t),βi(t),li) representing the cartesian coordinate (position) pi(t)=(xi,1(t),xi,2(t)) of robot i located at the mid-point of the rear-wheel axle, vi(t) is the translational driving speed, θi(t) is the orientation,
βi(t) the steering angle of the front wheels and li the distance between front and rear wheel axle. The goal is to control the robot to a desired orbit while spreading out. One can control the velocity vi through acceleration and the steering angle βi. The evolution of center point c and the radius r are given by the drift function bc(t),br(t). The connectivity in the circular graph for agent i is limited to two other agents : i−1 and i+1 modulo n. Each agent i is influenced only by its neighboring agents. The instantaneous cost is
|
Li(t)=ϵ1[cos(θi+1−θi)+cos(θi−θi−1)]+ϵ2(θi−π2−tan−1(xi,1−c1xi,2−c2)).
|
The first term in bracket says that agent i should spread out from i−1,i+1. The second in the bracket represents the orientation synchronization. The terminal cost is of mean-field type and is given by
|
Li(T)=ϵ3|vi|2d(xi,c)r+ϵ4|d(xi,c)−r|2+ϵ5var(vi),
|
representing a balance between the kinetic energy spent, the error adjustment for being on the new circle and the variance respectively.
The finite horizon cost functional of agent i is Ji(u,β)=Li(T)+∫T0Li(t)dt. Let C(c(0),r(0)) be the circle with center c(0) and radius r(0). The best-response problem of agent i is
|
{supui,βi −EJi(u,β)˙xi,1=vicosθi, ˙xi,2=visinθi,dθi=vitanβilidt+σtanβilidWi(t),vi=d(xi,c)r[ωi+n∑j=1Kij(θ)cos(θj−θi)+ui]xi(0)∈C(c(0),r(0))⊂R2
|
This is a mean-field-type optimization and the optimality system is easily derived from the stochastic maximum principle.
Application 8 (Energy-Efficient Buildings). Nowadays a large amount of the electricity consumed in buildings is wasted. A major reason for this wastage is inefficiencies in the building technologies, particularly in operating the HVAC (heating, ventilation and air conditioning) systems. These inefficiencies are in turn caused by the manner in which HVAC systems are currently operated. The temperature in each zone is controlled by a local controller, without regards to the effect that other zones may have on it or the effect it may have on others. Substantial improvement may be possible if inter-zone interactions are taken into account in designing control laws for individual zones [125,126,127,128,129]. The room/zone temperature evolution is a controlled stochastic process
|
dTi=[ϵ1(Text−Ti)+∑j∈Niϵ2ij(Tj−Ti)+ϵ3ui(Tref−Ti)]dt+σdWi,
|
where ϵ1,ϵ2ij,ϵ3 are positive real numbers. The control action ui in room i depends on the price of electricity p(demand,supply,location). The cost for driving to the comfort temperature zone (Figure 20) is (Ti−Ti,comfort)2+var(Ti−Ti,comfort). The payoff of consumer is a sort of tradeoff between comfort temperature and electricity cost uip. The instantaneous total cost of consumer i is
|
Li(t)=uip(.)⏟energy price+deviation to the comfort zone⏞(Ti−Ti,comfort)2+var(Ti−Ti,comfort)⏟risk.
|
Within the time horizon [0,τ], τ>0, consumer i minimizes in ui:
|
var(Ti(τ)−Ti,comfort)+E∫τ0Li(t)dt.
|
However, the electricity price p(.) depends on the demand D=∫Iconsumption(i)m1(t,di) and supply S=∫Jsupply(j)m2(t,dj). m1(t,.) is the population mean-field of consumers, i.e., the consumer distribution at time t. Note that m1 is an unnormalized measure. m2 is the distribution of suppliers. The building is served by a producer whose remaining energy dynamics is
|
dejk(t)=[cjk(t)1{k∈Acj(t)}−sjk(t)]dt+σdWjk,
|
The instant payoff of the producer j is its revenue minus the cost. The cost is decomposed as the cost due to mismatch between supply and demand and the production cost. The payoff is
|
rj=qjp(D,S)⏟revenue−mismatch cost⏞var(Dj−Sj)−c(qj)⏟production cost.
|
Producer j solves maxqjE∫τ0rjdt subject to the production constraint above. Explicit solutions to both problem can be obtained using the framework developed in [132,134].
3.5. General Engineering
Application 9 (Online Meeting). Group meeting online, even over video, is much different than sitting in a boardroom communicating face-to-face with someone. But they something in common: deciding to join Early or on Time the group meeting. In the context of online video group meeting, since the communication is over video, the opportunity for miscommunication is much higher, and thus, one should pay close attention to how the group meeting is conducted. Each group member aims to heighten the quality of her online meetings by acting professionally and by signing early or on time: Nothing throws off a meeting worse than scheduling woes. This is in particular widely observed for online group meetings.
Scheduling and synchronization is probably the hardest job in these meetings. The help scheduling groups from different sites can login to the meeting space at their convenience makes it easier to get meetings started on time. However, it does not mean that the meeting will start exactly at scheduled time. The group members can decide to be at convenient place early and prepare for the meeting to start, giving you time to settle down and get acquainted with the interface. We examine how agents decide when to join the group meeting in a basic setup. We consider several industry and academia aiming to collaborate on a research development. The companies are located at different sites. Each company from each site has appointed work package leader. In order to improve savings from long business trips, hotels/ accommodation and to reduce jet-lags effect the companies decided to organize an online meeting. After coordinating all the members availability, date and time is found and the meeting is initially scheduled to start at time ˉt. Each member has the starting time in his schedule and calendar remainders but in practice, the online meeting only begin when a certain number ˉn of representative group leaders and group members will connect online and will be seated in these respective rooms. Thus, the effective starting time T of the online meeting is unknown and people organize their behavior as a function of (ˉt,ˉn,T).
Each group member can move from her office to the meeting room (Figure 21). The dynamics of agent i is simply given by ˙xi=ui, where xi(0)∈D. Let n(t) be the number of people arrived (and seated) in the room before t. If the criterion is met (by all groups) before the initially scheduled time ˉt of the meeting, this latter starts exactly at ˉt. If on the other hand the criterion is met at a later time, T is determined by the self-consistency relation: T=inf{t | t≥ˉt, n(t)≥ˉn}. The instantaneous cost function is h(Gn(xi))‖ui‖2 and the terminal cost is c(th)=c1[th−ˉt]++c2[th−T]++c3[T−th]+ where ci are non-negative real numbers, and th=inf{t, | xi(t)∈MeetingRoom}. Let J(u)=c(th)+∫th0h(Gn(xi))‖ui‖2 dt where h(Gn(xi))‖ui‖2 quantifies a congestion-dependent kinetic energy spent to reach the meeting room of her group. [T−th]+ quantifies the useless waiting time, [th−T]+ quantifies of the time for missing of beginning of the online meeting, [th−ˉt]+ quantifies the sensitivity to her reputation of being late at the meeting. Given the strategies (u1,…,ui−1,ui+1,…,un), of the other agents, the best response problem of i is:
|
{supui −J(u)˙xi=ui, xi(0)∈D⊂R2ui=0 over ∂D⊂R2, ui=k at Exits⊂R2
|
Even if h(.) is constant, the agents interact because of a common term: the starting time of the online meeting T, and n(T)≥ˉn. For this reason, the choice of the other agents matters. The best response of agent i solves the Pontryagin maximum principle
|
˙pi=0, t<tih˙xi=u∗i=pi2,xi(0)∈Building⊂R3.
|
Hence, xi(t)=xi(0)+tpi(th)2 will at arrive at position xroom, at time th=2xroom−xi(0)pi(th) Thus, the optimal payoff of agent i starting from x at time 0 is −c(th)−∫th0‖p(th)‖24dt=−c(th)−th‖p(th)‖24. The optimal payoff of agent i starting from x at time t is −c(th)−(th−t)‖p(th)‖24 which is maximized for −c′(th)+‖p(th)‖24=0, i.e., ‖p(th)‖2=4c′(th) hence ‖p(th)‖=2√c′(th)=‖vx(th,x(th))‖. Knowing that the following two functions: ˜v1(x)=⟨x,p∗⟩, with ‖p∗‖∗=1, and ˜v2(x)=c2±‖x−y‖, with x≠y, solves the Eikonal equation, ‖˜vx‖=1, one deduces an explicit solution of the Bellman equation:
vt−‖vx‖22=0, v(th,x)=−c(th).
Proposition 6. The tradeoff value to the meeting room starting from point x at time t is v(t,x)=−2√c′(th)d(x(t),xroom)−2(th−t)c′(th)−c(th).
The next application uses MFTG theoretic modelling for smart cities.
Application 10 (Mobile CrowdSensing). The origins of crowdsourcing goes back at least to the nineteenth century and before [164,165]. Joseph Henry, the Smithsonian's first secretary, used the new networked technology of his day, the telegraph, to crowdsource weather reports from across the country, creating the first national weather map of the U.S. in 1856. Henry's successor, Spencer Baird, recruited citizen scientists to collect and ship natural history specimens to Washington, D.C. by the other revolutionary new technology of the day -the railroad -thus forming the bulk of the Institution's early scientific collections.
Today's mobile devices and vehicles not only serve as the key computing and communication device of choice, but it also comes with a rich set of embedded sensors, such as an accelerometer, digital compass, gyroscope, GPS, ambient light, dual microphone, proximity sensor, dual camera and many others. % (see all the available sensors on iPhone and Samsung Galaxy). Collectively, these sensors are enabling new applications across a wide variety of domains, creating huge data and give rise to a new area of research called mobile crowdsensing or mobile crowdsourcing [164,165,166]. Crowd sensing pertains to the monitoring of large-scale phenomena that cannot be easily measured by a single individual. For example, intelligent transportation systems may require traffic congestion monitoring and air pollution level monitoring. These phenomena can be measured accurately only when many individuals provide speed and air quality information from their daily commutes, which are then aggregated spatio-temporally to determine congestion and pollution levels in smart cities. Such a collected data from the crowd can be seen (up to a certain level) as a knowledge, which in turn, can be seen as a public good [167].
A great opportunity exists to fuse information from populations of privately-held sensors to create useful sensing applications will be public good. On the other hand, it is important to model, design, analyze and understand the behavior of the users and their concerns such as privacy issues and resource considerations limit access to such data streams. Two MFTGs where each user decides its level of participation to the crowdsensing: (ⅰ) public good, (ⅱ) information sharing, are presented below.
The smartphones are battery-operated mobile devices and sensors suffer from a limited battery lifetime. Hence, there is a need for solutions that will limit the energy consumptions of such mobile Internet-connected objects. Such an involvement is translated into a energy consumption cost.
All the data collected from these devices combine both voluntary participator sensing and opportunistic sensing from operators. The data is received by a network of cloud servers. For security and privacy concerns, several information are filtered, anonymized, aggregated and distributions (or mean-field) are computed. The model is a public good game with an extra reward for contributors. When decision-makers are optimizing their payoffs, a dilemma arises because individual and social benefits may not coincide. Since nobody can be excluded from the use of a public good, a user may not have an incentive to contribute to the public good. One way of solving the dilemma is to change the game by adding a second stage in which reward (fair) can be given to the contributors (non-free-riders).
The strategic form game with incomplete information denoted by G0, is described as follows: A stochastic state of the environment is represented by x. There are n0 potential participant to the mobile crowdsensing. The number n0 is arbitrary, and represent the number of users of the game G0. As we will see, the important number is not n0 but the number of active users (the ones with non-zero effort), who are contributing to the crowdsensing.
Each mobile user i equipped with sensing capabilities, can decide to invest a certain level of involvement and effort ui≥0. The action space of user i is Ui=R+. As we will see the degree of participation will be limited so that the action space can be included into a compact interval. The payoff of user i is additive and has three components: a public good component ˉGi(m−ˉR(x)), a resource sharing component ˉR(x)hi(ui)∑n0j=1hj(uj) and a cost component p(x,ui). Putting together, the function payoff is
|
r0i(x,u)=[ˉGi(m−ˉR(x))−p(x,ui)]1m≥ˉR(x)+ˉR(x)hi(ui)n0∑j=1hj(uj)1n0∑j=1hj(uj)≠0.
|
where m=∑n0j=1uj is the total contribution of all the users, where 1B(x) is the indicator function which is equal to 1 if x belongs to the set B and 0 otherwise. This creates a discontinuous payoff function. The function ˉGi is a smooth and nondecreasing, R(x) is a random non-negative number driven by x. The discontinuity of the payoffs due the two branches {u: m≥ˉR(x)} and {u: m<ˉR(x)} can be handled easily by eliminating the fact that the actions in {u: m≤ˉR(x)} cannot be equilibrium candidates.
Using standard concavity assumption with the respect to own-effort, one can guarantee that the game has an equilibrium in pure strategies. We analyze the equilibrium for ˉGi(z)=aizα,hi(z)==z where ai≥0, and α∈(0,1]. For any reward
|
ˉR(x)≥4m∗σ(1−σ)2, σ=ˉG′i(m)−1ˉG′j(m)−1>0
|
where m∗∈argmax[ˉG(m)−m], there exists a design parameter (ai)i such that the "new" lottery based scheme provides the global optimum level of contribution in the public good. We collect mobile crowdsensing users to form a network in which secondary users who willing to share their throughput for the benefit of the society or their friends and friends' of friends. This can be seen as a virtual Multiple-Inputs-Multiple-Outputs (MIMO) system with several cells, multiple users per cell, multiple antennas at the transmitters, multiple antennas at the receivers. The virtual MIMO system is a sharing network represented by a graph (V,E), where V is the set of users representing the vertices of the social graph and E is the set of edges. To an active connection (i,j)∈E is associated a certain value ϵij≥0. The term ϵij is strictly positive if j belongs to the altruistic outgoing network of i and i is concerned about the throughput of user j. The first-order outgoing neighborhood of i (excluding i) is Ni,−. Similarly, if i is receiving a certain portion from j then i∈Nj,− and ϵji>0. In the virtual MIMO system, each user i gets a potential initial throughput Thpi,t during the slot/frame t and can decide to share/rent some portion of it to its altruism subnetwork members in Ni,−. User i makes a sharing decision vector ui,t=(uij,t)j∈Ni, where uij,t≥0. The ex-post throughput is therefore
|
Thpi,t+=Thpi,t+∑j | i∈Nj,−uji,t−∑j∈Ni,−uij,t.
|
Denote {j | i∈Nj,−}=:Ni,+. Then,
|
Thpi,t+=Thpi,t+∑j∈Ni,+uji,t−∑j∈Ni,−uij,t.
|
(15)
|
Since we are dealing with sharing decisions, the mathematical expressions are not necessarily needed if the output can be observed or measured. Given a measured throughput, A user can decide to share or not based its own needs/demands. The term ∑j∈Ni,+uji,t represents the total extra throughput coming to user i from the other users in Ni,+ (excluding i). The term ∑j∈Ni,−uij,t represents the total outgoing throughput from user i to the other users in Ni,− (excluding i). In other word, user i has shared ∑j∈Ni,−uij,t to the others. If j∉Ni,− then uij,t=0 and for all i, uii,t=0. The balance equation is
|
∑iThpi,t+=∑iThpi,t+∑i,juji,t−∑i,juij,t=∑iThpi,t,
|
(16)
|
i.e., the system total throughput ex-post sharing is equal to the system total throughput ex-ante sharing. This means that the virtual MIMO throughput is redistributed and sharing among the users through individual sharing decisions s. Some users may care about the others because he may be in their situation in other slot/day. For these (altruistic) users, the preferences are better captured by an altruism term in the payoff. We model it through a simple and parameterized altruism payoff.
The payoff function of i at time t is represented by
|
r1i(x,ui,t,u−i,t)=ˆri(Thpi,t+)+∑j∈Niϵijˆrj(Thpj,t+).
|
(17)
|
Here, ϵij≥0 and represents a certain weight on how much i is helping j. The matrix (ϵij) plays an important role in the sharing game under consideration since it determines the social network and the altruistic relationship between the users over the network. The throughput Thp depends implicitly the random variable x. The static simultaneous act one-shot game problem over the network (V,E) is given by the collection G1,ϵ=(V,(Rn1−1+,r1i)i). The vector ui is in Rn1+, but the i-th component is uii=0. Therefore the choice vector reduces to be in Rn1−1+. and is denoted by (ui,1,…,ui,i−1,0,ui,i+1,…,ui,n1). An equilibrium of G1,ϵ in state w is a matrix s∈Rn21+ such that
|
r1i(x,ui,u−i)=maxu′ir1i(x,u′i,u−i).
|
(18)
|
We analyze the equilibria of G1,ϵ. Note that in practice the shared throughput cannot be arbitrary; it has to be feasible.
The set of actions can be restricted to
|
Ui={ui | uii=0, uij≥0, ∑juij≤C},
|
where ui=(ui,1,…,ui,i−1,0,ui,i+1,…,ui,n), and C>0 is large enough. For example, C can be taken as the maximum system throughput ∑jThpj,0. This way, the set of sharing actions Ui of user i is non-empty, convex and compact. Assuming that the functions ˆri are strictly concave, non-decreasing and continuous, one obtains that the game G1,ϵ has at least one equilibrium (in pure strategies).
As highlighted above, the set of actions can be made convex and compact. Since ˆri are continuous and strictly convex, it turns out that, each payoff function ri is jointly continuous and is concave in the individual variable ui (which is a vector) when fixing the other variables. We can apply the well-known fixed-point results which give the existence of constrained Nash equilibria. As we know that G1,ϵ has at least one equilibrium, the next step is to characterize them.
If the matrix u is an equilibrium of G1,ϵ then the following implications hold:
|
uij>0⟹ˆr′i(Thpi,0+)=ϵijˆr′j(Thpj,0+).
|
(19)
|
The equilibria may not be unique depending on the network topology. This is easily proved and it is due to the fact that one may have multiple ways to redistribute depending on the network structure and several redistributions can lead to the same sum Thpi,0+∑juji−∑juij. Even if the game has a set of equilibria, the equilibrium throughput and the equilibrium payoff turn out to be uniquely determined. The set of equilibria has a special structure as it is non-empty, convex and compact. The ex-post equilibrium throughput increases with the ex-ante throughput and stochastically dominates the initial distribution of throughput of the entire network. For ˆri=−1θe−θThpi, θ>0 let ϵij=ϵ where ϵ>0. Then, the fairness is improved in the network as ϵ increases. The topology of the network matters. The difference between the highest throughput and the lowest throughput in the network is given by the geodesic distance (strength) of the multi-hop connection.
4. Time Delayed States and Payoffs
This section presents MFTGs with time-delayed state dynamics. Delayed dynamical systems and delayed payoffs appear in many applications. They are characteristic of past-dependence, i.e., their behavior at time t not only depends on the situation at t, but also on their past history and or time delayed state. Some of such situations can be described with controlled stochastic differential delay equations. Networked systems suffer from intermittent, delayed, and asynchronous communications and sensing. To accommodate such systems, time delays need to be introduced.
Applications include
• Consensus and collective motion of Cucker-Smale [163] type with delayed information states
|
dxi=vidtdvi=∫(ˉx,ˉv)a(‖ˉx−xi‖2)(ˉv−vi)ρ(t−τi,dˉxdˉv) dt+c(∫ˉvˉvρ(t−τi,X,dˉv)) dt+uidt+σdWi,
|
where ρ(t,dxdv) is the distribution of states at time t.
• Delayed information processing, where the difference of the states ˉx−xi influences the dynamics after some time delay τi. Examples include Kuramoto-based oscillators [156]
|
dxi=[wi+∫ρ(t−τi,dˉx)sin(ˉx−xi(t−τi))+ui]dt+σdWi,
|
used to describe synchronization.
• Delayed information transmission, where agent i compares its state to the information coming from its neighbor j after some time delay τi. Information transmission delays arise naturally in many dynamical processes on networks.
|
dxi=[wi+∫ρ(t−τi,dˉx)sin(ˉx−xi(t))+ui]dt+σdWi.
|
Delayed information transmission has direct applications in opinion dynamics and opinion formation on social graph:
|
dxi=[∫B(xi,ϵi)ρ(t−τi,dˉx)−xi+ui]dt+σdWi,
|
• The Air Conditioning control towards a comfort temperature is influenced by integrated-state which represents the trend.
• Transmission and propagation delay affect the performance of both wireline and wireless networks both delayed information processing and delayed information transmission occur.
• In computer network security, the proportion of infected nodes at time t is a function of the delayed state, the topological delay, and the proportion of susceptible individuals and some time delay for the contamination period.
• In energy markets, there is an observed phenomenon for the dynamics of the price, which comes with a delayed effect.
4.1. Time-delayed mean-field game
We consider a mean-field game where agents interact within the time frame T. The best-response of a generic agent is
|
{supu∈UE[G(u,m1,m2)], subject to dx=b(t,x,y,z,u,m1,m2,ω)dt+σ(t,x,y,z,u,m1,m2,ω)dW+∫Θ γ(t,x,y,z,u,m1,m2,θ,ω)˜N(dt,dθ),x(t)=x0(t), t∈[−τ,0],
|
(20)
|
where τk>0 represents a time delay, x=x(t) is the state at time t of a generic agent,
y=(x(t−τk))1≤k≤D, is a D−dimensional delayed state vector,
z(t)=(∫tt−τλ(ds)ϕl(t,s)x(s))l≤I is the integral state vector of the recent past state over [t−τ,t]. This represents the trend of the state trajectory. The process ϕl(t,s) is an Fs−adapted locally bounded process. λ is a positive and σ−finite measure. m1 the average states of all the agents, m2 the average control actions of all the agents, x0 is a initial deterministic function of state. W(t)=W(t,ω) be a standard Brownian motion on T=[0,T] defined on a given filtered probability space (Ω,F,P,{Ft}t∈T).
Payoffs: G(u,m1,m2)=g1(T,x(T),m1(T),ω)+∫t∈Tg0(t,x,y,z,u,m1,m2,ω) dt, where the instantaneous payoff function is g0: T×X3×U×X×U×Ω→R, the terminal payoff function is g1: X2×Ω→R.
State dynamics: The drift coefficient function is b: T×X3×U×X×U×Ω→R, the diffusion coefficient function is σ: T×X3×U×X×U×Ω→R.
Jump process: Let N be a Poisson random measure with Lévy measure μ(dθ), independent of B and the measure μ is a σ−finite measure over Θ.
˜N(dt,dθ)=N(dt,dθ)−μ(dθ)dt. The function γ: T×X3×U×X×U×Θ×Ω→ R. The filtration Ft is the one generated by the union of events from W or N up time t.
The goal is to find or to characterize a best response strategy to mean-field (m1,m2):
u∗∈argmaxu∈UG(u,m1,m2).
Hypothesis H1: The functions b,σ,g are continuously differentiable with the respect to (x,m). Moreover, b,σ,g and all their first derivatives with the respect to (x,y,z,m) are continuous in (x,m,u) and bounded.
We explain below why the existing solution approaches cannot be used to solve (20). First, the presence of y,z lead to a delayed integro-McKean-Vlasov and the stochastic maximum principle developed in [33,34,36,37,171,174] does not apply. The dynamic programming principle for Markovian mean-field control cannot be directly used here because the state dynamics is non-Markovian due to the past and time delayed states. Hence, a novel solution approach or an extension is needed in order to solve (20). A chaos expansion methodology can be developed as in [160] using generalized polynomial of Wick and Poisson jump process. The idea is to develop a finite-dimensional optimality equation for (20). In this respect, a stochastic maximum principle could be a good candidate solution approach. Under H1, for each control u∈U, m1 and m2 the state dynamics admits a unique solution, x(t):=xu(t). The non-optimized Hamiltonian is H(t,x,y,z,u,m1,m2,p,q,ˉr,ω):T×X3×U×X×U×R2×J×Ω→R where ˉr(.)∈J and J is the set of functions on Θ such that ∫Θγˉr(t,θ)μ(t,dθ) is finite. The Hamiltonian is H=g0+bp+σq+∫Θγˉr(t,θ)μ(dθ). The first-order adjoint process (p,q,ˉr) is time-advanced and determined by
|
dp=E[−Hx1t≤T−D∑k=1Hyk(t+τk)1t≤T−τk | Ft]dt−I∑l=1E[λ(dt)∫t+τtϕl(t,s)Hz1s∈[0,T]ds | Ft]+qdW(t)+∫ˉr(t,dθ)˜N(dt,dθ),
|
(21)
|
|
p(T)=g1,x(x(T),m1(T)).
|
(22)
|
We now discuss the existence and uniqueness of the first-order adjoint equation.
Proposition 7. Assume that the coefficients are L2, the first order adjoint (22) has a unique solution such that
|
E[∫T0p2+q2+∫Θˉr2(t,θ)μ(dθ) dt]<+∞
|
Moreover, the solution (p,q,ˉr) can be found backwardly as follows:
• Within the time frame (T−τ,T), dp=E[−Hx | Ft]dt+qdW(t)+∫Θr(t,dθ)˜N(dt,dθ) with p(T).
• We fix p(T−τ) from the previous step and solve (21) on interval (T−2τ,T−τ).
• We inductively construct a procedure to compute p(t) on t∈[T−kτ,T−(k−1)τ], k≤Tτ ending with p(T−(k−1)τ).
Note that, if t∈[T−kτ,T−(k−1)τ] then t+τ∈[T−(k−1)τ,T−(k−2)τ] and hence, (p(t+τ),q(t+τ),ˉr(t+τ,θ)) is known from the previous step. However, p(t+τ) may not be Ft−adapted. Therefore a conditional expectation with the respect to the filtration Ft is used.
If U is a convex domain, we know that the second-order adjoint processes of Peng's type are not required, and if (x∗,u∗) is a best response to m1,m2 then there is a triplet of processes (p,q,ˉr), that satisfy the first order adjoint equation such that
|
H(t,x∗,y∗,z∗,u∗,m1,m2,p,q,ˉr)−H(t,x∗,y∗,z∗,u,m1,m2,p,q,ˉr)≥0,
|
(23)
|
for all u∈U, almost every t and P−almost surely (a.s.). A necessary condition for (interior) best response strategy is therefore E[Hu | Ft]=0 whenever Hu makes sense. A sufficient condition for optimality can be obtained, for example, in the concave case: g1,H are concave in (x,y,z,u) for each t almost surely.
4.2. Time delays effect in the Prosumers' Integration to Power Networks
Let c1(t),c2(t) and c3(t,z) be given bounded adapted processes, with c1 assumed to be deterministic and ∫c23ν(dz)<+∞. Consider the energy dynamic generated by a prosumer as
|
dei=(c1(t)ei(t−τ)−ui)dt+c2(t)ei(t−τ)dW(t)+ei(t−τ)∫c3(t,θ)˜N(dt,dθ),
|
ei(t)=ei0(t)1[−τ,0](t) where ei0 is deterministic and bounded function that is given. The energy ui is consumed by i. Prosumer i has a (random) satisfaction function s(t,ui,ω) which is σ(Wt′,N(t′), t′≤t)−adapted for each consumption strategy ui≥0, the random function s is assumed to be continuously differentiable and increasing with the respect to ui and its derivative sui(t,ui,ω) is decreasing in ui. The function sui(t,ui,ω) vanishes as the consumption ui grows without bound. Therefore, the maximum value of sui(t,ui,ω) is achieved when ui=0 and the maximum value is ˉm(t,ω):=sui(t,0,ω). The infinimum value of sui(t,ui,ω) is 0. It follows that ui↦sui(t,ui,ω) is a one-to-one mapping from R+ to (0,ˉm(t,ω)]. In particular, the function br: λ↦(sui(t,.,ω))−1[λ]1(0,ˉm(t,ω)](λ) is well-defined and is a measurable function. Prosumer i aims to maximize her satisfaction functional together with her profit E[g(ei(T))+∫T0s(t,ui,ω)+price(m)qi dt]
The Hamiltonian is
H(t,x,y,z,ui,m1,m2,p,q,ˉr)=s+(c1y−ui)p+c2yq+y∫Θc3ˉr(t,θ)μ(dθ).
|
dp=E[−Hy(t+τ)1t≤T−τ | Ft]dt+qdW(t)+∫ˉr(t,dθ)˜N(dt,dθ),p(T)=gx(x(T)),
|
(24)
|
where Hy(t+τ)=c1(t+τ)p(t+τ)+c2(t+τ)q(t+τ)+∫Θc3(t+τ)ˉr(t+τ,θ)μ(dθ).
We solve the solution explicitly with g(x)=c4x, c4≥0.
p(T)=c4≥0. Between time T−τ and T, the stochastic process p(t) must solve dp=qdW(t)+∫ˉr(t,dθ)˜N(dt,dθ) and it should be Ft-measurable. Therefore p(t)=c4 on t∈[T−τ,T]. For t<T−τ, the processes q and ˉr are zero and p is entirely deterministic and solves
Thus, for t∈[T−2τ,T−τ],
|
p(t)=p(T−τ)+∫T−τtc1(t′+τ)p(t′+τ) dt′.
|
This means that p(t)=c4[1+∫Tt+τc1(t″) dt″]. For t∈[T−(k+1)τ,T−kτ], and (k+1)τ≤T, one has p(t)=p(T−kτ)+∫T−(k−1)τt+τc1(t″)p(t″) dt″.
By assumption, sui(t,ui,ω) is decreasing in ui and from the above relationship it is clear that p is decreasing with τ. It follows that, if τ1<τ2,
p[τ1](t)>p[τ2](t). We would like to solve sui(t,ui,ω)=p[τ1](t)>p[τ2](t). By inverting the above equation one gets u∗i[τ1]<u∗i[τ2]. Thus, the optimal strategy u∗i increases if the time delay τ increases.
This proves the following result:
Proposition 8. The time delay decreases the prosumer market price. The optimal strategy u∗i increases as the time delay τ increases.
Numerical methods for delayed stochastic differential equations of mean-field type is not without challenge. Here we implement the Milstein scheme using MATLAB. We choose the following parameters γ=0,c1=c2=c3=1 and set the satisfaction function as
where μ>0 and ˉm2 is the average of all other agents' control actions. A typical shape of the satisfaction function is given in Figure 22. The optimal control is
|
u∗(t)=−logp(t)1+μˉm2(t)1(0,1](p(t)).
|
|
u∗(t)={−logc41+μˉm2(t) on t∈(T−τ,T],−logc4(1+T−t−τ)1+μˉm2(t) on t∈(T−2τ,T−τ],−11+μˉm2(t)log[c4(1+τ)+c4(1+T−τ)(T−t−2τ)−c42(T−t−2τ)(T+t)]on t∈(T−3τ,T−2τ].
|
The mean-field equilibrium solves the fixed-point equation E[u∗(t)]=ˉm2(t). Putting together one obtains
|
ˉm2(t)=−logp(t)1+μˉm2(t),
|
i.e., the root (in ˉm2) of ˉm2↦ˉm2(1+μˉm2)+logp(t). The quadratic polynomial has two roots: one positive and the other negative value. Since the consumption is nonnegative, the mean of the mean-field control action is hence given by
|
ˉm2(t)=−1+√1+4μlog[1p(t)]2μ.
|
Notice that the effect of the time delay τ in this specific example was through the adjoint process p which also enters into the control action u.
We plot the structure of the optimal strategy for T=1,τ=1/3,τ=2/3. The theoretical result of Proposition 2 is numerically observed in Figure 23. Figure 24 plots sample optimal state trajectories for T=1,τ=1/3 using Milstein scheme.
5. Decentralized Information and Partial Observation
Let FWt be the P-completed natural filtrations generated by W up to t. Set FW:={FWt, 0≤t≤T} and F:={Ft, 0≤t≤T}, where Ft=FWt∨σ(x0). An admissible control ui of agent i is an FWi-adapted process with values in a non-empty, closed and bounded subset (not necessarily convex) Ui of Rd and satisfies E[∫T0|ui(t)|2dt]<∞. Those are nonanticipative measurable functionals of the Brownian motions. Since each agent has a different information structure (decentralized information), let Ui be the set of admissible strategies of i (with decentralized partial information) such that Gi,t⊂Fi,t, i.e.,
Ui:={ui∈L2Gi,T([0,T],Rd), ui(t,.)∈Ui P−a.s}. Given a strategy ui∈Ui, and a (population) mean-field term m generated by other agents we consider the signal-observation xui,mi which satisfies the following stochastic differential equation of mean-field type to which we associate a best-response to mean-field [132,158,159]:
|
{ supui∈UiR(ui,m) subject to dxi(t)=b(t,xi(t),Exi(t),ui(t),m(t))dt+σ(t,xi(t),Exi(t),ui(t),m(t))dWi,t,xi(0)∼L(Xi,0),m(t)=population mean-field ,
|
(25)
|
|
b(t,x,y,u,m):[0,T]×Rd×Rd×Ui×Λ⟶R,
|
(26)
|
|
σ(t,xi,yi,ui,m):[0,T]×R×R×Ui×Λ⟶R.
|
(27)
|
|
R(ui,m)=g(xi(T),Exi(T),m(T))+∫T0r(t,xi(t),Exi(t),ui(t),m(t))dt,
|
g is the terminal payoff and r is the running payoff. Given m, any u∗i∈Ui which satisfies R(u∗i(⋅),m)=supui(⋅)∈UiR(ui,m) is called a pure best-response strategy to m, by agent i. In addition to the other coefficient we assume that γ satisfies H1. Under H1, the state dynamics admits a unique strong solution ([161], Proposition 1.2.) Given m, we apply the SMP for risk-neutral mean-field type control from ([162], Theorem 2.1) to the state dynamics x to derive the first order adjoint equation. Under the assumption H1, there exists a unique F-adapted pair of processes (p,q), which solves the Backward SDE:
|
p(t)=gx(T)+E[gy(T)]+∫Tt{Hx(s)+E[Hy(s)]}ds−∫Ttq(s)dW(s),
|
(28)
|
such that E[supt∈[0,T] |p(t)|2+∫T0|q(t)|2dt]<+∞. However, these processes (p,q) may not be adapted to decentralized information Gi,t. This is why their conditioning will appear in the maximum principle below. Again by ([162], Theorem 2.1), there exists a unique F-adapted pair of processes (P,Q), which solves the second order adjoint equation
|
+∫Tt{2bx(s)P(s)+σ2xP(s)+2σx(s)Q(s)+Hxx(s)}ds−∫TtQ(s)dW(s),
|
(30)
|
such that E[supt∈[0,T] |P(t)|2+∫T0|Q(t)|2dt]<+∞. Note that in the multi-dimensional setting, the term 2bx(s)P(s)+σ2xP(s)+2σx(s)Q(s) becomes b′xP+Pbx+σ′xPσx+σ′xQ+Qσx.
Proposition 9. Let H1 holds and m be a given population mean-field profile. If (x∗i,u∗i) is a best-response then, there are two pairs of F-adapted processes (p,q) and (P,Q) that satisfy (28) and (29) respectively, such that
|
i∈N: [δH(t)+12δσ(t)′P(t)δσ(t) | Gi,t]≤0,
|
(31)
|
for all ui∈Ui, almost every t and P−almost surely, where,
|
δH(t):=H(t,x∗(t),ui,m(t),p(t),q(t))−H(t,x∗(t),u∗i(t),m(t),p(t),q(t)),
|
(32)
|
and Hk(t):=bk(t)p+σk(t)q+rk(t), for k∈{x,y,xx}.
6. Limitations and Challenges
The examples above show that the continuum of agents assumption is rarely observed in engineering practice. The agents are not necessarily symmetric and a single agent may have a non-negligible effect on the mean field terms as illustrated in the HVAC application. Without having a broad set of facts on which to theorize, there is a certain danger of mean-field game models that are mathematically elegant, yet have little connection to actual behavior observed in engineering practice. At present, our empirical knowledge is inadequate to the main assumptions of the classical mean-field game theory. This is why a relaxed version is needed in order to better capture wide ranges of behaviors and constraints observed in engineering systems. MFTG relaxations include symmetry breaking, mixture between atomic and nonatomic agents, non-negligible effect on individual localized mean-field terms, and arbitrary number of decision-makers. In addition, behavioral and psychological factors should be incorporated for learning and information processes used by people-centric engineering systems. MFTG is still under development and is far from being a well-established tool for engineered systems. Until now, MFTG was not focused on behavioral and cognitively-plausible models of choices in humans, robots, machines, mobile devices and software-defined strategic interactions. Psychological and behavioral mean-field type game theories seem to explain behaviors that are better captured in experiments or in practice than classical game-theoretic equilibrium analysis. It allows to consider psychological aspects of the agent in addition to the traditional "material" payoff modelling. The value depends upon choice consequences, mean-field states, mean-field actions and on beliefs about what will happen. The psychological MFTG framework can link cognition and emotion. It expresses emotions, guilt, empathy, altruism, spitefulness (maliciousness) of the agents. It also include belief-dependent and other-regarding preferences in the motivations. It needs to be investigated how much the psychology of the people matters in their behaviors in engineering MFTGs. The answer to this question is particularly crucial when analyzing the quality-of-experience of the users in terms of MOS (mean opinion score) values. A preliminary result from a recent experiment conducted in [111,168] with 47 people carrying mobile devices with WiFi direct and D2D technology shows that the participation in forwarding the data of the users is correlated with their level of empathy towards their neighbors. This suggests the use of not only material payoffs but also non-material payoffs in order to better capture users behaviors. Another aspect of MFTGs is the complexity of the analysis (both equilibrium and non-equilibrium) when multiple agents (and multiple mean-field terms) are involved in the interaction [71,132,160,169,170].
7. Conclusion and Future Work
The article presented basic applications of mean-field-type game theory in engineering, covering key aspects such as de-congestion in intelligent transportation networks, control of virus spread over network, multi-level building evacuation, next generation wireless networks, incentive-based demand satisfaction in smart energy systems, synchronization and coordination of nodes, mobile crowdsourcing and cloud resource management. It appears from the wide ranges of applications and coverage that mean-field-type game theory is a promising tool for engineering problems. However, the framework is still under development and needs to be improved to capture realistic behavior observed in practice. Possible extensions of the work described in this article include the study of mean-field-type games for risk engineering, and an integrated mean-field-type game framework for smarter cities ranging from transportation to water distribution with ICT (Information Communication Technology), big data and human-in-the-loop among several other interesting directions.
Acknowledgments
This research work is supported by U.S. Air Force Office of Scientific Research
under grant number FA9550-17-1-0259. The authors would like to thank the Editor and the anonymous reviewers for interesting and constructive comments on the manuscript. The authors would like to thank the seminar participants at KTH Sweden for many extremely fruitful discussions and for their inputs on the first draft of the manuscript.
Conflict of Interest
The authors declare no conflict of interest in this paper.









 DownLoad:
DownLoad: