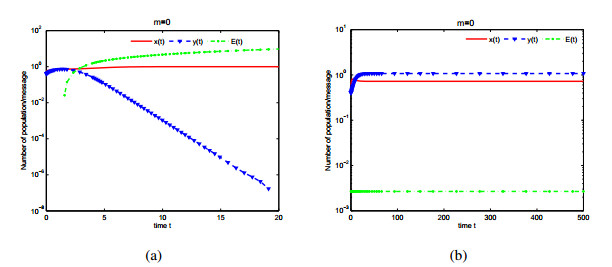
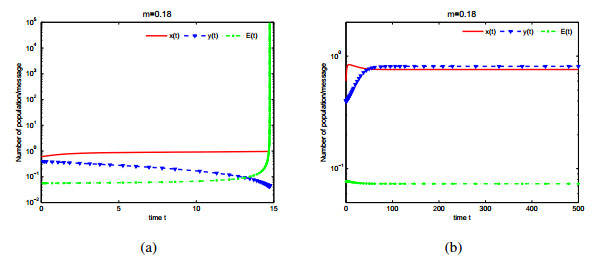
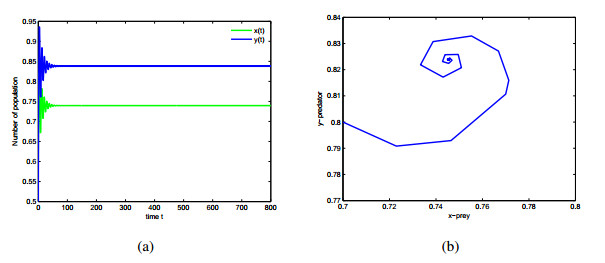
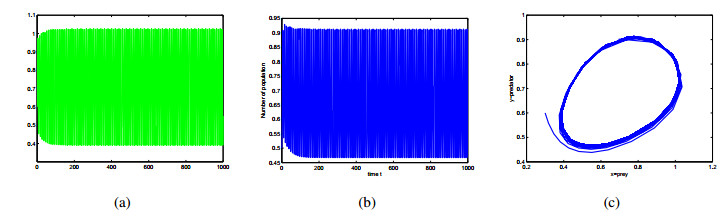
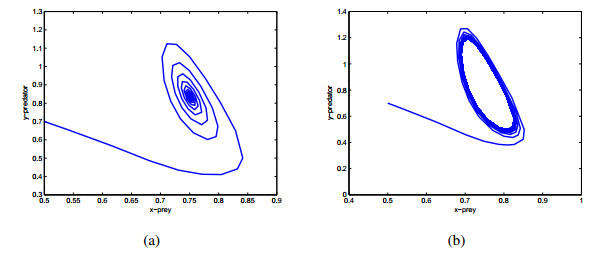
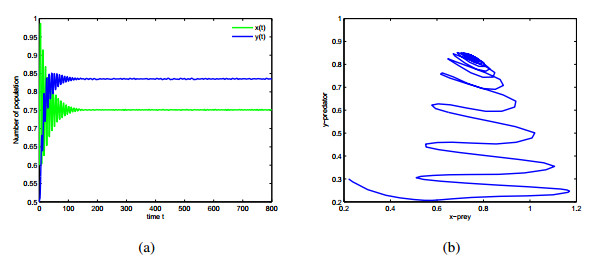
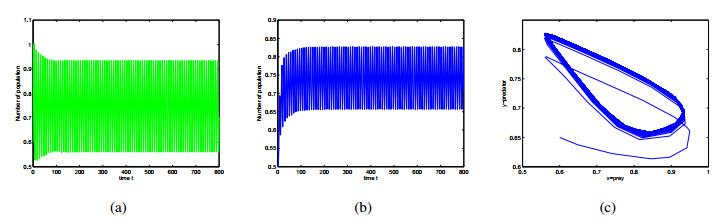
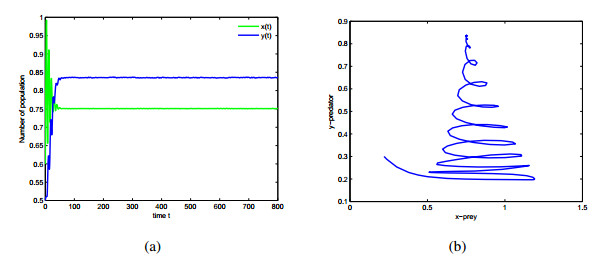
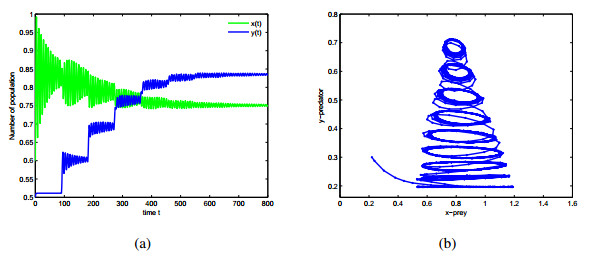
In this paper, a differential algebraic predator-prey model including two delays, Beddington-DeAngelis functional response and nonlinear predator harvesting is proposed. Without considering time delay, the existence of singularity induced bifurcation is analyzed by regarding economic interest as bifurcation parameter. In order to remove singularity induced bifurcation and stabilize the proposed system, state feedback controllers are designed in the case of zero and positive economic interest respectively. By the corresponding characteristic transcendental equation, the local stability of interior equilibrium and existence of Hopf bifurcation are discussed in the different case of two delays. By using normal form theory and center manifold theorem, properties of Hopf bifurcation are investigated. Numerical simulations are given to demonstrate our theoretical results.
1.
Introduction
Bone tumors, especially the benign tumors and tumor-like lesions were commonly located at the proximal femur, especially at the femoral head and neck [1]. The femoral head and neck endured the compression stress, shear force and torsion force of the hip, this special anatomic and biomechanical characteristic was very important for the overall mechanical transmission [2,3,4,5,6,7]. The normal bone, especially the trabecular bone might be destructed in the case of a tumor in the femoral head and neck, then pathological fracture might occur after a trauma, or gradual fatigue failures might occur over a long time. Besides, the blood supply to the femoral head and neck was fragile [8,9], and necrosis of the femoral head might occur after the invasion of the tumor or the operation of the surgery. The anterior approach, lateral approach, and posterior approach were the three main pathways for tumor of the femoral head and neck. Different surgical approach had different drilling site in the bone, and different drilling site meant different exposure of operative field and surgical operation [10,11,12,13,14,15], and different drilling site might influence the mechanical stability of the proximal femur differently.
With the application of arthroscopic technique, the tumor cavity could be curetted directly under the arthroscopy by tunneling through the proximal cortex of the femur to the femoral neck medullary canal without opening the joint capsule, therefore the tumor could be curetted completely, and the recurrence rate would be reduced greatly [16,17,18]. Therefore, surgeons focused on which site for drilling would influence the biomechanics of the proximal femur minimally, and the biomechanical stability of which site after reconstruction would be maximum. In our review of the literature, there was few reports to compare the biomechanical influence of drilling in the anterior femoral neck to that in the lateral proximal femur, and there were few reports to compare the biomechanical influence on the proximal femur of the two different drilling sites after the internal fixation. To evaluate these influences from a clinical treatment view, biomechanical experiments of the specimen and finite element studies were done.
2.
Materials and methods
2.1. Specimen preparation
Twelve paired formalin-fixed human cadaveric femora showing no deformities were obtained from Department of Human anatomy and histoembryology, Fudan University (average age: 79.9; range: 64–93 yrs.), leaving the bone devoid of any soft tissue.
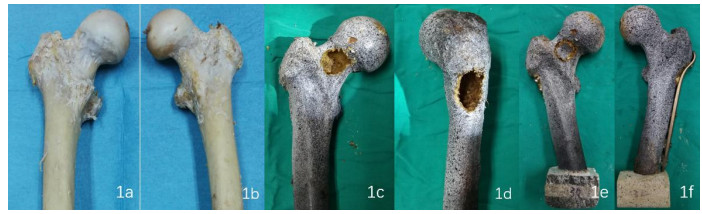
The femurs were grouped randomly into 2 groups of 6 pairs each, which were group 1 and group 2, and one of each pair of femora was grouped randomly to drill the hole in the anterior femoral neck (group 1 ADH and group 2 ADH), and the contralateral femur was assigned to drill the hole in the lateral of the proximal femur (group 1 LDH and group 2 LDH). The group 1 specimens had three stages during the experiment process, which were stage 1: Intact proximal femur (Figure 1a, b), stage 2: Drilled hole and curettage (Figure 1c, d), stage 3: Bone-grafting and fixation, with lag screws in anterior group or proximal femoral locking plate in lateral group (Figure 1e, f). While the group 2 specimens had two stages during the experiment process, which were stage 1: Intact proximal femur, stage 2: Drilled hole and curettage.
All the holes were oval-shaped, and we controlled the dimensions of these holes according to anatomical parameters of each femur, as to these holes in the anterior femoral neck, the length and width of the neck were designed as the two diameters of the oval (Figure 1c), then the bone was drilled according the elliptical column until the posterior cortex of the femoral neck to form an elliptical cylindrical bone defect. While to these holes in the lateral of the proximal femur, these holes were drilled on the lateral cortical bones intersected with the axis of the neck, and the thickness of this area and the width of the neck were designed as the two diameters of the oval (Figure 1d). Then the bone was drilled according the elliptical column until the junction of femoral head and neck to form an elliptical cylindrical bone defect too. Different femur had different hole.
The specimens were kept moist with 0.9% NaCl saline solution during the whole preparation and testing process.
All of the specimens of different stages were scanned with CT (Philips Brilliance 64 slice, Netherlands, slice thickness 0.65 mm) and X-ray from anterior-posterior and lateral.
2.2. Mechanical testing
All femora were embedded distally in polymethylmethacrylate (PMMA) in a Materials Testing Machine (Instron e10000; USA) to mimic the weight of the femur during one-legged stance (angle between loading axis and the proximal shaft 15°) [19,20] (Figure 2). As to the axial loading testing, the load was applied to the most cranial portion of the femoral head in the plane spanned by the neck axis and the proximal femur axis, and 10 mm of the femoral head was embedded in a PMMA cup, simulating the acetabulum, for load distribution according reports [19,21]. As to the torsional stiffness testing, the femoral head was fixed with a structure of three claws in the materials testing machine to allow rotation orthogonally to the loading axis through the femoral head (Figure 2).
Finally, a vertical load was applied to femora of group 1 on stage 3 and femora of group 2 on stage 2 to create axial compression until complete catastrophic failure of these femora occurred. Peak force was defined as axial strength. The locations of failure were observed and analyzed to evaluate the biomechanical stability of the proximal femur of different models.
In order to simulate natural hip articulation, the femoral head was not stabilized but was free to rotate within the PMMA cup during the axial loading. This mode of loading was actually a combination of axial compression and bending, which has been reported [19], since the load was applied off the axis of the femur shaft.
For torsion testing, every card slot of the three was screwed tightly onto the surface of the femoral head averagely for stabilization. The vertical axis of twist was through the femoral head, which was different from some reports which was through the long axis of the femoral shaft [22,23,24,25]. Figure 2 depicted the experimental setup for torsional loading, the set-up in axial loading was similar, except that a PMMA cup was used at the femoral head instead of card slots.
2.3. Test parameters
In order to keep the femora remained in the linear–elastic regime before the ultimate axial loading failure testing, the axial stiffness was determined by vertically applying a vertical displacement of 1 mm maximum using displacement control 1.5 mm/min during the axial loading testing. The machine was programmed to cease loading once 1 mm of displacement was reached, i.e., a maximum displacement criterion. While during the ultimate loading failure testing, the displacement control 1.5 mm/min was used until the loading failed.
Similarly, in order to keep the bones remained in the linear–elastic regime during torsion testing, torsional stiffness was determined by applying a maximum 7.5 Nm torque axial preload = 0.1 kN, pretorque = 0 Nm at the femoral head using angular displacement control 0.25 deg/ s in rotation. The machine was programmed to cease torque application using this maximum torque criterion.
To prevent permanent deformation or microcracks which might occur in a given loading, we monitored the load-displacement curve and torque-angle curve during the mechanical testing, if the curve became nonlinear suddenly, it meant the bone was no longer in a linear elastic regime, and if it happened before the axial loading failure testing, these data of this femur would be abandoned.
2.4. Finite element modeling
The serial CT images of the femur were acquired from one of the twelve paired formalin-fixed human cadaveric femora on stage 1. The slice thickness of the CT images was 0.65 mm in a 512 × 512 matrix. The DICOM data were imported into Mimics 17.0 software (Materialise, Belgium) to reconstruct the geometry of the femur. The femur bone was segmented into 2 partitions, the cortical layer and cancellous core, using a threshold of 600 Hounsfield units [26]. The material of the cortical and cancellous bone was assumed homogeneous and isotropic.
Two types of fixation/implants were modeled and simulated: Proximal lateral femur Locking Plate with 4.5 mm locking screw (PFLP) and 6.5 mm partially threaded cancellous screws. Three dimensional models of plate and screws were drawn according to the manufacturers' specifications using software UG NX 8.5 (SIEMENS Corp., Germany). The locking plate was modeled from a 4.5 mm plate (Kanghui, China) and the locking screws were modeled as 4.5 mm diameter solid cylinders. The partially threaded cancellous screws were modeled as 6.5 mm diameter.
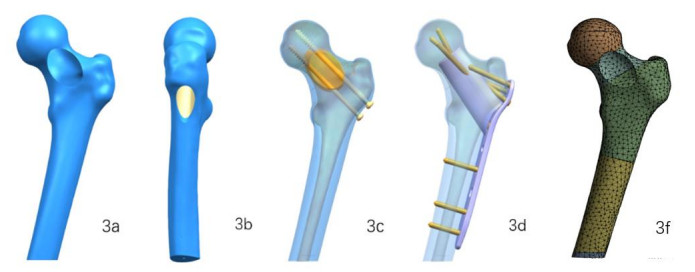
Two different oval shaped models were drawn to intersect with the intact femur FE model according to the methods of the specimen preparation, thus FE models of ADH and LDH were simulated (Figure 3a, b). Similarly, a model of ADH with bone-grafting and fixation (ADBF) and a model of LDH with bone-grafting and fixation (LDBF) were simulated by Boolean operation with PFLP or three 6.5 mm partially threaded cancellous screws (Figure 3c, d).
These models were processed by Geomagic Studio 2014 (3D System Inc., Rock Hill, SC, USA) and then, were input to the FE software ANSYS Workbench 15 (ANSYS Corp., USA), thus these models were assembled and meshed (Figure 3f). Due to the ease and robustness of performing automatic meshing, local and adaptive refinement with tetrahedral elements, linear tetrahedral elements were often used in the literature [27,28]. The 10-node tetrahedral element was a high-order form of a 4-node tetrahedral element, and its element boundary was a curved surface, which could mesh the structural irregular model well, while 8-node hexahedron element was often used to mesh the structural regular model [29]. We used the 10-node tetrahedral element to hand with multiple femoral interfaces in FE analysis [30]. The numbers of nodes and elements of femora, bone grafts and metallic implants were shown in Table 1. A mesh convergence test was conducted so that the deviation was less than 2%.
For the bone tissues, the constitutive elastic/plastic model was used [31]. Compared with a high Young's modulus of the fresh-frozen specimens [32], the formalin-fixed bones were reported to show a significantly lower Young's modulus compared to the fresh-frozen specimens [33], so we assigned a lower Young's modulus to the cortical bone of our FE model, and the material parameters of cancellous bone of the femur and implants were adopted from previous published reports [20,34,35,36,37,38,39] (Table 2). As to the bone grafts, we assigned a mechanical property of cancellous bone to them to simulate the mechanical testing and clinical operation. All contact pairs including bone grafts to femurs, metallic implants to femurs, metallic implants to bone grafts, were assigned with 0.3 coefficient of friction [40,41], except that the locking plate-locking screws interfaces were tied.
2.5. Boundary and loading conditions
For both torsional and axial loading, the distal bone was rigidly fixed i.e., zero displacement boundary condition to a distance of 25 cm below the proximal end. For the torsional loading scenario, coupling contact between the loading spot above the femur head and the femur head was assumed, and the spot was constrained in all degrees of freedom except the rotation. We marked a dot on the femoral head, and the angle of internal rotation of this dot was calculated automatically by ANSYS after the femoral head was rotated internally, and this angle was considered to the angle of internal rotation proximal femur. Then a torque of 7.5 Nm, perpendicular to the top surface of the spot was then applied, and the torsional stiffness was calculated by dividing the applied torque by the angular displacement of the loading spot.
For the axial loading scenario, frictionless sliding contact between the loading spot and the femur head was assumed, and the spot was prevented from moving in all degrees of freedom except vertical displacement. We assumed the quality of an adult was 60 kg, according to the report published [42], a vertical load of 1.56 kN (2.6 times of the weight) was applied to the spot, and the axial stiffness was calculated by dividing the applied load by the vertical displacement of the spot.
2.6. Normalization of data
To facilitate comparison between specimens of different length, the measured and FE predicted axial (kN/mm) and torsional stiffnesses (Nm/deg) were converted to effective axial (kN) and torsional rigidities (Nm2/deg), as has been done by previous investigators [20,43,44]. Simply stated, rigidity was a product of a stiffness timed femur length.
2.7. Statistical analysis
The data were analyzed by SAS software version 9.4 (SAS Institute, Cary, NC). Continuous variables with normal distribution were presented as mean (standard deviation [SD]); non-normal variables were reported as median (interquartile range [IQR]). Means of 2 continuous normally distributed variables were compared by independent samples Student's t test. Wilcoxon signed-rank test were used, respectively, to compare means of 2 and 3 or more groups of variables not normally distributed. P < 0.05 was considered statistically significant.
3.
Results
3.1. Cadaveric stiffness and effective rigidity
The data of measured stiffnesses and rigidities of the cadaveric specimens were shown in Tables 3-5.
Group 1 cadaveric femurs on stage 1 were stiffer (P = 0.0005) in axial compression than group 1 cadaveric femurs on stage 2, with P = 0.0313 in group 1 ADH and P = 0.0313 in group 1 LDH respectively, and the degree of decline made no statistical significance (P = 0.9715). And group 1 cadaveric femurs on stage 3 were stiffer (P = 0.0269) than group 1 cadaveric femurs on stage 2 in axial compression, with P = 0.0313 in group1 LDH, but P = 0.1294 in group 1 ADH. There was no statistical significance between the axial stiffnesses of group 1 femurs on stage 1 and stage 3 (P = 0.1514), with P = 0.6875 in group 1 ADH, but group 1 LDH cadaveric femurs on stage 3 were stiffer (P = 0.0313) in axial compression than group 1 cadaveric femurs on stage 1.
Similarly, in torsion the group 1 cadaveric femurs on stage 1 were stiffer (P = 0.0005) than the cadaver femurs on stage 2, with P = 0.03 in group 1 ADH and P = 0.03 in group 1 LDH respectively, and the degree of decline made no statistical significance (P = 0.8697). While there was no statistical significance between the group 1 cadaveric femurs on stage 3 and stage 2 (P = 0.1294) in torsion, with P = 0.4375 in group 1 ADH and P = 0.22 in group 1 LDH respectively.
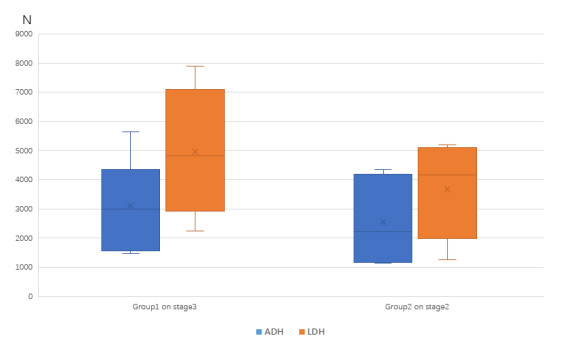
Although the medians of axial strength of group 1 cadaveric femurs, both of group 1 ADH and group 1 LDH, were much bigger than group 2 cadaveric femurs on stage 2, and the medians of axial strength of LDH cadaveric femurs, both of group 1 and group 2, were much bigger than ADH cadaveric femurs, there was no statistical significance between the axial strength of group 1 cadaveric femurs on stage 3 and group 2 on stage 2 (P = 0.2247), with P = 0.5276 in ADH and P = 0.2264 in LDH respectively (Figure 4).
3.2. Failure sites of the axial loading
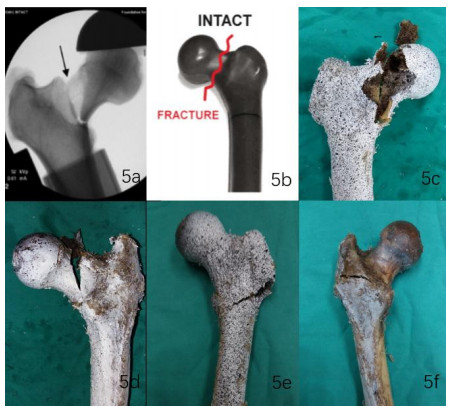
Due to the difficulty to achieve a lot of human cadaveric femora at one time, no femora on stage 1 were axial loaded to failure, so we referred to literatures [32,45], which showed that the fracture lines of intact femora began from the super-lateral region between the femoral head and neck, then went down straightly, and stopped on the lesser trochanter, with the lesser trochanter fractured (Figure 5a, b). And the fracture lines of the axial loading failure of group 2 ADH after drilling hole were similar to the fracture line on stage 1 (Figure 5c, d). While the fracture lines of the axial loading failure of group 2 LDH on stage 2 were on the lateral proximal femur, which went across the lateral cortical window and stopped on the lesser trochanter, with the lesser trochanter fractured too (Figure 5e, f).
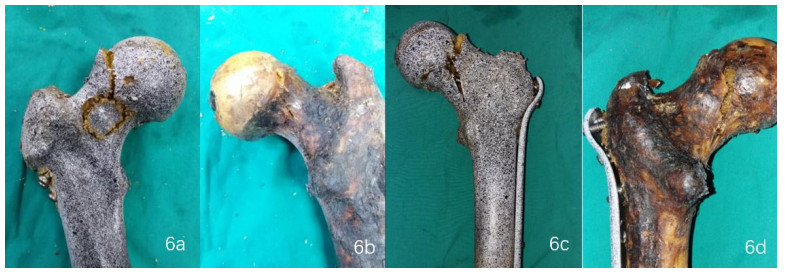
When it came to the group 1 ADH on stage 3 and group 1 LDH on stage 3, the locations of the axial loading failure of were similar, and the fracture lines began from the super-lateral region between the femoral head and neck, then went down straightly, and stopped above the lesser trochanter, with the lesser trochanter not involved (Figure 6). All of fracture lines of the axial loading failure of group 1 ADH on stage 3, group 2 ADH on stage 2 and group 2 LDH on stage 2 went across the cortical window.
3.3. Finite element analysis results
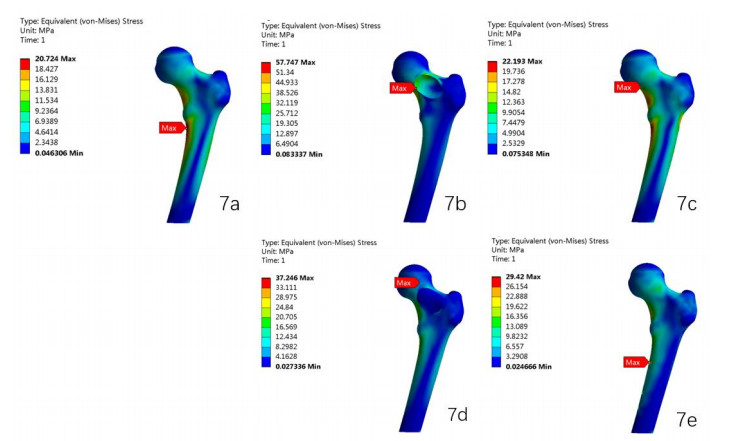
For the axial loading, equivalent (von-Mises) stress nephograms under axial loading were shown in Figure 7, and the results were shown in Table 6. The results showed that the axial stiffness of model of LDH was smaller than that of the intact proximal femur model, and the axial stiffness of model of ADH were smaller than that of model of LDH. Compared to the different drilling models respectively, the axial stiffness of LDBF model increased much more than that of ADBF model, even more stiff than the intact proximal femur model, and this trend was similar to the biomechanical testing of specimens. Only the location of the von-Mises stress in ADBF model was in the super-lateral region between the femoral head and neck, which were consistent with the site of axial loading failure in ADBF model in mechanical testing, none of the locations of the von-Mises stress in the rest of FE models were consistent with the site of axial loading failure in relevant model respectively in mechanical testing, which meant the locations of the von-Mises stress were consistent with the sites of axial loading failure in 20% models in Mechanical testing.
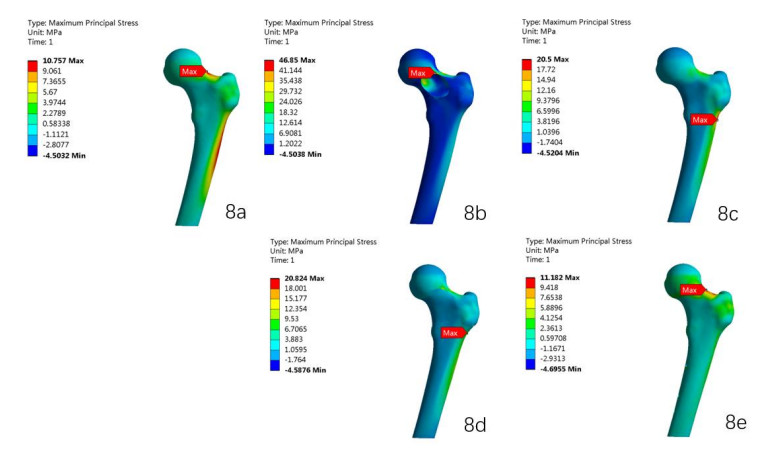
The maximum principal stress nephograms under axial loading were shown in Figure 8, and the locations of the maximum principal stress were consistent with the sites of axial loading failure in 80% models in Mechanical testing. The locations of the maximum principal stress in intact model and ADH model were in the super-lateral region between the femoral head and neck, which were consistent with these sites of axial loading failure in intact and ADH model in mechanical testing. And the location of the maximum principal stress in LDH model was in the lateral window of proximal femur, and it changed to the super-lateral region between the femoral head and neck in LDBF model, which were consistent with these sites of axial loading failure in LDH and LDBF model. While the location of the maximum principal stress in ADBF model was in the lateral window of proximal femur, which was different from these sites of axial loading failure in ADBF model in mechanical testing.
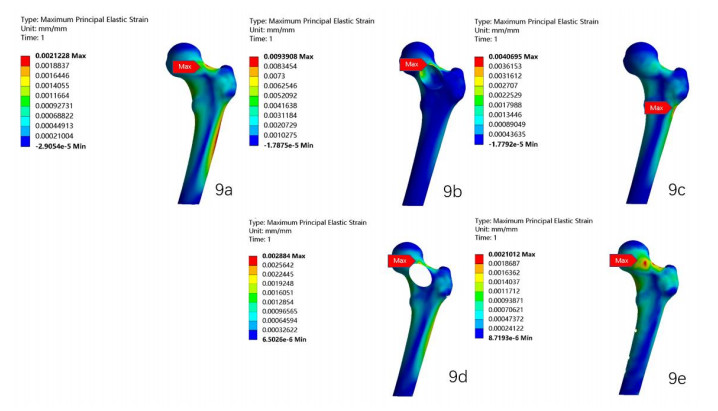
The maximum principal strain nephograms under axial loading were shown in Figure 9. All locations of the maximum principal strain of the five models were consistent with each site of axial loading failure of relevant model, which meant the locations of the maximum principal strain were consistent with the sites of axial loading failure in 100% models in Mechanical testing.
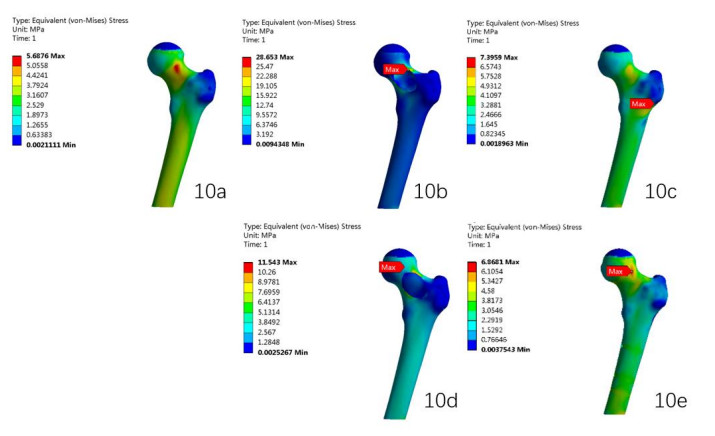
For the torsional loading, equivalent (von-Mises) stress nephograms were shown in Figure 10, and the results were shown in Table 7, which showed that the torsional stiffness of LDH model and ADH model were smaller than that of the intact proximal femur model, which was consistent with biomechanical testing of specimens.
4.
Discussion
4.1. Effects of different drilling sites with curettage
The femur was not only the most common long bone affected by cancerous metastasis, but also very common affected by benign tumors and tumor-like lesions, especially the proximal femur. Femoral tumor defects would affect the biomechanical stability, even fracture pathologically. Research showed that for a diaphyseal defect that destroyed 50% of the cortex, strength reductions of between 60 and 90% could occur pathologic fracture [46]. Another mechanical testing with human cadaver femurs showed that when the size of defected femoral necks reached 55%, the strength would decrease greatly [47]. Prior researches showed that many factors played a role in pathological fractures, besides the biomechanical properties of the bone itself, the size of the lesion [48,49], the shape [50], the type of lesion [51,52], and the defect site [21,45] were closely related too.
Sivasundaram R created circular tumor-like defects of 40 mm diameter proximally in the subtrochanteric region on the Anterior (n = 5), Posterior (n = 5), Medial (n = 5), and Lateral (n = 5) sides of 20 synthetic femurs, and intact femurs (n = 4) served as a control group, to examine the risk of pathological fracture with respect to the anterior, posterior, medial, and lateral surfaces on which a proximal tumor defect was located on the femur. The results showed that the Medial tumor-like defect group resulted in statistically lower stiffness values compared with Intact femurs and had lower strength than Anterior and Posterior groups in axial failure [45].
Similarly, Kaneko TS [53] found that defect site affected hip strength greatly. Lytic defects, modeled as spherical voids, were simulated at various locations within twelve matched pairs of human cadaveric proximal femora neck, and 564 finite element models were created to quantify the effect of location of femoral neck metastases on hip strength under single-limb stance loading, and the effectiveness of a proposed minimally invasive surgical repair technique for restoring hip strength was evaluated too. Defects in the inferomedial aspect of the neck and in the dense trabecular bone near the base of the femoral head had the greatest effect, with hip strengths 23 to 72% and 43 to 64% that of the intact strength, respectively, for 20 mm diameter defects.
All of these researches focused on predicting the risk of pathological fracture to simulated lesions in femoral neck and head, while our research focused on the treatment to simulate drilling and curettage in different sites.
Our mechanical testing results and FE results showed that the simulated operation of drilling for curettage decreased the axial stiffness and torsional stiffness of the intact proximal femur greatly, which suggested that the operation of bone-grafting and fixation were needed both in the model of ADH and LDH. But there was no statistical difference on the degree of the decline between different drilling sites, and there was no statistical difference between the model of ADH and LDH on the axial rigidity too. The axial loading failure testing on the intact femur was not performed because each one femur of each pair was used to simulated the model of ADH and the other femur of each pair was used to simulated the model of LDH.
4.2. Effects of bone-grafting and fixation in different drilling sites
Clinically, although autogenous nonvascularized fibula graft was used for lesions in the proximal femur after curettage and cryosurgery, higher incidence rate of the pathological fractures was reported with autogenous nonvascularized fibula graft compared to internal fixation. Four cases in sixteen presented with pathological fractures was reported with autogenous nonvascularized fibula graft after curettage and cryosurgery [54], while Nakamura T [14] suggested compression hip screw and synthetic bone graft as a safe and effective method for the treatment of the benign bone tumors including femoral neck lesion, all patients were allowed full weight-bearing with 12 weeks after surgery with no pathological fracture. Though endoprosthetic replacement was reported to be used in treatment of the benign femoral neck lesion, it was considered to be more suitable for agammaessive and recurrent lesions and served as an effective measure after internal fixation failure [55].
Although treatment of lesions of the proximal femur with internal fixation was suggested to lessen the risk of additional surgery [56], few basic researches on the stability after treatment on the lesion in the proximal femur were reported. We studied the stability of bone-grafting and fixation after curettage in different drilling sites. Although the simulated operation of bone-grafting and fixation in different drilling models increased the axial stiffness and torsional stiffness in mechanical testing, only in case of implanting bones and fixation for the lateral cortical window increased the axial stiffness greatly and made a statistical difference, even more stiff than the intact proximal femur model. The mechanical testing results suggested that only in case of drilling in the lateral cortex, the proximal femur could be more stable after the treatment of implanting bones and fixation.
FE analysis results showed that the simulated operation of bone-grafting and fixation increased the axial stiffness and torsional stiffness too. Compared with the axial stiffness of LDH model, the axial stiffness of LDBF model increased 362.487 N/mm (1675.618–1313.131 N/mm), which meant the operation of bone-grafting and fixation increased 27.82% of the axial stiffness of LDH model. When it came to the ADBF model, the axial stiffness of ADBF model increased 122.827 N/mm (1326.531–1203.704 N/mm) to the axial stiffness of ADH model, which meant the operation of bone-grafting and fixation increased 10.20% of the axial stiffness of ADH model. The increasing extent of axial stiffness of LDBF model from stage 3 to stage 2 (27.82%) was nearly three times more than that of ADBF model from stage 3 to stage 2 (10.20%). Although the fixation type might play a part, different drilling sites were the main reason, because the axial stiffness of ADBF model was only 1.02% bigger than that of LDH model, while the axial stiffness of LDBF model was 26.32% bigger than that of ADBF model, even 18.90% bigger than that of intact proximal femur model.
4.3. Failure sites of axial loading
The fracture line of axial loading in a single leg standing position of both new fresh-frozen intact proximal femurs [32] and intact third generation composite femurs [45] started from the tensional side of femur, which started from the super-lateral region between the femoral head and neck, then went down straightly, and stopped above the lesser trochanter, the lesser trochanter was not involved. While the fracture line of axial loading in both group 2 LDH and ADH on stage 2 went across the opening cortical window and stopped on the lesser trochanter, with the lesser trochanter fractured, which suggested that the operation of drilling decreased the axial stability of the femur. The fracture lines of axial loading in both Group1 LDH and ADH on stage 3 were similar to the intact proximal femur, with the lesser trochanter was not involved. [32,45], which suggested that the operation of bone-grafting and fixation increased the axial stability of the femur with cortical drilled and curettage.
As to the facture location predicted by FE analysis, Dragomir-Daescu's experiment showed fracture patterns of the FEA (83% agreement) correlated well with experimental data [57]. Yosibash's FE analysis showed that their predicted locations were accurate in 8 out of 14 fracture locations [54,58]. In Derikx's experiment, the FE ranking of load to failure corresponded very well with the actual experimental ranking (τ = 0.87; p < 0.001), and the location of the fracture was correctly predicted in the femora with metastatic lesions, while in intact femora there was a difference between the predicted and actual location of the fractures [59].
As we knew, the von Mises stress, the Drucker–Prager, maximum principal strain and maximum principal stress were used as 'yield criterions' to predict the 'yield' or 'fracture' load by FE analyses [60,61,62,63]. Zohar Yosibash [64] suggested that the surface average of the 'maximum principal strain' criterion in conjunction with the orthotropic FE model best predicted both the yield force and fracture location compared with other criteria. The surface average of the 'von Mises stress' criterion in conjunction with our FE models only predicted 20% fracture locations in our mechanical testing successfully, and the surface average of the 'maximum principal stress' criterion in conjunction with our FE models predicted 80% fracture locations in our mechanical testing successfully. When it came to the 'maximum principal strain' criterion, the locations of the maximum principal strain were consistent with the sites of axial loading failure in 100% models in Mechanical testing, which suggested that our research was consistent with Zohar Yosibash's study, and our FE models were reliable.
5.
Limitations
Due to the difficulty in obtaining a sufficient number of fresh-frozen human cadaveric femora at one time, we chose formalin-fixed specimens for our mechanical testing as previous researches [65,66], though the stiffness of the formalin-fixed femora might be weaker than the fresh-frozen femora, the formalin-fixed femora could also show the trend of drilling hole and fixing with bone graft and internal fixation very well. Another limitation was the FE-modeling of only one specimen, and the results of FE analysis had a certain reference value for our clinical operation.
6.
Conclusion
Despite these limitations, the results of this study confirmed that the operation of drilling and curettage decreased the stability of the proximal femur significantly, and the operation of bone-grafting and fixation after drilling in the lateral proximal femur increased the stability of the proximal femur significantly compared with drilling in the anterior femur neck. Our research suggested that the drilling site should be operated in the lateral proximal femur to get a bigger stability of the operation of drilling and bone-grafting and fixation for benign lesions in femoral head and neck.
Acknowledgments
This work was supported by the National Natural Science Foundation of China, Grant No. 61876109.
Conflicts of interest
There are no conflicts of interest.









 DownLoad:
DownLoad: