Mathematical Biosciences and Engineering, 2019, 16(4): 2650-2667. doi: 10.3934/mbe.2019132

Research article Special Issues

Export file:

Format

  • RIS(for EndNote,Reference Manager,ProCite)
  • BibTex
  • Text

Content

  • Citation Only
  • Citation and Abstract

TKRD: Trusted kernel rootkit detection for cybersecurity of VMs based on machine learning and memory forensic analysis

Xiao Wang, Jianbiao Zhang, Ai Zhang, Jinchang Ren

1 Faculty of Information Technology, Beijing University of Technology, Beijing 100124, China
2 Beijing Key Laboratory of Trusted Computing, Beijing 100124, China
3 Department of Computer Science & Engineering, UC San Diego, CA, USA
4 Department of Electronic and Electrical Engineering, University of Strathclyde, Glasgow, U.K.

Received: , Accepted: , Published:

Special Issues: Biological Models for Cybersecurity

Abstract    Full Text(HTML)    Figure/Table    Related pages

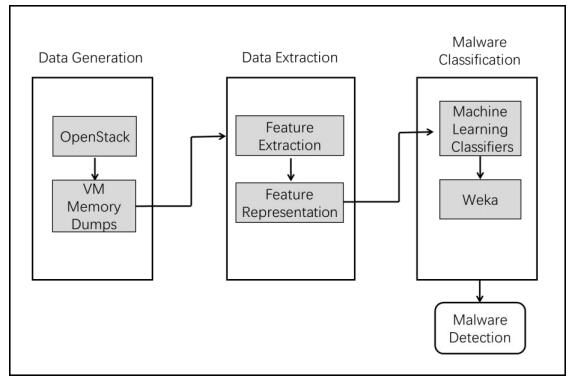
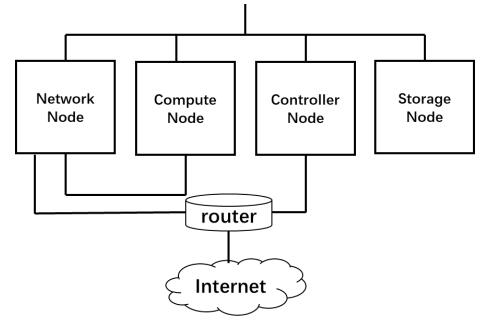
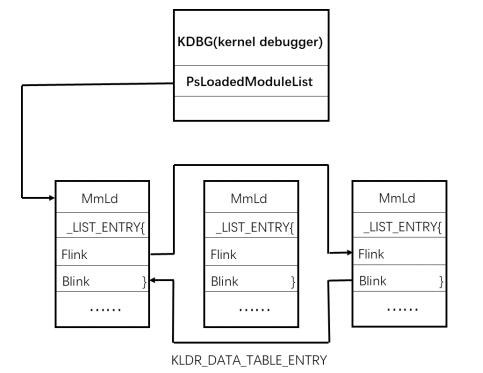
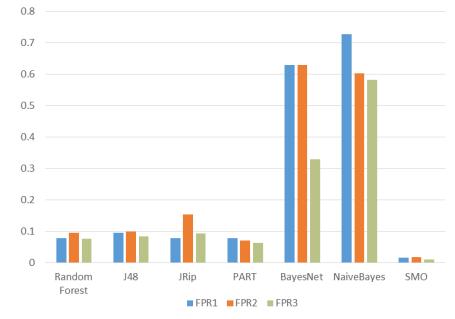
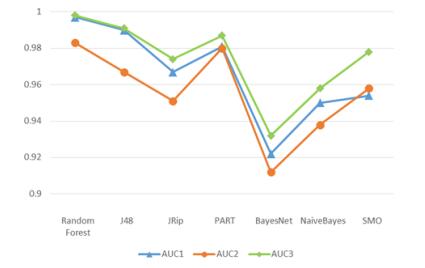
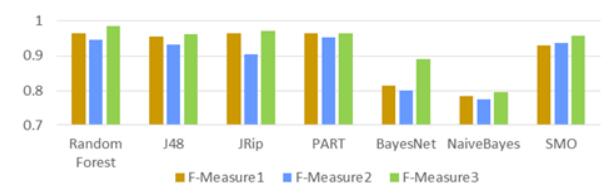
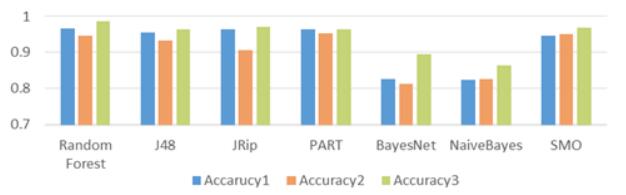
The promotion of cloud computing makes the virtual machine (VM) increasingly a target of malware attacks in cybersecurity such as those by kernel rootkits. Memory forensic, which observes the malicious tracks from the memory aspect, is a useful way for malware detection. In this paper, we propose a novel TKRD method to automatically detect kernel rootkits in VMs from private cloud, by combining VM memory forensic analysis with bio-inspired machine learning technology. Malicious features are extracted from the memory dumps of the VM through memory forensic analysis method. Based on these features, various machine learning classifiers are trained including Decision tree, Rule based classifiers, Bayesian and Support vector machines (SVM). The experiment results show that the Random Forest classifier has the best performance which can effectively detect unknown kernel rootkits with an Accuracy of 0.986 and an AUC value (the area under the receiver operating characteristic curve) of 0.998.
  Figure/Table
  Supplementary
  Article Metrics
Download full text in PDF

Export Citation

Article outline

Copyright © AIMS Press All Rights Reserved