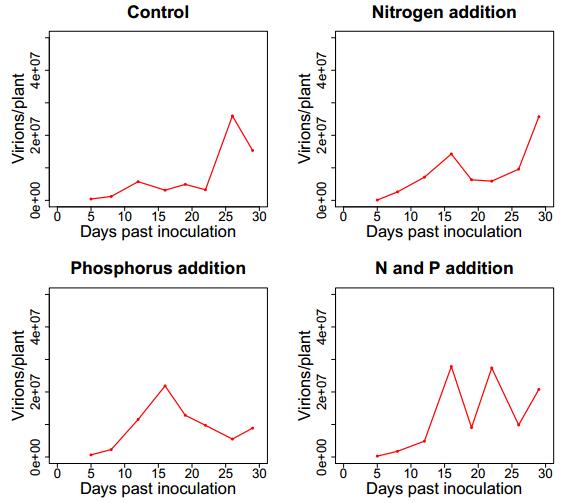
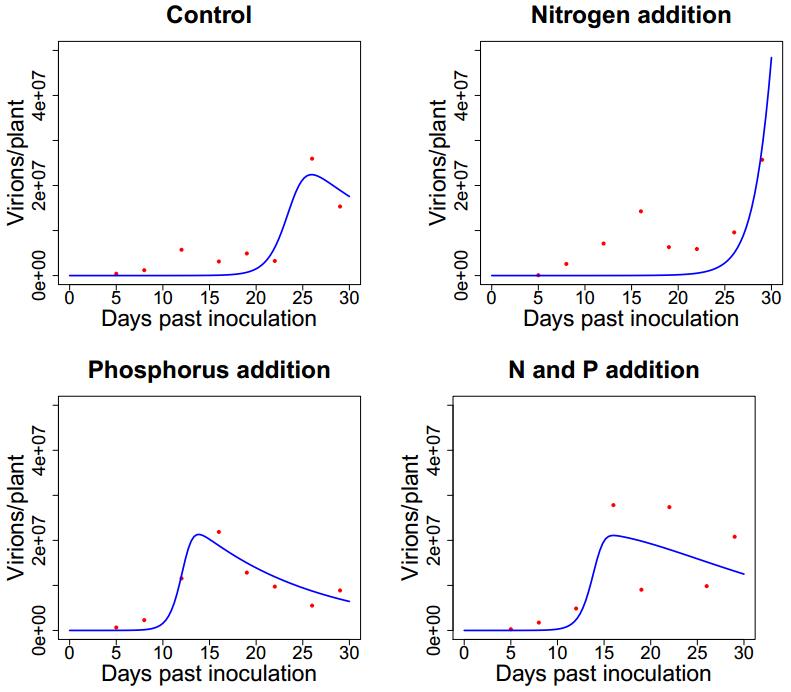
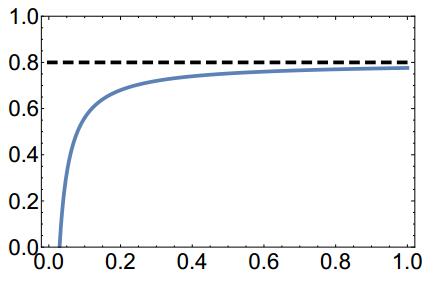
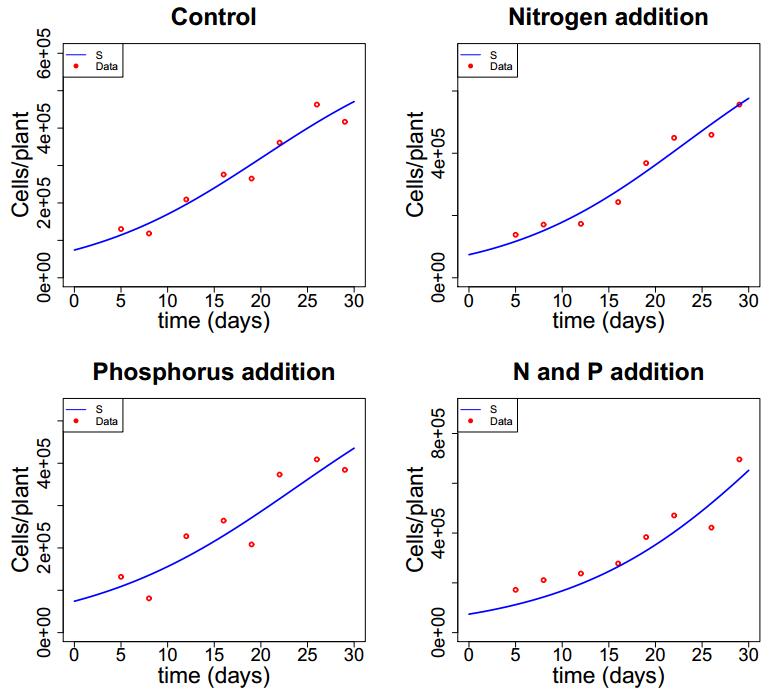
|
[1]
|
G. Ågren, Ideal nutrient productivities and nutrient proportions in plant growth, Plant Cell Environment, 11 (1988), 613–620.
|
|
[2]
|
M. Ali, S. Hameed, and M. Tahir, Luteovirus: insights into pathogenicity, Arc. Virol., 159 (2014), 2853–2860.
|
|
[3]
|
S. Alizon, M. van Baalen, A. E. J. Jokela, and E. M. A. Geber, Multiple infections, immune dynamics, and the evolution of virulence, Am. Nat., 172 (2008), E150–E168.
|
|
[4]
|
R. Antia, B. R. Levin, and R. M. May, Within-host population dynamics and the evolution and maintenance of microparasite virulence, Am. Nat., 144 (1994), 457–472.
|
|
[5]
|
N. Bacaër. The model of kermack and mckendrick for the plague epidemic in bombay and the type reproduction number with seasonality, J. Math. Biol., 64 (2012), 403–422.
|
|
[6]
|
M. Barfield, M. E. Orive, and R. D. Holt, The role of pathogen shedding in linking within-and between-host pathogen dynamics, Math. Biosci., 2015.
|
|
[7]
|
A. Béchette, T. Stojsavljevic, M. Tessmer, J. A. Berges, G. A. Pinter, and E. B. Young, Mathematical modeling of bacteria-virus interactions in lake michigan incorporating phosphorus content, J. Great Lake. Res., 39 (2013), 646–654.
|
|
[8]
|
E. Beretta and Y. Kuang, Modeling and analysis of a marine bacteriophage infection with latency period, Nonlinear Analys. Real World Appl., 2 (2001), 35–74.
|
|
[9]
|
E. Beretta and Y. Kuang, Geometric stability switch criteria in delay differential systems with delay dependent parameters, SIAM J. Math. Analys., 33 (2002), 1144–1165.
|
|
[10]
|
E. W. Birch, N. A. Ruggero, and M. W. Covert, Determining host metabolic limitations on viral replication via integrated modeling and experimental perturbation, 2012.
|
|
[11]
|
E. Borer, E. Seabloom, C. Mitchell, and A. Power, Local context drives infection of grasses by vector-borne generalist viruses, Ecol. Lett., 13 (2010), 810–818.
|
|
[12]
|
E. T. Borer, E. W. Seabloom, D. S. Gruner, W. S. Harpole, H. Hillebrand, E. M. Lind, P. B. Adler, J. Alberti, T. M. Anderson, J. D. Bakker, L. Biederman, D. Blumenthal, C. S. Brown, L. A. Brudvig, Y. M. Buckley, M. Cadotte, C. Chu, E. E. Cleland, M. J. Crawley, P. Daleo, E. I. Damschen, K. F. Davies, N. M. DeCrappeo, G. Du, J. Firn, Y. Hautier, R.W. Heckman, A. Hector, J. HilleRis- Lambers, O. Iribarne, J. A. Klein, J. M. H. Knops, K. J. La Pierre, A. D. B. Leakey, W. Li, A. S. MacDougall, R. L. McCulley, B. A. Melbourne, C. E. Mitchell, J. L. Moore, B. Mortensen, L. R. O'Halloran, J. L. Orrock, J. Pascual, S. M. Prober, D. A. Pyke, A. C. Risch, M. Schuetz, M. D. Smith, C. J. Stevens, L. L. Sullivan, R. J. Williams, P. D. Wragg, J. P. Wright, and L. H. Yang. Herbivores and nutrients control grassland plant diversity via light limitation, Nature, 508 (2014), 517.
|
|
[13]
|
E. T. Borer, E. W. Seabloom, C. E. Mitchell, and J. P. Cronin, Multiple nutrients and herbivores interact to govern diversity, productivity, composition, and infection in a successional grassland, Oikos, 123 (2014), 214–224.
|
|
[14]
|
G. Bratbak, A. Jacobsen, M. Heldal, K. Nagasaki, and F. Thingstad, Virus production in phaeocystis pouchetii and its relation to host cell growth and nutrition, Aquat. Microb. Ecol., 16 (1998),1–9.
|
|
[15]
|
L. Carrigan, H. Ohm, and J. Foster, Barley yellow dwarf virus translocation in wheat and oats, Crop Sci., 23 (1988), 611–612.
|
|
[16]
|
R. A. Chillakuru, D. D. Ryu, and T. Yilma, Propagation of recombinant vaccinia virus in hela cells: adsorption kinetics and replication in batch cultures, Biotechnol. Progress, 7 (1991), 85–92.
|
|
[17]
|
C. A. Clark, J. A. Davis, J. A. Abad, W. J. Cuellar, S. Fuentes, J. F. Kreuze, R. W. Gibson, S. B. Mukasa, A. K. Tugume, F. D. Tairo, AND J. P.T. Valkonen, Sweetpotato viruses: 15 years of progress on understanding and managing complex diseases, Plant Disease, 96 (2012), 168–185.
|
|
[18]
|
C. M. Clark and D. Tilman, Loss of plant species after chronic low-level nitrogen deposition to prairie grasslands, Nature, 451 (2008), 712.
|
|
[19]
|
J. L. Clasen and J. J. Elser, The effect of host Chlorella NC64A carbon:phosphorus ratio on the production of Paramecium bursaria Chlorella Virus-1, Freshwater Biol., 52 (2007), 112–122.
|
|
[20]
|
D. Coombs, M. A. Gilchrist, and C. L. Ball, Evaluating the importance of within- and betweenhost selection pressures on the evolution of chronic pathogens, Theoret. Popul. Biol., 72 (2007), 576–591.
|
|
[21]
|
D. Cordell, J.-O. Drangert, and S. White, The story of phosphorus: Global food security and food for thought, Global Environment. Change, 19 (2009), 292–305. Traditional Peoples and Climate Change.
|
|
[22]
|
T. Csorba, L. Kontra, and J. Burgyán, viral silencing suppressors: Tools forged to fine-tune hostpathogen coexistence, Virology, 479¢480 (2015), 85–103. 60th Anniversary Issue.
|
|
[23]
|
C. J. D'Arcy, P. A. Burnett, et al. Barley yellow dwarf: 40 years of progress. American Phytopathological Society (APS Press), 1995.
|
|
[24]
|
C. Dordas, Role of nutrients in controlling plant diseases in sustainable agriculture, Agron. Sustain. Develop., 428 (2008), 33–46.
|
|
[25]
|
M. Droop, Nutrient limitation in osmotrophic protista, Am. Zool., 13 (1973), 209–214.
|
|
[26]
|
M. Droop, Some thoughts on nutrient limitation in algae, J. Phycol., 9 (1973), 264–272.
|
|
[27]
|
M. Droop, The nutrient status of algal cells in continuous culture, J. Marine Biol. Asso. UK, 54 (1974), 825–855.
|
|
[28]
|
J. J. Elser, I. Loladze, A. L. Peace, and Y. Kuang, Lotka re-loaded: Modeling trophic interactions under stoichiometric constraints, Ecol. Modell., 245 (2012), 3–11.
|
|
[29]
|
G. G. Erion and W. E. Riedell, Barley yellow dwarf virus effects on cereal plant growth and transpiration, Crop Sci., 52 (2012), 2794–2799.
|
|
[30]
|
R. Everett, Applications of the Droop Cell Quota Model to Data Based Cancer Growth and Treatment Models, PhD thesis, Arizona State University, 2015.
|
|
[31]
|
R. Everett, J. Nagy, and Y. Kuang, Dynamics of a data based ovarian cancer growth and treatment model with time delay, J. Dynam. Different. Equat., (2015), 1–22.
|
|
[32]
|
R. Everett, A. Packer, and Y. Kuang, Can mathematical models predict the outcomes of prostate cancer patients undergoing intermittent androgen deprivation therapy? Biophys. Rev. Lett., 9 (2014), 173–191.
|
|
[33]
|
M. Eweida, P. Oxelfelt, and K. Tomenius, Concentration of virus and ultrastructural changes in oats at various stages of barley yellow dwarf virus infection, Ann. Appl. Biol., 112, 313–321.
|
|
[34]
|
K. Fuhrman, G. Pinter, and J. Berges, Dynamics of a virus–host model with an intrinsic quota, Math. Comput. Modell., 53 (2011), 716–730.
|
|
[35]
|
H. J. Gons, H. L. Hoogveld, S. G. Simis, and M. Tijdens, Dynamic modelling of viral impact on cyanobacterial populations in shallow lakes: implications of burst size, J. Marine Biol. Asso. UK, 86 (2006), 537–542.
|
|
[36]
|
S. A. Gourley, Y. Kuang, and J. D. Nagy, Dynamics of a delay differential equation model of hepatitis b virus infection, J. Biol. Dynam., 2 (2008), 140–153.
|
|
[37]
|
W. S. Harpole, L. L. Sullivan, E. M. Lind, J. Firn, P. B. Adler, E. T. Borer, J. Chase, P. A. Fay, Y. Hautier, H. Hillebrand, A. S. MacDougall, E. W. Seabloom, R. Williams, J. D. Bakker, M. W. Cadotte, E. J. Chaneton, C. Chu, E. E. Cleland, C. D¢¢Antonio, K. F. Davies, D. S. Gruner, N. Hagenah, K. Kirkman, J. M. H. Knops, K. J. La Pierre, R. L. McCulley, J. L. Moore, J. W. Morgan, S. M. Prober, A. C. Risch, M. Schuetz, C. J. Stevens, and P. D. Wragg, Addition of multiple limiting resources reduces grassland diversity, Nature, 537 (2016), 93.
|
|
[38]
|
W. R. Inc, Mathematica, Version 11.1. Champaign, IL, 2018.
|
|
[39]
|
J. D. Jones and J. L. Dangl, The plant immune system, Nature, 444 (2006), 323–329.
|
|
[40]
|
J. Karlsson, M. Anguelova, and M. Jirstrand, An efficient method for structural identifiability analysis of large dynamic systems, IFAC Proceed. Vol., 45 (2012), 941–946.
|
|
[41]
|
A. Kendig, E. Borer, E. Boak, T. Picard, and E. Seabloom, Plant virus coexistence occurs at multiple scales regardless of nutrient supply, Proceed. Royal Soc. B (submitted), 2018.
|
|
[42]
|
A. M. King, Virus taxonomy: classification and nomenclature of viruses: Ninth Report of the International Committee on Taxonomy of Viruses, volume 9. Elsevier, 2011.
|
|
[43]
|
Y. Kuang, Delay differential equations: with applications in population dynamics, volume 191. Academic Press, 1993.
|
|
[44]
|
Y. Kuang, J. Huisman and J. J. Elser, Stoichiometric plant-herbivore models and their interpretation, Math. Biosci. Engineer., 1 (2004), 215–222.
|
|
[45]
|
Y. Kuang, J. D. Nagy, and S. E. Eikenberry, Introduction to Mathematical Oncology. Chapman and Hall/CRC, 2016.
|
|
[46]
|
Y. Kuang, J. D. Nagy, and J. J. Elser, Biological stoichiometry of tumor dynamics: mathematical models and analysis, Discret. Cont. Dynam. Sys. Series B, 4 (2004), 221–240.
|
|
[47]
|
C. Lacroix, E.W. Seabloom, and E. T. Borer, Environmental nutrient supply alters prevalence and weakens competitive interactions among coinfecting viruses, New Phytol., 204 (2014), 424–433.
|
|
[48]
|
C. Lacroix, E. W. Seabloom, and E. T. Borer, Environmental nutrient supply directly alters plant traits but indirectly determines virus growth rate, Front. Microbiol., 8 (2017), 2116.
|
|
[49]
|
L. Mancio-Silva, K. Slavic, M. T. Grilo Ruivo, A. R. Grosso, K. K. Modrzynska, I. M. Vera, J. Sales-Dias, A. R. Gomes, C. R. MacPherson, P. Crozet, M. Adamo, E. Baena-Gonzalez, R. Tewari, M. Llinás, O. Billker, and M. M. Mota, Nutrient sensing modulates malaria parasite virulence, Nature, 547 (2017), 213–216.
|
|
[50]
|
E. Mitchell Charles, B. Reich Peter, T. David, and V. Groth James, Effects of elevated co2, nitrogen deposition, and decreased species diversity on foliar fungal plant disease, Global Change Biol., 9 (2018), 438–451.
|
|
[51]
|
G. Neofytou, Y. Kyrychko, and K. Blyuss, Mathematical model of plant-virus interactions mediated by rna interference, J. Theor. Biol., 403 (2016), 129–142.
|
|
[52]
|
G. Neofytou, Y. Kyrychko, and K. Blyuss, Time-delayed model of immune response in plants. J. Theoret. Biol., 389 (2016), 28–39.
|
|
[53]
|
H. Ogura, H. Sato, and M. Hatano, Relation of hvj (sendai virus) production to cell growth phase in persistently infected mouse 3t3 cells, Arc. Virol., 80 (1984), 47.
|
|
[54]
|
T. Pietschmann, V. Lohmann, G. Rutter, K. Kurpanek, and R. Bartenschlager, Characterization of cell lines carrying self-replicating hepatitis C virus RNAs, J. Virol., 75 (2001), 1252–1264.
|
|
[55]
|
T. Portz, Y. Kuang, and J. D. Nagy, A clinical data validated mathematical model of prostate cancer growth under intermittent androgen suppression therapy, Aip. Adv., 2 (2012), 011002.
|
|
[56]
|
R. Poulin and S. Morand, The diversity of parasites. Quarter. Rev. Biol., 75 (2000), 277–293. PMID: 11008700.
|
|
[57]
|
R Core Team, R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria, 2013.
|
|
[58]
|
Z. Rapti and C. E. Cáceres, Effects of intrinsic and extrinsic host mortality on disease spread, Bull. Math. Biol., 78 (2016), 235–253.
|
|
[59]
|
A. Raue, J. Karlsson, M. P. Saccomani, M. Jirstrand, and J. Timmer, Comparison of approaches for parameter identifiability analysis of biological systems, Bioinformatics, 2014.
|
|
[60]
|
A. Raue, C. Kreutz, T. Maiwald, J. Bachmann, M. Schilling, U. Klingm¨uller, and J. Timmer, Structural and practical identifiability analysis of partially observed dynamical models by exploiting the profile likelihood, Bioinformatics, 25 (2009), 1923–1929.
|
|
[61]
|
P. H. Raven, R. F. Evert, and S. E. Eichhorn, Biology of plants, Macmillan, 2005.
|
|
[62]
|
M. P. Saccomani, S. Audoly, and L. D'Angiò, Parameter identifiability of nonlinear systems: the role of initial conditions, Automatica, 39 (2003), 619–632.
|
|
[63]
|
E. Seabloom, E. Borer, C. Mitchell, and P. Alison, Viral diversity and prevalence gradients in north american pacific coast grasslands, Ecology, 91 (2010), 721–732.
|
|
[64]
|
E. W. Seabloom, C. D. Benfield, E. T. Borer, A. G. Stanley, T. N. Kaye, and P. W. Dunwiddie, Provenance, life span, and phylogeny do not affect grass species' responses to nitrogen and phosphorus, Ecol. Appl. Publ. Ecol. Soc. Am., 2011.
|
|
[65]
|
E. W. Seabloom, E. T. Borer, C. Lacroix, C. E. Mitchell, and A. G. Power, Richness and composition of niche-assembled viral pathogen communities, PLOS ONE, 8 (2013), 1–9.
|
|
[66]
|
H. Smith, An introduction to delay differential equations with applications to the life sciences, volume 57. Springer Science & Business Media, 2010.
|
|
[67]
|
H. L. Smith and P. D. Leenheer, Virus dynamics: A global analysis, SIAM J. Appli. Math., 63 (2003), 1313–1327.
|
|
[68]
|
V. H. Smith, R. D. Holt, M. S. Smith, Y. Niu, and M. Barfield, Resources, mortality, and disease ecology: importance of positive feedbacks between host growth rate and pathogen dynamics, Israel J. Ecol. Evol., 61 (2015), 37–49.
|
|
[69]
|
K. Soetaert and T. Petzoldt, Inverse modelling, sensitivity and monte carlo analysis in R using package FME, J. Statist. Software, 33 (2010), 1–28.
|
|
[70]
|
W. Steffen, K. Richardson, J. Rockström, S. E. Cornell, I. Fetzer, E. M. Bennett, R. Biggs, S. R. Carpenter, W. de Vries, C. A. de Wit, C. Folke, D. Gerten, J. Heinke, G. M. Mace, L. M. Persson, V. Ramanathan, B. Reyers, and S. Sörlin, Planetary boundaries: Guiding human development on a changing planet, Science, 347 2015.
|
|
[71]
|
C. L. Stewart, J. D. Pyle, C. C. Jochum, K. P. Vogel, G. Y. Yuen, and K.-B. G. Scholthof, Multiyear pathogen survey of biofuel switchgrass breeding plots reveals high prevalence of infections by panicum mosaic virus and its satellite virus, Phytopathology, 105 (2015), 1146–1154.
|
|
[72]
|
N. Tromas, M. P. Zwart, G. Lafforgue, and S. F. Elena, Within-host spatiotemporal dynamics of plant virus infection at the cellular level, PLoS Genet., 10 (2014), e1004186.
|
|
[73]
|
P. M. Vitousek, J. D. Aber, R. W. Howarth, G. E. Likens, P. A. Matson, D. W. Schindler, W. H. Schlesinger, and D. G. Tilman, Human alteration of the global nitrogen cycle: sources and consequences, Ecol. Appl., 7 (1997), 737–750.
|
|
[74]
|
R. O. Wayne, Plant cell biology: from astronomy to zoology, Academic Press, 2009.
|
|
[75]
|
B. Whitaker, M. Rúa, and C. Mitchell, Viral pathogen production in a wild grass host driven by host growth and soil nitrogen, New Phytol., 207 (2015), 760–768.
|
|
[76]
|
J. Wu, R. Dhingra, M. Gambhir, and J. V. Remais, Sensitivity analysis of infectious disease models: methods, advances and their application, J. Royal Soc. Int., 10 (2013), 186.
|
|
[77]
|
L. You, P. F. Suthers, and J. Yin, Effects of escherichia coli physiology on growth of phage t7 in vivo and in silico, J. Bacteriol., 184 (2002), 1888–1894.
|









 DownLoad:
DownLoad: