1. Introduction
Echinococcosis, which is often referred to as a hydatid disease, is a parasitic disease that affects both humans and other mammals, such as sheep, dogs, rodents and horses [3]. There are three different forms of Echinococcosis found in humans, each of which is caused by the larval stages of different species of the tapeworm of genus Echinococcus. The first of the three and also the most common form found in humans is cystic Echinococcosis, which is caused by Echinococcus granulosus. The second is alveolar Echinococcosis, which is caused by Echinococcus multilocularis and the third is polycystic Echinococcosis, which is caused by Echinococcus vogeli and very rarely, Echinococcus oligarthus. Alveolar and polycystic Echinococcosis are rarely diagnosed in humans and are not as widespread as cystic Echinococcosis. Thus, we focus on cystic Echinococcosis in this paper.
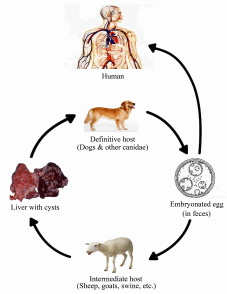
Echinococcus granulosus is an extremely small tapeworm, only 4-6 mm in length in its adult stage. This stage occurs in carnivore "definitive hosts, " generally dogs, wolves, coyotes, or wild dogs [17]. When mature, the adult tapeworm produces eggs that are passed in feces of the infected carnivore. The eggs contaminate foliage or vegetation which may be eaten by grazing animals, the "intermediate hosts, " generally ruminants such as sheep, goats, or cattle, although an extremely wide range of potential intermediate hosts exists. After the intermediate host ingests tapeworm eggs, the eggs hatch into tiny embryos in the small intestine of that host. These small mobile forms penetrate the intestinal mucosa, enter the circulatory tract, and are then transported via the bloodstream to various filtering organs in that host. The embryo lodges in those organs and there develops into a larval cystic form termed the "hydatid cyst". Eventually a thick wall develops around the hydatid cyst, and numerous tiny tapeworm heads are produced via asexual division within "brood capsules" from the germinal lining of each hydatid cyst. If parts of the viscera containing hydatid cysts are eaten by suitable carnivore hosts, then the tiny protoscolices are liberated from the brood capsules, evaginate their head region with its suckers and hooks, and move actively to eventually attach to the intestinal mucosa. There they grow within approximately 40 days to the adult stage to the tapeworm, which is then capable of producing eggs. Humans act as intermediate hosts for Echinococcus granulosus, and are infected when they ingest tapeworm eggs from the definitive host. The eggs may be eaten in foods such as vegetables, fruits or herbs, or drunk in contaminated water. The life cycle of Echinococcus granulosus is shown in Figure 1.
China is one of the countries in the world which have the most serious Echinococcosis. A national survey of important parasitic diseases in 2004 showed that the average prevalence of Echinococcosis in epidemic areas was about 1.08%. About 380000 people in the country are infected. During 2004-2008, China's 27 provinces and municipalities had Echinococcosis case reports, and 98.2% of reported cases distributed in Xinjiang, Inner Mongolia, Sichuan, Tibet, Gansu, Qinghai, Ningxia. At least 66 million people in China are threatened by Echinococcosis [20].
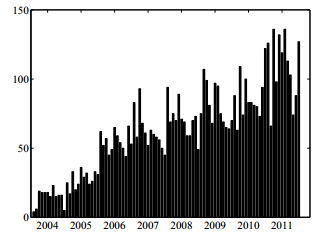
Echinococcosis is widely distributed and highly endemic in Xinjiang, China. Between 2004 and 2011, a total of 6086 human Echinococcosis cases were reported in Xinjiang, China (see Figure 2 [22]).
The average infection rates in sheep, cattle and dogs were 54.20%, 15.21% and 24.52%, respectively [9]. During 2008-2009, Xinjiang, China supervising agency for animal epidemic prevention examined Echinococcosis infection of liver and lung samples of cattle and sheep in fix point slaughter houses (see Table 2 [11]). Meanwhile, Echinococcus granulosus infection for dogs was also examined in various parts of Xinjiang, China (see Table 2 [23]).
Table 1. Infection of cattle and sheep liver/lung in Xinjiang, China.
| Region |
Infection rate |
| Sheep |
Cattle |
| Northern Xinjiang |
Ili |
70% |
41% |
| Tacheng |
63% |
25% |
| Altay |
65.8% |
27% |
| Changji |
50.78% |
9.23% |
| Southern Xinjiang |
Kashgar |
47% |
- |
| Hotan |
25% |
18% |
| Kezilesu Kirgiz Autonomous Prefecture |
38% |
6.2% |
| Aksu |
50.3% |
6.29% |
| Bayingolin Mongolia Autonomous Prefecture |
60.3% |
12.3% |
| Eastern Xinjiang |
Hami |
42% |
17% |
| Turpan |
36% |
16.68% |
Table 2. Infection of dog in Xinjiang, China.
| Region |
Infection rate |
| Northern Xinjiang |
Ili |
70% |
| Tacheng |
63% |
| Altay |
65.8% |
| Changji |
50.78% |
| Southern Xinjiang |
Kashgar |
47% |
| Hotan |
25% |
| Kezilesu Kirgiz Autonomous Prefecture |
38% |
| Aksu |
50.3% |
| Bayingolin Mongolia Autonomous Prefecture |
60.3% |
| Eastern Xinjiang |
Hami |
42% |
| Turpan |
36% |
Mathematical modeling is an important method of studying the spread of infectious disease qualitatively and quantitatively. Models can be used to understand how an infectious disease spreads in the real world, and how various complexities affect the dynamics. There have been some modeling studies on different aspects of Echinococcosis, and most of them are statistical models. A base-line survey was carried out on the transmission dynamics of Echinococcus granulosus, Taenia hydatigena and Taenia ovis in sheep in Uruguay by Cabrera et al. in [4]. The Echinococcus granulosus was only relative stable and the basic reproduction ratio was estimated about 1.2 in an endemic steady state. The effects of the different transmission levels of the parasites on potential control strategies were discussed. Torgerson et al. [16] examined the abundance and prevalence of infection of Echinococcus granulosus in cattle and sheep in Kazakhstan. Maximum likelihood techniques were used to define the parameters and their confidence limits in the model and the negative binomial distribution was used to define the error variance in the observed data. Lahmar et al. [8] examined the abundance and prevalence of infection of Echinococcus granulosus in camels in Tunisia.
Recently, dynamic models of Echinococcosis have been discussed in [19,21]. The work [19] proposed a deterministic model to study the transmission dynamics of Echinococcosis in Xinjiang, China. The results demonstrated that the dynamics of the model were completely determined by the basic reproductive number R0. The authors showed that Echinococcosis was endemic in Xinjiang, China with the current control measures. In [21] two mathematical models, the baseline model and the intervention model, were proposed to study the transmission dynamics of Echinococcosis. Applying these mathematical models to Qinghai Province, China, the authors showed that the infection of Echinococcosis was in an endemic state. In [19,21], the authors considered the density of Echinococcus eggs as a compartment in their models. However, it is hard to obtain the parameters of Echinococcus eggs in actual epidemiological surveys. To solve this problem, we take Echinococcus eggs in the environment as vectors and propose a novel spreading model for Echinococcosis with distributed time delays in this paper. We will evaluate the basic reproduction number R0 and analyze the dynamical behaviors of the model. According to human Echinococcosis cases from January 2004 to December 2011 in Xinjiang, China, we will estimate the parameters of the model and study the transmission trend of the disease in Xinjiang, China. We will also carry out some sensitivity analysis of the basic reproduction number R0 in terms of various model parameters. Finally, we shall suggest some strategies for control Echinococcosis infection in Xinjiang, China.
The article is organized as follows. The model is presented in Section 2. The basic properties on the positivity and boundedness of solutions, computation of the basic reproduction number and the existence of endemic equilibrium for the model are discussed in Section 3. In Section 4, we establish the global stability of the disease-free equilibrium for the model. In Section 5, we will apply the theory of permanence for infinite-dimensional systems to obtain the permanence of the model. The global stability theorem of the endemic equilibrium is stated and proved in Section 6. In Section 7, we estimate the parameters of the model and study the transmission trend of the disease in Xinjiang, China. A brief discussion is given in Section 8.
2. Model formulation
Based on the transmission mechanism of Echinococcosis, we consider dogs being the definitive hosts, livestock being the intermediate hosts, humans represented as an accidental intermediate hosts respectively.
The dogs population is subdivided into two classes: the susceptible population and the infected population denoted by SD(t) and ID(t), respectively. For livestock population, we separate the total livestock population into two classes: susceptible and infectious denoted by SL(t) and IL(t), respectively. Humans are infected when they ingest tapeworm eggs from the definitive host. We separate the total population into three classes: susceptible, exposed and infectious denoted by SH(t), EH(t) and IH(t), respectively.
To model the Echinococcosis infection delay from infected livestock to susceptible dogs, we let τ be the random variable that describes the time between infection offal thrown in the environment and eaten by dogs with a probability distribution f1(τ). h1 denotes the average survival time of larval cysts into the infection offal thrown in the environment. Here, f1: [0,h1]→[0,+∞) is continuous on [0,h1] satisfying ∫h10f1(τ)dτ=1. When infection offal was dropped in the environment at time t−h1, the number of infected dogs at time t is given by
|
β1SD(t)∫h10f1(τ)IL(t−τ)dτ.
|
To model the Echinococcosis infection delay from infected dogs to susceptible livestock, we let τ be the random variable that is the time between eggs produced by infected dogs and ingestion by susceptible livestock with a probability distribution f2(τ). h2 describes average life expectancy for Echinococcus eggs. f2(τ) is assumed to be non-negative and continuous on [0,h2] satisfying ∫h20f2(τ)dτ=1. When infected dogs produced Echinococcus eggs at time t−h2, the number of infected livestock at time t is given by
|
β2SL(t)∫h20f2(τ)ID(t−τ)dτ.
|
Humans act as an accidental intermediate host for Echinococcosis. Thus, similarly to the infection of livestock, the number of infected human at time t is given by
|
β3SH(t)∫h20f3(τ)ID(t−τ)dτ,
|
where f3(τ) is a probability distribution. Because the range of movement for humans and livestock is different, we choose distribution function in different forms. Hence, distribution f3(τ) is different from f2(τ). Similarly, f3(τ) is assumed to be non-negative and continuous on [0,h2] satisfying ∫h20f3(τ)dτ=1.
Based on the above discussions, a dynamical model of Echinococcosis with distributed time delays can be written as:
|
{dSD(t)dt=A1−β1SD(t)∫h10f1(τ)IL(t−τ)dτ−d1SD(t)+σID(t),dID(t)dt=β1SD(t)∫h10f1(τ)IL(t−τ)dτ−(d1+σ)ID(t),dSL(t)dt=A2−β2SL(t)∫h20f2(τ)ID(t−τ)dτ−d2SL(t),dIL(t)dt=β2SL(t)∫h20f2(τ)ID(t−τ)dτ−d2IL(t),dSH(t)dt=A3−β3SH(t)∫h20f3(τ)ID(t−τ)dτ−d3SH(t)+γIH(t),dEH(t)dt=β3SH(t)∫h20f3(τ)ID(t−τ)dτ−(d3+ω)EH(t),dIH(t)dt=ωEH(t)−(d3+μ+γ)IH(t).
|
(1)
|
All parameters in model (1) are assumed to be positive constants. For the dog population, A1 describes the annual recruitment rate; d1 is the natural death rate; σ denotes the recovery rate of transition from infected to non-infected dogs, including natural recovery rate and recovery due to anthelmintic treatment; For the livestock population, A2 is the annual recruitment rate; d2 is the death rate; For human population, A3 is the annual recruitment rate; d3 is the natural death rate; μ is the disease-related death rate; 1/ω denotes the incubation period of infected individuals; γ denotes the recovery rate.
Motivated by biological background of model (1), the initial conditions for model (1) are given as follows
|
{SD(θ)=ϕ1(θ), ID(θ)=ϕ2(θ), SL(θ)=ϕ3(θ), IL(θ)=ϕ4(θ),SH(θ)=ϕ5(θ), EH(θ)=ϕ6(θ), IH(θ)=ϕ7(θ),
|
(2)
|
where ϕ=(ϕ1,ϕ2,⋯,ϕ7)∈C([−h,0],R7+), h=max{h1,h2}. In this paper, for any integer n>0 we denote by C([−h,0],Rn+) the Banach space of all continuous functions ϕ:[−h,0]→Rn+ with sup-norm ‖.
3. Basic properties
For any \varepsilon>0, we define the region \Gamma_{\varepsilon} as follows.
|
\begin{array}{rl}
\Gamma_{\varepsilon}=&\displaystyle\{(S_D, I_D, S_L, I_L, S_H, E_H, I_H)\in
R_+^7,
\ S_D+I_D\leq \frac{A_1}{d_1}+\varepsilon, \\
&\displaystyle S_L+I_L\leq \frac{A_2}{d_2}+\varepsilon, \;
S_H+E_H+I_H\leq \frac{A_3}{d_3}+\varepsilon\}.
\end{array}
|
Firstly, on the positivity and ultimate boundedness of solutions for model (1), we have the following result.
Lemma 3.1. ( i ) The solution of model (1) with initial conditions (2) satisfy (S_D(t), I_D(t), S_L(t), I_L(t), S_H(t), E_H(t),
R_H(t))>0 for all t>0.
( ii ) All solutions of model (1) with initial conditions (2) ultimately turn into the region \Gamma_{\varepsilon} as t\to\infty.
The proof of Lemma 3.1 is simple, we hence omit it here.
Remark 3.2. According to Lemma 3.1, all feasible solutions of model (1) enter or remain in the region \Gamma_{\varepsilon} as t is large enough. Therefore, the dynamics of model (1) can be considered only in \Gamma_{\varepsilon}.
Simple algebraic calculation shows that model (1) always has a disease-free equilibrium E_0=(S_D^0, 0, S_L^0, 0, S_H^0, 0, 0), where
|
S_D^0=\frac{A_1}{d_1}, S_L^0=\frac{A_2}{d_2},
S_H^0=\frac{A_3}{d_3}.
|
Following the idea in [24,18], we can introduce the basic reproduction number for model (1) as follows
|
\mathcal{R}_0=\sqrt{\frac{\beta_1\beta_2A_1A_2}{d_1d_2^2(d_1+\sigma)}}.
|
Remark 3.3. To better understand the basic reproduction number, we rewrite it as
|
\mathcal{R}_0=\sqrt{\frac{A_2}{d_2}\cdot\frac{1}{d_1+\sigma}\cdot\beta_2
\cdot\frac{A_1}{d_1}\cdot\frac{1}{d_2}\cdot\beta_1}.
|
The biological meaning of \mathcal{R}_0 can be interpreted as follows, near the disease free equilibrium, the total number of livestock reaches at a stable state A_2/d_2 and every livestock will be susceptible. Then susceptible livestock is infected by infectious dogs over its expected infectious period 1/(d_1+\sigma) with probability \beta_2. Furthermore, the total number of dogs reaches stable state A_1/d_1 and every dog will be susceptible, which is infected by infectious livestock over its expected infectious period 1/d_2 with probability \beta_1. The square root arises from the two 'generations' required for an infected dogs or livestock to 'reproduce' itself.
It can be proved that if \mathcal{R}_0>1 then model (1) has a unique endemic equilibrium E^*(S_D^*, I_D^*, S_L^*, I_L^*, S_H^*, E_H^*, I_H^*), where
|
\begin{array}{rl}
S_D^*=&\displaystyle\frac{d_2(d_1+\sigma)(A_1\beta_2+d_1d_2)}
{\beta_2d_1(\beta_1A_2+d_1d_2+d_2\sigma)}, \\
I_D^*=&\displaystyle\frac{\beta_1\beta_2A_1A_2-
d_1d_2^2(d_1+\sigma)} {d_1\beta_2(\beta_1A_2+d_1d_2+d_2\sigma)}
=\frac{d_2^2(d_1+\sigma)}{\beta_2(\beta_1A_2
+d_1d_2+d_2\sigma)}(\mathcal{R}^2_0-1), \\
S_L^*=&\displaystyle\frac{d_1(\beta_1A_2
+d_1d_2+d_2\sigma)}{\beta_1(A_1\beta_2+d_1d_2)}, \\
I_L^*=&\displaystyle\frac{\beta_1\beta_2A_1A_2-d_1d_2^2(d_1+\sigma)}
{d_2\beta_1(A_1\beta_2+d_1d_2)}=
\frac{d_1d_2(d_1+\sigma)}{\beta_1(A_1\beta_2
+d_1d_2)}(\mathcal{R}^2_0-1), \\
S^*_H=&\displaystyle \frac{A_3(d_3+\omega)(d_3+\mu+\gamma)}
{(\beta_3I_D^*+d_3)(d_3+\omega)(d_3+\mu+\gamma)
-\gamma\omega\beta_3I_D^*}, \\
E^*_H=&\displaystyle\frac{\beta_3S^*_HI_D^*}{(d_3+\omega)}, \\
I^*_H=&\displaystyle\frac{\omega\beta_3S^*_HI_D^*}{(d_3+\omega)(d_3
+\mu+\gamma)}.
\end{array}
|
Therefore, we finally have the following theorem.
Theorem 3.4. ( i ) Model (1) always has a disease-free equilibrium E_0.
( ii ) Model (1) has a unique endemic equilibrium E^* if and only if \mathcal{R}_0>1.
4. Global stability of E_0
Regarding the stability of the disease-free equilibrium E_0, we have the following result.
Theorem 4.1. If \mathcal{R}_0<1, then the disease-free equilibrium E_0 of model (1) is globally asymptotically stable in \Gamma_{\varepsilon}.
Proof. Notice that the last three equations are independent of the first four equations, we start by considering the first four equations,
|
\left\{
\begin{array}{rl}
\displaystyle\frac{{\rm d}S_D(t)}{{\rm d}t}= &\displaystyle
A_1-\beta_1S_D(t)\int_0^{h_1}
f_1(\tau)I_L(t-\tau){\rm d}\tau-d_1S_D(t)+\sigma I_D(t),\\[8pt]
\displaystyle \frac{{\rm d}I_D(t)}{{\rm d}t}=
&\displaystyle\beta_1S_D(t)\int_0^{h_1}
f_1(\tau)I_L(t-\tau){\rm d}\tau-(d_1+\sigma)I_D(t),\\[8pt]
\displaystyle\frac{{\rm d}S_L(t)}{{\rm d}t}= &\displaystyle
A_2-\beta_2S_L(t)\int_0^{h_2}f_2(\tau)
I_D(t-\tau){\rm d}\tau-d_2S_L(t),\\[8pt]
\displaystyle\frac{{\rm d}I_L(t)}{{\rm d}t}=
&\displaystyle\beta_2S_L(t)\int_0^{h_2}f_2(\tau) I_D(t-\tau){\rm
d}\tau-d_2I_L(t).
\end{array}\right.
|
(3)
|
Since \mathcal{R}_0<1, it follows that
|
\frac{d_2^2(d_1+\sigma)}{\beta_2A_2}(\mathcal{R}_0^2-1)=\frac{\beta_1A_1}{d_1}
-\frac{d_2^2(d_1+\sigma)}{\beta_2A_2}<0.
|
Hence, there is a small enough constant \varepsilon>0 such that
|
\frac{\beta_1(A_1+d_1\varepsilon)}{d_1}
-\frac{d_2^2(d_1+\sigma)}{\beta_2(A_2+d_2\varepsilon)}<0.
|
Let (S_D(t), I_D(t), S_L(t), I_L(t), S_H(t), E_H(t), I_H(t)) be any solution of model (1) in \Gamma_{\varepsilon}. Then,
|
S_D(t)\leq \frac{A_1}{d_1}+\varepsilon, \ S_L(t)\leq\frac{A_2}{d_2}
+\varepsilon \;\; \mbox{for all}\;\; t\geq 0.
|
Consider the following Lyapunov functional
|
\begin{array}{rl}
V(t)=&\displaystyle
I_D(t)+\beta_1\int_0^{h_1}f_1(\tau)\int_{t-\tau}^tS_D(u+\tau)I_L(u){\rm
d}u{\rm d}\tau+\\
&\displaystyle\frac{d_2(d_1+\sigma)}{\beta_2(A_2+d_2\varepsilon)}
\Big(I_L(t)+\beta_2\int_0^{h_2}f_2(\tau)\int_{t-\tau}^tS_L(u+\tau)I_D(u){\rm
d}u{\rm d}\tau\Big),
\end{array}
|
calculating the derivative of V(t) along the solution of system (3), we have
|
\begin{array}{rl}
\dot{V}(t)=&\displaystyle \beta_1S_D(t)\int_0^{h_1}
f_1(\tau)I_L(t-\tau){\rm d}\tau-(d_1+\sigma)I_D(t)\\[8pt]
&\displaystyle+\beta_1I_L(t)\int_0^{h_1}f_1(\tau)S_D(t+\tau){\rm
d}\tau -\beta_1S_D(t)\int_0^{h_1}
f_1(\tau)I_L(t-\tau){\rm d}\tau\\[8pt]
&\displaystyle+\frac{d_2(d_1+\sigma)}{\beta_2(A_2+d_2\varepsilon)}
\Big(\beta_2S_L(t)\int_0^{h_2}f_2(\tau)
I_D(t-\tau){\rm d}\tau-d_2I_L(t)\\[8pt]
&\displaystyle+\beta_2I_D(t)\int_0^{h_2}f_2(\tau)S_L(t+\tau){\rm
d}\tau-\beta_2S_L(t)\int_0^{h_1}f_1(\tau)
I_D(t-\tau){\rm d}\tau\Big)\\[8pt]
=&\displaystyle-(d_1+\sigma)I_D(t)
+\beta_1I_L(t)\int_0^{h_1}f_1(\tau)S_D(t+\tau){\rm
d}\tau\\[8pt]
&\displaystyle+\frac{d_2(d_1+\sigma)}{\beta_2(A_2+d_2\varepsilon)}
\Big(-d_2I_L(t)+\beta_2I_D(t)\int_0^{h_2}f_2(\tau)S_L(t+\tau){\rm
d}\tau\Big)\\[8pt]
\leq&\displaystyle-(d_1+\sigma)I_D(t)
+\beta_1(\frac{A_1}{d_1}+\varepsilon)I_L(t)\\[8pt]
&\displaystyle+\frac{d_2(d_1+\sigma)}{\beta_2(A_2+d_2\varepsilon)}
\Big(-d_2I_L(t)+\beta_2(\frac{A_2}{d_2}+\varepsilon)I_D(t)\Big)\\[8pt]
=&\displaystyle\Big(\frac{\beta_1(A_1+d_1\varepsilon)}{d_1}
-\frac{d_2^2(d_1+\sigma)}{\beta_2(A_2+d_2\varepsilon)}\Big)I_L(t)\\[8pt]
\leq& 0.
\end{array}
|
Let E=\{(S_D, I_D, S_L, I_L): \dot{V}= 0\}. Then, we have E\subset
\{(S_D, I_D, S_L, I_L): I_L=0\}. Let M\subset E be the largest invariant set with respect to system (3) and let further (S_D(t), I_D(t), S_L(t), I_L(t)) be any solution of system (3) which retains in M for all t\in R, then (S_D(t), I_D(t),
S_L(t), I_L(t)) is defined and bounded on t\in R.
Since M\subset \{(S_D, I_D, S_L, I_L): I_L=0\}, we have I_L(t)\equiv0. Furthermore, from the fourth equation of system (3), we have S_L(t)\int_0^{h_2}f_2(\tau) I_D(t-\tau){\rm
d}\tau\equiv0. Therefore, we have
|
\begin{array}{rl}
\displaystyle\frac{dS_D(t)}{dt}=& A_1-d_1S_D(t)+\sigma I_D(t)\\
\displaystyle\frac{dI_D(t)}{dt}=&-(d_1+\sigma) I_D(t), \\
\displaystyle\frac{dS_L(t)}{dt}=& A_2-d_2S_L(t).
\end{array}
|
Solving second equation, we have
|
I_D(t)=I_D(0)\exp(-(d_1+\sigma)t)\;\;\mbox{for all}\;\; t\in R.
|
Hence, I_D(t)\equiv0. Otherwise, I_D(t) will be unbounded on R.
Since
|
S_D(t)=\frac{A_1}{d_1}+S_D(0)\exp(-d_1t) \;\; \mbox{for all}\;\;
t\in R,
|
then we also have S_D(0)\equiv0. Otherwise S_D(t) will be unbounded on R. Therefore S_D(t)\equiv A_1/d_1. Similarly, we can obtain S_L(t)\equiv A_2/d_2. Finally, we have (S_D(t), I_D(t), S_L(t), I_L(t))=(A_1/d_1, 0, A_2/d_2, 0). This shows that M\equiv\{(A_1/d_1, 0, A_2/d_2, 0)\}. By the LaSalle invariance principle, (A_1/d_1, 0, A_2/d_2, 0) of system (3) is globally asymptotically stable.
Next, we consider the last three equations
|
\left\{
\begin{array}{rl}
\displaystyle\frac{{\rm d}S_H(t)}{{\rm d}t}= &\displaystyle
A_3-\beta_3S_H(t)\int_0^{h_2}f_3(\tau)
I_D(t-\tau){\rm d}\tau-d_3S_H(t)+\gamma I_H(t),\\[8pt]
\displaystyle\frac{{\rm d}E_H(t)}{{\rm d}t}= &\displaystyle
\beta_3S_H(t)\int_0^{h_2}f_3(\tau)
I_D(t-\tau){\rm d}\tau-(d_3+\omega)E_H(t),\\[8pt]
\displaystyle\frac{{\rm d}I_H(t)}{{\rm d}t}= &\displaystyle \omega
E_H(t)-(d_3+\mu+\gamma)I_H(t).
\end{array}\right.
|
(4)
|
Since I_D(t)\to0 as t\to\infty, we obtain that E_H(t)\to 0 as t\to \infty by the second equation of system (4). Furthermore, from the third equation of system (4) we also have I_H(t)\to 0 as t\to \infty. Lastly, from the first equation of system (4) we finally have that S_H(t)\to A_3/d_3 as t\to\infty. Therefore, (A_3/d_3, 0, 0) is globally attractive with respect to system (4). Thus, according to the theory of asymptotic autonomous system [15], we finally obtain that the disease-free equilibrium E_0 is globally asymptotically stable for model (1) when \mathcal{R}_0<1. This completes the proof of Theorem 4.1.
5. Permanence
In this section, we will apply the theory of persistence for infinite-dimensional dynamical system from [7] to obtain the permanence of model (1).
Let X be a complete metric space with metric d. Suppose that T(t): X\to X, \;t\geq 0, is a C^0-semigroup on X. For any x\in X, the positive orbit \gamma^+(x) through x is defined as \gamma^+(x)=\{T(t)x: t\geq 0\}, and its \omega-limit set is \omega(x)=\{y\in X: there is a time sequence t_k\to\infty such that \lim_{k\to\infty}T(t_k)x=y\}. Let X^0 and X_0 be two nonempty subsets such that X=X^0\cup X_0 and X^0\cap X_0=\emptyset. Further, we assume that C^0-semigroup T on X satisfies
|
T(t): X^0\to X^0, T(t): X_0\to X_0.
|
We denote T^0(t)=T(t)|_{X^0} and T_0(t)=T(t)|_{X_0}. We further assume that there is a global attractor A_0 for T_0 in X_0, and let
|
\tilde{A}_0=\bigcup\{\omega(x): x\in A_0\}.
|
Furthermore, the definitions of the compactness, point dissipativity and the uniform persistence for C^0-semigroup T on X, and the definitions of the isolated invariance and acyclic covering for a subset A\subset X, can be found in Kuang [7].
Now, we state the following lemma, which can be found in ([7], Theorem 2.4).
Lemma 5.1. Assume that
( i ) there is a t_0\geq0 such that T(t) is compact in X for t>t_0;
( ii ) T(t) is point dissipative in X;
( iii ) \tilde{A}_0 is isolated and has an acyclic covering M=\cup_{i=1}^kM_i.
Then T(t) is uniform persistent if and only if
|
W^s(M_i)\cap X^0=\emptyset, i=1, 2, \cdots, k,
|
where W^s(M_i)=\{x\in X: \omega(x)\neq\emptyset, \omega(x)\subset M_i\} is the stable set of M_i.
In the following, as an application of this lemma, we establish the result on the permanence of model (1).
Theorem 5.2. If \mathcal{R}_0>1, then model (1) is permanent.
Proof. We firstly prove the permanence of system (3). To apply Lemma 5.1, we choose space X=C([-h, 0], R^4_+), and sets X^0 and X_0 are defined by
|
\begin{array}{l}
X^0=\{(\phi_1, \phi_2, \phi_3, \phi_4)\in X: \phi_2(\theta^*)>0\
\mbox{or}\ \phi_4(\theta^*)>0\ \mbox{for some}\
\theta^*\in[-h, 0]\}, \\
X_0=\{(\phi_1, \phi_2, \phi_3, \phi_4)\in X: \phi_2(\theta)\equiv0, \
\phi_4(\theta)\equiv 0\ \mbox{for all}\ \theta\in[-h, 0]\}.
\end{array}
|
Denote \phi=(\phi_1, \phi_2, \phi_3, \phi_4) and x=(S_D, I_D, S_L, I_L). Let x(t, \phi)=(S_D(t, \phi), I_D(t, \phi), S_L(t, \phi), I_L(t, \phi)) be the solution of system (3) with initial value \phi at t=0. We define C^0-semigroup T(t) in Lemma 5.1 as follows
|
T(t)\phi=x_t(\phi), \phi\in X, \; t\geq 0,
|
where x_t(\phi)=x(t+s, \phi) with s\in[-h, 0].
Now, we verify that all the conditions of Lemma 5.1 are satisfied.
Firstly, we show that X^0 and X_0 are positively invariant sets. Let \phi=(\phi_1, \phi_2, \phi_3, \phi_4)\in X^0, from system (3) we can obtain
|
\begin{array}{l}
\displaystyle S_D(t,\phi)\geq S_D(0,\phi)\exp(-\beta_1\int_0^t\int_0^{h_1}f_1(\tau)I_L(s-\tau,\phi)d\tau ds-d_1t),\\[8pt]
\displaystyle
I_D(t,\phi)=e^{-(d_1+\sigma)t}\Big\{I_D(0,\phi)+\int_0^t\beta_1S_D(\rho,\phi)\int_0^{h_1}
f_1(\tau)I_L(\rho-\tau,\phi){\rm d}\tau e^{(d_1+\sigma)\rho}{\rm
d}\rho\Big\},\\[8pt]
\displaystyle S_L(t,\phi)\geq S_L(0,\phi)\exp(-\beta_2\int_0^t\int_0^{h_2}f_2(\tau)I_D(s-\tau,\phi)d\tau ds-d_2t),\\[8pt]
\displaystyle
I_L(t,\phi)=e^{-d_2t}\Big\{I_L(0,\phi)+\int_0^t\beta_2S_L(\rho,\phi)
\int_0^{h_2}f_2(\tau)I_D(\rho-\tau,\phi){\rm d}\tau
e^{d_2\rho}{\rm d}\rho\Big\}
\end{array}
|
(5)
|
for all t>0. Obviously, S_D(t, \phi)\geq 0 and S_L(t, \phi)\geq 0 for all t\geq 0. If there is a t_1>0 such that I_D(t_1)=0 and I_L(t_1)=0, then from (5) we can obtain I_D(0, \phi)=I_L(0, \phi)=0 and for any s\in[0, t_1]
|
\int_0^{h_2}f_2(\tau)I_D(s-\tau, \phi)d\tau=0, \int_0^{h_1}f_1(\tau)I_L(s-\tau, \phi)d\tau=0.
|
Hence, we have \phi_2(\theta)=\phi_4(\theta)=0 for all \theta\in[-h, 0]. This leads to a contradiction with \phi=(\phi_1, \phi_2, \phi_3, \phi_4)\in X^0. Therefore, I_D(t, \phi)>0 and I_L(t, \phi)>0 for all t\geq 0. This shows that x_t(\phi)=(S_{Dt}(\phi), I_{Dt}(\phi), S_{Lt}(\phi), I_{Lt}(\phi))\in X^0 for all t\geq 0. This implies that X^0 is positively invariant.
Let \phi=(\phi_1, \phi_2, \phi_3, \phi_4)\in X_0. Since \phi_2=\phi_4=0, by the existence and uniqueness theorem of solutions for the functional differential equations, we have
|
I_D(t, \phi)\equiv 0, I_L(t, \phi)\equiv 0\;\;\mbox{for all}\;\; t\geq0.
|
From this, we obtain that X_0 also is positively invariant.
Denote by \omega(\phi) the \omega-limit set of the solution of model (3) starting at t=0 with initial value \phi\in X. Let
|
\Omega=\bigcup\{\omega(\phi): \phi\in X_0\},
E'_0=(\frac{A_1}{d_1}, 0, \frac{A_2}{d_2}, 0).
|
Restricting system (3) to X_0, we obtain
|
\left\{
\begin{array}{l}
\displaystyle\frac{{\rm d}S_D(t)}{{\rm d}t}=A_1-d_1S_D(t)\\
\displaystyle\frac{{\rm d}S_L(t)}{{\rm d}t}=A_2-d_2S_L(t).
\end{array}\right.
|
(6)
|
It is easy to verify that system (6) has a unique equilibrium (A_1/d_1, A_2/d_2), which is globally asymptotically stable. Therefore, we have \Omega=\{E_0'\}, and E_0' is a covering of \Omega, which is isolated (since E_0' is the unique equilibrium) and is acyclic (since there exists no solution in X_0 which links E_0' to itself). It remains to show that
|
W^s(E_0')\cap X^0=\emptyset,
|
(7)
|
where W^s(E_0') denotes the stable manifold of E_0'. Suppose that (7) does not hold, then there exists a solution (S_D(t), I_D(t), S_L(t), I_D(t)) of model (3) with initial conditions in X^0, such that
|
\lim\limits_{t\to\infty}S_D(t)=\frac{A_1}{d_1}, \ \
\lim\limits_{t\to\infty}I_D(t)=0, \ \
\lim\limits_{t\to\infty}S_L(t)=\frac{A_2}{d_2}, \ \
\lim\limits_{t\to\infty}I_L(t)=0.
|
(8)
|
Since \mathcal{R}_0=\sqrt{\frac{\beta_1\beta_2A_1A_2}{d_1d_2^2(d_1+\sigma)}}>1, we can choose a small enough constant \epsilon>0 such that A_1/d_1-\epsilon>0, A_2/d_2-\epsilon>0 and
|
\mathcal{R}_0^{\epsilon}\triangleq
\sqrt{\frac{\beta_1\beta_2(A_1-d_1\epsilon)(A_2
-d_2\epsilon)}{d_1d_2^2(d_1+\sigma)}}>1.
|
For this \epsilon>0, by (8), there exists a t_1>0 such that
|
S_D(t)>\frac{A_1}{d_1}-\epsilon,
S_L(t)>\frac{A_2}{d_2}-\epsilon \;\;\mbox{for all}\;\; t\geq
t_1.
|
Hence, by system (3), we have
|
\begin{array}{rl}
\displaystyle\frac{{\rm d}I_D(t)}{{\rm d}t}&\geq \displaystyle
\beta_1(\frac{A_1}{d_1}-\epsilon)\int_0^{h_1}f_1(\tau)I_L(t-\tau){\rm
d}\tau-(d_1+\sigma)I_D(t),\\
\displaystyle\frac{{\rm d}I_L(t)}{{\rm d}t}&\geq \displaystyle
\beta_2(\frac{A_2}{d_2}-\epsilon)\int_0^{h_2}f_2(\tau)I_D(t-\tau){\rm
d}\tau-d_2I_L(t)
\end{array}
|
for all t\geq t_1. Consider the following auxiliary system
|
\begin{array}{rl}
\displaystyle\frac{{\rm d}U(t)}{{\rm d}t}&= \displaystyle
\beta_1(\frac{A_1}{d_1}-\epsilon)\int_0^{h_1}f_1(\tau)V(t-\tau){\rm
d}\tau-(d_1+\sigma)U(t), \\
\displaystyle\frac{{\rm d}V(t)}{{\rm d}t}&= \displaystyle
\beta_2(\frac{A_2}{d_2}-\epsilon)\int_0^{h_2}f_2(\tau)U(t-\tau){\rm
d}\tau-d_2V(t).
\end{array}
|
(9)
|
Let (U(t), V(t)) be the solution of system (9) with initial conditions U(t_1+\theta)=I_D(t_1+\theta) and V(t_1+\theta)
=I_L(t_1+\theta) for all \theta\in[-\tau, 0], by the comparison theorem of functional differential equations([12], Chapter 5, Theorem 1.1) we have
|
I_D(t)\geq U(t), I_L(t)\geq V(t)\;\; \mbox{for all}\;\;
t\geq t_1.
|
From (8), we further have
|
\lim\limits_{t\to\infty}U(t)=0, \lim\limits_{t\to\infty}V(t)=0.
|
(10)
|
Consider the following auxiliary function
|
W(t)=W_1(t)+\frac{d_1+\sigma}{\beta_2(\frac{A_2}{d_2}-\epsilon)}W_2(t),
|
where
|
W_1(t)=U(t)+\beta_1(\frac{A_1}{d_1}-\epsilon)\int_0^{h_1}
f_1(\tau)\int_{t-\tau}^tV(\rho){\rm d}\rho{\rm d}\tau
|
and
|
W_2(t)=V(t)+\beta_2(\frac{A_2}{d_2}-\epsilon)\int_0^{h_2}
f_2(\tau)\int_{t-\tau}^tU(\rho){\rm
d}\rho{\rm d}\tau.
|
Then, from (10) we have
|
\lim\limits_{t\to\infty}W(t)=0.
|
Calculating the derivative of W(t) along the solution of system (9), we have
|
\begin{array}{rl}
\dot{W}(t)&\displaystyle=\dot{W}_1(t)+\frac{d_1+\sigma}{\beta_2(\frac{A_2}{d_2}
-\epsilon)}\dot{W}_2(t)\\
&\displaystyle=
\beta_1(\frac{A_1}{d_1}-\epsilon)\Big[1-\frac{d_1d_2^2(d_1+\sigma)}
{\beta_1\beta_2(A_1-d_1\epsilon)(A_2-d_2\epsilon)}\Big]V(t)\\
&\displaystyle=\beta_1(\frac{A_1}{d_1}-\epsilon)(1-\frac{1}
{(\mathcal{R}_0^{\epsilon})^2})V(t)\\
&>0.
\end{array}
|
Therefore, W(t) increases as t increases. This shows that W(t) does not tend to zero as t\to\infty, which leads a contradiction. Therefore, (7) holds and system (3) satisfies all conditions of Lemma 2. Therefore, system (3) is permanent. Then there exists a constant \eta>0 such that \liminf_{t\to\infty}I_D(t)>\eta. For any positive number \varepsilon<\eta, there is a T>0 such that I_D(t)>\eta-\varepsilon, for all t\geq T.
Next, we prove that system (4) is also permanent. From system (4), we have
|
\frac{{\rm d}S_H(t)}{{\rm d}t}\geq
A_3-\big(\beta_3(\eta-\varepsilon)+d_3\big)S_H, \mbox{for all
}t\geq T+h,
|
it follows that
|
\liminf\limits_{t\to\infty}S_H(t)\geq
\frac{A_3}{\beta_3(\eta-\varepsilon)+d_3}.
|
Using a similar argument as above, we can obtain that
|
\liminf\limits_{t\to\infty}E_H(t)\geq
\frac{\beta_3A_3(\eta-\varepsilon)}{(d_3+\omega)
\big(\beta_3(\eta-\varepsilon)+d_3\big)}
|
and
|
\liminf\limits_{t\to\infty}S_H(t)\geq
\frac{\beta_3\omega A_3(\eta-\varepsilon)}{(d_3+\omega)
\big(\beta_3(\eta-\varepsilon)+d_3\big)(d_3+\mu+\gamma)}.
|
This implies that model (1) is permanent.
6. Global stability of E^*
In this section, we will obtain the stability of endemic equilibrium of model (1). We will use the theory of cooperative systems to prove the global stability of system.
Consider the functional differential equations
|
\frac{d x(t)}{dt}=f(x_t)
|
(11)
|
where f: U\to R^n is a continuously differentiable map on the open subset U of C_r. Denote x(t, \phi) for the unique solution of (11) satisfying x_0=\phi and let [0, \sigma_{\phi}] be its maximal interval of existence. Now we have the following lemma, which can be found in ([26], Theorem 3.2).
Lemma 6.1. Let f:\; C_{\tau}^+\to R^n be a continuously differentiable cooperative map, and let F:\; R^n_+\to R^n be defined by F(x)=f(\hat{x}), x\in R^n_+. Assume that
(1) for any \phi\in C_{\tau}^+ with \phi_i(0)=0, f_i(\phi)\geq 0 and f maps bounded sets into bounded sets;
(2) f:\; C_{\tau}^+\to R^n is sublinear, i.e., for any \alpha\in (0, 1), \phi\in C_r^+, f(\alpha\phi)>\alpha f(\phi), and F:\;R^n_+\to R is strictly sublinear, i.e., for any \alpha\in (0, 1), x\in R^n_+ with x\gg0, F(\alpha x)>\alpha F(x);
(3) f(\hat{0})=0, df(\hat{0}) satisfies (R), and for any x\in R^n_+, DF(x) is irreducible.
(a) If s(DF(0))\leq 0, then \hat{0} is globally asymptotically stable for (11) with respect to c_r^+;
(b) If s(DF(0))>0, then either
( i ) for any \phi\in C_r^+\setminus\{\hat{0}\}, \lim_{t\to\infty}\|x_t(\phi)\|=+\infty, or alternatively,
( ii ) (11) admits a unique positive steady state \hat{x}^* with \hat{x}^*\gg 0 and \hat{x}^* is globally asymptotically stable with respect to C_r^+\setminus\{\hat{0}\}.
We further have the following result on the stability of the endemic equilibrium.
Theorem 6.2. If \mathcal{R}_0>1, then endemic equilibrium E^* of model (1) is globally asymptotically stable.
Proof. We still start by considering system (3). It is easily proved that S_D(t)+I_D(t)\to A_1/d_1 and S_L(t)+I_L(t)\to A_2/d_2 as t\to\infty. Therefore, in system (4) we can represent S_D(t) and S_L(t) by A_1/d_1-I_D(t) and A_2/d_2-S_L(t), respectively, then system (3) reduces to the following system with two equations:
|
\left\{
\begin{array}{rl}
\displaystyle \frac{{\rm d}I_D(t)}{{\rm d}t}=
&\displaystyle\beta_1\Big(\frac{A_1}{d_1}-I_D(t)\Big)\int_0^{h_1}
f_1(\tau)I_L(t-\tau){\rm d}\tau-(d_1+\sigma)I_D(t), \\
\displaystyle\frac{{\rm d}I_L(t)}{{\rm d}t}=
&\displaystyle\beta_2\Big(\frac{A_2}{d_2}-I_L(t)\Big)\int_0^{h_2}f_2(\tau)
I_D(t-\tau){\rm d}\tau-d_2I_L(t).
\end{array}\right.
|
(12)
|
By Lemma 3.1, the dynamics of system (12) can be focused on the following restricted region
|
\Omega=\{(I_D, I_L):0\leq I_D\leq \frac{A_1}{d_1},
\ 0\leq I_L\leq \frac{A_2}{d_2}\}.
|
We will use Lemma 6.1 to prove the global stability of system (12). We only need to verify all assumptions in Lemma 6.1 for system (12). Consider the following equation
where x(t)=\big(I_D(t), I_L(t)\big)^T and f: C([-h, 0], R^2_+)\to
R^2 is defined by
|
f(\phi)=\left(\begin{array}{c}
f_1(\phi)\\
f_2(\phi)
\end{array}\right)=\left(\begin{array}{c}
\displaystyle\beta_1\Big(\frac{A_1}{d_1}-\phi_1(0)\Big)\int_{t-h_1}^{t}
f_1(t-s)\phi_2(s){\rm d}s-(d_1+\sigma)\phi_1(0)\\
\displaystyle\beta_2\Big(\frac{A_2}{d_2}-\phi_2(0)\Big)\int_{t-h_1}^{t}f_2(t-s)
\phi_1(s){\rm d}s-d_2\phi_2(0)
\end{array}\right).
|
Let
|
F(x)=\left(\begin{array}{c} F_1(x_1, x_2)\\
F_2(x_1, x_2)
\end{array}\right)=\left(\begin{array}{c}
\displaystyle\beta_1\big(\frac{A_1}{d_1}-x_1\big)x_2-(d_1+\sigma)x_1\\
\displaystyle\beta_2\big(\frac{A_2}{d_2}-x_2\big)x_1-d_2x_2
\end{array}\right).
|
For any \phi, \psi\in C([-h, 0], R^2_+), we have
|
\begin{array}{rcl}
df_1(\psi)\phi&=&\displaystyle-\beta_1\phi_1(0)
\int_{t-h_1}^tf_1(t-s)\psi_2(s)ds\\
&&\displaystyle+\beta_1\Big(\frac{A_1}{d_1}-\psi_1(0)\Big)
\int_{t-h_1}^tf_1(t-s)\phi_2(s)ds
-(d_1+\sigma)\phi_1(0), \\
df_2(\psi)\phi&=&\displaystyle-\beta_2\phi_2(0)
\int_{t-h_2}^tf_2(t-s)\psi_1(s)ds\\
&&\displaystyle+\beta_2\Big(\frac{A_2}{d_2}-\psi_2(0)\Big)
\int_{t-h_2}^tf_2(t-s) \phi_1(s)ds -d_2\phi_2(0).
\end{array}
|
Hence, for any \psi(0)\in (0, A_1/d_1) and \phi\in
C([-h, 0], R^2_+) with \phi(0)=0, we have
|
df_1(\psi)\phi=\beta_1\Big(\frac{A_1}{d_1}-\psi_1(0)\Big)
\int_{t-h_1}^tf_1(t-s)\phi_2(s)ds>0
|
and
|
df_2(\psi)\phi=
\beta_2\Big(\frac{A_2}{d_2}-\psi_2(0)\Big)\int_{t-h_2}^tf_2(t-s)
\phi_1(s)ds>0,
|
which imply that f is a cooperative map. For any \phi\in
C([-h, 0], R^2_+) with \phi(0)=0, we have
|
\begin{array}{c}
\displaystyle f_1(\phi)=\frac{\beta_1A_1}{d_1}\int_{t-h_1}^{t}
f_1(t-s)\phi_2(s){\rm d}s\geq0, \\
\displaystyle f_2(\phi)= \frac{\beta_2A_2}{d_2}
\int_{t-h_1}^{t}f_2(t-s) \phi_1(s){\rm d}s\geq0.
\end{array}
|
It is easy to see from the expression of f that f maps bounded sets in C([-h, 0], R^2_+) into bounded sets in R^2_+. For any \alpha\in (0, 1) and \phi\in C([-h, 0], R^2_+) we have
|
\begin{array}{rcl}
f_1(\alpha\phi)&=&\displaystyle\beta_1\Big(\frac{A_1}{d_1}
-\alpha\phi_1(0)\Big)\int_{t-h_1}^{t}
f_1(t-s)\alpha\phi_2(s){\rm d}s-(d_1+\sigma)\alpha\phi_1(0)\\
&\geq&\displaystyle\beta_1\Big(\frac{A_1}{d_1}
-\phi_1(0)\Big)\int_{t-h_1}^{t}
f_1(t-s)\alpha\phi_2(s){\rm d}s-(d_1+\sigma)\alpha\phi_1(0)\\
&=&\alpha f_1(\phi).
\end{array}
|
Using the same argument, we can show that f_2(\alpha\phi)\geq\alpha f_2(\phi). Therefore, the functional f is sublinear. For x\in R_+^2 with x\gg 0, we have
|
\begin{array}{rcl}
F_1(\alpha x)&=&\displaystyle\beta_1\big(\frac{A_1}{d_1}-\alpha
x_1\big)\alpha x_2-(d_1+\sigma)\alpha x_1\\
&>&\displaystyle
\alpha[\beta_1\big(\frac{A_1}{d_1}-x_1\big)x_2-(d_1+\sigma)x_1]=\alpha
F_1(x)
\end{array}
|
and
|
\begin{array}{rcl}
F_2(\alpha x)&=&\displaystyle\beta_2\big(\frac{A_2}{d_2}-\alpha x_2\big)\alpha
x_1-d_2\alpha x_2\\
&>&\displaystyle
\alpha[\beta_2\big(\frac{A_2}{d_2}-x_2\big)x_1-d_2x_2]=\alpha
F_2(x).
\end{array}
|
This shows that F is strictly sublinear. Since f(\hat{0})=0 and for any \phi\in C([-h, 0], R^2_+),
|
\begin{array}{rcl}
df_1(\hat{0})\phi&=&\displaystyle\frac{\beta_1A_1}{d_1}
\int_{t-h_1}^tf_1(t-s)\phi_2(s)ds
-(d_1+\sigma)\phi_1(0), \\
df_2(\hat{0})\phi&=&\displaystyle\frac{\beta_2A_2}{d_2}\int_{t-h_2}^tf_2(t-s)
\phi_1(s)ds -d_2\phi_2(0),
\end{array}
|
it is easy to see that df(\hat{0}) satisfies assumption (R) in [26]. By computing DF(x), we have
|
DF(x)=\left(\begin{array}{cc}
\displaystyle-(d_1+\sigma)-\frac{\beta_1A_1}{d_1}x_2&
\displaystyle\beta_1(\frac{A_1}{d_1}-x_1)\\
\displaystyle\beta_2(\frac{A_2}{d_2}-x_2)&
\displaystyle-d_2-\frac{\beta_2A_2}{d_2}x_1
\end{array}\right).
|
Clearly, DF(x) is irreducible for x\in \Omega. Since
|
DF(0)=\left(\begin{array}{cc}
\displaystyle-(d_1+\sigma)&\displaystyle\frac{\beta_1A_1}{d_1}\\
\displaystyle\frac{\beta_2A_2}{d_2}&\displaystyle-d_2
\end{array}\right),
|
the characteristic equation of DF(0) is
|
\det(\lambda I-DF(0))=\lambda^2+a_1\lambda+a_0=0,
|
where
|
\begin{array}{l}
\displaystyle a_1=d_1+d_2+\sigma, \\
\displaystyle
a_0=d_2(d_1+\sigma)-\frac{\beta_1\beta_2A_1A_2}{d_1d_2}=d_2(d_1+\sigma)
(1-\mathcal{R}_0^2).
\end{array}
|
When \mathcal{R}_0>1, we have a_0<0. Hence, s(DF(0)):=\max\{\mbox{Re}\;\lambda: \det(\lambda I-DF(0))=0\}>0. By Lemma 6.1, one can conclude that the equilibrium (I_D^*, I_L^*) of system (12) is globally asymptotically stable. According to the theory of asymptotic autonomous systems [15], we further obtain that endemic equilibrium (S_D^*, I_D^*, S_L^*, I_L^*) is globally attractive for system (3).
Next, when t\to\infty, the limiting system of equation (4) is
|
\left\{\begin{array}{rcl}
\displaystyle \frac{dS_H(t)}{dt}&=&A_3-\beta_3S_H I_D^*-d_3 S_H
+\gamma I_H,\\
\displaystyle \frac{dE_H(t)}{dt}&=&\beta_3S_H I_D^*-(d_3+\omega)E_H, \\
\displaystyle \frac{dI_H(t)}{dt}&=&\omega E_H-(d_3+\mu+\gamma)I_H.
\end{array}\right.
|
(13)
|
Let U(t)=S_H(t)-S_H^*, V(t)=I_H(t)-I_H^*, W(t)=E_H(t)-E_H^*, we can transform equation (13) into the following system
|
\left\{\begin{array}{rcl}
\displaystyle \frac{dU(t)}{dt}&=&-(\beta_3I_D^*+d_3)U(t)+\gamma V(t), \\
\displaystyle \frac{dW(t)}{dt}&=&\beta_3I_D^*U(t)-(d_3+\omega)W(t), \\
\displaystyle \frac{dV(t)}{dt}&=&\omega W(t)-(d_3+\mu+\gamma)V(t).
\end{array}\right.
|
(14)
|
The Jacobian matrix of equation (14) at (0, 0, 0) is
|
J|_{(0, 0, 0)}=\left(\begin{array}{ccc}
-\beta_3I_D^*-d_3& 0& \gamma\\
\beta_3I_D^*&-(d_3+\omega)&0\\
0&\omega&-(d_3+\mu+\gamma)
\end{array}\right).
|
The characteristic equation is
|
\phi(\lambda)=\lambda^3+a_2\lambda^2+a_1\lambda+a_0=0,
|
where
|
\begin{array}{l}
a_2=3d_3+\beta_3I_D^*+\omega+\mu+\gamma, \\
a_1=(\beta_3I_D^*+d_3)(d_3+\omega)+(\beta_3I_D^*+d_3)(d_3+\mu+\gamma)
+(d_3+\omega)(d_3+\mu+\gamma), \\
a_0=(\beta_3I_D^*+d_3)(d_3+\omega)(d_3+\mu+\gamma)-\beta_3I_D^*\omega\gamma.
\end{array}
|
It is clear that a_0, a_1, a_2>0, and by simple computation, we have
|
\begin{array}{rl}
a_1a_2-a_0=&6d_3\omega\gamma+2\omega\mu\gamma+4d_3\mu\gamma
+6d_3\omega\mu+6\beta_3I_D^*d_3\omega+6\beta_3 I_D^*d_3\mu\\
&+6\beta_3I_D^*d_3\gamma+2\beta_3I_D^*\omega\mu+2\beta_3I_D^*\omega\gamma
+2\beta_3I_D^*\mu\gamma+2\beta_3^2{I_D^*}^2d_3\\
&+8\beta_3I_D^*d_3^2+\beta_3^2{I_D^*}^2\omega
+\beta_3I_D^*\omega^2+\beta_3^2{I_D^*}^2\mu+\beta_3I_D^*\mu^2\\
&+\beta_3^2{I_D^*}^2\gamma+\beta_3I_D^*\gamma^2+8d_3^3
+8d_3^2\omega+8d_3^2\mu+8d_3^2\gamma+2d_3\omega^2\\
&+2d_3\mu^2+2d_3\gamma^2+\omega^2\mu+\omega\mu^2
+\omega^2\gamma+\omega\gamma^2\\
>&0.
\end{array}
|
Hence, by Routh-Hurwitz criteria, all roots of \phi(\lambda)=0 have negative real parts. Furthermore, by the stability theory of linear differential equations, it follows that (0, 0, 0) is globally attractive for equation (14). Therefore, (S_H^*, E_H^*, I_H^*) is also globally attractive for equation (13). According to theory of asymptotic autonomous systems [15], we finally obtain that endemic equilibrium E^*(S_D^*, I_D^*, S_L^*, I_L^*, S_H^*, E_H^*, I_H^*) of model (1) is globally asymptotically stable.
7. Numerical simulations
In this section, we shall estimate the parameters of model (1) and study the transmission trend of the disease in Xinjiang, China. From Xinjiang Center for Disease Control and Prevention (Xinjiang CDC) [22], we have obtained the monthly numbers of reported Echinococcosis cases from January 2004 to December 2011 (see Figure 2).
As an illustration, we take the parameters in Table 3 and give a few necessary comments:
Table 3. Parameters and their values (unit: month−1).
| Parameters |
Value |
Comments |
Source |
| A_1 |
1.34\times 10^4 |
recruitment rate for dog |
[25] |
| d_1 |
0.0067 |
dog natural mortality rate |
[1] |
| \beta_1 |
6.3\times10^{-10} |
livestock to dog transmission rate |
fitting |
| \sigma |
1/6 |
recovery rate from infected to non-infected dogs |
[13] |
| A_2 |
8.7\times10^{6} |
recruitment rate for livestock |
[10] |
| d_2 |
0.0275 |
livestock mortality rate |
assumption |
| \beta_2 |
2.8\times10^{-8} |
parasite egg-to-livestock transmission rate |
fitting |
| h_1 |
1/3 |
survival time of larval cysts into the infection offal |
[6] |
| h_2 |
1.17 |
average life expectancy for Echinococcus eggs |
[17] |
| A_3 |
2\times10^{4} |
human annual birth population |
[2] |
| d_3 |
0.0012 |
human natural mortality rate |
[14] |
| \omega |
1/(14\times12) |
human incubation period |
[13] |
| \mu |
0.0793% |
human disease-related death rate |
[5] |
| \gamma |
0.0625 |
treatment/recovery rate |
assumption |
| \beta_3 |
2.96\times10^{-12} |
parasite egg-to-human transmission rate |
fitting |
(a) The number of dogs in Xinjiang, China was estimated to be 2 millions in 2004 [25]. The average life expectancy of dogs was 12.5 years [1]. Thus, d_1=1/(12.5\times12)=0.0067. We estimated the capacity of dogs in Xinjiang, China to be 2 millions. Thus, A_1\thickapprox2000000\times0.0067=1.34\times 10^4. The adult Echinococcus granulosus resided in the small bowel of the dogs and its life expectancy was about 5-6 months [13]. We select 6 months. So, the recovery rate \sigma=1/6.
(b) According to China Statistical Yearbook [10], the recruitment rate A_2 for livestock population was estimated to be 8.7\times 10^6 and the mortality rate of livestock d_2 was estimated to be 0.0275.
(c) The average survival time of larval cysts into the infection offal thrown in the environment is assumed to be 7-10 days [6]. We select h_1=1/3. Life expectancy is assumed to be 35 days for parasite eggs [17]. So h_2=35/30=1.17.
(d) The average life expectancy of people in Xinjiang Uygur Autonomous Region of China was 71.12 years in 2005 [14]. We take it as the current average life expectancy. Thus, d_3=1/
(71.12\times12)=0.0012. According to the data of the Sixth Census of China [2], human annual birth population in Xinjiang, China was 2.4\times10^5, that is A_3=(2.4\times10^5)/12=2\times10^4. The incubation period of Echinococcosis can be months to years or even decades. We select 14 years [13].
(e) The parameters \beta_1, \beta_2 and \beta_3 are obtained by fitting the model to data. We first apply the Runge-Kutta method to obtain the numerical expression formula of model (1) with parameters \beta_1, \beta_2 and \beta_3, then by the least-square estimation the estimation values of \beta_1, \beta_2 and \beta_3 are given through MATLAB implementation.
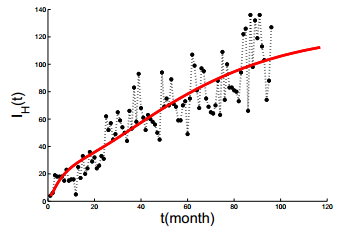
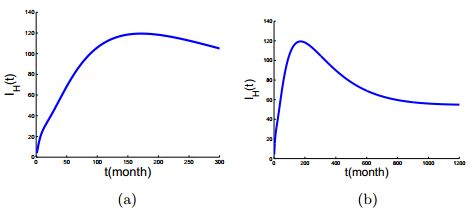
The numerical simulation of the model on the number of human Echinococcosis cases is shown in Figure 3. We can predict the general tendency of the epidemic in a long term according to the current situation, which is presented in Figure 4. It shows that the number of human Echinococcosis cases will increase steadily in the next 6 or 7 years, then reach the peak (about 120) in 2017 and begin a slow decline, and finally become stable.
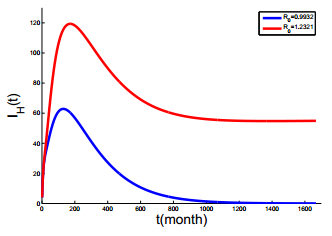
Moreover, with these parameter values, we can roughly estimate the basic reproduction number \mathcal{R}_0=1.23 for model (1) under the current circumstances in Xinjiang, China. This indicates that human Echinococcosis is endemic in Xinjiang, China: it stabilizes and is approaching its equilibrium. Therefore, if no further effective prevention and control measures are taken, the disease will not vanish. From Figure 5, we can see that when \mathcal{R}_0<1 the number of Echinococcosis humans I_H(t) tends to 0. On the contrary, when \mathcal{R}_0>1, I_H(t) tends to a stable equilibrium. We can see that \mathcal{R}_0 is really the threshold for the establishment of the disease and the number of infections increases with the increase of \mathcal{R}_0.
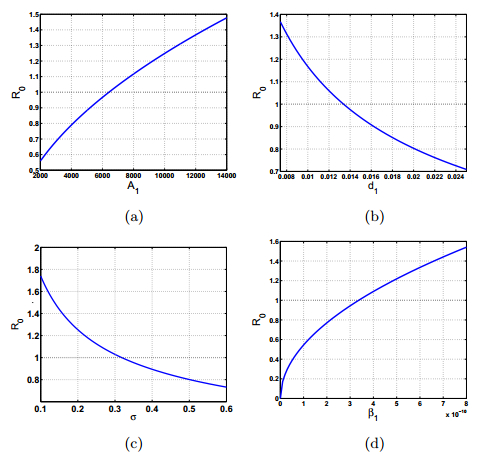
Next, to find better control strategies for Echinococcosis infection, we perform some sensitivity analysis to determine the influence of parameters A_1, d_1, \sigma and \beta_1 on \mathcal{R}_0. From Figure 6 we can see that \mathcal{R}_0 decreases if A_1 decreases, or d_1 increases, or \sigma increases, or \beta_1 decreases. From Figure 6(a), it is obvious that when A_1 is less than 6500, \mathcal{R}_0 can be less than 1. However, the recruitment rate of dogs can achieve 13400 in Xinjiang, China. This indicates that human Echinococcosis in Xinjiang, China cannot be eradicated if recruitment rate of dogs cannot be controlled under 6500. From Figure 6(d), we can see that when \beta_1 is less than 3.5\times 10^{-10}, \mathcal{R}_0 can be less than 1. In order to decrease the parameter \beta_1, we have the following measures. Dogs should be barred from slaughter houses and should not be fed uncooked offal. Infection carcasses and offal should be burned or buried. The parameter \sigma can be increased through increasing the frequency of dog anthelmintic.
8. Discussion
In this paper, in order to understand how Echinococcosis spreads in the real world and forecast the disease trends, we propose a novel spreading model for Echinococcosis with distributed time delays. We calculated the basic reproduction number \mathcal{R}_0. The mathematical results show that the dynamics of the model is completely determined by \mathcal{R}_0. If \mathcal{R}_0<1, the disease-free equilibrium is globally asymptotically stable, and if \mathcal{R}_0>1, the model is permanence and endemic equilibrium is globally asymptotically stable.
With suitable parameter values, we estimated the basic reproduction number to be R_0=1.23 in Xinjiang, China for model (1). Moreover, sensitivity analysis demonstrates that Echinococcosis can be controlled with several strategies which can change four parameters A_1, d_1, \beta_1 and \sigma(see Figure 6). From Figure 3 we can see that our model matches the trend of monthly data for human Echinococcosis cases well. However, model (1) cannot simulate the oscillations of the data. Therefore, extension of our framework to include the stochastic disturbance is an interesting future work. We hope this work would lead to a better understanding of transmission of Echinococcosis.
Acknowledgments
This research was supported by the The Natural Science Foundation of Xinjiang [2015211C031].









 DownLoad:
DownLoad: