Mathematical Biosciences and Engineering, 2017, 14(3): 709-733. doi: 10.3934/mbe.2017040

Export file:

Format

RIS(for EndNote,Reference Manager,ProCite)
BibTex
Text

Content

Citation Only
Citation and Abstract

Mathematical analysis and dynamic active subspaces for a long term model of HIV

1. School of Mathematics, University of Minnesota-Twin Cities, 127 Vincent Hall, 206 Church St. SE, Minneapolis, MN 55455, USA
2. Department of Applied Mathematics and Statistics, Colorado School of Mines, 1500 Illinois St, Golden, CO 80401, USA

Received: , Accepted: , Published:

Abstract Full Text(HTML) Figure/Table Related pages

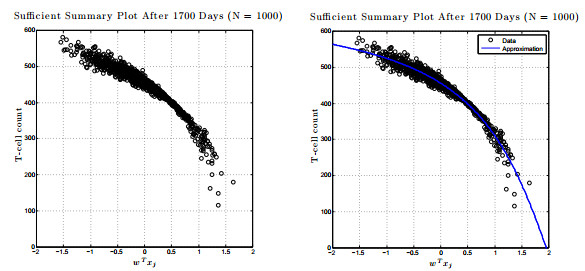
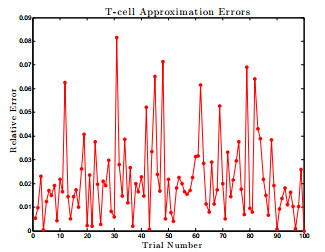
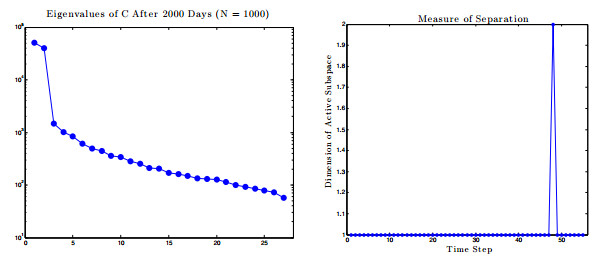
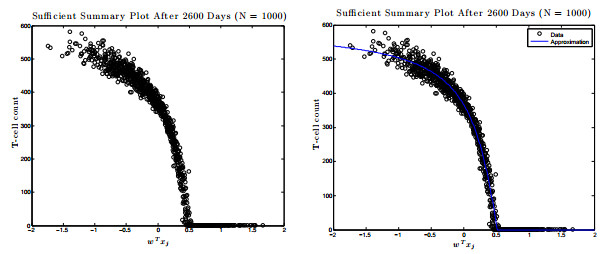
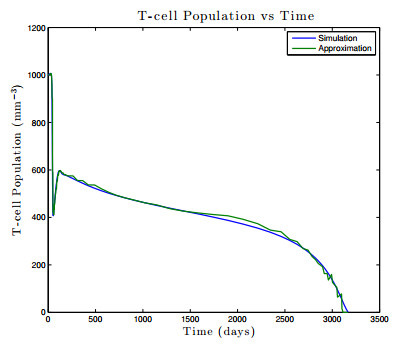
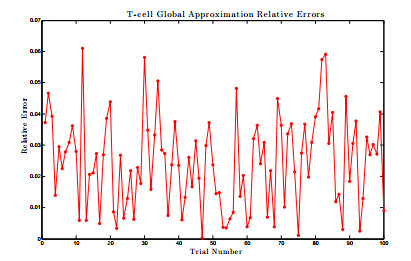
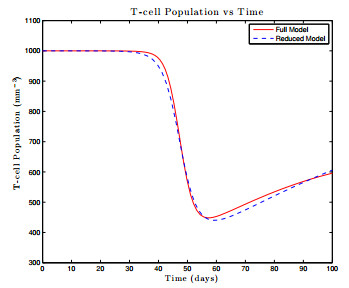
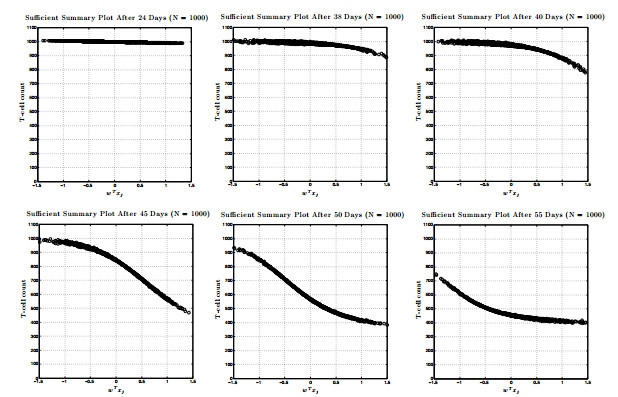
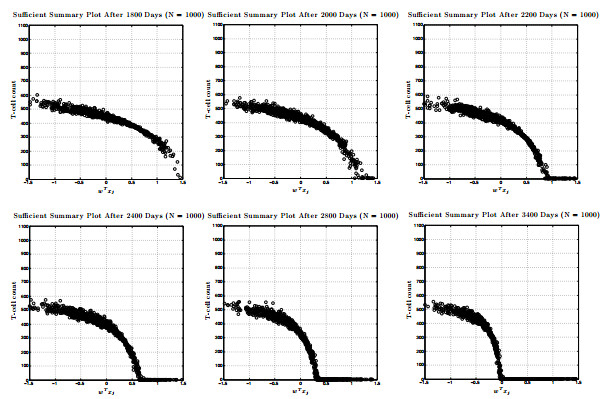
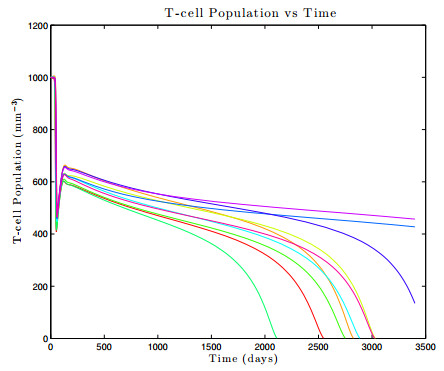
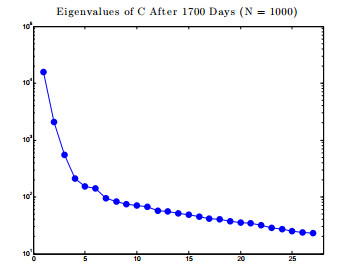
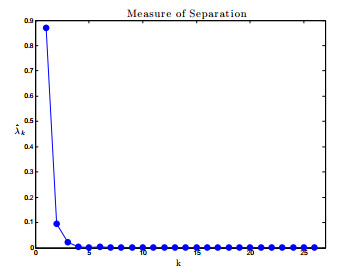
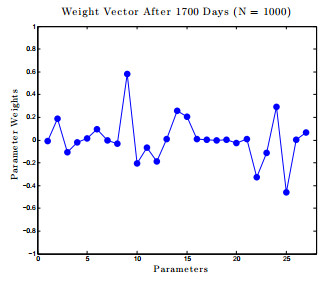
Recently, a long-term model of HIV infection dynamics [8] was developed to describe the entire time course of the disease. It consists of a large system of ODEs with many parameters, and is expensive to simulate. In the current paper, this model is analyzed by determining all infection-free steady states and studying the local stability properties of the unique biologically-relevant equilibrium. Active subspace methods are then used to perform a global sensitivity analysis and study the dependence of an infected individual's T-cell count on the parameter space. Building on these results, a global-in-time approximation of the T-cell count is created by constructing dynamic active subspaces and reduced order models are generated, thereby allowing for inexpensive computation.

Figure/Table

Supplementary

Article Metrics

References

[1] D. Callaway,A. Perelson, HIV-1 infection and low steady state viral loads, Bull.Math.Biol., 64 (2002): 29-64.

[2] P. Constantine, Active Subspaces: Emerging Ideas for Dimension Reduction in Parameter Studies SIAM, 2015.

[3] P. Constantine and D. Gleich, Computing active subspaces with monte carlo, arXiv: 1408.0545

[4] P. Constantine,B. Zaharatos,M. Campanelli, Discovering an active subspace in a single-diode solar cell model, Statistical Analysis and Data Mining: The ASA Data Science Journal, 8 (2015): 264-273.

[5] A. S. Fauci,G. Pantaleo,S. Stanley, Immunopathogenic mechanisms of HIV infection, Annals of Internal Medicine, 124 (1996): 654-663.

[6] T. C. Greenough,D. B. Brettler,F. Kirchhoff, Long-term non-progressive infection with Human Immunodeficiency Virus in a Hemophilia cohort, J Infect Dis, 180 (1999): 1790-1802.

[7] A. B. Gumel,P. N. Shivakumar,B. M. Sahai, A mathematical model for the dynamics of HIV-1 during the typical course of infection, Nonlinear Analysis, 47 (2001): 1773-1783.

[8] M. Hadjiandreou,R. Conejeros,V. S. Vassiliadis, Towards a long-term model construction for the dynamic simulation of HIV infection, Mathematical Biosciences and Engineering, 4 (2007): 489-504.

[9] E. Hernandez-Vargas,R. Middleton, Modeling the three stages in HIV infection, J TheorBiol., 320 (2013): 33-40.

[10] T. Igarashi,C. R. Brown,Y. Endo, Macrophages are the principal reservoir and sustain high virus loads in Rhesus Macaques following the depletion of CD4+ T-cells by a highly pathogenic SIV: Implications for HIV-1 infections of man, Proc Natl Acad Sci., 98 (2001): 658-663.

[11] E. Jones and P. Roemer (sponsors: S. Pankavich and M. Raghupathi), Analysis and simulation of the three-component model of HIV dynamics, SIAM Undergraduate Research Online, 7 (2014), 89–106

[12] D. Kirschner, Using mathematics to understand HIV immunodynamics, Am. Math. Soc., 43 (1996): 191-202.

[13] D. E. Kirschner and A. S. Perelson, A model for the immune response to HIV: AZT treatment studies, Mathematical Population Dynamics: Analysis of Heterogeneity, Volume One: Theory of Epidemics Eds. O. Arino, D. Axelrod, M. Kimmel, and M. Langlais, Wuerz Publishing Ltd., Winnipeg, Canada, (1993), 295–310.

[14] D. Kirschner,G. F. Webb, Immunotherapy of HIV-1 infection, J Biological Systems, 6 (1998): 71-83.

[15] D. Kirschner,G. F. Webb,M. Cloyd, A model of HIV-1 disease progression based on virus-induced lymph node homing-induced apoptosis of CD4+ lymphocytes, J Acquir Immune Dec Syndr, 24 (2000): 352-362.

[16] J. M. Murray,G. Kaufmann,A. D. Kelleher, A model of primary HIV-1 infection, Math Biosci, 154 (1998): 57-85.

[17] M. Nowak and R. May, Virus Dynamics: Mathematical Principles of Immunology and Virology Oxford University Press, NewYork, 2000.

[18] S. Pankavich, The effects of latent infection on the dynamics of HIV, Differential Equations and Dynamical Systems, 24 (2016): 281-303.

[19] S. Pankavich,D. Shutt, An in-host model of HIV incorporating latent infection and viral mutation, Dynamical Systems, Differential Equations, and Applications, AIMS Proceedings, null (2015): 913-922.

[20] S. Pankavich, N. Neri and D. Shutt, Bistable dynamics and Hopf bifurcation in a refined model of the acute stage of HIV infection, submitted, (2015).

[21] S. Pankavich,C. Parkinson, Mathematical analysis of an in-host model of viral dynamics with spatial heterogeneity, Discrete and Continuous Dynamical Systems B, 21 (2016): 1237-1257.

[22] E. Pennisi and J. Cohen, Eradicating HIV from a patient: Not just a dream?, Science, 272 (1996), 1884.

[23] A. S. Perelson, Modeling the Interaction of the Immune System with HIV, Lecture Notes in Biomath. Berlin: Springer, 1989.

[24] A. Perelson,P. Nelson, Mathematical analysis of HIV-1 dynamics in vivo, SIAM Rev., 41 (1999): 3-44.

[25] T. M. Russi, Uncertainty Quantification with Experimental data and Complex System Models, Ph. D. thesis, UC Berkeley, 2010.

[26] W. Y. Tan,H. Wu, Stochastic modeing of the dynamics of CD4+ T-cell infection by HIV and some monte carlo studies, Math Biosci, 147 (1997): 173-205.

[27] E. Vergu,A. Mallet,J. Golmard, A modeling approach to the impact of HIV mutations on the immune system, Comput Biol Med., 35 (2005): 1-24.

Copyright Info: © 2017, Stephen Pankavich, et al., licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution Licese (http://creativecommons.org/licenses/by/4.0)

Download full text in PDF

Export Citation

Article outline

Show full outline