Figure 1.
The solution curves of (5.1) with $ b_2 = -0.3 $ and $ \det(C) = 0\geq0 $.
Citation: Guihong Fan, Yijun Lou, Horst R. Thieme, Jianhong Wu. Stability and persistence in ODE modelsfor populations with many stages[J]. Mathematical Biosciences and Engineering, 2015, 12(4): 661-686. doi: 10.3934/mbe.2015.12.661
| [1] | Gonzalo Robledo . Feedback stabilization for a chemostat with delayed output. Mathematical Biosciences and Engineering, 2009, 6(3): 629-647. doi: 10.3934/mbe.2009.6.629 |
| [2] | Yun Hu, Qianqian Duan . Solving the TSP by the AALHNN algorithm. Mathematical Biosciences and Engineering, 2022, 19(4): 3427-3448. doi: 10.3934/mbe.2022158 |
| [3] | Masaki Sekiguchi, Emiko Ishiwata, Yukihiko Nakata . Dynamics of an ultra-discrete SIR epidemic model with time delay. Mathematical Biosciences and Engineering, 2018, 15(3): 653-666. doi: 10.3934/mbe.2018029 |
| [4] | Luyao Li, Licheng Fang, Huan Liang, Tengda Wei . Observer-based event-triggered impulsive control of delayed reaction-diffusion neural networks. Mathematical Biosciences and Engineering, 2025, 22(7): 1634-1652. doi: 10.3934/mbe.2025060 |
| [5] | Yuan Ma, Yunxian Dai . Stability and Hopf bifurcation analysis of a fractional-order ring-hub structure neural network with delays under parameters delay feedback control. Mathematical Biosciences and Engineering, 2023, 20(11): 20093-20115. doi: 10.3934/mbe.2023890 |
| [6] | Huaying Liao, Zhengqiu Zhang . Finite-time stability of equilibrium solutions for the inertial neural networks via the figure analysis method. Mathematical Biosciences and Engineering, 2023, 20(2): 3379-3395. doi: 10.3934/mbe.2023159 |
| [7] | Bingrui Zhang, Jin-E Zhang . Fixed-deviation stabilization and synchronization for delayed fractional-order complex-valued neural networks. Mathematical Biosciences and Engineering, 2023, 20(6): 10244-10263. doi: 10.3934/mbe.2023449 |
| [8] | Sheng Wang, Lijuan Dong, Zeyan Yue . Optimal harvesting strategy for stochastic hybrid delay Lotka-Volterra systems with Lévy noise in a polluted environment. Mathematical Biosciences and Engineering, 2023, 20(4): 6084-6109. doi: 10.3934/mbe.2023263 |
| [9] | Toshikazu Kuniya, Tarik Mohammed Touaoula . Global stability for a class of functional differential equations with distributed delay and non-monotone bistable nonlinearity. Mathematical Biosciences and Engineering, 2020, 17(6): 7332-7352. doi: 10.3934/mbe.2020375 |
| [10] | Yuanpei Xia, Weisong Zhou, Zhichun Yang . Global analysis and optimal harvesting for a hybrid stochastic phytoplankton-zooplankton-fish model with distributed delays. Mathematical Biosciences and Engineering, 2020, 17(5): 6149-6180. doi: 10.3934/mbe.2020326 |
It is well known that stability properties of Hopfield-type neural networks (see, for example, [1], [2]) have been widely used in optimization problems, associative memory, pattern recognition and signal processing (see, for example, [3], [4], [5], [6], [7]). Early researches on stability of the equilibria of Hopfield-type neural networks mainly involves ordinary differential equations. However, time delays are inevitable in the propagation of electrical signals between neurons or in complex signal processing. Therefore, time delays are commonly found in artificial neural networks. At the same time, a large number of theoretical studies show that time delays may have complicated and unpredictable impacts on local or global dynamics of neural networks. Time delays may destroy stability properties of the equilibria of neural networks and cause their orbits to oscillate and even become chaotic etc.
Due to both the universality of time delays in the real world and the importance of constructing the neural networks, many mathematical researchers have paid great attention to Hopfield-type neural networks with time delays and a great amount of results have been achieved (see, for example, [8], [9], [10], [11], [12], [13], [14], [15], [16], [17], [18]).
Compared with continuous Hopfield-type neural networks, theoretical studies on discrete Hopfield-type neural networks are much less. However, discrete Hopfield-type neural networks may have rich kinetic behavior.
In an ideal case, the discrete Hopfield-type neural networks should be produced in a way to reflect the dynamics of the continuous counterparts. Specifically, the discrete networks should inherit the dynamical characteristics of the continuous networks, and also maintain functional similarity to the continuous system and any physical or biological reality that the continuous has[19]. However, unfortunately, as pointed out in [20], discrete neural networks can hardly maintain the dynamics of continuous counterparts even during very short sampling periods. Therefore, it is crucial to study the similarity of the dynamic properties between the discrete neural networks and the continuous counterparts.
It should be mentioned that, based on the analytical method on the distribution of the roots of transcendental functions developed in [24], some sharp conditions are obtained for delay independent stability of a class of additive neural networks are given in [25].
In [26], [27], [28] and [29], by constructing suitable nonlinear algebraic equations and using the results in [25] and the properties of $ M $-matrix in [30], some sufficient conditions and necessary conditions for global attractivity of retarded and neutral Hopfield-type neural networks are obtained.
The purpose of the short paper is to extend the methods in [24], [25], [26], [27], [28] and [29] to the analysis for global attractivity of a class of discrete Hopfield-type neural networks with time delays. This paper is organized as follows. In Section 2, a class of discrete Hopfield-type neural networks with time delays and some basic assumptions are given. Then, ultimate boundedness of the solutions of the discrete neural networks is considered by establishing a class of related nonlinear algebraic equations. At the same time, for convenience, some equivalent conditions of $ M $-matrix are introduced. In Section 3, global attractivity of the discrete neural networks is discussed, and a sufficient condition is given. In Section 4, necessary conditions for stability of the discrete neural networks are obtained. To prove the necessary conditions, several important lemmas similar to [24] and [25] have been extended to the discrete neural networks. Finally, in Section 5, a $ 3 $-dimensional discrete Hopfield-type neural networks with time delays is considered by the method of numerical simulations. The numerical simulations show that, under certain conditions, the sufficient condition is very close to the necessary condition.
The following $ n $-dimensional discrete Hopfield-type neural networks with time delays is considered,
| $ Ui(k+1)=biUi(k)+n∑j=1aijfj(Uj(k−τij))(i=1,2,⋯,n;k∈Z+). $ | (2.1) |
In (2.1), $ \mathbb{Z_+} $ denotes the set of all nonnegative integers. $ U_{i}(k) $ denotes the potential(or voltage) of the $ i $th neuron at time $ k $. $ b_{i} $ is the real constant which represents the $ i $th neuron receives itself's feedback. $ a_{ij} $ is the real constant which represents the synaptic connection weight between the $ j $th neuron and the $ i $th neuron. $ f_{j}(U) $ denotes the nonlinear processing function in the dendrites of neurons. The time delay $ \tau_{ij} $ is the nonnegative integer which represents the signal propagation delay from $ j $th neuron to $ i $th neuron. As pointed out in [1], $ f_{j}(U) $ can be regarded as a smooth input-output function because the biological information in neurons often lies in a short-time average of the firing rate[21]. Hence, $ f_{j}(U) $ can be regarded as a continuously differentiable function with respect to the variable $ U $. Based on biological meanings, it is assumed that the following conditions are satisfied.
(H$ _{\text{1}} $) $ |b_{i}| < 1\; (i = 1, 2, ..., n) $.
(H$ _{\text{2}} $) $ f_{i}(0) = 0, $ $ |f_{i}(U)|\leq 1 $ $ (U \in \mathbb{R}) $, $ \mathop {\lim }\limits_{U \to -\infty}f_{i}(U) = -1, $ $ \mathop {\lim }\limits_{U \to +\infty}f_{i}(U) = 1 $ $ (i = 1, 2, ..., n). $
(H$ _{\text{3}} $) $ f_{i}^{\prime }(U) > 0 $ $ (U \in \mathbb{R}) $, $ f_{i}^{\prime }(0) = \mathop{\sup}\limits_{U\in\mathbb{R}} f_{i}^{\prime }(U) = 1 $ $ (i = 1, 2, ..., n). $
Remark 2.1. Based on [22] and [23], the constant $ b_{i} $ represents the rate with which the $ i $th neuron will reset its potential(or voltage) to the resting state in isolation when disconnected from the networks. Hence, the assumption (H$ _{\text{1}} $) is reasonable in biology. Moreover, according to [2] the nonlinear processing function $ f_{j} $ can be considered as some sigmoidal function with saturation properties. Therefore, the assumptions (H$ _{\text{2}} $) and (H$ _{\text{3}} $) have rationality in biology.
Remark 2.2 For convenience, and without losing the generality of theoretical analysis, it is assumed that the external inputs are equal to $ 0 $ in (2.1). When there are constant external inputs in (2.1), similar to [22] and [25], the neural networks can be transformed to a system similar to (2.1) without external inputs.
The initial condition for (2.1) is given as $ u_{i}(s) = \phi_{i}(s), \; \; (s = -r, -r+1, \cdots, 0, \; i = 1, 2, \cdots, n), $ where $ \phi_{i}(s) $ are given real constants, $ r = \max \{\tau_{ij}\; |\; i, j = 1, 2, \cdots, n\} $. It is clear that the solution $ U(k) = (U_{1}(k), U_{2}(k), \cdots, U_{n}(k))^{\text{T}} $ of (2.1) with the above initial condition is existent and unique for all $ k\in \mathbb{Z_+} $.
(2.1) always has the equilibrium $ U = (0, 0, \cdots, 0)^{\text{T}}\equiv 0 $. This paper mainly discusses sufficient conditions for global attractivity of $ U = 0 $ and necessary conditions for stability of $ U = 0 $.
First, similar to [26] and [27], we have the following important result on dissipation of (2.1).
Lemma 2.1. If (H$ _{\mathit{\text{1}}} $) - (H$ _{\mathit{\text{3}}} $) hold, then any solution $ U(k) $ of (2.1) satisfies $ \limsup_{k\rightarrow +\infty} $ $ |U_{i}(k)| $$ \leq M_{i}, \; $ where each $ M_{i} $ satisfies the following nonlinear algebraic equations,
| $ M_{i} = \frac{1}{1-|b_{i}|} \sum\limits_{j = 1}^n |a_{ij}| \bar{f_{j}}(M_{j})\; (i = 1, 2, \cdots, n), $ |
where $ \bar{f_{j}}(M_{j}) = \max \{ f_{j}(M_{j}), -f_{j}(-M_{j})\}\; (i = 1, 2, \cdots, n). $
Proof. By (2.1) and (H$ _{\text{2}} $), it has
| $ |Ui(k+1)|≤|bi||Ui(k)|+n∑j=1|aij|(i=1,2,⋯,n,k∈Z+). $ |
Note that $ |b_{i}| < 1 $ by (H$ _{\text{1}} $), it further has
| $ \limsup\limits_{k\rightarrow +\infty} |U_{i}(k)| \leq \frac{1}{1-|b_{i}|} \sum\limits_{j = 1}^n |a_{ij}| \triangleq M_{i, 0}\; (i = 1, 2, \cdots, n). $ |
For $ \forall \varepsilon > 0 $, there is a positive integer $ K_0 $, such that $ |U_{i}(k-\tau_{ij})|\leq M_{i, 0}+\varepsilon\; $ $ (i = 1, 2, \cdots, n, \; k > K_0). $ According to (H$ _{\text{3}} $), it has
| $ |Ui(k+1)|≤|bi||Ui(k)|+n∑j=1|aij|¯fj(Mj,0+ε)(i=1,2,⋯,n,k>K0). $ |
Hence,
| $ \limsup\limits_{k \rightarrow +\infty}|U_{i}(k)| \leq \frac{1}{1-|b_{i}|} \sum\limits_{j = 1}^n |a_{ij}| \bar{f_{j}}(M_{j, 0}+\varepsilon) \; (i = 1, 2, \cdots, n). $ |
Let $ \varepsilon \rightarrow 0 $. It has $ \limsup_{k\rightarrow +\infty} |U_{i}(k)| \leq M_{i, 1}, $ where
| $ M_{i, 1} = \frac{1}{1-|b_{i}|} \sum\limits_{j = 1}^n |a_{ij}|\bar{f_{j}}(M_{j, 0}) \leq M_{i, 0}\; (i = 1, 2, \cdots, n). $ |
Repeating the above process, there has a decreasing sequence $ \{ M_{i, p}\} $, which satisfies $ \limsup_{k\rightarrow +\infty} |U_{i}(k)|\leq M_{i, p}, $ where
| $ M_{i, p} = \frac{1}{1-|b_{i}|} \sum\limits_{j = 1}^n |a_{ij}| \bar{f_{j}}(M_{j, p-1})\; (i = 1, 2, \cdots, n, \; p = 1, 2, \cdots). $ |
Denote $ \mathop {\limsup }\limits_{p \to +\infty}M_{i, p} = M_{i} $ $ (i = 1, 2, \cdots, n) $. It has $ \lim_{k \rightarrow +\infty}\sup_{k} |U_{i}(k)|\leq M_{i}, $ where
| $ M _{i} = \frac{1}{1-|b_{i}|} \sum\limits_{j = 1}^n |a_{ij}| \bar{f_{j}}(M_{j})\; (i = 1, 2, \cdots, n). $ |
Lemma 2.2. ([30]) Define the set of real matrices $ Z^{n\times n}\triangleq \{ Z = (z_{ij})|z_{ij}\leq 0, i\neq j, \ i, j = 1, 2, \cdots, n\} $. For any $ C\in Z^{n\times n} $, the following conditions are equivalent:
(i) All the principle minors of $ C $ are nonnegative.
(ii) For any vector $ x\neq 0 $, let $ y = Cx $, then there is some $ i\in \{1, 2, \cdots, n\} $ such that $ x_{i}\neq 0 $ and $ x_{i}y_{i}\geq 0. $
If $ C\in Z^{n\times n} $ satisfies any of the above conditions, then $ C $ is called an $ M $-matrix.
In this section, we will give sufficient conditions for global attractivity of $ U = 0 $ of (2.1).
Define the matrix $ C\in Z^{n\times n} $ as follows:
| $ C = [1−|b1|−|a11|−|a12|⋯−|a1n|−|a21|1−|b2|−|a22|⋯−|a2n|⋮⋮⋱⋮−|an1|−|an2|⋯1−|bn|−|ann|] = (c_{ij})_{n\times n}. $ |
Using the similar method in [28], it has the following result for global attractivity of $ U = 0 $ of (2.1).
Theorem 3.1. If $ C $ is an $ M $-matrix, then $ U = 0 $ of (2.1) is globally attractive for any time delays $ \tau_{ij} $ $ (i, j = 1, 2, \cdots, n) $.
Proof. According to Lemma 2.1, any solution $ U(k) $ of (2.1) satisfies $ \limsup_{k\rightarrow +\infty} |U_{i}(k)|\leq M_{i}, $ where
| $ Mi=11−|bi|n∑j=1|aij|¯fj(Mj)(i=1,2,⋯,n). $ | (3.1) |
Subsequently, it will be shown that there must be $ M_{i} = 0 $ for all $ i = 1, 2, \cdots, n $.
Firstly, it assumes that $ M_{i} > 0 $ for all $ i = 1, 2, \cdots, n $. Then according to (3.1), (H$ _{\text{2}} $) and (H$ _{\text{3}} $), it has that $ \sum \limits_{j = 1}^{n}|a_{ij}| > 0 $ $ (i = 1, 2, ..., n) $. Hence, it has that $ \bar{f_{j}}(M_{j}) < M_{j}\; (j = 1, 2, ..., n). $ which further implies that
| $ M_{i} (1-|b_{i}) = \sum\limits_{j = 1}^n |a_{ij}| \bar{f_{j}}(M_{j}) \lt \sum\limits_{j = 1}^n |a_{ij}| M_{j}\; (i = 1, 2, \cdots , n), $ |
i.e., $ CM < 0, $ here $ M = (M_{1}, M_{2}, \cdots, M_{n})^{\text{T}} > 0 $.
Denote $ x = M > 0 $ and $ y = CM $. Then for all $ i \in \{1, 2, \cdots, n\} $, it has
| $ x_{i}y_{i} = M_{i}\sum\limits_{j = 1}^n c_{ij} M_{j} \lt 0, $ |
which contradicts to the condition (ⅱ) in Lemma 2.2. Therefore, it must have that there is at least some $ j $ such that $ M_{j} = 0 $.
Without loss of generality, it is assumed that $ M_{n} = 0 $. Afterwards, it can be shown from (3.1) that
| $ M_{i} = \frac{1}{1-|b_{i}|} \sum\limits_{j = 1}^{n-1} |a_{ij}| \bar{f_{j}}(M_{j})\; (i = 1, 2, \cdots, n-1). $ |
With the same method as discussed above, it has that $ M_{2} = M_{3} = \cdots = M_{n-1} = M_{n} = 0 $. Finally, it has from (3.1) that
| $ M_{1} = \frac{1}{1-|b_{1}|} |a_{11}| \bar{f_{1}}(M_{1}). $ |
If $ a_{11} = 0 $, it is clear that $ M_{1} = 0 $. If $ a_{11}\neq 0 $, it has that
| $ M_{1} = \frac{1}{1-|b_{1}|} |a_{11}| \bar{f_{1}}(M_{1}) \lt \frac{1}{1-|b_{1}|} |a_{11}| M_{1}, $ |
i.e., $ (1-|b_{1}|-|a_{11}|) M_{1} < 0, $ which is a contradiction to $ C $ being an $ M $-matrix (hence $ 1-|b_{1}|-|a_{11}|\geq 0 $). Therefore, there must be $ M_{1} = 0 $. In summary, it has that $ M_{1} = M_{2} = \cdots = M_{n} = 0 $.
In this section, we will consider the necessary conditions for stability of $ U = 0 $ of (2.1). First of all, from (H$ _{\text{2}} $) and (H$ _{\text{3}} $), it has the following linearized system of (2.1) at $ U = 0 $,
| $ Ui(k+1)=biUi(k)+n∑j=1aijUj(k−τij)(i=1,2,⋯,n;k∈Z+). $ | (4.1) |
The characteristic equation of (4.1) is
| $ P(λ)≜det[λ−b1−a11λ−τ11−a12λ−τ12⋯−a1nλ−τ1n−a21λ−τ21λ−b2−a22λ−τ22⋯−a2nλ−τ2n⋮⋮⋱⋮−an1λ−τn1−an2λ−τn2⋯λ−bn−annλ−τnn]=0. $ | (4.2) |
Motivated by the results in [24] and [25], it has the following important Lemmas 4.1, 4.2 and 4.3.
Lemma 4.1. Assume that $ b_{i}\leq 0 $ $ (i = 1, 2, \cdots, n) $. If $ \det (C) < 0 $, then there exist the time delays $ \tau_{ij} \in \mathbb{N}\ (i, j = 1, 2, \cdots, n) $ such that the characteristic equation (4.2) has a root $ \lambda $ with $ |\lambda| > 1 $.
Proof. Let us assume that $ \lambda \neq 0 $. Consider the following equation,
| $ λnP(λ)=λndet[λ−b1−a11λ−τ11−a12λ−τ12⋯−a1nλ−τ1n−a21λ−τ21λ−b2−a22λ−τ22⋯−a2nλ−τ2n⋮⋮⋱⋮−an1λ−τn1−an2λ−τn2⋯λ−bn−annλ−τnn]=det[λ2−b1λ−a11λ−τ11+1−a12λ−τ12+1⋯−a1nλ−τ1n+1−a21λ−τ21+1λ2−b2λ−a22λ−τ22+1⋯−a2nλ−τ2n+1⋮⋮⋱⋮−an1λ−τn1+1−an2λ−τn2+1⋯λ2−bnλ−annλ−τnn+1]. $ |
Let us define the function,
| $ Fε(z)≜det[(z+ε)2−b1(z+ε)−a11(z+ε)−τ11+1⋯−a1n(z+ε)−τ1n+1−a21(z+ε)−τ21+1⋯−a2n(z+ε)−τ2n+1⋮⋱⋮−an1(z+ε)−τn1+1⋯(z+ε)2−bn(z+ε)−ann(z+ε)−τnn+1], $ | (4.3) |
where
| $ τij={even number,aij<0,odd number,aij≥0(i,j=1,2,...,n). $ | (4.4) |
For $ z = re^{\pi i}\ (r\in \mathbb{R_+}) $ and $ \varepsilon = 0 $, (4.3) becomes
| $ R(r)≜F0(reπi)=det[r2+b1r−|a11|r−τ11+1−|a12|r−τ12+1⋯−|a1n|r−τ1n+1−|a21|r−τ21+1r2+b2r−|a22|r−τ22+1⋯−|a2n|r−τ2n+1⋮⋮⋱⋮−|an1|r−τn1+1−|an2|r−τn2+1⋯r2+bnr−|ann|r−τnn+1]=det[r2−|b1|r−|a11|r−τ11+1−|a12|r−τ12+1⋯−|a1n|r−τ1n+1−|a21|r−τ21+1r2−|b2|r−|a22|r−τ22+1⋯−|a2n|r−τ2n+1⋮⋮⋱⋮−|an1|r−τn1+1−|an2|r−τn2+1⋯r2−|bn|r−|ann|r−τnn+1]. $ |
According to $ b_i\leq0 $, it has $ R(1) = \det C < 0. $ Furthermore, $ R(+\infty) = +\infty > 0. $ Since $ R(r) $ is continuous in $ \mathbb{R} $, it has from Lagrangian mean value theorem that there exists $ r^{\ast} > 1 $ such that $ R(r^{\ast}) = 0 $. Therefore, $ z^{\ast} = r^{\ast} e^{\pi i} $ is a root of $ F_{0}(z) = 0 $. Obviously, for small $ \varepsilon > 0 $, $ |F_{\varepsilon}(z)-F_{0}(z)| $ is also small enough. By Rouché's Theorem, $ F_{\varepsilon}(z) = 0 $ has a root $ \hat{z^{\ast}}(\varepsilon) $ in the neighborhood of $ z^{\ast} $ such that $ |\hat{z^{\ast}}| > 1 $.
Denote $ \lambda^{\ast}\triangleq \hat{z^{\ast}}+\varepsilon $. Obviously, it has $ |\lambda^{\ast}| > 1 $ as $ \varepsilon $ is small enough. According to the selection method of $ \tau_{ij} $ in (4.4), it has from (4.3) that
| $ 0=Fε(^z∗)=det[(^z∗+ε)2−b1(^z∗+ε)−a11(^z∗+ε)−τ11+1⋯−a1n(^z∗+ε)−τ1n+1−a21(^z∗+ε)−τ21+1⋯−a2n(^z∗+ε)−τ2n+1⋮⋱⋮−an1(^z∗+ε)−τn1+1⋯(^z∗+ε)2−bn(^z∗+ε)−ann(^z∗+ε)−τnn+1]=det[(λ∗)2−b1λ∗−a11(λ∗)−τ11+1⋯−a1n(λ∗)−τ1n+1−a21(λ∗)−τ21+1⋯−a2n(λ∗)−τ2n+1⋮⋱⋮−an1(λ∗)−τn1+1⋯(λ∗)2−bnλ∗−ann(λ∗)−τnn+1]=(λ∗)nP(λ∗). $ |
This proves that $ \lambda^{\ast} $ is a root of the characteristic equation (4.2) such that $ |z^{\ast}| > 1 $.
Lemma 4.2. Assume that $ b_{i}\leq 0 $ $ (i = 1, 2, \cdots, n) $. If $ C $ is not an $ M $-matrix, then there exist the time delays $ \tau_{ij} \in \mathbb{N}\ (i, j = 1, 2, \cdots, n) $ such that the characteristic equation (4.2) has a root $ \lambda $ with $ |\lambda| > 1 $.
Proof. From Lemma 2.2, if $ C $ is not an $ M $-matrix, then there exists at least one negative principal minor of $ C $. Without loss of generality, it is assumed that the sequential principal minor $ C_l $ of order $ l $ of $ C $ is negative, namely, $ \det (C_{l}) < 0 $.
The characteristic equation of $ C_{l} $ is as follows,
| $ Pl(λ)≜det[λ−b1−a11λ−τ11−a12λ−τ12⋯−a1lλ−τ1l−a21λ−τ21λ−b2−a22λ−τ22⋯−a2lλ−τ2l⋮⋮⋱⋮−al1λ−τl1−al2λ−τl2⋯λ−bl−allλ−τll]=0. $ | (4.5) |
By method similar to the proof of Lemma 4.1, there exist time delays $ \tau_{ij} \in \mathbb{N_+}\ (i, j = 1, 2, \cdots, l) $ which satisfy (4.4) such that the characteristic equation (4.5) has a root satisfying $ |\lambda^{\ast}| > 1 $.
Applying Laplace expansion, $ P(\lambda) $ can be written as
| $ P(λ)=Pl(λ)[n∏m=l(λ−bm−ammλ−τmm)+S(λ,λ−τij)]+T(λ,λ−τij). $ | (4.6) |
Observing (4.2), it is easy to see that, both $ S(\lambda, \lambda^{-\tau_{ij}}) $ and $ T(\lambda, \lambda^{-\tau_{ij}}) $ contain the terms $ a_{ij}\lambda^{-\tau_{ij}}\; (i, j = l+1, \cdots, n) $. Therefore, when $ |\lambda| > 1 $, $ |S(\lambda, \lambda^{-\tau_{ij}})| $ and $ |T(\lambda, \lambda^{-\tau_{ij}})| $ can become sufficiently small by choosing $ \tau_{ij} $ $ (i, j = l+1, l+2, \cdots, n) $ to be large enough. Again using Rouché's Theorem, it has that (4.2) has a root $ \tilde{\lambda}^{\ast} $ in the neighborhood of $ \lambda^{\ast} $ satisfying $ |\tilde{\lambda}^{\ast}| > 1 $.
Lemma 4.3. ([31]) If the system (4.1) has a characteristic eigenvalue $ \lambda $ satisfying $ |\lambda| > 1 $, then $ U = 0 $ of (2.1) is not stable.
From Lemma 4.2, Lemma 4.3 and Lemma 4.3, it has the following result.
Theorem 4.1. Assume that $ b_{i}\leq 0 $ $ (i = 1, 2, \cdots, n) $. If $ C $ is not an $ M $-matrix, then there exist time delays $ \tau_{ij} \in \mathbb{N_+}\ (i, j = 1, 2, \cdots, n) $ such that $ U = 0 $ of (2.1) is not stable.
Remark 4.1. Based on [2], the $ U_{i}(k) $ of (2.1) refers to the potential of the $ i $th neuron at time $ k $. The sign of $ U_{i}(k) $ indicates the neuron being at the action potential or the resting potential. In terms of a single neuron (ignoring the interactions among neurons), when a neuron at resting potential receives a stimulus input, the neuron's potential will be at an action potential at next time. Similarly, when neuron's stimulation at the action potential is terminated, the neuron will be resting at next time. Therefore, to a certain extent, this explains the biological significance of the condition $ b_{i}\leq 0 $ $ (i = 1, 2, ..., n) $ in Theorem 4.1.
In this paper, global attractivity and stability of the equilibrium $ U = 0 $ of (2.1) have been considered. In Theorem 3.1, sufficient conditions are given for global attractivity of $ U = 0 $ for any time delays $ \tau_{ij} $ $ (i, j = 1, 2, ..., n) $. In Theorem 4.1, under certain conditions, necessary conditions are presented for stability of $ U = 0 $ for any time delays $ \tau_{ij} $ $ (i, j = 1, 2, ..., n) $.
Theorem 3.1 shows that, under certain conditions, for global attractivity of the equilibrium, the discrete Hopfield-type neural networks (2.1) can maintain consistent conditions with continuous counterparts in [25] and [28]. Meanwhile, it is also confirmed that the discrete Hopfield-type neural networks can inherit some of biological dynamic properties of the continuous ones. Furthermore, based on [1] and [2], when the discrete Hopfield-type neural networks (2.1) behaves as an associative memory or a content addressable memory, the state near the equilibrium contains information about the memory. Hence, under the conditions in Theorem 3.1, the memory is truly addressable and allows information to be stored around the equilibrium. On the other hand, according to the following numerical simulations, it can be showed that when a discrete Hopfield-type neural networks does not satisfy the conditions in Theorem 4.1, the potential (voltage) of the neurons will not reset in the resting state, but becomes oscillatory.
It should be pointed out that the condition "$ b_{i}\leq 0 $ $ (i = 1, 2, ..., n) $" in Theorem 4.1 may be a technical condition and is likely to be further improved.
Finally, as a simple application of the conclusions of this paper, let us consider the following $ 3 $-dimensional discrete Hopfield neural networks with time delays,
| $ {U1(k+1)=−310U1(k)−130f(U1(k−τ11))−13f(U2(k−τ12))+13f(U3(k−τ13)),U2(k+1)=b2U2(k)+13f(U1(k−τ21))+130f(U2(k−τ22))−13f(U3(k−τ23)),U3(k+1)=−310U3(k)−13f(U1(k−τ31))−13f(U2(k−τ32))−130f(U3(k−τ33)), $ | (5.1) |
where $ b_2\leq0 $, $ f(x) = \tanh(x) $.
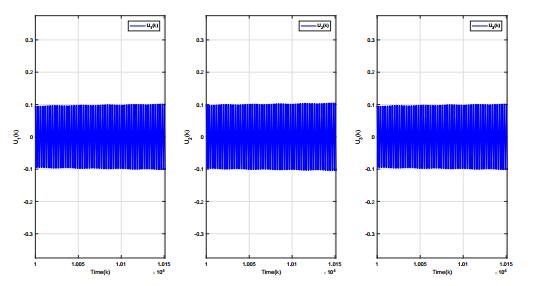
Let $ b_2 = -0.3 $, (5.1) satisfies the conditions of Theorem 3.1, and $ \det C = 0 $. Hence, $ U = 0 $ is globally attractive for any time delays $ \tau_{ij} $ $ (i, j = 1, 2, 3) $. Figure 1 is corresponding numerical simulation.
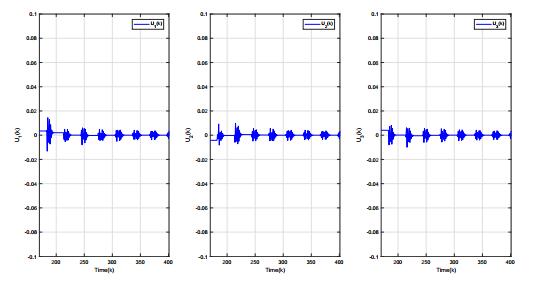
On the other hand, let us change the value of $ b_2 $ from $ b_2 = -0.3 $ to $ b_2 = -0.33 $, it has $ \det C = -0.01 < 0 $. According to (4.4), the time delays $ \tau_{ij} $ $ (i, j = 1, 2, 3) $ are selected as follows,
| $ \tau_{ij} = {30,aij<0,29,aij≥0(i,j=1,2,3). $ |
From Theorem 4.1, it has that $ U = 0 $ is unstable. Figure 2 is corresponding numerical simulation, which shows that the solution becomes oscillatory.
This work is supported by National Key R & D Program of China (2017YFF0207401) and NNSF of China (No.11471034) for W. Ma.
The author declares no conflicts of interest in this paper.
| [1] | J. Differential Equations, 217 (2005), 431-455. |
| [2] | SIAM J. Appl. Math., 66 (2006), 1339-1365. |
| [3] | Sinauer Associates Inc, Sunderland, MA, 2001. |
| [4] | J. Differential Equations, 247 (2009), 956-1000. |
| [5] | Discrete Contin. Dyn. Syst., 33 (2013), 4891-4921. |
| [6] | CBMS-NSF regional conference series in applied mathematics, 71, SIAM, 1998. |
| [7] | Academic Press, 2003. |
| [8] | Springer, Berlin Heidelberg, 1985. |
| [9] | J. Math. Biol., 61 (2010), 277-318. |
| [10] | Wiley, New York, 2000. |
| [11] | J. Math. Anal. Appl., 242 (2000), 255-270. |
| [12] | Math. Model. Nat. Phenom., 2 (2007), 69-100. |
| [13] | J. Math. Biol., (to appear). |
| [14] | Math. Biosci. Eng., 8 (2011), 503-513. |
| [15] | Vol. Two, Chelsea Publishing Company, New York, 1989. |
| [16] | Structured population models in biology and epidemiology, Lecture Notes in Math., Springer, Berlin, 1936 (2008), 165-208. |
| [17] | Theor. Popul. Biol., 28 (1985), 150-180. |
| [18] | The American Nat., 171 (2008), 743-754. |
| [19] | Comm. Pure Appl. Math., 38 (1985), 733-753. |
| [20] | Math. Biosci., 155 (1999), 77-109. |
| [21] | Can. Appl. Math. Quart., 19 (2011), 65-77. |
| [22] | Springer Verlag, Berlin Heidelberg, 2008. |
| [23] | SIAM J. Math. Anal., 37 (2005), 251-275. |
| [24] | Springer Verlag, Berlin Heidelberg, 1986. |
| [25] | Statistical Methods in Medical Research, 9 (2000), 279-301. |
| [26] | Int. J. Parasit., 35 (2005), 375-389. |
| [27] | Journal of Theoretical Biology, 224 (2003), 359-376. |
| [28] | Mathematical Biosciences, 208 (2007), 216-240. |
| [29] | Computers and Mathematics with Applications, 15 (1988), 565-594. |
| [30] | SIAM J. Appl. Math., 52 (1992), 541-576. |
| [31] | American Mathematical Society, Providence, RI, 1995. |
| [32] | Springer New York, 2011. |
| [33] | Cambridge University Press, Cambridge, 1995. |
| [34] | Amer. Math. Soc., Providence, 2011. |
| [35] | J. Math. Biology, 26 (1988), 299-317. |
| [36] | Princeton University Press, Princeton, NJ, 2003. |
| [37] | SIAM J. Appl. Math., 70 (2009), 188-211. |
| [38] | SIAM J. Appl. Math., 48 (1988), 549-591. |
| [39] | Springer, 1997. |
| [40] | Math. Biosc., 180 (2002), 29-48. |
| [41] | Structured population models in biology and epidemiology, Lecture Notes in Math., Springer, Berlin, 1936 (2008), 1-49. |
| [42] | Parasitology Today, 15 (1999), 258-262. |
| [43] | 2010 International Congress on Environmental Modelling and Software Modelling for Environment's Sake (D.A. Swayne, W. Yang, A. A. Voinov, A. Rizzoli, T. Filatova, eds.), 2010. |
| [44] | Journal of Theoretical Biology, 319 (2013), 50-61. |
| [45] | Springer, New York, 2003. |
| 1. | Lu Junxiang, Hong Xue, Adaptive synchronization for fractional stochastic neural network with delay, 2021, 2021, 1687-1847, 10.1186/s13662-020-03170-2 | |
| 2. | Duc Thuan Do, Thai Son Doan, Viet Cuong Le, A characterization of delay independent stability for linear off-diagonal delay difference equations, 2023, 171, 01676911, 105428, 10.1016/j.sysconle.2022.105428 | |
| 3. | Sourav Kumar Sasmal, Yasuhiro Takeuchi, Editorial: Mathematical Modeling to Solve the Problems in Life Sciences, 2020, 17, 1551-0018, 2967, 10.3934/mbe.2020167 | |
| 4. | José J. Oliveira, Global exponential stability of discrete-time Hopfield neural network models with unbounded delays, 2022, 28, 1023-6198, 725, 10.1080/10236198.2022.2073820 | |
| 5. | António J.G. Bento, José J. Oliveira, César M. Silva, Existence and stability of a periodic solution of a general difference equation with applications to neural networks with a delay in the leakage terms, 2023, 126, 10075704, 107429, 10.1016/j.cnsns.2023.107429 | |
| 6. | A. Elmwafy, José J. Oliveira, César M. Silva, Existence and exponential stability of a periodic solution of an infinite delay differential system with applications to Cohen–Grossberg neural networks, 2024, 135, 10075704, 108053, 10.1016/j.cnsns.2024.108053 |
Guihong Fan, Yijun Lou, Horst R. Thieme, Jianhong Wu. Stability and persistence in ODE modelsfor populations with many stages[J]. Mathematical Biosciences and Engineering, 2015, 12(4): 661-686. doi: 10.3934/mbe.2015.12.661
DownLoad:
