1. Introduction
The interest to colloidal nanocrystals (NCs) is highly motivated by their potential application in optoelectronics, photovoltaics, biology, medicine, etc. [1]. Luminescent NCs based on II-VI compounds (CdSe, CdS, CdTe and their alloys) are characterized by a high photoluminescence (PL) quantum yield, narrow excitonic emission band and a broad absorption spectrum, which makes them well suited to the multicolor bio-labeling [2]. In turn, the NCs of I-III-VI materials (CuInS2, AgInS2 and their alloys) also show a high PL quantum yield, but comprise the less-toxic elements which is especially important for the in vivo bio-imaging [2].
A range of the methods has been developed for the synthesis of II-VI and I-III-VI NCs [3,4,5,6,7,8,9,10,11,12]. The high temperature injection and colloidal solution (precipitation) methods are among the most followed practices [3,4]. Another convenient and effective route used for the preparation of II-VI and I-III-VI NCs or thin films is the thermal decomposition of a single-molecule precursor, including the chemical vapour deposition and colloidal thermolysis [5,6]. Other methods applied for the fabrication of the NCs are the solvothermal/hydrothermal process [7], sonochemical [8], microwave assisted routes [9], spray pyrolysis [10], chemical bath deposition [11], etc. Recently we have proposed a new method for the fabrication of non-stoichiometric Ag-In-S NPs via the synthesis of Ag-doped indium(III) sulfide NCs stabilized by mercaptoacetate anions in water and glycerol [12] which is particularly relevant for the bio-sensing applications.
To improve the stability of the NCs, different polymer materials are applied as surface stabilizing and coating agents [2,13]. Among them, polyvinyl alcohol (PVA), a hydrophilic non-carcinogenic and optically transparent polymer, is considered as a good host material for metal nanoparticles and semiconductor NCs [14,15].
We have found earlier that the PL intensity of CdSe NCs embedded in PVA films can be enhanced by more than an order of magnitude upon illumination with visible light at elevated temperatures [16]. Those NCs were produced in gelatine and then transferred to PVA matrix. In order to eliminate possible effect of gelatine, the photostability of the NC-PVA composite with the NCs of different types produced in an aqueous media were investigated. In the present work the effect of photo-induced enhancement of the deep-trap emission in CdSe NCs is confirmed but the magnitude of the effect is found to be smaller presumably owing to a different route of NC synthesis. It is found that photostability of the NC-PVA composite depends strongly on the material of NC core. Specifically, the photoinduced PL quenching occurs for the Ag-In-S NCs in contrast to the photo-enhancement effect found for the CdSe NCs.
2. Materials and Method
The films of pure PVA and PVA hosting CdSe or Ag-In-S NCs were studied. The film thickness was about 0.2 mm. The CdSe NCs were synthesized similar to [17], while the Ag-In-S NCs were synthesized at room temperature in aqueous media in the presence of mercaptoacetic acid as a stabilizer as described in [12]. The molar Ag:In ratio was maintained at 1:4. All the reagents were purchased from Sigma-Aldrich and used as supplied. After the dialysis the NCs solution was mixed with 20 w% aqueous solution of PVA, deposited onto glass slides and left for natural drying. The dried films were detached from the glass and subjected to heating in the air at 100 °C for 5 min. The annealing was performed both in the dark and under illumination of 409-nm LED.
The optical properties of the films were studied at room temperature by the PL, optical transmission and micro-Raman spectroscopy. The PL was excited with a 409-nm LED and recorded using a prism monochromator equipped with a photomultiplier. The optical absorption spectra were recorded with a double beam spectrophotometer Specord-210. The micro-Raman spectra were collected with a triple Raman spectrometer T-64000 Horiba Jobin-Yvon or a Renishaw Micro-Raman Spectrometer, using for the excitation the 488.0-nm line of an Ar-Kr ion laser or 785-nm line of a High Power Near Infrared Diode Laser, respectively. Laser beam was focused at 2.5 µm diameter spot, while a diode beam was focused at about 3 mm diameter spot. The structural properties of the films were investigated by X-ray diffraction (XRD) using a D-8 ADVANCE (Bruker) single-crystal X-ray diffractometer operating with the Cu Kα irradiation.
3. Results
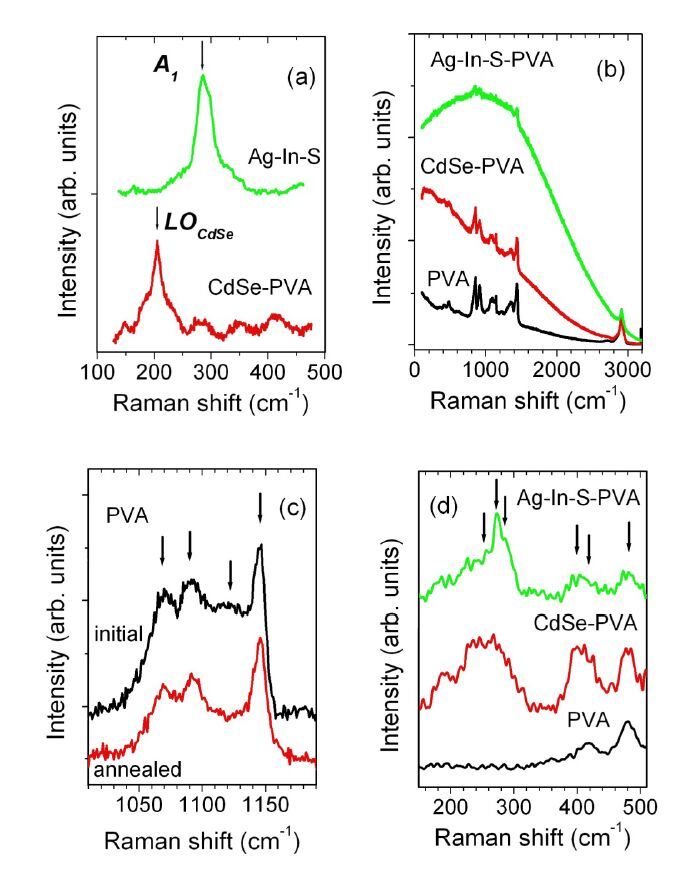
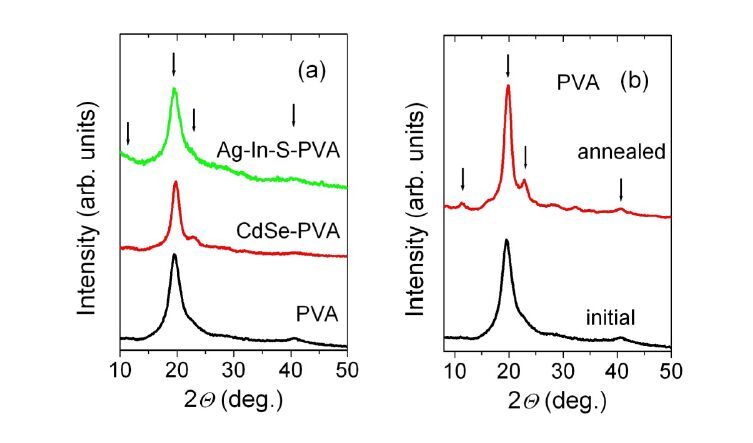
The XRD patterns of pure PVA and NC-PVA composites (Figure 1) show the signals from partially crystallized PVA matrix [14] with the most intense peak at 2θ = 19.5° and the peaks at 2θ = 11.5°, 22.8° and 40.6° of a much lower intensity. The PVA is known to be composed of the chain-like-connected -CH2-CH-OH- units with multiple H-bonds binding the OH-groups either within the same chain or those of the neighboring macro-chains. The latter binding type is responsible for the crystallization of PVA. The diffraction peaks from crystalline NC phase are not observed apparently because of a low NC concentration (less than 1% w/v). The heating of the films of pure PVA and NC-PVA composites both in the dark and under illumination increases the intensity of the peaks at 2θ =11.5° and 22.8°, indicating an increase of the PVA crystallinity degree.
The micro-Raman spectrum of the CdSe-PVA composite shows a peak at 205.8 cm−1ascribed to the CdSe LO phonon mode (Figure 2a). The peak is shifted towards the low-frequency region as compared to the position of bulk CdSe peak at 210 cm-1 apparently due to spatial phonon confinement and compressive strains in the NCs [18]. The micro-Raman spectrum of the Ag-In-S NCs (Figure 2a) demonstrates a strong peak at about 285 cm-1 assigned to the chalcopyrite characteristic mode A1 caused by the vibration of the anion sublattice [19].
The micro-Raman spectra of pristine and heated under illumination pure PVA and NC-PVA composite films are shown in Figure 2b-d. The spectra are recorded under 785 nm excitation which is below the band gap of both CdSe and Ag-In-S NCs and does not produce PL in the NCs.
The vibrational spectra presented in Figure 2b show several strong scattering peaks characteristic of the PVA polymer. The peaks are caused by stretching, bending and wagging vibrations of the O-H, C-H, C-C, C-O and CH2 groups. The frequencies for major Raman bands in the pure PVA and NC-PVA composites as well as the assignment of the bands done in accordance with [20] are listed in Table 1. The Raman peaks are found on a broad background signal. The nature of this feature is not clear at the moment. Incorporation of the NCs into the PVA matrix increases this background. The most intense background is observed for the Ag-In-S-PVA composite.
Table 1. The vibrational bands obtained from the micro-Raman spectra of pure PVA and NC-PVA composite films and their assignment in accordance with [20]
|
Frequency, cm-1
|
Assignment
|
|
PVA
|
CdSe-PVA
|
Ag-In-S-PVA
|
|
-
|
250
|
250
|
-
|
|
-
|
-
|
273
|
-
|
|
-
|
-
|
284
|
-
|
|
-
|
400
|
400
|
-
|
| 416
|
416
|
412
|
C-O wagging
|
| 480
|
480
|
480
|
C-O bending
|
| 619
|
619
|
618
|
O-H stretching
|
| 854
|
854
|
854
|
C-C stretching
|
| 915
|
915
|
915
|
C-C stretching
|
| 1071
|
1069
|
-
|
C-O stretching
|
| 1091
|
1091
|
1091
|
C-O stretching, O-H bending
|
| 1121
|
1121
|
-
|
C-OH valence asymmetric ring vibrations
|
| 1146
|
1146
|
1146
|
C-O stretching, C-C stretching
|
| 1360
|
1360
|
1361
|
C-H bending, O-H bending
|
| 1372
|
1372
|
-
|
CH2 wagging
|
| 1439
|
1442
|
1442
|
C-H bending, O-H bending
|
| 2715
|
2715
|
-
|
unassigned
|
| 2910
|
2910
|
2910
|
C-H stretching
|
The intensities of the sharp Raman peak at 1146 cm-1 and the less pronounced band at about 1121 cm-1 (Figure 2c) are used as an indicator of crystallinity and “amorphicity” of the polymer, respectively [21]. The ratio of the intensities of these bands is typical for partially crystallized PVA.
The vibrational frequencies of PVA matrix vary slightly in the composites as compared with the pure PVA (Table 1). Besides, in the low frequency region of the Raman spectra of the NC-PVA films, additional phonon bands appear (Figure 1d). The wide bands at about 250 and 400 cm-1 as well as the sharp band at 272 cm-1 with a shoulder at 284 cm-1 can be tentatively assigned to residual substances of the NC synthesis.
The heating of the films both in the dark and under illumination does not change noticeably the Raman peak frequencies, but alters slightly the intensity of all the Raman bands and the PL background. The heating decreases also the relative intensity of the band at about 1 121 cm-1 (Figure 2c) indicating further crystallization of the PVA matrix that is in agreement with the XRD results.
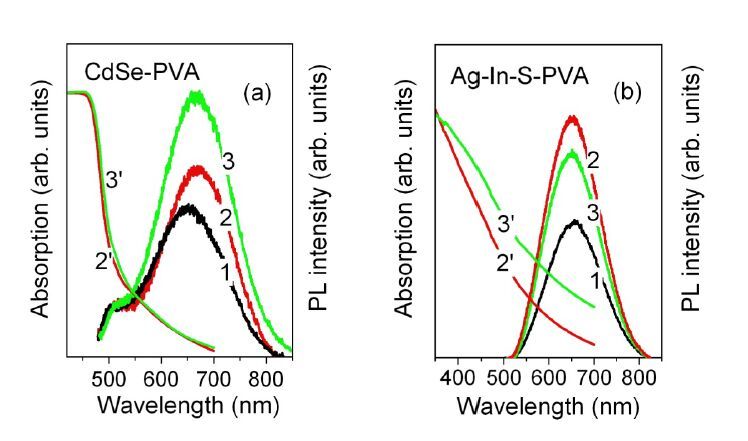
Figure 3 presents optical absorption and PL spectra of the CdSe-PVA and Ag-In-S-PVA composites. The absorption spectra of the CdSe-PVA films show a broad band with a kink at about 460 nm and a blurred edge, which corresponds to optical absorption by the CdSe NCs with a quite broad size distribution and an average diameter of around 3 nm [22].The absorption spectra of the Ag-In-S-PVA films show a long “tail” in the long-wavelength spectral region. The tail is usually explained by a size/shape inhomogeneity of the NC ensemble and/or by the optical transitions via intra-band-gap states in the NCs [23]. It should be noted that our previous investigations have shown that the average diameter of the Ag-In-S NCs is about4 nm [24].
The annealing in the dark and under illumination produces qualitatively opposite effects on the optical absorption spectra of the composites. While the annealing in the dark does not change noticeably the absorption spectra, the annealing under illumination results in a darkening of the films. The most pronounced changes occur in the absorption spectra of the Ag-In-S-PVA composite, where a shift of the absorption edge to longer wavelengths as well as a decrease of the film transmission in the long-wavelength region are observed (Figure 3b). At the same time, the transparency of pure PVA film does not change after the annealing under illumination.
The PL spectra of the CdSe-PVA composite (Figure 3a) show two bands at about 515 and 667 nm, which can be ascribed to the band-edge emission and to the emission caused by the carrier recombination via deep acceptor levels introduced by NC surface defects, respectively [25]. The PL spectra of the Ag-In-S-PVA film (Figure 3b) demonstrate an intense broad PL band at about 650 nm caused by the carrier recombination via NC defect levels [24]. This broad PL band is often ascribed to bound-to-bound transitions in the donor-acceptor (DA) pairs.
Thermal treatment of the films in the dark enhances the defect-related emissions for both composites. The band-edge emission of CdSe NCs remains almost unchanged upon treatment. In some places of the CdSe-PVA film, it grows too, the increase being much smaller than that of the defect-related band. No clear correlation of the changes in the band-edge emission on sample parameters is found. In contrast to the effect of annealing per se, illumination of the films during thermal treatment produces qualitatively opposite effects on the PL intensity of the CdSe and Ag-In-S NCs - increasing the PL intensity for the CdSe NCs and decreasing it for the Ag-In-S NCs.
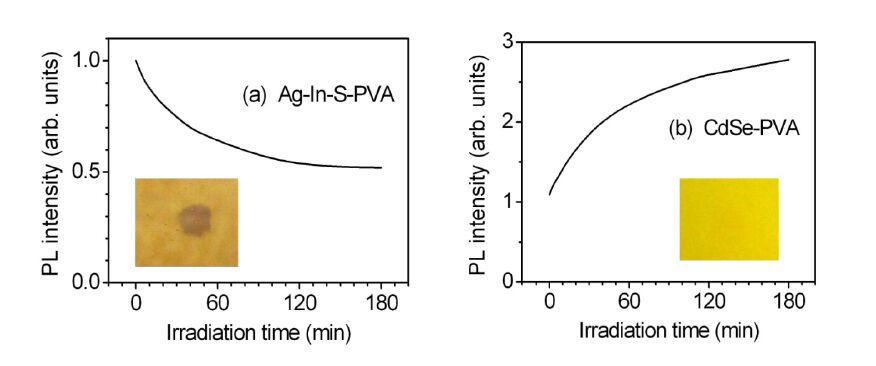
To distinguish the effect of irradiation, the films were illuminated with a 409-nm LED at room temperature for several hours. The PL intensity of the CdSe NCs increases gradually under irradiation, and that of the Ag-In-S NCs decreases (Figure 4). The color of the CdSe-PVA film changes slightly, while pronounced darkening of the Ag-In-S-PVA composite occurs (inserts in Figure 4). The changes in the PL and optical absorption spectra of the CdSe-PVA composite were irreversible. At the same time, both the color and PL intensity of the Ag-In-S-PVA composite restored during a storage of the films at ambient conditions for several weeks.
4. Discussion
The results of both structural and optical investigations show that the heating of the NCs-PVA composites induces chemical and structural transformations in the PVA matrix. The heat treatment of PVA can result in breaking of the hydrogen bonds, both inter- and intra-molecular, freeing hydroxyl groups in the backbone of PVA chains. The heating can also release the H2O molecules bounded to PVA molecules by H-bonds. The process of evaporation of water was visually observed during the film heating. The rearrangement of polymer chains and formation of new interchain bridging by H-bonding is expected to produce aligned ordered regions and increase the degree of polymer crystallinity. The increase of PVA matrix crystallinity in the heat treated films is confirmed by both XRD and Raman spectra investigations.
Besides, both thermal dehydration and oxidation of the PVA molecules upon the annealing can be expected. The former process manifests itself in the appearance of isolated and conjugated C=C bonds, while the latter causes transformation of hydroxyl groups into carbonyls and stimulates further oxidation of double carbon bonds. The C=O groups are known to produce the IR absorption bands at 1700-1800 cm-1, while the C=C bonds are responsible for the absorption at 1660 cm-1. However, we do not observe Raman peaks in the above mentioned frequency regions both for the pristine and heated films. Therefore, the Raman spectra do not provide clear evidence of thermal dehydration or oxidation of the PVA matrix.
At the same time, thermally stimulated increase of the luminescence intensity of CdSe and Ag-In-S NCs is observed. The effect can be explained by (i) the reconstruction of the surface atoms of the NC by removing the dangling bonds acting as the centers of nonradiative recombination [26] or (ii) the improvement of passivation of non-radiative surface defects of the NCs by the functional groups of PVA. In the latter case, formation of complexes between under-coordinated NC surface atoms and free hydroxyl groups can be supposed to be the reason of PL intensity increase. The photoinduced enhancement of this effect observed for CdSe NCs can be understood if supposing that photocarriers generated in the NCs initiate transformations in the nearby polymer chains and molecular species similar to those produced by the heating [17]. In fact, the process of the PL intensity increase under illumination is tentatively explained by different models: (i) passivation of surface traps by oxygen and/or by water molecules adsorbed on QD surface; (ii) recharging of the trapping centers on the QD surface; (iii) passivation of non-radiative surface defects caused by surface reconstruction or rearrangement of the surfactant molecules or other ligands [26]. Since the increase of the PL intensity accompanied with a small shifting of the absorption edge and PL band maxima to longer wavelengths is an irreversible process, it can be ascribed mainly to the improvement of QD surface defect passivation by the functional groups or the fragments of the polymer chains of PVA matrix.
In contrast, in the Ag-In-S-PVA composite, the darkening of the films occurs without change of the PL band position, and this effect is found to be reversible. If we suppose the presence of residual Ag-related compounds in the Ag-In-S-PVA composite, we can propose the next mechanism of the effect. The photocarriers formed by photoexcitation of the NCs can reduce silver(I)-containing species in the films, both Ag-In-S and residuals of AgCl or Ag2O in the PVA matrix to the metallic silver. The photoproduced Ag(0) renders the films colored presumably due to surface plasmon resonance (SPR). Similar effect of photoinduced darkening of PVA-ZnO-BiCl3 composite under UV light is described in [27] and assigned to formation of metallic bismuth. If colored film is kept in the dark, a reverse reaction of silver oxidation can happen and the films restore their original color and transparency. The absorption of a portion of LED’s light by metallic silver can be the reason of the decreasing of the NC luminescence intensity. Currently, it is not clear where these Ag-related residues are located. Taking into account the dialysis of the NC solution, we can suppose that these residues are located on a surface of the NCs.
It is well reported that the absorption spectra of silver nanoparticles in a broad range of sizes in aqueous media and other polar solvents show the SPR maximum located typically at 390-440 nm and the long-wavelength tail extended to 500-600 nm [28]. These can cause the effect of film darkening. The presence of oxygen and formation of the Ag species on the semiconductor NC surface can cause further broadening of the SPR band and thus the contribution of the visible light absorption will be increased as well. We have observed the former effect for Ag nanoparticles grown photocatalytically on ZnO NCs [29] and the latter—for the Ag nanoparticles grown in a catalytic regime on the surface of Ag2S NCs [30]. Typically, the SPR band of the Ag nanoparticles grown on the surface of metal chalcogenide NCs is broadened and red-shifted as also could be the case for the present Ag-In-S NCs. Passivation of the Ag nanoparticle surface by polymer molecules as PVA in the present case can also contribute to the SPR band broadening and deepening of the film coloration.
An alternative explanation of the darkening may be in formation of very small (most probably charged) silver clusters. Gradual extinction of the coloration at storage of the films in the dark can be caused by slow oxidation of such clusters by air oxygen. As suggested by the reports of A. Henglein’s group even a-few-atom silver clusters reveal absorption bands in the visible spectral range and can, therefore, contribute to the films darkening, observed in the present work. For example, a charged Ag42+ cluster is quite stable toward oxidation by oxygen and reveals a two-band absorption spectrum with the first band peaked at around 250-300 nm and the second band being broad and having an indistinct maximum at 490-500 nm [28]. According to [31], the Ag82+ and Ag142+ clusters reveal multiple absorption bands with the maxima extending down to ~600 nm. Therefore, starting from even such small species as Ag42+ the silver clusters can contribute to the visible light absorption and so induce the darkening of the films observed by the naked eye.
5. Conclusion
In the present study, the photoinduced variations of the optical properties of NC-PVA composites with CdSe or Ag-In-S NCs were investigated. It is found that heating of the composites to 100 °C results in an increase of the NC luminescence intensity. The illumination of the films during thermal treatment enhances this effect for CdSe NCs, but hampers it for Ag-In-S NCs. The latter fact is supposed to be due to formation of some light-absorbing species from the residual Ag-related compounds, most probably the metallic silver.
The transformations occurred in PVA matrix upon heating and light illuminations were studied with micro-Raman and XRD methods. The heating is found to promote crystallization of PVA matrix while the illumination has no effect on it. No clear spectral evidences of thermal dehydration or oxidation of PVA matrix are found.
Acknowledgments
This work was supported by the National Academy of Science of Ukraine via the project III-41-12.
Conflict of Interest
The authors declare no conflicts of interest regarding this paper.









 DownLoad:
DownLoad: