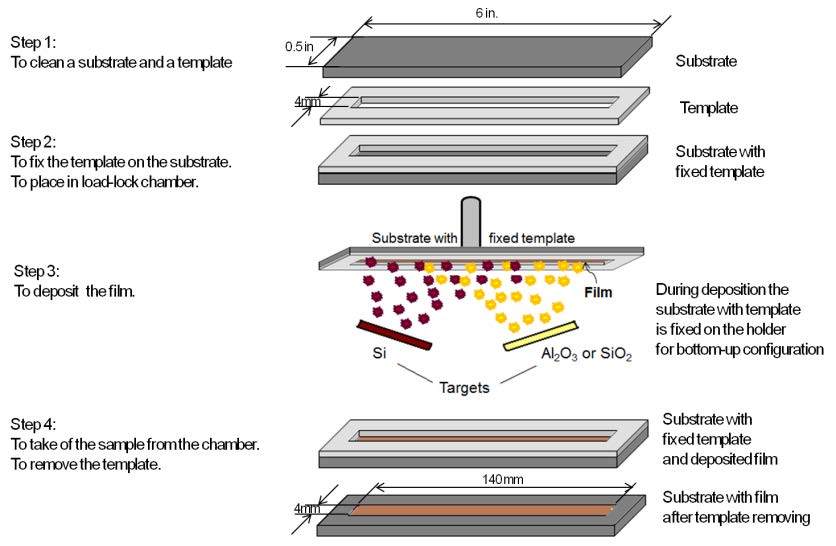
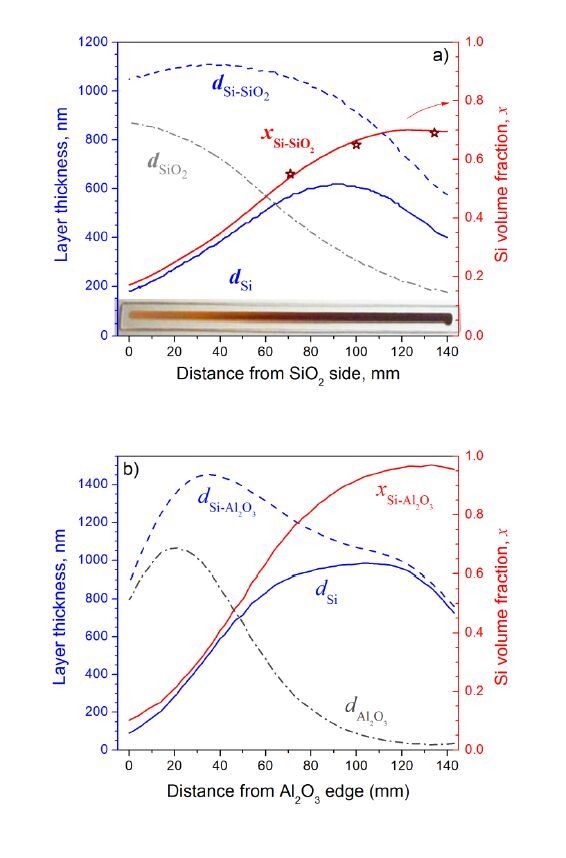
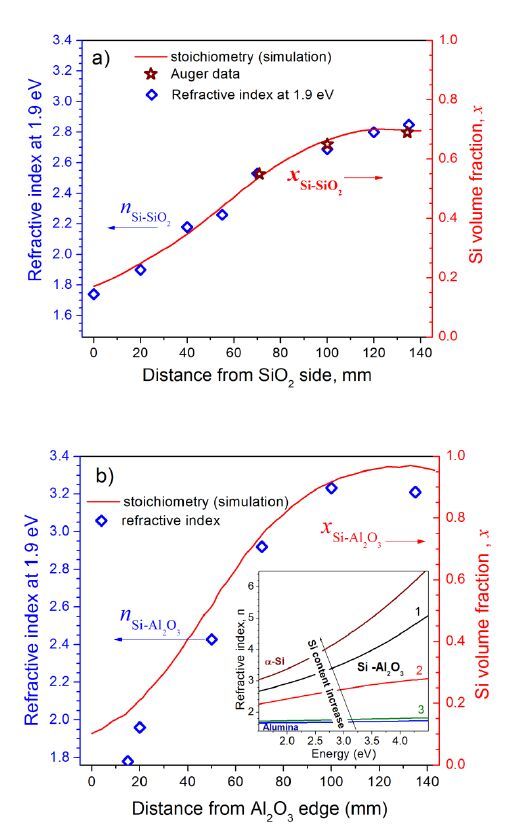
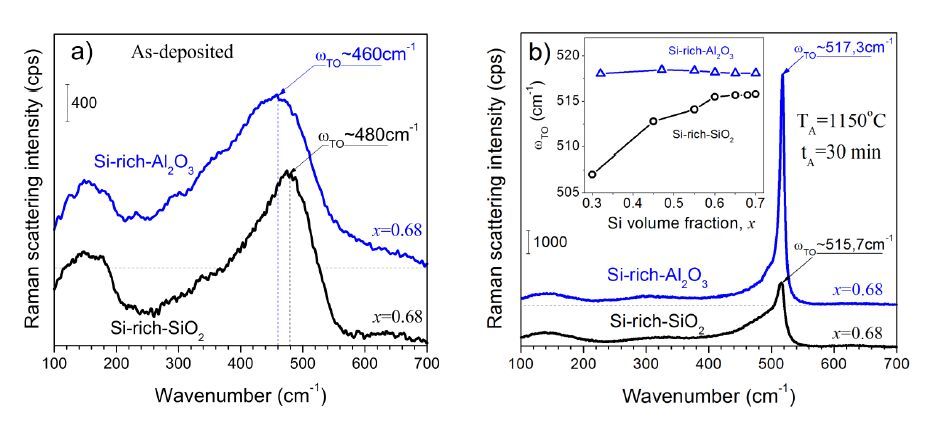
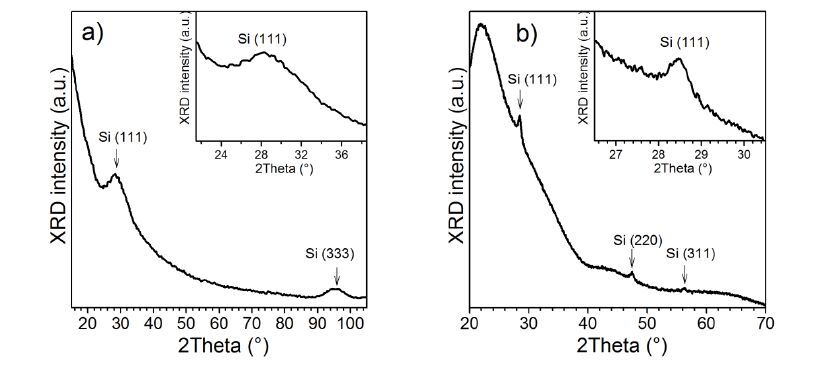
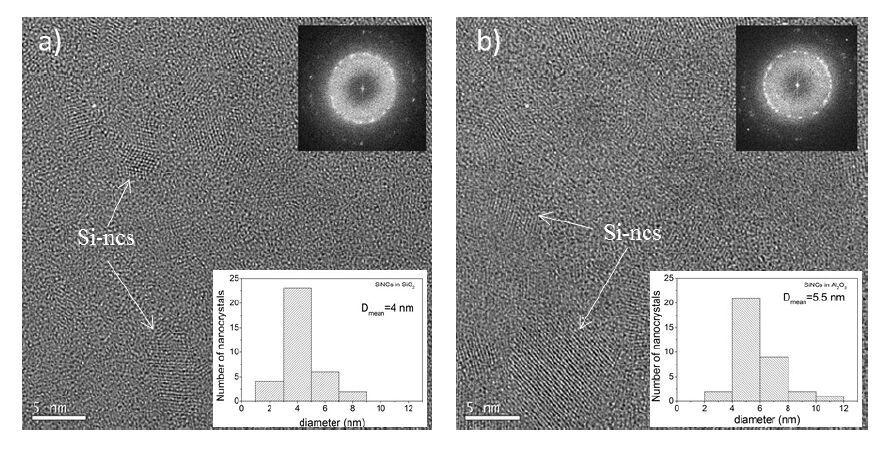
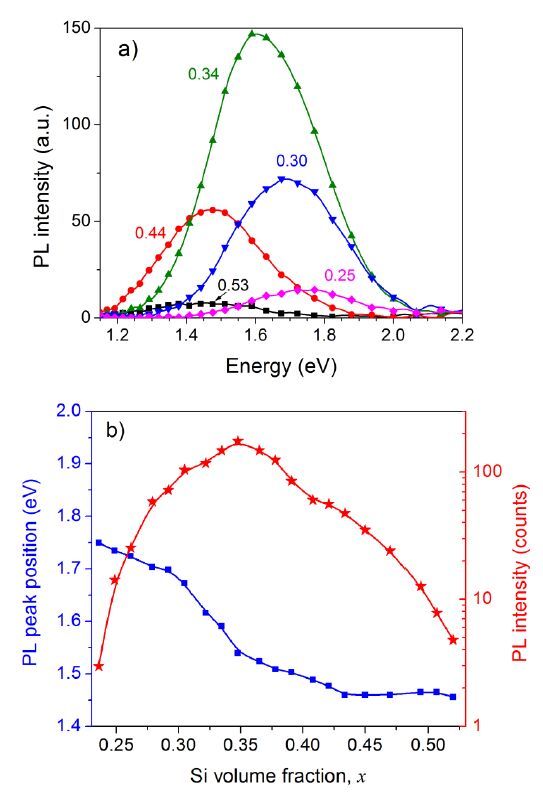
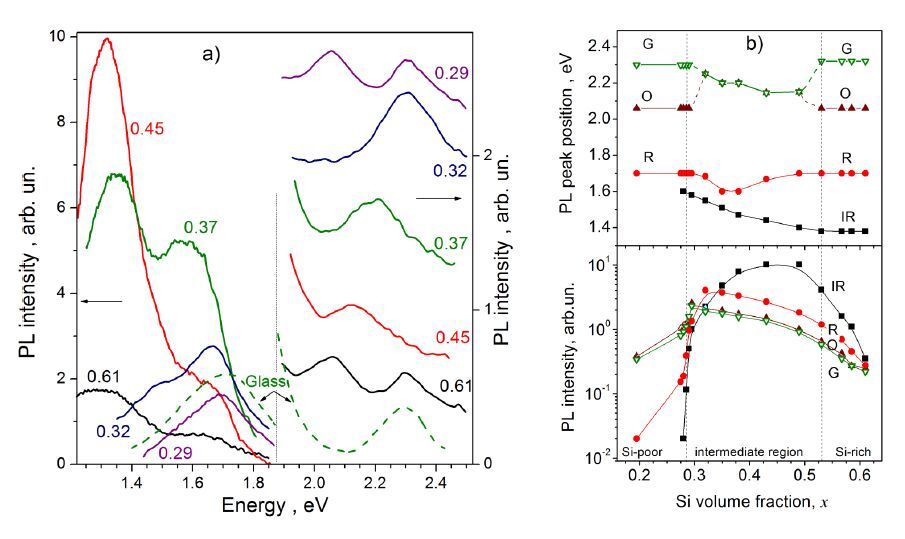
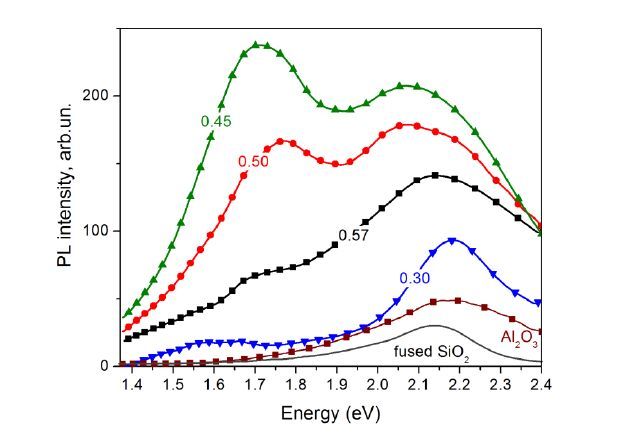
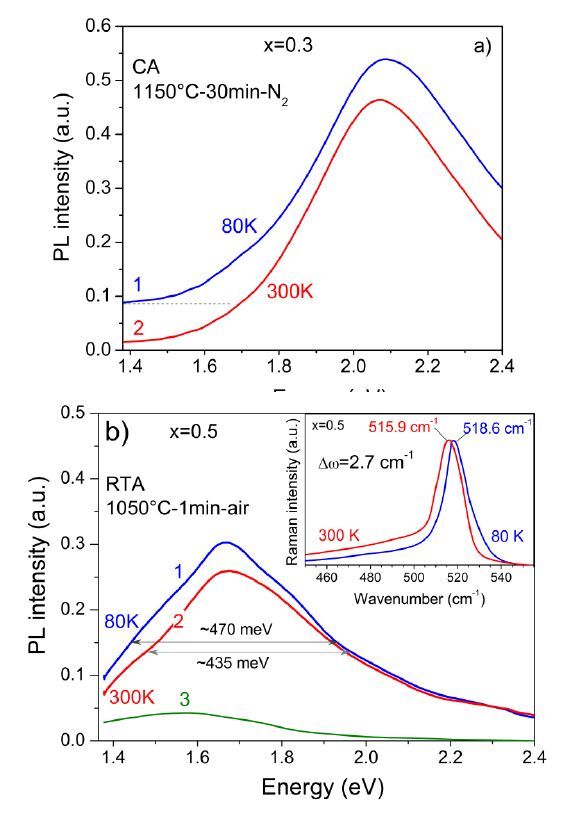
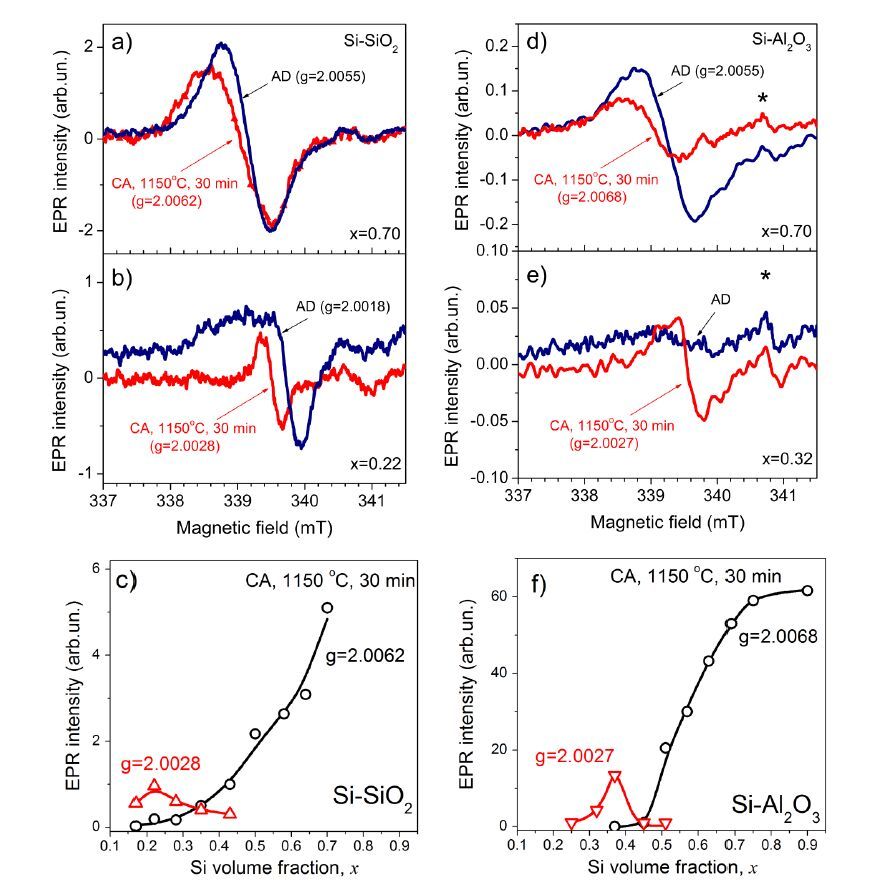
This paper presents a comparison of the results that we obtained and reported over the last few years on the structural, optical and light emitting properties of Si-SiO2 and Si-Al2O3 films that were fabricated using a specific configuration of RF magnetron sputtering. In these films the Si volume fraction, x, varies along the film (which is typically 14 cm long) from a value of ~0.1 at one end to ~0.9 at the other end. For the films with x > 0.3, the formation of amorphous Si clusters was observed in as-deposited Si-SiO2 and Si-Al2O3 films. Si nanocrystals (Si-ncs) were generated by high-temperature annealing of the films in nitrogen atmosphere. We found that two processes can contribute to the Si-ncs formation: (i) the crystallization of the existing amorphous Si inclusions in the as-deposited films, and (ii) the thermally stimulated phase separation. Process (i) can be responsible for the independence of Si-ncs mean sizes on x in annealed films with x > 0.5. At the same time, difference in the structural and the light emitting properties of the two types of films was observed. For the samples of the same x, the Si-ncs embedded in the Al2O3 host were found to be larger than the Si-ncs in the SiO2 host. This phenomenon can be explained by the lower temperature required for phase separation in Si-Al2O3 or by the lower temperature of the crystallization of Si-ncs in alumina. The latter suggestion is supported by Raman scattering and electron paramagnetic resonance spectra. In contrast with the Si-SiO2, the Si-ncs embedded in Si-Al2O3 films were found to be under tensile stress. This effect was explained by the strains at the interfaces between the film and silica substrate as well as between the Si inclusions and the Al2O3 host. It was also shown that exciton recombination in Si-ncs is the dominant radiative channel in Si-SiO2 films, while the emission from the oxide defects dominates in Si-Al2O3 films. This can be due to the high number of non-radiative defects at Si-ncs/Al2O3 interface, which is confirmed by our electron paramagnetic resonance data and is consistent with our above suggestion of mechanical stresses in the Si-Al2O3 films.
1.
Introduction
Predation is a ubiquitous interaction among species and thus it has been studied extensively. Most predator-prey models are extensions and modifications of the classical Lotka-Volterra model by incorporating many other factors. The obtained theoretical results can guide us to make appropriate policies on ecological protection and ecological sustainable development [1]. One important modification is the Leslie-Gower model described by
where $ x(t) $ and $ y(t) $ stand for the densities of the prey and predator at time $ t $, respectively. Here both species have the logistic growths with respective intrinsic growth rates $ r $ and $ s $ and with the carrying capacities $ K $ for the prey and $ nx $ for the predator (which depends on the density of the prey). $ n $ is a measure of the quality of the prey and $ nx $ is called the Leslie-Gower term [2]. $ P(x) $ is the functional response of predators to prey. Model (1.1) has been extensively studied and promoted (see, for example, [3,4]). Recently, the influence of fear effect and Allee effect on the dynamical behaviors of predator-prey models has attracted many researchers' attention.
Fear effect of predator is a form of indirect predation impacting the prey population [5,6,7]. To some extent, the physiological states of prey are disturbed by the fear effect. As a result, in the long run, the fear effect may lead to a loss in prey population. Meanwhile, the prey suffered from scare usually forage less and then their birth rate decreases which may be not good for the survival of prey's population. There is an example that some birds make anti-predator defenses against the sound of the predator and once perceive danger, they flee from their nests. As far as prey is concerned, frequent exposure to fear and anti-predation behavior will affect their birth rate. Therefore, it is necessary to take into account of fear factor in the predator-prey interaction [8,9,10]. In [11], Wang et al. first modeled the fear effect by introducing a factor $ f(k, y) $, where $ k $ represents the intensity of anti-predator behaviors of the prey caused by fear. See the paper for more detail on the properties of $ f(k, y) $. A recent experiment designed by Elliott et al. [12] demonstrated that Allee effect [13,14,15] can be induced by the fear effect. Moreover, the strong Allee effects [16,17] should be paid more attention, because too large fear intensity will drive the species to extinction.
Allee effect mainly signifies that individual fitness is directly proportionate to population density. Due to the variety of species, the causes of Allee effect are also different. Such as sperm limitation, reproduction facilitation, cooperative breeding, anti-predator behavior and predator satiation. During the last decades, lots have been done for predator-prey models with Allee effects. For example, Merdan [18] investigated the stabilityof a Lotka-Volterra type predator-prey system involving Allee effect; Liu and Dai [19] considered an impulsive predator-prey model with double Allee effects; Wu et al. [20] tried to understand the Allee effect in a commensal symbiosis mode; studied Guan and Chen [21] studied an amensalism model with Allee effect on the second species; and Naik et al. [22] explored the effect of strong Allee effect in a discrete predator-prey model.
On the one hand, based on the experimental observations of Elliott et al. [12], Sasmal [15] proposed and investigated the following predator-prey model with prey subject to Allee effect and fear effect,
where $ \theta $ and $ f $ are Allee constant and fear factor, respectively. They showed that the cost of fear has no influence on the stability of equilibria. On the other hand, González-Olivares et al. [23] studied the following Leslie-Gower model with Allee effect in prey,
where $ m $ represents the Allee effect threshold. Without Allee effect, there is a unique equilibrium, which is globally asymptotically stable. However, with the presence of strong Allee effect, the number of equilibria varies with respect to $ m $. It is shown that the system exhibits local bifurcations including Hopf bifurcation and Bogdanov-Takens bifurcation.
Inspired by these two works [15,23], it is natural and interesting to investigate the combined influence of both Allee effect and fear effect on dynamics of Leslie-Gower predator-prey models. In other words, whether the qualitative structure and bifurcation phenomena will become more complex? The thoretical results will help humans manage ecosystems. Precisely, the model to be studied in this paper is
where $ r $, $ K $, $ f $, $ q $, $ n $, $ s $, and $ m $ are all positive constants and $ 0 < m < K $. For simplicity of analysis, we introduce new variables
and denote
Then system (1.2) becomes
(note that we have dropped the bars here), where $ m $, $ f $, $ q $, and $ s $ are positive constants with $ 0 < m < 1 $.
Though not defined at $ x = 0 $, the dynamical behavior of (1.3) in the absence of prey is of interest. For this end, we take the time scaling $ d t = (1+fy)x d \tau $ to get a new system (still label $ \tau $ as $ t $),
This new system with the time scale reaches stable equilibria much faster than the original one. As a result, in the following we only focus on (1.4). Due to the biological background, the initial conditions $ (x(0), y(0))\in\mathbb{R}_+^2 $. Obviously, for such an initial condition, (1.4) has a unique global solution which stays in $ \mathbb{R}_+^2 $.
In the following, we first present the results on boundedness of solutions and the attraction of the origin. Followed is the existence and local stability of equilibria. The results indicate possible occurrence of bifurcations. We thus explore the detail on saddle-node bifurcation of codimension 1, Hopf bifurcation of codimension 1, and Bogdanov-Takens bifurcation of codimension 2. A brief conclusion ends the paper.
2.
Preliminaries
We first show the ultimate boundedness of solutions of (1.4).
Proposition 1. Let $ (x(t), y(t)) $ be a solution of (1.4). Then
Proof. We show $ \limsup_{t\to\infty}x(t)\le 1 $ by distinguishing two cases. Firstly, we assume $ x(t)\ge 1 $ for $ t\ge 0 $. Then it follows from (1.4a) that $ x $ is a decreasing function. Denote $ \lim_{t\to\infty}x(t) $ by $ l $. It is easy to see that $ l = 1 $. Next, we assume that $ x(t_0) < 1 $ for some $ t_0\ge 0 $. We claim that, for $ t\ge t_0 $, $ x(t)\le 1 $. Otherwise, there exists a $ t^* > t_0 $ such that $ x(t^*) > 1 $. Let $ x(\hat{t}) = \max\{x(t)\vert t_0\le t\le t^*\} $. As $ \frac{dx(t^*)}{dt} < 0 $, we have $ \hat{t}\in (t_0, t^*) $ and hence $ \frac{dx(\hat{t})}{dt} = 0 $. This is impossible as $ x(\hat{t}) > 1 $, which gives $ \frac{dx(\hat{t})}{dt} < 0 $. The claim is proved. To sum up, $ \limsup_{t\to\infty}x(t)\le 1 $ is proved. Now, for $ \varepsilon_0 > 0 $, there exists $ \breve{t}\ge 0 $ such that $ x(t)\le 1+\varepsilon_0 $ for $ t\ge \breve{t} $. It follows that, for $ t\ge \breve{t} $,
Then arguing similarly as for $ \limsup_{t\to\infty}x(t)\le 1 $, we can get $ \limsup_{t\to\infty}y(t)\le 1+\varepsilon_0 $. As $ \varepsilon_0 $ is arbitrary, we immediately have $ \limsup_{t\to\infty}y(t)\le 1 $.
3.
Existence and local stability of equilibria
We start with finding the equilibria to (1.4), which are determined by solutions to
Clearly, (1.4) always admits two positive boundary equilibria $ P_1(m, 0) $ and $ P_2(1, 0) $. Moreover, for a positive equilibrium $ (x, x) $ (or coexistence equilibrium), $ x $ satisfies
If $ m-q+1\le 0 $ then (3.1) has no positive roots and hence (1.4) has no positive equilibria. Now assume that $ m-q+1 > 0 $, which implies that $ q < m+1 < 2 $. Denote the discriminant of (3.1) by $ \Delta $ and it can be expressed as a quadratic function of $ m $,
Note that $ \Delta(1) = q(q-4-4f) < 0 $ and $ \Delta(q-1) = 2(1-q)(2+fq) $. It follows that if $ q\ge 1 $ then $ \Delta(m) < 0 $, which again implies that (1.4) has no positive equilibrium. Finally, if $ 0 < q < 1 $, then $ \Delta(m) > 0 $ only when $ 0 < m < m_1 $ while $ \Delta(m) = 0 $ only when $ m = m_1 $, where
In the former, (3.1) has two positive roots, $ x_3 = \frac{m-q+1-\sqrt{\Delta(m)}}{2(1+fq)} $ and $ x_4 = \frac {m-q+1+\sqrt{\Delta(m)}}{2(1+fq)} $, which are in $ (0, 1) $ while in the latter, $ \bar{x} = 1-\sqrt{\frac{fq+q}{fq+1}}\in (0, 1) $ is the unique positive root. The above discussion is summarized as follows.
Theorem 2. (ⅰ) There are always three boundary equilibria $ (0, 0) $, $ P_1(m, 0) $, and $ P_2(1, 0) $ for system (1.4).
(ⅱ) Besides the three boundary equilibria, for (1.4) to have positive equilibria it is necessary that $ 0 < q < 1 $. In this case,
(a) if $ m_1 < m < 1 $, there is no positive equilibrium;
(b) if $ m = m_1 $, there is a unique positive equilibrium $ \bar{P}(\bar{x}, \bar{x}) $, where $ \bar{x} = 1-\sqrt{\frac{fq+q}{fq+1}} $;
(c) if $ 0 < m < m_1 $, there are distinct positive equilibria $ P_3(x_3, x_3) $ and $ P_4(x_4, x_4) $, where $ x_3 = \frac{m-q+1-\sqrt{\Delta(m)}}{2(1+fq)} $ and $ x_4 = \frac{m-q+1+\sqrt{\Delta(m)}}{2(1+fq)} $.
Remarks 3. Considering $ f = 0 $, we have $ q+1-2\sqrt{q}: = m_0 $. Obviously, $ m_1 < m_0 $, which means that influenced by fear effect, Allee threshold value decreases. In other words, prey are more likely to die out at low density.
Next, we consider the attractivity of the origin.
Theorem 4. The origin is a non-hyperbolic attractor for (1.4).
Proof. Note that the technique of linearization is inapplicable as $ J(0, 0) $ is the zero matrix for (1.4). The approach here is the blow-up method. With the horizontal blow-up
along the invariant line $ x = 0 $, we rewrite system (1.4) as
On the nonnegative $ u $-axis, the above system admits two equilibria $ C_1(0, 0) $ and $ C_2(0, \frac{m+s}{s}) $. The corresponding Jacobian matrices are
respectively. Obviously, $ C_1 $ is a saddle while $ C_2 $ is an attractor. After blow-down, the origin is an attractor.
Theorem 5. $ P_1 $ is a hyperbolic repeller node while $ P_2 $ is a saddle.
Proof. At $ P_1 $ and $ P_2 $, the Jacobian matrices are respectively
respectively. Clearly, since $ m < 1 $, $ J_{P_1} $ has two positive eigenvalues while $ J_{P_2} $ has one positive and one negative eigenvalues. Then the results follow immediately.
The result below indicates that the stability of the positive equilibrium $ \bar{P} $ depends on $ s $.
Theorem 6. Suppose that $ 0 < q < 1 $ and $ m = m_1 $, which guarantee the existence of $ \bar{P} $. Then we have the following statements.
(i) $ \bar{P} $ is a saddle-node with an attracting parabolic sector when $ s > s_* $, where $ s_* = \frac {q\bar{x}(1+2f\bar{x})}{f\bar{x}+1} $;
(ii) $ \bar{P} $ is a saddle-node with a repelling parabolic sector when $ s < s_* $;
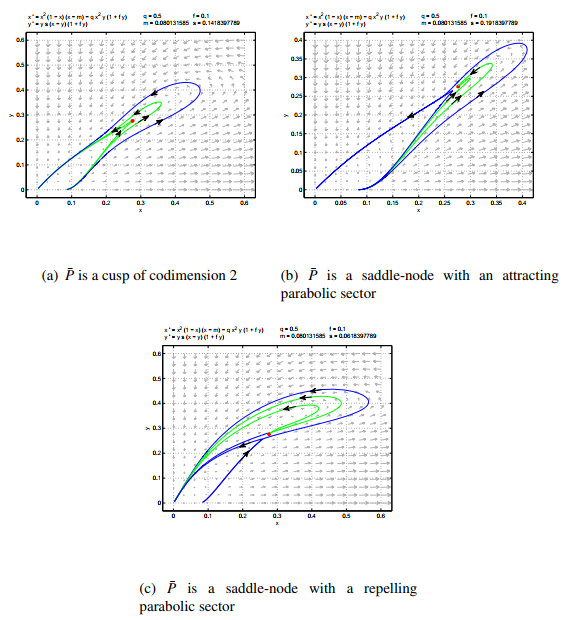
(iii) $ \bar{P} $ is a degenerate equilibrium when $ s = s_* $. Furthermore, if either ($ 0 < \bar{x} < 2-\sqrt{3} $ and $ f\neq f_1 $) or $ 2-\sqrt{3}\leq\bar{x} < 1 $, then $ \bar{P} $ is a cusp of codimension two; if $ 0 < \bar{x} < 2-\sqrt{3} $ and $ f = f_1 $, then $ \bar{P} $ is a cusp of codimension at least three, where
Fig. 1 shows the phase portraits.
Proof. Note that the Jacobian matrix of (1.4) at $ \bar{P} $ is
We easily see that
and hence $ J_{\bar{P}} $ has zero as an eigenvalue.
First of all, we use the transformation
to translate $ \bar{P} $ into $ (0, 0) $ and system (1.4) into
where
Now, assume that $ s \neq s_* $. Then the linear transformation
is nonsingular. This, combined with the time scale $ d \tau = (a_{10}+b_{01}) d t $, transforms system (3.2) into (we still denote $ \tau $ as $ t $)
where
Since $ a^{\prime}_{20} > 0 $, with the center manifold method [24], the equation near the center manifold can be approximated by
Making use of [25,Theorem 7.1], the degenerate equilibrium $ \bar{P} $ is a saddle-node where the parabolic sector is located at the right half plane. From the time scaling $ d\tau = (a_{10}+b_{01})dt $, we see that if $ s > s_* $, the parabolic sector is attracting while if $ s < s_* $ the parabolic sector is repelling.
Next, we assume $ s = s_* $. It follows from
that
Obviously, $ m_1\in(0, 1) $, $ q_* > 0 $, and $ s_* > 0 $ still hold under the assumptions that $ f > 0 $ and $ \bar{x}\in(0, 1) $. Then $ (X, Y) = (u, -\frac{a_{01}}{a_{10}}u+\frac{1}{a_{10}}v) $ transforms (3.2) into
where
Thus the $ C^\infty $ change of coordinates in a small neighborhood of $ (0, 0) $,
produces the normal form of system (3.5),
where
Obviously, $ f_{20} < 0 $ and the sign of $ f_{11} $ relies on the sign of
Note that $ 2\bar{x}^4-4\bar{x}^3 < 0 $ since $ 0 < \bar{x} < 1 $. Denote
Then
Thus $ \varphi(f) < 0 $ if $ \frac{2-\sqrt{2}}{2} < \bar{x} < 1 $. If $ \bar{x} = \frac{2-\sqrt{2}}{2} $, then $ \varphi(f) = \frac{2\sqrt{2}-3}{2}(f+1)^2 < 0 $ since $ f > 0 $. Now consider the case where $ 0 < \bar{x} < \frac{2-\sqrt{2}}{2} $. Notice that
and
It follows that $ \varphi(f) < 0 $ if $ 2-\sqrt{3} < \bar{x} < \frac{2-\sqrt{2}}{2} $ and $ \varphi(f) = f[(90-52\sqrt{3})f+(38-22\sqrt{3})] < 0 $ when $ \bar{x} = 2-\sqrt{3} $ since $ f > 0 $. If $ 0 < \bar{x} < 2-\sqrt{3} $, then
where
Then the results follow and this completes the proof.
At last, we consider the positive equilibria $ P_3 $ and $ P_4 $.
Theorem 7. Suppose $ 0 < q < 1 $ and $ 0 < m < m_1 $. Then $ P_3 $ is always a saddle point while $ P_4 $ is a sink if $ s > {\frac {x_4 \left(-2\, x_4+m+1 \right) }{f x_4+1}} $, is a source if $ s < {\frac {x_4 \left(-2\, x_4+m+1 \right) }{f x_4+1}} $, and a center or fine focus if $ s = {\frac {x_4 \left(-2\, x_4+m+1 \right) }{f x_4+1}} $.
Proof. After a simple calculation, we can get
where $ J_{P_3} $ and $ J_{P_4} $ are the Jacobian matrices of (1.4) at $ P_3 $ and $ P_4 $, respectively. It follows immediately that $ P_3 $ is always a saddle. For the stability of $ P_4 $, we need the trace of $ J_{P_4} $, which is
Then the results follow easily.
4.
Bifurcation analysis
The goal of this section is to analyse the saddle-node bifurcation, Hopf bifurcation, and Bogdanov-Takens bifurcation that may occur in system (1.4).
4.1. Saddle-node bifurcation
From Theorems 6 and 7, it is not difficult to obtain the saddle-node surface,
The phase of the saddle-node bifurcation corresponding to the ecology system has obvious critical Allee value $ m_1 $. When $ m > m_1 $, the prey will face the risk of extinction; when $ m < m_1 $, the dynamic behavior of system (1.4) becomes complex since the saddle and anti-saddle come out in the phase, which means that the density of prey must be large enough for survival.
4.2. Hopf bifurcation
From Theorem 7, the local stability of $ P_4 $ will change as the parameter $ s $ varies. Besides, there exists an $ s_H = {\frac {x_4 \left(-2\, x_4+m+1 \right) }{f x_4+1}} $ which satisfies $ Tr(J_{P_4})\vert_{s_{H}} = 0 $ and then $ P_4 $ becomes a non-hyperbolic equilibrium which loses its stability. Meanwhile, it is easy to verify the transversality condition,
Therefore, there exists a Hopf bifurcation in a small neighbourhood of $ P_{4} $. This is summarized as follows.
Theorem 8. Let $ s $ be the Hopf bifurcation parameter. When $ s $ crosses the threshold value $ s_H = {\frac {x_4 \left(-2\, x_4+m+1 \right) }{f x_4+1}} $, system (1.4) undergoes a non-degenerate Hopf bifurcation around $ P_{4} $.
There is at least one limit cycle which appears around $ P_4 $ due to the occurrence of Hopf bifurcation. The stability of the limit cycle is very significant for ecology systems and we can use the sign of the Lyapunov number to determine it. In order to simplify the computation, we translate $ P_4 (x_4, x_4) $ to $ (1, 1) $ with the following state variable scaling and time rescaling:
After dropping the bars and relabelling $ \tau $ as $ t $, we transform system (1.4) into
Because system (4.2) has an equilibrium $ \bar{P_4}(1, 1) $ (i.e., $ P_4(x_4, x_4) $ of (1.4)), we have $ q = \frac{(K-1)(1-m)}{K(1+f)} > 0 $. Then we can get another positive equilibrium $ \bar{P_3}(\bar{x}_3, \bar{x}_3) $, where $ \bar{x}_3 $ and $ \bar{x}_4 $ are positive distinct roots of the equation
By Vieta theorem [26], $ \bar{x}_3 \bar{x}_4 = {\frac {Km \left(1+f \right) }{-Kfm+Kf+fm+1}} < 1 $. From the scalings (4.1), we see that the parameters in system (4.2) satisfy
With $ q $ being replaced by $ \frac{(K-1)(1-m)}{K(1+f)} $, system (4.2) becomes
where the parameters $ K $, $ m $, $ f $, and $ s $ satisfy (4.3). Therefore, we study the stability of the weak focus $ \bar{P_4}(1, 1) $ for system (4.4) to acquire the stability of the weak focus $ P_4(x_4, y_4) $ in system (1.4).
The Jacobian matrix of system (4.4) at $ \bar{E_4}(1, 1) $ is
It follows that
and
With the help of (4.3), we see that $ \det(J_{\bar{P_4}}) > 0 $. Thus the necessary conditions on parameters for Hopf bifurcation occurring around $ \bar{E_4} $ are
Note that at $ s = s_{hf}\triangleq \frac{m+K-2}{K(1+f)} $, $ J_{\bar{P_4}} $ has a pair of conjugate pure imaginary eigenvalues. Moreover,
that is, the transversality condition holds.
Now translating $ \bar{P_4}(1, 1) $ to the origin $ (0, 0) $ by the change $ (\hat{x}, \hat{y}) = (x-1, y-1) $ when $ s = s_{hf} $, we rewrite (4.4) as
where
We now make another transformation $ \hat{u} = -\hat{x} $, $ \hat{v} = \frac{1}{\sqrt{D}}(\hat{a_{10}}\hat{x}+\hat{a_{01}}\hat{y}) $, and $ \mathrm{d}\tau = \sqrt{D}\mathrm{d}t $ to change system (4.6) into
where
Here we have omitted the expressions of $ \hat{c_{ij}} $ and $ \hat{d_{ij}} $.
Applying the formal series method in [25] and calculating the first Lyapunov number with the help of MAPLE, we get
where
Under condition (4.5), we have $ p_4 > 0 $. Thus the sign of $ l_{1} $ depends on that of
Theorem 9. If $ l_{11} > 0 $ then system (4.4) exhibits a subcritical Hopf bifurcation around $ \bar{P_4} $ at $ s = s_{hf} $ (see Fig. 2(a)) while if $ l_{11} < 0 $ then it exhibits a supercritical Hopf bifurcation around $ \bar{P_4} $ at $ s = s_{hf} $ (see Fig. 2(b)).
When $ l_{11} = 0 $, we should consider the second Lyapunov number $ l_2 $ to determine the stability of the order-two weak focus. The expression of $ l_2 $ is too complicated, so we just provide a numerical example with $ (K, f, m, s) = (2, \frac{36281}{21430}, \frac{2}{5}, \frac{4286}{57711}) $. For such a set of parameter values, we have $ l_1 = 0 $ and $ l_2 = 0.4025314467 > 0 $, which means that system (4.4) undergoes a multiple Hopf bifurcation of codimension two and there are two limit cycles (the inner one is stable and the outer one is unstable) bifurcated from $ \bar{P_4}(1, 1) $ when the bifurcation parameters $ (f, s) = (\frac{36281}{21430}, \frac{4286}{57711}) $ is disturbed (see Fig. 2(c)).
4.3. Bogdanov-Takens bifurcation
From Theorem 6, system (1.4) admits that $ \bar{P} $ is a cusp of codimension 2 when $ m = m_1 $, $ s = s_* $, $ q = q_* $, and $ \varphi (f)\neq0 $. In the following, we show that Bogdanov-Takens bifurcation around $ \bar{P} $ can occur.
Theorem 10. Under the condition that $ \bar{P} $ is a cusp of codimension 2, we choose the parameters $ m $ and $ s $ as bifurcation parameters. As the parameters $ (m, s) $ vary around $ (m_1, s_*) $, system (1.4) experiences Bogdanov-Takens bifurcation in a small neighborhood of\ $ \bar{P} $. Furthermore,
(i) Given $ \varphi (f) > 0 $, system (1.4) exhibits a supercritical Bogdanov -Takens bifurcation, which accompanies with the appearance of a stable limit cycle originated from the supercritical Hopf bifurcation followed by a stable homoclinic loop;
(ii) Given $ \varphi (f) < 0 $, system (1.4) exhibits a subcritical Bogdanov -Takens bifurcation, which accompanies with the appearance of an unstable limit cycle originated from the subcritical Hopf bifurcation followed by an unstable homoclinic loop.
Proof. We give the unfolding system of system (1.4),
where $ \lambda_1 $ and $ \lambda_2 $ are disturbed in a small neighbourhood of the origin. For convenience, we should find the versal unfolding of system (4.7), which is helpful to study the change of the topological structure. We make some transformations as follows to achieve it.
Firstly, use the transformation $ u_1 = x-\bar{x} $ and $ u_2 = y-\bar{x} $ to translate the positive equilibrium $ \bar{P} $ to $ (0, 0) $ and transform system (4.7) into
where
Next, letting $ u_3 = u_2 $, $ u_4 = \frac{du_2}{dt} $, we transform system (4.8) into
where
In order to remove the $ \tilde{c}_{02}u_4^2 $ term in system (4.9), we make a new time variable $ \tau $ by $ d t = (1-\tilde{c}_{02}u_3) d \tau $ and let $ u_5 = u_3 $, $ u_6 = u_4(1-\tilde{c}_{02}u_3) $. We still denote $ \tau $ as $ t $ to get from (4.9) that
where
Notice that $ \tilde{d}_{20}\to -\frac{(\bar{x}-1)^2(2\bar{x}f+1)\bar{x}^4(f+1)} {(\bar{x}^2f-2\bar{x}f-1)^2} < 0 $ when $ (\lambda_1, \lambda_2)\to (0, 0) $. Then we employ the transformation
to change $ \tilde{d}_{20} $ into $ -1 $. Meanwhile with this transform and relabelling $ \tau $ as $ t $, system (4.10) becomes
where
Now eliminate $ u_7 $ by the transformation $ u_9 = u_7-\frac{\tilde{e}_{10}}{2} $, $ u_{10} = u_8 $ to change system (4.11) into
where
Lastly, to obtain the versal unfolding of (4.7), we need to make $ \tilde{f_{11}} $ be 1. Since $ \tilde{f}_{11}\to \frac{\bar{x}\varphi(f)}{(\bar{x}f+1)(1-\bar{x}^2f+2\bar{x}f)} \neq 0 $ as $ (\lambda_1, \lambda_2) \to (0, 0) $, we can perform the transformation
Relabelling $ \tau $ as $ t $, we can rewrite (4.12) as
where
With the assistance of MAPLE,
which implies that $ \tilde{g}_{00} $ and $ \tilde{g}_{10} $ are independent parameters. Therefore, system (4.14) is the versal unfolding of system (4.7) such that both have the same topological structure. As $ \tilde{g}_{00} $ and $ \tilde{g}_{10} $ vary, the topological structure of system (4.14) will change and system (1.4) will undergo Bogdanov-Takens bifurcation. Noticing that there exists time scale $ t = -\tilde{f_{11}}\tau $ in the transformation (4.13), we have the following conclusions:
(i) if $ \varphi (f) > 0 $, then $ -\tilde{f}_{11} < 0 $. Thus system (1.4) undergoes a supercritical Bogdanov-Takens bifurcation of codimension 2, which consists of saddle-node bifurcation of codimension 1, supercritical Hopf bifurcation of codimension 1, and homoclinic bifurcation of codimension 1.
(ii) if $ \varphi (f) < 0 $, then $ -\tilde{f}_{11} > 0 $. Thus system (1.4) undergoes a subcritical Bogdanov-Takens bifurcation of codimension 2, which consists of saddle-node bifurcation of codimension 1, subcritical Hopf bifurcation of codimension 1, and homoclinic bifurcation of codimension 1.
Before drawing the phase portraits, we need to acquire the expression of the bifurcation curves within Bogdanov-Takens bifurcation in the $ (\lambda_1, \lambda_2) $-plane.
By the conclusion in Bogdanov [27] and Takens [28] (see also Chow et al. [29] and Perko [24]), we can obtain the following local representations of the bifurcation curves.
(i) The saddle-node bifurcation curve $ SN = \{(\tilde{g}_{00}, \tilde{g}_{01}):\tilde{g}_{00} = 0, \tilde{g}_{01}\neq 0 \} $;
(ii) the Hopf bifurcation curve $ H = \{(\tilde{g}_{00}, \tilde{g}_{01}):\tilde{g}_{01} = \sqrt{-\tilde{g}_{00}}, \tilde{g}_{00} < 0 \} $;
(iii) the homoclinic bifurcation curve $ HL = \{(\tilde{g}_{00}, \tilde{g}_{01}):\tilde{g}_{01} = \frac{5}{7}\sqrt{-\tilde{g}_{00}}, \tilde{g}_{00} < 0 \} $.
In the case of repelling Bogdanov-Takens bifurcation ($ \varphi (f) > 0 $), we will use $ \lambda_1 $ and $ \lambda_2 $ to describe the bifurcation curves $ SN $, $ H $, and $ HL $. By (4.15) and the Implicit Function Theorem, we get the expressions of $ \lambda_1 $ and $ \lambda_2 $ in terms of $ \tilde{g_{00}} $ and $ \tilde{g_{10}} $,
where
For the saddle-node bifurcation curve $ SN $, let $ \Lambda_1 \triangleq \tilde{g_{00}}(\lambda_1, \lambda_2) = 0 $. Due to
turning to the Implicit Function Theorem, there exists a unique function $ \lambda_1(\lambda_2) $, which satisfies $ \lambda_1(0) = 0 $ and $ \Lambda_1(\lambda_1(\lambda_2), \lambda_2) = 0 $. It follows that
Furthermore, on the curve $ \Lambda_1 = 0 $, from (4.16), we know $ \lambda_2 = b_2\tilde{g_{10}}+O(\mid\tilde{g_{10}}\mid^2) $, which implies that $ \lambda_2 > 0 $ if $ \tilde{g_{10}} > 0 $ and $ \lambda_2 < 0 $ if $ \tilde{g_{10}} < 0 $. Therefore, we acquire
For the Hopf bifurcation curve $ H $, let $ \Lambda_2 \triangleq \tilde{g_{00}}(\lambda_1, \lambda_2) +\tilde{g_{10}}^2(\lambda_1, \lambda_2) = 0 $. Due to
there exists a unique function $ \lambda_1(\lambda_2) $, which satisfies $ \lambda_1(0) = 0 $ and $ \Lambda_2(\lambda_1(\lambda_2), \lambda_2) = 0 $. Then
Furthermore, on the curve $ \Lambda_2 = 0 $, from (4.16), we know $ \lambda_2 = b_2\tilde{g_{10}}+O(\mid\tilde{g_{10}}\mid^2) $, which implies that $ \lambda_2 < 0 $ if $ \tilde{g_{10}} < 0 $. Therefore, we get
For the Homoclinic bifurcation curve $ HL $, let $ \Lambda_3 \triangleq \frac{25}{49}\tilde{g_{00}}(\lambda_1, \lambda_2) +\tilde{g_{10}}^2(\lambda_1, \lambda_2) = 0 $. Due to
there exists a unique function $ \lambda_1(\lambda_2) $, which satisfies $ \lambda_1(0) = 0 $ and $ \Lambda_3(\lambda_1(\lambda_2), \lambda_2) = 0 $. Then
Moreover, on the curve $ \Lambda_3 = 0 $, from (4.16), we know $ \lambda_2 = b_2\tilde{g_{10}}+O(\mid\tilde{g_{10}}\mid^2) $, which implies that $ \lambda_2 < 0 $ if $ \tilde{g_{10}} < 0 $. Therefore,
Analogously, the Bogdanov-Takens bifurcation curve in terms of $ \lambda_1 $ and $ \lambda_2 $ can be described.
To end this section, we present two sets of numerical simulations to verify the theoretical results with the help of MATLAB.
First, let $ \bar{x} = 0.5 $ and $ f = 3 $. Then $ m_1 = \frac{4}{13} $, $ q_* = \frac{1}{13} $, $ s_* = \frac{4}{65} $, and $ \varphi(f) = -\frac{57}{8} < 0 $. Therefore, system (1.4) undergoes a repelling Bogdanov-Takens bifurcation. With the disturbance of $ (\lambda_1, \lambda_2) $ in a small neighborhood of $ (0, 0) $, the repelling Bogdanov-Takens bifurcation diagram and its local phase portraits are shown in Fig 3.
Next, let $ \bar{x} = 0.1 $ and $ f = 8 $. Then $ m_1 = \frac{1}{28} $, $ q_* = \frac{9}{28} $, $ s_* = \frac{13}{280} $, and $ \varphi(f) = 1.1988 > 0 $. Therefore, system (1.4) undergoes an attracting Bogdanov-Takens bifurcation. With the disturbance of $ (\lambda_1, \lambda_2) $ in a small neighborhood of $ (0, 0) $, the attracting Bogdanov-Takens bifurcation diagram and its local phase portraits are illustrated by Fig. 4.
5.
Conclusion
In the present study, the dynamical behavior of a Leslie-Gower model with linear (Holling Type I) functional response and with both Allee effect and fear effect in prey is investigated. Although the model is not defined when the density of the prey is zero, the origin is an attractor with the help of the blow-up method and the technique of time scaling. Correspondingly, prey will die out at low densities. Moreover, solutions are bounded. Based on the work of Korobeinikov [30] that system (1.4) admits a unique globally asymptotically stable positive equilibrium when $ m = 0 $ and $ f = 0 $, qualitative analysis reveals that Allee effect results in complex dynamics. The number and stability of equilibria in system (1.4) depend on the Allee constant. The model has two boundary equilibria, one an unstable node and the other a saddle which means that the prey population will not fully reach the environmental capacity. There is a cusp coexistence equilibrium of codimension 2 or 3 if Theorem 6 holds. Furthermore, with the help of the formal series method in [25], we calculated the order of the weak focus to determine the stability of limit cycles bifurcated from Hopf bifurcation, which means that there is the possibility of periodic distributions of prey and predator populations. Choosing the Allee constant and intrinsic growth rate of the predator as bifurcation parameters and by means of a series of near-identity transformations, it was demonstrated that system (1.4) undergoes Bogdanov-Takens bifurcation of codimension 2 through calculating the versal unfolding.
Compared to the work of González-Olivares et al. [23], we focus on the cost of the anti-predation response in the prey reproduction. Our investigation indicates that the cost of fear still does not chang the stability of equilibria. This is similar to the result that the stability of positive equilibrium will not be influenced and the system still undergoes analogous bifurcation.
Different from the work of Sasmal [15], we considered a Leslie-Gower model where the carrying capacity of the predator relies on the abundance of prey. The model has abundant bifurcation phenomena. Through rigorous mathematical analysis, as the Allee constant varies, the model experiences saddle-node bifurcation and there are at most two equilibria in the phase diagram. Meanwhile, the model can undergo more complex bifurcation, Bogdanov-Takens bifurcation, than the traditional predator-prey model. Further, the model undergoes subcritical or supercritical Hopf bifurcation, which means that there is a stable or unstable limit cycle around a positive equilibrium. The model can even exhibit multiple Hopf bifurcations by a set of numerical simulations when the first Lyapunov number is zero.
Acknowledgments
This work was supported partially by the Natural Science Foundation of Fujian Province (Nos. 2020J01499, 2021J01613) and the National Natural Science Foundation of China (No. 12071418).
Conflict of interest
The authors declare there is no conflict of interest.









 DownLoad:
DownLoad: