1.
Introduction
The problem of estimating urban traffic flow has always been a matter of great concern, and it is also a core issue that needs to be paid attention to in the context of traffic congestion problems [1,2,3]. As urban traffic demand increasingly exceeds the capacity of existing infrastructure, merely expanding roadways is inadequate for mitigating congestion [4,5,6]. Instead, more sustainable and efficient solutions depend on the strategic planning and management of the current network [7]. Central to this effort is traffic assignment, which determines the flow distribution pattern in a given network [8,9,10]. Accurate assignment relies on understanding travelers' route-choice behavior [11,12], since individual decisions shape overall traffic flow distribution [13,14]. User Equilibrium (UE), based on Wardrop's first principle [15], provides the theoretical framework: in equilibrium, no traveler can unilaterally switch routes to reduce their travel cost. The UE traffic assignment problem (UE-TAP) can be formulated as a convex nonlinear program [16] and solved by the Frank-Wolfe algorithm [17]. However, owing to the classical method's high complexity and limited efficiency, three main streams of solution algorithms have emerged: link-based algorithms [18,19,20], bush-based methods [21,22,23], and path-based algorithms [24,25,26]. More recently, parallel computing strategies have been explored to enhance both efficiency and scalability in solving UE-TAP [27,28,29,30,31].
In addition to the above mechanism-based methods, data-driven deep learning methods have been increasingly adopted in transportation research, demonstrating significant potential for addressing complex and nonlinear traffic problems [32,33,34,35,36,37,38,39,40,41,42]. Rahman and Hasan [43] employed the graph convolutional network (GCN) to address stochastic flow diffusion under traffic randomness. However, capturing flow patterns purely from observations is constrained by data availability and quality, resulting in limited generalization to new networks. To address this limitation, physical information such as UE theory can be embedded directly in the learning process to enhance behavior realism [44,45]. For example, Fang et al. [46] proposed a long short-term memory (LSTM)-based traffic assignment model that retains the initialization step of the Frank-Wolfe algorithm.
This study offers a different perspective on addressing generalization challenge, especially across different network structures. Liu et al. [47] explored out-of-distribution (OOD) challenges by testing their model on networks with added links or adjusted capacities; however, these networks still share broadly similar topologies. The central question we address is: how to design a trained UE-learning model that can be applied to networks with significantly different node and link structures. If this generalization can be achieved, the dependence on data availability and accessibility could be significantly reduced in future studies. To the best of our knowledge, this study is the first to develop an end-to-end learning-based framework for user equilibrium prediction under variable network topologies. Compared to previous work [48], our approach models the propagation of node information across the graph while preserving both node and edge attributes, thereby capturing the underlying network topology more comprehensively. In addition to origin-destination (OD) demand, our model also incorporates link attributes and network topology as inputs, enabling a more detailed representation of traffic assignment dynamics. Table 1 summarizes recent machine learning-based UE-TAP literature, highlighting the innovation of this study.
More specifically, the main contributions of this study are as follows:
(1) Existing research has typically relied on classical optimization methods or data-driven approaches that lack behavioral interpretability to address the UE-TAP. This study introduces a GCN-based model that explicitly encodes the travelers' cost-minimizing behavior into its learning framework and trains it to directly predict equilibrium traffic flows from OD demand inputs, thereby bypassing the need for iterative optimization.
(2) Previous studies primarily assume fixed network topologies, limiting the applicability of these methods when faced with changes or disruptions in the network structure. This study utilizes network partitioning and subgraph training, explicitly incorporating network attributes such as free-flow travel time and link capacity, and employing a variable adjacency matrix as input, thereby making the model adapt dynamically to varying network topologies and significantly improving model robustness.
(3) This study generates and utilizes multiple randomized datasets based on two widely used benchmark networks: SF and EMA. Extensive numerical experiments demonstrate the proposed model's robustness and generalizability across different network scales and topologies. Notably, a model pretrained on data-rich networks can be effectively transferred to improve training efficiency and accuracy on networks with limited data, highlighting the potential of transferable learning in traffic assignment modeling.
The remainder of this study is organized as follows. Section 2 introduces the UE-TAP formulation and the proposed model. In Section 3, the methodology of the proposed model is described. Subsequently, Section 4 introduces the study network and the results obtained using the proposed model. Finally, Section 5 concludes the paper and outlines directions for future research.
2.
Problem statement
The equilibrium flow pattern throughout a traffic network can be seen as the outcome of traffic assignment. In this section, we define the UE-TAP and establish its role in obtaining equilibrium flows. Since real-world link flows is often difficult to obtain, we first employ the traditional optimization-based UE model to compute equilibrium flows as a reliable approximation. See Section 2.1. We then leverage a deep learning-based approach to learn the underlying mapping between the input attributes and the equilibrium flow distribution in Section 2.2. Table 2 summarizes the notations used in this study.
2.1. Traditional UE-TAP for obtaining the stable equilibrium flows
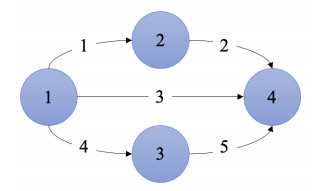
The road network is modeled as a directed graph G(N,M,A), where each element of A equals 1 when the two nodes in the road network are adjacent; it is 0 otherwise. We illustrate an example in Figure 1, consisting of four nodes and five links. For travelers who travel from node 1 to node 4 (OD pair o), Ko={0,1,2} (path 0 denotes nodes 1–2–4, path 1 denotes nodes 1–4, and path 2 denotes nodes 1–3–4). Total demand of this OD pair is denoted as qo, with fo0, fo1, and fo2 representing the traffic flows on path 0, 1, and 2, respectively. In this graph, we denote traffic flows on link 1 as f1 and travel time on this link as t1. We represent the formal UE formulation using the Beckmann's transformation in Eqs (1)–(5).
Subject to:
where Eq (1) is a convex optimization problem with a flow conservation constraint (traffic flow on links is determined by path flows) in Eq (2), an OD demand constraint to ensure all demand is assigned in Eq (3), and a nonnegativity constraint is in Eq (4). Finally, the binary variables define the association between links and paths, indicating whether a specific link belongs to a given path. Then, we use traditional algorithm (e.g., Frank-Wolfe algorithm) to iteratively update flows until convergence, while the solution satisfies:
Equation (6) means that all paths have equal travel time for each OD pair and no traveler can reduce their travel time by switching routes. Thus, the UE condition is satisfied, and we get the optimal equilibrium flows of our UE-TAP.
2.2. Learning-based approach to learn the underlying mapping between OD demand and stable equilibrium flows
Traditional optimization-based methods are computationally expensive and inefficient when applied to large-scale transportation networks. So, we try to propose a data-driven method for solving the UE-TAP using deep-learning. The goal is to develop a model that can efficiently learn the mapping between OD demand and equilibrium traffic flows in the network, thereby reducing computational time while maintaining high accuracy. We represent the problem as:
Here, f(⋅) is a GCN-based model in this study that learns the relationship between the input data (OD demand matrix Q, adjacency matrix A) and the output ˆy (predicted set of equilibrium flows).
3.
GCN-based learning framework
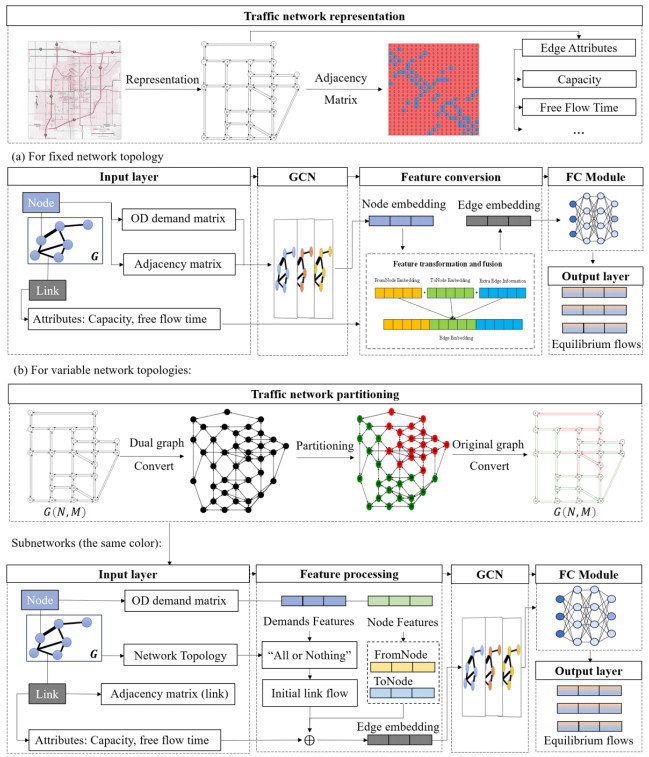
Given OD demand and link attribute information, we applied GCN [51] to estimate the equilibrium traffic flows distribution in this study. We first show our basic GCN model in a fixed network in Section 3.1, then we transfer this approach to variable network topologies in Section 3.2. Whole workflow of this study is shown in Figure 2.
3.1. GCN for fixed network topology
GCN relies on message passing and neighbor aggregation to capture spatial dependencies in graph-structured data. In the context of UE-TAP, GCN is used to estimate the equilibrium traffic flows on each road segment, given a specific travel demand distribution. The hidden representation at layer l+1 in the GCN can be expressed as:
where Hl is the feature matrix at layer l, Wl is the trainable weight matrix at layer l, and h(⋅) is the propagation function that aggregates information from neighboring nodes.
The GCN propagation rule follows:
where ˜A=A+I denotes the adjacency matrix augmented with the identity matrix to incorporate self-loops, ˜D is the degree matrix of ˜A, and σ(⋅) is the activation function.
In our UE-TAP, we predict equilibrium traffic flows, so no activation function is applied to the last layer. Instead, we use a regression-based approach, and the predicted equilibrium flow ˆy is given by:ˆy=f(Q,A;θ)
where θ denotes the set of all learnable parameters in the GCN-based model, including the weights and biases of both the graph convolution layers and the fully connected layers.
The model is trained using mean squared error (MSE) to minimize the difference between the predicted and actual equilibrium flows, with loss function:
In Figure 2(a), OD demand features are passed through GCN to derive new node features that incorporate graph structure information. When the topology of the traffic network is fixed, the focus is solely on the network itself, without the need to consider additional information. The model takes the OD demand between nodes, the adjacency matrix A of nodes, and link attributes as input.
In this study, the goal is to obtain the approximate equilibrium flow on each edge; therefore, node features must be converted into edge features in the feature processing stage. The transformation process follows these rules: the features of two nodes connected by an edge are concatenated, and feature fusion is performed by combining the edge features with additional edge information. After processing through the GCN, the edge features encapsulate node information, structural details, and intrinsic attributes of the edge. Finally, after passing through the fully connected layer, the model predicts the equilibrium flows for the traffic network.
3.2. Scalable GCN for variable network topologies
The GCN-based traffic assignment model proposed in Section 3.1 cannot be directly applied to variable topologies, as deep learning models typically require fixed input and output dimensions. To overcome this limitation, we introduce traffic network partitioning, as illustrated in Figure 2(b), enabling our approach to be adaptable and transferable across different traffic networks. Once trained, the model can be fine-tuned and applied to new networks while maintaining predictive accuracy.
The road network is initially partitioned into subnetworks, each containing an equal number of edges. If a subnetwork has fewer edges than required, a zero-padding operation is applied to maintain a consistent input dimension. The different colors of the arrows in the subsequent figures represent distinct subnetworks identified through the partitioning process, helping to visualize the structural segmentation more clearly. The partitioned subnetworks are then used to train the traffic assignment model. For a new traffic network, we only need to partition the network into subnetworks with an equal number of edges and either fine-tune the trained model or train a new deep learning model, ensuring predictive consistency in UE-TAP.
(1) Traffic network partitioning based on dual graph representation
The traffic network is partitioned such that adjacent edges in close proximity are grouped into the same subnetwork, ensuring each subnetwork remains a contiguous unit. To achieve this, we consider the dual graph representation of the traffic network, where the roles of edges and nodes are reversed, transforming the network into an undirected graph. The nodes in the dual graph (representing links in the original network) are then clustered into partitions, which are subsequently mapped back to the original traffic network to define subnetwork boundaries. Notably, all edges connecting the same pair of nodes are assigned to the same subnetwork to preserve network continuity.
(2) Adjacency matrix for road segments
To enable traffic assignment across variable topologies, we redefine the adjacency matrix to represent road segment connectivity rather than traditional node connectivity. This allows the GCN to process edge-level interactions, capturing the spatial dependencies among road segments. The adjacency matrix A′ for road segments is formulated as:
where r and s represent the starting point and end point of segment i and j.
(3) Model construction
Unlike fixed-topology traffic assignment model, the proposed variable-topology model directly accounts for road segments' characteristics. To ensure input consistency across networks, we first integrate OD demand information into the road network using an "all-or-nothing" assignment [52]. For each OD pair, we assign the entire demand to the shortest path (i.e., the path with the lowest travel cost based on free-flow travel times). This process is repeated for all OD pairs, and the resulting link flows are aggregated across all shortest paths to obtain a single edge-level demand vector. The resulting demand information, originally defined at the OD level, is thereby projected onto road segments. Each road segment is then represented by a feature vector that combines both its intrinsic attributes (link capacity, free-flow travel time, and initial link flow from "all-or-nothing" operation) and the derived demand features (FromNode: the total outgoing demand from the tail node; ToNode: the total incoming demand to the head node). These vectors are subsequently processed through a feature embedding layer to obtain low-dimensional representations. Since this model focuses on road segments level, a GCN layer with a segment adjacency matrix A′ is employed to aggregate information from adjacent links. This enables the model to capture spatial dependencies among neighboring road segments, ultimately facilitating accurate traffic flow estimation under variable network topologies.
4.
Discussion
4.1. Data description
To evaluate the effectiveness of our proposed data-driven UE-TAP model, we constructed and utilized three datasets for model training and validation. Since the problem described in Section 2 is based on supervised learning, labeled data is essential for training the model. In this context, we employed the improved gradient projection (iGP) algorithm [26] to compute traffic equilibrium flows under varying demand conditions and road segment attributes.
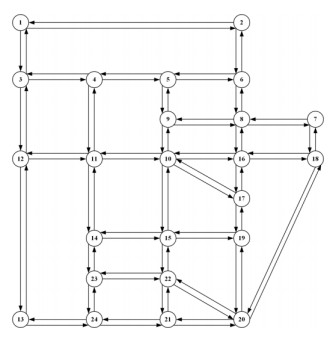
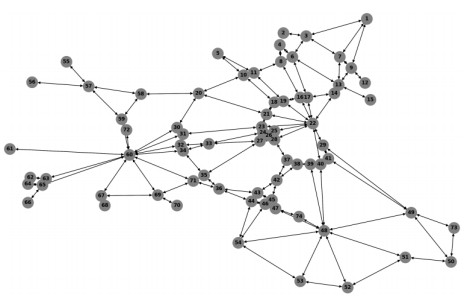
We generated datasets using two benchmark networks: the SF network in Figure 3 and the EMA network in Figure 4. A comparison of the network sizes is provided in Table 3, where the EMA network has significantly more nodes and links than the SF network, enabling evaluation under both small-scale and large-scale network scenarios.
To introduce variability in OD demand and road segment capacities, we applied randomization techniques to generate a diverse dataset for training and evaluation. The baseline OD demand matrix Q and initial road segment capacities C was collected from Transportation Networks for Research Core Team (2023). To create multiple samples, we introduced random scaling factors drawn from a uniform distribution:
where Q∗i denotes the randomized OD demand matrix for the ith sample, μi U(0.1,1) is the random scaling factor vector, and each OD pair o has an individual scaling coefficient μo, ensuring diverse demand patterns across samples.
Similarly, the initial road segment capacities are randomized using a uniform distribution:
where C∗i denotes the randomized OD demand matrix for the ith sample, ηi U(0.1,1) is the random scaling factor vector, and each link m has an individual capacity coefficient ηm, ensuring heterogeneous capacity constraints across samples.
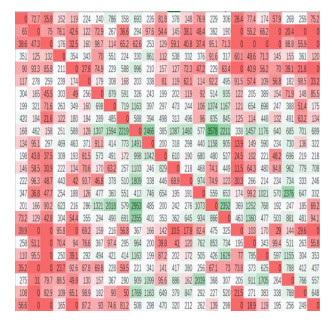
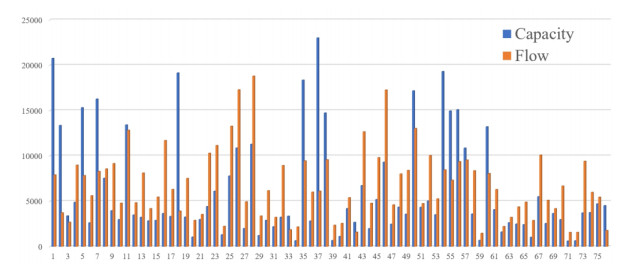
Note that the choice of a uniform distribution is not a modeling assumption but a data generation strategy. It provides a simple and unbiased way to simulate diverse traffic scenarios within realistic bounds. The proposed framework does not rely on any specific distributional form and can be adapted to empirical data or alternative distributions as they become available. Figure 5 and Figure 6 provide examples of the OD demand matrix, adjacency matrix, and capacity-flow statistics in the generated dataset. The demand matrix has a N×N shape, for example, an entry 72.7 in the first row and second column in Figure 5 represents a demand of 72.7 trips from node 1 to node 2. And the shape of the adjacency matrix is also N×N. Figure 7 provides an overview of road segment capacities and traffic flows, highlighting the diversity of network conditions introduced through randomization.
The generated dataset is divided into three subsets as shown in Table 4, each designed to test different aspects of the proposed model.
4.2. Model estimation results and analysis for fixed network topology
To explore the feasibility of our proposed model in UE-TAPs, we first use Dataset A to construct a basic GCN model consisting of a single graph convolutional layer and two fully connected layers (input-output structure: (N, N) → (N, M) → (N, 1)). Before the final fully connected layer, the data must be transposed to transform node features into road segment features. In the generated data, we use 9000 samples for training, 500 for verification, and the remaining 500 for testing. The performance indicators include mean absolute percentage error (MAPE), mean absolute error (MAE), and root mean square error (RMSE), as defined in Eqs (15)–(17).
where yi denotes the actual equilibrium traffic flow on segment i, ˆyi represents the estimated traffic flow on segment i, and n is the total number of road segments in the network.
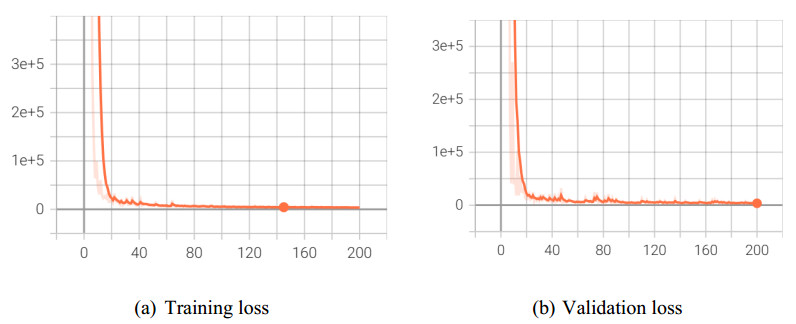
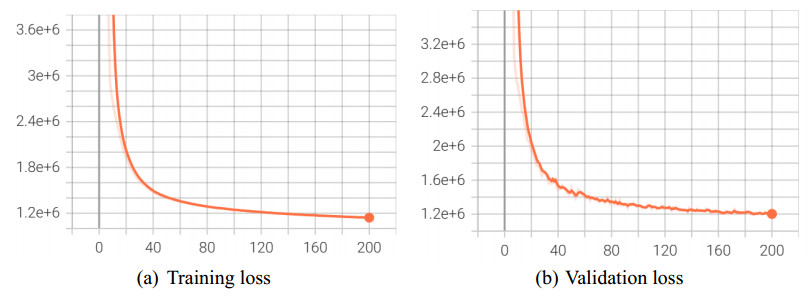
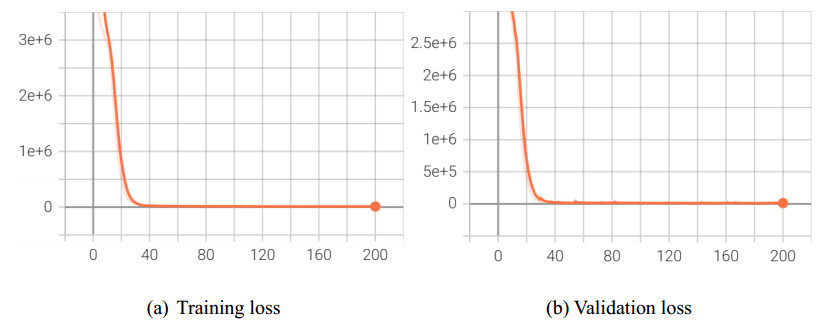
The loss curves for the training and verification sets on the SF network are shown in Figure 8. As summarized in Table 5, experiments conducted on both SF and EMA networks demonstrate that MAPE remains stable at approximately 1%, while R2 consistently reaches 0.99. The observed discrepancy between the RMSE and MAE metrics can be attributed to the larger scale and the greater number of road segments in the EMA network. Once equilibrium is achieved, the estimated flow on each segment in EMA is generally lower than that in the SF network.
Experiments conducted on this dataset demonstrate that the GCN effectively captures the distribution pattern of OD demand. However, the basic GCN struggles to integrate edge attributes, particularly when the traffic network edges contain critical information, making the simple GCN ineffective in such scenarios.
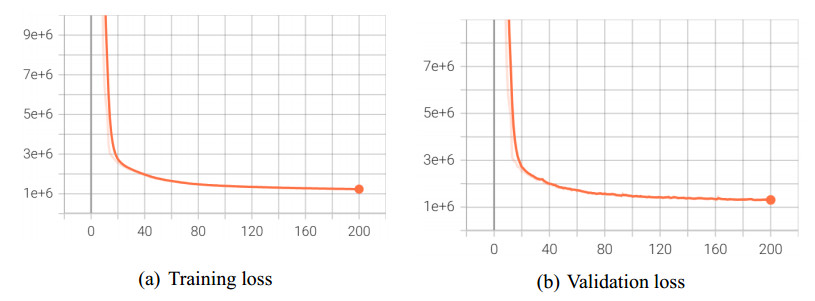
To address this limitation, we introduce a traffic assignment model that incorporates link features. This model consists of three main components: a three-layer GCN with the following architecture: (N, 64) → (64, 64) → (64, 64); two fully connected layers for processing of road segment features, structured as: (2, 16) → (16, 32); three fully connected layers for final prediction, structured as: (160,256) → (256,128) → (128, 1). To evaluate model performance, we utilized Dataset B, where 90% of the samples were used for training, 5% for validation, and 5% for testing. The results of the proposed GCN-based deep learning model across varying sample sizes are summarized in Table 6. MAPE stabilized at approximately 14%, while R2 remained around 0.90, indicating strong model fitting capabilities. Additionally, the loss function curves for training with 10,000 and 20,000 samples are presented in Figure 9 and Figure 10, respectively.
The proposed model integrates road segment features and effectively captures traffic flow variations induced by changes in link characteristics. To demonstrate the advantages of our approach, we designed two baseline models: a standard artificial neural network (ANN) and a conventional GCN. Table 7 shows the results of comparison experiments. Traditional deep learning models such as ANN are unable to capture the topological structure of the traffic network or incorporate the intrinsic attributes of road segments, making them unsuitable for solving the UE-TAP. The GCN model, while capable of modeling topological relationships, does not adequately incorporate edge-level features. Therefore, these two baselines represent a step-by-step progression toward the motivation of this study: to develop a GCN-based framework that effectively leverages both the structural and physical characteristics of traffic networks for efficient UE flow estimation. By leveraging graph-based deep learning techniques, our model effectively learns spatial dependencies and complex feature interactions, thereby delivering improved prediction accuracy in diverse traffic assignment scenarios.
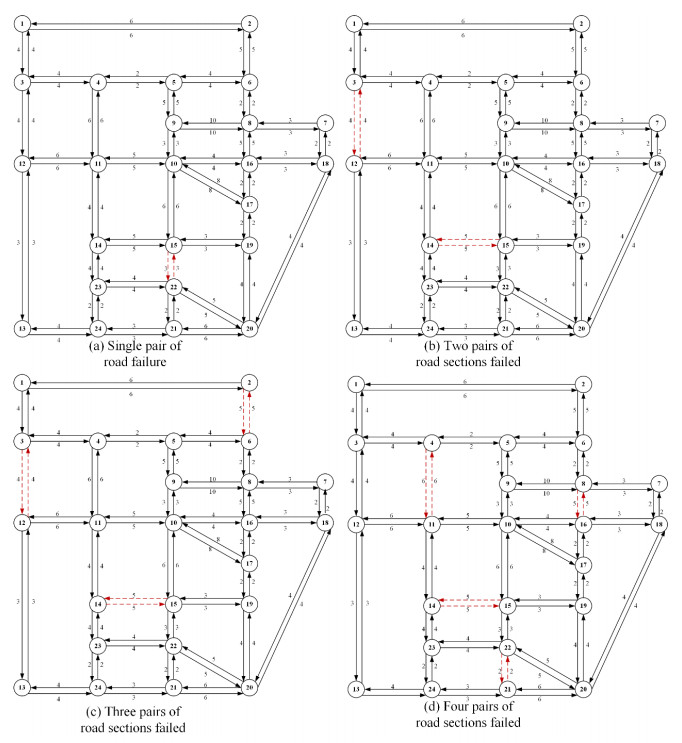
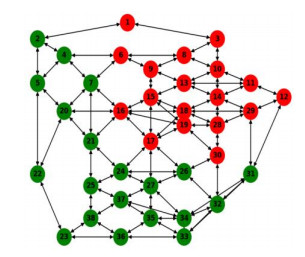
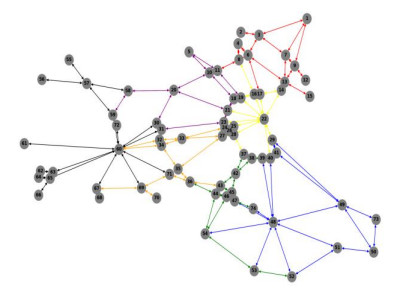
We examine the scenario of road segment failures in the traffic network and assess the model's adaptability to topological disruptions. During the data generation process, road segments were randomly removed in pairs, meaning that both roads connecting a node pair fail simultaneously. Although these failures introduce minor structural modifications, the overall network connectivity remains intact, ensuring that no isolated nodes emerge. For the experiment, we generated 100 network topologies using the random road segment failure method, with each topology producing 1000 random OD demand samples (Dataset C). The resulting randomly generated network topology is illustrated in Figure 11, where red dotted lines indicate the failed road segments.
To assess the robustness of the model under road segment failures, the features of all failed road segments are replaced with zero vectors after feature fusion. The newly generated data was directly fed into the model, which has been trained on the fixed topology. Table 8 summarizes the performance of the GCN-based model across different sample sizes. Shown in this table, the model demonstrates improved adaptability to variable topologies under the current parameter settings. Additionally, increasing the training sample size significantly enhances model performance. With only 10,000 samples, the model achieves an estimated R2 of 0.72. As the sample size increases to 100,000, R2 improves to 0.84, and all performance metrics show notable improvement. Due to the random nature of failed road segments in terms of location and frequency, a small dataset does not provide sufficient training diversity for the model to generalize effectively. To further enhance model estimation performance, a larger dataset with more samples should be generated to capture a wider range of failure scenarios.
4.3. Model estimation results and analysis for variable network topology
The graph convolution-based neural network model, as constructed above, is designed to process inputs with a fixed number of nodes. However, it encounters scalability challenges when applied to networks with varying node counts. In particular, when severe disruptions occur in the traffic network and result in disconnected subgraphs, the existing model fails to accommodate these structural changes. To overcome this limitation, we propose an algorithm for subgraph training, which modifies the input representation to enhance the model's adaptability and scalability. In our extended experiments, Dataset A is used to test the feasibility of the proposed approach.
(1) Graph partitioning
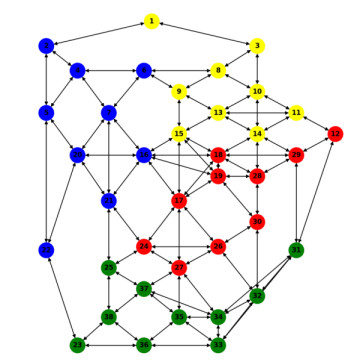
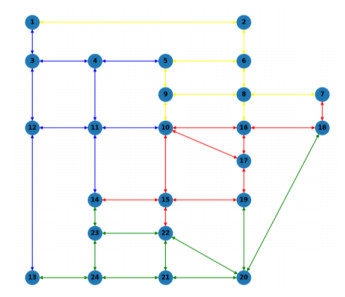
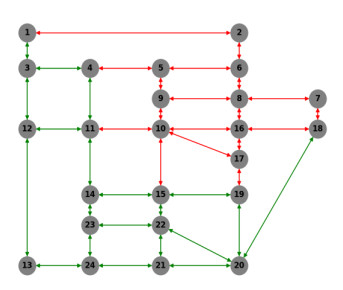
In this experiment, we apply the multilevel k-way partitioning algorithm provided by Metis [53] to divide the traffic network into multiple subgraphs. Specifically, the SF network is partitioned into 4 blocks. The original traffic network is first transformed into its dual graph representation, in which nodes represent road segments and edges indicate adjacency between segments. The partitioning is then performed on the dual graph to ensure spatially coherent subgraphs. The results of the partitioning on both the dual graph and the corresponding original traffic network are shown in Figure 12 and Figure 13. Since the resulting subgraphs may contain different numbers of nodes, we apply a zero-padding operation to standardize the input dimensions, thereby ensuring compatibility with the neural network architecture.
(2) Edge attribute model considered in this study
This study aims to train an end-to-end deep learning model capable of approximating equilibrium traffic flows under varying OD demand conditions. To facilitate this, the OD demand matrix is first transformed into edge-level features using an "all-or-nothing" traffic assignment operation. The edge attribute set includes the resulting all-or-nothing flow, road capacity, and free flow time. In addition, node-level features are incorporated to enhance spatial representation. For each edge, we compute node demand feature based on its origin and destination nodes, defined as the total outgoing demand from the origin node and the total incoming demand to the destination node. These features are appended to the edge feature set, forming a comprehensive input representation. The adjacency matrix used in the model is constructed based on edge-to-edge relationships, enabling the GCN layer to propagate information across adjacent road segments.
(3) Evaluation of subgraph-based training on the SF network
We evaluate the model's performance under subgraph-based training using the SF network, as summarized in Table 9. The input features include both intrinsic edge attributes and, in some cases, node-level demand characteristics, such as the total outbound and inbound demand at each node. First, the comparison between training on 2 subgraphs and 4 subgraphs shows that as the number of partitions increases, the model's prediction accuracy declines. This suggests that while subgraph partitioning helps standardize input dimensions, it also leads to a loss of global structural information, which negatively affects model performance. Second, incorporating node-level demand features significantly mitigates this information loss and enhances the model's accuracy under subgraph-based training. Third, to further address the limitations of partition-based modeling, future research will explore mechanisms for inter-subgraph communication, aiming to recover lost global context and improve the robustness of subgraph-trained models. The training loss curve for this experiment is shown in Figure 14.
(4) Evaluation of subgraph results on the EMA network
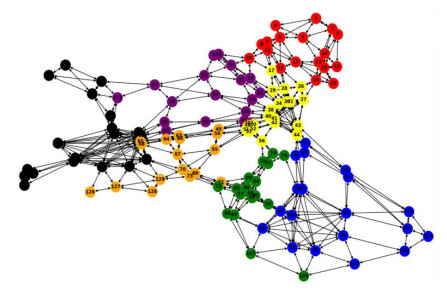
To evaluate the generalizability of the proposed model across different traffic networks, we further analyzed the EMA network and compared its structural characteristics to those of the SF network, as discussed in the previous subsection. Ensuring consistent input dimensions across networks requires partitioning each network into subgraphs of uniform size. The partitioning results for both networks are illustrated in Figures 15–18. Specifically, the SF network is divided into 2 subgraphs, containing 36 and 40 edges, respectively. In contrast, the larger EMA network is partitioned into 7 subgraphs, each containing either 36 or 38 edges, thereby maintaining input shape consistency while preserving topological structure.
We first evaluated the performance of subgraph-based training on the EMA network, using 7 subgraphs. Two experimental settings were tested: one with node-level features included, and the other without. As shown in Table 10, incorporating node demand features significantly improves model accuracy. However, due to the relatively large number of subgraphs, the overall estimation performance did not reach optimal levels.
The OD demand distributions in the SF and EMA networks differ substantially. As a result, a model trained on the SF network cannot be directly applied to the EMA network due to significant discrepancies in road segment capacities and free-flow travel times. To investigate this transferability, we conducted an experiment where a model pretrained on 1000 samples from the SF network (with node-level features included) was fine-tuned using 1000 samples from the EMA network. The results are summarized in Table 11, which compares two scenarios: one where the model is initialized with pretrained weights from the SF network, and another where training starts from random initialization. The results show that loading the pretrained model improves training efficiency and accuracy under the current settings. This suggests that models trained on networks with abundant data can be effectively leveraged to accelerate and enhance learning on networks with limited data. Naturally, the closer the demand patterns and OD distributions between the two networks, the greater the benefit of pretraining is expected to be.
In summary, this section constructs a diverse set of datasets and proposes two deep learning-based traffic assignment models built upon GCN. The proposed models demonstrate strong performance on data with fixed network topologies, but encounter limitations when applied to scenarios involving random link failures. Due to the high degree of uncertainty in Dataset C, accurate flow estimation cannot be achieved solely based on link-level features. To improve model performance in such cases, a larger volume of topologically diverse training data is required. Meanwhile, the subgraph-based deep learning model introduced in this study presents a promising and scalable solution, as it is capable of adapting to networks with varying node counts, thereby extending the applicability of GCNs to more complex and dynamic transportation systems.
5.
Conclusions
Conventional traffic assignment models often rely on complex and computationally intensive algorithms. This study proposes a novel approach to the UE-TAP based on GCN, offering an end-to-end deep learning solution that bypasses the intricacies of traditional methods. The proposed model directly maps OD demand, link attributes, and network topology to the equilibrium traffic flow, enabling fast and accurate prediction. First, we demonstrate the feasibility of using deep learning to address UE-TAPs and introduce two GCN-based model frameworks. The baseline model is designed for fixed network topologies, incorporating intrinsic link features to effectively estimate equilibrium flows under varying road segment conditions. Building upon this, we develop an enhanced framework that employs dual graph partitioning and subgraph-based training, enabling the model to adapt to networks with varying node counts and topologies. This flexible model structure also supports transfer learning, allowing a pretrained model on one network to be fine-tuned for another with limited data availability.
To validate our approach, multiple datasets were generated based on the SF network, and experiments were conducted across various scenarios, including fixed topology, randomized OD demand, and random link failures. The results confirm that the proposed model can accurately approximate equilibrium flows and exhibits robustness in the face of network disruptions. Notably, the subgraph-based model for variable topologies remains effective even when link failures lead to significant changes in network structure. However, this flexibility may come at the cost of reduced prediction accuracy due to the loss of global structural information.
While the proposed GCN-based framework demonstrates strong performance in estimating equilibrium flows under both fixed and variable network topologies, several limitations remain. First, the model has primarily been validated in synthetic environments, where the network topology and intrinsic road segment attributes (e.g., capacity, free-flow time) are readily available and well-defined. In real-world applications, however, both the abstraction of traffic network topology and the collection of intrinsic link properties present significant challenges due to data heterogeneity, incompleteness, and noise. These factors may affect model generalizability and reliability in practice. Moreover, the current subgraph-based framework does not yet support explicit communication between subgraphs, which may lead to information loss and reduced accuracy, especially as the number of subgraphs increases. Future work will focus on addressing these limitations by developing methods for inter-subgraph information exchange and improving the adaptability to real-world network complexities of this model. Additionally, while the proposed method offers substantial gains in inference speed compared to traditional traffic assignment algorithms, a comprehensive evaluation of its end-to-end computational efficiency, including training cost, inference time, and scalability to large-scale networks, remains an important direction for future work.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
This study is supported by the National Natural Science Foundation of China (52131203, 5240120175, 72471057), the Natural Science Foundation of Jiangsu Province (BK20232019), the Jiangsu Provincial Scientific Research Center of Applied Mathematics (BK20233002), Humanities and Social Sciences Research Project of the Ministry of Education (24YJCZH357), China Postdoctoral Science Foundation (2024M761430).
Conflict of interest
The authors declare there is no conflict of interest.









 DownLoad:
DownLoad: