AIMS Materials Science, 2016, 3(2): 324-338. doi: 10.3934/matersci.2016.2.324

Research article Topical Section

Export file:

Format

  • RIS(for EndNote,Reference Manager,ProCite)
  • BibTex
  • Text

Content

  • Citation Only
  • Citation and Abstract

The effect of nanocrystalline Ni-W coating on the tensile properties of copper

C. N. Panagopoulos, E. P. Georgiou, D.A. Lagaris, V. Antonakaki

1 Laboratory of Physical Metallurgy, National Technical University of Athens, Zografos, 15780, Athens, Greece
2 KU Leuven, Dept. Materials Engineering (MTM), Kasteelpark Arenberg 44, B-3001, Leuven, Belgium
3 Falex Tribology NV, Wingepark 23B, 3110, Rotselaar, Belgium

Received: , Accepted: , Published:

Topical Section: Metal ceramic (Cermets)

Abstract    Full Text(HTML)    Figure/Table    Related pages

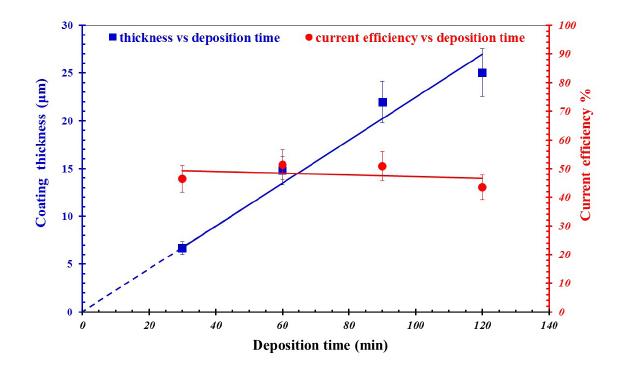
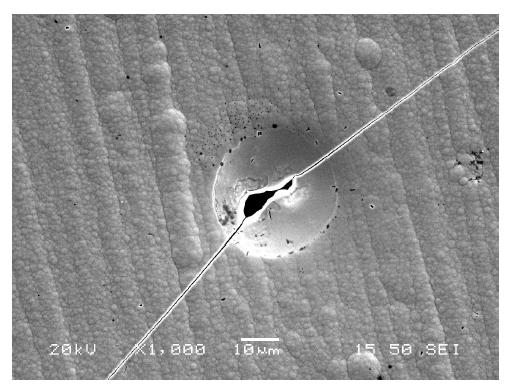
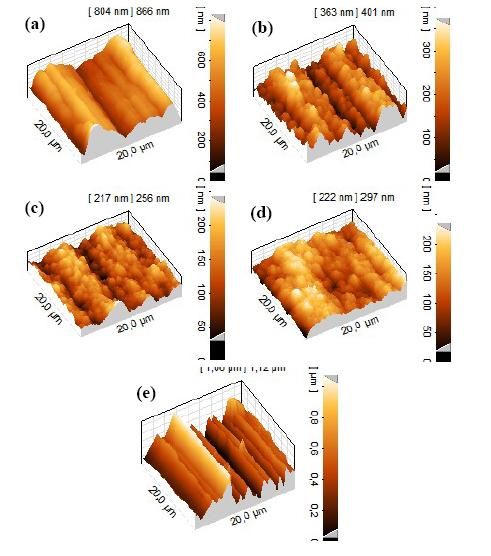
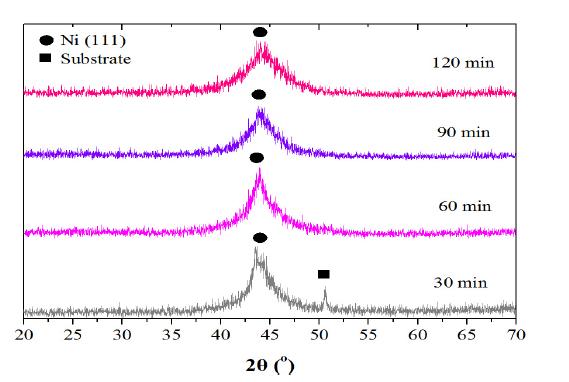
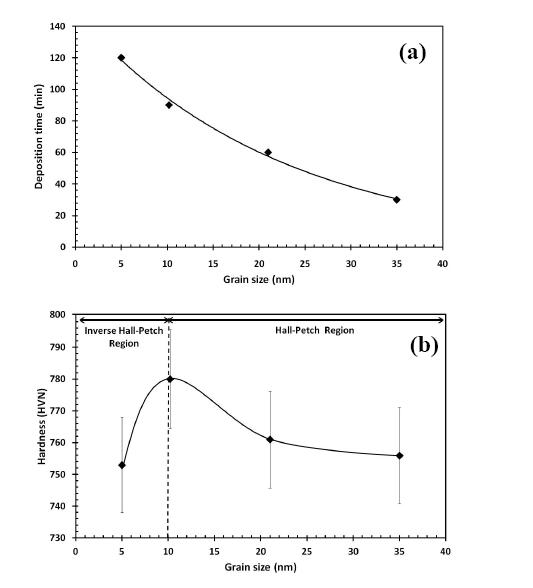
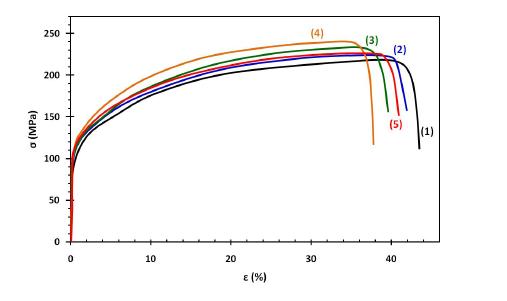
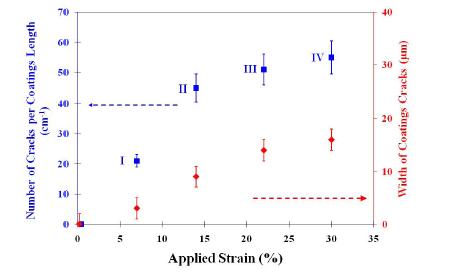
Nanostructured Ni-W alloy coatings containing approximately 40 wt.% tungsten were electrodeposited onto copper substrates. The effect of the coatings thickness on the surface topography, microstructure and grain size was investigated with the aid of Atomic Force Microscopy (AFM), Scanning Electron Microscopy (SEM) and X-ray Diffraction (XRD) techniques respectively. In addition, this research work aims in understanding the influence and correlation between microstructure and thickness of these Ni-W coatings with the bulk mechanical properties of coated specimens. The experimental results indicated that the micro-hardness and Ultimate Tensile Strength (UTS) of the Ni-W coated copper were higher than that of bare copper, whereas both slightly increased with increasing coating thickness up to 21 μm. On the other hand, the ductility of Ni-W coated copper decreased significantly with increasing coating thickness. Thus it could be said that when applying Ni-W coatings there are certain limitations not only in terms of their composition, but their thickness, grain size and coating structure should be also taken into consideration, in order to obtain an understanding of their mechanical behavior.
  Figure/Table
  Supplementary
  Article Metrics
Download full text in PDF

Export Citation

Article outline

Copyright © AIMS Press All Rights Reserved