Effect of Hydrological Properties on the Energy Shares of Reflected&nbsp;Waves at the Surface of a Partially Saturated Porous Solid

Mahabir Barak; Manjeet Kumari; Manjeet Kumar

doi:10.3934/geosci.2017.1.67

AIMS Geosciences, 2017, 3(1): 67-90. doi: 10.3934/geosci.2017.1.67. Research article

Export file:

Format

RIS(for EndNote,Reference Manager,ProCite)
BibTex
Text

Content

Citation Only
Citation and Abstract

Effect of Hydrological Properties on the Energy Shares of Reflected Waves at the Surface of a Partially Saturated Porous Solid

Mahabir Barak, Manjeet Kumari, Manjeet Kumar

1 Dept. of Mathematics, Indira Gandhi University Meerpur, India-122503
2 Dept. of Mathematics, C.M.R.J Govt. College, Ellenabad, India-125102

Received: , Accepted: , Published:

Abstract Full Text(HTML) Figure/Table Related pages

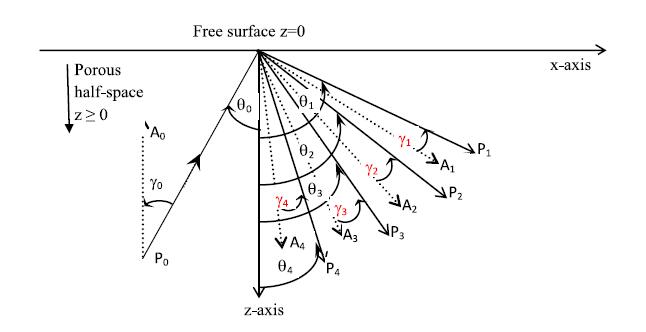
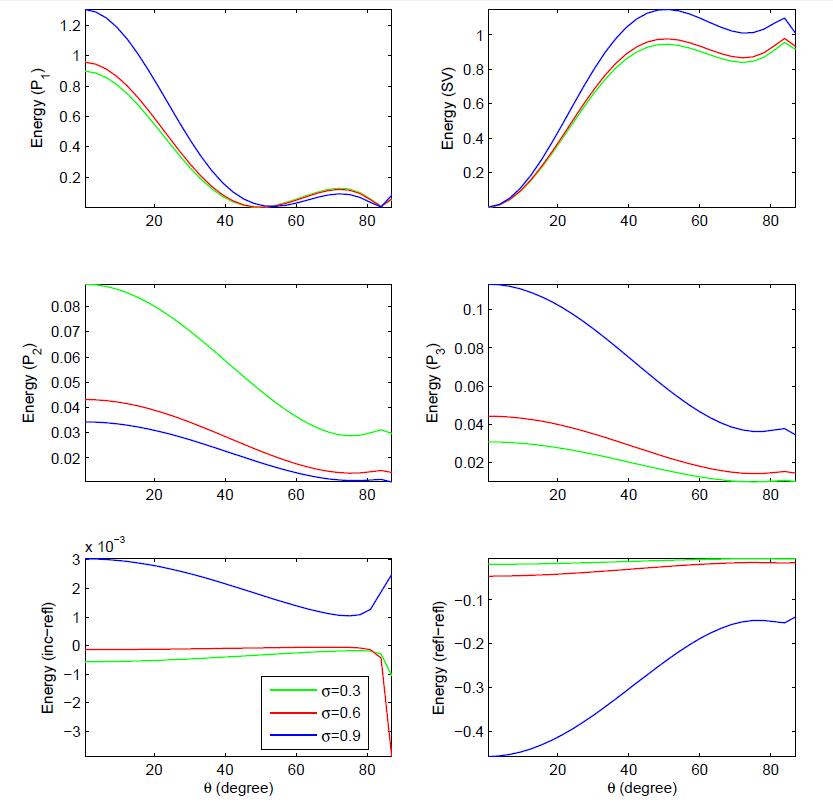
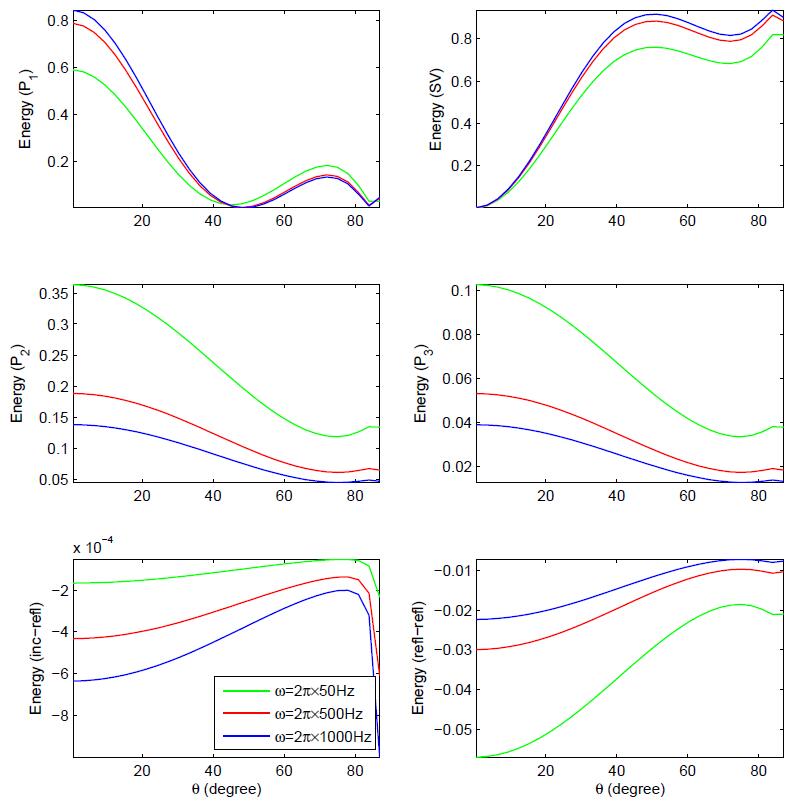
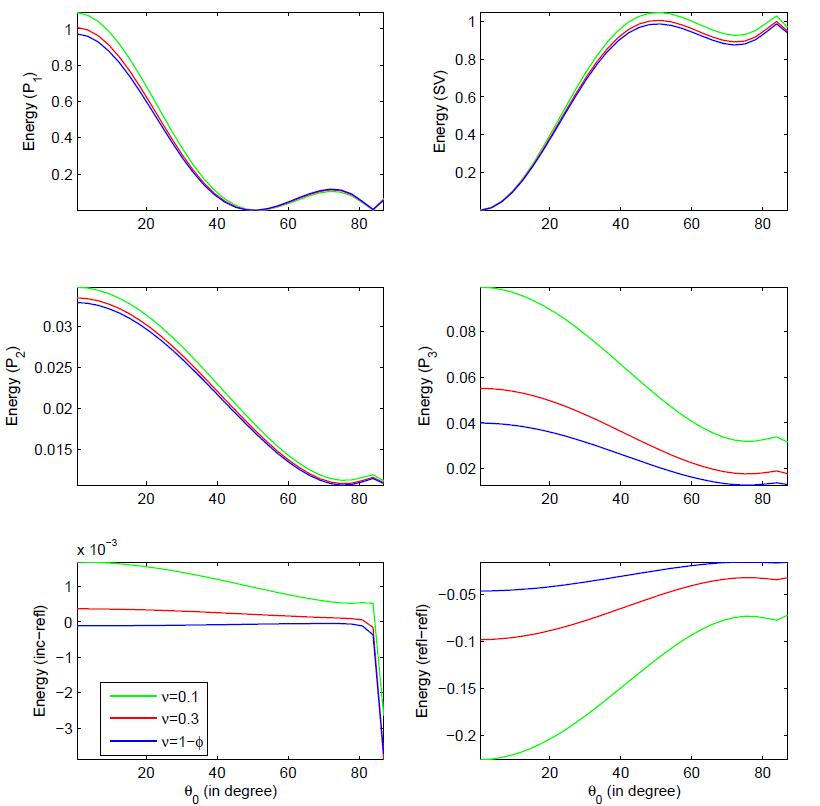
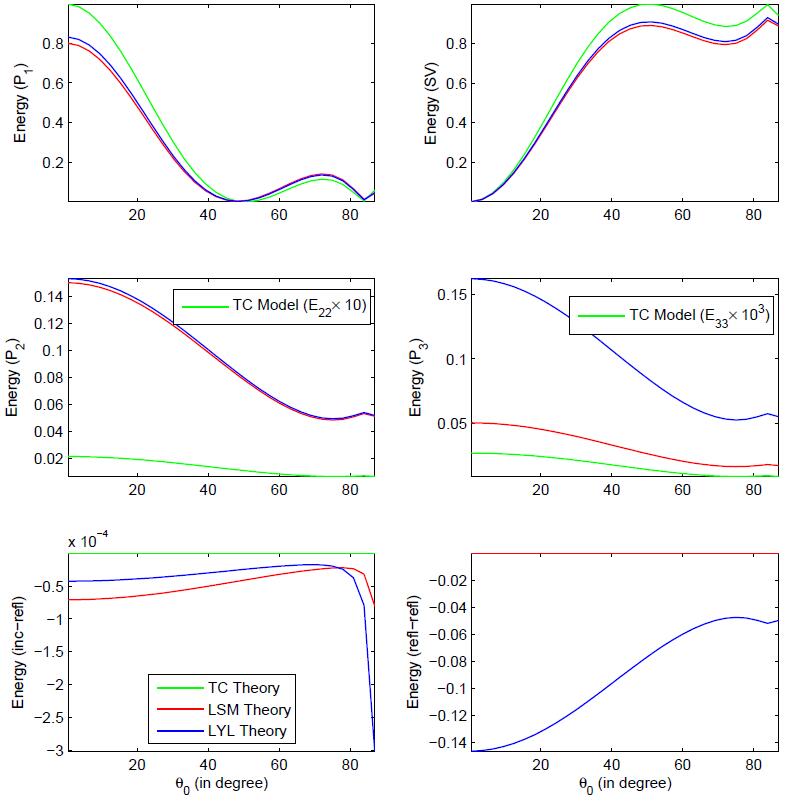
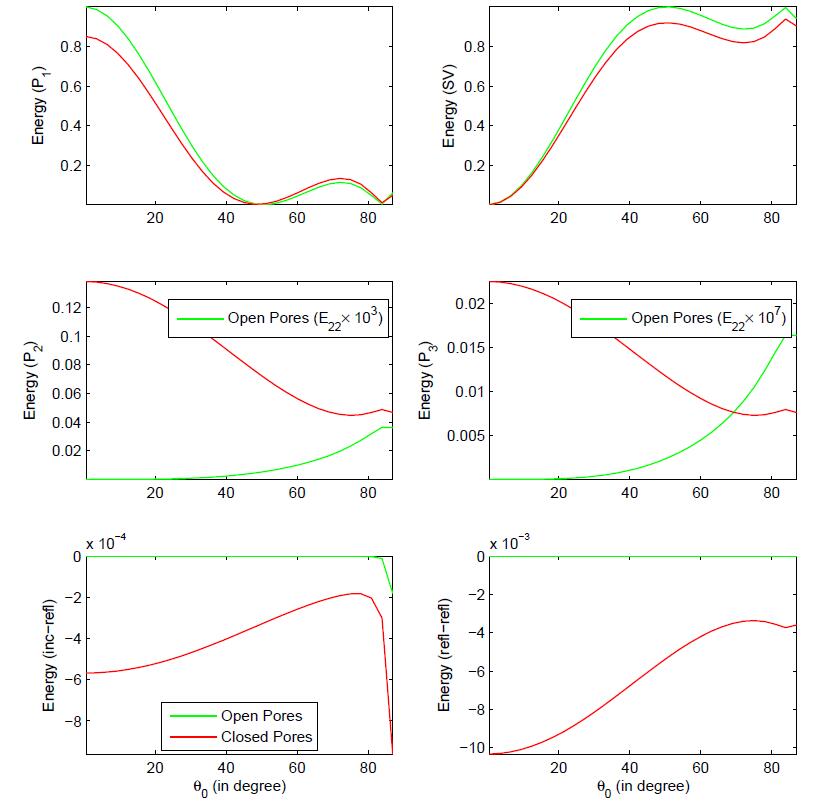
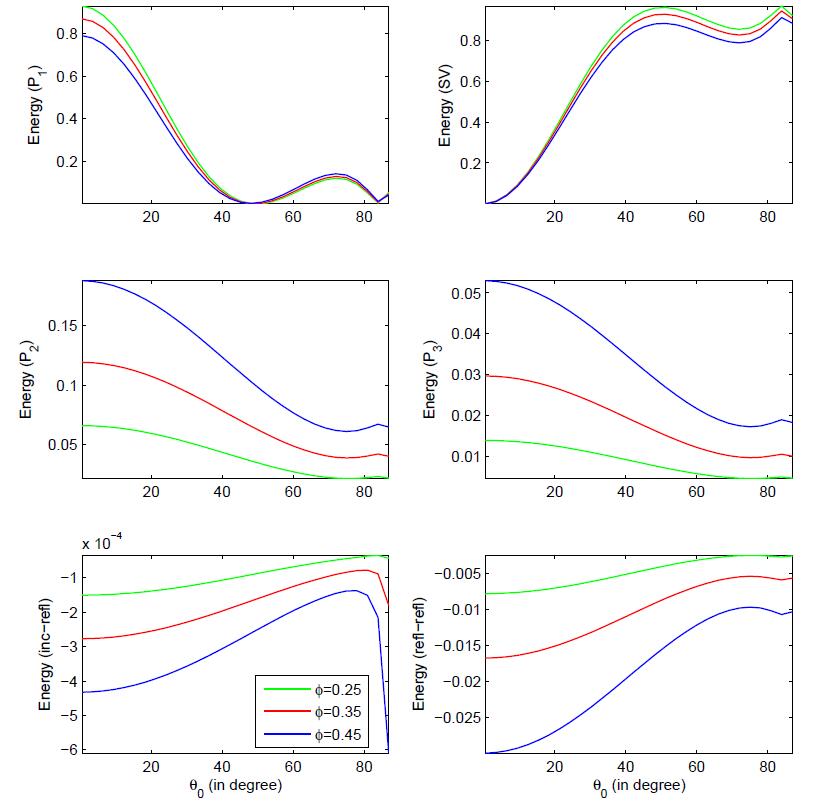
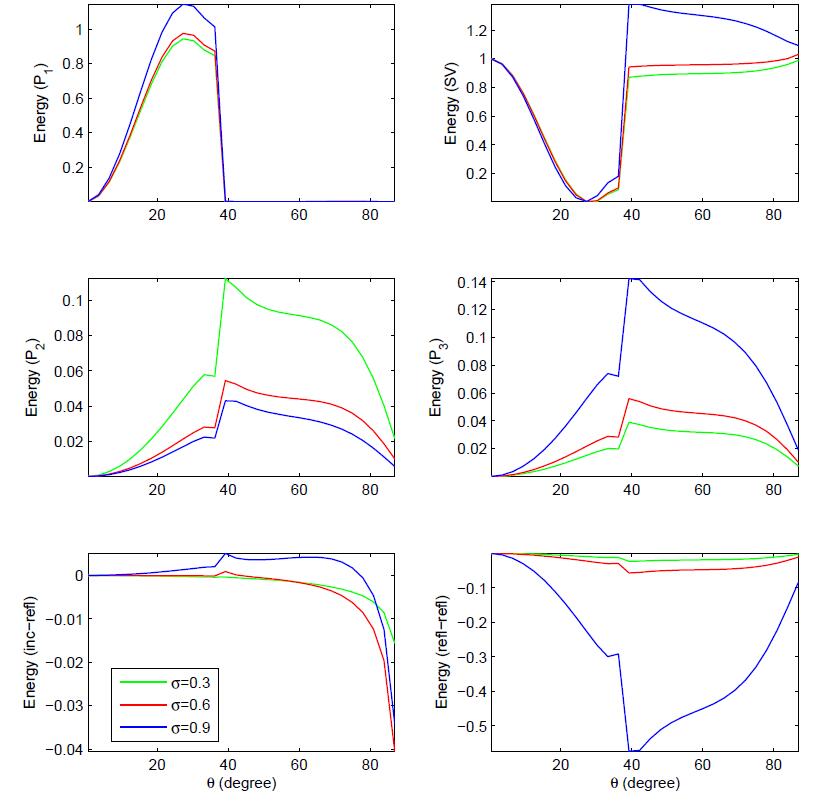
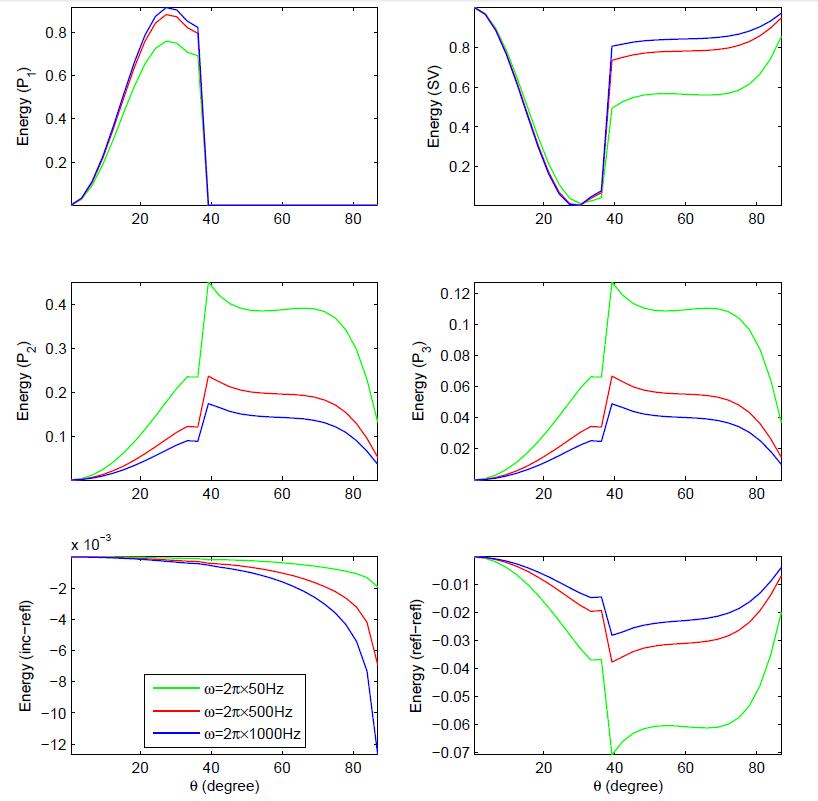
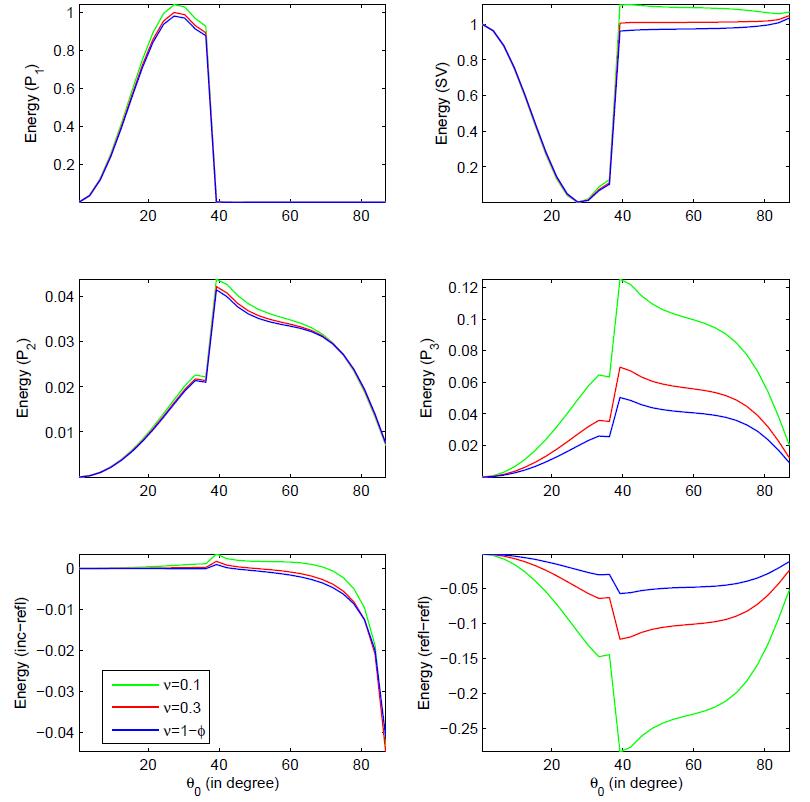
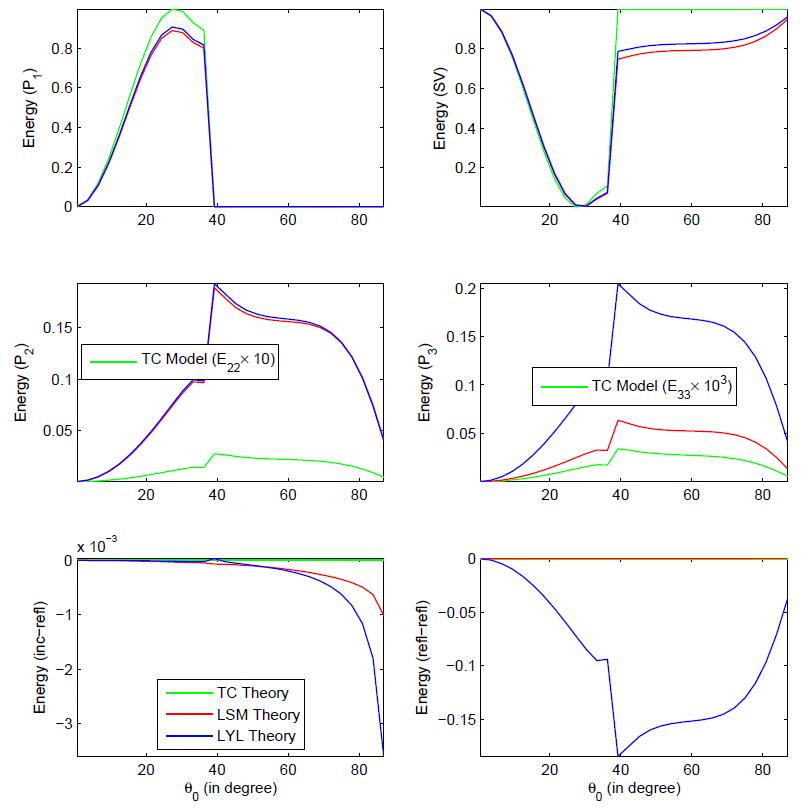
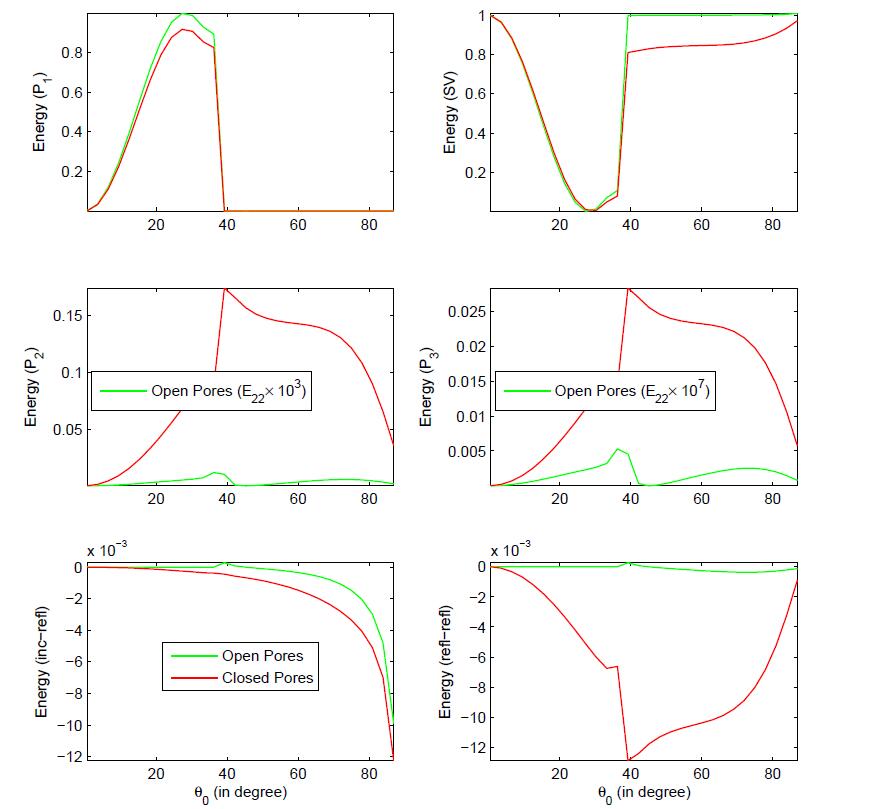
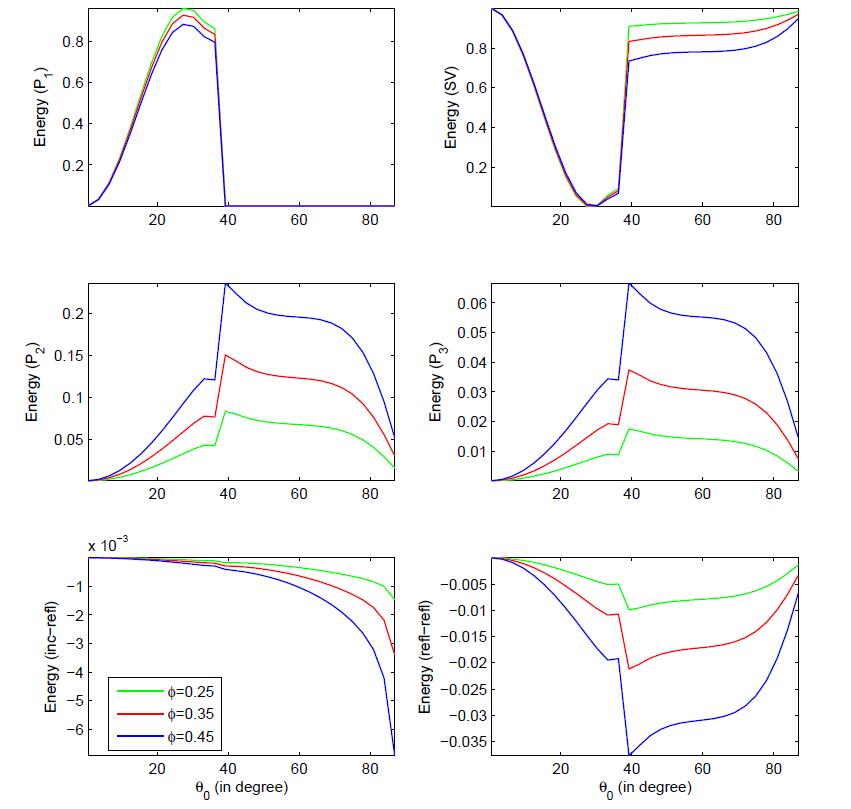
In the present study, the reflection of inhomogeneous waves is investigated at the stress-free plane surface based on multiphase poroelasticity theory. The porous medium is considered as dissipative due to the presence of viscosity in pores fluid. Four inhomogeneous (i.e. different direction of propagation and attenuation) reflected waves (three longitudinal and one shear) exists due to an incident wave. By using the appropriate boundary conditions, closed-form analytical expressions for the reflection coeffcients are derived at the stress-free surface. These reflection coeffcients are used to drive the analytical expressions for the energy shares of various reflected inhomogeneous waves. In mathematical framework, the conservation of incident energy is confirmed by considering an interaction energy between two dissimilar waves. It validates that the numerical calculations are analytically correct. Finally, a numerical example is considered to study the effects of viscous cross-coupling, porosity, saturation of gas, pore-characteristics and wave frequency on the energy shares of various reflected inhomogeneous waves and depicted graphically.

Figure/Table

Supplementary

Article Metrics

Keywords: viscous cross-coupling; partially saturated porous solid; immiscible pore-fluids; inhomogeneous wave; reflection coefficients

Citation: Mahabir Barak, Manjeet Kumari, Manjeet Kumar. Effect of Hydrological Properties on the Energy Shares of Reflected Waves at the Surface of a Partially Saturated Porous Solid. AIMS Geosciences, 2017, 3(1): 67-90. doi: 10.3934/geosci.2017.1.67

References:

1. Biot MA (1956) Theory of propagation of elastic waves in a fluid saturated porous solid, I. Lowfrequency range. J Acoust Soc Am 28: 168-178.
2. BiotMA(1956) Theory of propagation of elastic waves in a fluid saturated porous solid, II. Higher frequency range. J Acoust Soc Am 28: 179-191.
3. Biot MA (1962) Mechanics of deformation and acoustic propagation in porous media. J Appl Phys 33: 1482-1498.
4. Biot MA (1962) Generalized theory of acoustic propagation in porous dissipative media. J Acoust Soc Am 34: 1254-1264.
5. Brutsaert W (1964) The propagation of elastic waves in unconsolidated unsaturated granular mediums. J Geophy Res 69: 243-257.
6. Brutsaert W and Luthin JN (1964) The velocity of sound in sgass near the surface as a function of the moister content. J Geophy Res 69: 643-652.
7. Bedford A and Drumheller DS (1983) Theories of immiscible and structured mixtures. Int J Eng Sci 21: 863-960.
8. Garg SK and Nayfeh AH (1986) Compressional wave propagation in liquid and/or gas saturated elastic porous media. J Appl Phys 60: 3045-3055.
9. Berryman JG, Thigpen L, Chin RCY (1988) Bulk elastic wave propagation in partially saturated porous solids. J Acoust Soc Am 84: 360-373.
10. Santos JE, Corbero JM, et al. (1990) Static and dynamic behavior of a porous solid saturated by a two phase fluid. J Acoust Soc Am 87: 1428-1438.
11. Santos JE, Douglas J, Corbero JM, Lovera OM (1990) A theory for wave propagation in a porous medium saturated by a two phase fluid. J Acoust Soc Am 87: 1439-1448.
12. Corapcioglu MY and Tuncay K (1996) Propagation of waves in porous media, Advances in Porous Media, Vol. 3, M.Y. Corapcioglu ed., Elsevier, Amsterdam.
13. Tuncay K and Corapcioglu MY (1997) Wave propagation in poroelastic media saturated by two fluids. J Appl Mech 64: 313-319.
14. Wei C and Muraleetharan KK (2002) A continuum theory of porous media saturated by multiple immiscible fluids: I. Linear poroelasticity. Int J Eng Sci 40: 1807-1833.
15. Wei C and Muraleetharan KK (2002) A continuum theory of porous media saturated by multiple immiscible fluids: II. Lagrangian description and variational structure. Int J of Eng Sci 40: 1835-1854.
16. Hanyga A (2004) Two fluid porous flow in a single temperature approximation. Int J Eng Sci 42: 1521-1545.
17. Lu JF and Hanyga A (2005) Linear dynamic theory for porous media saturated by two immiscible fluids. Int J Solids and Struct 42: 2689-2709.
18. Lo WC (2008) Propagation and attenuation of Rayleigh waves in a semi-infinite unsaturated poroelastic medium. Adv Water Resour 31: 1399-1410.
19. Lo WC, Sposito G, Majer E (2005) Wave propagation through elastic porous media containing two immiscible fluids. Water Resour Res 41: 1-20.
20. Lo WC, Sposito G, Majer E (2009) Analytical decoupling of poroelasticity equations for acousticwave propagation and attenuation in a porous medium containing two immiscible fluids. J Eng Math 64: 219-235.
21. Lo WC, Sposito G, Majer E, et al. (2010) Motional modes of dilatational waves in elastic porous media containing two immiscible fluids. Adv Water Resour 33: 304-311.
22. Sharma MD and Kumar M (2011) Reflection of attenuated waves at the surface of a porous solid saturated with two immiscible viscous fluids. Geophys J Int 184: 371-384.
23. KumarMand KumariM(2014) Reflection of attenuated waves at the surface of a fractured porous solid saturated with two immiscible viscous fluids. Latin Am J Solids Struct 11: 1206-1237.
24. Sharma MD (2013) Effect of local fluid flow on reflection of plane elastic waves at the boundary of a double-porosity medium. Adv Water Resour 61: 62-73.
25. Sharma MD (2015) Constitutive relations for wave propagation in a double porosity solids. Mech Mater 91: 263-276.
26. Tomer SK and Goyal S (2013) Elastic waves in swelling porous media. Transp Porous Media 100: 39-68.
27. Carcione JM (2007) Wave Field in Real Media. Wave Propagation in Anisotropic, Anelastic, Porous and Electromagnetic Media. Pergamon, Amsterdam.
28. Lo WC, Yeh CL, Lee JW (2015) Effect of viscous cross coupling between two immiscible fluids on elastic wave propagation and attenuation in unsaturated porous media. Adv Water Resour 83: 207-222.
29. Borcherdt RD (2009) Viscoelastic waves in layered media. Cambridge University Press, New York.
30. Achenbach JD (1973)Wave Propagation in Elastic Solids, 1st Edition, North-Holland Publishing, Amsterdam.
31. Krebes ES (1983) The viscoelastic reflection/ transmission problem: two special cases. Bull Seismol Soc Am 73: 1673-1683.
32. Ainslie MA and Burns PW (1995) Energy-conserving reflection and transmission coeffcients for a solid-solid boundary. J Acoust Soc Am 98: 2836-2840.
33. Ayub M and Bentsen RG (2005) Experimental testing of interfacial coupling in two-phase flow in porous media. Pet Sci Technol 23: 863-897.

show all references

This article has been cited by:

1. Weihua Li, Jie Zheng, Mihailo D. Trifunac, Saturation effects on ground motion of unsaturated soil layer-bedrock system excited by plane P and SV waves, Soil Dynamics and Earthquake Engineering, 2018, 110, 159, 10.1016/j.soildyn.2018.04.005

Reader Comments

your name: * your email: *

Copyright Info: 2017, Manjeet Kumari, et al., licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution Licese (http://creativecommons.org/licenses/by/4.0)

Download full text in PDF

Associated material

Metrics