1. Introduction
Rainfall variability has led to the occurrence of extreme weather and climate events like droughts, floods, microbursts, thunderstorms and tornadoes in Zimbabwe [1]. Under scarce rainfall conditions, droughts and prolonged dry spells have resulted in reduced crop yields leading to the increase in frequency of drought occurrences to almost an annual event [2,3,4]. The drought of 1982 to 1984 caused massive crop failure as crop and livestock production declining to about 10% of historical levels [5,6]. This was also stressed by Zhakata [7] who pointed out that the dry period of 1981 to 1985 caused severe social and economic stress. According to him, the 1982 to 1983 season was one of the worst on record since the 1901 to 1902 season for Zimbabwe. Furthermore, the 1991 to 1992 dry season received only about 50% of normal rainfall over South Eastern Africa, surpassing the 1982 to 1983 drought in severity [8]. The recent dry spell of 2014 to 2016 caused acute food shortages in Zimbabwe and Southern Africa. Dam levels at Lake Kariba became extremely low at 12% leading to a massive decrease in power generation for both Zimbabwe and Zambia (Climate.gov, Financial Gazette, of February 2, 2017). The effect of droughts has continued to torment resource constrained nations. There is need to enhance understanding of weather systems which lead to prolonged dry spells and droughts.
Besides the frequent low rainfall years, Zimbabwe has also suffered from adverse impact of floods. For example, the year 2000 was characterized by floods due to tropical cyclone Eline which left a trail of destruction in areas like Chipinge, Masvingo and Beitbridge [9,10,11]. These floods led to loss of life (70 people), affected 266,000 people and caused an estimated US$72,900,000 in economic damages [12]. The flood prone region of Tokwe-Mukosi was to suffer from flooding when incessant rains caused dam levels of the Tokwe-Mukosi dam which was under construction to rise from 15.8 m on 26 January to 61.5 m on 14 February 2014. This led to most houses in the dam basin to be inundated, the dam wall partially collapsed and the resultant induced flooding affecting about 40,000 people downstream. Another tropical cyclone in the year 2017 caused massive damages to roads, bridges and dam failures in areas like Lupane and Tsholotsho [13]. Flooding leads to soil leaching reducing crop yields, affects the smooth transportation of goods and disrupts power grid lines hence greatly reducing the economic output of affected areas [14,15]. Low economic activity caused by climatic extremes results in job losses, hunger and poverty leading to increased criminal activity [16]. The strong link between Zimbabwe's GDP, droughts and floods occurrence places great importance on the understanding of the mechanisms behind such occurrences [13,17].
Among the systems responsible for moisture advection and therefore convergence in Zimbabwe, the Inter Tropical Convergence Zone (ITCZ) is the dominant system during the summer season [18]. The effects of the ITCZ are strongest in January hence most of the flooding also occurs around late January to February when the soil is also very saturated with moisture [19]. The ITCZ responds to pressure fluctuations to the north and south of the country, modulating rainfall patterns [20]. Westerly waves, easterly waves and mid-tropospheric high pressure systems enhance or suppress ITCZ induced rainfall during summer [21]. For example, a blocking high pressure system to the south of Madagascar inhibits the movement of the westerly waves prolonging wet or dry periods over Zimbabwe [22]. However, not all rainfall events can be attributed to the behaviour of the ITCZ. Other circulation patterns also lead to drought or flood occurrence and these have largely been understudied.
Previous studies carried out on the circulation mechanisms behind extreme rainfall events over Zimbabwe focused on external forcing mechanisms [21,23,24,25]. Most of these studies covered influence of large parts of the ocean resulting in large homogenous regions which fail to adequately explain the temporal and spatial distribution of extreme rainfall events [26,27]. Mamombe et al., for instance, concentrated on the broad scale effects of El Nino Southern Oscillation (ENSO) on drought and flooding in Zimbabwe [21]. They observed that positive ENSO years correspond to extreme dry summer while negative ENSO years correspond to extreme wet summers. Nangombe et al. looked at both external and internal forcing circulation patterns and embedded weather systems in the Indian and Pacific Oceans during the pre-summer season which are precursors to drought occurrence [28]. They got strong correlation between SSTs, Wind, temperature and geopotential height anomalies with extreme drought events over Zimbabwe. However, Manatsa et al. [29] noted that ENSO-based approaches do not adequately explain the occurrence of extreme rainfall events especially during weak ENSO signal years. ENSO-rainfall relationships have undergone significant variations in various parts of the world in the last century. Simmonds & Hope argued that the ENSO effects on Australian summer rainfall has significantly diminished in the last thirty or so years [30]. Some authors argue that the Indian Ocean Dipole Zonal Mode explains rainfall characteristics better than ENSO signal [24]. Recently Manatsa et al. [31] discovered that sea level pressure anomalies in the Pacific basin are better indicators for rainfall patterns over Southern Africa than IODZ and ENSO. The deficiency of these past approaches was in focusing on large areas which overshadow influence of small and very localized SSTs variations on rainfall events [22,26]. These limitations result in limited understanding and understudying of local SSTs variations which might exhibit very strong relationship with dry or wet summers in Zimbabwe and Southern Africa. Previous approaches stressed on the influence of large scale atmospheric and oceanic circulation over regions such as Pacific ignoring effect of circulation patterns of regions in the vicinity of the study area. The contribution of circulation patterns in the eastern Atlantic and Western Indian oceans which are close to the study area may be more significant that of regions further away. We hypothesize that an analysis, incorporating circulation of nearby regions, can provide better understanding of the forcing mechanism behind dry or wet summer occurrences.
The objectives of this paper are to (i) enhance understanding of the forcing mechanisms behind dry or wet summer occurrences over Zimbabwe due to ocean and land based circulations patterns over regions close to the country. (ii) Ascertain the level of correlation between SSTs of western Indian Ocean, Eastern Atlantic Ocean and Zimbabwe summer rainfall.
2. Data sources and methodology
2.1. Description of the study area
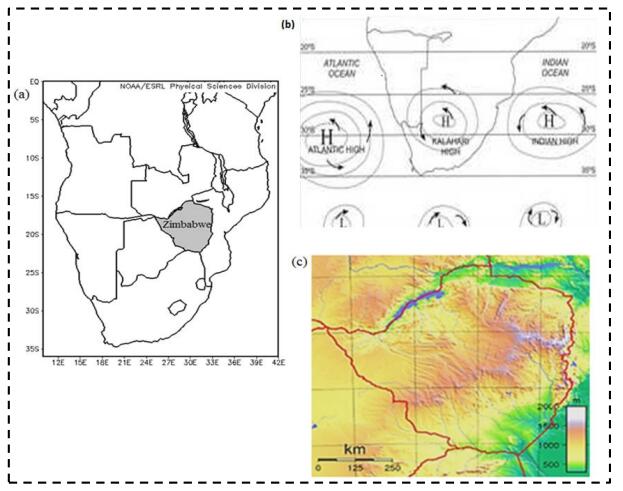
Zimbabwe is a landlocked country which is located in southern Africa (Figure 1a). The terrain ranges from the high altitudes (around 2500 m above sea level) in the eastern and central parts of the country to the very low altitudes (about 400 m above sea level) in the extreme northern, western and southern areas. High altitude areas receive the lots of rainfall in summer (above 1200 mm seasonal total) which makes them susceptible to cases of flush flooding. The low altitude areas are prone to flooding especially in areas like Muzarabani and Tsholotsho during extreme wet periods [15,32,33,34]. These low altitude areas also receive very low amounts of rainfall resulting in semi-arid conditions [35]. Such areas suffer from extreme drought events during dry summers.
Zimbabwe's summer rainfall seasonal runs from mid-November through to late March [21]. Heaviest precipitation occurs around January hence the effects of floods or the outcome of a drought usually depends on the rainfall patterns around this period. Long term mean seasonal rainfall shows a north–south, and west–east gradient. This is in response to the country's topography and airflow that approach Zimbabwe from the northwest, north and northeast promoting warm and moist air inflow from the humid equatorial source region [32,36]. The Inter Tropical Convergence Zone (ITCZ) is the dominant feature responsible for moisture advection into Zimbabwe during the summer season [18]. The effects of the Inter Tropical Convergence Zone (ITCZ) are strongest in January [19]. Most of the rainfall occurs around this period and so most of the flooding also occurs late January to February when the soil is already saturated. The behaviour of the ITCZ, which responds to pressure fluctuations to the north and south of the country, modulates rainfall patterns [20]. The start and end of the summer season are variable both spatially and temporally. Sometimes the season starts in October and ends late April [32]. In other seasons, it commences in November and ends early March [21]. Westerly waves enhance or suppress rainfall during summer [21]. Sometimes a blocking high pressure system to the south of Madagascar inhibits the movement of the westerly waves prolonging wet or dry periods over Zimbabwe [22]. The occurrence of floods or droughts can be attributed to the weakening or strengthening of pressure systems to the northeast, northwest, south east and south west of the country. South Atlantic Ocean High (SAOH), South Indian Ocean High (SIOH) [37], Angola Low Pressure (ALP) system [38,39], the ITCZ [20], the quasi low pressure system in the Mozambican channel, number and strength of tropical cyclones passing in the Mozambican channel all regulate the occurrence of extreme rainfall summer events. All these features modulate the summer mid tropospheric westerly or easterly wave behavior, times and areas of surface convergence or divergence, moist or dry air advection into different parts of the country. This affects cumulative rainfall and intensities in different segments of the season as well as different locations of the country.
Figure 1a shows the geographical location of Zimbabwe in Southern Africa while Figure 1b shows the relative positions of the dominant pressure systems responsible for modulating summer rainfall over Zimbabwe. Figure 1c is the topographic map of Zimbabwe.
2.2. Data collection and processing
2.2.1. Rainfall data
Rainfall data used in the study was obtained from gridded merged station and model data from Global Precipitation Climatology Centre (GPCC). The precipitation data were at a spatial resolution of 0.5º × 0.5º and at monthly time-steps covering period from 1975 to 2013. This data is provided free of charge by the NOAA to OAR to ESRL PSD, Boulder, Colorado, USA, from their website (http:totowww.esrl.noaa.govtopsd) [40]. The high resolution merged station and model dataset is suitable for the study area where topography plays a crucial role in modulating precipitation events. The rainfall station density for Zimbabwe is not sufficient to depict rainfall variability on its own.
2.2.2. The geopotential height, meridional and zonal wind datasets
The geopotential height, meridional and zonal winds (for determining moisture transport) data used in the study was obtained from ERA-interim reanalysis datasets, gridded at 0.75º × 0.75º resolution for the period 1980 to 2015. This data is provided free of charge by the European Centre for Medium-Range Weather Forecasts (ECMWF), from their website (http:totoapps.ecmwf.inttodatasetstodatatointerim-full-dailytolevtype=sfcto) [41]. The National Center for Environmental Prediction to National Center for Atmospheric research (NCEP to NCAR) reanalysis datasets were chosen because they are suitable for a study area such as Zimbabwe with very few upper air stations and a very low density network of surface meteorological stations [42].
2.2.3 Sea Surface Temperature data (SST)
The SST data at 0.5º × 0.5º resolution used in the study was obtained from the Extended Reconstructed Sea Surface Temperature (ERSST) version 3b. This data is provided free of charge by the National Ocean and Atmospheric Administration to National Climatic Data Center (NOAA to NCDC) their website (https:totowww.ncdc.noaa.gov) [43]. The ERSST data is also suitable for ocean analysis where meteorological stations are sparse especially for the southern hemisphere where very few data from ships can be obtained.
2.3. Methodology
2.3.1. Monthly spatial rainfall analysis using the standardized precipitation index
Monthly rainfall data from GPCC were formulated into their standardized departures using the historical means and standard deviations for each. Hence, the seasonal cycle was removed based on averages calculated for the period 1980 to 2013. The standardized data has a mean of zero and a variance of one. In this way diverse grid points are combined into indices and compared. A number of grid points' individual time series from the various natural regions of the study area were cross correlated and those showing strong positive values at statistically significant levels of 95% retained [22]. The time series of Zimbabwe's monthly and seasonal precipitation was evaluated. The dry and wet years are filtered out by choosing years with a standardized anomaly greater than 1 representing wet years and those with a standardized anomaly less than −1 during dry years [22]. The grid point's precipitation indices are averaged to come up with one precipitation index for Zimbabwe (December–February). This area index is used to identify dry and wet years according to the following criteria:
For all dry years, Zi ≤ −1 and for all wet years, Zi ≥ +1. Normal years are categorized as those years with −1 < Zi < +1.
From this characterization, 7 wet years (1980/81, 1995/96, 1996/97, 1998/99, 1999/00, 2005/06 and 2007/08) and 7 dry years (1982/83, 1983/84, 1986/87, 1991/92, 1994/95, 2001/02 and 2002/03) are identified. The circulation mechanisms for these selected wet and dry years were then investigated.
2.3.2. Characterization of wet or dry summers using composite analysis techniques
Monthly climatic data from the different datasets for previously identified wet or dry summers from the Standardized Precipitation Index method at the grid points were composited together. The composites involved summing together the selected climatic fields and dividing by the total number of cases to get the average precipitation value at each grid point [22,26]. Composites are useful for indicating pronounced and common features and patterns in variables. They also reduce the number of maps and figures associated with each case study. Results of these composites are then used to generate hypotheses for patterns which may be associated with the individual scenarios [26,44]. This method has been used by many researchers in the fields of meteorology and climatology [45,46,47,48]. For example Jury and Levey [48], used this method in their study to highlight meteorological features of flood events over the eastern mountains of South Africa. Recently this method was used to investigate circulation and temperature anomalies associated with sever and extreme droughts occurrence over Zimbabwe [28]. The indices of each climatic field (Wind, Geopotential Height and SSTs) are correlated with Zimbabwe Standardized Precipitation Index and only those results at 95% level of confidence are presented. In this study composite maps are used to retrieve the forcing circulation patterns for rainfall, SSTs, wind and geopotential heights of dry and wet years. However, extreme caution must be exercised since such composites might not be sufficient on their own for the occurrence of wet or dry summers over Zimbabwe [49]. These composites plus other mechanisms might be necessary for the occurrence of such events. Nevertheless this method is still powerful in the field of meteorology in explaining relationships between different parameters with similar characteristics.
2.3.3. Effects of Eastern Atlantic and Western Indian Ocean SSTs on Zimbabwe summer rainfall using correlation analysis
Correlation analysis reveals simple relationship between pairs of variables [23]. The tool is used to retrieve the level of cause and effect relationship between SSTs and Zimbabwe summer rainfall. Such relationships are so useful in developing regression models useful in the development of Numerical Weather Prediction (NWP) [22]. Anomalous warm SSTs over the western Pacific and western Indian Oceans have been found to favor the occurrence of dry conditions over South eastern Africa whilst SSTs in the Atlantic Ocean has no effect on rainfall over the same region [50]. In this study, the analysis was used to come up with correlation maps aimed at establishing whether there are some significant relationships between Zimbabwe summer rainfall and SSTs of West Indian Ocean and East Atlantic Ocean.
3. Results and discussions
3.1. Composite summer season rainfall mean and anomaly maps for wet and dry years
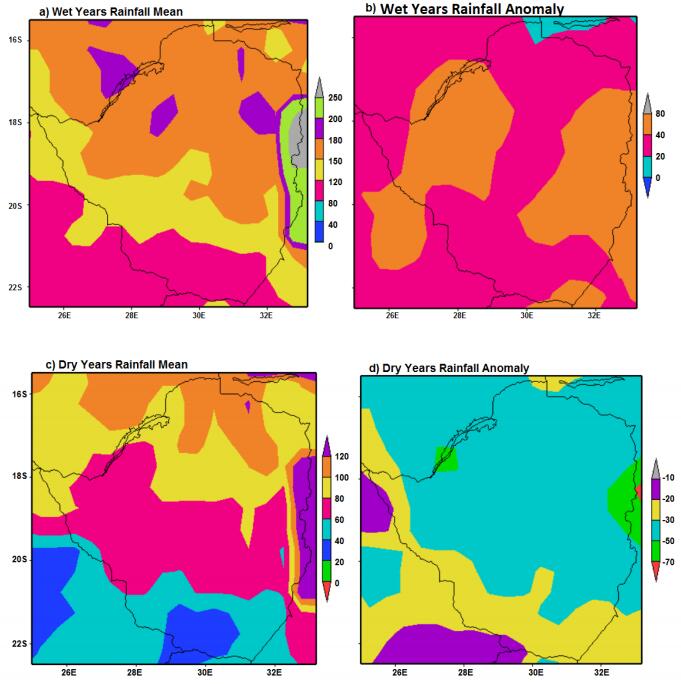
From the composite summer season rainfall mean and anomaly maps for wet and dry years of rainfall over Zimbabwe between 1980 to 2013 (Figure 2), the precipitation gradient decrease in a north east (above 250 mm for wet seasons and 120 mm for dry seasons) to south west (below 160 mm for wet seasons and 60 mm for dry seasons) direction. These results show the importance of the Inter Tropical Convergence Zone (ITCZ) as the major rainfall bearing feature for Zimbabwe summer rainfall in agreement with the results of Beilfuss [20]. Highest precipitation occurs along the central watershed showing the critical influence of topography on the spatial distribution of Zimbabwe summer rainfall. This is agreement with Meteorological Services Department of Zimbabwe [32] who showed that topography plays a dominant role in the spatial distribution of Zimbabwe's rainfall. However, the wettest regions in wet seasons become driest during dry seasons. During dry years, the weakening of the ITCZ is more than the weakening of westerly cloud bands. Therefore, since westerly cloud bands weaken north-eastwards that results in more precipitation in the south and south western than other areas during dry years. Contrastingly, during wet years the ITCZ strengthens and far exceeds the influence of westerly cloud bands resulting in more rainfall to the north than south of the central watershed.
3.2. Summer season wind anomalies for composite wet and dry years
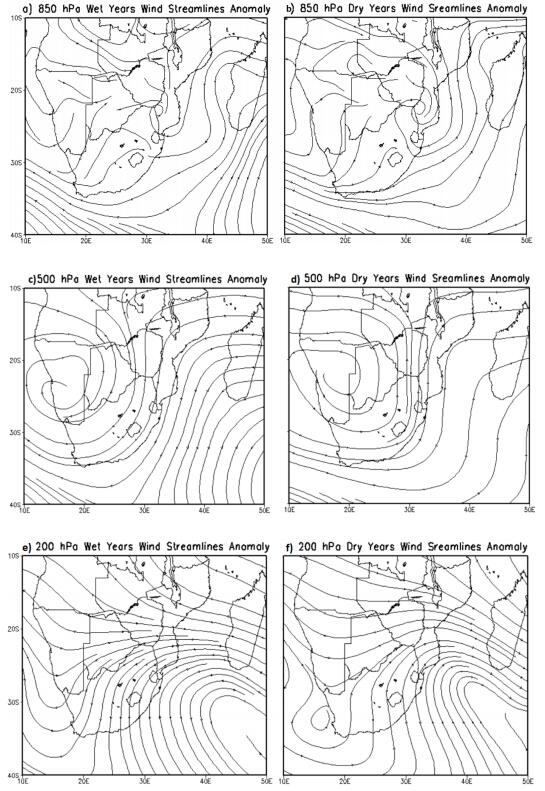
Figure 3 shows the composite wind anomaly pattern for both wet and dries years over Zimbabwe derived from 1980 to 2013 events. The composite anomaly maps are for the lower troposphere (850 hPa), middle troposphere (500 hPa) and upper troposphere (200 hPa).
3.2.1. Wet summers wind anomaly patterns
Wet summers are characterized by weak wind anomalies in all levels of the troposphere (Figure 3a, c, e). Northerly airflow is dominant in the lower levels right up to the middle levels of the troposphere (Figure 3a, c). Easterly flow then dominates in the upper troposphere (Figure 3e). The pattern also depicts marked convergence in the lower levels right through to the 500 hPa level. The convergence can be explained by the cyclonic circulation to the west and anticyclonic airflow to the south east of the country at the 500 hPa level. Such patterns favor moisture advection and convergence hence vertical uplift of moist air which results in cloud development hence lots of precipitation [51]. Although the results are slightly different from those found by Nicholson [22] and Preston-Whyte & Tyson [52] over Southern Africa, they, however, can be justified by that such airflow promotes strong advection of warm and moist air from the Congo basin in the lower and middle troposphere resulting in enhanced convective activity.
3.2.2. Dry summer wind anomaly patterns
Dry summers are characterized by stronger wind anomalies in the middle levels of the troposphere (Figure 3d). Southerly airflow is dominant in the lower troposphere right up to the 200 hPa level (Figure 3d, f). These results are different from observation by Mwafulirwa [22] in Malawi that westerly airflow dominates at all levels in dry summers. Contrasting findings were also obtained by [52,53] who found that easterly airflow dominate in the lower troposhere for dry years and westerly airflow at upper levels. The difference in results can be attributed to differences in geographical locations of the different study areas although they are all located in Southern Africa. This highlights the dangers of generalizing results of large inhomogeneous areas as rainfall varies tremendously over small spatial scales. The same pressure systems which drive easterly winds into south eastern Africa will veer into a southerly airflow into Zimbabwe which will turns into a westerly wind as they enter into Zambia and Malawi. Therefore, directions of wind patterns cannot be generalized over large areas like southern Africa. There is also marked divergence in the lower levels of the troposphere in the northern half of the country (Figure 3b, d). Convergence does exist from the middle troposphere right up to the upper levels especially in the southern half of the country (Figure 3d, f). This is in agreement with earlier argument that the southern and south western parts are wetter than the rest of the country during dry years. It is also important to note the anticyclonic circulation to the west and cyclonic airflow to the east of the country at the 500 hPa level (Figure 3e). Such airflow promotes advection of cold, moist air from the Indian Ocean in the eastern half of the country and hot, dry air from the arid areas to the south west of the country in the South western areas. These two circulation patterns enhance cold, moist air from the ocean converging with dry hot air from arid areas at this level. Such patterns favor a stable atmosphere and hence results in very little precipitation.
3.3. Geopotential height summer season mean for composite wet and dry years
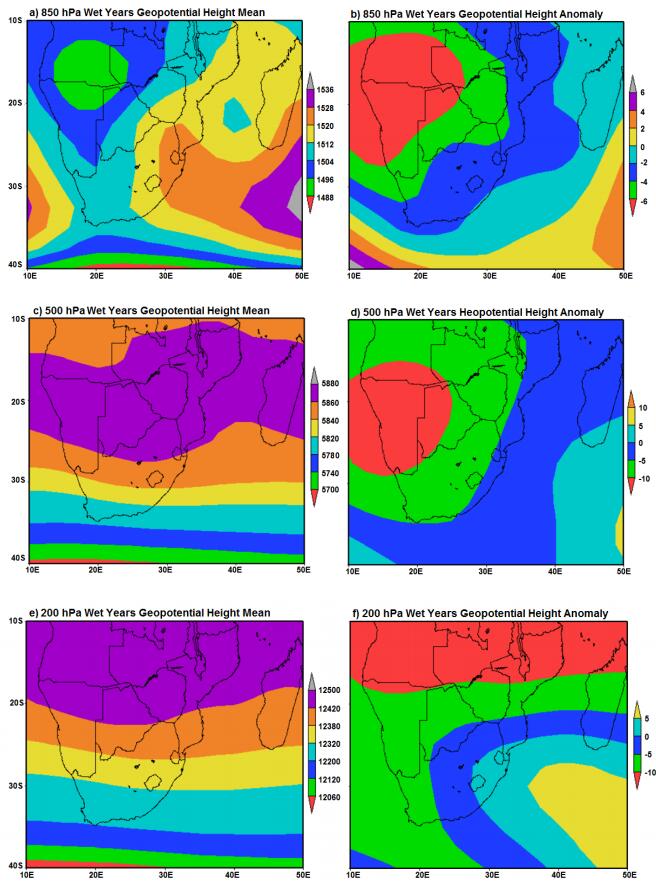
Figure 4 shows the composite geopotential mean and anomaly patterns for both wet years over Zimbabwe during 1980 to 2013. The composite maps are for the 850,500 and 200 hPa levels respectively.
3.3.1. Geopotential height mean pattern during wet summers
Wet summers are characterized by low geopotential heights in the between the 850 and 500 hPa levels (Figure 4a, c). A deep low pressure cell sits over Botswana and Namibia at the 850 hPa level (Figure 4a). At the 500 hPa level, a trough extends all the way from the Atlantic to the Indian Ocean (Figure 4c). Cyclonic circulation is thus enhanced right from the lower through to the middle troposphere. These results agree with those of many previous studies for Southern Africa (e.g. [52,22]). Such conditions promote vertical uplift hence cloud development and significant amounts of precipitation during wet years.
3.3.2. Geopotential height anomaly pattern for wet summers
Figure 4b, d illustrate that wet summers are characterized by negative geopotential height anomalies (lowest anomaly being below −6 and −10 hPa respectively) at the 850 and 500 hPa levels to the west of the country centered over Botswana. A trough exists to the south of the country with positive anomalies forming ridges both to the south west and south east of the country at both 850 and 500 hPa levels. Similar findings were also obtained for the southern Africa region by Preston-Whyte & Tyson [52]. Positive anomalies exist at the 200 hPa level promoting moisture advection and convergence in the lower and middle troposphere and divergence in the upper troposphere hence favoring cloud development and precipitation.
3.4. Geopotential height summer season mean and anomaly for composite dry years
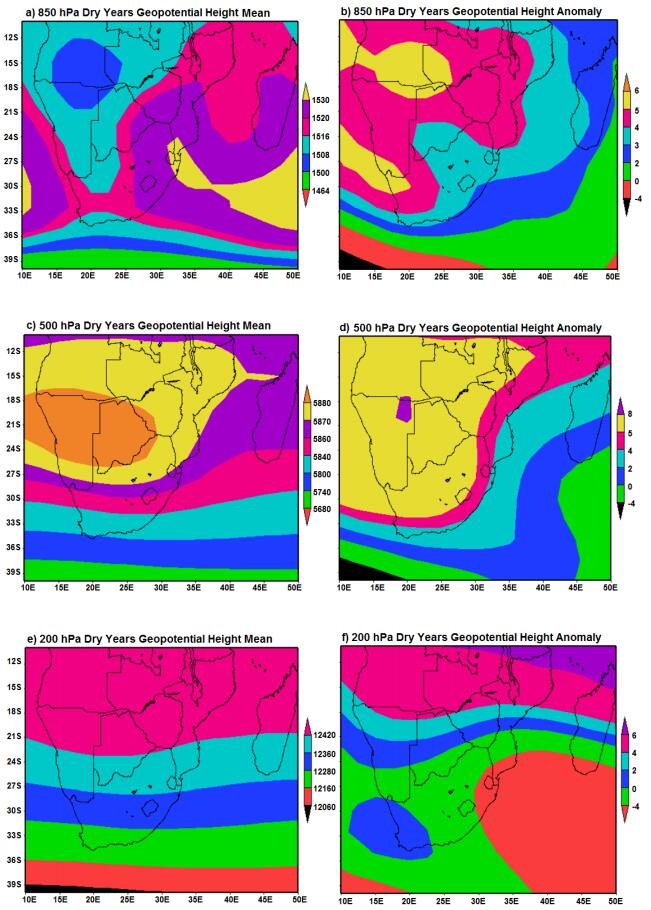
Figure 5 shows the composite geopotential anomaly pattern for both wet and dry years over Zimbabwe during 1980 to 2013. The composite anomaly maps are for the 850,500 and 200 hPa levels respectively.
3.4.1. Geopotential height mean pattern for dry summers
Dry summers are characterized by high geopotential heights from the 850 hPa level extending to the middle troposphere (Figure 5a, c). A high pressure cell (popular Botswana upper high) sits over Botswana and Namibia at the 500 hPa level (Figure 4c). A ridge extends all the way from the Atlantic Ocean to the Indian Ocean at this level enhancing anticyclonic circulation and influx of dry air in the middle troposphere. Such conditions promote subsidence and cloud suppression at this level leading to very little precipitation.
3.4.2. Geopotential height anomaly pattern for dry summers
As shown in Figure 5b, d, f, dry summers are characterized by positive geopotential height anomalies which form a belt running in a south east to north west direction, extending all the way from south of Madagascar to the Eastern Atlantic Ocean on the Angola-Namibia border at all levels of the troposphere. Negative anomalies are found on either side of this belt indicating the presence of a strong anticyclone in the lower and middle troposphere. This creates a strong inversion hence cloud formation is suppressed. This concurs with Preston-Whyte & Tyson [52] who also gave similar explanation for dry summer over the entire Southern Africa region.
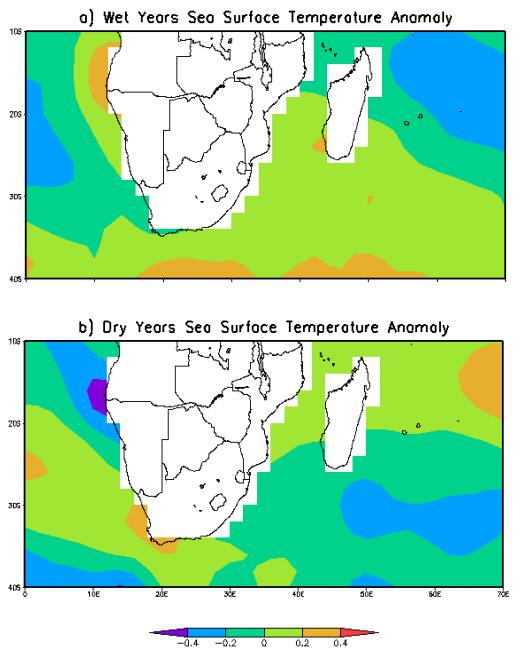
3.5. SSTs summer season composite anomaly maps for wet and dry years
The SSTs pattern for wet summer seasons shows distinct patterns for wet and dry seasons. On both oceans, the anomaly pattern shows interesting results for wet and dry summer seasons over Zimbabwe.
3.5.1. SSTs anomaly patterns during wet summer
Wet summers are characterized by negative SST anomalies in the West Central Indian Ocean forming a belt starting at the Mozambican-Tanzania border extending in a south east direction (Figure 6a). These results are different from earlier observation for Southern Africa by Nicholson & Entekhabi [54]. Nicholson & Entekhabi [54] observed that positive SST anomaly for same sea region occur during wet years. The negative anomalies also found in the eastern Atlantic Ocean off the Namibian border for wet years concur with findings of Mwafulirwa et al. [22]. Just adjacent to this belt in the western Indian Ocean is a belt of positive SSTs anomalies whose center is just to the south east of Madagascar. Another center is found in the Eastern Atlantic Ocean just on the Namibian coast. Large parts of the ocean extending from south of Madagascar to south west of South Africa are all under positive anomalies. Although in contrast with Nicholson & Entekhabi [54] such a pattern sets up a strong land-sea temperature gradient to the north east and north west of the country. On the other hand, to the South west and south east, weak land-sea temperature gradients are set up. Therefore strong north westerly and north easterly airflow are prevalent promoting warm moist air advection during wet summers. Weak south westerly and south easterly airflow are also favored meaning the convergence zone occurs further southwards over Zimbabwe. In general, warm moist air advection from the equator is promoted. Warmer oceans to the south of the sub-continent mean more evaporation. Stable conditions are therefore suppressed and unstable conditions promoted.
3.5.2. SST anomaly patterns for dry summers
Dry summers are characterized by alternating belts of negative and positive SSTs anomalies both in the West Indian and East Atlantic Oceans (Figure 6b). The SSTs anomaly pattern for dry years differ from that for wet summers in that the SST belts for wet summers shift westwards. The positive SSTs center will now be located just off the western coast of the sub-continent while that for negative anomalies will be on the Angola-Namibia coast and the other just off the south western coast of the subcontinent. Vast parts of both oceans are under positive anomalies north of the subcontinent while portions of the ocean to the south east of Madagascar are under negative anomalies. Such a pattern sets up weak land-sea temperature gradient to the north east and northwest of the country and a weak land-sea temperature gradient to the south east. Therefore weak north westerly and north easterly airflow as well as strong southerly and south easterly airflow are favored. This implies that the convergence zone occur further northward establishing stable conditions over Zimbabwe. In general, cold moist air advection from the ocean will be promoted.
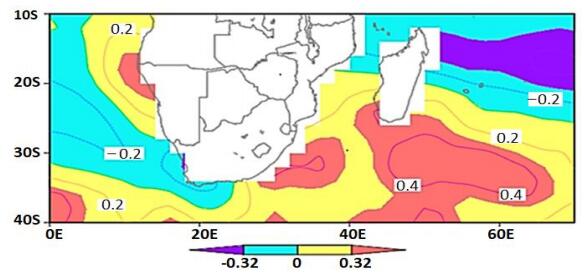
3.6. Correlation of Zimbabwe summer rainfall with SSTs of the Western Indian Ocean and Eastern Atlantic Ocean
Figure 7 shows that positive correlation (maximum is +0.4) exists between Zimbabwe summer rainfall and SSTs of ocean waters where the South Atlantic Ocean-, South Indian Ocean- as well as the bud-off high pressure systems are usually located. Positive correlation (above +3.2) also exists on the Namibian-Angola coast. Negative correlation exists just to the west of the sub-region touching the southern coast of Cape Town and to the eastern side of the sub-region with the strongest negative correlation of about −0.4 forming a belt around 15° south of the equator. Such results agree with those from the composite maps of SST behavior for both wet and dry summer seasons (Figure 6). Such results agree with those of other authors for the western Indian Ocean region but differ for the Eastern Atlantic Ocean region where they found no significant relationships between Atlantic Ocean SSTs anomalies and South East Africa rainfall [50]. Warmer SSTs to the south of the sub-region favor weak meridional flow into Zimbabwe while cooler SSTs to the East of the sub-region favor strong zonal flow during summer. This results in enhanced moisture convergence over the study area hence the resultant wet seasons. Cooler SSTs to the south of the sub-region favor strong meridional flow while warmer SSTs to the East of the sub-region leads to weak zonal flow into Zimbabwe during summer. The result is enhanced stable air inflow from the south into the country which results in dry summer seasons.
4. Conclusion
The study analyzed the circulation forcing mechanisms responsible for wet and dry summer seasons in Zimbabwe using GPCC and ERA1-interim re-analysis datasets from NCEP to NCAR joint project. Composite analysis and correlation techniques were applied on monthly SSTs, geopotential height and wind data covering the period 1980 to 2013. Based on the external forcing (SST) results, it was concluded that warmer waters at the Atlantic and West Indian Ocean boundary sets up a weak south to north temperature gradient hence weak southerly flow strongly associated with dry summers in Zimbabwe. Cooler ocean waters around 15º S of the equator results in a strong east to west temperature gradient hence strong easterly flow and enhanced warm moist air advection into the country during wet seasons. Conversely, cooler ocean surface waters to the south East Madagascar together with warm ocean water around 15º S results in strong southerly flow and weak easterly flow which enhances stable condition resulting in dry summer seasons over Zimbabwe. It was also concluded that considerable correlation exists between the SSTs of these ocean waters and annual rainfall amounts received in Zimbabwe. Therefore since SSTs take longer to evolve with time, SSTs of these regions can be used to predict the incoming summer season at lead times of about 3 months. Future studies may develop new SSTs indices based on these ocean regions and incorporate them in local seasonal forecast models to improve accuracy of such forecasts. This study focused on Zimbabwe, forming a basis upon which similar studies can be done in regions with similar rainfall patterns to Zimbabwe to verify these findings.
Acknowledgments
Sincere gratitude is extended to my supervisors; Prof Zhu Wei Zhun, Dr. A. Makarau and colleagues; Dr. V. Musara and C. Mutasa for their tireless guidance, support and immense contribution towards the successful production of this paper. Their suggestions and corrections were greatly valuable for the successful completion of this paper. Lastly I would like to give thanks to my family and friends who are always urging me on. I gratefully also acknowledge the GPCC and NOAA/NCDC for providing datasets for my research.
Conflict of interest
The authors declare there is no conflict of interest.









 DownLoad:
DownLoad: