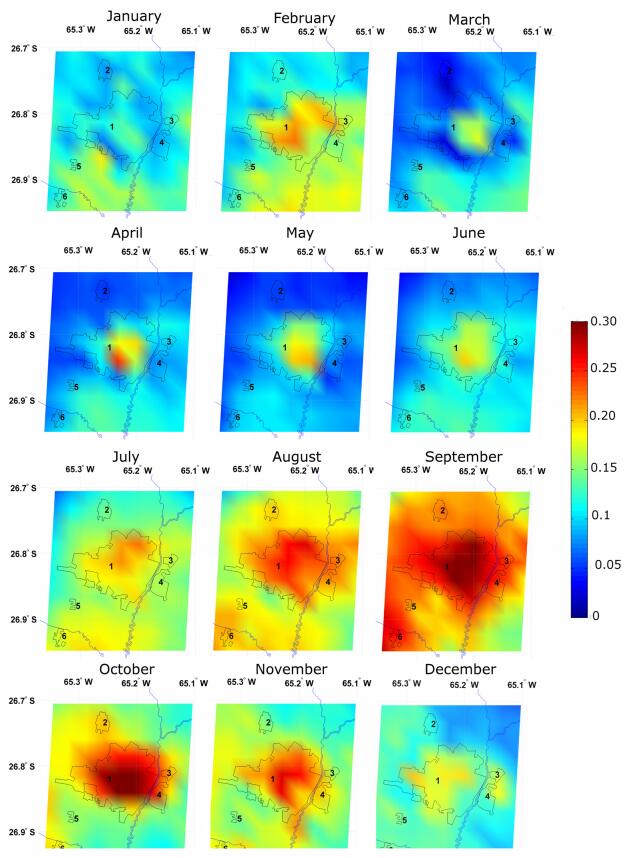
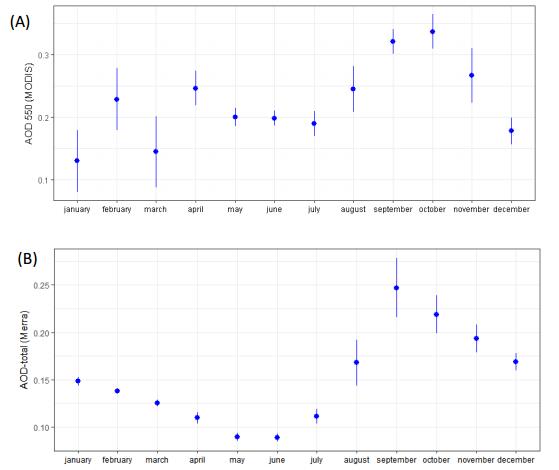
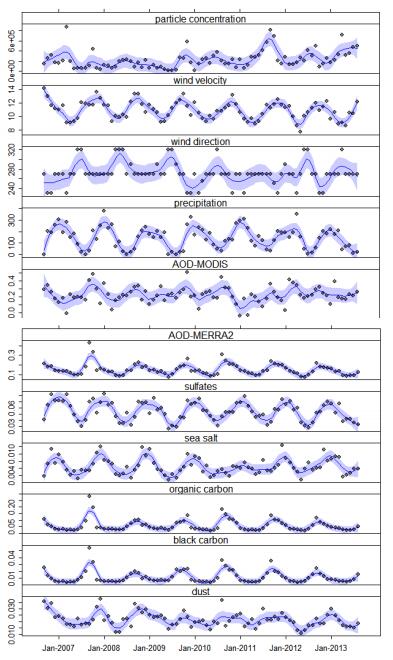
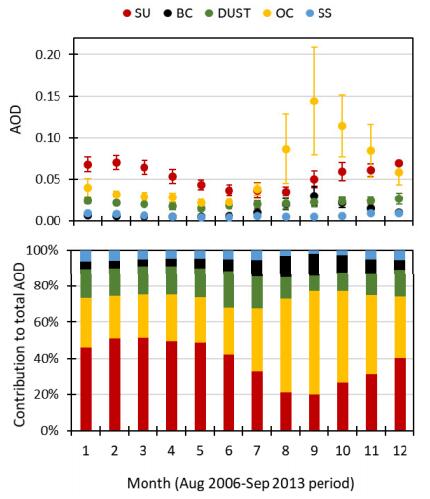
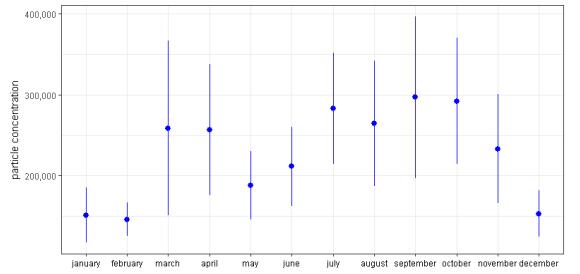
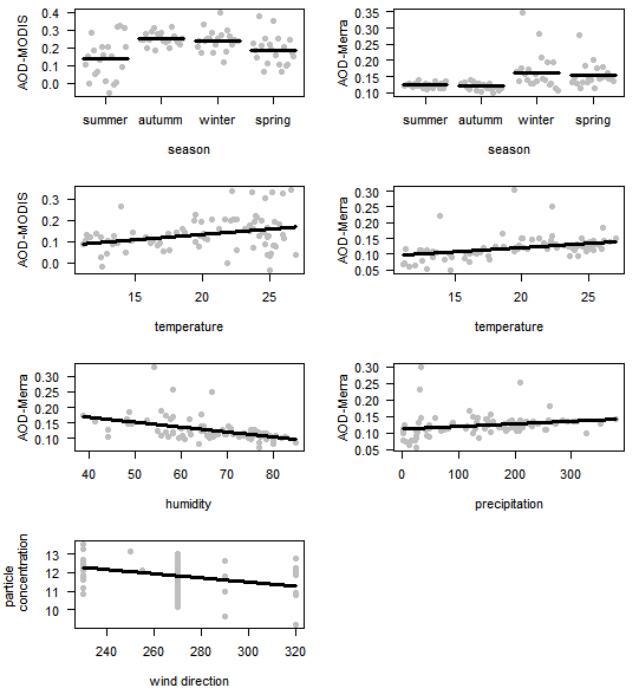
The analysis of atmospheric particles (aerosols) is of special interest due to their potential effects on human health and other applications. In this paper the climatic and seasonal effects on aerosols have been characterized in Tucumán city (26°50’ S, 65° 13’ W,450 masl),Argentina, for the 2006–2013 period. The atmospheric aerosols in Tucumán city result from both stationary and mobile sources such as: industrial activity of sugar cane and alcohol distilleries, paper industry, biomass burning (mainly sugarcane waste crop and grasslands), household waste burning and transport emissions. The peak of industrial activity is seasonal, coincident with the austral winter (July-August-September), when accumulation of particles in the lower atmosphere occurs. In this region, there are no studies like the present one that evaluate, using “in situ” equipment, the temporal variation of aerosols and its causes, by applying modern analytical techniques. A continuous volumetric and isokinetic sampler of Hirst type (Burkard), was used for atmospheric particle sampling, in weekly records between 2006 and 2013. The particle concentration (number of particles per cubic meter) showed an increasing trend in the studied period. The monthly variation of: the particle concentration; the aerosol optical thickness at a wavelength of 550 nm (AOD550) obtained from the Moderate Resolution Imaging Spectroradiometer (MODIS) sensors onboard Aqua (NASA) satellite, and the AOD from different aerosol tracers (black and organic carbon, sea salt, sulfates, dust) obtained from the Modern-Era Retrospective Analysis for Research and Applications (MERRA-2), were also analyzed. The temporal variation in particle concentration was explained mostly by wind direction, while the corresponding variation for AOD550(MODIS) was explained by temperature and seasonality (as by-product of climatic variation and anthropogenic particle emission sources). The variation in the AOD550(MERRA-2) data series were explained by temperature, humidity, precipitation, and seasonality, with less effect of wind speed and direction. Particle concentration, AOD550(MODIS), and AOD550(MERRA-2) were highly variable. The cross-correlation between AOD550(MODIS) and AOD550(MERRA-2) time series was significantly positive at lag zero. Other contribution was the determination of the space-time distribution of aerosols on a monthly basis considering AOD550 MODIS (3 km × 3 km) data. The present study suggests that these variables are affected by temperature and wind dynamics driven by seasonal and high-order autoregressive non-linear processes.
1.
Introduction
Fractional differential equations have played an important role and have presented valuable tools in the modeling of many phenomena in various fields of science and engineering [6,7,8,9,10,11,12,13,14,15,16]. There has been a significant development in fractional differential equations in recent decades [2,3,4,5,26,23,33,37]. On the other hand, many authors studied the stability of functional equations and established some types of Ulam stability [1,17,18,19,20,21,22,24,27,28,29,30,31,32,33,34,35,36,37] and references there in. Moreover, many authors discussed local and global attractivity [8,9,10,11,34].
Benchohra et al. [13] established some types of Ulam-Hyers stability for an implicit fractional-order differential equation.
A. Baliki et al. [11] have given sufficient conditions for existence and attractivity of mild solutions for second order semi-linear functional evolution equation in Banach spaces using Schauder's fixed point theorem.
Benchohra et al. [15] studied the existence of mild solutions for a class of impulsive semilinear fractional differential equations with infinite delay and non-instantaneous impulses in Banach spaces. This results are obtained using the technique of measures of noncompactness.
Motivated by these works, in this paper, we investigate the following initial value problem for an implicit fractional-order differential equation
where CDα is the Caputo fractional derivative, h:J×R⟶R,g1:J×R×R⟶R and g2:J×R⟶R are given functions satisfy some conditions and J=[0,T].
we give sufficient conditions for the existence of solutions for a class of initial value problem for an neutral differential equation involving Caputo fractional derivatives. Also, we establish some types of Ulam-Hyers stability for this class of implicit fractional-order differential equation and some applications and particular cases are presented.
Finally, existence of at least one mild solution for this class of implicit fractional-order differential equation on an infinite interval J=[0,+∞), by applying Schauder fixed point theorem and proving the attractivity of these mild solutions.
By a solution of the Eq (1.1) we mean that a function x∈C2(J,R) such that
(i) the function t→[x(t)−h(t,x(t))]∈C2(J,R) and
(ii) x satisfies the equation in (1.1).
2.
Preliminaries
Definition 1. [23] The Riemann-Liouville fractional integral of the function f∈L1([a,b]) of order α∈R+ is defined by
and when a=0, we have Iαf(t)=Iα0f(t).
Definition 2. [23] For a function f:[a,b]→R the Caputo fractional-order derivative of f, is defined by
where where n=[α]+1 and [α] denotes the integer part of the real number α.
Lemma 1. [23]. Let α≥0 and n=[α]+1. Then
Lemma 2. Let f∈L1([a,b]) and α∈(0,1], then
(i) CDαIαf(t)=f(t).
(ii) The operator Iα maps L1([a,b]) into itself continuously.
(iii) For γ,β>0, then
For further properties of fractional operators (see [23,25,26]).
3.
Main results
Consider the initial value problem for the implicit fractional-order differential Eq (1.1) under the following assumptions:
(i) h:J×R⟶R is a continuous function and there exists a positive constant K1 such that:
(ii) g1:J×R×R⟶R is a continuous function and there exist two positive constants K,H such that:
(iii) g2:J×R⟶R is a continuous function and there exists a positive constant K2 such that:
Lemma 3. Let assumptions (i)-(iii) be satisfied. If a function x∈C2(J,R) is a solution of initial value problem for implicit fractional-order differential equation (1.1), then it is a solution of the following nonlinear fractional integral equation
Proof. Assume first that x is a solution of the initial value problem (1.1). From definition of Caputo derivative, we have
Operating by Iα−1 on both sides and using Lemma 2, we get
Then
Using initial conditions, we have
Integrating both sides of (1.1), we obtain
Then
Conversely, assume that x satisfies the nonlinear integral Eq (3.1). Then operating by CDα on both sides of Eq (3.1) and using Lemma 2, we obtain
Putting t=0 in (3.1) and since g1 is a continuous function, then we obtain
Also,
Then we have
Hence the equivalence between the initial value problem (1.1) and the integral Eq (3.1) is proved. Then the proof is completed.
Definition 3. The Eq (1.1) is Ulam-Hyers stable if there exists a real number cf>0 such that for each ϵ>0 and for each solution z∈C2(J,R) of the inequality
there exists a solution y∈C2(J,R) of Eq (1.1) with
Definition 4. The Eq (1.1) is generalized Ulam-Hyers stable if there exists ψf∈C(R+,R+),ψf(0)=0, such that for each solution z∈C2(J,R) of the inequality
there exists a solution y∈C2(J,R)of Eq (1.1) with
Definition 5. The Eq (1.1) is Ulam-Hyers-Rassias stable with respect to φ∈C(J,R+) if there exists a real number cf>0 such that for each ϵ>0 and for each solution z∈C2(J,R) of the inequality
there exists a solution y∈C2(J,R) of Eq (1.1) with
Definition 6. The Eq (1.1) is generalized Ulam-Hyers-Rassias stable with respect to φ∈C(J,R+) if there exists a real number cf,φ>0 such that for each solution z∈C2(J,R) of the inequality
there exists a solution y∈C2(J,R) of Eq (1.1) with
Now, our aim is to investigate the existence of unique solution for (1.1). This existence result will be based on the contraction mapping principle.
Theorem 1. Let assumptions (i)-(iii) be satisfied. If K1+KTαΓ(α+1)+K2HTα+βΓ(β+1)Γ(α+1)<1, then there exists a unique solution for the nonlinear neutral differential equation of fractional order.
Proof. Define the operator N by:
In view of assumptions (i)-(iii), then N:C2(J,R)→C2(J,R) is continuous operator.
Now, let x and ,˜x∈C2(J,R), be two solutions of (1.1)then
Then
Since K1+KTαΓ(α+1)+K2HTα+βΓ(β+1)Γ(α+1)<1. It follows that N has a unique fixed point which is a solution of the initial value problem (1.1) in C2(J,R).
4.
Stability of solutions of the IVP (1.1)
4.1. Ulam-Hyers stability
Theorem 2. Let assumptions of Theorem 1 be satisfied. Then the fractional order differential Eq (1.1) is Ulam-Hyers stable.
Proof. Let y∈C2(J,R) be a solution of the inequality
Let x∈C2(J,R) be the unique solution of the initial value problem for implicit fractional-order differential Eq (1.1). By using Lemma 3, The Cauchy problem (1.1) is equivalent to
Operating by Iα−1 on both sides of (4.1) and then integrating, we get
Also, we have
Then
thus the intial value problem (1.1) is Ulam-Heyers stable, and hence the proof is completed. By putting ψ(ε)=cε,ψ(0)=0 yields that the Eq (1.1) is generalized Ulam-Heyers stable.
4.2. Ulam-Hyers-Rassias stability
Theorem 3. Let assumptions of Theorem 1 be satisfied, there exists an increasing function φ∈C(J,R) and there exists λφ>0 such that for any t∈J, we have
then the Eq (1.1) is Ulam-Heyers-Rassias stable.
Proof. Let y∈C2(J,R) be a solution of the inequality
Let x∈C2(J,R) be the unique solution of the initial value problem for implicit fractional-order differential Eq (1.1). By using Lemma 3, The Cauchy problem (1.1) is equivalent to
Operating by Iα−1 on both sides of (4.2) and then integrating, we get
Also, we have
Then
then the initial problem (1.1) is Ulam-Heyers-Rassias stable, and hence the proof is completed.
5.
Existence and attractivity of solutions on half line
In this section, we prove some results on the existence of mild solutions and attractivity for the neutral fractional differential equation (1.1) by applying Schauder fixed point theorem. Denote BC=BC(J),J=[0,+∞) and consider the following assumptions:
(I) h:J×R⟶R is a continuous function and there exists a continuous function Kh(t) such that:
where K∗h=supt≥0Kh(t)<1,limt→∞Kh(t)=0, and limt→∞h(t,0)=0.
(II) g1:J×R×R⟶R satisfies Carathéodory condition and there exist an integrable function a1:R+⟶R+ and a positive constant b such that:
(III) g2:J×R⟶R satisfies Carathéodory condition and there exists an integrable function
a2:R+⟶R+ such that:
(IV) Let
By a mild solution of the Eq (1.1) we mean that a function x∈C(J,R) such that x satisfies the equation in (3.1).
Theorem 4. Let assumptions (I)-(IV) be satisfied. Then there exists at least one mild solution for the nonlinear implicit neutral differential equation of fractional order (1.1). Moreover, mild solutions of IVP (1.1) are locally attractive.
Proof. For any x∈BC, define the operator A by
The operator A is well defined and maps BC into BC. Obviously, the map A(x) is continuous on J for any x∈BC and for each t∈J, we have
Then
Thus A(x)∈BC. This clarifies that operator A maps BC into itself.
Finding the solutions of IVP (1.1) is reduced to find solutions of the operator equation A(x)=x. Eq (5.1) implies that A maps the ball BM:=B(0,M)={x∈BC:||x(t)||BC≤M} into itself. Now, our proof will be established in the following steps:
Step 1: A is continuous.
Let {xn}n∈N be a sequence such that xn→x in BM. Then, for each t∈J, we have
Assumptions (II) and (III) implies that:
Using Lebesgue dominated convergence theorem, we have
Step 2: A(BM) is uniformly bounded.
It is obvious since A(BM)⊂BM and BM is bounded.
Step 3: A(BM) is equicontinuous on every compact subset [0,T] of J,T>0 and t1,t2∈[0,T],t2>t1 (without loss of generality), we get
Thus, for ai=supt∈[0,T]ai,i=1,2 and from the continuity of the functions ai we obtain
Continuity of h implies that
Step 4: A(BM) is equiconvergent.
Let t∈J and x∈BM then we have
In view of assumptions (I) and (IV), we obtain
Then A has a fixed point x which is a solution of IVP (1.1) on J.
Step 5: Local attactivity of mild solutions. Let x∗ be a mild solution of IVP (1.1). Taking x∈B(x∗,2M), we have
We have
Hence A is a continuous function such that A(B(x∗,2M))⊂B(x∗,2M).
Moreover, if x is a mild solution of IVP (1.1), then
Then
In view of assumption of (IV) and estimation (5.2), we get
Then, all mild solutions of IVP (1.1) are locally attractive.
6.
Applications
As particular cases of the IVP (1.1), we have
● Taking g1(t,x,y)=g1(t,x), we obtain the initial value problem
● Letting α→2,β→1, as a particular case of Theorem 1 we can deduce an existence result for the initial value problem for implicit second-order differe-integral equation
As particular cases we can deduce existence results for some initial value problem of second order differential equations (when h=0) and α→2, we get:
● Taking g1(t,x,y)=−λ2x(t),λ∈R+, then we obtain a second order differential equation of simple harmonic oscillator
● Taking g1(t,x,y)=(t2−kt2)x+q(x),k∈R where q(x) is continuous function, then we obtain Riccati differential equation of second order
● Taking g1(t,x,y)=−(t2−2lt−k)x+q(x),k∈R where q(x) is continuous function and l is fixed, then we obtain Coulomb wave differential equation of second order
● Taking g1(t,x,y)=(−8π2mℏ2)(Ex−kt22x)+q(x),k∈R where q(x) is continuous function and ℏ is the Planket's constant and E,k are positive real numbers, then we obtain of Schrödinger wave differential equation for simple harmonic oscillator
7.
Conclusions
Sufficient conditions for the existence of solutions for a class of neutral integro-differential equations of fractional order (1.1) are discussed which involved many key functional differential equations that appear in applications of nonlinear analysis. Also, some types of Ulam stability for this class of implicit fractional differential equation are established. Some applications and particular cases are presented. Finally, the existence of at least one mild solution for this class of equations on an infinite interval by applying Schauder fixed point theorem and the local attractivity of solutions are proved.
Acknowledgements
The authors express their thanks to the anonymous referees for their valuable comments and remarks.
Conflict of interest
The authors declare that they have no competing interests.













 DownLoad:
DownLoad: