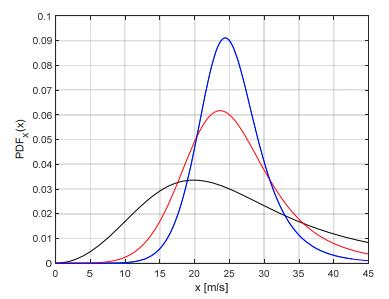
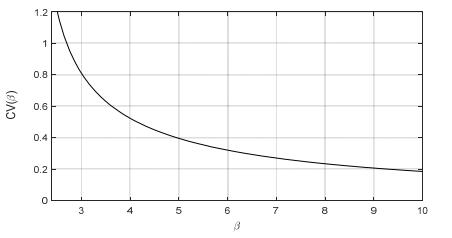
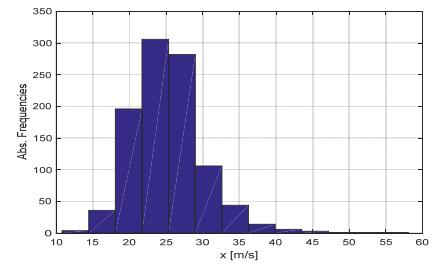
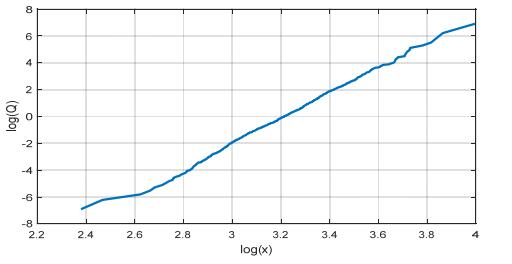
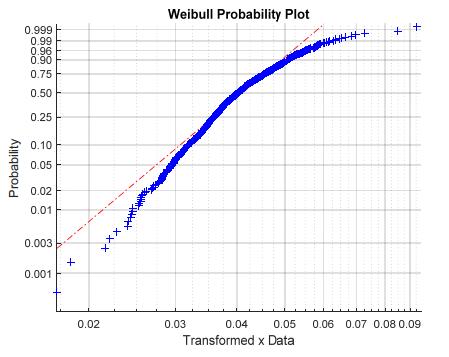
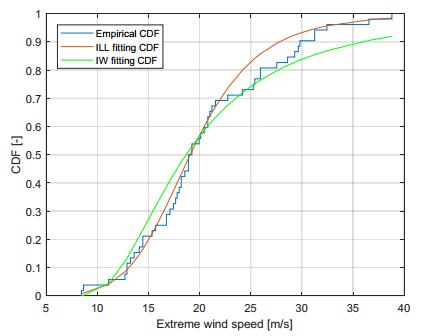
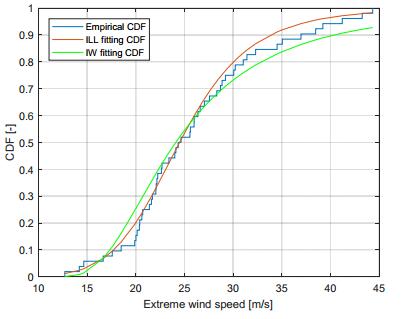
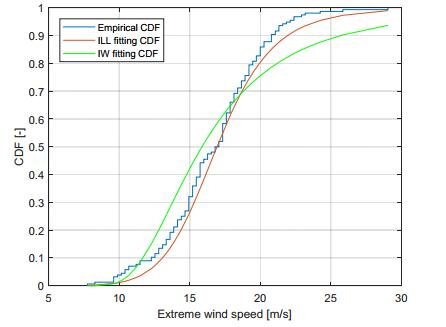
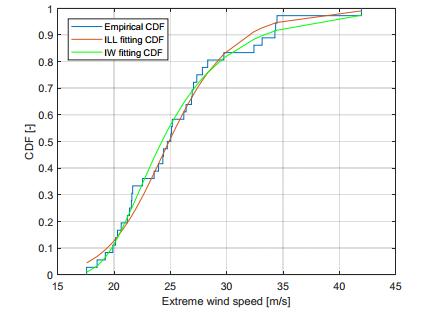
Extreme Wind Speed modeling, i.e. the probabilistic characterization of extreme values of wind speed, is a key tool for properly understanding the destructive wind forces which may affect mechanical safety and reliability of wind power systems, but it is also extremely useful for the purpose of achieving accurate wind energy production estimations. Indeed, the need of more accurate wind estimations has been often highlighted in the literature, especially for Extreme Wind Speed, since classical adopted models, such as the Weibull distribution, behave poorly in the range of Extreme Wind Speed values. In the paper, a new model, generated by a proper mixture of the established Inverse Weibull distribution, is proposed and illustrated. The proposal is the “Inverse Log-logistic” distribution, whose adequacy in interpreting some sets of real Extreme Wind Speed data is shown after giving some hints to its identification. This study also develops a peculiar Bayesian statistical inference approach for the estimation of the above model from available data, using different prior distributions, i.e. the Lognormal, the Generalized Gamma and the Uniform distribution. Extensive numerical simulations confirm that the proposed estimation technique constitutes a very fast, efficient and robust method for the Extreme Wind Speed modeling.
1.
Introduction
In recent years, complex networks research has aroused particular concern in many different realms of science. With the development of the telecommunication, internet and international exchange, the conception of complex networks increasingly appears in human's productive activity, scientific research and daily life, such as e-commerce warehouse logistics, multinational social media and unmanned aerial vehicle (UAV) formation. Erdös and Rényi Explored a random graph model firstly in 1959 [1]. In a random graph, the probability of a connection emerged between a pair of nodes is a random constant. Watts and Strogatz [2] investigated the mechanism that a regular graph gradually converts to a random graph and proposed a small-world network model. Newman and Watts [3] modified it to generate another variant of the small-world model. In 1999 [4], Barabási and Albert proposed a scale-free network model that aroused intense scholarly interest. The degree distribution of nodes in a scale-free network follows a power-law form. The founding of scale-free networks is significant since plenty of real-word systems have the power-law property.
The research of complex networks simultaneously raised the attention on synchronization. Pecora and Carroll's work was the early research on synchronization [5]. Wu studied a linearly coupled identical dynamical system and obtained synchronization sufficient conditions of the system [6]. Louis M. Pecora and Thomas L studied a coupled oscillator array described as a complex network [7]. The author put the complex network into a simple form so that the determination of the stability of the synchronous state can be done by a master stability function. Substantial work has been devoted to the study of synchronization since there are many systems in real-word that can be described by complex networks [8,9]. A synchronization of heterogeneous dynamics networks via three-layer communication framework was established in [10]. An explicit synchronization algorithm was proposed, in which the synchronization errors of all the agents are decoupled. In [11], the author addresses the leader-follower consensus for linear and nonlinear multi-agent systems with three-layer network framework and dynamic interaction jointly connected topology. Wang [12] studied heterogeneous uncertain dynamical networks under switching communication typologies. This work established an explicit synchronization framework and solved the zero error synchronization problem. Based on this work, Wang further studied the leader-follower consensus of a high-order nonlinear complex system [13]. In [14], A united directed complex network with multi-links was studied and exponential synchronization conditions were obtained. Multi-agent systems are typical complex networks. Li utilized linear feedback control and adaptive linear feedback control to achieve successive lag synchronization in a multi-agent system.
The works as mentioned above have studied the synchronization of complex networks in various angles, however, most of which focus on the networks with time-invariant couplings under the global control and pinning synchronization of complex networks with time-varying coupling have been seldom explored. Many systems in the real word have time-varying feature. Time-varying exists in interior parts of systems, links and coupling among systems. Besides, it is impossible to control all nodes in a system to achieve global synchronization. Yu [15] investigated how the local controllers on pinned nodes affect global network synchronization. The research gave a general criterion for ensuring network synchronization and obtained appropriate coupling strengths for achieving network synchronization. Today, many results of pinning synchronization have been established [16,17]. Zhang [18] investigated the synchronization of complex networks with time-varying coupling matrices and established suitable linear controllers and adaptive controllers. Furthermore, a large amount of research on synchronization with the time-varying feature have been proposed [19,20]. Time-varying inner coupling and outer coupling are common and complicated situations in complex networks. In a single system, state variables do not transform separately. We regard variables affecting each other from different angles along the entire dynamic process as the inner coupling of systems. In large-scale systems and complex systems, small components and parts are not isolated. They are often connected by electric wires or signal wires. That is, they are coupled by each other and their states depend on the neighbors' states, external magnetic field and electric field. We regard this situation as the outer coupling of systems. Complicated inner coupling and outer coupling lead systems hardly to be controlled or be stabilized. It prompts us to find effective methods to decompose the coupling and design feedback controllers. Motivated by Yu and Zhang's contributions, this paper aims to the synchronization of time-varying random networks by respectively setting linear pinning controllers and adaptive pinning controllers. We take inner, outer coupling and stochastic behaviors into consideration. Potential correlations among the parameters are also investigated in this paper.
The rest of this paper is organized as follows. In Section 2, some preliminaries are outlined. In Section 3, the main theorems and corollaries for pinning synchronization on complex networks are given. In Section 4, simulation examples are shown to demonstrate the effectiveness of the proposed method. Finally, conclusions are drawn in Section 5.
2.
Preliminaries
Consider a complex network consisting of N identical coupled nodes, described by
where, i=1,2,...,N, xi(t)=(xi1(t),xi2(t),...,xin(t))T∈Rn is the state vector of the ith node. The node in the system is an n dimensional nonlinear time-varying dynamical system. c(t) is the time-varying outer coupling strength. f:Rn×R+→Rn is a nonlinear continuously differentiable vector function. Γ(t)∈Rn×n is the time-varying inner coupling matrix. G(t)=[Gij(t)]ni,j=1∈RN×N represents the topological structure and the coupling strength of the the complex network at time t, where Gij(t) is defined as follows: If there is a connection between nodes j to i time, then Gij(t)>0; otherwise Gij(t)=Gji(t)=0(j≠i). The corresponding Laplacian matrix with respect to this complex network is given by
Definition 1 ([33]). The matrix L(t) is said to be dissipative if
Obviously, L(t) in Eq (2.2) satisfies the dissipative condition.
In this paper, the complex network is an random network in which the probability that Gij=1 is a constant p∈[0,1]. When p=0, all nodes in are isolated; when p=1, the complex network is a fully coupled network; and when p∈(0,1) the coupling strength between nodes i and j is the expectation of the connection
Remark 1. In random networks, the existence of links between nodes depends on the probability value p. Large p creates dense complex networks and vice versa. Note that isolated nodes do not have information exchange with other nodes and it is hard to synchronize in complex networks if there is no common equilibrium in the nonlinear dynamic. If the number of links are too small, nodes in complex networks turn to hardly achieve synchronization since the information exchanging is ineffective. Therefore, p can be regarded as an external condition. As the value of p changes, the controllability of the complex systems changes accordingly. In this paper, the complex network is a jointly connected network. The complex network topology is under arbitrary switching during the entire dynamic process and may be not connected in every single switching state since the value of p could be very small that leads some isolated nodes. However, in the entire dynamic process, the superposition of all switching states is a connected network. Equivalently, Eq (2.1) can be simplified as follows
Set s(t) be the solution of an isolated node with
whose trajectory may be may be an equilibrium point, a periodic orbit, or a chaotic orbit of the nonlinear function f(xi(t),t). The aim of this paper is to find out some appropriate controllers such that the state of all nodes in complex network with time-varying inner and outer coupling Eq (2.5) synchronize with the solution of Eq (2.6)
where ‖⋅‖ is the Euclidean vector norm.
Assumption 1 ([21]). The nonlinear function satisfies the Lipschitz condition, that is, for any time, there exists a constant matrix K and ∀x,y∈Rn, such that
Lemma 1 ([22]). Assume that A is a dissipative coupling matrix and satisfies aij>0(i≠j), then the following results hold
(1) 0 is an eigenvalue of matrix A and the associated eigenvector is (1,1⋯1)T,
(2) The real parts of all eigenvalues of matrix A are less than or equal to 0 and all possible eigenvalues with zero real part are the real eigenvalue 0,
(3) If A is irreducible, then 0 is its eigenvalue of multiplicity 1.
Lemma 2 ([23]). Let λ1,λ2⋯λn be eigenvalues of matrix A∈Rn and μ1,μ2⋯μn are eigenvalues of matrix B∈Rn, then, there is |λmin||μmin|Inm×mn⩽A⊗B⩽|λmax||μmax|Inm×mn in which ⊗ is the Kronecker product, λmax and λmin are the maximum and the minimum eigenvalues of A, while μmax and μmin are the maximum and the minimum eigenvalues of B.
To realize the synchronization, pinning control will be used in part of nodes. As the complex network is a jointly connected network, without loss of generality, we randomly choose one node in minimal spanning tree of every connected component as the controlled node. Suppose nodes i1,i2,...,il are selected to be controlled, where l represents the integer part of the real number N. The complex network with pinning control can be rewritten as
where
The error dynamic equation can be described by
where ei(t)=xi(t)−s(t),(i=1,2...,N). Denote e(t)=(eT1(t),eT2(t),...,eTN(t))T.
3.
Pinning synchronization of complex networks
3.1. Pinning synchronization
In this section, some general criterion of pinning synchronization are derived.
Theorem 1. Suppose that Assumption 1 is established, under the control of linear controllers (2.10), complex network (2.9) can achieve synchronization and the synchronous solution is asymptotically stable if the following condition is satisfied
where IN is the N-dimensional identity matrix and D=diag(d1,d2,⋯,dl,0⋯0)∈Rn×n.
Proof. For simplicity, we first investigate the connected network with l randomly choosed controlled nodes. Consider the Lyapunov functional candidate
The declarative of V(t) along the trajectories of Eq (2.11) gives
If L(t)+D is large such that IN⊗KΓ(t)−pc(t)(L(t)+D)⊗Γ(t)<0 hold, then ˙V(t)<0 and complex network (2.9) is globally synchronized.
When the connected network degrades into a jointly connected network mentioned in Remark 1, arbitrary one single node in minimal spanning tree of all connected components are chosen as pinning controlled nodes. Suppose that complex nework (2.9) contains l connected component and the sth component contains Ns nodes, namely ∑qs=1Ns=N. Each component is associated with a zero eigenvalue and l zero eigenvalues are associated with the l dimensions zero eigen-subspace that is spun by the corresponding eigenvectors ζ1,⋯,ζl. The base vectors satisify
where ζij=1Ni, if j=i, otherwise ζij=0Nj. 1n(0n) indicate the n-dimensional column vector with each entry being 1(0). col{ζi1,⋯,ζil} means column a vector composed by ζi1,⋯,ζik. There exists a set of constants ℓi,i=1,⋯,N such that arbitrary nonzero vector ∀ζ≠0 can be decomposed as ζi1,⋯,ζil and ζTiζj=0. Set D=diag{D1,⋯,Dk} be a block diagonal matrix, where each Di,i=1,⋯,l are all diagonal matrices. Since arbitrary single node in minimal spanning tree of all connected components are chosen as pinning controlled nodes, there is at least 1 nonzero element in the main diagonal of each Di,i=1,⋯,l. If i>l, for ∀ζ≠0.
ζ≠0 and at least one ℓi≠0. If there exis ts one ℓi≠0,i=k+1,⋯,N, the right-hand side of Eq (3.5) is positive. If not, Eq (3.5) can be simplified as
Therefore, jointly connected network status remains the L(t)+D conditon in Eq (3.3) that guarantees the complex network synchronization. The proof is completed.
Remark 2. Equation (3.1) is a general condition to ensure the pinning synchronization of complex networks. Note that Eq (3.1) is a N×n dimension matrix and it contains multiple parameters. Therefore, it is difficult to realize these parameter conditions simultaneously. To solve this problem, based on Eq (3.1), we will seek to derive a more practicable condition to guarantee the synchronization of complex networks. Let Γ be a positive definite matrix. If Γ and K are commutable, let θ=‖K‖>0 [33].
Corollary 1. Suppose that Assumption 1 is established and Γ(t) is a positive definite matrix. Under the control of linear controllers (2.10), complex network (2.9) can achieve synchronization and the synchronous solution is asymptotically stable if the following condition is satisfied
where θ=‖K‖ defined in Assumption 1. λi and λmax are the eigenvalues and maximum eigenvalue of L(t). Lλi is the diagonal matrix of L(t) satisfies Φ−1L(t)Φ=Lλi. Lλmax is a diagonal matrix composed by λmax.
Proof. First based on Eq (3.1) and Remark 2, the following inequality holds
Taking the similarity transformation on both sides of Eq (3.5) yields
On the right-hand side, we have
Γ(t) is a positive definite matrix. According to the property of Kronecker product, matrix multiplication and similarity transformation, if θIN−pc(t)(λmaxIN+Φ−1DΦ)<0, then Φ−1((θIN−pc(t)(L(t)+D))⊗Γ(t))Φ<0. Furthermore, we can easily obtain Φ−1(IN⊗KΓ(t)−pc(t)(L(t)+D)⊗Γ(t))Φ<0 and IN⊗KΓ(t)−pc(t)(Lij(t)+D)⊗Γ(t)<0. Therefore, condition (3.1) is satisfied, complex network (2.7) can achieve synchronization. The proof is completed.
Remark 3. Equation (3.7) is distinctly simpler. To ensure the global synchronization of the complex networks, appropriate maximum eigenvalues of L(t) and outer coupling strength c(t) need to be determined. Another problem is that the value of c(t) often determines the speed of the network synchronization.The required theoretical value for the L(t) is too conservative, usually much more extensive than that needed in practice.
3.2. Connection possibility and coupling strength in pinning synchronization
In this subsection, correlation between the random network connection possibility and coupling strength are derived.
Corollary 2. Suppose that Assumption Assumption 1 is established, under the control of linear controllers (2.10), complex network (2.9) can achieve synchronization and the synchronous solution is asymptotically stable if one of the following condition is satisfied
where λmax and λmin are the norms of the maximum and minimum eigenvalues of L(t). ηmax and ηmin are the norms of the maximum and minimum eigenvalues of D, respectively.
Proof. First, based on Lemma 1 and Lemma 2, Eq (3.1) satisfies the following inequality
where μmin=0 is the minimum eigenvalues of Γ(t). If |λmax|+pc(t)|λmin||ηmin|<0, then IN⊗KΓ(t)−pc(t)(Lij(t)+D)⊗Γ(t)<0 holds. Condition (3.1) is satisfied, completing the proof.
Remark 4. In Corollary 2, condition (i) reveals that a cluster of appropriate pinning controllers can synchronize the complex networks under the fixed topological structure and outer coupling strength. Condition (ii) reveals that there is a lower bound of the connection probability, under the fixed topological structure and outer coupling strength. Condition (iii) proposes a way to choose the coupling strength with fixed network structure and pinning scheme (2.9).
From Corollary 2, we can see that random network connection possibility p has a inversely proportional relationship with coupling strength c(t). When the network is sparse, strong coupling strength is needed to synchronize all nodes and vice versa. However, we are interested in the question if connection possibility is fixed and how to adequately lower the coupling strength c(t). Let cp(t)=c(t)p. Next, adaptive technique are utilized to reduce the value of cp(t).
With the pinning controllers (2.10) and the adaptive coupling law, complex network (2.9) can be expressed as
Theorem 2. Suppose that Assumption 1 holds and Γ is a positive definite matrix. Then, the adaptively controlled undirected network (2.9) is globally synchronized for a small constant ρ>0.
Proof. Consider the Lyapunov functional candidate
where φ and c∗ are positive constants. Based on lemma 1 and lemma 2, we yield
where μmin=0 is the minimum eigenvalues of Γ(t). If θIN−cp(t)(φIN−D)−φc∗IN<0 then the ˙V(t)<0 is negative definite. Complex network (2.9) can achieve synchronization, and the synchronous solution is asymptotically stable.
Remark 5. cp(t) can be caculated through the adaptive technique. Consequently, c(t) can be obtained under a fixed p. Note that the value of feedback gain is another factor, which determines the speed of network synchronization and the required theoretical value for the feedback gain is probably much larger than that needed in practice. Therefore, in the same way, an adaptive technique is exploited to compute the lower bound of feedback gain for achieving the complex network synchronization.
3.3. Adaptive controllers in pinning synchronization
The pinning controllers selected by Eq (2.9) yield the following controlled network
where qi are positive constants.
Theorem 3. Suppose that Assumption 1 holds and Γ is a positive definite matrix, then the undirected network (3.15) is globally synchronized under the adaptive scheme.
Proof. Consider the Lyapunov functional candidate
where d is a positive constant. Based on Lemma 1 and Lemma 2, the derivative of V(t) gives
where ˜IN=diag(1,...,1,⏟l0,...,0)⏟N−l. If INθ−pc(t)L(t)−pd˜IN<0, then ˙V(t)=eT(t)[[INθ−pc(t)L(t)−pd˜IN]⊗Γ(t)]e(t)<0. Note that pc(t)L(t) and pd˜IN are negative definite. INθ−pc(t)L(t)−pd˜IN is also negative definite when p is sufficiently small. Therefore we can select an appropriate d to guarantee ˙V(t)<0. This completes the proof.
In the adaptive control process, if the initial value ofdi(0) is very large, then di(t) increases very slowly according to the change of ei(t). Finally, the synchronization can be achieved when di(t) is large enough and converges to a constant d∗. d∗ is the bound of adaptive controllers di(t).
4.
Simulation examples
In this section, some numerical simulations are presented to verify the criteria established above. Consider complex network (2.9) that consists of N identical Chen systems, described by
where Γ=[3+sin2(t)0002+sin2(t)0005sin2(t)], and f(xi,t)={35(xi2−xi1)−7xi1−xi1xi3+28xi2xi1xi2−3xi3.
It is found that the chaotic attractor (s1,s2,s3) of the Chen system satisfies |S1|<M1, |S2|<M2, and |S3|<M3, M1=23, M2=32, and M3=61. Based on Lemma 3
υ and ε are chosen as 1.3139 and 0.4715, then θ=31.0122.
4.1. Pinning synchronization of complex networks with linear controllers
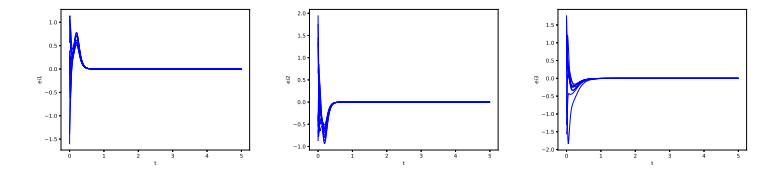
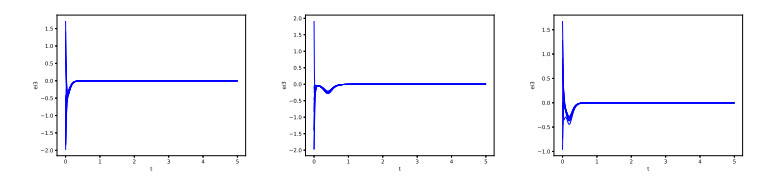
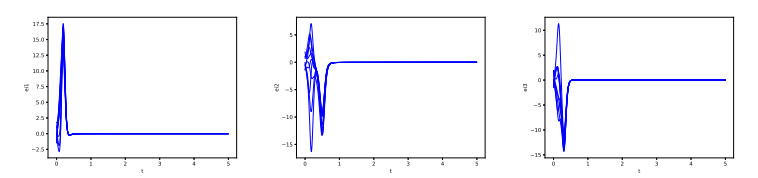
According to Theorem 1 and Corollary 2, when maximum eigenvalues of feedback matrix D satisfies ηmax>|λmax|pc(t)|λmin|, complex networks can realize synchronization. The states of error are under different value of linear controllers illustrated in Figures 1 and 2.
4.2. Pinning synchronization of complex networks with adaptive controllers
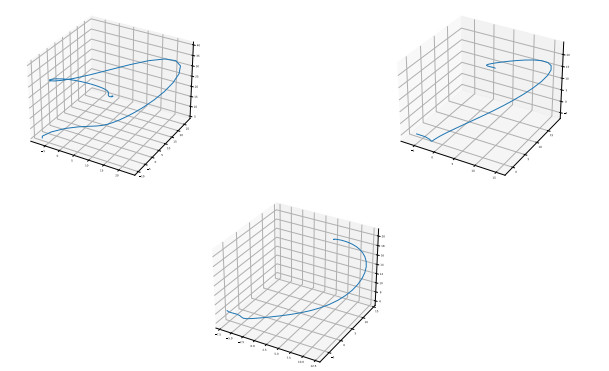
According to Theorem 3, same parameters are chosen to simulate complex network (2.8) with adaptive controllers. With different adaptive control factors, complex network can realize synchronization. The states of error eit are illustrated in Figure 2. Moreover, state trajectories were simulated to show the rate of convergence under different controllers in Figure 4. The graphs from left to right and top to bottom illustrate the system state evolution corresponding to Figures 1–3.
5.
Conclusions
In this paper, we investigated the pinning synchronization problem for complex networks with time-varying inner and outer coupling. We derived a general criterion for ensuring network synchronization. Pinning controllers and adaptive pinning controllers were respectively obtained based on the Lyapunov function theory. We found that the complex networks with two kinds of time-varying coupling can achieve global synchronization by adaptively adjusting the coupling strength or feedback gain. Simulations on random networks verify well the theoretical results.
Acknowledgments
This work are supported by National Natural Science Foundation of China (No. 61633019) and Shaanxi Provincial Key Project, China (2018ZDXM-GY-168).
Conflict of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad: