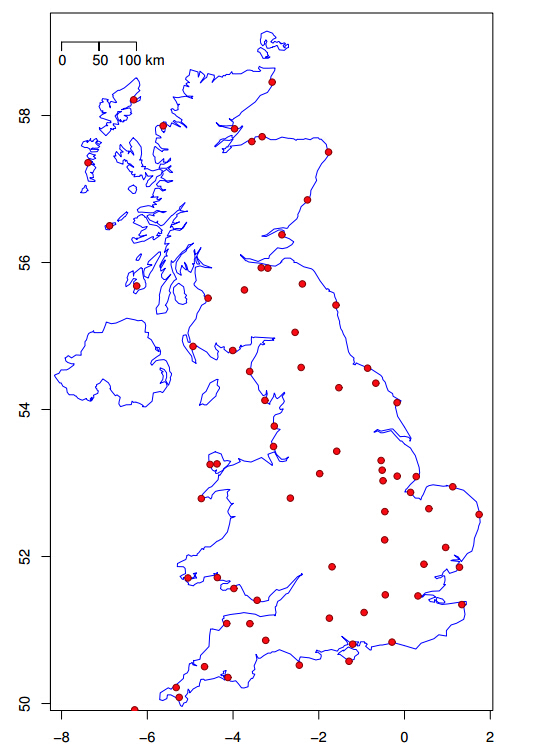
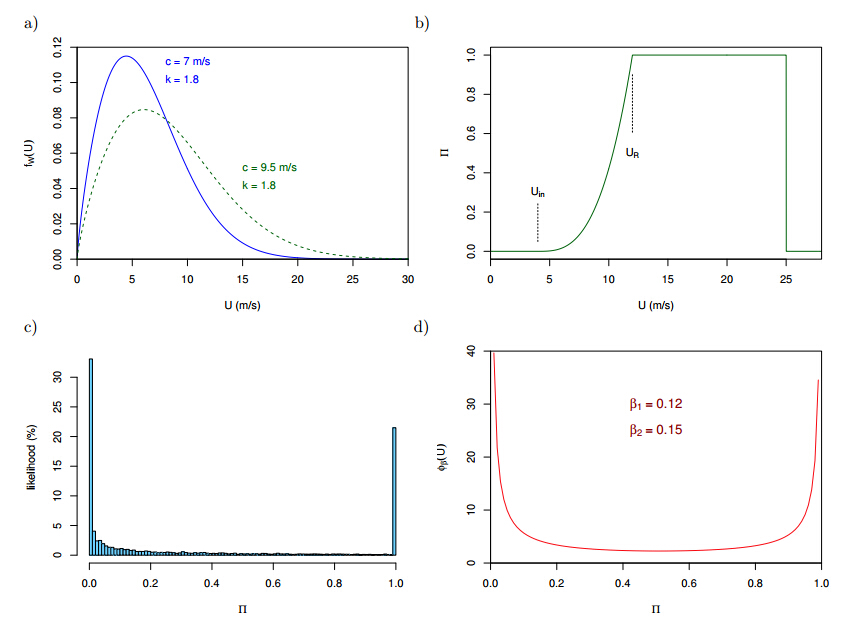
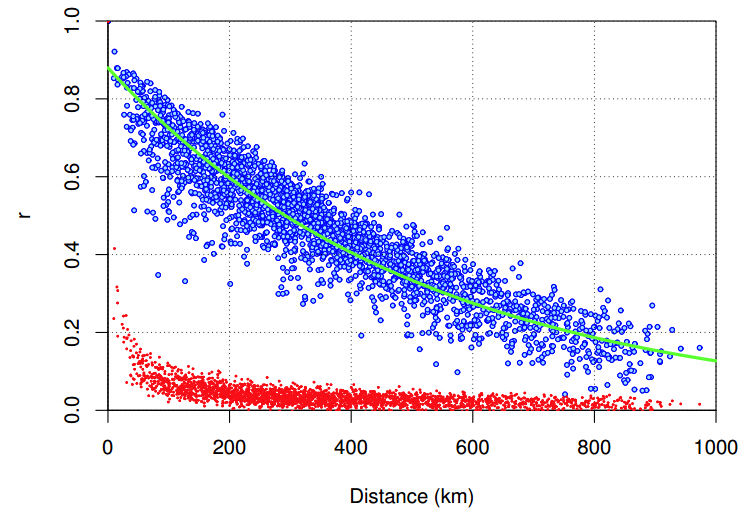
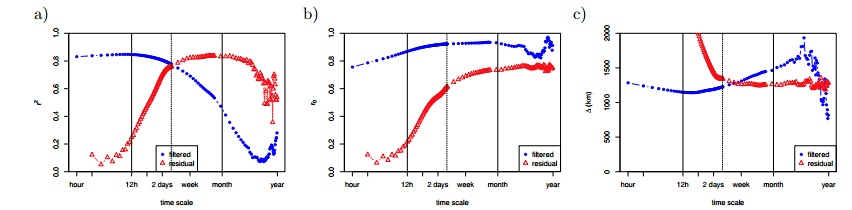
Wind power is one of the most established renewable power resources yet it is also one of the most volatile resources. This poses a key challenge for successfully integrating wind power at a large scale into the power grid. Here we present an analysis of the time scales associated with wind power from hourly to seasonal fluctuations and how combining spatially distributed wind power sources helps to reduce its volatility. The analysis, based on observed wind speeds, is then generalised in a simple statistical model to develop a tool which can estimate the power output profile from a particular consortium of wind power sources. As the estimator only uses the local, or the mean national, wind resource and the mean distance between the sites to estimate the joint power output profile, it can be used by developers to estimate the reliability of their joint power output and to form the most effective consortium.
1.
Introduction
In many biomedical applications, the primary interest centers on predicting a survival outcome, for instance, the $ t $-year survival probability, or the median survival time for future patients. For some diseases, it may be of much relevance to predict the survival function over a continuum of time for better treatment and surveillance. The problem of survival prediction is often tackled by first formulating a regression model that relates the survival time to the covariates and then making the prediction according to the fitted model. The commonly used approaches to assess the survival rate (or disease risk) are either based on modeling the association between the baseline covariates and the failure times (e.g. [1,2,3,4]) or through modeling the relationship between the hazard function and baseline covariates (e.g. [5,6,7]). As an alternative, the censored quantile regression [8,9,10] provides a valuable complement to the aforementioned methods. The censored quantile regression method has great advantages in the interpretation of regression coefficients which are derived under distribution-free assumptions. However, the censored quantile regression method focuses on a single quantile at a time, hence fails to make full use of the quantile information of the target distribution.
The regression-based prediction directly models the conditional hazard function or the conditional regression function. The information of the covariates is incorporated and the resulting model can also be used for quantifying the risks for individual patients. However, the prediction accuracy of the regression approach relies heavily on whether the model is correctly specified. When a misspecified model is used, the prediction results can be misleading. However, in practice, it is often difficult to specify a correct model, especially when patients population are heterogeneous, or the data structure is complex. Furthermore, predicting the conditional survival outcome for individual patients is often too difficult or unrealistic. For example, Henderson and Keiding [11] convincingly showed that statistical models and indices can be useful at the group or population level, but may have limited predictive values for individual survival since human survival is so uncertain. Therefore throughout the paper, we focus on predicting unconditional survival outcomes. For such purposes, the conditional approach does not directly target the quantity to predict and is hence less ideal.
So far, to the best of our knowledge, there is very limited research discussing the survival-rate (or disease-risk) assessment by matching quantiles or survival distributions. For complete data, the idea of matching quantiles is explored in many contexts (e.g. [12,13,14]). The matching quantiles estimation (MQE) method is proved to be an effective approach to assess the target distribution. For regression models, the MQE method shares certain similarities in form with the ordinary least squares estimation (OLS) and the quantile regression (QR) method [12,15]. But the MQE method is quite different from the classical methods such as the QR method. To be specific, the MQE is proposed to assess the (unconditional) target distribution, while the QR method is used for estimating regression coefficients based on conditional quantile functions. The MQE method makes use of both information of the order and the distance between quantiles of the target distribution and those used for matching.
One advantage of the MQE method is that it can be implemented by matching the local quantiles between $ \tau_1 $ and $ \tau_2 $ only ($ 0 < \tau_1 < \tau_2 < 1 $). This could be very attractive if we are only interested in studying a specific part of the target distribution, such as the middle or the lower end of the target distribution. Another advantage is that it does not require the observations being paired, i.e., the size of the sample from the target distribution and that of the counterpart are allowed to be unequal. It makes the MQE method more appealing and practical than traditional methods, especially for missing data. Sgouropoulos et al. [14] propose a MQE method by matching the sample quantiles of target distribution with that of a linear combination of covariates, which uses an iterative procedure based on permutation and OLS in computation. Although the iterative algorithm is fast, it inherits several disadvantages from OLS such as being sensitive to outliers, inapplicable to unpaired observations as well as the incomplete data due to censoring.
Motivated by the MQE method, we propose a matching censored quantiles approach for predicting the survival rates and assessing the target distribution of interest. Particularly, the proposed method not only bears certain similarities with the classical quantile regression method and the composite quantile regression method [16], but also maintains major advantages of the aforementioned MQE methods for complete data. In addition, the proposed method avoids using permutations in the computational algorithm and can be easily extended to match a complex transformation of the target distribution. Last but not the least, the proposed method provides an alternative to assess or predict the target distribution in the presence of right-censored data.
The rest of the article is organized as follows. In Section 2, we first present some notations, and then introduce the matching censored quantiles method. In Section 3, we provide the asymptotic properties of the proposed estimator. Section 4 discusses the matching measurement criteria. Section 5 presents extensive simulation studies. An illustrative example is provided in Section 6. Finally, Section 7 concludes with some remarks.
2.
Estimation procedure
Let $ T_i $ be the failure time of the $ i $-th subject, and $ C_i $ be the censoring time. Denote the observed time as $ Y_i = \min(T_i, C_i) $, and the censoring indicator as $ \Delta_i = I (T_i \leq C_i) $. Let $ Z_i = (1, Z_{i1}, \ldots, Z_{ip})^T $ be a $ (p+1) \times 1 $ vector of covariates for the $ i $th subject. The observations of $ \{(Y_i, \Delta_i, Z_i), i = 1, \ldots, n \} $ are independent and identically distributed copies of $ (Y, \Delta, Z) $. The censoring mechanism is assumed to be non-informative, i.e., $ T_i $ and $ C_i $ are independent of each other, or $ T_i $ and $ C_i $ are conditionally independent of each other given $ Z $.
To assess the survival rates of $ T $, we aim to find a transformation $ G(\beta^T Z) $ such that its distribution matches the distribution of $ T $ as close as possible, where $ G(\cdot) $ is a known, continuous and strictly increasing function, and $ \beta \in {R}^{p+1} $ is a $ (p+1) $-dimensional coefficient. Denote the cumulative distribution function of $ T $ and $ \beta^T Z $ as $ F_T (t) = { \rm{Pr}} (T \leq t) $ and $ F_{G(\beta^T Z)}(t) = { \rm{Pr}} \{G(\beta^T Z) \leq t \} $, respectively. Correspondingly, we write the survival function of $ T $ and $ \beta^T Z $ as $ S_T (t) = 1 - F_T (t) $ and $ S_{G(\beta^T Z)}(t) = 1 - F_{G(\beta^T Z)}(t) $.
Let $ H(t) = G^{-1}(t) $ be the inverse function of $ G(t) $, then $ H(\cdot) $ is also a known, continuous and strictly increasing function. Note the fact that
hence, to search $ \beta $ such that $ F_{G(\beta^T Z)} $ matches $ F_T $ is equivalent to find a linear combination $ \beta^T Z $ such that its distribution matches the distribution of $ H(T) $.
2.1. Matching censored quantiles
With complete data, Sgouropoulos et al. [14] proposed to use the distribution of a linear combination $ \beta^T Z $ to match the target distribution, and $ \beta $ is estimated by minimizing the objective function,
where $ T_{(1)} \leq \cdots \leq T_{(n)} $ are the order statistics of $ T_1, \ldots, T_n $, and $ (\beta^T Z)_{(1)} \leq \cdots \leq (\beta^T Z)_{(n)} $ are the order statistics of $ \beta^T Z_{1}, \ldots, \beta^T Z_{n} $. Here, $ (\beta^T Z)_{(i)} $ is also known as the $ (i/n) $th sample quantile of $ \beta^T Z $. However, $ T_{(i)} $ is not fully observed due to right censoring, and naively treating $ Y_{(i)} $, the order statistic of the observed time $ Y $, as $ T_{(i)} $ would cause bias.
Denote $ X_{\beta} = G(\beta^T Z) $. Let $ F_{X_{\beta}}(t) = { \rm{Pr}} \{ G(\beta^T Z) \leq t \} $ be the cumulative distribution function of the survival time $ X_{\beta} $. Let $ Q_T (\tau) = \inf \{ y: F_T (y) \geq \tau\} $ be the $ \tau $-quantile of $ F_T(\cdot) $, and $ Q_{X_{\beta}} (\tau) = \inf \{ y: F_{X_{\beta}} (y) \geq \tau\} $ be the $ \tau $-quantile of $ F_{X_{\beta}} $. Motivated by [14], we define the objective function $ M_n(\beta) $
where $ \alpha_L \leq \tau_1 < \cdots < \tau_{K_n} \leq \alpha_{U} < 1 $ are $ K_n $ quantile points, $ 0 < \delta_{k} = \tau_k - \tau_{k-1} $, $ K_n \leq n $, and $ K_n \uparrow \infty $, $ \max\{\delta_{k} \} \downarrow 0 $ as $ n \rightarrow \infty $, $ \widehat{Q}_T (\tau) $ is the estimated $ \tau $-quantile with right-censored observations, and $ \widehat{Q}_{X_{\beta}} (\tau) $ is the sample $ \tau $-quantile of $ G(\beta^T Z_1), \ldots, G(\beta^T Z_n) $. Here we confine the range of study in $ [0, \tau_{U}] $, where $ \tau_{U} \in (0, 1) $ is a deterministic constant subject to certain identifiability constraints due to censoring. By matching censored quantiles, the estimator defined in Eq (2.2) forces the distribution $ F_{X_{\beta}} $ to be as close as possible to the target distribution $ F_T $. Define $ \widehat{\beta} $ as a minimizer of $ \min_{\beta} M_n(\beta) $. We call the proposed estimator $ \widehat{\beta} $ as the matching censored quantiles (MCQ) estimator.
Remark 1. The proposed MCQ method has certain similarity with the idea of maximum rank correlation (MRC) estimator [17,18] which is given by minimizing
The MRC approach also matches the orders of event times and covariate effects. However, there are essential differences between MCR and MCQ. The MRC method aims to match only the order of event times and covariate effects, not the quantiles, leading to a clear difference with MCQ in the form of objective functions. The objective function of MRC is a U-statistics, while the objective function of MCQ is a simple square summation. The MCQ method focus on minimizing the distance of the quantiles, so it allows the occurence of mismatch at some orders while the MRC method does not allow any mismatch. When there exist missing observations in $ Z $, the MCQ method works normally but the MRC fails. Khan and Tamer [19] proposed a partial rank estimation (PRE) procedure which was a generalization of [17,18] for censored data. In Section 4, we compare the performance of the proposed method with that of the PRE method.
The key to construct Eq (2.2) is to estimate the quantiles $ \{ Q_T (\tau_k): k = 1, \ldots, K_n \} $, for which the redistribution-of-mass technique (e.g., [8,10,20]) is adopted. This method redistributes the mass of each censored observation to $ Y^{+\infty} $, where $ Y^{+\infty} $ is a sufficiently large constant. We start with constructing an augmented data set $ \{(Y_i, \Delta_i, Z_i), i = 1, \ldots, n + n_c \} $, where $ \{ (Y_i, \Delta_i, Z_i), i = 1, \ldots, n \} $ represent the original data, and $ \{ (Y_i = Y^{+\infty}, \Delta_i = 0, Z_i), i = n+1, \ldots, n + n_c \} $ are $ n_c $ pseudo paired observations corresponding to the censored data.
For the case of conditional independent censoring, given a fixed quantile $ \tau $, we define the local weight function as
for $ i = 1, \ldots, n $. Here, $ F_T(t |Z) $ is the cumulative distribution function of $ T $ given $ Z $. Let $ \{ w_1(F_T; Z_i, \tau), \ldots, w_n(F_T; Z_i, \tau), 1 - w_{c_{1}}(F_T; Z_i, \tau), \ldots, 1 - w_{c_{n_c}}(F_T; Z_i, \tau) \} $ be the weights assigned to the augmented data, where $ \{ c_1, \ldots, c_{n_c} \} $ are subscripts of the $ n_c $ censored observations. Using these weights, we can estimate $ Q_T (\tau) $ by
In practice, $ F_T(t |Z) $ is unknown, and thus need to be estimated. Using the method in [21], we can estimate $ F_T(t |Z) $ nonparametrically by $ \widehat{F}_T(t|Z = z) = 1-\widehat{S}_T(t |Z = z) $ with $ \widehat{S}_T(t |Z = z) $ being the local Kaplan-Meier estimator,
where $ B_{ni} (z) = K_p \left\{ (z - Z_i)/h_n \right\}/\sum_{i = 1}^{n} K_p \left\{ (z - Z_i)/h_n \right\} $ is the Nadaraya-Watson type of weight, $ K_p (z_i) = \prod_{j = 1}^{p} K(z_{ij}) $, $ K(\cdot) $ is a univariate density kernel function, and $ h_n $ is the bandwidth that converges to zero as $ n \rightarrow \infty $.
For the case of independent censoring, we can still use the above framework for conditional independent censoring, and we only need to change the $ B_{ni} (z) $ in Eq (2.5) as $ B_{ni} (z) = 1/n $, for all $ i $. In this case, $ \widehat{S}_T(t |Z = z) = \widehat{S}_T(t) $ exactly reduces to the Kaplan-Meier estimator, and the $ \tau $-quantile estimator by Eq (2.4) is equivalent to $ \widehat{Q}_{\mathrm{KM}} (\tau) = \inf \{ y: \widehat{F}_{\mathrm{KM}} (y) \geq \tau\} $, where $ \widehat{F}_{\mathrm{KM}} $ equals to 1 minus the Kaplan-Meier estimator.
2.2. Computational algorithm
Since $ H(\cdot) $ is a known and strictly monotonic function, in practical computation, people commonly assume $ H $ is from the class of Box-Cox transformation functions with a parameter $ \lambda $ as follows
or other class of transformation functions such as logarithmic transformation function (Cheng et al. [3]). If there is no specific claim in the sequel, we assume $ H_{\lambda} = G_{\lambda}^{-1} $ is from the Box-Cox transformations class in default.
Let $ X_{\beta, \lambda} = G_{\lambda}(\beta^T Z) $, then, correspondingly, Eq (2.2) can be rewritten as
where $ Q_{X_{\beta, \lambda}} (\tau) = \inf \{ y: F_{X_{\beta, \lambda}} (y) \geq \tau\} $ and $ F_{X_{\beta, \lambda}} (t) = { \rm{Pr}} \{ G_{\lambda}(\beta^T Z) \leq t \} $. Let $ U(\cdot) $ be the probability distribution function of the random variable $ F_T (X_{\beta, \lambda}) $. If $ T $ and $ X_{\beta, \lambda} $ have the same distribution, $ F_T (X_{\beta, \lambda}) $ is a random variable uniformly distributed on the interval $ [0, 1] $, hence $ U(x) = x $, for $ x \in [0, 1] $. We define a measurement for the goodness of match as
It is obvious that $ \rho \in [0, 1] $, and $ \rho = 1 $ if and only if the matching is perfect in the sense that $ T $ and $ X_{\beta, \lambda} $ have exactly the same distribution. When the difference between $ dU(x) $ and 1 increases, $ \rho $ decreases. Hence the larger the difference between the distributions of $ T $ and $ X_{\beta, \lambda} $, the smaller the value of $ \rho $.
Let $ \widehat{F}_{T}(t) = n^{-1} \sum_{i = 1}^{n} I \left(T_i \leq t \right) $ if there is no censoring, otherwise $ \widehat{F}_{T}(t) = \widehat{F}_{\mathrm{KM}} (t) $, where $ \widehat{F}_{\mathrm{KM}}(t) = 1 - \widehat{S}_{\mathrm{KM}} (t) $ and $ \widehat{S}_{\mathrm{KM}} $ is the Kaplan-Meier estimator. Denote $ V_i = \widehat{F}_{T} (X_{\widehat{\beta}, \widehat{\lambda}}) $, and define
where $ D_s = n^{-1} \sum_{i = 1}^{n} I \left\{ (s-1)k/n < V_i \leq sk/n \right\} $, and $ \lfloor n/k \rfloor $ represents the largest integer smaller than or equal to $ n/k $.
Considering that $ \widehat{\rho} $ can be used to measure the goodness of match between the distribution of $ X_{\widehat{\beta}, \widehat{\lambda}} $ and that of $ T $, we shall use $ \widehat{\rho} $ as a criterion to choose the optimal value of $ \lambda $ for the transformation link functions in the sequel. We present the details of the proposed algorithm are as follows.
Step 1. Given $ \lambda^{(1)} = 0 $, we update $ \beta $ by
using the coordinate descent algorithm.
Step 2. Calculate the value of goodness measurement of match, $ \widehat{\rho}^{(1)} $, based on $ \lambda^{(1)} $ and the obtained $ \widehat{\beta}^{(1)} $.
Step 3. Repeat Step 1 and Step 2 rest on the $ \lambda $ grid-searched in $ [0, L] $ with 0.1 as footstep, where $ L $ is a positive constant. At the same time, record all the values of $ \{ (\lambda^{(m)}, \widehat{\beta}^{(m)}, \widehat{\rho}^{(m)}): m = 1, \ldots, \sharp\} $, where $ \sharp $ stands for the number of the grid points of $ \lambda $ in $ [0, L] $.
Step 4. Finally, take $ (\lambda^{(m)}, \widehat{\beta}^{(m)}) $ with $ m $ corresponding to the maximum $ \widehat{\rho}^{(m)} $ among all as the estimate $ (\widehat{\lambda}, \widehat{\beta}) $.
With the estimators $ (\widehat{\lambda}, \widehat{\beta}) $, we then estimate the survival probability of $ T $ using
The computation in Step 1 involves bandwidth selection, which is critical for the local Kaplan-Meier estimator. In our numerical study, we use the leave-$ q $-out cross-validation method on quantiles to choose $ h_n $. Specifically, we take $ K_n -q $ quantiles as the training set and the remaining $ q $ quantiles as the validation set (denoted as $ \mathcal{V}_{-q} $). Given $ \lambda $, we minimize Eq (2.7) using the $ K_n -q $ training quantiles, and then use the resulting coefficients $ \widehat{\beta}_{ \mbox{Training}} $ to predict the matching error at the validation quantiles by calculating the loss,
Repeat the above procedure and calculate the averaged prediction error until all the quantiles are scanned through. The bandwidth $ h_n $ that yields the smallest averaged prediction error is selected. We set $ q = 1 $ for the sequel numerical examples.
2.3. Prediction of disease risk
Given the value of covariate $ Z_{new} $ of a new patient and the obtained estimates $ \widehat{\beta} $ and $ \widehat{\lambda} $, we can predict the disease risk of a patient using the proposed method with following procedure:
(ⅰ) Calculate the value of $ \widehat{\beta}^T Z_{new} $ and denote it as $ t_{new} $, calculate the empirical quantile $ \tau_{new} $ of $ t_{new} $ among the values of $ \{\widehat{\beta}^T Z_{i}:\; i = 1, \cdots, n \} $.
(ⅱ) Calculate $ \widehat{S}(t) = \widehat{P} (T > t) = 1 - {n}^{-1} \sum_{i = 1}^n I \left\{ G_{\widehat{\lambda}} (\widehat{\beta}^T Z_i) \leq t \right\}. $
Then, we predict the disease time for the patient by the value of $ \widehat{Q}_T (\tau_{new}) $ and the disease risk by $ \widehat{S}(t_{new}) $. In the sequel, we mainly interested in predicting the disease risk.
3.
Asymptotic properties
In a general setting, suppose we are interested in matching a part of the target distribution, such as the segment between the $ \alpha_{L} $th quantile and the $ \alpha_{U} $th quantile, where $ \alpha_{L} $ and $ \alpha_{U} $ are prefixed and satisfy $ 0 \leq \alpha_{L} < \alpha_{U} < 1 $. Let $ M(\beta) = \int_{\alpha_{L}}^{\alpha_{U}} \big\{ Q_T (\tau) - Q_{X_{\beta}} (\tau) \big\}^2 d\tau $. Define $ \beta_0 = \arg\min_{\beta} M (\beta) $, then $ \beta_0 $ can be regarded as the theoretical true value to be estimated, although $ \beta_0 $ may not be unique. Similar to the theoretical counterpart $ \beta_0 $, the estimator $ \widehat{\beta} $ may not be unique either. We show below that $ M_n(\beta) $ converges to $ M(\beta) $ which is equivalent to show that the distribution of $ X_{\widehat{\beta}} $ provides an optimal approximation to the distribution of $ T $. Denote $ \mathcal{B} = \{ \beta: M(\beta) = M (\beta_0) \} $, where $ \| \cdot \| $ is the Euclidean norm.
Denote $ F_C(t) = P (C \leq t) $ as the cumulative distribution function of censoring time $ C $. Denote $ f_{\xi}(\cdot) $ and $ f'_{\xi}(\cdot) $ as the density function and its first derivative function of a random variable $ \xi $ conditional on $ Z $, respectively, where $ \xi $ could be $ T $, $ C $ or $ Z $. We impose the following regularity conditions.
$ (C1) $ Assume $ \mathcal{B} $ is a compact subsets of $ R^{p+1} $, and $ T $ has a bounded support.
$ (C2) $ The density functions $ f_{T}(\cdot) $, $ f_{C}(\cdot) $, $ f_{X_{\beta}}(\cdot) $, $ f_{T}(\cdot|Z) $ and $ f_{C}(\cdot|Z) $ are uniformly bounded away from 0 and infinity, and $ F_T (t) $ and $ F_C (t) $ have uniformly bounded second-order partial derivatives with respect to $ Z $.
$ (C3) $ For any fixed $ \beta $, it holds that
$ (C4) $ The kernel function $ K(\cdot) \geq 0 $ has a compact support, $ K(\cdot) $ is Lipschitz continuous of order 1 and satisfies $ \int K(u) du = 1 $, $ \int u K(u) du = 0 $, $ \int K^2(u) du < \infty $, and $ \int |u|^2 K(u) du < \infty $.
$ (C5) $ The bandwidth satisfies $ h_n = O(n^{-v}) $, where $ 0 < v < 1/p $.
$ (C6) G $ is a thrice continuously differentiable and strictly increasing function.
The first part of condition (C1) imposes a regular assumption on the true parameter space. Considering that the follow-up study is typically restricted to some limited time, the second part of condition (C1) which assumes $ T $ has a bounded support is also reasonable. Condition (C2) is necessary for the Kaplan-Meier estimator, and it shall be used to derive the consistency of the proposed estimators. Condition (C3) is the Kiefer condition [22] that ensures the uniform Bahadur–Kiefer bounds for empirical quantile processes with independent and identically distributed samples. Conditions (C4) and (C5) are regular assumptions for kernel-based smoothing estimators in terms of the bandwidth and the kernel function. Condition (C6) is satisfied by $ G(x) = (\lambda x + 1)^{1/\lambda} - 1 $ with $ \lambda > 0 $, which corresponds to $ H(x) $ being the Box-Cox transformation function. Under the conditions above, we have the following two theorems.
Theorem 1. Under conditions (C1)–(C6), $ M_n(\widehat{\beta}) \rightarrow M (\beta_0) $ in probability, and $ d(\widehat{\beta}, \mathcal{B}) \rightarrow 0 $ in probability.
The consistency shown in Theorem 1 indicates that the distribution of $ G(\widehat{\beta}^T Z) $ shall provides an optimal approximation to the distribution of $ T $ when the sample size is sufficiently large, although both of them may not converge exactly to the true distribution $ F_T $. Proof of Theorem 1 is sketched in the Supplementary.
4.
Simulation study
To illustrate the finite sample performance of the proposed methods, we conduct the following two simulation studies.
Example 1. Consider a normal error transformation model
where $ H_{\lambda}(\cdot) $ is a Box-Cox transformation function with parameter $ \lambda = 0, 0.5 $ or $ 1 $, $ Z_i = (Z_{i1}, Z_{i2})^T $, $ \beta = (\sqrt{2}, 1)^T $, $ Z_{i1} $ and $ Z_{i2} $ are independent and follow the normal distribution with mean 5 and standard deviation 1, and $ \epsilon_i $ independently follows the standard normal distribution. The right censoring time $ C_i $ is generated independently from uniform distributions to yield the censoring rates of 20 and 40%, correspondingly.
Example 2. We compare the proposed method with a regression method using Cox proportional hazard model under the samples generated from three different models:
where $ H_{\lambda}(\cdot) $ is a logarithmic transformation function,
$ \Lambda_0(t) = t $, $ Z_i = (Z_{i1}, Z_{i2})^T $, $ \beta = (\sqrt{2}, 1)^T $, $ Z_{i1} $, $ Z_{i2} $ and $ \epsilon_i $ are independent and follow the standard normal distribution. The right censoring time $ C_i $ is generated independently from exponential distributions to yield the censoring rates of 20 and 40%, correspondingly. Specifically, Model Ⅰ corresponds to the log-normal AFT model, Model Ⅱ with $ \lambda = 0 $ corresponds to the Cox's proportional hazards model, and Model Ⅲ corresponds to the proportional odds model.
Example 3. Consider the same model and parameter settings as in Example 1 except that the censoring time $ C_i $ is generated independently from exponential distributions to yield the censoring rates of 20 and 40%, respectively. Besides, we let the values of $ Z_i $s be missing completely at random with a missing rates of 20 and 40%, respectively, thus the simulated observations in Example 3 are unpaired.
Example 4. To assess the robustness of the proposed method, we compare the proposed method with three alternative methods in this example. For convenience, we consider a same model $ \log(T_i) = \beta^T Z_i + \epsilon_i $, $ i = 1, \cdots, n $, used in Example 2. Consider two scenarios with $ \epsilon_i \sim N(0, 1) $ and $ \epsilon_i \sim t(3) $, respectively. We compare the proposed method with the PRE method, rank-based estimation (AFT.rank) [23], and the regular least squares estimation of AFT for censored data [24]. The last one is a non-robust method, so we choose it as a benchmark. To evaluate the accuracy of prediction of the proposed method, we independently generate $ 20\% n $ testing samples from the model, and then predict the potential risk at each testing observation using the well established predictor using training data.
In the simulation, we choose a quadratic (biweight) kernel function, $ K(x) = 15/16 (1-x^2)^2 I(|x| \leq 1) $, for the MCQ method. Other kernel functions, such as the Epanechnikov kernel, can also be used, while our experience shows that the numerical results by different kernel functions have little difference. We adopt a product kernel for the multivariate scenario. For example, we use $ K(x_1, x_2) = K (x_1) K (x_2) $ for bivariate cases, where $ K(\cdot) $ is a univariate quadratic kernel function. We set $ \alpha_L = 0 $ and $ \alpha_U = 0.90 $. We take $ L = 2 $ for searching the optimal transformation function. The simulation results are based on 1000 replications with sample sizes of 200,400 and 800.
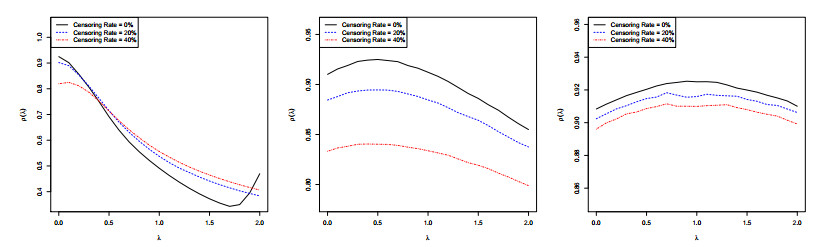
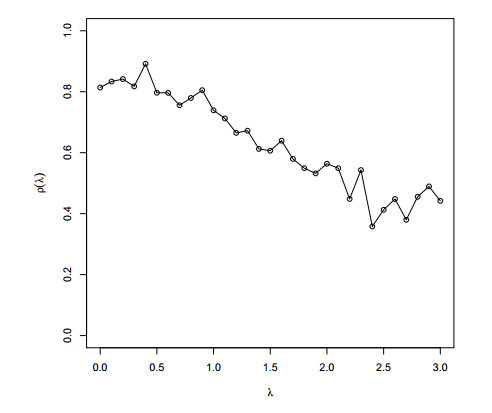
Table 1 presents the simulation results of Example 1, from which we can observe that the proposed MCQ method performs well overall on assessing the target distribution in terms of the estimated values at the prefixed $ \tau $-quantiles. Although the bias of the estimated survival rates tends to be increasing as the censoring rate increases under small sample sizes, the estimation accuracy is improved significantly as the sample size increases. On the other hand, from the estimated values of $ \lambda $, the method used for searching the parameter $ \lambda $ in the function $ G $ based on the criterion $ \hat{\rho} $ also works considerably well. Figure 1 shows the curves of the estimated $ \rho $ along with $ \lambda $ with the true values of $ \lambda $ equal to 0, 0.5 and 1.0, respectively. The plots show the clear modes of the maximum points around the true values.
In Example 2, we compare the proposed method with the other two methods of estimating survival rates under three models. The results are summarized in Table 2. To be specific, 'Pro' is the prediction by the proposed matching censored quantiles method; 'Cox' stands of the survival predictor based on the maximum partial likelihood estimation method for proportional hazards model; 'K-M' is survival prediction using the Kaplan-Meier estimator. The K-M values can be regarded as the benchmark estimator, which are considerably accurate under all the scenarios. Naturally, the Cox method performs well under the true model while show underperforms with misspecified models. Compared to the Cox method, the proposed method performs relatively stable. In Example 3, we demonstrate that the proposed method can handle the unpaired observations caused by missing data. The simulation results in Table 3 show that MCQ performs well in assessing the values of $ F_T $ at the 0.25-quantile, 0.50-quantile and 0.75-quantile, which demonstrates their special advantages in dealing with unpaired observations over the traditional methods.
In Example 4, we compare the robustness and efficiency of the proposed method with three alternative approaches in terms of estimation and prediction. The simulation results are summarized in Table 4. From the estimation results, we see that the proposed method and the AFT.rank method perform almost equally well in terms of robustness and better than the other two methods under the heavy-tail scenario of $ t(3) $ model errors. Khan's method provides larger bias estimation than the proposed method, which shows that the proposed method could gain more flexibility by allowing certain mismatch of orders at some quantiles and hence can improve both the estimation and prediction of the disease risk. Moreover, we also see that the proposed method has a clear advantage in efficiency compared to the traditional robust method based on rank estimation. From the prediction results in Table 4, we know the prediction accuracy of proposed method is better than that of Khan's method.
5.
Application
We apply the proposed methods to analyze Veterans' administration lung cancer data collected from the patients with advanced inoperable lung cancer [25]. This data set consists of 137 patients who were randomized to either a standard or test chemotherapy, among them 128 were followed to death. In this study, one primary endpoint for the therapy comparison is the time to death. In addition to the treatment indicator, several covariates are included, such as the Karnofsky performance score (Karnofsky), the time in months from the diagnosis to randomization (diagtime), the prior therapy (yes or no), and the patient's age in years and the lung cancer cell type (squamous cell = 1, small cell = 2, adenocarcinoma cell = 3, large cell = 4). According to existing literature, all the above covariates are important factors affecting the survival time.
The goal is to estimate $ \beta $ and $ \lambda $ such that the distribution of $ G_{\lambda} (\beta^T Z) $ matches the distribution of $ T $, i.e., the survival time in days. The covariate $ Z_i = (1, Z_{i1}, \ldots, Z_{i8})^T $ are defined as follows: $ Z_{i1} = \mbox{age}/100 $, $ Z_{i2} = \mbox{Karnofsky}/10 $, $ Z_{i3} = \mbox{diagtime}/100 $, and $ Z_{i4} = 0 $ if no prior therapy and $ 1 $ otherwise; $ Z_{ij} = 1 $, $ j = 5, 6, 7 $, if the cell type is squamous, small or large, respectively, and $ 0 $ otherwise; $ Z_{i8} = 1 $ if the patient is given the test chemotherapy treatment, otherwise $ Z_{i8} = 0 $. To apply the proposed methods, we set $ \alpha_L = 0 $ and $ \alpha_U = \widehat{F}_{\mathrm{KM}} (1000) = 0.985 $ for the MCQ method. Considering the fact that the estimated coefficients by the proposed method may not be unique, we compare the estimated survival curve by the proposed methods with that by the Kaplan-Meier estimator and the Cox proportional hazards model. To be specific, we calculate $ \widehat{S}_{ \widehat{\beta}} (t) = 1 - n^{-1} \sum_{i = 1}^n I \{G_{\widehat{\lambda}}(\widehat{ \beta}^T Z_i) \leq t \} $ using the estimated regression coefficients $ \widehat{\beta} $. Then, we use $ \widehat{ S}_{ \widehat{\beta}} $ to assess or approximate the survival probability of $ T $. For the Cox proportional hazards model, we use $ \bar{S} (t|Z) = n^{-1} \sum_{i = 1}^n \exp \{ - \widehat{\Lambda}_0 (t) \exp(\widehat{\beta}_{\mathrm{Cox}}^T Z_i) \} $ to estimate the survival function of $ T $, where $ \widehat{\Lambda}_0 $ is the estimated baseline cumulative hazard function, and $ \widehat{\beta}_{\mathrm{Cox}} $ is the estimated regression coefficient.
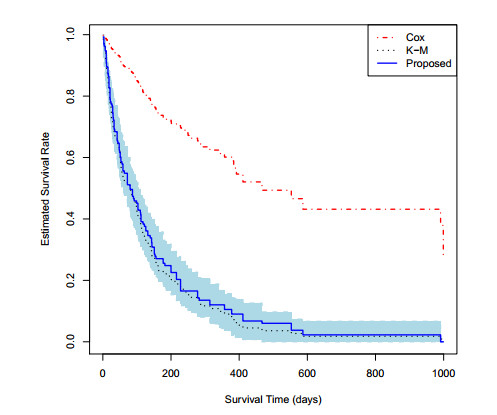
The estimated value of $ \lambda $ for the transformation function $ G_{\lambda} $ is $ 0.4 $ which corresponds to the value of $ \rho = 0.892 $. The estimated values of $ \rho $ indicate that the proposed method performs considerably well in matching $ \widehat{F}_{\mathrm{KM}} $. Table 5 presents the estimated survival rates of the survival time with 95% confidence intervals (CI), and Figure 3 displays the estimated survival curves of $ T $ by MCQ with 95% pointwise confidence bands (CB). Here, both the 95% CIs and the 95% CBs are constructed by the 0.025 and 0.975 quantiles of the estimated survival rates through the bootstrap method with 1000 bootstrap samples. Overall, the estimated survival curves by MCQ and KM are considerably close to each other, except for minor differences at the tail. Compared with the survival curve by the Cox proportional hazards model, the MCQ curve is much closer to the Kaplan-Meier curve, which indicates that the estimated survival probability by the proposed methods might be more accurate than that by the Cox proportional hazards model.
Remark 2. Here we assume, without any proof, that the proposed estimator converges to an asymptotic distribution, hence we could use the bootstrap method under this assumption. In other words, the bootstrap method used here is not rigorous from the theoretical point of view.
6.
Discussions
In this paper, we propose a matching censored quantiles estimator to study the relationship between the observed event times and the covariates in the presence of right censoring. The proposed method provides a new option to predict the disease risks for survival events of interest.
Under the MCQ framework, we adopt a locally weighted approach to estimate the censored quantiles. Other options such as the inverse probability weighting or the Buckley-James method [1] can also be considered. Yet, it still lacks efficient approaches for statistical inference and hypothesis testing on the obtained estimators which warrant further research. Last but not least, new algorithms are also needed to combine the proposed methods with sparse model selection using penalty functions.
Acknowledgments
This research was supported by the Fundamental Research Funds for the Central Universities, Beijing Natural Science Foundation (No. 1204031), and the National Natural Science Foundation of China (No. 11901013).
Conflict of Interests
All authors declare no conflicts of interest in this paper.
Appendix
Lemma 1. Under conditions (C2), (C4) and (C5), we have
where $ 0 < l_0 < 1/4 $.
Proof. Lemma 1 follows from the result of Theorem 2.1 of [26] and Lemma A.1 of [27].
Lemma 2. If $ M_{n}(\widehat{\beta}_n) \rightarrow M (\beta_0) $ in probability, where the estimator $ \widehat{\beta}_n $ is defined by minimizing $ M_{n}(\beta) $, then $ d(\widehat{\beta}_n, \mathcal{B}) \rightarrow 0 $ in probability as $ n \rightarrow \infty $.
Proof. To prove this lemma is equivalent to prove that $ { \rm{Pr}} \{ d(\widehat{\beta}_n, \mathcal{B}) \geq \epsilon \} \rightarrow 0 $ for any constant $ \epsilon > 0 $. Suppose there exists an $ \epsilon > 0 $ such that $ {\lim\sup}_{n \rightarrow \infty} { \rm{Pr}} \{ d(\widehat{\beta}_n, \mathcal{B}) \geq \epsilon \} > 0 $, then there exists a subsequence of $ \{ \widehat{\beta}_n\} $, denoted by $ \{ \widehat{\beta}_{n_k}\} $, such that $ \lim_k { \rm{Pr}} \{ d(\widehat{\beta}_{n_k}, \mathcal{B}) \geq \epsilon \} = \eta > 0 $. Define $ \mathcal{B}_{\epsilon} = \{ \beta: d(\beta, \mathcal{B}) \geq \epsilon \} $, hence $ \mathcal{B}_{\epsilon} $ is a compact set. Because $ \mathcal{B} = \{ \beta: M(\beta) = M (\beta_0) \} $, then $ \inf_{\beta \in \mathcal{B}_{\epsilon}} M(\beta) = \eta + M(\beta_0) $. Hence, it holds
Hence, we have
This contradicts to the assumption that $ M_{n}(\widehat{\beta}_n) \rightarrow M (\beta_0) $ in probability. This completes the proof of Lemma 2.
Proof of Theorem 1. By the definition of $ M_n(\beta) $, we have
where $ C_1 > 0 $ and $ C_2 > 0 $ are some constants. According to the definition of the Riemann integral, the last term on the right-hand side of the above equation tends to 0 as $ K_n \rightarrow \infty $ and $ \max \{ \delta_{k} \} \rightarrow 0 $ for any finite $ \beta $. We only need to consider the rear terms.
Firstly, because $ \sum_{k = 1}^{K_n} \delta_{k} \big\{ \widehat{Q}_T(\tau_k) - Q_T(\tau_k) \big\}^2 I(\alpha_L \leq \tau_k \leq \alpha_U) = \int_{\alpha_{L}}^{\alpha_{U}} \big\{ \widehat{Q}_T(t) - Q_T(t) \big\}^2 dt + o(1) $, and
where the last equation is by the mean value theorem, $ d Q_T (t) /dt $ is the first derivative of $ Q_T(t) $, and $ t^* $ is a point between $ F_T \{\widehat{Q}_T(t)\} $ and $ t $. By conditions (C1)–(C3), we know $ |d Q_T(t^*)/dt| $ can be bounded by a positive constant. According to Lemma 1, the proof of Theorem 1 in [10] and the dominated convergence theorem, we have $ \sum_{k = 1}^{K_n} \delta_{k} \{ \widehat{Q}_T(\tau_k) - Q_T(\tau_k) \}^2 I(\alpha_L \leq \tau_k \leq \alpha_U) = o_P(1) $. Using the same argument, we can also conclude that $ \sum_{k = 1}^{K_n} \delta_{k} | \widehat{Q}_T(\tau_k) - Q_T(\tau_k) | I(\alpha_L \leq \tau_k \leq \alpha_U) = o_P(1) $. Second, note that the condition (C3) entails that $ X_{\beta} $ has a bounded support for any $ \beta $, even in the extreme case with $ \alpha_{L} = 0 $ and $ \alpha_{U} $ close to 1. Using the same argument above and the Glivenko-Cantelli theorem, for any fixed $ \beta $ we can also obtain $ \sum_{k = 1}^{K_n} \delta_{k} \big\{ \widehat{Q}_{X_{\beta}}(\tau_k) - Q_{X_{\beta}}(\tau_k) \big\}^2 I(\alpha_L \leq \tau_k \leq \alpha_U) = o_P(1) $ and $ \sum_{k = 1}^{K_n} \delta_{k} | \widehat{Q}_{X_{\beta}}(\tau_k) - Q_{X_{\beta}}(\tau_k) | I(\alpha_L \leq \tau_k \leq \alpha_U) = o_P(1) $. Hence, $ | M_n (\beta) - M (\beta) | \rightarrow 0 $ in probability as $ n \rightarrow \infty $ for any fixed and finite $ \beta $.
By conditions (C1) and (C2), the matching censored quantiles estimator defined by Eq (2.2) is finite in $ {R}^{p+1} $, hence there exists a compact neighborhood $ \mathcal{B} \subset {R}^{p+1} $ such that $ \widehat{\beta} \in \mathcal{B} $. Next, we show $ \sup_{\beta \in \mathcal{B}} | M_{n} (\beta) - M (\beta) | \rightarrow 0 $ in probability. Because $ M(\beta) $ is a continuous function with respect to $ \beta $. According to the Heine–Borel theorem, for any $ \epsilon > 0 $, there exist finite elements $ \beta_1, \ldots, \beta_m \in \mathcal{B} $, $ m $ is a finite integer, such that $ \| \beta - \beta_j \| < C \epsilon $ and $ | M(\beta) - M(\beta_j) | < \epsilon $, where $ C $ is a constant, $ j = 1, \ldots, m $. By conditions (C2), (C3) and the Glivenko-Cantelli theorem, we have
Hence, $ \sup_{\beta \in \mathcal{B}} | M_{n} (\beta) - M (\beta) | \; \leq\; O(\epsilon) + \sum_{j = 1}^m | M_{n} (\beta_j) - M (\beta_j) | $, by the arbitrariness of $ \epsilon $, we conclude that $ \sup_{\beta \in \mathcal{B}} | M_{n} (\beta) - M (\beta) | \rightarrow 0 $ in probability for a compact neighborhood $ \mathcal{B} \subset {R}^{p+1} $. Finally, by the inequation
and the fact that $ |M_n (\beta_0) - M (\beta_0)| \rightarrow 0 $ and $ |M_n (\widehat{\beta}) - M (\widehat{\beta})| \rightarrow 0 $ in probability, it holds that $ |M_n (\widehat{\beta}) - M (\beta_0)| \rightarrow 0 $ in probability. Using the same argument in the proof of Lemma 2, the second part of Theorem 1 is proved.









 DownLoad:
DownLoad: