1.
Introduction
Rough set [26,27] is one of a nonstatistical technique to deal with the problems of uncertainty in data and incompleteness of knowledge. The rationale of this set is depended on that the human knowledge is categorized into three fundamental regions, inside, outside and boundary. Therefore, the essential idea of this set focuses on the lower and upper approximations which are used to define the boundary region and accuracy measure. In the classical rough set model approximations are based on the equivalence relations, but this condition does not always hold in many practical problems and also this restriction limits the wide applications of this set. In the recent times, lots of researchers are interested to generalize this set in many fields of applications [9,15,16,23]. It was also generalized by the topological point of view [20,21,29,31] by replacing the equivalence relations in the lower and upper approximations by the open and closed sets, respectively. In the past few years mathematicians turned their attention towards to near (or nearly) open concept as generalization of open sets to topological spaces [1,19,24,25,30]. In this direction, numerous generalizations of the rough set were offered using the nearly open concepts instead of open sets [4,5,6,32]. In 2017, Amer et al. [8] utilized the $ J $-nearly open concepts and introduced the notions of $ J $-nearly approximations. After that, Hosny [11] improved Amer et al.'s approximations [8] by proposing the notions of the $ {\delta\beta}_J $-open sets and $ {\bigwedge_{\beta}}_J $-sets which were used to define the $ \delta\beta_{J} $-approximations and $ {\bigwedge_{\beta}}_{J} $-approximations.
An ideal is a nonempty collection of sets which is closed under hereditary property and the finite additivity [18,33]. In view of the recent applications of ideals in the rough set theory, it seems very natural to extend the interesting concept of rough set further by using ideals. As, the notions of ideals are pivotal tool helping in removing imprecision and ambiguous of a concept by minimizing the vagueness of uncertainty regions at their borders by increasing the lower approximations and decreasing the upper approximations which automatically implies to increase the accuracy measure of the uncertainty regions [7,13,14]. Recently, Hosny [12] presented the concepts of $ J $-nearly open sets and $ J $-nearly approximations with respect to ideals. She proved that these new sort of $ J $-nearly open sets were generalized the preceding ones [8,11]. Moreover, Hosny's approximations [12] were improvement of Abd El-Monsef et al.'s approximations [2] and Amer et al.'s approximations [8]. Furthermore, the $ J $-nearly rough membership relations and functions with respect to ideals were introduced in [12] as generalization of the other types [3,22,28].
This work indicates that the rough set has a purely topological nature and emphasizes the importance of using ideal in the study of this set because it demystifies the concept. So, a more general notion of a topological rough set via ideal is suggested. In this paper, Section 2 covers some fundamental principles of concepts which are needed in the current work. Meantime, Sections 3 and 5 introduce and study new $ J $-near open sets with respect to ideals namely, $ {\mathcal{I}} $-$ {\delta\beta}_J $-open sets and $ {\mathcal{I}} $-$ {\bigwedge_{\beta}}_J $-sets. The basic properties, characterizations and the relationships among of these definitions are derived. These definitions are more general than the previous ones [8,11,12]. It should be noted that the generalization of $ \mathcal{I} $-$ {\beta}_{J} $-open sets [12] by using the $ \mathcal{I} $-$ \bigwedge_{\beta} $-sets is very different from the generalization of the $ \mathcal{I} $-$ {\beta}_{J} $-open sets by using the $ \mathcal{I} $-$ {\delta\beta}_{J} $-open sets. The main difference is that the family of all $ \mathcal{I} $-$ {\delta\beta}_{J} $-open sets does not form a topology, as the intersection of two $ \mathcal{I} $-$ {\delta\beta}_{J} $-open sets does not need to be an $ \mathcal{I} $-$ {\delta\beta}_{J} $-open set as shown in Example 3.1. While, the family of all $ \mathcal{I} $-$ \bigwedge_{\beta} $-sets forms a topology as it is shown in Lemma 5.2. Moreover, it is shown that the concepts of $ \mathcal{I} $-$ {\delta\beta}_{J} $-open sets and $ \mathcal{I} $-$ \bigwedge_{\beta} $-sets are independent (see Remark 5.5). Furthermore, if $ {\mathcal{I}} = \{\phi\} $, then the current definitions are coincided with Hosny's definitions [11]. So, Hosny's definitions [11] are special case of the current definitions. The main object of Sections 4 and 6 is to propose two different and independent of new approximations. These approximations are based on $ \mathcal{I} $-$ {\delta\beta}_{J} $-open sets and $ \mathcal{I} $-$ \bigwedge_{\beta} $-sets. The properties of the present approximations and the connections among them are established and constructed in these sections. They are compared to the prior ones [2,8,11,12] and shown that the accuracy measure which deduced by the current approximations is the best. The goal of Section 7 is to define new kind of the rough membership functions via ideal namely, $ \mathcal{I} $-$ {\delta\beta}_{J} $-rough membership functions and $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J} $-rough membership functions. It is proved that these functions are better than the previous ones such as Abd El-Monsef et al. [3], Hosny [12], Lin [22], Pawlak and Skowron [28] (see Lemmas 7.2, 7.3 and Remark 7.8). Section 8 demonstrates the importance of this paper by some real life applications. Finally, Section 9 aims to outline the essential findings and a plan for the future work.
2.
Preliminaries
Definition 2.1. [17] Let $ X $ be a non-empty set. $ \mathcal{I}\neq\phi, $ $ \mathcal{I}\in P(X) $ is an ideal on $ X, $ if
(i) $ A\in \mathcal{I} $ and $ B\in\mathcal{I}\Rightarrow A\cup B\in\mathcal{I}. $
(ii) $ A\in \mathcal{I} $ and $ B\subseteq A \Rightarrow B\in \mathcal{I}. $
Definition 2.2. [2] Let $ X $ be a non-empty finite set and $ \mathcal{R} $ be an arbitrary binary relation on $ X $. The $ J $-neighborhood of $ x \in X $ ($ J $-nd) $ (n_J (x)), J \in \{R, L, < R > , < L > , I, U, < I > , < U > \} $ defined as:
(i) $ R $-nd: $ n_R(x) = \{y\in X : x\mathcal{R} y\}. $
(ii) $ L $-nd: $ n_L(x) = \{y\in X : y\mathcal{R} x\}. $
(iii) $ < R > $-nd: $ n_{ < R > }(x) = \cap _{x\in n_R (y) }n_R(y). $
(iv) $ < L > $-nd: $ n_{ < L > }(x) = \cap _{x\in n_L (y) }n_L(y). $
(v) $ I $-nd: $ n_I (x) = n_R (x) \cap n_L (x). $
(vi) $ U $-nd: $ n_U (x) = n_R (x)\cup n_L (x). $
(vii) $ < I > $-nd: $ n_{ < I > }(x) = n_{ < R > }(x)\cap n_{ < I > }(x). $
(viii) $ < U > $-nd: $ n_{ < U > }(x) = n_{ < R > }(x) \cup n_{ < I > }(x). $
From the following concepts and throughout this paper $ J \in \{R, L, < R > , < L > , I, U, < I > , < U > \}. $
Definition 2.3. [2] Let $ X $ be a non-empty finite set, $ \mathcal{R} $ be an arbitrary binary relation on $ X $ and $ \Xi_J : X\rightarrow P(X) $ assigns each $ x $ in $ X $ its $ J $-nd in $ P(X) $. $ (X, \mathcal{R}, \Xi_J) $ is a $ J $-neighborhood space ($ J $-ndS).
Theorem 2.1. [2] Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS and $ A \subseteq X. $ Then, $ \tau_J = \{A \subseteq X:\forall a\in A, n_J (a) \subseteq A\} $ is a topology on $ X. $ The elements of $ \tau_{J} $ are called $ J $-open set and the complement of $ J $-open set is $ J $-closed set. The family $ \Gamma_{J} $ of all $ J $-closed sets defined by $ \Gamma_{J} = \{F \subseteq X:F^{'}\in \tau_{J}\}, F^{'} $ is the complement of $ F. $
Definition 2.4. [2] Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS and $ A \subseteq X $. The $ J $-lower, $ J $-upper approximations, $ J $-boundary regions and $ J $-accuracy of $ A $ are defined respectively by:
$ \underline{\mathcal{R}}_J(A) $ is the union of all $ J $-open sets which are subset of $ A = int_J (A) $, where $ int_J (A) $ represents $ J $-interior of $ A $.
$ \overline{\mathcal{R}}_J(A) $ is the intersection of all $ J $-closed sets which are superset of $ A = cl_J(A) $, where $ cl_J (A) $ represents $ J $-closure of $ A $.
$ {\mathcal{BND}}_J(A) = \overline{\mathcal{R}}_J(A)-\underline{\mathcal{R}}_J(A). $
$ {ACC}_J(A) = \frac{|\underline{\mathcal{R}}_J(A)|}{|\overline{\mathcal{R}}_J(A)|}, $ where $ |\overline{\mathcal{R}}_J(A)|\neq0. $
Definition 2.5. [2] Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS. $ A \subseteq X $ is $ {J} $-exact if $ {\overline{\mathcal{R}}}_{J}(A) = {\underline{\mathcal{R}}}_{J}(A). $ Otherwise, $ A $ is $ {J} $-rough.
Definition 2.6. [8] Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS. $ A \subseteq X $ is
(i) $ J $-preopen ($ P_J $-open), if $ int_J(cl_J(A)) \supseteq A. $
(ii) $ J $-semiopen ($ S_J $-open), if $ cl_J (int_J(A))\supseteq A. $
(iii) $ \alpha_J $-open, if $ A \subseteq int_J[cl_J(int_J(A))]. $
(iv) $ \beta_J $-open (semi preopen), if $ A \subseteq cl_J[int_J(cl_J(A))]. $
These sets are called $ J $-nearly open sets, the families of $ J $-nearly open sets of $ X $ denoted by $ \eta_{J}O(X) $, the complements of the $ J $-nearly open setsare called $ J $-nearly closed sets and the families of $ J $-nearly closed sets of $ X $ denoted by $ \eta_{J}C(X) $, $ \forall \eta \in \{ P, S, \alpha, \beta\}. $
Remark 2.1. [8] The implications between $ \tau_J, \Gamma_J, \eta_{J}O(X) $ and $ \eta_{J}C(X) $ are in Figure 1.
From the following concepts and throughout this paper $ \eta \in \{P, S, \alpha, \beta\}. $
Definition 2.7. [8] Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS and $ A \subseteq X. $ The $ J $-nearly lower, $ J $-nearly upper approximations, $ J $-nearly boundary regions and $ J $-nearly accuracy of $ A $ are defined respectively by:
$ \underline{\mathcal{R}}^{\eta}_J(A) $ is the union of all $ J $-nearly open sets which are subset of $ A = J $-nearly interior of $ A $.
$ \overline{\mathcal{R}}^{\eta}_J(A) $ is the intersection of all $ J $-nearly closed sets which are superset of $ A = J $-nearly closure of $ A $.
$ {\mathcal{BND}}^{\eta}_J(A) = \overline{\mathcal{R}}^{\eta}_J(A)-\underline{\mathcal{R}}^{\eta}_J(A). $
$ {ACC}^{\eta}_J(A) = \frac{|\underline{\mathcal{R}}^{\eta}_J(A)|}{|\overline{\mathcal{R}}^{\eta}_J(A)|}, $ where $ |\overline{\mathcal{R}}^{\eta}_J(A)|\neq0, |\overline{\mathcal{R}}^{\eta}_J(A)| $ denotes to the cardinality of $ \overline{\mathcal{R}}^{\eta}_J(A). $
Definition 2.8. [11] Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS and $ A \subseteq X. $ The $ \delta $-$ J $-closure of $ A $ is defined by $ cl^{\delta}_{J} (A) = \{x \in X :A\cap int_J(cl_J(G))\neq\phi, G \in\tau_J $ and $ x\in G\}. $ A set $ A $ is called $ {\delta}_{J} $-closed if $ A = cl^{\delta}_{J}(A) $. The complement of a $ {\delta}_{J} $-closed set is $ {\delta}_{J} $-open. Notice that $ int^{\delta}_{J}(A) = X-cl^{\delta}_{J} (X-A). $
Definition 2.9. [11] Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS and $ A \subseteq X. $ A subset $ A $ is called $ {\delta\beta}_J $-open, if $ A \subseteq cl_J[int_J(cl^{\delta}_{J}(A))]. $ The complement of a $ {\delta\beta}_J $-open set is a $ {\delta\beta}_J $-closed set. The family of all $ {\delta\beta}_J $-open and $ {\delta\beta}_J $-closed are denoted by $ {\delta\beta}_{J}O(X) $ and $ {\delta\beta}_{J}C(X) $ respectively.
Proposition 2.1. [11] Every $ {\beta}_J $-open is $ {\delta\beta}_J $-open.
Definition 2.10. [11] Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS and $ A \subseteq X $ Then, the $ \delta\beta_{J} $-lower, $ \delta\beta_{J} $-upper approximations, $ \delta\beta_{J} $-boundary and $ \delta\beta_{J} $-accuracy of $ A $ are defined respectively by:
$ {\underline{\mathcal{R}}}^{\delta\beta}_{J}(A) = \cup\{G \in {\delta\beta}_{J}O(X) : G \subseteq A\} = {\delta\beta}_{J} $-interior of $ A $.
$ {\overline{\mathcal{R}}}^{\delta\beta}_{J}(A) = \cap\{H \in {\delta\beta}_{J}C(X) : A \subseteq H\} = {\delta\beta}_{J} $-closure of $ A $.
$ {\mathcal{BND}}^{\delta\beta}_{J}(A) = {\overline{\mathcal{R}}}^{\delta\beta}_{J}(A)-{\underline{\mathcal{R}}}^{\delta\beta}_{J}(A). $
$ {ACC}^{\delta\beta}_{J}(A) = \frac{|{\underline{\mathcal{R}}}^{\delta\beta}_{J}(A)|}{|{\overline{\mathcal{R}}}^{\delta\beta}_{J}(A)|}, $ where $ |{\overline{\mathcal{R}}}^{\delta\beta}_{J}(A)|\neq0. $
Theorem 2.2. [11] Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS and $ A \subseteq X. $ Then
(i) $ {\underline{\mathcal{R}}}^{\alpha}_{J}(A)\subseteq {\underline{\mathcal{R}}}^{p}_{J}(A)\subseteq{\underline{\mathcal{R}}}^{\gamma}_{J}(A)\subseteq{\underline{\mathcal{R}}}^{\beta}_{J}(A)\subseteq {\underline{\mathcal{R}}}^{\delta\beta}_{J}(A). $
(ii) $ {\underline{\mathcal{R}}}^{\alpha}_{J}(A)\subseteq {\underline{\mathcal{R}}}^{s}_{J}(A)\subseteq{\underline{\mathcal{R}}}^{\gamma}_{J}(A)\subseteq{\underline{\mathcal{R}}}^{\beta}_{J}(A)\subseteq {\underline{\mathcal{R}}}^{\delta\beta}_{J}(A). $
(iii) $ {\underline{\mathcal{R}}}_{J}(A)\subseteq {\underline{\mathcal{R}}}^{\delta\beta}_{J}(A). $
(iv) $ {\overline{\mathcal{R}}}^{\delta\beta}_{J}(A)\subseteq {\overline{\mathcal{R}}}^{\beta}_{J}(A)\subseteq {\overline{\mathcal{R}}}^{\gamma}_{J}(A)\subseteq {\overline{\mathcal{R}}}^{p}_{J}(A)\subseteq {\overline{\mathcal{R}}}^{\alpha}_{J}(A). $
(v) $ {\overline{\mathcal{R}}}^{\delta\beta}_{J}(A)\subseteq {\overline{\mathcal{R}}}^{\beta}_{J}(A)\subseteq {\overline{\mathcal{R}}}^{\gamma}_{J}(A)\subseteq {\overline{\mathcal{R}}}^{s}_{J}(A)\subseteq {\overline{\mathcal{R}}}^{\alpha}_{J}(A). $
(vi) $ {\overline{\mathcal{R}}}^{\delta\beta}_{J}(A)\subseteq {\overline{\mathcal{R}}}_{J}(A). $
Corollary 2.1. [11] Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS and $ A \subseteq X. $ Then
(i) $ {\mathcal{BND}}^{\delta\beta}_{J}(A)\subseteq {\mathcal{BND}}^{\beta}_{J}(A)\subseteq {\mathcal{BND}}^{\gamma}_{J}(A)\subseteq {\mathcal{BND}}^{p}_{J}(A)\subseteq {\mathcal{BND}}^{\alpha}_{J}(A). $
(ii) $ {\mathcal{BND}}^{\delta\beta}_{J}(A)\subseteq {\mathcal{BND}}^{\beta}_{J}(A)\subseteq {\mathcal{BND}}^{\gamma}_{J}(A)\subseteq {\mathcal{BND}}^{s}_{J}(A)\subseteq {\mathcal{BND}}^{\alpha}_{J}(A) $.
(iii) $ {\mathcal{BND}}^{\delta\beta}_{J}(A)\subseteq {\mathcal{BND}}_{J}(A). $
(iv) $ {ACC}^{\alpha}_{J}(A)\leqslant {ACC}^{p}_{J}(A)\leqslant {ACC}^{\gamma}_{J}(A)\leqslant {ACC}^{\beta}_{J}(A)\leqslant {ACC}^{\delta\beta}_{J}(A). $
(v) $ {ACC}^{\alpha}_{J}(A)\leqslant {ACC}^{s}_{J}(A)\leqslant {ACC}^{\gamma}_{J}(A)\leqslant {ACC}^{\beta}_{J}(A)\leqslant {ACC}^{\delta\beta}_{J}(A). $
(vi) $ {ACC}_{J}(A)\leqslant {ACC}^{\delta\beta}_{J}(A). $
Definition 2.11. [11] Let $ (X, R, \Xi_J) $ be a $ J $-ndS and $ A \subseteq X. $ A subset $ A $ is called
(i) $ {\delta\beta}_{J} $-definable ($ \delta\beta_{J} $-exact) if $ {\overline{\mathcal{R}}}^{\delta\beta}_{J}(A) = {\underline{\mathcal{R}}}^{\delta\beta}_{J}(A) $ or $ {\mathcal{BND}}^{\delta\beta}_{J}(A) = \phi. $
(ii) $ {\delta\beta}_{J} $-rough if $ {\overline{\mathcal{R}}}^{\delta\beta}_{J}(A)\neq{\underline{\mathcal{R}}}^{\delta\beta}_{J}(A) $ or $ {\mathcal{BND}}^{\delta\beta}_{J}(A)\neq\phi. $
Definition 2.12. [11] Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS and $ A \subseteq X. $ A subset $ {\bigwedge_{\beta}}_{J} $ is defined as follows: $ {\bigwedge_{\beta}}_{J}(A) = \cap\{ G:A\subseteq G, G\in \beta_{J}O(X)\}. $ The complement of $ {\bigwedge_{\beta}}_{J}(A) $-set is called $ {\bigvee_{\beta}}_{J}(A) $-set.
Definition 2.13. [11] Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS and $ A \subseteq X. $ A subset $ A $ is called $ {\bigwedge_{\beta}}_{J} $-set if $ A = {\bigwedge_{\beta}}_{J}(A). $ The family of all $ {\bigwedge_{\beta}}_J $-set and $ {\bigvee_{\beta}}_J $-set are denoted by $ \tau^{{\bigwedge_{\beta}}}_{J} $ and $ \Gamma^{{\bigvee_{\beta}}}_{J} $ respectively.
Proposition 2.2. [11] Every $ {\beta}_J $-open set is $ {\bigwedge_{\beta}}_J $-set.
Definition 2.14. [11] Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS, $ A \subseteq X. $ The $ {\bigwedge_{\beta}}_{J} $-lower, $ {\bigwedge_{\beta}}_{J} $-upper approximations, $ {\bigwedge_{\beta}}_{J} $-boundary and $ {\bigwedge_{\beta}}_{J} $-accuracy of $ A $ are defined respectively by:
$ {\underline{\mathcal{R}}}^{\bigwedge_{\beta}}_{J}(A) = \cup\{G \in \tau^{{\bigwedge_{\beta}}}_{J} : G \subseteq A\} = {\bigwedge_{\beta}}_{J} $-interior of $ A $.
$ {\overline{\mathcal{R}}}^{\bigwedge_{\beta}}_{J}(A) = \cap\{H \in \Gamma^{{\bigvee_{\beta}}}_{J} : A \subseteq H\} = {\bigwedge_{\beta}}_{J} $-closure of $ A $.
$ {\mathcal{BND}}^{\bigwedge_{\beta}}_{J}(A) = {\overline{\mathcal{R}}}^{\bigwedge_{\beta}}_{J}(A)-{\underline{\mathcal{R}}}^{\bigwedge_{\beta}}_{J}(A). $
$ {ACC}^{\bigwedge_{\beta}}_{J}(A) = \frac{|{\underline{\mathcal{R}}}^{\bigwedge_{\beta}}_{J}(A)|}{|{\overline{\mathcal{R}}}^{\bigwedge_{\beta}}_{J}(A)|}, $ where $ |{\overline{\mathcal{R}}}^{\bigwedge_{\beta}}_{J}(A)|\neq0. $
Theorem 2.3. [11] Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS and $ A \subseteq X. $ Then
(i) $ {\underline{\mathcal{R}}}^{\alpha}_{J}(A)\subseteq {\underline{\mathcal{R}}}^{p}_{J}(A)\subseteq{\underline{\mathcal{R}}}^{\gamma}_{J}(A)\subseteq{\underline{\mathcal{R}}}^{\beta}_{J}(A)\subseteq {\underline{\mathcal{R}}}^{\bigwedge_{\beta}}_{J}(A). $
(ii) $ {\underline{\mathcal{R}}}^{\alpha}_{J}(A)\subseteq {\underline{\mathcal{R}}}^{s}_{J}(A)\subseteq{\underline{\mathcal{R}}}^{\gamma}_{J}(A)\subseteq{\underline{\mathcal{R}}}^{\beta}_{J}(A)\subseteq {\underline{\mathcal{R}}}^{\bigwedge_{\beta}}_{J}(A). $
(iii) $ {\underline{\mathcal{R}}}_{J}(A)\subseteq {\underline{\mathcal{R}}}^{\bigwedge_{\beta}}_{J}(A). $
(iv) $ {\overline{\mathcal{R}}}^{\bigwedge_{\beta}}_{J}(A)\subseteq {\overline{\mathcal{R}}}^{\beta}_{J}(A)\subseteq {\overline{\mathcal{R}}}^{\gamma}_{J}(A)\subseteq {\overline{\mathcal{R}}}^{p}_{J}(A)\subseteq {\overline{\mathcal{R}}}^{\alpha}_{J}(A). $
(v) $ {\overline{\mathcal{R}}}^{\bigwedge_{\beta}}_{J}(A)\subseteq {\overline{\mathcal{R}}}^{\beta}_{J}(A)\subseteq {\overline{\mathcal{R}}}^{\gamma}_{J}(A)\subseteq {\overline{\mathcal{R}}}^{s}_{J}(A)\subseteq {\overline{\mathcal{R}}}^{\alpha}_{J}(A). $
(vi) $ {\overline{\mathcal{R}}}^{\bigwedge_{\beta}}_{J}(A)\subseteq {\overline{\mathcal{R}}}_{J}(A). $
Corollary 2.2. [11] Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS and $ A \subseteq X. $ Then
(i) $ {\mathcal{BND}}^{\bigwedge_{\beta}}_{J}(A)\subseteq {\mathcal{BND}}^{\beta}_{J}(A)\subseteq {\mathcal{BND}}^{\gamma}_{J}(A)\subseteq {\mathcal{BND}}^{p}_{J}(A)\subseteq {\mathcal{BND}}^{\alpha}_{J}(A). $
(ii) $ {\mathcal{BND}}^{\bigwedge_{\beta}}_{J}(A)\subseteq {\mathcal{BND}}^{\beta}_{J}(A)\subseteq {\mathcal{BND}}^{\gamma}_{J}(A)\subseteq {\mathcal{BND}}^{s}_{J}(A)\subseteq {\mathcal{BND}}^{\alpha}_{J}(A). $
(iii) $ {\mathcal{BND}}^{\bigwedge_{\beta}}_{J}(A)\subseteq {\mathcal{BND}}_{J}(A). $
(iv) $ {ACC}^{\alpha}_{J}(A)\leqslant {ACC}^{p}_{J}(A)\leqslant {ACC}^{\gamma}_{J}(A)\leqslant {ACC}^{\beta}_{J}(A)\leqslant {ACC}^{\bigwedge_{\beta}}_{J}(A). $
(v) $ {ACC}^{\alpha}_{J}(A)\leqslant {ACC}^{s}_{J}(A)\leqslant{ACC}^{\gamma}_{J}(A)\leqslant {ACC}^{\beta}_{J}(A)\leqslant {ACC}^{\bigwedge_{\beta}}_{J}(A). $
(vi) $ {ACC}_{J}(A)\leqslant {ACC}^{\bigwedge_{\beta}}_{J}(A). $
Definition 2.15. [11] Let $ (X, R, \Xi_J) $ be a $ J $-ndS and $ A \subseteq X. $ A subset $ A $ is called
(i) $ {\bigwedge_{\beta}}_{J} $-definable ($ {\bigwedge_{\beta}}_{J} $-exact) if $ {\overline{\mathcal{R}}}^{\bigwedge_{\beta}}_{J}(A) = {\underline{\mathcal{R}}}^{\bigwedge_{\beta}}_{J}(A) $ or $ {\mathcal{BND}}^{\bigwedge_{\beta}}_{J}(A) = \phi. $
(ii) $ {\bigwedge_{\beta}}_{J} $-rough if $ {\overline{\mathcal{R}}}^{\bigwedge_{\beta}}_{J}(A)\neq{\underline{\mathcal{R}}}^{\bigwedge_{\beta}}_{J}(A) $ or $ {\mathcal{BND}}^{\bigwedge_{\beta}}_{J}(A)\neq\phi. $
Definition 2.16. [12] Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS and $ \mathcal{I} $ be an ideal on $ X $. $ A \subseteq X $ is called
(i) $ {\mathcal{I}} $-$ \alpha_J $-open, if $ \exists\; G\in \tau_J $ such that $ (A - int_J(cl_J((G)) \in\mathcal{I} $ and $ (G - A) \in\mathcal{I}. $
(ii) $ {\mathcal{I}} $-$ {J} $-Preopen (briefly $ {\mathcal{I}} $-$ P_J $-open), if $ \exists\; G\in \tau_J $ such that $ (A - G)\in \mathcal{I} $ and $ (G - cl_J(A)) \in\mathcal{I}. $
(iii) $ {\mathcal{I}} $-$ {J} $-Semi open (briefly $ {\mathcal{I}} $-$ S_J $-open), if $ \exists\; G\in \tau_J $ such that $ (A - cl_J (G))\in\mathcal{I} $ and $ (G- A) \in\mathcal{I}. $
(iv) $ {\mathcal{I}} $-$ \beta_J $-open, if $ \exists\; G\in \tau_J $ such that $ (A - cl_J(G))\in\mathcal{I} $ and $ (G- cl_J(A)) \in\mathcal{I}. $
These sets are called $ \mathcal{I} $-$ J $-nearly open sets, the complement of the $ \mathcal{I} $-$ J $-nearly open sets is called $ \mathcal{I} $-$ J $-nearly closed sets, the families of $ \mathcal{I} $-$ J $-nearly open sets of $ X $ denoted by $ \mathcal{I} $-$ \eta_{J}O(X) $ and the families of $ \mathcal{I} $-$ J $-nearly closed sets of $ X $ denoted by $ \mathcal{I} $-$ \eta_{J}C(X) $, $ \forall \eta \in \{P, S, \alpha, \beta\}. $
Proposition 2.3. [12] Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS and $ \mathcal{I} $ be an ideal on $ X. $ Then, the following implications hold:
Proposition 2.4. [12] Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS and $ \mathcal{I} $ be an ideal on $ X $. Then, the following implications hold:
Definition 2.17. [12] Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS, $ \mathcal{I} $ be an ideal on $ X $ and $ A \subseteq X. $ The $ \mathcal{I} $-$ J $-nearly lower, $ \mathcal{I} $-$ J $-nearly upper approximations, $ \mathcal{I} $-$ J $-nearly boundary regions and $ \mathcal{I} $-$ J $-nearly accuracy of $ A $ are defined respectively by:
$ {\underline{\mathcal{R}}^{\mathcal{I}-\eta}_{J}}(A) = \cup\{G \in {\mathcal{I}} $-$ {\eta}_JO(X) : G \subseteq A\} = \mathcal{I} $-$ J $-nearly interior of $ A $.
$ {\overline{\mathcal{R}}^{\mathcal{I}-\eta}_{J}}(A) = \cap\{H \in {\mathcal{I}} $-$ {\eta}_JC(X): A \subseteq H\} = \mathcal{I} $-$ J $-nearly closure of $ A $.
$ {{\mathcal{BND}}^{\mathcal{I}-\eta}_{J}}(A) = {\overline{\mathcal{R}}^{\mathcal{I}-\eta}_{J}}(A)-{\underline{\mathcal{R}}^{\mathcal{I}-\eta}_{J}}(A). $
$ {{ACC}^{\mathcal{I}-\eta}_{J}}(A) = \frac{|{\underline{\mathcal{R}}^{\mathcal{I}-\eta}_{J}}(A)|}{|{\overline{\mathcal{R}}^{\mathcal{I}-\eta}_{J}}(A)|}, $ where $ |{\overline{\mathcal{R}}^{\mathcal{I}-\eta}_{J}}(A)|\neq0. $
Definition 2.18. [12] Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS, $ \mathcal{I} $ be an ideal on $ X $ and $ A \subseteq X. $ $ A $ is an $ \mathcal{I} $-$ \eta_{J} $-nearly definable ($ \mathcal{I} $-$ \eta_{J} $-nearly exact) set if $ {\overline{\mathcal{R}}^{\mathcal{I}-\eta}_{J}}(A) = {\underline{\mathcal{R}}^{\mathcal{I}-\eta}_{J}}(A). $ Otherwise, $ A $ is an $ \mathcal{I} $-$ \eta_{J} $-nearly rough set.
Theorem 2.4. [12] Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS, $ \mathcal{I} $ be an ideal on $ X $ and $ A \subseteq X. $ Then
(i) $ {\underline{\mathcal{R}}}^{\eta}_{J}(A)\subseteq {\underline{\mathcal{R}}^{\mathcal{I}-\eta}_{J}}(A). $
(ii) $ {\underline{\mathcal{R}}}_{J}(A)\subseteq {\underline{\mathcal{R}}^{\mathcal{I}-\eta}_{J}}(A). $
(iii) $ {\overline{\mathcal{R}}^{\mathcal{I}-\eta}_{J}}(A)\subseteq {\overline{\mathcal{R}}}^{\eta}_{J}(A). $
(iv) $ {\overline{\mathcal{R}}^{\mathcal{I}-\eta}_{J}}(A)\subseteq {\overline{\mathcal{R}}}_{J}(A) $.
Corollary 2.3. [12] Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS, $ \mathcal{I} $ be an ideal on $ X $ and $ A \subseteq X. $ Then
(i) $ {\mathcal{BND}}^{\mathcal{I}-\eta}_{J}(A)\subseteq {\mathcal{BND}}^{\eta}_{J}(A). $
(ii) $ {\mathcal{BND}}^\eta_{J}(A)\subseteq {\mathcal{BND}}_{J}(A). $
(iii) $ {ACC}^\eta_{J}(A)\leqslant {ACC}^{\mathcal{I}-\eta}_{J}(A). $
(iv) $ {ACC}_{J}(A)\leqslant {ACC}^{\mathcal{I}-\eta}_{J}(A). $
Proposition 2.5. [12] Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS, $ \mathcal{I} $ be an ideal on $ X $ and $ A \subseteq X. $ Then
(i) $ {\underline{\mathcal{R}}^{\mathcal{I}-P}_J}(A)\subseteq {\underline{\mathcal{R}}^{\mathcal{I}-\beta}_J}(A). $
(ii) $ {\underline{\mathcal{R}}^{\mathcal{I}-\alpha}_J}(A)\subseteq {\underline{\mathcal{R}}^{\mathcal{I}-S}_J}(A)\subseteq {\underline{\mathcal{R}}^{\mathcal{I}-\beta}_J}(A) $.
(iii) $ {\overline{\mathcal{R}}^{\mathcal{I}-\beta}_J}(A)\subseteq {\overline{\mathcal{R}}^{\mathcal{I}-P}_J}(A). $
(iv) $ {\overline{\mathcal{R}}^{\mathcal{I}-\beta}_J}(A)\subseteq {\overline{\mathcal{R}}^{\mathcal{I}-S}_J}(A)\subseteq {\overline{\mathcal{R}}^{\mathcal{I}-\alpha}_J}(A). $
Corollary 2.4. [12] Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS, $ \mathcal{I} $ be an ideal on $ X $ and $ A \subseteq X. $ Then
(i) $ {{\mathcal{BND}}^{\mathcal{I}-\beta}_J}(A)\subseteq {{\mathcal{BND}}^{\mathcal{I}-P}_J}(A). $
(ii) $ {{\mathcal{BND}}^{\mathcal{I}-\beta}_J}(A)\subseteq {{\mathcal{BND}}^{\mathcal{I}-S}_J}(A)\subseteq {{\mathcal{BND}}^{\mathcal{I}-\alpha}_J}(A). $
(iii) $ {{ACC}^{\mathcal{I}-P}_J}(A)\leqslant {{ACC}^{\mathcal{I}-\beta}_J}(A) $.
(iv) $ {{ACC}^{\mathcal{I}-\alpha}_J}(A)\leqslant {{ACC}^{\mathcal{I}-S}_J}(A)\leqslant {{ACC}^{\mathcal{I}-\beta}_J}(A). $
Definition 2.19. [28] Let $ \mathcal{R} $ be an equivalence relation on $ X $ and $ A \subseteq X $. Then the rough membership functions of $ A \subseteq X $ are defined as $ \mu^{A}:X\rightarrow [0, 1], $ where
$ [x]_{\mathcal{R}} $ denotes to an equivalence classes.
Definition 2.20. [3] Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS, $ A \subseteq X $ and $ x \in X. $ Then the $ J $-rough membership functions of $ A $ are defined by $ \mu^{{J}}_{A}\rightarrow [0, 1], $ where
Definition 2.21. [3] Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS, $ A \subseteq X $ and $ x \in X. $ Then the $ J $-rough nearly membership functions of $ A $ are defined by $ \mu^{{{\eta}_J}}_{A}\rightarrow [0, 1], $ where
Definition 2.22. [12] Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS, $ \mathcal{I} $ be an ideal on $ X, A \subseteq X $ and $ x \in X. $ The $ \mathcal{I}-J $-nearly rough membership functions of $ A $ are defined by $ \mu^{\mathcal{I}-{{\eta}_J}}_{A}\rightarrow [0, 1], $ where
Lemma 2.1. [12] Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS, $ \mathcal{I} $ be an ideal on $ X $ and $ A \subseteq X. $ Then
(i) $ \mu^{J}_{A}(x) = 1\Rightarrow \mu^{{{\eta}_J}}_{A}(x) = 1\Rightarrow \mu^{\mathcal{I}-{\eta_{J}}}_{A}(x) = 1, \forall\; x\in X. $
(ii) $ \mu^{J}_{A}(x) = 0\Rightarrow \mu^{{\eta_{J}}}_{A}(x) = 0\Rightarrow \mu^{\mathcal{I}-{\eta_{J}}}_{A}(x) = 0, \forall\; x\in X. $
Definition 2.23. [3] Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS, $ x\in X $ and $ A \subseteq X $:
(i) If $ x\in{\underline{\mathcal{R}}_{J}}(A) $, then $ x $ is $ J $-surely belongs to $ A $, denoted by $ x\; {\underline{\in}}_{J} A $.
(ii) If $ x\in{\overline{\mathcal{R}}_{J}}(A) $, then $ x $ is $ J $-possibly belongs to $ A $, denoted by $ x\; {\overline{\in}}_{J} A $.
(iii) If $ x\in{\underline{\mathcal{R}}^{\eta}_{J}}(A), $ then $ x $ is $ J $-nearly surely ($ {{\eta}_J} $-surely) belongs to $ A, $ denoted by $ x\; {\underline{\in}}^{{\eta}}_{J} A $.
(iv) If $ x\in{\overline{\mathcal{R}}^{\eta}_{J}}(A), $ then $ x $ is $ J $-nearly possibly ($ {{\eta}_J} $-possibly) belongs to $ A, $ denoted by $ x\; {\overline{\in}}^{{\eta}}_{J} A $.
It is called $ J $-(nearly) strong and $ J $-(nearly) weak membership relations respectively.
Definition 2.24. [12] Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS, $ \mathcal{I} $ be an ideal on $ X, x\in X $ and $ A \subseteq X: $
(i) If $ x\in{\underline{\mathcal{R}}^{\mathcal{I}-\eta}_{J}}(A), $ then $ x $ is $ J $-nearly surely with respect to $ \mathcal{I} $ ($ \mathcal{I}-{{\eta}_J} $-surely) belongs to $ A $, denoted by $ x\; {\underline{\in}}^{\mathcal{I}-{\eta}}_{J} A. $
(ii) If $ x\in{\overline{\mathcal{R}}^{\mathcal{I}-\eta}_{J}}(A), $ then $ x $ is $ J $-nearly possibly with respect to $ \mathcal{I} $ (briefly $ \mathcal{I}-{{\eta}_J} $-possibly) belongs to $ A $, denoted by $ x\; {\overline{\in}}^{\mathcal{I}-{\eta}}_{J} A. $
It is called $ J $-nearly strong and $ J $-nearly weak membership relations with respect to $ \mathcal{I} $ respectively.
Proposition 2.6. [12] Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS, $ \mathcal{I} $ be an ideal on $ X $ and $ A \subseteq X. $ Then
(i) If $ x\; {\underline{\in}}_{J} A\Rightarrow x\; {\underline{\in}}^{{\eta}}_{J} A\Rightarrow x\; {\underline{\in}}^{\mathcal{I}-{\eta}}_{J} A. $
(ii) If $ x\; {\overline{\in}}^{\mathcal{I}-{\eta}}_{J} A\Rightarrow x \; {\overline{\in}}^{{\eta}}_{J} A\Rightarrow x \; {\overline{\in}}_{J} A. $
3.
$ \mathcal{I} $-$ {\delta\beta}_{J} $-open sets
In this section, the concept of $ \mathcal{I} $-$ {\delta\beta}_{J} $-open sets is presented as generalization of the $ J $-nearly open sets in Definitions 2.6 [8], 2.9 [11] and also generalization of the $ \mathcal{I} $-$ J $-nearly open sets in Definition 2.16 [12]. This concept is based on the notions of ideals. Moreover, the principle properties of this concept is studied and compared to the previous concepts.
Definition 3.1. Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS and $ \mathcal{I} $ be an ideal on $ X $. $ A \subseteq X $ is called $ {\mathcal{I}} $-$ {\delta\beta}_{J} $-open, if $ \exists\; G\in \tau_J $ such that $ (A-cl_J(G))\in\mathcal{I} $ and $ (G-cl^{\delta}_J(A)) \in\mathcal{I}. $ The complement of the $ \mathcal{I} $-$ {\delta\beta}_{J} $-open sets is called $ \mathcal{I} $-$ {\delta\beta}_{J} $-closed sets. The family of all $ \mathcal{I} $-$ {\delta\beta}_J $-open and $ \mathcal{I} $-$ {\delta\beta}_J $-closed are denoted by $ \mathcal{I} $-$ {\delta\beta}_{J}O(X) $ and $ \mathcal{I} $-$ {\delta\beta}_{J}C(X) $ respectively.
Example 3.1. Let
and
be a binary relation defined on $ X, $ thus $ a\mathcal{R} = b\mathcal{R} = \{a, b\}, c\mathcal{R} = \{c\} $ and $ d\mathcal{R} = X. $ Then, the topology associated with this relation is $ \tau_R = \{X, \phi, \{c\}, \{a, b\}, \{a, b, c\}\} $ and $ \mathcal{I} $-$ \delta\beta_{R}O(X) = P(X). $
The following proposition shows that the concept of $ \mathcal{I} $-$ {\delta\beta}_{J} $-open sets is an extension of the concept of $ {\delta\beta}_{J} $-open sets in Definition 2.9 [11].
Proposition 3.1. Every $ {\delta\beta}_{J} $-open is $ {\mathcal{I}} $-$ {\delta\beta}_{J} $-open.
Proof. By using Definitions 2.9 [11] and 3.1.
Remark 3.1. (i) The converse of Proposition 3.1 is not necessarily true as shown in Example 3.1, $ {\mathcal{I}} $-$ \delta\beta_{R}O(X) = P(X) $ and $ \delta\beta_{R}O(X) = P(X)-\{\{d\}\}. $ It is clear that $ \{d\} $ is an $ {\mathcal{I}} $-$ {\delta\beta}_{R} $-open set, but it is not a $ {\delta\beta}_{R} $-open set.
(ii) According to Remark 2.1 [8] and Propositions 2.1 [11], 3.1, the current Definition 3.1 is also a generalization of Definition 2.6 [8].
The following theorem shows that Hosny's Definition 2.9 [11] is a special case of the current definition.
Theorem 3.1. Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS and $ \mathcal{I} $ be an ideal on $ X $. If $ \mathcal{I} = \{\phi\} $ in the current Definition 3.1, then I get Hosny's Definition 2.9 [11].
Proof. Straightforward.
The following proposition shows that the $ \mathcal{I} $-$ {\delta\beta}_{J} $-open sets are generalization of the $ \mathcal{I} $-$ {\beta}_{J} $-open sets [12]. Consequently, they are also generalization of any $ \mathcal{I} $-$ J $-near open sets in Definition 2.16 [12] such as, $ {\mathcal{I}} $-$ P_J $-open, $ {\mathcal{I}} $-$ S_J $-open and $ {\mathcal{I}} $-$ \alpha_J $-open sets.
Proposition 3.2. Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS and $ \mathcal{I} $ be an ideal on $ X. $ Then, the following implications hold:
Proof. Straightforward by Proposition 2.3 [12], Definitions 2.16 [12] and 5.2.
It should be noted that, Proposition 3.2 shows that, every $ \mathcal{I} $-$ {\beta}_{J} $-open is $ \mathcal{I} $-$ {\delta\beta}_{J} $-open, but the converse is not necessarily true as shown in the following example.
Example 3.2. Let $ X = \{a, b, c\}, \mathcal{I} = \{\phi, \{b\}\} $ and $ \mathcal{R} = \{(a, a), (a, c), (b, a), (b, c), (c, c)\} $ is a binary relation defined on $ X $ thus $ a\mathcal{R} = b\mathcal{R} = \{a, b\} $ and $ c\mathcal{R} = \{c\}. $ Then, the topology associated with this relation is $ \tau_R = \{X, \phi, \{c\}, \{a, b\}\}. $ It is clear that $ \{b\} $ is an $ \mathcal{I} $-$ \delta\beta_{R} $-open set, but it is not an $ \mathcal{I} $-$ \beta_{R} $-open set.
Proposition 3.3. Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS and $ \mathcal{I} $ be an ideal on $ X $. Then, the following implications hold:
Proof. By Propositions 2.4 and 3.2 [12], the proof is obvious.
Theorem 3.2. Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS and $ \mathcal{I} $ be an ideal on $ X. $ Then, the union of two $ \mathcal{I} $-$ {\delta\beta}_{J} $-open sets is also $ \mathcal{I} $-$ {\delta\beta}_{J} $-open set.
Proof. Let $ A $ and $ B $ be $ \mathcal{I} $-$ {\delta\beta}_{J} $-open sets. Then, $ \exists\; G, H $ such that $ (A - cl_J (G))\in \mathcal{I}, (G - cl^{\delta}_{J}(A))\in \mathcal{I}, (B -cl_J (H))\in \mathcal{I} $ and $ (H-cl^{\delta}_{J}(B))\in \mathcal{I}. $ Hence, $ (G - cl^{\delta}_{J}(A\cup B))\subseteq(G - cl^{\delta}_{J}(A))\in \mathcal{I}, $ $ (H - cl^{\delta}_{J}(A\cup B))\subseteq(H - cl^{\delta}_{J}(B))\in \mathcal{I} $ and so, $ (G -cl^{\delta}_{J} (A\cup B))\cup(H - cl^{\delta}_{J} (A\cup B))\in \mathcal{I} $. Let $ W = G\cup H $, then $ (W- cl^{\delta}_{J}(A\cup B))\in \mathcal{I} $. Also, $ (A -cl_J (W))\subseteq (A - cl_J (G)) \in \mathcal{I} $ and $ (B -cl_J (W))\subseteq (B - cl_J (H)) \in \mathcal{I} $. Then, $ (A - cl_J (W))\cup (B -cl_J (W)) \subseteq (A -cl_J (G))\cup (B - cl_J (H)) \in \mathcal{I} $ and so $ ((A\cup B) -cl_J(W)) \subseteq (A -cl_J (G))\cup (B - cl_J (H))\in \mathcal{I} $. Thus, $ A\cup B $ is an $ \mathcal{I} $-$ {\delta\beta}_{J} $-open set. The rest of the proof is similar.
Remark 3.2. The family of all $ {\mathcal{I}} $-$ {\delta\beta}_J $-open sets in a space $ X $ does not form a topology as it is shown in the following example.
Example 3.3. Let
and
It is clear that the intersection of two $ \mathcal{I} $-$ {\delta\beta}_R $-open sets is not an $ \mathcal{I} $-$ {\delta\beta}_R $-open set. Take $ A = \{a, e\} $ and $ B = \{b, e\}\in \mathcal{I} $-$ \delta\beta_{R}O(X), $ then $ A\cap B = \{e\}\not\in\mathcal{I} $-$ \delta\beta_{R}O(X) = P(X)-\{\{e\}\}. $
Remark 3.3. Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS, $ \mathcal{I} $ be an ideal on $ X $ and $ A \subseteq X. $ Then the following statements are not true in general:
(i) $ \mathcal{I} $-$ {\delta\beta}_{U}O(X) \subseteq \mathcal{I} $-$ {\delta\beta}_{R}O(X) \subseteq \mathcal{I} $-$ {\delta\beta}_{I}O(X). $
(ii) $ \mathcal{I} $-$ {\delta\beta}_{U}O(X) \subseteq \mathcal{I} $-$ {\delta\beta}_{L}O(X) \subseteq \mathcal{I} $-$ {\delta\beta}_{I}O(X). $
(iii) $ \mathcal{I} $-$ {\delta\beta}_{ < U > }O(X) \subseteq \mathcal{I} $-$ {\delta\beta}_{ < R > }O(X) \subseteq \mathcal{I} $-$ {\delta\beta}_{ < I > }O(X). $
(iv) $ \mathcal{I} $-$ {\delta\beta}_{ < U > }O(X) \subseteq \mathcal{I} $-$ {\delta\beta}_{ < L > }O(X) \subseteq \mathcal{I} $-$ {\delta\beta}_{ < I > }O(X). $
(v) $ \mathcal{I} $-$ {\delta\beta}_{R}O(X) $ is the dual of $ \mathcal{I} $-$ {\delta\beta}_{L}O(X). $
(vi) $ \mathcal{I} $-$ {\delta\beta}_{ < R > }O(X) $ is the dual of $ \mathcal{I} $-$ {\delta\beta}_{ < L > }O(X). $
So, the relationships among $ \mathcal{I} $-$ {\delta\beta}_{J} $- open sets are not comparable as in Example 3.3:
(i) $ \mathcal{I} $-$ {\delta\beta}_{R}O(X) = P(X)-\{\{e\}\}. $
(ii) $ \mathcal{I} $-$ {\delta\beta}_{L}O(X) = \mathcal{I} $-$ {\delta\beta}_{ < L > }O(X) = P(X)-\{\{b\}\}. $
(iii) $ \mathcal{I} $-$ {\delta\beta}_{I}O(X) = \mathcal{I} $-$ {\delta\beta}_{U}O(X) = \mathcal{I} $-$ {\delta\beta}_{ < R > }O(X) = \mathcal{I} $-$ {\delta\beta}_{ < I > }O(X) = \mathcal{I} $-$ {\delta\beta}_{ < U > }O(X) = P(X). $
It is clear that
● $ \mathcal{I} $-$ {\delta\beta}_{U}O(X) \nsubseteq \mathcal{I} $-$ {\delta\beta}_{R}O(X). $
● $ \mathcal{I} $-$ {\delta\beta}_{I}O(X) \nsubseteq \mathcal{I} $-$ {\delta\beta}_{R}O(X). $
● $ \mathcal{I} $-$ {\delta\beta}_{U}O(X) \nsubseteq \mathcal{I} $-$ {\delta\beta}_{L}O(X). $
● $ \mathcal{I} $-$ {\delta\beta}_{I}O(X) \nsubseteq \mathcal{I} $-$ {\delta\beta}_{L}O(X). $
● $ \mathcal{I} $-$ {\delta\beta}_{ < U > }O(X) \nsubseteq \mathcal{I} $-$ {\delta\beta}_{ < L > }O(X). $
● $ \mathcal{I} $-$ {\delta\beta}_{ < I > }O(X) \nsubseteq \mathcal{I} $-$ {\delta\beta}_{ < L > }O(X). $
● $ \mathcal{I} $-$ {\delta\beta}_{R}O(X) $ is not the dual of $ \mathcal{I} $-$ {\delta\beta}_{L}O(X) $ and $ \mathcal{I} $-$ {\delta\beta}_{ < R > }O(X) $ is not the dual of $ \mathcal{I} $-$ {\delta\beta}_{ < L > }O(X). $
● In a similar way, I can add examples to show that $ \mathcal{I} $-$ {\delta\beta}_{L}O(X) \nsubseteq \mathcal{I} $-$ {\delta\beta}_{I}O(X), \mathcal{I} $-$ {\delta\beta}_{R}O(X) \nsubseteq \mathcal{I} $-$ {\delta\beta}_{U}O(X), \mathcal{I} $-$ {\delta\beta}_{R}O(X) \nsubseteq \mathcal{I} $-$ {\delta\beta}_{I}O(X), \mathcal{I} $-$ {\delta\beta}_{L}O(X) \nsubseteq \mathcal{I} $-$ {\delta\beta}_{U}O(X), \mathcal{I} $-$ {\delta\beta}_{I}O(X) \nsubseteq \mathcal{I} $-$ {\delta\beta}_{L}O(X), \mathcal{I} $-$ {\delta\beta}_{ < L > }O(X) \nsubseteq \mathcal{I} $-$ {\delta\beta}_{ < I > }O(X), \mathcal{I} $-$ {\delta\beta}_{ < L > }O(X) \nsubseteq \mathcal{I} $-$ {\delta\beta}_{ < U > }O(X), \mathcal{I} $-$ {\delta\beta}_{ < R > }O(X) \nsubseteq \mathcal{I} $-$ {\delta\beta}_{ < I > }O(X) $ and $ \mathcal{I} $-$ {\delta\beta}_{ < U > }O(X)\nsubseteq \mathcal{I} $-$ {\delta\beta}_{ < R > }O(X). $
4.
Approximations spaces by using $ \mathcal{I} $-$ {\delta\beta}_{J} $-open sets
The purpose of this section is to generalize the previous approximations in Definitions 2.4 [2], 2.7 [8], 2.10 [11] and 2.17 [12]. The current approximations are depended on the $ \mathcal{I} $-$ {\delta\beta}_{J} $-open sets. The fundamental properties of these approximations are obtained. Furthermore, the current findings are compared to the previous approaches.
Definition 4.1. Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS, $ \mathcal{I} $ be an ideal on $ X $ and $ A \subseteq X. $ The $ \mathcal{I} $-$ {\delta\beta}_{J} $-lower, $ \mathcal{I} $-$ {\delta\beta}_{J} $-upper approximations, $ \mathcal{I} $-$ {\delta\beta}_{J} $-boundary regions and $ \mathcal{I} $-$ {\delta\beta}_{J} $-accuracy of $ A $ are defined respectively by:
$ {\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}(A) = \cup\{G \in {\mathcal{I}} $-$ {\delta\beta}_JO(X) : G \subseteq A\} = \mathcal{I} $-$ {\delta\beta}_{J} $-interior of $ A $.
$ {\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}(A) = \cap\{H \in {\mathcal{I}} $-$ {\delta\beta}_JC(X): A \subseteq H\} = \mathcal{I} $-$ {\delta\beta}_{J} $-closure of $ A $.
$ {{\mathcal{BND}}^{\mathcal{I}-{\delta\beta}}_{J}}(A) = {\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}(A)-{\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}(A). $
$ {{ACC}^{\mathcal{I}-{\delta\beta}}_{J}}(A) = \frac{|{\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}(A)|}{|{\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}(A)|}, $ where $ |{\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}(A)|\neq0. $
The following proposition presents the main properties of the current $ \mathcal{I} $-$ {\delta\beta}_{J} $-lower and $ \mathcal{I} $-$ {\delta\beta}_{J} $-upper approximations.
Proposition 4.1. Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS, $ \mathcal{I} $ be an ideal on $ X $ and $ A, B \subseteq X. $ Then,
(i) $ {\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}(A)\subseteq A\subseteq{\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}(A) $ equality hold if $ A = \phi $ or $ X. $
(ii) $ A\subseteq B\Rightarrow {\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}(A)\subseteq {\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}(B). $
(iii) $ A\subseteq B\Rightarrow {\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}(A)\subseteq {\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}(B). $
(iv) $ {\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}(A\cap B)\subseteq{\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}(A)\cap{\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}(B). $
(v) $ {\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}(A\cup B)\supseteq{\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}(A)\cup{\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}(B). $
(vi) $ {\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}(A\cup B)\supseteq {\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}(A)\cup{\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}(B). $
(vii) $ {\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}(A\cap B)\subseteq{\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}(A)\cap{\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}(B). $
(viii) $ {\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}(A) = ({\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}(A^{'}))^{'} $, $ {\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}(A) = ({\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}(A^{'}))^{'} $.
(ix) $ {\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}({\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}(A)) = {\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}(A). $
(x) $ {\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}({\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}(A)) = {\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}(A). $
(xi) $ {\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}({\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}(A))\subseteq {\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}({\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}(A)). $
(xii) $ {\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}({\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}(A))\subseteq {\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}({\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}(A)). $
(xiii) $ x\in{\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}(A)\Leftrightarrow G\cap A\neq\phi, \forall G\in \mathcal{I} $-$ {{\delta\beta}}_{J}O(X), x\in G. $
(xiv) $ x\in{\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}(A)\Leftrightarrow \exists \; G\in \mathcal{I} $-$ {\delta\beta}_{J}O(X), x\in G, G\subseteq A. $
The proof of this proposition is simple using the $ \mathcal{I} $-$ {\delta\beta}_{J} $-interior and $ \mathcal{I} $-$ {\delta\beta}_{J} $-closure, so I omit it.
Remark 4.1. Example 3.3 shows that
(a) the inclusion in Proposition 4.1 parts (i), (iv), (v), (vi), (vii), (xi) and (xii) can not be replaced by equality relation:
(i) For part (i), if $ A = \{a, b, c, d\}, {\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{R}}(A) = X, $ then $ {\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{R}}(A)\nsubseteq A, $ take $ A = \{e\}, {\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{R}}(A) = \phi $. Then, $ A\nsubseteq {\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{R}}(A). $
(ii) For part (iv), if $ A = \{a, b, c, d\}, B = \{b, c, d, e\}, A\cap B = \{b, c, d\}, {\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{R}}(A) = X, {\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{R}}(B) $$= B, {\overline{\mathcal{R}}}^{\delta\beta}_{R}(A\cap B) = A\cap B $, then $ {\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{R}}(A)\cap {\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{R}}(B) = \{b, c, d, e\}\nsubseteq \{b, c, d\} = {\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{R}}(A\cap B). $
(iii) For part (v), if $ A = \{a\}, B = \{e\}, A\cup B = \{a, e\}, {\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{R}}(A) = A, {\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{R}}(B) = \phi, {\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{R}}(A\cup B) = A\cup B $, then $ {\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{R}}(A\cup B) = \{a, e\} \nsubseteq \{a\} = {\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{R}}(A)\cup {\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{R}}(B). $
(iv) For part (vi), if $ A = \{a, c\}, B = \{b, d\}, A\cup B = \{a, b, c, d\}, {\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{R}}(A) = A, {\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{R}}(B) = B, \\ {\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{R}}(A\cup B) = X $, then $ {\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{R}}(A\cup B) = X\nsubseteq \{a, b, c, d\} = {\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{R}}(A)\cup {\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{R}}(B). $
(v)For part (vii), if $ A = \{a, e\}, B = \{c, e\}, A\cap B = \{e\}, {\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{R}}(A) = A, {\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{R}}(B) = B, {\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{R}}(A\cap B) = \phi $, then $ {\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{R}}(A)\cap {\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{R}}(B) = \{e\}\nsubseteq \phi = {\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{R}}(A\cap B). $
(vi) For part (xi), if $ A = \{a, b, c, d\}, {\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{R}}({\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{R}}(A)) = A, {\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{R}}({\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{R}}(A)) = X $, then $ {\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{R}}({\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{R}}(A)) \nsubseteq {\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{R}}({\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{R}}(A)). $
(vii) For part (xii), if $ A = \{e\}, {\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{R}}({\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{R}}(A)) = A, {\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{R}}({\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{R}}(A)) = \phi $, then $ {\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{R}}({\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{R}}(A)) \nsubseteq {\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{R}}({\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{R}}(A)). $
(b) the converse of parts (ii) and (iii) is not necessarily true:
(i) For part (ii), if $ A = \{e\}, B = \{a, b, c, d\}, $ then $ {\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{R}}(A) = A, {\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{R}}(B) = X $. Therefore, $ {\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{R}}(A)\subseteq {\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{R}}(B) $, but $ A\nsubseteq B. $
(ii) For part (iii), if $ A = \{e\}, B = \{c, d\}, $ then $ {\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{R}}(A) = \phi, {\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{R}}(B) = B $. Therefore, $ {\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{R}}(A)\subseteq {\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{R}}(B) $, but $ A\nsubseteq B. $
Definition 4.2. Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS, $ \mathcal{I} $ be an ideal on $ X $ and $ A \subseteq X. $ $ A $ is an $ \mathcal{I} $-$ {\delta\beta}_{J} $-definable (an $ \mathcal{I} $-$ {\delta\beta}_{J} $-exact) set if $ {\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}(A) = {\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}(A). $ Otherwise, $ A $ is an $ \mathcal{I} $-$ {\delta\beta}_{J} $-rough set.
In Example 3.3 $ A = \{c\} $ is $ \mathcal{I} $-$ {\delta\beta}_{R} $-exact, while $ B = \{e\} $ is $ \mathcal{I} $-$ {\delta\beta}_{R} $-rough.
Remark 4.2. Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS, $ \mathcal{I} $ be an ideal on $ X $ and $ A \subseteq X. $ Then the intersection of two $ \mathcal{I} $-$ {\delta\beta}_{R} $-exact sets does not need to be an $ \mathcal{I} $-$ {\delta\beta}_{R} $-exact set as in Example 3.3 $ \{a, e\} $ and $ \{c, e\} $ are $ \mathcal{I} $-$ {\delta\beta}_{R} $-exact sets, but $ \{a, e\}\cap\{c, e\} = \{e\} $ is not an $ \mathcal{I} $-$ {\delta\beta}_{R} $-exact set.
The following theorem and corollary present the relationships between the current approximations in Definition 4.1 and the previous ones in Definitions 2.4 [2], 2.7 [8] and 2.10 [11].
Theorem 4.1. Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS and $ A \subseteq X. $ Then
(i) $ {\underline{\mathcal{R}}}^{\alpha}_{J}(A)\subseteq {\underline{\mathcal{R}}}^{p}_{J}(A)\subseteq{\underline{\mathcal{R}}}^{\gamma}_{J}(A)\subseteq{\underline{\mathcal{R}}}^{\beta}_{J}(A)\subseteq {\underline{\mathcal{R}}}^{\delta\beta}_{J}(A)\subseteq {\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}(A). $
(ii) $ {\underline{\mathcal{R}}}^{\alpha}_{J}(A)\subseteq {\underline{\mathcal{R}}}^{s}_{J}(A)\subseteq{\underline{\mathcal{R}}}^{\gamma}_{J}(A)\subseteq{\underline{\mathcal{R}}}^{\beta}_{J}(A)\subseteq {\underline{\mathcal{R}}}^{\delta\beta}_{J}(A)\subseteq {\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}(A). $
(iii) $ {\underline{\mathcal{R}}}_{J}(A)\subseteq {\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}(A). $
(iv) $ {\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}(A)\subseteq{\overline{\mathcal{R}}}^{\delta\beta}_{J}(A)\subseteq {\overline{\mathcal{R}}}^{\beta}_{J}(A)\subseteq {\overline{\mathcal{R}}}^{\gamma}_{J}(A)\subseteq {\overline{\mathcal{R}}}^{p}_{J}(A)\subseteq {\overline{\mathcal{R}}}^{\alpha}_{J}(A). $
(v) $ {\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}(A)\subseteq{\overline{\mathcal{R}}}^{\delta\beta}_{J}(A)\subseteq {\overline{\mathcal{R}}}^{\beta}_{J}(A)\subseteq {\overline{\mathcal{R}}}^{\gamma}_{J}(A)\subseteq {\overline{\mathcal{R}}}^{s}_{J}(A)\subseteq {\overline{\mathcal{R}}}^{\alpha}_{J}(A). $
(vi) $ {\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}(A)\subseteq {\overline{\mathcal{R}}}_{J}(A). $
Proof. (i) By Theorem 2.2 [11], $ {\underline{\mathcal{R}}}^{\alpha}_{J}(A)\subseteq {\underline{\mathcal{R}}}^{p}_{J}(A)\subseteq{\underline{\mathcal{R}}}^{\gamma}_{J}(A)\subseteq{\underline{\mathcal{R}}}^{\beta}_{J}(A)\subseteq {\underline{\mathcal{R}}}^{\delta\beta}_{J}(A), $ and $ {\underline{\mathcal{R}}}^{\delta\beta}_{J}(A) = \cup\{G \in {\delta\beta}_JO(X):G \subseteq A\}\subseteq \cup\{G \in {\mathcal{I}} $-$ {\delta\beta}_JO(X) : G \subseteq A\} = {\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}(A) $ (by Proposition 3.1).
(ii) It is similar to (i).
(iii) By Theorem 2.2 [11], $ {\underline{\mathcal{R}}}_{J}(A)\subseteq {\underline{\mathcal{R}}}^{\delta\beta}_{J}(A), $ and by (1) $ {\underline{\mathcal{R}}}^{\delta\beta}_{J}(A)\subseteq {\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}(A). $ Hence, $ {\underline{\mathcal{R}}}_{J}(A)\subseteq {\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{J}}(A). $
(iv)–(vi) They are similar to (i)–(iii).
Corollary 4.1. Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS and $ A \subseteq X. $ Then
(i) $ {\mathcal{BND}}^{\mathcal{I}-{\delta\beta}}_{J}(A)\subseteq{\mathcal{BND}}^{\delta\beta}_{J}(A)\subseteq {\mathcal{BND}}^{\beta}_{J}(A)\subseteq {\mathcal{BND}}^{\gamma}_{J}(A)\subseteq {\mathcal{BND}}^{p}_{J}(A)\subseteq {\mathcal{BND}}^{\alpha}_{J}(A). $
(ii) $ {\mathcal{BND}}^{\mathcal{I}-{\delta\beta}}_{J}(A)\subseteq{\mathcal{BND}}^{\delta\beta}_{J}(A)\subseteq {\mathcal{BND}}^{\beta}_{J}(A)\subseteq {\mathcal{BND}}^{\gamma}_{J}(A)\subseteq {\mathcal{BND}}^{s}_{J}(A)\subseteq {\mathcal{BND}}^{\alpha}_{J}(A) $.
(iii) $ {\mathcal{BND}}^{\mathcal{I}-{\delta\beta}}_{J}(A)\subseteq {\mathcal{BND}}_{J}(A). $
(iv) $ {ACC}^{\alpha}_{J}(A)\leqslant {ACC}^{p}_{J}(A)\leqslant {ACC}^{\gamma}_{J}(A)\leqslant {ACC}^{\beta}_{J}(A)\leqslant {ACC}^{\delta\beta}_{J}(A)\leqslant {ACC}^{\mathcal{I}-{\delta\beta}}_{J}(A). $
(v) $ {ACC}^{\alpha}_{J}(A)\leqslant {ACC}^{s}_{J}(A)\leqslant {ACC}^{\gamma}_{J}(A)\leqslant {ACC}^{\beta}_{J}(A)\leqslant {ACC}^{\delta\beta}_{J}(A)\leqslant {ACC}^{\mathcal{I}-{\delta\beta}}_{J}(A). $
(vi) $ {ACC}_{J}(A)\leqslant {ACC}^{\mathcal{I}-{\delta\beta}}_{J}(A). $
Remark 4.3. Example 3.1 shows that the converse of the implications in Theorem 4.1 and Corollary 4.1 is not true in general. Take $ A = \{d\}, $ then $ {\underline{\mathcal{R}}}_{R}(A) = {\underline{\mathcal{R}}}^{\delta\beta}_{R}(A) = \phi, {\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{R}}(A) = \{d\} $ and if $ A = \{a, b, c\}, $ then $ {\overline{\mathcal{R}}}_{R}(A) = {\overline{\mathcal{R}}}^{\delta\beta}_{R}(A) = X, {\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_{R}}(A) = \{a, b, c\}. $ Moreover, take $ A = \{a, b, c\}, $ then the boundary and accuracy by the present method in Definition 4.1 are $ \phi $ and $ 1 $ respectively. Whereas, the boundary and accuracy by using Abd El-Monsef et al.'s method 2.4 [2], Amer et al.'s method 2.7 [8] and Hosny's method 2.10 [11] are $ \{d\} $ and $ 0 $ respectively.
Corollary 4.2. Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS, $ \mathcal{I} $ be an ideal on $ X $ and $ A \subseteq X. $ Then
(i) $ A $ is $ \alpha_J $-exact $ \Rightarrow $ $ A $ is $ S_J $-exact $ \Rightarrow $ $ A $ is $ \beta_J $-exact $ \Rightarrow $ $ {\delta\beta}_J $-exact $ \Rightarrow $ $ A $ is $ \mathcal{I} $-$ {\delta\beta}_J $-exact.
(ii) $ A $ is $ P_J $-exact $ \Rightarrow $ $ A $ is $ \beta_J $-exact $ \Rightarrow $ $ A $ is $ {\delta\beta}_J $-exact $ \Rightarrow $ $ A $ is $ \mathcal{I} $-$ {\delta\beta}_J $-exact.
(iii) $ A $ is $ {J} $-exact $ \Rightarrow $ $ A $ is $ \mathcal{I} $-$ {\delta\beta}_{J} $-exact.
(iv) $ A $ is $ \mathcal{I} $-$ {\delta\beta}_{J} $-rough $ \Rightarrow $ $ A $ is $ {\delta\beta}_J $-rough $ \Rightarrow $ $ A $ is $ {\beta}_{J} $-rough $ \Rightarrow $ $ A $ is $ S_J $-rough $ \Rightarrow $ $ A $ is $ \alpha_J $-rough.
(v) $ A $ is $ \mathcal{I} $-$ {\delta\beta}_{J} $-rough $ \Rightarrow $ $ A $ is $ {\delta\beta}_J $-rough $ \Rightarrow $ $ A $ is $ {\beta}_{J} $-rough $ \Rightarrow $ $ A $ is $ P_J $-rough.
(vi) $ A $ is $ \mathcal{I} $-$ {\delta\beta}_{J} $-rough $ \Rightarrow $ $ A $ is $ {J} $-rough.
Remark 4.4. The converse of parts of Corollary 4.2 is not necessarily true as in Example 3.1:
(i) If $ A = \{d\} $, then it is $ \mathcal{I} $-$ {\delta\beta}_{R} $-exact, but it is neither $ {\delta\beta}_{R} $-exact nor $ {R} $-exact.
(ii) If $ A = \{a, b, c\} $, then it is $ {R} $-rough and $ {\delta\beta}_{R} $-rough, but it is not $ \mathcal{I} $-$ {\delta\beta}_{R} $-rough.
The following proposition and corollary are introduced the relationships between the current approximations in Definition 4.1 and the previous one in Definition 2.17 [12].
Proposition 4.2. Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS, $ \mathcal{I} $ be an ideal on $ X $ and $ A \subseteq X. $ Then
(i) $ {\underline{\mathcal{R}}^{\mathcal{I}-P}_J}(A)\subseteq {\underline{\mathcal{R}}^{\mathcal{I}-\beta}_J}(A)\subseteq {\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_J}(A). $
(ii) $ {\underline{\mathcal{R}}^{\mathcal{I}-\alpha}_J}(A)\subseteq {\underline{\mathcal{R}}^{\mathcal{I}-S}_J}(A)\subseteq {\underline{\mathcal{R}}^{\mathcal{I}-\beta}_J}(A)\subseteq {\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_J}(A) $.
(iii) $ {\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_J}(A)\subseteq{\overline{\mathcal{R}}^{\mathcal{I}-\beta}_J}(A)\subseteq {\overline{\mathcal{R}}^{\mathcal{I}-P}_J}(A). $
(iv) $ {\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_J}(A)\subseteq{\overline{\mathcal{R}}^{\mathcal{I}-\beta}_J}(A)\subseteq {\overline{\mathcal{R}}^{\mathcal{I}-S}_J}(A)\subseteq {\overline{\mathcal{R}}^{\mathcal{I}-\alpha}_J}(A). $
Proof. By Proposition 3.2, the proof is obvious.
Corollary 4.3. Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS, $ \mathcal{I} $ be an ideal on $ X $ and $ A \subseteq X. $ Then
(i) $ {{\mathcal{BND}}^{\mathcal{I}-{\delta\beta}}_J}(A)\subseteq {{\mathcal{BND}}^{\mathcal{I}-\beta}_J}(A)\subseteq {{\mathcal{BND}}^{\mathcal{I}-P}_J}(A). $
(ii) $ {{\mathcal{BND}}^{\mathcal{I}-{\delta\beta}}_J}(A)\subseteq {{\mathcal{BND}}^{\mathcal{I}-\beta}_J}(A)\subseteq {{\mathcal{BND}}^{\mathcal{I}-S}_J}(A)\subseteq {{\mathcal{BND}}^{\mathcal{I}-\alpha}_J}(A). $
(iii) $ {{ACC}^{\mathcal{I}-P}_J}(A)\leqslant {{ACC}^{\mathcal{I}-\beta}_J}(A)\leqslant {{ACC}^{\mathcal{I}-{\delta\beta}}_J}(A) $.
(iv) $ {{ACC}^{\mathcal{I}-\alpha}_J}(A)\leqslant {{ACC}^{\mathcal{I}-S}_J}(A)\leqslant {{ACC}^{\mathcal{I}-\beta}_J}(A)\leqslant {{ACC}^{\mathcal{I}-{\delta\beta}}_J}(A). $
Corollary 4.4. Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS, $ \mathcal{I} $ be an ideal on $ X $ and $ A \subseteq X. $ Then
(i) $ A $ is $ \mathcal{I} $-$ \alpha_J $-exact $ \Rightarrow $ $ A $ is $ \mathcal{I} $-$ S_J $-exact $ \Rightarrow $ $ A $ is $ \mathcal{I} $-$ \beta_J $-exact $ \Rightarrow $ $ A $ is $ \mathcal{I} $-$ {\delta\beta}_J $-exact.
(ii) $ A $ is $ \mathcal{I} $-$ P_J $-exact $ \Rightarrow $ $ A $ is $ \mathcal{I} $-$ \beta_J $-exact $ \Rightarrow $ $ A $ is $ \mathcal{I} $-$ {\delta\beta}_J $-exact.
(iii) $ A $ is $ \mathcal{I} $-$ {\delta\beta}_{J} $-rough $ \Rightarrow $ $ A $ is $ \mathcal{I} $-$ {\beta}_{J} $-rough $ \Rightarrow $ $ A $ is $ \mathcal{I} $-$ S_J $-rough $ \Rightarrow $ $ A $ is $ \mathcal{I} $-$ \alpha_J $-rough.
(iv) $ A $ is $ \mathcal{I} $-$ {\delta\beta}_{J} $-rough $ \Rightarrow $ $ A $ is $ \mathcal{I} $-$ {\beta}_{J} $-rough $ \Rightarrow $ $ A $ is $ \mathcal{I} $-$ P_J $-rough.
In Table 1, the lower, upper approximations, boundary regions and accuracy are calculated by using Hosny's approximations 2.17 [12] and the current approximations in Definition 4.1 by using Example 3.2.
For example, take $ A = \{a, b\}, $ then the boundary and accuracy by the present method in Definition 4.1 are $ \phi $ and $ 1 $ respectively. Whereas, the boundary and accuracy by using Hosny's method 2.17 [12] are $ \{a, b\} $ and $ 0 $ respectively.
Remark 4.5. Example 3.2 shows that the converse of the implications in Corollary 4.4 is not true in general. For example, if take $ A = \{a\}, $ then it is $ \mathcal{I} $-$ {\delta\beta}_R $-exact, but it is not $ \mathcal{I} $-$ \beta_R $-exact and consequently, not $ \mathcal{I} $-$ S_R $-exact, not $ \mathcal{I} $-$ \alpha_R $-exact and not $ \mathcal{I} $-$ P_R $-exact, also $ A = \{a\}, $ is $ \mathcal{I} $-$ \beta_R $-rough, but not $ \mathcal{I} $-$ {\delta\beta}_R $-rough.
Remark 4.6. Theorem 4.1 and Proposition 4.2 show that the present method in Definition 4.1 reduces the boundary region by increasing the $ \mathcal{I} $-$ {\delta\beta}_{J} $-lower approximations and decreasing the $ \mathcal{I} $-$ {\delta\beta}_{J} $-upper approximations with the comparison of Abd El-Monsef et al.'s method 2.4 [2], Amer et al.'s method 2.7 [8], Hosny's method 2.10 [11] and Hosny's method 2.17 [12]. Moreover, Corollaries 4.1 and 4.3 show that the current accuracy in Definition 4.1 is greater than the previous ones in Definitions 2.4 [2], 2.7 [8], 2.10 [11] and 2.17 [12].
5.
$ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J} $-sets
The idea of generalization of $ J $-nearly open sets and $ \mathcal{I} $-$ J $-nearly open sets is developed and extended in this section by proposing the concept of $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J} $-sets. The main characterizations of this concept and the connections among them are investigated and analyzed. The concepts of $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J} $-sets and $ \mathcal{I} $-$ {\delta\beta}_{J} $-open sets are different and independent (see Remark 5.5).
Definition 5.1. Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS, $ \mathcal{I} $ be an ideal on $ X $ and $ A \subseteq X $. A subset $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J} $ is defined as follows: $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J}(A) = \cap\{ G:A\subseteq G, G\in{\mathcal{I}} $-$ {\beta}_JO(X)\}. $ The complement of $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J}(A) $-set is called $ \mathcal{I} $-$ {\bigvee_{\beta}}_{J}(A) $-set.
In the following lemma I summarize the fundamental properties of the subset $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J}. $
Lemma 5.1. For subsets $ A, B $ and $ A_{\alpha} (\alpha \in \Delta) $ of a $ J $-ndS $ (X, \mathcal{R}, \Xi_J), $ the following implications hold:
(i) $ A\subseteq \mathcal{I} $-$ {\bigwedge_{\beta}}_{J}(A) $.
(ii) If $ A \subseteq B $, then $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J}(A)\subseteq \mathcal{I} $-$ {\bigwedge_{\beta}}_{J}(B). $
(iii) $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J}(\mathcal{I} $-$ {\bigwedge_{\beta}}_{J}(A)) = \mathcal{I} $-$ {\bigwedge_{\beta}}_{J}(A). $
(iv) If $ A \in {\mathcal{I}} $-$ {\beta}_JO(X) $, then $ A = \mathcal{I} $-$ {\bigwedge_{\beta}}_{J}(A). $ (v) $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J}(\cup\{A_{\alpha}:\alpha \in \Delta\}) = \cup\{\mathcal{I} $-$ {\bigwedge_{\beta}}_{J}(A_{\alpha}):\alpha \in \Delta\}. $
(vi) $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J}(\cap\{A_{\alpha}:\alpha \in \Delta\})\subseteq\cap\{\mathcal{I} $-$ {\bigwedge_{\beta}}_{J}(A_{\alpha}):\alpha \in \Delta\}. $
Proof. I prove only (v) and (vi) since the other are consequences of Definition 5.1.
(v) First for each $ \alpha \in \Delta, \mathcal{I} $-$ {\bigwedge_{\beta}}_{J}(A_{\alpha})\subseteq \mathcal{I} $-$ {\bigwedge_{\beta}}_{J}({\cup}_{\alpha \in \Delta}A_{\alpha}). $ Hence, $ {\cup}_{\alpha \in \Delta} \mathcal{I} $-$ {\bigwedge_{\beta}}_{J}(A_{\alpha})\subseteq \mathcal{I} $-$ {\bigwedge_{\beta}}_{J}({\cup}_{\alpha \in \Delta}A_{\alpha}). $ Conversely, suppose that $ x\not \in {\cup}_{\alpha \in \Delta} \mathcal{I} $-$ {\bigwedge_{\beta}}_{J}(A_{\alpha}). $ Then, $ x\not \in \mathcal{I} $-$ {\bigwedge_{\beta}}_{J}(A_{\alpha}) $ for each $ \alpha \in \Delta $ and hence there exists $ G_{\alpha} \in {\mathcal{I}} $-$ {\beta}_JO(X) $ such that $ A_{\alpha} \subseteq G_{\alpha} $ and $ x\not\in G_{\alpha} $ for each $ \alpha \in \Delta. $ I have that $ {\cup}_{\alpha \in \Delta} A_{\alpha} \subseteq {\cup}_{\alpha \in \Delta} G_{\alpha} $ and $ {\cup}_{\alpha \in \Delta} G_{\alpha} $ is $ {\mathcal{I}} $-$ {\beta}_J $-open set which does not contain $ x. $ Therefore, $ x\not\in \mathcal{I} $-$ {\bigwedge_{\beta}}_{J}({\cup}_{\alpha \in \Delta}A_{\alpha}). $ Thus, $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J}({\cup}_{\alpha \in \Delta}A_{\alpha}) \subseteq {\cup}_{\alpha \in \Delta}\mathcal{I} $-$ {\bigwedge_{\beta}}_{J}(A_{\alpha}). $
(vi) Suppose that, $ x\not\in \cap\{\mathcal{I} $-$ {\bigwedge_{\beta}}_{J}(A_{\alpha}):\alpha \in \Delta\}. $ There exists $ \alpha_{0}\in \Delta $ such that $ x\not\in \mathcal{I} $-$ {\bigwedge_{\beta}}_{J}(A_{{\alpha}_{0}}) $ and there exists $ {\mathcal{I}} $-$ {\beta}_J $-open set $ G $ such that $ x\not\in G $ and $ A_{{\alpha}_{0}} \subseteq G. $ I have that $ {\cap}_{\alpha \in \Delta}A_{{\alpha}}\subseteq A_{{\alpha}_{0}}\subseteq G $ and $ x\not\in G. $ Therefore, $ x\not\in \mathcal{I} $-$ {\bigwedge_{\beta}}_{J}(\cap\{A_{\alpha}:\alpha \in \Delta\}). $
Remark 5.1. The inclusion in Lemma 5.1 parts (i) and (vi) can not be replaced by equality relation. Moreover, the converse of part (ii) is not necessarily true as shown in Example 3.3 that:
(i) For part (i), if $ A = \{a\}, $ then $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J}(A) = \{a, b\} $ and $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J}(A)\nsubseteq A. $
(ii) For part (vi), if $ A = \{b\} $ and $ B = \{a\}, $ then $ A\cap B = \phi $ and $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J}(A) = \{b\}, \mathcal{I} $-$ {\bigwedge_{\beta}}_{J}(B) = \{a, b\}, \mathcal{I} $-$ {\bigwedge_{\beta}}_{J}(A\cap B) = \phi $ and $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J}(A)\cap \mathcal{I} $-$ {\bigwedge_{\beta}}_{J}(B) = \{b\}\nsubseteq \mathcal{I} $-$ {\bigwedge_{\beta}}_{J}(A\cap B) = \phi. $
(iii) For part (ii), if $ A = \{a\} $ and $ B = \{b\}, $ then $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J}(A) = \{a, b\} $ and $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J}(B) = \{b\} $. Therefore, $ \mathcal{I} $-$ {\bigwedge_{\beta}}(A)\subseteq \mathcal{I} $-$ {\bigwedge_{\beta}}_{J}(B), $ but $ A\nsubseteq B. $
Definition 5.2. Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS, $ \mathcal{I} $ be an ideal on $ X $ and $ A \subseteq X $. A subset $ A $ is called an $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J} $-set if $ A = \mathcal{I}-{\bigwedge_{\beta}}_{J}(A). $ The family of all $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J} $-sets and $ \mathcal{I} $-$ {\bigvee_{\beta}}_{J} $-sets are denoted by $ \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{J} $ and $ \Gamma^{\mathcal{I}-{\bigvee_{\beta}}}_{J} $ respectively.
Example 5.1. In Example 3.1, $ \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{R} = P(X), $ in Example 3.2, $ \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{R} = P(X)-\{\{a\}, \{b\}, \{a, b\}\} $ and in Example 3.2, $ \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{R} = \{X, \phi, \{b\}, \{c\}, \{d\}, \{e\}, \{a, b\}, \{b, c\}, \{b, d\}, \{b, e\}, \{ c, d\}, \{c, e\}, \{d, e\}, \{a, b, c\}, \{a, b, \\ e\}, \{a, b, d\}, \{b, c, d\}, \{b, c, e\}, \{b, d, e\}, \{c, d, e\}, \{a, b, c, d\}, \{a, b, c, e\}, \{a, b, d, e\}, \{b, c, d, e\}\}. $
The following proposition shows that the concept of $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J} $-sets is an extension of the concept of $ {\bigwedge_{\beta}}_{J} $-sets.
Proposition 5.1. Every $ {\bigwedge_{\beta}}_{J} $-set is $ {\mathcal{I}} $-$ {\bigwedge_{\beta}}_{J} $-set.
Proof. By using Definitions 2.13 [11] and 5.2.
Remark 5.2. (i) According to Remark 2.1 [8] and Propositions 2.2 [11], 5.1 the current Definition 5.2 is also generalization of any $ J $-near open sets in Definition 2.6 [8] such as, $ P_J $-open, $ S_J $-open and $ \alpha_J $-open sets.
(ii) The converse of Proposition 5.1 is not necessarily true as shown in the following example.
Example 5.2. Let
and
be a binary relation defined on $ X $ thus $ a\mathcal{R} = b\mathcal{R} = \{a, c\}, c\mathcal{R} = \{c\} $ and $ d\mathcal{R} = \{d\}. $ Then, the topology associated with this relation is $ \tau_R = \{X, \phi, \{c\}, \{d\}, \{a, c\}, \{c, d\}, \{a, c, d\}\}. $ It is clear that $ \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{R} = P(X) $ and $ \tau^{\bigwedge_{\beta}}_{R} = \{X, \phi, \{b\}, \{c\}, \{d\}, \{a, c\}, \{b, c\}, \{b, d\}, \{c, d\}, \{a, b, c\}, \{a, c, d\}, \{b, c, d\}\}. $
The following theorem shows that Hosny's Definition 2.13 [11] is a special case of the current definition.
Theorem 5.1. Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS and $ \mathcal{I} $ be an ideal on $ X $. If $ \mathcal{I} = \{\phi\} $ in the current Definition 5.2, then I get Hosny 's Definition 2.13 [11].
Proof. Straightforward.
The following proposition shows that $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J} $-sets are generalization of $ \mathcal{I} $-$ {\beta}_{J} $-open sets in Definition 2.16 [12]. Consequently, it is also generalization of any $ {\mathcal{I}} $-$ J $-near open sets in Definition 2.16 [12] such as, $ {\mathcal{I}} $-$ P_J $-open, $ {\mathcal{I}} $-$ S_J $-open and $ {\mathcal{I}} $-$ \alpha_J $-open sets.
Proposition 5.2. Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS and $ \mathcal{I} $ be an ideal on $ X. $ Then, the following implications hold:
Proof. Straightforward by Proposition 2.3 [12], Definitions 2.16 [12] and 29.
Remark 5.3. The converse of Proposition 5.2 is not necessarily true as shown in Example 3.3, $ \{e\} $ is an $ {\mathcal{I}} $-$ {\bigwedge_{\beta}}_{R} $-set, but it is not an $ {\mathcal{I}} $-$ {\beta}_{R} $-open set.
Proposition 5.3. Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS and $ \mathcal{I} $ be an ideal on $ X $. Then, the following implications hold:
Proof. By Propositions 2.4 [12] and 5.2, the proof is obvious.
In the following lemma I summarize the fundamental properties of $ {\mathcal{I}} $-$ {\bigwedge_{\beta}}_{J} $-sets.
Lemma 5.2. For subsets $ A, B $ and $ A_{\alpha} (\alpha \in \Delta) $ of a $ J $-ndS $ (X, \mathcal{R}, \Xi_J), $ the following implications hold:
(i) $ X, \phi $ are $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J} $-sets.
(ii) If $ A_{\alpha} $ is an $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J} $-set $ \forall \alpha \in \Delta, $ then $ {\cup}_{\alpha \in \Delta}A_{\alpha} $ is an $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J} $-set.
(iii) If $ A_{\alpha} $ is an $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J} $-set $ \forall \alpha \in \Delta, $ then $ {\cap}_{\alpha \in \Delta}A_{\alpha} $ is an $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J} $-set.
Proof. This follows from Lemma 5.1.
Remark 5.4. It is clear from (i)–(iii) in Lemma 5.2 that the family of all $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J} $-sets forms a topology.
Remark 5.5. The $ \mathcal{I} $-$ {\delta\beta}_{J} $-open sets of Definition 3.1 and the current Definition 5.2 of $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J} $-sets are different and independent. Example 3.3 shows that $ \{a\} $ is an $ \mathcal{I} $-$ {\delta\beta}_{J} $-open set, but it is not an $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J} $-set. Moreover, it shows that $ \{e\} $ is an $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J} $-set, but it is not an $ \mathcal{I} $-$ {\delta\beta}_{J} $-open set.
Remark 5.6. Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS, $ \mathcal{I} $ be an ideal on $ X $ and $ A \subseteq X. $ Then the following statements are not true in general:
(i) $ \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{U} \subseteq \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{R} \subseteq \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{I}. $
(ii) $ \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{U} \subseteq \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{L} \subseteq \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{I}. $
(iii) $ \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{ < U > } \subseteq \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{ < R > } \subseteq \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{ < I > }. $
(iv) $ \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{ < U > } \subseteq \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{ < L > } \subseteq \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{ < I > }. $
(v) $ \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{R} $ is the dual of $ \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{L}. $
(vi) $ \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{ < R > } $ is the dual of $ \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{ < L > }. $
So, the relationships among $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J} $-sets are not comparable as in Example 3.3:
(i) $ \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{R} = \{X, \phi, \{b\}, \{c\}, \{d\}, \{e\}, \{a, b\}, \{b, c\}, \{b, d\}, \{b, e\}, \{ c, d\}, \{c, e\}, \{d, e\}, \{a, b, c\}, $$\{a, b, d\}, \{a, b, e\}, \\\{b, c, d\}, \{b, c, e\}, \{b, d, e\}, \{c, d, e\}, \{a, b, c, d\}, \{a, b, c, e\}, \{a, b, d, e\}, \{b, c, d, e\}\}. $
(ii) $ \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{L}(X) = \{X, \phi, \{a\}, \{b\}, \{c\}, \{e\}, \{a, b\}, \{a, c\}, \{a, e\}, \{b, c\}, \{b, e\}, $$\{c, e\}, \{d, e\}, \{a, b, c\}, \{a, b, e\}, \\\{a, c, e\}, \{a, d, e\}, \{b, c, e\}, \{b, d, e\}, \{c, d, e\}, \{a, c, d, e\}, \{a, b, c, e\}, \{a, b, d, e\}, \{b, c, d, e\}\}. $
(iii) $ \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{I}(X) = P(X). $
(iv) $ \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{U}(X) = P(X). $
(v) $ \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{ < R > }(X) = \{X, \phi, \{b\}, \{c\}, \{d\}, \{e\}, \{a, b\}, \{b, c\}, \{b, d, \},$$ \{b, e\}, \{ c, d\}, \{c, e\}, \{d, e\}, \{a, b, c\}, \{a, b, d\}, \\\{a, b, e\}, \{b, c, d\}, \{b, c, e, \}, \{b, d, e\}, \{ c, d, e\}, \{a, b, c, d\}, \{a, b, c, e\}, \{a, b, d, e\}, \{b, c, d, e\}\}. $
(vi) $ \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{ < L > }(X) = P(X). $
(vii) $ \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{ < I > }(X) = P(X). $
(viii) $ \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{ < U > }(X) = \{X, \phi, \{e\}, \{a, e\}, \{b, e\}, \{c, e\}, \{d, e\}, \{a, b, e\}, $$\{ a, c, e\}, \{a, d, e\}, \{b, c, e\}, \{b, d, e\}, \{ c, d, e\}, \\\{a, b, c, e\}, \{a, c, d, e\}, \{a, b, d, e\}, \{b, c, d, e\}\}. $
It is clear that
● $ \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{U}(X) \nsubseteq \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{R}(X). $
● $ \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{I}(X) \nsubseteq \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{R}(X). $
● $ \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{U}(X)\nsubseteq \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{L}X). $
● $ \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{I}(X)\nsubseteq \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{L}X). $
● $ \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{ < U > }(X) \nsubseteq \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{ < R > }(X). $
● $ \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{ < R > }(X) \nsubseteq \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{ < U > }(X). $
● $ \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{ < L > }(X) \nsubseteq \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{ < U > }(X). $
● $ \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{ < I > }(X) \nsubseteq \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{ < U > }(X). $
● $ \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{ < L > }(X) \nsubseteq \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{ < I > }(X). $
● $ \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{ < I > }(X) \nsubseteq \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{ < L > }(X). $
● $ \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{R}(X) $ is not the dual of $ \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{L} $ and $ \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{ < R > }(X) $ is not the dual of $ \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{ < L > }(X). $
● In a similar way, I can add examples to show that, $ \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{L}(X)\nsubseteq \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{I}(X), \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{R}(X)\nsubseteq \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{I}(X),τI−⋀βR(X)⊈τI−⋀βU(X),τI−⋀β<R>(X)⊈τI−⋀β<I>(X),τI−⋀β<U>(X)⊈τI−⋀β<I>(X),
\tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{ < U > }(X)\nsubseteq \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{ < L > }(X) $ and $ \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{ < L > }(X)\nsubseteq\tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{ < I > }(X). $
6.
Approximations spaces by using $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J} $-sets
The aim of this section is to present a new technique to define the approximations of rough sets by using the notion of $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J} $-sets. Some important significant properties of these approximations are investigated and compared to the previous approximations in Definitions 2.4 [2], 2.7 [8], 2.14 [11] and 2.17 [12]. The techniques in this section and Section 4 are different and independent.
Definition 6.1. Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS, $ \mathcal{I} $ be an ideal on $ X $ and $ A \subseteq X. $ The $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J} $-lower, $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J} $-upper approximations, $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J} $-boundary regions and $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J} $-accuracy of $ A $ are defined respectively by:
$ {\underline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A) = \cup\{G \in \tau^{{\mathcal{I}-{\bigwedge_{\beta}}}}_{J} : G \subseteq A\} = \mathcal{I} $-$ {\bigwedge_{\beta}}_{J} $-interior of $ A $.
$ {\overline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A) = \cap\{H \in \Gamma^{{\mathcal{I}-{\bigwedge_{\beta}}}}_{J}: A \subseteq H\} = \mathcal{I} $-$ {\bigvee_{\beta}}_{J} $-closure of $ A $.
$ {{\mathcal{BND}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A) = {\overline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A)-{\underline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A). $
$ {{ACC}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A) = \frac{|{\underline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A)|}{|{\overline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A)|}, $ where $ |{\overline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A)|\neq0. $
The following proposition studies the main properties of the current $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J} $-lower and $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J} $-upper approximations.
Proposition 6.1. Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS, $ \mathcal{I} $ be an ideal on $ X $ and $ A, B \subseteq X. $ Then,
(i) $ {\underline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A) < /italic > < italic > \subseteq A\subseteq{\overline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A) $ equality hold if $ A = \phi $ or $ X. $
(ii) $ A\subseteq B\Rightarrow {\overline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A)\subseteq {\overline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(B). $
(iii) $ A\subseteq B\Rightarrow {\underline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A)\subseteq {\underline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(B). $
(iv) $ {\overline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A\cap B)\subseteq{\overline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}}_{J}}(A)\cap{\overline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(B). $
(v) $ {\underline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}}_{J}}(A\cup B)\supseteq{\underline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A)\cup{\underline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(B). $
(vi) $ {\overline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A\cup B) = {\overline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A)\cup{\overline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(B). $
(vii) $ {\underline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A\cap B) = {\underline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A)\cap{\underline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(B). $
(viii) $ {\underline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A) = ({\overline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A^{'}))^{'} $, $ {\overline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A) = ({\underline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A^{'}))^{'} $.
(ix) $ {\overline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}({\overline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A)) = {\overline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A). $
(x) $ {\underline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}({\underline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A)) = {\underline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A). $
(xi) $ {\underline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}({\underline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A))\subseteq {\overline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}({\underline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A)). $
(xii) $ {\underline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}({\overline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A))\subseteq {\overline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}({\overline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A)). $
(xiii) $ x\in{\overline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A)\Leftrightarrow G\cap A\neq\phi, \forall G\in \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{J}, x\in G. $
(xiv) $ x\in{\underline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A)\Leftrightarrow \exists\; G\in \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{J}, x\in G, G\subseteq A. $
The proof of this proposition is simple using $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J} $-interior and $ \mathcal{I} $-$ {\bigvee_{\beta}}_{J} $-closure, so I omit it.
Remark 6.1. Example 3.3 shows that
(a) The inclusion in Proposition 6.1 parts (i), (iv), (v), (xi) and (xii) can not be replaced by equality relation:
(i) For part (i), if $ A = \{b, c, e\}, {\overline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{R}}}(A) = \{a, b, c, e\}, $ then $ {\overline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{R}}}(A)\nsubseteq A, $ take $ A = \{a\}, {\underline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{R}}}(A) = \phi $. Then, $ A\nsubseteq {\underline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{R}}}(A). $
(ii) For part (iv), if $ A = \{b, c, d, e\}, B = \{a, c, d, e\}, A\cap B = \{c, d, e\}, {\overline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{R}}}(A) = X, {\overline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{R}}}(B) = $$B, {\overline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{R}}}(A\cap B) = A\cap B, $ then $ {\overline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{R}}}(A)\cap {\overline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{R}}}(B) = \{a, c, d, e\}\nsubseteq\{c, d, e\} = {\overline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{R}}}(A\cap B). $
(iii) For part (v), if $ A = \{a\}, B = \{b\}, A\cup B = \{a, b\}, {\underline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{R}}}(A) = \phi, {\underline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{R}}}(B) = B, {\underline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{R}}}(A\cup B) = A\cup B $, then $ {\underline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{R}}}(A\cup B) = \{a, b\} \nsubseteq \{b\} = {\underline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{R}}}(A)\cup {\underline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{R}}}(B). $
(iv) For part (xi), if $ A = \{b, c, d, e\}, {\underline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{R}}}({\underline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{R}}}(A)) = A, {\overline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{R}}}({\underline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{R}}}(A)) = X $, then $ {\overline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{R}}}({\underline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{R}}}(A)) \nsubseteq {\underline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{R}}}({\underline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{R}}}(A)). $
(v) For part (xii), if $ A = \{a\}, {\overline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{R}}}({\overline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{R}}}(A)) = A, {\underline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{R}}}({\overline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{R}}}(A)) = \phi $, then $ {\overline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{R}}}({\overline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{R}}}(A)) \nsubseteq {\underline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{R}}}({\overline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{R}}}(A)). $
(b) The converse of parts (ii) and (iii) is not necessarily true:
(i) For part (ii), if $ A = \{a, b, c, e\}, B = \{b, c, d, e\}, $ then $ {\overline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{R}}}(A) = A, {\overline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{R}}}(B) = X $. Therefore, $ {\overline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{R}}}(A)\subseteq {\overline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{R}}}(B) $, but $ A\nsubseteq B. $
(ii) For part (iii), if $ A = \{a\}, B = \{c, d, e\}, $ then $ {\underline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{R}}}(A) = \phi, {\underline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{R}}}(B) = B $. Therefore, $ {\underline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{R}}}(A)\subseteq {\underline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{R}}}(B) $, but $ A\nsubseteq B. $
Definition 6.2. Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS, $ \mathcal{I} $ be an ideal on $ X $ and $ A \subseteq X. $ $ A $ is an $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J} $-definable ($ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J} $-exact) set if $ {\overline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A) = {\underline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A). $ Otherwise, $ A $ is an $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J} $-rough set.
In Example 3.3 $ A = \{c\} $ is $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{R} $-exact, while $ B = \{a\} $ is $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{R} $-rough.
Remark 6.2. Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS, $ \mathcal{I} $ be an ideal on $ X $ and $ A \subseteq X. $ Then the intersection of two $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J} $-rough sets does not need to be an $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J} $-rough set as in Example 3.3, $ \{c, d\} $ and $ \{c, e\} $, are $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{R} $-rough sets, but $ \{c, d\}\cap\{c, e\} = \{c\} $ is not an $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{R} $-rough set.
The following theorem and corollary present the relationships between the current approximations in Definition 6.1 and the previous ones in Definitions 2.4 [2], 2.7 [8] and 2.14 [11].
Theorem 6.1. Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS, $ \mathcal{I} $ be an ideal on $ X $ and $ A \subseteq X. $ Then
(i) $ {\underline{\mathcal{R}}}^{\alpha}_{J}(A)\subseteq {\underline{\mathcal{R}}}^{p}_{J}(A)\subseteq{\underline{\mathcal{R}}}^{\gamma}_{J}(A)\subseteq{\underline{\mathcal{R}}}^{\beta}_{J}(A)\subseteq{\underline{\mathcal{R}}}^{\bigwedge_{\beta}}_{J}(A)\subseteq {\underline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A). $
(ii) $ {\underline{\mathcal{R}}}^{\alpha}_{J}(A)\subseteq {\underline{\mathcal{R}}}^{s}_{J}(A)\subseteq{\underline{\mathcal{R}}}^{\gamma}_{J}(A)\subseteq{\underline{\mathcal{R}}}^{\beta}_{J}(A)\subseteq{\underline{\mathcal{R}}}^{\bigwedge_{\beta}}_{J}(A)\subseteq {\underline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A). $
(iii) $ {\underline{\mathcal{R}}}_{J}(A)\subseteq {\underline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A). $
(iv) $ {\overline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A)\subseteq {\overline{\mathcal{R}}}^{\bigwedge_{\beta}}_{J}(A)\subseteq {\overline{\mathcal{R}}}^{\beta}_{J}(A)\subseteq {\overline{\mathcal{R}}}^{\gamma}_{J}(A)\subseteq {\overline{\mathcal{R}}}^{p}_{J}(A)\subseteq {\overline{\mathcal{R}}}^{\alpha}_{J}(A). $
(v) $ {\overline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A)\subseteq {\overline{\mathcal{R}}}^{\bigwedge_{\beta}}_{J}(A)\subseteq {\overline{\mathcal{R}}}^{\beta}_{J}(A)\subseteq {\overline{\mathcal{R}}}^{\gamma}_{J}(A)\subseteq {\overline{\mathcal{R}}}^{s}_{J}(A)\subseteq {\overline{\mathcal{R}}}^{\alpha}_{J}(A). $
(vi) $ {\overline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A)\subseteq {\overline{\mathcal{R}}}_{J}(A). $
Proof. (i) By Theorem 2.3 [11], $ {\underline{\mathcal{R}}}^{\alpha}_{J}(A)\subseteq {\underline{\mathcal{R}}}^{p}_{J}(A)\subseteq{\underline{\mathcal{R}}}^{\gamma}_{J}(A)\subseteq{\underline{\mathcal{R}}}^{\beta}_{J}(A)\subseteq {\underline{\mathcal{R}}}^{\bigwedge_{\beta}}_{J}(A), $ and $ {\underline{\mathcal{R}}}^{\bigwedge_{\beta}}_{J}(A) = \cup\{G \in \tau^{\bigwedge_{\beta}}_{J} : G \subseteq A:G \subseteq A\}\subseteq \cup\{G \in \tau^{{\mathcal{I}-{\bigwedge_{\beta}}}}_{J} : G \subseteq A\} = {\underline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A) $ (by Proposition 5.1).
(ii) It is similar to (i).
(iii) By Theorem 2.3 [11], $ {\underline{\mathcal{R}}}_{J}(A)\subseteq {\underline{\mathcal{R}}}^{\bigwedge_{\beta}}_{J}(A), $ and by (1) $ {\underline{\mathcal{R}}}^{\bigwedge_{\beta}}_{J}(A)\subseteq {\underline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A). $ Hence, $ {\underline{\mathcal{R}}}_{J}(A)\subseteq {\underline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A). $
(iv)–(vi) They are similar to (i)–(iii).
Corollary 6.1. Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS, $ \mathcal{I} $ be an ideal on $ X $ and $ A \subseteq X. $ Then
(i) $ {{\mathcal{BND}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A)\subseteq {\mathcal{BND}}^{\bigwedge_{\beta}}_{J}(A)\subseteq {\mathcal{BND}}^{\beta}_{J}(A)\subseteq {\mathcal{BND}}^{\gamma}_{J}(A)\subseteq {\mathcal{BND}}^{p}_{J}(A)\subseteq {\mathcal{BND}}^{\alpha}_{J}(A). $
(ii) $ {{\mathcal{BND}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A)\subseteq {\mathcal{BND}}^{\bigwedge_{\beta}}_{J}(A) \subseteq {\mathcal{BND}}^{\beta}_{J}(A)\subseteq {\mathcal{BND}}^{\gamma}_{J}(A)\subseteq {\mathcal{BND}}^{s}_{J}(A)\subseteq {\mathcal{BND}}^{\alpha}_{J}(A) $.
(iii) $ {{\mathcal{BND}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A)\subseteq {\mathcal{BND}}_{J}(A). $
(iv) $ {ACC}^{\alpha}_{J}(A)\leqslant {ACC}^{p}_{J}(A)\leqslant {ACC}^{\gamma}_{J}(A)\leqslant {ACC}^{\beta}_{J}(A)\leqslant{ACC}^{\bigwedge_{\beta}}_{J}(A)\leqslant {ACC}^{\mathcal{I}-{\bigwedge_{\beta}}}_{J}(A). $
(v) $ {ACC}^{\alpha}_{J}(A)\leqslant {ACC}^{s}_{J}(A)\leqslant {ACC}^{\gamma}_{J}(A)\leqslant {ACC}^{\beta}_{J}(A)\leqslant{ACC}^{\bigwedge_{\beta}}_{J}(A)\leqslant {{ACC}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A). $
(vi) $ {ACC}_{J}(A)\leqslant {{ACC}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A). $
Corollary 6.2. Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS, $ \mathcal{I} $ be an ideal on $ X $ and $ A \subseteq X. $ Then
(i) $ A $ is $ \alpha_J $-exact $ \Rightarrow $ $ A $ is $ S_J $-exact $ \Rightarrow $ $ A $ is $ \beta_J $-exact $ \Rightarrow $ $ A $ is $ {\bigwedge_{\beta}}_{J} $-exact $ \Rightarrow $ $ A $ is $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J} $-exact.
(ii) $ A $ is $ P_J $-exact $ \Rightarrow $ $ A $ is $ \beta_J $-exact $ \Rightarrow $ $ A $ is $ {\bigwedge_{\beta}}_{J} $-exact $ \Rightarrow $ $ A $ is $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J} $-exact.
(iii) $ A $ is $ {J} $-exact $ \Rightarrow $ $ A $ is $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J} $-exact.
(iv) $ A $ is $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J} $-rough $ \Rightarrow $ $ A $ is $ {\bigwedge_{\beta}}_{J} $-rough $ \Rightarrow $ $ A $ is $ {\beta}_{J} $-rough $ \Rightarrow $ $ A $ is $ S_J $-rough $ \Rightarrow $ $ A $ is $ \alpha_J $-rough.
(v) $ A $ is $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J} $-rough $ \Rightarrow $ $ A $ is $ {\bigwedge_{\beta}}_{J} $-rough $ \Rightarrow $ $ A $ is $ {\beta}_{J} $-rough $ \Rightarrow $ $ A $ is $ P_J $-rough.
(vi) $ A $ is $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J} $-rough $ \Rightarrow $ $ A $ is $ {J} $-rough.
The converse of parts of Corollary 6.2 is not necessarily true as in Example 5.2:
(i) If $ A = \{a\}, $ then it is $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{R} $-exact, but it is neither $ {\bigwedge_{\beta}}_{R} $-exact nor $ {R} $-exact.
(ii) If $ A = \{b\}, $ then it is $ {R} $-rough and $ {\bigwedge_{\beta}}_{R} $-rough, but it is not $ \mathcal{I} $-$ \beta_{R} $-rough.
The following proposition and corollary are introduced the relationships between the current approximations in Definition 6.1 and the previous one in Definition 2.17 [12].
Proposition 6.2. Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS, $ \mathcal{I} $ be an ideal on $ X $ and $ A \subseteq X. $ Then
(i) $ {\underline{\mathcal{R}}^{\mathcal{I}-P}_J}(A)\subseteq {\underline{\mathcal{R}}^{\mathcal{I}-\beta}_J}(A)\subseteq {\underline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A). $
(ii) $ {\underline{\mathcal{R}}^{\mathcal{I}-\alpha}_J}(A)\subseteq {\underline{\mathcal{R}}^{\mathcal{I}-S}_J}(A)\subseteq {\underline{\mathcal{R}}^{\mathcal{I}-\beta}_J}(A)\subseteq {\underline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A) $.
(iii) $ {\overline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A)\subseteq{\overline{\mathcal{R}}^{\mathcal{I}-\beta}_J}(A)\subseteq {\overline{\mathcal{R}}^{\mathcal{I}-P}_J}(A). $
(iv) $ {\overline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A)\subseteq{\overline{\mathcal{R}}^{\mathcal{I}-\beta}_J}(A)\subseteq {\overline{\mathcal{R}}^{\mathcal{I}-S}_J}(A)\subseteq {\overline{\mathcal{R}}^{\mathcal{I}-\alpha}_J}(A). $
Proof. By Proposition 5.2, the proof is obvious.
Corollary 6.3. Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS, $ \mathcal{I} $ be an ideal on $ X $ and $ A \subseteq X. $ Then
(i) $ {{\mathcal{BND}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A)\subseteq {{\mathcal{BND}}^{\mathcal{I}-\beta}_J}(A)\subseteq {{\mathcal{BND}}^{\mathcal{I}-P}_J}(A). $
(ii) $ {{\mathcal{BND}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A)\subseteq {{\mathcal{BND}}^{\mathcal{I}-\beta}_J}(A)\subseteq {{\mathcal{BND}}^{\mathcal{I}-S}_J}(A)\subseteq {{\mathcal{BND}}^{\mathcal{I}-\alpha}_J}(A). $
(iii) $ {{ACC}^{\mathcal{I}-P}_J}(A)\leqslant {{ACC}^{\mathcal{I}-\beta}_J}(A)\leqslant {{ACC}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A) $.
(iv) $ {{ACC}^{\mathcal{I}-\alpha}_J}(A)\leqslant {{ACC}^{\mathcal{I}-S}_J}(A)\leqslant {{ACC}^{\mathcal{I}-\beta}_J}(A)\leqslant {{ACC}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A). $
Corollary 6.4. Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS, $ \mathcal{I} $ be an ideal on $ X $ and $ A \subseteq X. $ Then
(i) $ A $ is $ J $-exact $ \Rightarrow $ $ A $ is $ \mathcal{I} $-$ \alpha_J $-exact $ \Rightarrow $ $ A $ is$ \mathcal{I} $-$ S_J $-exact $ \Rightarrow $ $ A $ is $ \mathcal{I} $-$ \beta_J $-exact $ \Rightarrow $ $ A $ is $ \mathcal{I} $-$ {\bigwedge_{\beta}}_J $-exact.
(ii) $ A $ is $ \mathcal{I} $-$ P_J $-exact $ \Rightarrow $ $ A $ is $ \mathcal{I} $-$ \beta_J $-exact $ \Rightarrow $ $ A $ is $ \mathcal{I} $-$ {\bigwedge_{\beta}}_J $-exact.
(iii) $ A $ is $ \mathcal{I} $-$ {\bigwedge_{\beta}}_J $-rough $ \Rightarrow $ $ A $ is $ \mathcal{I} $-$ {\beta}_{J} $-rough $ \Rightarrow $ $ A $ is $ \mathcal{I} $-$ S_J $-rough $ \Rightarrow $ $ A $ is $ \mathcal{I} $-$ \alpha_J $-rough.
(iv) $ A $ is $ \mathcal{I} $-$ {\bigwedge_{\beta}}_J $-rough $ \Rightarrow $ $ A $ is $ \mathcal{I} $-$ {\beta}_{J} $-rough $ \Rightarrow $ $ A $ is $ \mathcal{I} $-$ P_J $-rough.
Remark 6.3. Example 3.3 shows that the converse of the implications in Corollaries 6.3, 6.4 and Proposition 6.2 is not true in general.
In Table 2, the lower, upper approximations, boundary region and accuracy are calculated by using Hosny's method 2.17 [12] and the current approximations in Definition 6.1 by using Example 3.3.
For example, take $ A = \{e\}, $ then the boundary and accuracy by the present method in Definition 6.1 are $ \phi $ and $ 1 $ respectively. Whereas, the boundary and accuracy by using Hosny's method 2.17 [12] are $ \{e\} $ and $ 0 $ respectively.
Remark 6.4. It should be noted that the $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J} $-approximations in this section and the $ \mathcal{I} $-$ {\delta\beta}_{J} $-approximations in Section 4 are different and independent. As, the concepts of $ \mathcal{I} $-$ {\delta\beta}_{J} $-open sets and $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J} $-sets are different and independent as shown in Remark 5.5.
7.
$ \mathcal{I} $-$ {\delta\beta}_{J} $-rough membership functions and $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J} $-rough membership functions
This section concentrates on generalization the concept of rough membership functions by introducing the concepts of $ \mathcal{I} $-$ {\delta\beta}_{J} $-rough membership functions and $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J} $-rough membership functions.
Definition 7.1. Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS, $ \mathcal{I} $ be an ideal on $ X, x\in X $ and $ A \subseteq X: $
(i) If $ x\in {\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_J}(A), $ then $ x $ is $ J $-$ {\delta\beta} $-surely with respect to $ \mathcal{I} $ ($ \mathcal{I}-{\delta\beta}_J $-surely) belongs to $ A $, denoted by $ x\; {\underline{\in}}^{\mathcal{I}-{\delta\beta}_J} A. $
(ii) If $ x\in{\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_J}(A), $ then $ x $ is $ J $-$ {\delta\beta} $-possibly with respect to $ \mathcal{I} $ (briefly $ \mathcal{I}-{\delta\beta}_J $-possibly) belongs to $ A $, denoted by $ x\; {\overline{\in}}^{\mathcal{I}-{\delta\beta}_J} A. $
(iii) If $ x\in {\underline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A), $ then $ x $ is $ J $-$ {\bigwedge_{\beta}} $-surely with respect to $ \mathcal{I} $ ($ \mathcal{I}-{\bigwedge_{\beta}}_J $-surely) belongs to $ A $, denoted by $ x\; {\underline{\in}}^{\mathcal{I}-{\delta\beta}_J} A. $
(iv) If $ x\in{\overline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A), $ then $ x $ is $ J $-$ {\bigwedge_{\beta}} $-possibly with respect to $ \mathcal{I} $ (briefly $ \mathcal{I}-{\bigwedge_{\beta}}_J $-possibly) belongs to $ A $, denoted by $ x\; {\overline{\in}}^{\mathcal{I}-{\bigwedge_{\beta}}_J} A. $
It is called $ J $-$ {\delta\beta} $-strong ($ J $-$ {\bigwedge_{\beta}} $-strong) and $ J $-$ {\delta\beta} $-weak ($ J $-$ {\bigwedge_{\beta}} $-weak) membership relations with respect to $ \mathcal{I} $ respectively.
Remark 7.1. According to Definitions 4.1 and 6.1, the $ \mathcal{I} $-$ {\delta\beta}_{J} $-lower, $ \mathcal{I} $-$ {\delta\beta}_{J} $-upper approximations, $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J} $-lower and $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J} $-upper approximations for any $ A\subseteq X $ can be written as:
(i) $ {\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_J}(A) = \{x\in X: x\; {\underline{\in}}^{\mathcal{I}-{\delta\beta}_J} A\}. $
(ii) $ {\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_J}(A) = \{x\in X: x\; {\overline{\in}}^{\mathcal{I}-{\delta\beta}_J} A\}. $
(iii) $ {\underline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A) = \{x\in X: x\; {\underline{\in}}^{\mathcal{I}-{\bigwedge_{\beta}}_J} A\}. $
(iv) $ {\overline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A) = \{x\in X: x\; {\overline{\in}}^{\mathcal{I}-{\bigwedge_{\beta}}_J} A\}. $
Lemma 7.1. Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS, $ \mathcal{I} $ be an ideal on $ X $ and $ A \subseteq X. $ Then
(i) If $ x\; {\underline{\in}}^{\mathcal{I}-{\delta\beta}_J} A, $ then $ x \in A. $
(ii) If $ x \in A, $ then $ x\; {\overline{\in}}^{\mathcal{I}-{\delta\beta}_J} A. $
(iii) If $ x\; {\underline{\in}}^{\mathcal{I}-{\bigwedge_{\beta}}_J} A, $ then $ x \in A. $
(iv) If $ x \in A, $ then $ x\; {\overline{\in}}^{\mathcal{I}-{\bigwedge_{\beta}}_J} A. $
Proof. Straightforward.
Remark 7.2. The converse of Lemma 7.1 is not true in general, as it is shown in Example 3.3 that if:
(i) $ A = \{a, b, c, d\}, $ then $ a \in A, $ but $ a{\underline{\not\in}}^{\mathcal{I}-{\delta\beta}_R}A. $
(ii) $ A = \{a, b, c, d\}, $ then $ e\; {\overline{\in}}^{\mathcal{I}-{\delta\beta}_R} A, $ but $ e \not\in A. $
(iii) $ A = \{a, c, d, e\}, $ then $ a \in A, $ but $ a\; {\underline{\not\in}}^{\mathcal{I}-{\bigwedge_{\beta}}_R} A. $
(iv) $ A = \{b, c, d\}, $ then $ e\; {\overline{\in}}^{\mathcal{I}-{\bigwedge_{\beta}}_R} A, $ but $ e \not\in A. $
Proposition 7.1. Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS, $ \mathcal{I} $ be an ideal on $ X $ and $ A \subseteq X. $ Then
(i) If $ x\; {\underline{\in}}_{J} A\Rightarrow x\; {\underline{\in}}^{{\eta}}_{J} A\Rightarrow x\; {\underline{\in}}^{\mathcal{I}-{\eta}}_{J} A\Rightarrow x\; {\underline{\in}}^{\mathcal{I}-{\delta\beta}_J} A. $
(ii) If $ x\; {\overline{\in}}^{\mathcal{I}-{\delta\beta}_J} A\Rightarrow x\; {\overline{\in}}^{\mathcal{I}-{\eta}}_{J} A\Rightarrow x \; {\overline{\in}}^{{\eta}}_{J} A\Rightarrow x \; {\overline{\in}}_{J} A. $
(iii) If $ x\; {\underline{\in}}_{J} A\Rightarrow x\; {\underline{\in}}^{{\eta}}_{J} A\Rightarrow x\; {\underline{\in}}^{\mathcal{I}-{\eta}}_{J} A\Rightarrow x\; {\underline{\in}}^{\mathcal{I}-{\bigwedge_{\beta}}_J} A. $
(iv) If $ x\; {\overline{\in}}^{\mathcal{I}-{\bigwedge_{\beta}}_J} A\Rightarrow x\; {\overline{\in}}^{\mathcal{I}-{\eta}}_{J} A\Rightarrow x \; {\overline{\in}}^{{\eta}}_{J} A\Rightarrow x \; {\overline{\in}}_{J} A. $
Proof. I prove (i) and the other similarly. $ x\; {\underline{\in}}_{J} A\Rightarrow x\; {\underline{\in}}^{{\eta}}_{J} A\Rightarrow x\; {\underline{\in}}^{\mathcal{I}-{\eta}}_{J} A $ by Proposition 2.6. Let $ x\; {\underline{\in}}^{\mathcal{I}-{\eta}}_{J} A. $ Then, $ x\in{\underline{\mathcal{R}}^{\mathcal{I}-\eta}_{J}}(A)\Rightarrow x\in {\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_J}(A) (\; by\; Theorem\; 4.1) \Rightarrow x\; {\underline{\in}}^{\mathcal{I}-{\delta\beta}_J} A. $
Remark 7.3. The converse of Proposition 7.1 is not true in general, as it is shown in
(i) Example 3.2 that if $ A = \{b, c\}, $ then $ b\; {\underline{\in}}^{\mathcal{I}-{\delta\beta}_R} A, $ but $ b\; {\underline{\not\in}}^{{\beta}}_{R} A. $
(ii) Example 3.2 that if $ A = \{b, c\}, $ then $ a\; {\overline{\in}}^{\mathcal{I}-{\beta}}_{R} A, $ but $ a\; {\overline{\not\in}}^{\mathcal{I}-{\delta\beta}_R} A. $
(iii) Example 3.3 that if $ A = \{e\}, $ then $ e\; {\underline{\in}}^{\mathcal{I}-{\bigwedge_{\beta}}_R} A, $ but $ e\; {\underline{\not\in}}^{{\beta}}_{R} A. $
(iv) Example 3.3 that if $ A = \{a, b, c, d\}, $ then $ e\; {\overline{\in}}^{\mathcal{I}-{\beta}}_{R} A, $ but $ e\; {\overline{\not\in}}^{\mathcal{I}-{\bigwedge_{\beta}}_R}. $
Definition 7.2. Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS, $ \mathcal{I} $ be an ideal on $ X, A \subseteq X $ and $ x \in X. $ The $ {\mathcal{I}-{\delta\beta}_J} $-rough membership functions of $ A $ are defined by $ \mu^{{\mathcal{I}-{\delta\beta}_J}}_{A}\rightarrow [0, 1], $ where
Remark 7.4. The $ {\mathcal{I}-{\delta\beta}_J} $-rough membership functions are used to define the $ \mathcal{I} $-$ {\delta\beta}_{J} $-lower and $ \mathcal{I} $-$ {\delta\beta}_{J} $-upper approximations as follows:
(i) $ {\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_J}(A) = \{x\in X:\mu^{{\mathcal{I}-{\delta\beta}_J}}_{A}(x) = 1\}. $
(ii) $ {\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_J}(A) = \{x\in X:\mu^{{\mathcal{I}-{\delta\beta}_J}}_{A}(x) > 0\}. $
(iii) $ {{\mathcal{BND}}^{\mathcal{I}-{\delta\beta}}_{J}}(A) = \{x\in X:0 < \mu^{{\mathcal{I}-{\delta\beta}_J}}_{A}(x) < 1\}. $
The following results give the fundamental properties of the $ {\mathcal{I}-{\delta\beta}_J} $-rough membership functions.
Proposition 7.2. Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS, $ \mathcal{I} $ be an ideal on $ X $ and $ A, B \subseteq X. $ Then
(i) If $ \mu^{{\mathcal{I}-{\delta\beta}_J}}_{A}(x) = 1\Leftrightarrow x\; {\underline{\in}}^{\mathcal{I}-{\delta\beta}_J} A. $
(ii) If $ \mu^{{\mathcal{I}-{\delta\beta}_J}}_{A}(x) = 0\Leftrightarrow x\in X-{\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_J}(A). $
(iii) If $ 0 < \mu^{{\mathcal{I}-{\delta\beta}_J}}_{A}(x) < 1\Leftrightarrow x\in {{\mathcal{BND}}^{\mathcal{I}-{\delta\beta}}_{J}}(A). $
(iv) If $ \mu^{{\mathcal{I}-{\delta\beta}_J}}_{A^{'}}(x) = 1-\mu^{{\mathcal{I}-{\delta\beta}_J}}_{A}(x), \forall\; x\in X. $
(v) If $ \mu^{{\mathcal{I}-{\delta\beta}_J}}_{A \cup B}(x)\geq max(\mu^{\mathcal{I}-{{\zeta}_J}}_{A}(x), \mu^{{\mathcal{I}-{\delta\beta}_J}}_{B}(x)), \forall\; x\in X. $
(vi) If $ \mu^{{\mathcal{I}-{\delta\beta}_J}}_{A \cap B}(x)\leq min(\mu^{{\mathcal{I}-{\delta\beta}_J}}_{A}(x), \mu^{{\mathcal{I}-{\delta\beta}_J}}_{B}(x)), \forall\; x\in X. $
Proof. I prove (i), and the others similarly.
$ x\; {\underline{\in}}^{\mathcal{I}-{\delta\beta}_J} A \Leftrightarrow x\in {\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_J}(A). $ Since $ {\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_J}(A) $ is $ \mathcal{I}-{\delta\beta}_{J} $-open set contained in $ A $, thus $ \frac{|{\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_J}(A) \cap A|}{| {\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_J}(A)(A)|} = \frac{| {\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_J}(A)|}{| {\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_J}(A)|} = 1. $ Then, $ 1\in \psi^{{\mathcal{I}-{\delta\beta}_J}}_{A}(x) $ and accordingly $ \mu^{{\mathcal{I}-{\delta\beta}_J}}_{A}(x) = 1. $
The following lemma is very interesting since it is given the relations between the $ J $-rough membership relations [3], $ J $-nearly rough membership relations [3], $ J $-nearly rough membership relations with respect to $ \mathcal{I} $ [12] and $ \mathcal{I} $-$ {\delta\beta}_{J} $-rough membership functions.
Lemma 7.2. Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS, $ \mathcal{I} $ be an ideal on $ X $ and $ A \subseteq X. $ Then
(i) $ \mu^{J}_{A}(x) = 1\Rightarrow \mu^{{{\eta}_J}}_{A}(x) = 1\Rightarrow \mu^{\mathcal{I}-{\eta_{J}}}_{A}(x) = 1\Rightarrow \mu^{{\mathcal{I}-{\delta\beta}_J}}_{A}(x) = 1, \forall\; x\in X. $
(ii) $ \mu^{J}_{A}(x) = 0\Rightarrow \mu^{{\eta_{J}}}_{A}(x) = 0\Rightarrow \mu^{\mathcal{I}-{\eta_{J}}}_{A}(x) = 0\Rightarrow \mu^{{\mathcal{I}-{\delta\beta}_J}}_{A}(x) = 0, \forall\; x\in X. $
Proof. (i) $ \mu^{J}_{A}(x) = 1\Rightarrow \mu^{{{\eta}_J}}_{A}(x) = 1\Rightarrow \mu^{\mathcal{I}-{\eta_{J}}}_{A}(x) = 1 $ directly from Lemma 2.1. Let $ \mu^{\mathcal{I}-{\eta_{J}}}_{A}(x) = 1, $ then $ x\in{\underline{\mathcal{R}}^{\mathcal{I}-\eta}_{J}}(A)\Rightarrow x\in {\underline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_J}(A)\Rightarrow \mu^{{\mathcal{I}-{\delta\beta}_J}}_{A}(x) = 1, \forall\; x\in X. $
(ii) $ \mu^{J}_{A}(x) = 0\Rightarrow \mu^{{\eta_{J}}}_{A}(x) = 0 $ directly from Lemma 2.1. Let $ \mu^{{\eta_{J}}}_{A}(x) = 0, $ then $ x\in X-{\overline{\mathcal{R}}^{\mathcal{I}-\eta}_{J}}(A)\Rightarrow x\in X-{\overline{\mathcal{R}}^{\mathcal{I}-{\delta\beta}}_J}(A)\Rightarrow \mu^{{\mathcal{I}-{\delta\beta}_J}}_{A}(x) = 0, \forall\; x\in X. $
Remark 7.5. The converse of Lemma 7.2 is not true in general, as it is shown in Example 3.2.
Definition 7.3. Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS, $ \mathcal{I} $ be an ideal on $ X, A \subseteq X $ and $ x \in X. $ The $ {\mathcal{I}-{\bigwedge_{\beta}}_J} $-rough membership functions of a $ J $-ndS on $ X $ for a $ A $ are defines by $ \mu^{{\mathcal{I}-{\bigwedge_{\beta}}_J}}_{A}\rightarrow [0, 1], $ where
Remark 7.6. The $ \mathcal{I} $-$ J $-nearly rough membership functions are used to define the $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J} $-lower and $ \mathcal{I} $-$ {\bigwedge_{\beta}}_{J} $-upper approximations as follows:
(i) $ {\underline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A) = \{x\in X:\mu^{{\mathcal{I}-{\bigwedge_{\beta}}_J}}_{A}(x) = 1\}. $
(ii) $ {\overline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A) = \{x\in X:\mu^{{\mathcal{I}-{\bigwedge_{\beta}}_J}}_{A}(x) > 0\}. $
(iii) $ {{\mathcal{BND}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A) = \{x\in X:0 < \mu^{{\mathcal{I}-{\bigwedge_{\beta}}_J}}_{A}(x) < 1\}. $
The following results give the fundamental properties of the $ {\mathcal{I}-{\bigwedge_{\beta}}_J} $-rough membership functions.
Proposition 7.3. Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS, $ \mathcal{I} $ be an ideal on $ X $ and $ A, B \subseteq X. $ Then
(i) If $ \mu^{{\mathcal{I}-{\bigwedge_{\beta}}_J}}_{A}(x) = 1\Leftrightarrow x {\underline{\in}}^{\mathcal{I}-{\bigwedge_{\beta}}_J} A. $
(ii) If $ \mu^{{\mathcal{I}-{\bigwedge_{\beta}}_J}}_{A}(x) = 0\Leftrightarrow x\in X-{\overline{\mathcal{R}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A). $
(iii) If $ 0 < \mu^{{\mathcal{I}-{\bigwedge_{\beta}}_J}}_{A}(x) < 1\Leftrightarrow x\in {{\mathcal{BND}}^{\mathcal{I}-{\bigwedge_{\beta}}_{J}}}(A). $
(iv) If $ \mu^{{\mathcal{I}-{\bigwedge_{\beta}}_J}}_{A^{'}}(x) = 1-\mu^{{\mathcal{I}-{\bigwedge_{\beta}}_J}}_{A}(x), \forall\; x\in X. $
(v) If $ \mu^{{\mathcal{I}-{\bigwedge_{\beta}}_J}}_{A \cup B}(x)\geq max(\mu^{{\mathcal{I}-{\bigwedge_{\beta}}_J}}_{A}(x), \mu^{{\mathcal{I}-{\bigwedge_{\beta}}_J}}_{B}(x)), \forall\; x\in X. $
(vi) If $ \mu^{{\mathcal{I}-{\bigwedge_{\beta}}_J}}_{A \cap B}(x)\leq min(\mu^{{\mathcal{I}-{\bigwedge_{\beta}}_J}}_{A}(x), \mu^{{\mathcal{I}-{\bigwedge_{\beta}}_J}}_{B}(x)), \forall\; x\in X. $
Proof. It is similar to Proposition 7.2.
Lemma 7.3. Let $ (X, \mathcal{R}, \Xi_J) $ be a $ J $-ndS, $ \mathcal{I} $ be an ideal on $ X $ and $ A \subseteq X. $ Then
(i) $ \mu^{J}_{A}(x) = 1\Rightarrow \mu^{{{\eta}_J}}_{A}(x) = 1\Rightarrow \mu^{\mathcal{I}-{\eta_{J}}}_{A}(x) = 1 \Rightarrow \mu^{{\mathcal{I}-{\bigwedge_{\beta}}_J}}_{A}(x) = 1, \forall\; x\in X. $
(ii) $ \mu^{J}_{A}(x) = 0\Rightarrow \mu^{{\eta_{J}}}_{A}(x) = 0\Rightarrow \mu^{\mathcal{I}-{\eta_{J}}}_{A}(x) = 0\Rightarrow \mu^{{\mathcal{I}-{\bigwedge_{\beta}}_J}}_{A}(x) = 0, \forall\; x\in X. $
Proof. It isimilar to Lemma 7.2.
Remark 7.7. The converse of Lemma 7.3 is not true in general, as it is shown in Example 3.3.
Remark 7.8. According to Lemmas 7.2 and 7.3, the current Definitions 7.2 and 7.3 are also generalization of the approaches in [22] and 2.19 [28].
8.
Applications
Finally in this section, an applied example in Chemistry field is introduced by applying the present Definition 3.1 and the previous one 2.6 in [8]. Furthermore, a practical example uses an equivalence relation that induced from an information system is introduced to compare between the current approach in Definition 7.2 and the previous approach for Pawlak and Skoworn 2.19 [28].
Example 8.1. Let $ X = \{x_1, x_2, x_3, x_4, x_5\} $ be five amino acids (for short, AAs). The (AAs) are described in terms of seven attributes: $ a_1 = $ PIE and $ a_2 = $ SAC = surface area, $ a_3 = $ MR = molecular refractivity, $ a_4 = $ LAM = the side chain polarity and $ a_5 = $ Vol = molecular volume ([10,34]). Table 3 shows all quantitative attributes of five AAs.
I consider the relations on $ X $ defined as: $ \mathcal{R}_i = \{(x_i, x_j) : x_i(a_k)-x_j(a_k) < \frac{\sigma_{k}}{2}, i, j, k = 1, 2, ..., 5\} $ where $ \sigma_{k} $ represents the standard deviation of the quantitative attributes.
The right neighborhoods $ \forall x\in X $ with respect to the relations are shown in Table 4.
The intersection of all right neighborhoods $ \forall x\in X $ is:
$ x_1\mathcal{R} = {\cap}_{k = 1}^{5}(x_1\mathcal{R}_k) = \{x_1, x_4\}, x_2\mathcal{R} = {\cap}_{k = 1}^{5}(x_2\mathcal{R}_k) = \{x_2, x_5\}, x3R=∩5k=1(x3Rk)={x2,x3,x4,x5},
x_4\mathcal{R} = {\cap}_{k = 1}^{5}(x_4\mathcal{R}_k) = \{x_4\}, x_5\mathcal{R} = {\cap}_{k = 1}^{5}(x_5\mathcal{R}_k) = \{x_5\}. $ Then, $ \tau_{R} = \{\phi, X, \{x_4\}, \{x_5\}, \{x_4, x_5\},
{x1,x4},{x2,x5},{x1,x4,x5},{x2,x4,x5},{x1,x2,x4,x5},{x1,x3,x4,x5}},βRO(X)=
\{\phi, X, \{x_4\}, \{x_5\}, \{x_1, x_4\}, \{x_1, x_5\}, \{x_2, x_5\}, \{x_3, x_4\}, \{x_3, x_5\}, \{x_4, x_5\}, \{x_1, x_3, x_5\},
{x1,x4,x5},{x2,x3,x5},{x2,x4,x5},,{x3,x4,x5},{x1,x2,x4,x5},{x1,x3,x4,x5},
\{x_2, x_3, x_4, x_5\}\}. $ Let $ \mathcal{I} = \{\phi, \{x_1\}\}, $ then $ \mathcal{I} $-$ {\delta\beta}_{R}O(X) = P(X). $
(i) It is clear that every $ \beta_R $-open is $ \mathcal{I} $-$ {\delta\beta}_{R} $-open, but the converse is not necessary to be true. For example take $ A = \{x_1\} $ which is $ \mathcal{I} $-$ {\delta\beta}_{R} $-open, but it is not $ \beta_R $-open. Hence, the current concept generalize and extend the previous one 2.6 in [8].
(ii) The current approximations which are depended on $ \mathcal{I} $-$ {\delta\beta}_{R} $-open is better than the previous approximations 2.7 [8] which depended on $ {\beta}_{R} $-open. As for any concept $ A\subseteq X $ (collection of Amino Acid), this concept is determine by the lower and upper approximations which defines its boundary. Moreover, the accuracy increases by the decreases of the boundary region. Clearly the accuracy measure by using the suggested class $ \mathcal{I} $-$ {\delta\beta}_{R} $-open in general is greater than the accuracy measure by using $ \beta_R $-open. For example take $ A = \{x_1, x_4, x_5\}, $ Then,
(a) by the current Definition 4.1, $ {{\mathcal{BND}}^{\mathcal{I}-{\delta\beta}}_{R}}(A) = \phi $ and $ {{ACC}^{\mathcal{I}-{\delta\beta}}_{R}}(A) = 1 $;
(b) by the previous one in Definition 2.7 [8], $ {\mathcal{BND}}^{\beta}_R(A) = \{2, 3\} $ and $ {ACC}^{\beta}_R(A) = \frac{3}{5}. $
(iii) Similarly, it is easy to calculate $ \mathcal{I} $-$ {\beta}_{R}O(X), \tau^{\mathcal{I}-{\bigwedge_{\beta}}}_{R} $ and their approximations by the same manner in Tables 1 and 2. This also shows that the present methods is better than the previous ones in [2,8,11,12].
Example 8.2. Consider the following information system as in Table 5. The data about six students is given as shown below:
From Table 5:
(i) The set of universe: $ X = \{x_1, x_2, x_3, x_4, x_5, x_6\}. $
(ii) The set of attributes: AT $ = \{Science, \; German, \; Mathematics\}. $
(iii) The sets of values:
and
I take the set of condition attributes, $ C = \{Science, German, Mathematics\}. $ Thus, the corresponding equivalence relation is $ \mathcal{R} = \{(x_1, x_1), (x_2, x_5), (x_3, x_3), (x_4, x_4), (x_5, x_2), (x_6, x_6)\}, $ let $ \mathcal{I} = \{\phi, \{x_1\}\}. $ Then, $ {\mathcal{I}} $-$ {\delta\beta}_{R}O(X) = P(X). $ Let $ A $ (Decision: Accept) $ = \{x_1, x_2, x_3, x_6\}. $ Then
(i) The rough membership functions with respect to the Definition of Pawlak and Skowron 19 [28] are computed as follows:
(ii) The $ \mathcal{I} $-$ {\delta\beta}_{R} $-rough membership functions in Definition 7.2 are calculated as follows:
Obviously, the current Definition 7.2 is accurate more than the Definition of Pawlak and Skowron 2.19 [28].
Remark 8.1. It should be noted that for some elements that have decision (Reject) such that $ x_5 $
(i) The rough membership function with respect to the Definition of Pawlak and Skowron 2.19 [28] is $ \mu^{A}(x_5) = \frac{1}{2}. $ This means that $ x_5 $ may belong to the set $ A $ (Decision: Accept), $ A = \{x_1, x_2, x_3, x_6\} $ and this contradicts to Table 5.
(ii) The $ \mathcal{I} $-$ {\delta\beta}_{R} $-rough membership function in Definition 7.2 is $ \mu^{{\mathcal{I}-{\delta\beta}_{R}}}_{A}(x_5) = 0. $ This means that $ x_{5}\not\in A $ (Decision: Accept) $ = \{x_1, x_2, x_3, x_6\} $ which is coincide with Table 5.
9.
Conclusions
Rough set theory is a vast area that has varied inventions, applications and interactions with many other branches of mathematical sciences. Deriving rough sets from topology is one such interaction. There is a close homogeneity between rough set theory and general topology. Topology is a rich source for constructs that can be helpful to enrich the original model of approximation spaces. Ideal is a fundamental concept in topological spaces and played an important role in the study of a generalization of rough set. Since the advent of the ideals, several research papers with interesting results in different respects came to existence. In the current results, ideals were very helpful for increasing the current lower approximations and decreasing the current upper approximations. Consequently, they reduced the boundary region and increased the accuracy measure. So, they removed the vagueness of a concept that is an essential goal for the rough set. The properties of the proposed concepts and methods were studied. It should be noted that the two methods in this paper were different and independent as it was shown. I gave not only their characterizations but also discussed the relationships among them and between the previous ones and shown to be more general. The present accuracy measures were more accurate and higher than the previous ones. Since, the boundary regions were decreased (or empty) by increasing the lower approximations and decreasing the upper approximations. Further, two kind of the rough membership functions with respect to ideals were introduced as extension of the former functions. Moreover, an applied example in chemical field was suggested by applying the current methods to illustrate the concepts in a friendly way. Finally, a particle example was provided to clarify the technique of the present rough membership functions and demonstrate their utility and efficiency. I hope the beauty of this work can pave way to many other research fields such as:
(i) Fuzzy topologies, soft topologies and Multiset topologies.
(ii) New applications of these new approximations in various real-life fields.
This is a part of the future research.
Acknowledgments
The author extend her appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through research groups program under grant (R.G.P.1/15/42). She also would like to express her sincere thanks to the editor and anonymous reviewers for their valuable comments and suggestions which have helped immensely in improving the quality of the paper.
Conflict of interest
This work does not have any conflicts of interest.
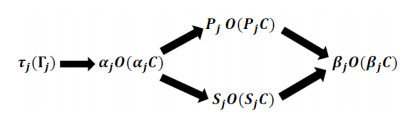









 DownLoad:
DownLoad:



