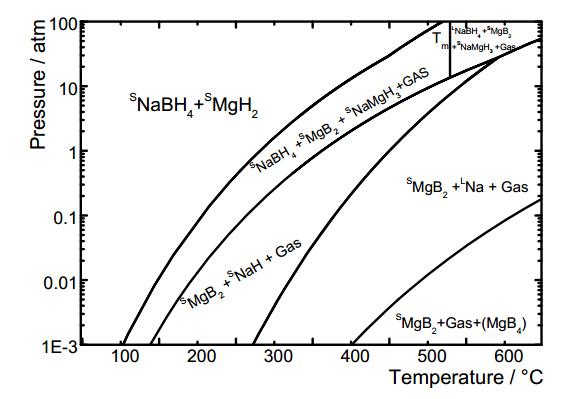
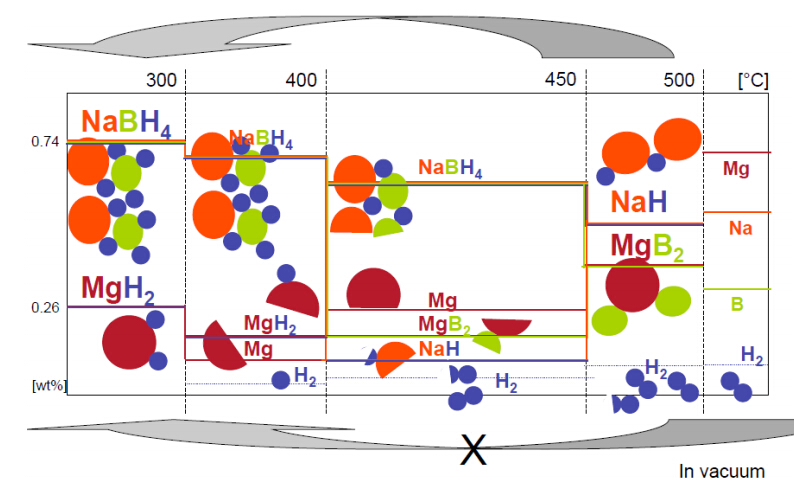
This review on materials for hydrogen storage in the solid state gives a brief discussion underlying reasons and driving forces of this specific field of research and development (the why question). This scenario is followed by an outline of the main materials investigated as options for hydrogen storage (the what exactly). Then, it moves into breakthroughs in the specific case of solid state storage of hydrogen, regarding both materials (where to store it) and properties (how it works). Finally, one of early model systems, namely NaBH4/MgH2 (the case study), is discussed more comprehensively to better elucidate some of the issues and drawbacks of its use in solid state hydrogen storage.
1.
Introduction
The study of the long term symbiosis and complex dynamics among different interacting species is a hot topic and has attracted more and more attention of mathematicians and biologists over decades. Under the observations of interactions between various species, researchers purposed many appropriated mathematical models. Among these models, the Lotka-Volterra predator-prey model proposed by Lotka[1] and Volterra[2] is a widely known model due to its universal application and significance. Now, the various Lotka-Volterra models are developed to study the complex population dynamics in different ecological situations. Hence, taking into consideration prey competition and different functional responses, the original Lotka-Volterra model is extended to the generalized Gause type case[3,4]
where $ u $ and $ v $ separately represent the amount of prey and predators; $ a $ and $ b $ separately represent the intrinsic growth rate and compete rate of prey; $ c $ and $ d $ separately represent the death rate and maximal growth rate of predators; $ p(u) $ is the functional response describes the variation of the amount of prey affected by the attacks of predators.
However, it is worth noticing that not only is there competition among prey, but predators also compete each other for the limited resource such as the size of the habitat to live and reproduce [5]. Hence, by introducing predator competition, system (1.1) can be rewritten as
where $ h $ is the competition rate of predators. This is the well-known Bazykin's predator-prey model proposed in [6].
The functional response $ p(u) $ is usually classified into four types firstly purposed by the biologist Holling [7,8], for example the Holling Type Ⅰ functional response
where $ m $ is a maximal per capita consumption rate and $ \alpha $ is the half-saturation constant-the prey's number at which the per capita consumption rate is half of its maximum $ m $, and other three Holling Type functional responses, see Table 1. Note that these functional response are all bounded function which is suitable for actual field data and the Holling type Ⅰ functional response (1.3) is continuous but not smooth, which is also called the piecewise-smooth Holling type Ⅰ functional response.
Recent researches related to the Bazykin's model with different functional responses obtain some interesting complex dynamics and bifurcations. For example, Bzaykin [9] showed that there is a threshold value $ c_1 $ such that system (1.2) with the functional response $ p(u) = mu $ has the globally asymptotically stable boundary equilibrium $ (\frac{a}{b}, 0) $ if $ c > c_1 $ and the unique globally asymptotically stable positive equilibrium if $ c < c_1 $; many researchers [5,6,9,10,11,12,13,14,15,16,17] including Bazykin et al.[5,6,9,10], Hainzl et al.[11,12] and Lu and Huang[13] investigated system (1.2) with Holling type Ⅱ functional response by the theoretical analysis or numerical methods and got complex dynamics and rich bifurcation phenomenons such as the location and stability of equilibriums, the existence of limit cycles, the degenerate Bogdanov-Takens bifurcation, the Hopf bifurcation, etc.
In this paper, we investigate Bazykin's predator-prey model (1.2) with piecewise smooth Holling type Ⅰ functional response (1.3). Before going into details, we apply the following rescaling transformation
and removing the bar notation, then the system (1.2) can be rewrote as the following non-dimensional system
with
where $ u $ and $ v $ are the non-dimensional variables; $ b = \dfrac{bd}{a} $, $ \epsilon = \dfrac{dm}{a} $, $ h = \dfrac{ha\alpha}{dm^2} $ and $ c = \dfrac{c}{dm} $ are non-dimensional parameters. Furthermore, we assume the growth rate of predators is much smaller than that of prey which means that system (1.4) is a piecewise-smooth slow-fast system with the small parameter $ 0 < \epsilon\ll1 $. Note that our assumption is reasonable because species at different trophic levels have different growth rates, which may vary several orders of magnitude, and the growth time of individuals increases gradually from the bottom of the food chain to the top [18]. Moreover, many observations of interactions between prey and predators such as hares and lynx [19], phytoplankton and zooplankton [20], insects and birds [21], etc. indicate the prey grow much faster than predators.
So far, there are few studies on the slow-fast Bazykin's model and these studies mainly focus on the dynamics of the model (1.2) with smooth Holling Ⅱ functional response [15,16] such as relaxation oscillation cycles, canard phenomenon and so on. Hence, Our main aim in this paper is to study the dynamics of the slow-fast Bazykin's model with a piecewise-smooth functional response (1.4) by using the geometrical singular perturbation theory [22,23,24,25,26,27,28,29] and piecewise-smooth dynamical system theory [30,31,32,33,34,35]. For the various values of parameters, we will show that there are the coexistence of two relaxation oscillation cycles with different stability, an unstable relaxation oscillation cycle surrounded by a stable homoclinic cycle and a heteroclinic cycle enclosing an unstable relaxation oscillation cycle. Furthermore, the system (1.4) undergoes a series of bifurcations such as Saddle-node bifurcation and Discontinuous saddle-node bifurcation of codimension $ 1 $. Moreover, we also give some conditions of the global stability of the unique positive equilibrium. Numerical simulations with the help of the "PPlane8" tool of Matlab [36] are presented to illustrate the theoretical results.
The rest of this paper is organized as follows. In Section $ 2 $, we study the critical manifold and the existence and types of equilibriums of system (1.4). In Section $ 3 $, we show that the dynamics and bifurcations of system (1.4) such as relaxation oscillation cycles, homoclinic cycle, heteroclinic cycle, etc. A brief discussion is given in the last section.
2.
The critical manifold and equilibriums
Based on the ecological viewpoint, we are keen on the dynamics of the system (1.4) in the first quadrant $ R^2_{+} = \{(u, v)\mid u\geq0, v\geq0\} $ and the switching boundary $ \Sigma = \{(u, v)\mid u = 1\} $ splits the first quadrant into two regions denoted by $ \Sigma^{(-)} = \{(u, v)\mid 0 < u < 1, v\geq0\} $ and $ \Sigma^{(+)} = \{(u, v)\mid u > 1, v\geq0\} $. The system (1.4) is smooth in $ \Sigma^{(\mp)} $ and determined by the following systems
and
Since the vector field is locally Lipschitz, the fundamental existence and uniqueness theory is true for the system (1.4) [31]. Note that the trajectories of the system (1.4) transversally pass through the switching boundary $ \Sigma $. Moreover, in order to guarantee the density of preys can support the growth of predators, we assume throughout the paper that $ 0 < b < \frac{1}{4} $ and $ 0 < c < 1 $. These are also the necessary condition for the existence of relaxation oscillation cycles. Hence, we will study the system (1.4) in the parametric region
Before going into the detail dynamics, we firstly show some basic properties of the system (1.4).
Lemma 2.1. The system (1.4) has the invariant set
and it also has no limit cycle which is entirely lied in the region $ \Sigma^{(-)} $.
Proof. It is clear that $ u = 0 $ and $ v = 0 $ are two invariant straight lines of system (1.4) and the boundary of set $ \Omega $ is
For $ (u, v)\in\partial\Omega $, we have
which means that the vector field of the system (1.4) in the line $ \partial\Omega $ never points outside. Hence, any trajectories of the system (1.4) are confined in the set $ \Omega $ as they enter $ \Omega $ in finite time.
For $ (u, v)\in\Sigma^{(-)} $, we construct the Dulac function $ \varphi(u, v) = \frac{1}{uv} $ and have
which implies the system (1.4) has no limit cycles in the region $ \Sigma^{(-)} $ because of the Dulac's criteria. □
Hence, if the system (1.4) has a limit cycle, it will either entirely locate in the region $ \Sigma^{(+)} $ or consist of trajectories in the regions $ \Sigma^{(+)} $ and $ \Sigma^{(-)} $ and transversally pass through the switching boundary $ \Sigma $.
2.1. Critical manifold
Under the time scale transformation $ \tau = \epsilon t $, we can get the equivalent system
The systems (1.4) and (2.1) are individually known as the fast system and the slow system because of their different time scales. By setting $ \epsilon = 0 $ in systems (1.4) and (2.1), we get the degenerate system
and the layer system
Hence, the critical manifold is
which is composed of the singular points of layer system (2.3) and can be divided into three parts as follows, see Figure 1,
Note that the sub-manifold $ S^2_0 $ is a normally hyperbolic attracting sub-manifold and the non-normally hyperbolic points $ A(0, 1) $ and $ M(\frac{1}{2b}, \frac{1}{4b}) $ separately split the sub-manifolds $ S^1_0 $ and $ S^3_0 $ into the normally hyperbolic attracting sub-manifolds
and normally hyperbolic repelling sub-manifolds
For $ 0 < \epsilon\ll1 $, the Fenichel theory [22,23] indicates the normally hyperbolic attracting sub-manifolds $ S^2_0 $, $ S^{1a}_0 $ and $ S^{3a}_0 $ can be perturbed to the attracting slow manifolds $ S^2_{\epsilon} $, $ S^{1a}_{\epsilon} $ and $ S^{3a}_{\epsilon} $ and the normally hyperbolic repelling sub-manifolds $ S^{1r}_0 $ and $ S^{3r}_0 $ can be perturbed to the repelling slow manifolds $ S^{1r}_{\epsilon} $ and $ S^{3r}_{\epsilon} $. Hence, the trajectory starting near $ S^{1a}_0 $ is attracted to the $ v $-axis, then it moves down with $ O(\epsilon) $ speed. It is clear that the trajectory passes the non-hyperbolic point $ A(0, 1) $ and leaves the $ O(\epsilon) $ neighborhood of $ S^{1r}_0 $ at the point $ (0, p_\epsilon(v)) $ satisfying $ \lim\limits_{\epsilon\to0}p_{\epsilon}(v) = p_0(v) $. The function $ p_0(v) $ is called the entry-exit function [28,29] and satisfies the following lemma.
Lemma 2.2. For system (1.4) and $ v_0\in(1, +\infty) $, there is a unique $ p_0(v_0)\in (0, 1) $ satisfying
Proof. Let
it is easy to verify that $ I(1) < 0 $ and $ \lim\limits_{\tilde{v}\to0}I(\tilde{v}) = +\infty $. Since
there is a unique $ \tilde{v}^*\in(0, 1) $ such that $ I(v^*) = 0 $ which implies $ p_0(v_0) = v^* $.
□
Note that the above proof indicates the entry-exit function $ p_0(v_0) $ is monotone decreasing function in $ (1, +\infty) $.
2.2. Equilibriums and their types
In this subsection, we mainly study the existence and stability of equilibriums of system (1.4). We can get the equilibriums by a straight calculation of the following equations
and the dynamics of system (1.4) near these equilibriums are determined by the Jacobian matrix of system (1.4) at these equilibriums, which is given by
and
here $ (u^*, v^*) $ is the coordinate of these equilibriums. Now, set
we give the following lemmas about the existence and stability of equilibriums.
Lemma 2.3. For system (1.4), the following conclusions hold.
1) System (1.4) always has two trivial equilibriums $ O(0, 0) $ and $ B(\frac{1}{b}, 0) $ which are both saddle.
2) If $ h < h_1 $ or $ h > h_2 $, then system (1.4) has a stable equilibrium $ E_{1}(u_1, v_1) $ which are separately located in $ S_0^2 $ and $ S_0^{3a} $, see Figure 1(a), (e). More precisely, the equilibrium $ E_{1}(u_1, v_1) $ is a globally stable node when $ h > h_2 $, see Figure 2(a).
Proof. The number and locations of equilibriums of system (1.4) can be obtained by the straight calculation of Eq (2.6). Next, we determine the types of equilibriums $ O(0, 0) $, $ B(\frac{1}{b}, 0) $ and $ E_{1}(u_1, v_1) $. For equilibrium $ O(0, 0) $, the eigenvalues of the Jacobian matrix $ J^{(-)} $ are $ \lambda_1 = 1 $ and $ \lambda_2 = -\epsilon c < 0 $ which implies the equilibrium $ O(0, 0) $ is a saddle point. Similarly, the eigenvalues of the Jacobian matrix $ J^{(+)} $ at $ B(\frac{1}{b}, 0) $ are $ \lambda_1 = -1 $ and $ \lambda_2 = \epsilon(1-c) > 0 $ which indicates the equilibrium $ B(\frac{1}{b}, 0) $ is a saddle point. For equilibrium $ E_{1}(u_1, v_1)\in S_0^{3a} $, the similar calculation gives the eigenvalues of the Jacobian matrix $ J^{(+)} $ as $ \lambda_1 = 1-2bu_1 < 0 $ and $ \lambda_2 = \epsilon (c-1) < 0 $, which implies $ E_{1}(u_1, v_1)\in S_0^{3a} $ is a stable node. For equilibrium $ E_{1}(u_1, v_1)\in S_0^{2} $, we calculate the determinant and trace of Jacobian matrix $ J^{(-)} $ as
which implies $ E_{1}(u_1, v_1)\in S_0^{2} $ is stable.
Next, we will prove the global stability of equilibrium $ E_{1} $ when $ h > h_2 $. We construct the trapping region
and assert that the vector field of system (1.4) point inside at the boundary $ \partial\Omega_1 $. So the trajectories cannot leave after entering the region $ \Omega_1 $. Furthermore, we construct the same Dulac function in Lemma 2.1 as $ \varphi(u, v) = \frac{1}{uv} $ and have
Hence, based on the Dulac's criteria, the system (1.4) has no limit cycles in the region $ \Omega_1 $, which indicate the equilibrium $ E_1 $ is globally stable in $ \Omega_1 $. Moreover, the trajectories starting in the region $ \Sigma\backslash\Omega_1 $ enter into the region $ \Omega $ in finite time because of the Fenichel theory and Lemma 2.2. Then we can assert that system (1.4) has a globally stable node $ E_1 $ when $ h > h_2 $.
□
Lemma 2.4. If $ h = h_1 $ or $ h = h_2 $, then system (1.4) has two positive equilibriums. More precisely,
1) If $ h = h_1 $, then system (1.4) has a stable equilibrium $ E_{1}(u_1, v_1) $ located in $ S_0^2 $ and an attracting saddle-node $ E_M(\frac{1}{2b}, \frac{1}{4b}) $ which is the vertex point in $ S_0^3 $, see Figure 1(b).
2) If $ h = h_2 $, then system (1.4) has a stable equilibrium $ E_{1}(u_1, v_1) $ located in $ S_0^2 $ and a boundary equilibrium $ E_B(1, 1-b) $ located in the switching boundary $ \Sigma $, see Figures 1(d) and 2(b).
Proof. The existence and location of two positive admissible equilibriums follows from the straight calculation of Eq (2.6). By some simple calculations, we get
and the eigenvalues of equilibrium $ E_M(\frac{1}{2b}, \frac{1}{4b}) $ are $ \lambda_1 = 0 $ and $ \lambda_2 = -\epsilon(1-c) < 0 $. Hence, the equilibrium $ E_1 $ is stable and the equilibrium $ E_M $ is an attracting saddle-node which can be proven based on the conditions in [37].
□
Lemma 2.5. If $ h_1 < h < h_2 $, then system (1.4) has three positive equilibriums $ E_1(u_1, v_1) $, $ E_2(u_2, v_2) $ and $ E_3(u_3, v_3) $. More precisely, $ E_1(u_1, v_1) $ is a stable equilibrium in $ S_0^2 $; $ E_2(u_2, v_2) $ is a saddle in $ S_0^{3r} $ and $ E_3(u_3, v_3) $ is a stable node in $ S_0^{3a} $, see Figure 1(c).
The proof of Lemma 2.5 is similar to that given in Lemmas 2.3 and 2.4 and so is omitted.
3.
Dynamics of the slow-fast system
In this section, we are keen on various possible dynamics of the slow-fast system (1.4) including relaxation oscillation, saddle-node bifurcation, boundary equilibrium bifurcation and so on.
3.1. Saddle-node bifurcation
According to Lemmas 2.3–2.5, we know that
is a saddle-node bifurcation surface. When parameters change from one side of the surface $ SN $ to another one, the number of positive equilibriums of system (1.4) in $ \Sigma^{(+)} $ changes from zero to two. So there is a critical competition rate $ h_1 $ such that the two species coexist in the form of a positive equilibrium for suitable choices of initial values when $ h = h_1 $
In what follows, we show that system (1.4) has homoclinic orbit, heteroclinic orbit and relaxation oscillation cycles in both sides of saddle-node bifurcation surface $ SN $.
First, we investigate the relaxation oscillation cycles of system (1.4) when $ h < h_1 $. Now, we denote the function $ \hat{I}(\tilde{v}) $ as the function (2.5) with $ v_0 = \frac{1}{4e} $ and state the main theorem as follows
Theorem 3.1. When $ 0 < b < \frac{1}{4} $, $ 0 < c < 1 $ and $ 0 < h < h_1 $, system (1.4) has a positive equilibrium $ E_1(u_1, v_1) $ which is stable. Moreover, if
then system (1.4) has a hyperbolically stable relaxation oscillation cycle $ \Gamma^{1}_{\epsilon} $ and a hyperbolically unstable relaxation oscillation cycle $ \gamma_{\epsilon} $ which separately converges to
and
in the Hausdorff distance as $ \epsilon\to0 $, see Figures 3(a) and 4(a).
Proof. Our first goal is to prove the existence of the stable relaxation oscillation cycle $ \Gamma^{1}_{\epsilon} $. To begin with, it is easy to see that the vertex point $ M(\frac{1}{2b}, \frac{1}{4b}) $ is a general fold and there exists $ \hat{v}^*\in(0, 1-b) $ such that $ p_0(\frac{1}{4b}) = \hat{v}^* $ based on $ \hat{I}(1-b) < 0 $ and the properties of function $ \hat{I}(\tilde{v}) $. Hence, we construct the singular slow-fast cycle $ \Gamma^{1}_0 $, see Figure 3(a), as
where $ M(\frac{1}{2b}, \frac{1}{4b}) $, $ K_{1}(0, \frac{1}{4b}) $, $ Q_1(0, \hat{v}^*) $, $ D_1(\hat{u}^*, \hat{v}^*) $ and $ \hat{u}^* $ is the larger root of equation $ H_2(u) = \hat{v}^* $.
Set
which separately are vertical region of $ \overset{\LARGE\frown}{MK_1} $ and $ \overset{\LARGE\frown}{Q_1D_1} $ and $ \delta $ is a small positive parameter. We construct the Poincaré map $ \Pi $ as
which consists of two maps $ \Pi_0:\Delta_0\to\Delta_1 $ and $ \Pi_1:\Delta_1\to\Delta_0 $. For the trajectory starting in $ \Delta_0 $, it will arrive at the neighborhood of critical manifold $ S^{1a}_{0} $ and move downwards until reach the neighborhood of $ Q_1 $. The trajectory will move along the layers of system (2.3) and pass through the region $ \Delta_1 $ before reaching near the critical manifold $ S^{3a}_{0} $ because system (1.4) is continuous on the switching boundary $ \Sigma $. Then the trajectory will move along $ S^{3a}_{0} $ and jump into $ \Delta_0 $ in the neighborhood of fold point $ M $. Hence, the relaxation oscillation cycle $ \Gamma_{\epsilon}^{1} $ is equivalent to the fixed point of Poincaré map $ \Pi $ which is a contraction map with exponential contraction rate $ O(\mathrm{e}^{-\frac{1}{\epsilon}}) $ by Lemma 2.2 and Theorem 2.1 in [26]. According to the Contraction Mapping Theorem, there is an unique fixed point of $ \Pi $ corresponding to the relaxation oscillation cycle $ \Gamma_{\epsilon}^{1} $. Furthermore, it is clear that $ \Gamma_{\epsilon}^{1} $ is a hyperbolically stable limit cycle and converges to the singular slow-fast cycle $ \Gamma_{0}^{1} $ as $ \epsilon\to0 $.
Next we prove the existence of the unstable relaxation oscillation cycle $ \gamma_{\epsilon} $. Since $ E_{1}(u_1, v_1) $ is stable and the relaxation oscillation cycle $ \Gamma_{\epsilon}^{1} $ is hyperbolically stable, we can conclude that there exists at least an unstable limit cycle inside $ \Gamma_{\epsilon} $ based on Poincaré-Bendixson Theorem. According to the Geometric Singular Perturbation Theory [23], the limit cycles of slow-fast system (1.4) are usually perturbed by singular slow-fast cycles. Clearly, system (1.4) has an unique singular slow-fast cycle $ \gamma_0 $ inside the relaxation oscillation cycle $ \Gamma_{\epsilon}^1 $ for $ \epsilon\to0 $, see Figure 3(a), which are constructed as
with $ Q_2(0, 1-b) $, $ B(1, 1-b) $, $ D_2(\bar{u}^*, \bar{v}^*) $ and $ K_2(0, \bar{v}^*) $. Note that $ p_0(\bar{v}^*) = 1-b $ and $ \bar{u}^* $ is the smaller root of equation $ H_2(u) = \bar{v}^* $. Hence, if the limit cycles exist, they must be in the neighborhood of $ \gamma_0 $. By the Corollary 4.3 in [38], the sign of the following integral
determines the limit cycle is hyperbolically unstable if it exists. Thus, we can claim that there is an unique relaxation oscillation cycle $ \gamma_{\epsilon} $ near $ \gamma_0 $ because two adjacent limit cycles don't have the same stabilities.
□
Combined with the above analysis and applying numerical simulations by the "PPlane8" tool in Matlab, we give the phase portrait of system (1.4) when $ b = 0.2 $, $ c = 0.5 $ and $ h = 0.3 $, see Figure 4(a). Note that system (1.4) has a hyperbolically unstable relaxation oscillation cycle $ \gamma_{\epsilon} $ surrounded by a hyperbolically stable relaxation oscillation cycle $ \Gamma_{\epsilon}^{1} $.
Second, we investigate the existence of a homoclinic cycle of system (1.4) with $ h = h_1 $ and have the following theorem.
Theorem 3.2. When $ 0 < b < \frac{1}{4} $, $ 0 < c < 1 $ and $ h = h_1 $, system (1.4) has a stable equilibrium $ E_1(u_1, v_1) $ and a attracting saddle-node $ E_M(\frac{1}{2b}, \frac{1}{4b}) $. Moreover, if $ \hat{I}(1-b) < 0 $, then system (1.4) has a stable homoclinic cycles $ \Gamma^{2}_{\epsilon} $ and a unstable relaxation oscillation cycle $ \gamma_{\epsilon} $ which separately converge to
and
in Hausdorff distance as $ \epsilon\to0 $, see Figures 3(b) and 4(b).
Proof. For $ \epsilon = 0 $, it is clear that there is a singular orbit $ \Gamma^2_0 $ in saddle-node $ E_M $, which can be constructed by the same way of $ \Gamma^1_0 $ in Theorem 3.1, see Figure 3(b). Furthermore, the layer of system (2.3) at $ E_M $ will be perturbed to one dimensional unstable manifold $ W^{u}_{\epsilon}(E_M) $ of system (1.4) at $ E_M $ if $ 0 < \epsilon\ll1 $. By Lemma 2.2, the unstable manifold $ W^{u}_{\epsilon}(E_M) $ will be attracted to the neighborhood of $ S_0^{1a} $ and move down until it reach near $ Q_1 $. Then $ W^{u}_{\epsilon}(E_M) $ move quickly from the neighborhood of $ S_0^{1r} $ to the neighborhood of $ S_0^{3a} $. Next, we show that the unstable manifold $ W^{u}_{\epsilon}(E_M) $ tends to saddle-node $ E_M $. We construct the trapping region $ \Omega_1 $ which is same to (2.7) in Lemma 2.4 and the orbit cannot leave if it enters the region $ \Omega_1 $. Since the unstable manifold $ W^{u}_{\epsilon}(E_M) $ enter this region $ \Omega_1 $ and the orbits is monotone increasing in $ v $, the unstable manifold $ W^{u}_{\epsilon}(E_M) $ tends to saddle-node $ E_{M} $ along its stable manifold $ W^{s}_{\epsilon}(E_M) $ which is perturbed by $ W^{s}(S^{3a}_0) $ based on the Fenichel theorem. Hence, when $ 0 < \epsilon\ll1 $, there is a homoclinic cycle $ \Gamma^{2}_{\epsilon} $ which converges to singular orbit $ \Gamma^2_0 $ as $ \epsilon\to0 $.
Based on the Theorem 5 in [37], the stability of the homoclinic cycle $ \Gamma_{\epsilon}^2 $ is determined by the sign of the following integral
Hence, the homoclinic cycle $ \Gamma_{\epsilon}^2 $ is stable.
The proof of existence and stability of the relaxation oscillation cycle $ \gamma_{\epsilon} $ is omitted because it is similar to that in Theorem 3.1. □
According to the analysis of Theorem 3.2 and using numerical simulation by the "PPlane8" tool in Matlab, the phase portrait of system (1.4) with $ b = 0.2 $, $ c = 0.5 $ and $ h = 0.4 $ is presented in Figure 4(b). Note that system (1.4) has a stable homoclinic cycle $ \Gamma_{\epsilon}^2 $ enclosing a hyperbolically unstable relaxation oscillation cycle $ \gamma_{\epsilon} $.
Third, we study the existence of a heterocilinic cycle of system (1.4) when $ h > h_2 $. Similarly, we denote $ \tilde{I}(\tilde{u}) $ as the function (2.5) with $ v_0 = \frac{1-c}{h} $. By applying the similar analysis methods in Theorem 3.2 and Lemma 1 in [39], we can derive the following theorem.
Theorem 3.3. When $ 0 < b < \frac{1}{4} $, $ 0 < c < 1 $ and $ h_1 < h < h_2 $, system (1.4) has a saddle point $ E_2(u_2, v_2) $ and two stable equilibirums $ E_1(u_1, v_1) $ and $ E_3(u_3, v_3) $. Moreover, if
then system (1.4) has a heteroclinic cycle $ \Gamma^{3}_{\epsilon} $ and a unstable relaxation oscillation cycle $ \gamma_{\epsilon} $ which separately converge to
and
in Hausdorff distance as $ \epsilon\to0 $, see Figures 3(c) and 4(c).
According to the above analysis and some numerical simulations by the "PPlane8" tool in Matlab, we give the phase portrait of system (1.4) with $ b = 0.2 $, $ c = 0.5 $ and $ h = 0.45 $, see Figure 4(c). Note that the two unstable manifolds of saddle $ E_2(u_2, v_2) $ tend to the stable node $ E_{3}(u_3, v_3) $ and form the heteroclinic cycle. From Figure 4, we know that the number of equilibriums of system (1.4) changes from one to three when parameters pass through the saddle-node bifurcation surface. Furthermore, under some conditions, system (1.4) always has a small relaxation oscillation cycle $ \gamma_{\epsilon} $ which is separately surrounded by a big relaxation oscillation cycle, homoclinic cycle and heteroclinic cycle for different values of parameter $ h $ in the neighborhood of $ h_1 $.
3.2. Boundary equilibrium bifurcation
In this subsection, we will discuss the boundary equilibrium bifurcation of system (1.4). From Lemma 2.4, we know that the boundary equilibrium $ E_B(1, 1-b) $ is an admissible equilibrium for both systems in $ \Sigma^{(-)} $ and $ \Sigma^{(+)} $, which is a mark of boundary equilibrium bifurcation of codimension $ 1 $. Hence, incorporating Lemmas 2.3 and 2.5, we present the discontinuous saddle-node bifurcation surface as follows
When the parameters vary from one side of the surface to another, system (1.4) has two positive equilibriums $ E_1(u_1, v_1) $ and $ E_2(u_2, v_2) $ which are separately located in regions $ \Sigma^{(-)} $ and $ \Sigma^{(+)} $. Then the discontinuous saddle-node bifurcation gets two positive equilibriums.
4.
Discussion
In this paper, we consider the slow-fast Bazykin's predator-prey model with piecewise smooth Holling Ⅰ functional response. Our qualitative analysis on system (1.4) reveals that system has complex dynamics and bifurcations and the competition rate $ h $ plays a critical role which affects not only the number and type of equilibriums but also the type of bifurcations in this model. When the values of parameters vary, system (1.4) undergoes the saddle-node bifurcation and the discontinuous saddle-node bifurcation. For different values of parameters, it is clear that system (1.4) has a hyperbolically unstable relaxation oscillation cycle which is respectively surrounded by a hyperbolically stable relaxation oscillation cycle, a homoclinic cycle and a heteroclinic cycle. These complex dynamics cannot occur in the system (1.4) with single time scale and smooth Holling type Ⅰ functional response. In fact, the system (1.4) with $ \epsilon > 1 $ and smooth Holling type Ⅰ functional response [9] has at least one positive equilibrium which is globally stable if $ c < c_1 $, here $ c_1 $ is a threshold value. Hence, compared with our result in this paper, it is clear that the different time scale and piecewise-smooth functional response in system (1.4) can introduce more complex dynamical behaviour.
These complex dynamical phenomenons of system (1.4) show that the complexity of dynamical behaviors of the Bazykin's model. For the biological interpretations of these complex dynamical phenomenons, we interpret biological meaning of the big relaxation oscillation cycle in Theorem 3.1 as an example. By Figure 4(a), it is clear that the big relaxation oscillation cycle is hyperbolically stable, which indicates that that the prey and predator will coexist in system (1.4). The slow manifolds represent the density of prey and predator vary slowly under the influence of interactions or low prey density, and the fast movements implies the fast changes of prey density. The existence of the limit cycle suggests that the predator density increases slowly with sufficient food, and once the predator density exceeds the vertex point, the prey density decreases rapidly but not extinct due to large consumption. In the absence of food, the predator density also slowly declines until the prey density increases again quickly enough to support predator's reproduction, where the cycle begins again. Therefore, the relaxation oscillation cycle may show sudden outbreaks of pests in biology many years after extinction.
It is worth noticing that Kooij and Zegeling [40] extend the piecewise-smooth Holling type Ⅰ functional response, which replace the linear function $ p(x) = x $, $ 0 < x < 1 $ by cubic function $ p(x) = x(1+(x-1)(a_0+a_1x)) $, $ 0 < x < 1 $. Note that the new functional response is not only a non-monotonic function but also contains different cases for different values of $ a_1 $ and $ a_2 $. Furthermore, there may be more complex dynamics and bifurcations for system (1.4) with this new function response. We leave these for future consideration.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgements
The first author is supported by the Fundamental Research Funds for the Central Universities (No.2232023D-22, No.2232022G-13) and The third author was supported by the National Natural Science Foundation of China (12271088) and the Natural Science Foundation of Shanghai (21ZR1401000).
Conflict of interest
The authors declare there is no conflict of interest.









 DownLoad:
DownLoad: