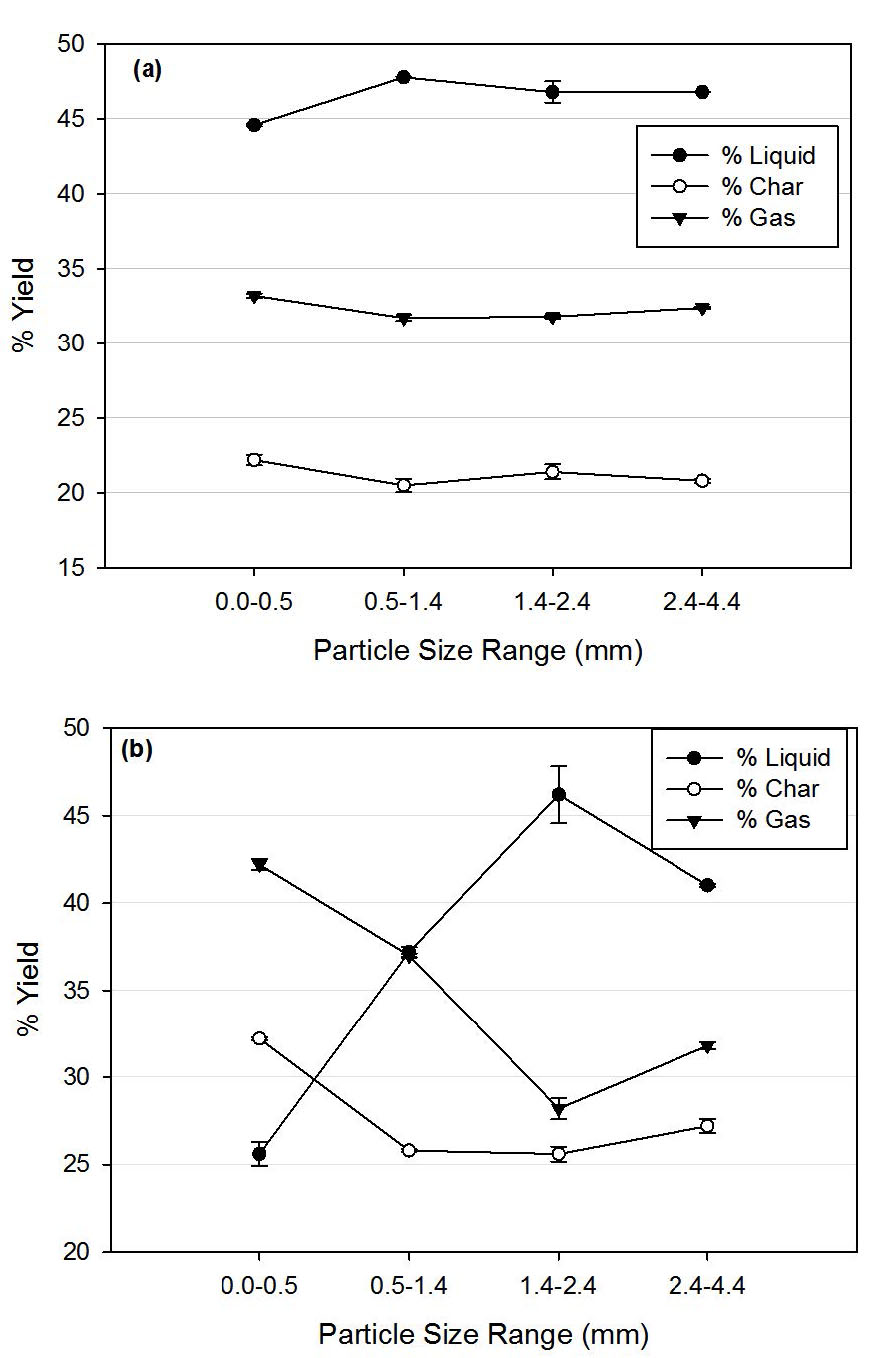
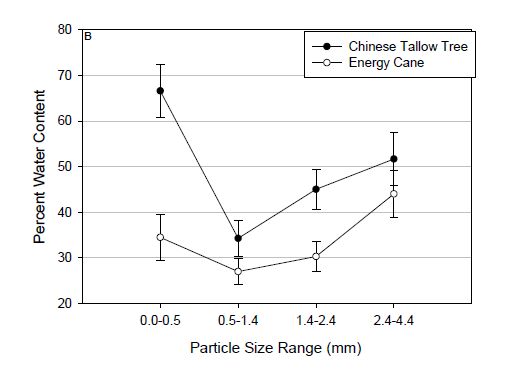
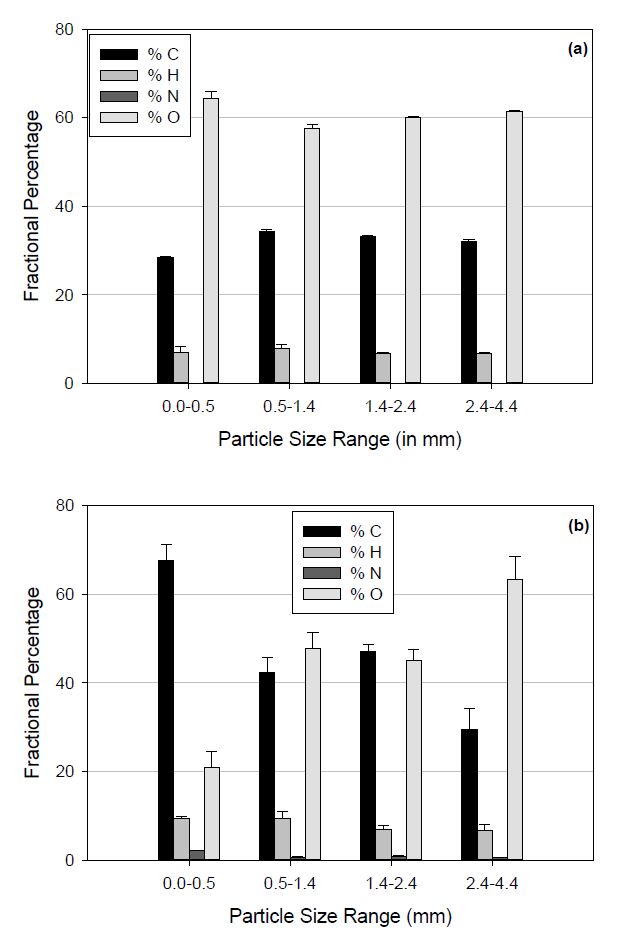
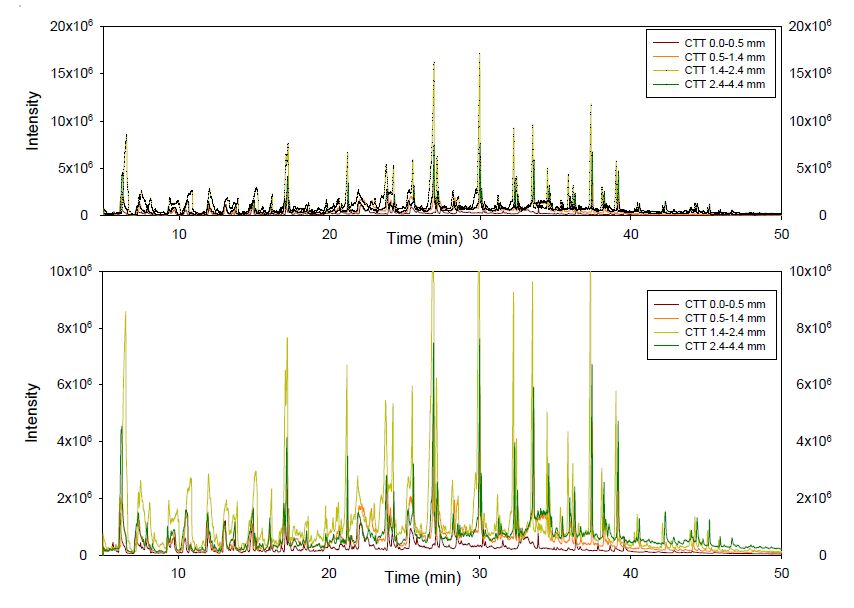
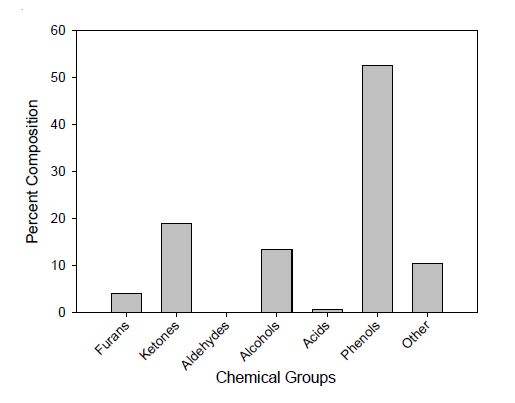
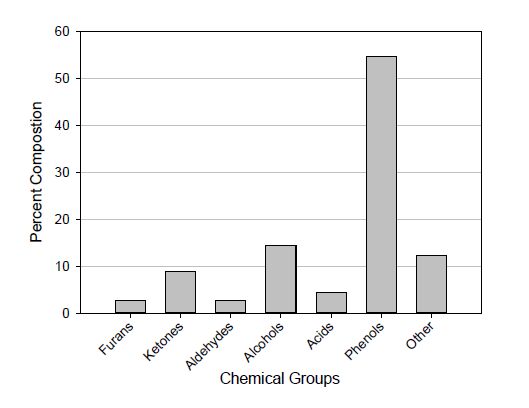
In the face of fluctuating petroleum costs and a growing demand for energy, the need for an alternative and sustainable energy source has increased. A viable solution for this problem can be attained by using thermochemical conversion, pyrolysis, of existing biomass sources for the production of liquid fuels. This study focuses on the effect that biomass particle size has on the conversion of biomass into liquid pyrolysis oil. Energy cane and Chinese tallow tree biomass were pyrolyzed at 550 ℃. The particle size ranges studied were < 0.5, 0.5 to 1.4, 1.4 to 2.4 and, 2.4 to 4.4 mm. The results indicate that the range from 0.5-1.4 mm is a better range for optimizing bio-oil production while keeping water content low.
1.
Introduction
The centrality of necessary conditions in optimal control is well-known and has originated an immense literature in the fields of optimization and nonsmooth analysis, see, e.g., [3,16,17,29,33,35].
In control theory, the celebrated Pontryagin Maximum Principle plays the role of the classical Euler-Lagrange equations in the calculus of variations. In the case of unrestricted state space, such conditions provide Lagrange multipliers---the so-called co-states---in the form of solutions to a suitable adjoint system satisfying a certain transversality condition. Among various applications of necessary optimality conditions is the deduction of further regularity properties for minimizers which, a priori, would just be absolutely continuous.
When state constraints are present, a large body of results provide adaptations of the Pontryagin Principle by introducing appropriate corrections in the adjoint system. The price to pay for such extensions usually consists of reduced regularity for optimal trajectories which, due to constraint reactions, turn out to be just Lipschitz continuous while the associated co-states are of bounded variation, see [20].
The maximum principle under state constraints was first established by Dubovitskii and Milyutin [17] (see also the monograph [35] for different forms of such a result). It may happen that the maximum principle is degenerate and does not yield much information (abnormal maximum principle). As explained in [8,10,18,19] in various contexts, the so-called "inward pointing condition" generally ensures the normality of the maximum principle under state constraints. In our setting (calculus of variation problem, with constraints on positions but not on velocities), this will never be an issue. The maximum principle under state constraints generally involves an adjoint state which is the sum of a $W^{1, 1}$ map and a map of bounded variation. This latter mapping may be very irregular and have infinitely many jumps [32], which allows for discontinuities in optimal controls. However, under suitable assumptions (requiring regularity of the data and the affine dynamics with respect to controls), it has been shown that optimal controls and the corresponding adjoint states are continuous, and even Lipschitz continuous: see the seminal work by Hager [22] (in the convex setting) and the subsequent contributions by Malanowski [31] and Galbraith and Vinter [21] (in much more general frameworks). Generalization to less smooth frameworks can also be found in [9,18].
Let $\Omega\subset \mathbb{R}^n $ be a bounded open domain with $C^2$ boundary. Let $\Gamma$ be the metric subspace of $AC(0, T;\mathbb{R}^n)$ defined by
with the uniform metric. For any $x\in\overline{\Omega}$, we set
We consider the problem of minimizing the classical functional of the calculus of variations
Let $U\subset \mathbb{R}^n$ be an open set such that $\overline{\Omega}\subset U$. Given $ x\in \overline \Omega$, we consider the constrained minimization problem
where $f: [0, T]\times U\times \mathbb{R}^n\rightarrow \mathbb{R}$ and $g:U\rightarrow \mathbb{R}$.In this paper, we obtain a certain formulation of the necessary optimality conditions for the above problem, which are particularly useful to study the regularity of minimizers. More precisely, given a minimizer $\gamma^\star \in \Gamma[x]$ of (1.1), we prove that there exists a Lipschitz continuous arc $p:[0, T]\rightarrow \mathbb{R}^n$ such that
where $\Lambda$ is a bounded continuous function independent of $\gamma^\star$ and $p$ (Theorem 3.1). By the above necessary conditions we derive a sort of maximal regularity, showing that any solutions $\gamma^\star$ is of class $C^{1, 1}$. As is customary in this kind of problems, the proof relies on the analysis of suitable penalized functional which has the following form:
Then, we show that all solutions of the penalized problem remain in $\overline{\Omega}$ (Lemma3.7).
A direct consequence of our necessary conditions is the Lipschitz regularity of the value function associated to (1.1) (Proposition 4.1).
Our interest is also motivated by application to mean field games, as we explain below. Mean field games (MFG) theory has been developed simultaneously by Lasry and Lions ([25,26,27]) and by Huang, Malhamé and Caines ([23,24]) in order to study differential games with an infinite number of rational players in competition. The simplest MFG model leads to systems of partial differential equations involving two unknown functions: the value function $u$ of an optimal control problem of a typical player and the density $m$ of the population of players. In the presence of state constraints, the usual construction of solutions to the MFG system has to be completely revised because the minimizers of the problem lack many of the good properties of the unconstrained case. Such constructions are discussed in detail in [11], where a relaxed notion of solution to the constrained MFG problem was introduced following the so-called Lagrangian formulation (see [4,5,6,7,13,14]. In this paper, applying our necessary conditions, we deduce the existence of more regular solutions than those constructed in [11], assuming data to be Lipschitz continuous.
This paper is organised as follows. In Section 2, we introduce the notation and recall preliminary results. In Section 3, we derive necessary conditions for the constrained problem. Moreover, we prove the $C^{1, 1}$-smoothness of minimizers. In Section 4, we apply our necessary conditions to obtain the Lipschitz regularity of the value function for the constrained problem. Furthermore, we deduce the existence of more regular constrained MFG equilibria. Finally, in the Appendix, we prove a technical result on limiting subdifferentials.
2.
Preliminaries
Throughout this paper we denote by $|\cdot|$ and $\langle \cdot \rangle$, respectively, the Euclidean norm and scalar product in $\mathbb{R}^n$. Let $A\in\mathbb{R}^{n\times n}$ be a matrix. We denote by $||\cdot||$ the norm of $A$ defined as follows
For any subset $S \subset \mathbb{R}^n$, $\overline{S}$ stands for its closure, $\partial S$ for its boundary, and $S^c$ for $\mathbb{R}^n\setminus S$. We denote by ${\bf 1}_{S}:\mathbb{R}^n\rightarrow \{0, 1\}$ the characteristic function of $S$, i.e.,
We write $AC(0, T;\mathbb{R}^n)$ for the space of all absolutely continuous $\mathbb{R}^n$-valued functions on $[0, T]$, equipped with the uniform norm $||\gamma||_\infty = {\rm sup}_{[0, T]}\ |\gamma(t)|$. We observe that $AC(0, T;\mathbb{R}^n)$ is not a Banach space.
Let $U$ be an open subset of $\mathbb{R}^n$. $C(U)$ is the space of all continuous functions on $U$ and $C_b(U)$ is the space of all bounded continuous functions on $U$. $C^k(U)$ is the space of all functions $\phi:U\rightarrow\mathbb{R}$ that are k-times continuously differentiable. Let $\phi\in C^1(U)$. The gradient vector of $\phi$ is denoted by $D\phi = (D_{x_1}\phi, \cdots , D_{x_n}\phi)$, where $D_{x_i}\phi = \frac{\partial \phi}{\partial x_i}$. Let $\phi \in C^k(U)$ and let $\alpha = (\alpha_1, \cdots, \alpha_n) \in \mathbb{N}^n$ be a multiindex. We define $D^\alpha \phi = D^{\alpha_1}_{x_1}\cdots D^{\alpha_n}_{x_n}\phi$. $C^k_b(U)$ is the space of all function $\phi\in C^k(U)$ and such that
Let $\Omega$ be a bounded open subset of $\mathbb{R}^n$ with $C^2$ boundary. $C^{1, 1}(\overline{\Omega})$ is the space of all the functions $C^1$ in a neighborhood $U$ of $\Omega$ and with locally Lipschitz continuous first order derivates in $U$.
The distance function from $\overline{\Omega}$ is the function $d_\Omega :\mathbb{R}^n \rightarrow [0, + \infty[$ defined by
We define the oriented boundary distance from $\partial \Omega$ by
We recall that, since the boundary of $\Omega$ is of class $C^2$, there exists $\rho_0>0$ such that
Throughout the paper, we suppose that $\rho_0$ is fixed so that (2.1) holds.
Take a continuous function $f: \mathbb{R}^n\rightarrow \mathbb{R}$ and a point $x\in \mathbb{R}^n$. A vector $p\in\mathbb{R}^n$ is said to be a proximal subetaadient of $f$ at $x$ if there exists $\epsilon>0$ and $C\geq 0$ such that
The set of all proximal subetaadients of $f$ at $x$ is called the proximal subdifferential of $f$ at $x$ and is denoted by $\partial^p f(x)$. A vector $p\in\mathbb{R}^n$ is said to be a limiting subetaadient of $f$ at $x$ if there exist sequences $x_i\in \mathbb{R}^n$, $p_i\in \partial^p f(x_i)$ such that $x_i\rightarrow x$ and $p_i\rightarrow p$ ($i\rightarrow \infty$).
The set of all limiting subetaadients of $f$ at $x$ is called the limiting subdifferential and is denoted by $\partial f(x)$.In particular, for the distance function we have the following result.
Lemma 2.1. Let $\Omega$ be a bounded open subset of $\mathbb{R}^n$ with $C^2$ boundary. Then, for every $x\in \mathbb{R}^n$ it holds
where $\rho_0$ is as in (2.1) and $D{b_\Omega}(x)[0, 1]$ denotes the set $\{ D{b_\Omega}(x)\alpha~:~\alpha\in [0, 1]\}$.
The proof is given in the Appendix.
Let $X$ be a separable metric space. $C_b(X)$ is the space of all bounded continuous functions on $X$. We denote by $\mathscr{B}(X)$ the family of the Borel subset of $X$ and by $\mathcal{P}(X)$ the family of all Borel probability measures on $X$. The support of $\eta \in \mathcal{P}(X)$, $supp(\eta)$, is the closed set defined by
We say that a sequence $(\eta_i)\subset \mathcal{P}(X)$ is narrowly convergent to $\eta \in \mathcal{P}(X)$ if
We denote by $d_1$ the Kantorovich-Rubinstein distance on $X$, which---when $X$ is compact---can be characterized as follows
for all $m, m'\in\mathcal{P}(X)$.
Let $\Omega$ be a bounded open subset of $\mathbb{R}^n$ with $C^2$ boundary. We write ${\rm Lip}(0, T;\mathcal{P}(\overline{\Omega}))$ for the space of all maps $m:[0, T]\rightarrow \mathcal{P}(\overline{\Omega})$ that are Lipschitz continuous with respect to $d_1$, i.e.,
for some constant $C\geq 0$. We denote by ${\rm Lip}(m)$ the smallest constant that verifies (2.3).
3.
Necessary conditions and smoothness of minimizers
3.1. Assumptions and main result
Let $\Omega \subset \mathbb{R}^n$ be a bounded open set with $C^2$ boundary. Let $\Gamma$ be the metric subspace of $AC(0, T;\mathbb{R}^n)$ defined by
For any $x\in\overline{\Omega}$, we set
Let $U\subset \mathbb{R}^n$ be an open set such that $\overline{\Omega}\subset U$. Given $ x\in \overline \Omega$, we consider the constrained minimization problem
We denote by $\mathcal{X}[x]$ the set of solutions of (3.1), that is
We assume that $f: [0, T]\times U\times \mathbb{R}^n\rightarrow \mathbb{R}$ and $g:U\rightarrow \mathbb{R}$ satisfy the following conditions.
(g1) $g\in C^1_b(U)$
(f0) $f\in C\big([0, T]\times U\times \mathbb{R}^n\big)$ and for all $t\in[0, T]$ the function $(x, v)\mapsto f(t, x, v)$ is differentiable. Moreover, $D_xf$, $D_vf$ are continuous on $[0, T]\times U\times \mathbb{R}^n$ and there exists a constant $M\geq 0$ such that
(f1) For all $t\in[0, T]$ the map $(x, v)\mapsto D_{v}f(t, x, v)$ is continuously differentiable and there exists a constant $\mu\geq 1$ such that
for all $(t, x, v)\in [0, T]\times U\times \mathbb{R}^n$, where $I$ denotes the identity matrix.
(f2) For all $(x, v)\in U\times\mathbb{R}^n$ the function $t\mapsto f(t, x, v)$ and the map $t\mapsto D_vf(t, x, v)$ are Lipschitz continuous. Moreover, there exists a constant $\kappa\geq 0$ such that
for all $t$, $s\in [0, T]$, $x\in U$, $v\in\mathbb{R}^n$.
Remark 3.1. By classical results in the calculus of variation (see, e.g., [15, Theorem 11.1i]), there exists at least one minimizer of (3.1) in $\Gamma$ for any fixed point $x\in\overline{\Omega}$.
In the next lemma we show that (f0)-(f2) imply the useful growth conditions for $f$ and for its derivatives.
Lemma 3.1. Suppose that (f0)-(f2) hold. Then, there exists a positive constant $C(\mu, M)$ depending only on $\mu$ and $M$ such that
for all $(t, x, v)\in [0, T]\times U\times \mathbb{R}^n$.
Proof. By (3.2), and by (3.3) one has that
and so (3.7) holds. Furthermore, by (3.2), and by (3.4) we have that
Therefore, (3.8) holds. Moreover, fixed $v\in \mathbb{R}^n$ there exists a point $\xi$ of the segment with endpoints $0$, $v$ such that
By (3.2), (3.3), and by (3.7) we have that
and so (3.9) holds. This completes the proof.
In the next result we show a special property of the minimizers of (3.1).
Lemma 3.2. For any $x\in\overline{\Omega}$ and for any $\gamma^\star\in\mathcal{X}[x]$ we have that
where
Proof. Let $x\in\overline{\Omega}$ and let $\gamma^\star\in \mathcal{X}[x]$. By comparing the cost of $\gamma^\star$ with the cost of the constant trajectory $\gamma^\star(t)\equiv x$, one has that
Using (3.2) and (3.9) in (3.11), one has that
where
We denote by $H:[0, T]\times U\times\mathbb{R}^n \rightarrow \mathbb{R}$ the Hamiltonian
Our assumptions on $f$ imply that $H$ satisfies the following conditions.
(H0) $H\in C\big([0, T]\times U\times \mathbb{R}^n\big)$ and for all $t\in[0, T]$ the function $(x, p)\mapsto H(t, x, p)$ is differentiable. Moreover, $D_xH$, $D_pH$ are continuous on $[0, T]\times U\times \mathbb{R}^n$ and there exists a constant $M'\geq 0$ such that
(H1) For all $t\in[0, T]$ the map $(x, p)\mapsto D_{p}H(t, x, p)$ is continuously differentiable and
for all $(t, x, p)\in [0, T]\times U\times \mathbb{R}^n$, where $\mu$ is the constant given in (f1) and $C(\mu, M')$ depends only on $\mu$ and $M'$.
(H2) For all $(x, p)\in U\times\mathbb{R}^n$ the function $t\mapsto H(t, x, p)$ and the map $t\mapsto D_pH(t, x, p)$ are Lipschitz continuous. Moreover
for all $t$, $s\in [0, T]$, $x\in U$, $p\in\mathbb{R}^n$, where $\kappa$ is the constant given in (f2) and $C(\mu, M')$ depends only on $\mu$ and $M'$.
Remark 3.2. Arguing as in Lemma 3.1 we deduce that
for all $(t, x, p)\in[0, T]\times U\times\mathbb{R}^n$ and $C(\mu, M')$ depends only on $\mu$ and $M'$.
Under the above assumptions on $\Omega$, $f$ and $g$ our necessary conditions can be stated as follows.
Theorem 3.1. For any $x\in\overline{\Omega}$ and any $\gamma^\star \in\mathcal{X}[x]$ the following holds true.
(i) $\gamma^\star$ is of class $C^{1, 1}([0, T];\overline{\Omega})$.
(ii) There exist:
(a) a Lipschitz continuous arc $p:[0, T]\rightarrow \mathbb{R}^n$,
(b) a constant $\nu\in\mathbb{R}$ such that
which satisfy the adjoint system
and the transversality condition
where $\Lambda:[0, T]\times\Sigma_{\rho_0}\times\mathbb{R}^n\rightarrow \mathbb{R}$ is a bounded continuous function independent of $\gamma^\star$ and $p$.
Moreover,
(iii) the following estimate holds
where $L^\star = L^\star(\mu, M', M, \kappa, T, ||Dg||_\infty, ||g||_\infty)$.
The (feedback) function $\Lambda$ in (3.20) can be computed explicitly, see Remark 3.4 below.
3.2. Proof of Theorem 3.1 for $U=\mathbb{R}^n$
In this section, we prove Theorem 3.1 in the special case of $U = \mathbb{R}^n$. The proof for a general open set $U$ will be given in the next section.
The proof is based on [12, Theorem 2.1] where the Maximum Principle under state constraints is obtained for a Mayer problem. The reasoning requires several intermediate steps.
Fix $x\in \overline{\Omega}$. The key point is to approximate the constrained problem by penalized problems as follows
Then, we will show that, for $\epsilon>0$ and $\delta\in (0, 1]$ small enough, the solutions of the penalized problem remain in $\overline{\Omega}$.
Observe that the Hamiltonian associated with the penalized problem is given by
for all $(t, x, p)\in [0, T]\times \mathbb{R}^n\times \mathbb{R}^n$.
By classical results in the calculus of variation (see, e.g., [15, Section 11.2]), there exists at least one mimimizer of (3.22) in $AC(0, T;\mathbb{R}^n)$ for any fixed initial point $ x\in\overline{\Omega}$. We denote by $\mathcal{X}_{\epsilon, \delta}[x]$ the set of solutions of (3.22).
Remark 3.3. Arguing as in Lemma 3.2 we have that, for any $x\in \overline{\Omega}$, all $\gamma\in\mathcal{X}_{\epsilon, \delta}[x]$ satisfy
where $K$ is the constant given in (3.10).
The first step of the proof consists in showing that the solutions of the penalized problem remain in a neighborhood of $\overline{\Omega}$.
Lemma 3.3. Let $\rho_0$ be such that (2.1) holds. For any $\rho\in(0, \rho_0]$, there exists $\epsilon(\rho)>0$ such that for all $\epsilon\in (0, \epsilon(\rho)]$ and all $\delta\in(0, 1]$ we have that
Proof. We argue by contradiction. Assume that, for some $\rho>0$, there exist sequences $\{\epsilon_k\}$, $\{\delta_k\}$, $\{t_k\}$, $\{x_k\}$ and $\{\gamma_k\}$ such that
By Remark 3.3, one has that for all $k\geq1$
where $K$ is the constant given in (3.10). The above inequality implies that $\gamma_k$ is $1/2-$Hölder continuous with Hölder constant $(4\mu K)^{1/2}$. Then, by the Lipschitz continuity of $d_{\Omega}$ and the regularity of $\gamma_k$, we have that
Since $d_{ \Omega}(\gamma_k(t_k))> \rho$, one has that
Hence, $d_{\Omega}(\gamma_k(s))\geq \rho/2$ for all $s\in J: = [t_k-\frac{\rho^2}{16\mu K}, t_k+ \frac{\rho^2}{16\mu K}]\cap [0, T]$ and all $k\geq 1$. So,
But the above inequality contradicts the fact that $\epsilon_k\downarrow 0$. So, (3.25) holds true.
In the next lemma, we show the necessary conditions for the minimizers of the penalized problem.
Lemma 3.4. Let $\rho\in(0, \rho_0]$ and let $\epsilon\in(0, \epsilon(\rho)]$, where $\epsilon(\rho)$ is given by Lemma 3.3. Fix $\delta\in(0, 1]$, let $ x_0\in\overline{\Omega}$, and let $\gamma\in\mathcal{X}_{\epsilon, \delta}[ x_0]$. Then,
(i) $\gamma$ is of class $C^{1, 1}([0, T];\mathbb{R}^n)$;
(ii) there exists an arc $p\in {\rm Lip}(0, T;\mathbb{R}^n)$, a measurable map $\lambda:[0, T]\rightarrow [0, 1]$, and a constant $\beta\in [0, 1]$ such that
where
and
Moreover,
(iii) the function
belongs to $AC(0, T;\mathbb{R})$ and satisfies
where $K$ is the constant given in (3.10) and $\mu$, $\kappa$ are the constants in (3.5) and (3.9), respectively;
(iv) the following estimate holds
where $C_1 = 8\mu+8\mu||Dg||_\infty^2+2C(\mu, M')+ \kappa(T+4\mu K)$.
Proof. In order to use the Maximum Principle in the version of [35, Theorem 8.7.1], we rewrite (3.22) as a Mayer problem in a higher dimensional state space. Define $X(t)\in \mathbb{R}^n\times \mathbb{R}$ as
where $z(t) = \int_0^t \big[f(s, \gamma(s), \dot \gamma(s)) +\frac{1}{\epsilon}\ d_{\Omega}(\gamma(s))\big]\, ds$. Then the state equation becomes
where
and $\mathcal{L}_{\epsilon}(t, x, u) = f(t, x, u)+\frac{1}{\epsilon}\ d_{{\Omega}}(x)$ for $X = (x, z)$ and $(t, x, z, u)\in [0, T]\times \mathbb{R}^n\times \mathbb{R} \times \mathbb{R}^n$. Thus, (3.22) can be written as
where $\Phi(X) = g(x) + \frac{1}{\delta}\ d_{{\Omega}}(x) + z$ for any $X = (x, z)\in \mathbb{R}^n\times \mathbb{R}$. The associated unmaximized Hamiltonian is given by
We observe that, as $\gamma(\cdot)$ is minimizer for (3.22), $X$ is minimizer for (3.30). Hence, the hypotheses of [35, Theorem 8.7.1] are satisfied. It follows that there exist $P(\cdot) = (p(\cdot), b(\cdot)) \in AC(0, T;\mathbb{R}^{n+1})$, $r(\cdot) \in AC(0, T;\mathbb{R})$, and $\lambda_0\geq 0$ such that
(ⅰ) $\big(P, \lambda_0\big)\not \equiv \big(0, 0\big)$,
(ⅱ) $\big(\dot r(t), \dot{P}(t)\big)\in co \ \partial_{t, X}\mathcal{H}_\epsilon\big(t, X(t), P(t), \dot{\gamma}(t)\big)$, a.e $t\in[0, T]$,
(ⅲ) $P(T)\in \lambda_0 \partial \Phi(X^u(T))$,
(ⅳ) $\mathcal{H}_\epsilon \big(t, X(t), P(t), \dot{\gamma}(t)\big) = \max_{u\in \mathbb{R}^n} \mathcal{H}_\epsilon \big(t, X(t), P(t), u\big)$, a.e. $t\in [0, T]$,
(ⅴ)$\mathcal{H}_\epsilon\big(t, X(t), P(t), \dot{\gamma}(t)\big) = r(t)$, a.e. $t\in [0, T]$,
where $\partial_{t, X}\mathcal{H}_\epsilon$ and $\partial\Phi$ denote the limiting subdifferential of $\mathcal{H}_\epsilon$ and $\Phi$ with respect to $(t, X)$ and $X$ respectively, while $co$ stands for the closed convex hull. Using the definition of $\mathcal{H}_\epsilon$ we have that
where $\partial_{t, x}\mathcal{L}_{\epsilon}$ and $\partial(g+\frac{1}{\delta}\ d_{\Omega})$ stands for the limiting subdifferential of $\mathcal{L}_{\epsilon}(\cdot, \cdot, u)$ and $g(\cdot)+\frac{1}{\delta} d_{\Omega}(\cdot)$. We claim that $\lambda_0>0$. Indeed, suppose that $\lambda_0 = 0$. Then $b\equiv 0$ by (3.33) and (3.35). Moreover, $p(T) = 0$ by (3.34). It follows from (3.32) that $p\equiv 0$, which is in contradiction with (3.31). So, $\lambda_0> 0$ and we may rescale $p$ and $b$ so that $b(t) = \lambda_0 = 1$ for any $t\in [0, T]$.
Note that the Weierstrass Condition (ⅳ) becomes
Therefore
By Lemma 2.1, by the definition of $\rho$, and by (3.5) we have that
Thus (3.32) implies that there exists $\lambda(t)\in [0, 1]$ as in (3.27) such that
Hence, by (3.39), and by Remark 3.3 we conclude that
Moreover, by Lemma 2.1, and by assumption on $g$, one has that
So, by (3.34), there exists $\beta\in [0, 1]$ as in (3.28) such that
Finally, by well-known properties of the Legendre transform one has that
So, recalling (3.38), (3.40) can be rewritten as
We have to prove estimate (3.29). Recalling (3.23) and (3.19), we have that
So, using (3.41) one has that
Moreover, (3.42) implies that $|p(T)|\leq \frac{1}{\delta}+||Dg||_\infty$. Therefore, using again (3.19), we obtain
Hence,
where $C_1 = 8\mu+8\mu||Dg||_\infty^2+2C(\mu, M')+\kappa(T+4\mu K)$. This completes the proof of (3.29).
Finally, by the regularity of $H$, we have that $p\in {\rm Lip}(0, T;\mathbb{R}^n)$. So, $\gamma\in C^{1, 1}([0, T];\mathbb{R}^n)$. Observing that the right-hand side of the equality $\dot{\gamma}(t) = -D_pH(t, \gamma(t), p(t))$ is continuous we conclude that this equality holds for all $t$ in $[0, T]$.
Lemma 3.5. Let $\rho\in(0, \rho_0]$ and let $\epsilon\in(0, \epsilon(\rho)]$, where $ \epsilon(\rho)$ is given by Lemma 3.3. Fix $\delta\in(0, 1]$, let $ x\in\overline{\Omega}$, and let $\gamma\in\mathcal{X}_{\epsilon, \delta}[ x]$. If $\gamma(\overline{t})\notin \partial\Omega$ for some $\overline{t}\in [0, T]$, then there exists $\tau>0$ such that $\gamma\in C^2\left(\left(\overline{t}-\tau, \overline{t}+\tau\right)\cap [0, T];\mathbb{R}^n\right)$.
Proof. Let $\gamma\in\mathcal{X}_{\epsilon, \delta}[x]$ and let $\overline{t}\in [0, T]$ be such that $\gamma(\overline{t})\in \Omega \cup(\mathbb{R}^n\setminus \overline{\Omega})$. If $\gamma(\overline{t})\in\mathbb{R}^n\setminus\overline{\Omega}$, then there exists $\tau>0$ such that $\gamma(t)\in \mathbb{R}^n\setminus\overline{\Omega}$ for all $t\in I: = (\overline{t}-\tau, \overline{t}+\tau)\cap[0, T]$. By Lemma 3.4, we have that there exists $p\in {\rm Lip}(0, T;\mathbb{R}^n)$ such that
for $t\in I$. Since $p(t)$ is Lipschitz continuous for $t\in I$, and $\dot{\gamma}(t) = -D_pH(t, \gamma(t), p(t))$, then $\gamma$ belongs to $C^1\left(I;\mathbb{R}^n\right)$. Moreover, by the regularity of $H$, ${b_\Omega}$, $p$, and $\gamma$ one has that $\dot{p}(t)$ is continuous for $t\in I$. Then $p\in C^1\left(I;\mathbb{R}^n\right)$. Hence, $\dot{\gamma}\in C^1\left(I;\mathbb{R}^n\right)$. So, $\gamma\in C^2\left(I;\mathbb{R}^n\right)$. Finally, if $\gamma(\overline{t})\in\Omega$, the conclusion follows by a similar argument.
In the next two lemmas, we show that, for $\epsilon>0$ and $\delta\in(0, 1]$ small enough, any solution $\gamma$ of problem (3.22) belongs to $\overline{\Omega}$ for all $t\in[0, T]$. For this we first establish that, if $\delta\in(0, 1]$ is small enough and $\gamma(T)\notin \overline{\Omega}$, then the function $t\mapsto {b_\Omega}(\gamma(t))$ has nonpositive slope at $t = T$. Then we prove that the entire trajectory $\gamma$ remains in $\overline{\Omega}$ provided $\epsilon$ is small enough. Hereafter, we set
Lemma 3.6. Let
where
Fix any $\delta_1 \in (0, \delta]$ and let $ x\in \overline{\Omega}$. Let $\epsilon\in(0, \epsilon_0]$. If $\gamma\in\mathcal{X}_{\delta_1, \epsilon}[ x]$ is such that $\gamma(T)\notin\overline{\Omega}$, then
Proof. As $\gamma(T) \notin \overline{\Omega}$, by Lemma 3.4 we have that $p (T) = Dg(\gamma(T))+\frac{1}{\delta}\ D{b_\Omega}(\gamma(T))$. Hence,
Recalling that $D^2_{pp}H(t, x, p)\geq \frac{I}{\mu}$, one has that
So,
Therefore, we obtain
Thus, choosing $\delta$ as in (3.43) gives the result.
Lemma 3.7. Fix $\delta$ as in (3.43). Then there exists $\epsilon_1\in(0, \epsilon_0]$, such that for any $\epsilon\in(0, \epsilon_1]$
Proof. We argue by contradiction. Assume that there exist sequences $\{\epsilon_k\}$, $\{t_k\}$, $\{x_k\}$, $\{\gamma_k\}$ such that
Then, for each $k\geq 1$ one could find an interval with end-points $0\leq a_k <b_k\leq T$ such that
Let $\overline{t}_k\in(a_k, b_k]$ be such that
We note that, by Lemma 3.5, $\gamma_k$ is of class $C^2$ in a neighborhood of ${\tilde t_k}$.
Step 1
We claim that
Indeed, (3.45) is trivial if $\overline{t}_k\in(a_k, b_k)$. Suppose $\overline{t}_k = b_k$. Since $\overline{t}_k$ is a maximum point of the map $t\mapsto d_\Omega(\gamma_k(t))$ and $\gamma_k(\overline{t}_k)\notin\overline{\Omega}$, we have that $d_\Omega(\gamma_k(\overline{t}_k))\neq 0$. So, $b_k = T = \overline{t}_k$ and we get
Moreover, Lemma 3.6 yields
So,
and we have that (3.45) holds true at $\overline{t}_k = T$.
Step 2
Now, we prove that
where $C_1 = 8\mu+8\mu||Dg||_\infty^2+2C(\mu, M')+\kappa(T+4\mu K)$ and the constant $C(\mu, M', \kappa)$ depends only on $\mu$, $M'$ and $\kappa$. Indeed, since $\gamma$ is of class $C^2$ in a neighborhood of $\overline{t}_k$ one has that
Developing the second order derivative of $d_\Omega\circ\gamma$, by (3.47) and the expression of the derivatives of $\gamma$ and $p$ in Lemma 3.4 one has that
We now use the growth properties of $H$ in (3.14), and (3.16)-(3.18), the lower bound for $D_{pp}^2H$ in (3.13), and the regularity of the boundary of $\Omega$ to obtain:
where the constant $C(\mu, M', \kappa)$ depends only on $\mu$, $M'$ and $\kappa$. By our estimate for $p$ in (3.29) we get:
where $C_1 = 8\mu+8\mu||Dg||_\infty^2+2C(\mu, M')+\kappa(T+4\mu K)$.
Conclusion
Let $\rho = \min\left\{\rho_0, \frac{1}{32 C(\mu, M', \kappa) \mu^2}\right\}$. Owing to Lemma 3.3, for all $\epsilon\in(0, \epsilon(\rho)]$ we have that
Hence, using (3.46), we deduce that
Since the above inequality fails for $k$ large enough, we conclude that (3.44) cannot hold true. So, $\gamma(t)$ belongs to $\overline{\Omega}$ for all $t\in[0, T]$.
An obvious consequence of Lemma 3.7 is the following:
Corollary 3.1. Fix $\delta$ as in (3.43) and take $\epsilon = \epsilon_1$, where $\epsilon_1$ is defined as in Lemma 3.7. Then an arc $\gamma(\cdot)$ is a solution of problem (3.22) if and only if it is also a solution of (3.1).
We are now ready to complete the proof of Theorem 3.1.
Proof of Theorem 3.1. Let $ x\in\overline{\Omega}$ and $\gamma^\star\in \mathcal{X}[ x]$. By Corollary 3.1 we have that $\gamma^\star$ is a solution of problem (3.22) with $\delta$ as in (3.43) and $\epsilon = \epsilon_1$ as in Lemma 3.7. Let $p(\cdot)$ be the associated adjoint map such that $(\gamma^\star(\cdot), p(\cdot))$ satisfies (3.26). Moreover, let $\lambda(\cdot)$ and $\beta$ be defined as in Lemma 3.4. Define $\nu = \frac{\beta}{\delta}$. Then we have $0\leq \nu \leq \frac{1}{\delta}$ and, by (3.26),
By Lemma 3.4 $\gamma^\star\in C^{1, 1}([0, T];\overline{\Omega})$ and
Moreover, $p(\cdot)\in {\rm Lip}(0, T;\mathbb{R}^n)$ and by (3.29) one has that
where $C_1 = 8\mu+8\mu||Dg||_\infty^2+2C(\mu, M')+\kappa(T+4\mu K)$. Hence, $p$ is bounded. By (3.49), and by (3.17) one has that
where $L^\star = L^\star(\mu, M', M, \kappa, T, ||Dg||_\infty, ||g||_\infty)$. Thus, (3.21) holds
Finally, we want to find an explicit expression for $\lambda(t)$. For this, we set
where $\rho_0$ is as in assumption (2.1). Note that $\psi(t): = {b_\Omega}\circ\gamma^\star$ is of class $C^{1, 1}$ on the open set $D_{\rho_0}$, with
Since $p\in {\rm Lip}(0, T;\mathbb{R}^n)$, $\dot{\psi}$ is absolutely continuous on $D_{\rho_0}$ with
Let $N_{\gamma^\star} = \{t\in D\cap (0, T)|\ \dot{\psi}(t)\neq 0\}$. Let $t\in N_{\gamma^\star}$, then there exists $\sigma>0$ such that $\gamma^\star(s)\notin \partial\Omega$ for any $s\in ((t-\sigma, t+\sigma)\setminus\{t\})\cap (0, T)$. Therefore, $N_{\gamma^\star}$ is composed of isolated points and so it is a discrete set. Hence, $\dot{\psi}(t) = 0$ a.e. $t\in D\cap (0, T)$. So, $\ddot{\psi}(t) = 0$ a.e. in $D$, because $\dot \psi$ is absolutely continuous. %$\ddot{\psi}(t) = 0$ a.e. in $D$. Moreover, since $D_{pp}^2 H(t, x, p)>0$ and $|D{b_\Omega}(\gamma^\star(t))| = 1$, we have that
So, for a.e. $t\in D$, $\lambda(t)$ is given by
Since $\lambda(t) = 0$ for all $t\in[0, T]\setminus D$ by (3.27), taking $\Lambda(t, \gamma^\star(t), p(t)) = \frac{\lambda(t)}{\epsilon}$, we obtain the conclusion.
Remark 3.4. The above proof gives a representation of $\Lambda$, i.e., for all $(t, x, p) \in[0, T]\times\Sigma_{\rho_0}\times \mathbb{R}^n$ one has that
where $\theta(t, x, p): = \langle D{b_\Omega}(x), D_{pp}^2 H(t, x, p)D{b_\Omega}(x)\rangle$. Observe that (3.13) ensures that $\theta(t, x, p)>0$ for all $t\in [0, T]$, for all $x\in\Sigma_{\rho_0}$ and for all $p\in \mathbb{R}^n$.
3.3. Proof of Theorem 3.1 for general $U$
We now want to remove the extra assumption $U = \mathbb{R}^n$. For this purpose, it suffices to show that the data $f$ and $g$---a priori defined just on $U$---can be extended to $\mathbb{R}^n$ preserving the conditions in (f0)-(f2) and (g1). So, we proceed to construct such an extension by taking a cut-off function $\xi\in C^\infty(\mathbb{R})$ such that
Lemma 3.8. Let $\Omega\subset\mathbb{R}^n$ be a bounded open set with $C^2$ boundary. Let $U$ be a open subset of $\mathbb{R}^n$ such that $\overline{\Omega}\subset U$ and set
Suppose that $f:[0, T]\times U\times \mathbb{R}^n\rightarrow \mathbb{R}$ and $g:U\rightarrow \mathbb{R}$ satisfy (f0)-(f2) and (g1), respectively. Set $\sigma = \sigma_0\wedge \rho_0$. Then, the function $f$ admits the extension
that satisfies conditions (f0)-(f2) with $U = \mathbb{R}^n$. Moreover, $g$ admits the extension
that satisfies condition (g1) with $U = \mathbb{R}^n$.
Note that, since $\Omega$ is bounded and $U$ is open, the distance between $\overline \Omega$ and $\mathbb{R}^n\setminus U$ is positive.
Proof. By construction we note that $\widetilde{f}\in C([0, T]\times \mathbb{R}^n\times\mathbb{R}^n)$. Moreover, for all $t\in[0, T]$ the function $(x, v)\mapsto \widetilde{f}(t, x, v)$ is differentiable and the map $(x, v)\mapsto D_{v}\widetilde{f}(t, x, v)$ is continuously differentiable by construction. Furthermore, $D_x\widetilde{f}$, $D_v\widetilde{f}$ are continuous on $[0, T]\times \mathbb{R}^n\times \mathbb{R}^n$ and $\widetilde{f}$ satisfies (3.2). In order to prove (3.3) for $\widetilde{f}$, we observe that
and
Hence, by the definition of $\xi$ and (3.3) we obtain that
Since $\mu\geq 1$, we have that $\widetilde{f}$ verifies the estimate in (3.3).
Moreover, since
and by (3.4) we obtain that
For all $(x, v)\in\mathbb{R}^n\times\mathbb{R}^n$ the function $t\mapsto\widetilde{f}(t, x, v)$ and the map $t\mapsto D_v\widetilde{f}(t, x, v)$ are Lipschitz continuous by construction. Moreover, by (3.5) and the definition of $\xi$ one has that
for all $t$, $s\in [0, T]$, $x\in\mathbb{R}^n$, $v\in\mathbb{R}^n$. Now, we have to prove that (3.6) holds for $\widetilde{f}$. Indeed, using (3.6) we deduce that
for all $t$, $s\in[0, T]$, $x\in\mathbb{R}^n$, $v\in \mathbb{R}^n$. Therefore, $\widetilde{f}$ verifies the assumptions (f0)-(f2).
Finally, by the regularity of ${b_\Omega}$, $\xi$, and $g$ we have that $\widetilde{g}$ is of class $C^1_b(\mathbb{R}^n)$. This completes the proof.
4.
Applications of Theorem 3.1
4.1. Lipschitz regularity for constrained minimization problems
Suppose that $f:[0, T]\times U\times \mathbb{R}^n\rightarrow \mathbb{R}$ and $g:U\rightarrow \mathbb{R}$ satisfy the assumptions (f0)-(f2) and (g1), respectively. Let $(t, x)\in [0, T]\times \overline{\Omega}$. Define $u:[0, T]\times \overline{\Omega}\rightarrow\mathbb{R}$ as the value function of the minimization problem (3.1), i.e.,
Proposition 4.1. Let $\Omega$ be a bounded open subset of $\mathbb{R}^n$ with $C^2$ boundary. Suppose that $f$ and $g$ satisfy (f0)-(f2) and (g1), respectively. Then, $u$ is Lipschitz continuous in $[0, T]\times\overline{\Omega}$.
Proof. First, we shall prove that $u(t, \cdot)$ is Lipschitz continuous on $\Omega$, uniformly for $t\in[0, T]$. Since $u(T, \cdot) = g$, it suffices to consider the case of $t \in [0, T)$. Let $x_0\in\Omega$ and choose $0<r<1$ such that $B_r(x_0)\subset B_{2r}(x_0)\subset B_{4r}(x_0)\subset \Omega$. To prove that $u(t, \cdot)$ is Lipschitz continuous in $B_r(x_0)$, take $x\neq y$ in $B_r(x_0)$. Let $\gamma$ be an optimal trajectory for $u$ at $(t, x)$ and let ${\bar \gamma}$ be the trajectory defined by
where $\tau = \frac{|x-y|}{2L^\star}<T-t$. We claim that
(a) ${\bar \gamma}(t+\tau) = \gamma(t+\tau)$;
(b) ${\bar \gamma}(s) = \gamma(s)$ for any $s\in[t+\tau, T]$;
(c) $|{\bar \gamma}(s)-\gamma(s)|\leq |y-x|$ for any $s \in [t, t+\tau]$;
(d) ${\bar \gamma}(s)\in \overline{\Omega}$ for any $s \in [t, T]$.
Indeed, by the definition of ${\bar \gamma}$ we have that
and this gives (a). Moreover, by (a), and by the definition of ${\bar \gamma}$ one has that ${\bar \gamma}(s) = \gamma(s)$ for any $s\in[t+\tau, T]$. Hence, ${\bar \gamma}$ verifies (b). By the definition of ${\bar \gamma}$, for any $s\in [t, t+\tau]$ we obtain that
and so (c) holds. Since $\gamma$ is an optimal trajectory for $u$ and by ${\bar \gamma}(s) = \gamma(s)$ for all $s\in [t+\tau, T]$, we only have to prove that ${\bar \gamma}(s)$ belongs to $\overline{\Omega}$ for all $s\in[t, t+\tau]$. Let $s\in [t, t+\tau]$, by Theorem 3.1 one has that
Recalling that $\tau = \frac{|x-y|}{2L^\star}$ one has that
Therefore, ${\bar \gamma}(s)\in B_{4r}(x_0)\subset \overline{\Omega}$ for all $s\in[t, t+\tau]$.
Now, owing to the dynamic programming principle, by (a) one has that
Since $\gamma$ is an optimal trajectory for $u$ at $(t, x)$, we obtain that
By (3.7), (3.8), and the definition of ${\bar \gamma}$, for $s\in [t, t+\tau]$ we have that
By Theorem 3.1 one has that
Using (4.3), (4.4), and (c), by the definition of $\overline{\gamma}$ one has that
for a.e. $s\in[t, t+\tau]$. By (4.5), and the choice of $\tau$ we deduce that
where $C_{L^\star} = C(\mu, M)(1+4L^\star)+\frac{1}{2L^\star}C(\mu, M)(1+(L^\star)^2)$. Thus, $u$ is locally Lipschitz continuous in space and one has that $||Du||_\infty\leq \vartheta$, where $\vartheta$ is a constant not depending on $\Omega$. Owing to the smoothness of $\Omega$, $u$ is globally Lipschitz continuous in space, uniformly for $t\in[0, T]$.
In order to prove Lipschitz continuity in time, let $x \in \overline\Omega$ and fix $t_1$, $t_2 \in [0, T]$ with $t_2\geq t_1$. Let $\gamma$ be an optimal trajectory for $u$ at $(t_1, x)$. Then,
The first term on the right-side of (4.6) can be estimated using the Lipschitz continuity in space of $u$ and Theorem 3.1. Thus, we get
We only have to estimate the second term on the right-side of (4.6). By the dynamic programming principle, (3.9), and the assumptions on $F$ we deduce that
Using (4.7) and (4.8) to bound the right-hand side of (4.6), we obtain that $u$ is Lipschitz continuous in time. This completes the proof.
4.2. Lipschitz regularity for constrained MFG equilibria
In this section we want to apply Theorem 3.1 to a mean field game (MFG) problem with state constraints. Such a problem was studied in [11], where the existence and uniqueness of constrained equilibria was obtained under fairly general assumptions on the data. Here, we will apply our necessary conditions to deduce the existence of more regular equilibria than those constructed in [11], assuming the data $F$ and $G$ to be Lipschitz continuous.
Assumptions
Let $\Omega$ be a bounded open subset of $\mathbb{R}^n$ with $C^2$ boundary. Let $\mathcal{P}(\overline{\Omega})$ be the set of all Borel probability measures on $\overline\Omega$ endowed with the Kantorovich-Rubinstein distance $d_1$ defined in (2.2). Let $U$ be an open subset of $\mathbb{R}^n$ and such that $\overline{\Omega}\subset U$. Assume that $F:U\times\mathcal{P}(\overline{\Omega})\rightarrow \mathbb{R}$ and $G:U\times \mathcal{P}(\overline{\Omega})\rightarrow \mathbb{R}$ satisfy the following hypotheses.
(D1) For all $x\in U$, the functions $m\mapsto F(x, m)$ and $m\mapsto G(x, m)$ are Lipschitz continuous, i.e., there exists a constant $\kappa\geq 0$ such that
for any $m_1$, $m_2 \in\mathcal{P}(\overline{\Omega})$.
(D2) For all $m\in \mathcal{P}(\overline{\Omega})$, the functions $x\mapsto G(x, m)$ and $x\mapsto F(x, m)$ belong to $C^1_b(U)$. Moreover
Let $L:U\times\mathbb{R}^n\rightarrow \mathbb{R}$ be a function that satisfies the following assumptions.
(L0) $L\in C^1(U\times \mathbb{R}^n)$ and there exists a constant $M\geq 0$ such that
(L1) $D_vL$ is differentiable on $U\times\mathbb{R}^n$ and there exists a constant $\mu\geq 1$ such that
for all $(x, v)\in U\times \mathbb{R}^n$.
Remark 4.1. (ⅰ) $F$, $G$ and $L$ are assumed to be defined on $U\times \mathcal{P}(\overline{\Omega})$ and on $U\times \mathbb{R}^n$, respectively, just for simplicity. All the results of this section hold true if we replace $U$ by $\overline{\Omega}$. This fact can be easily checked by using well-known extension techniques (see, e.g. [1, Theorem 4.26]).
(ⅱ) Arguing as Lemma 3.1 we deduce that there exists a positive constant $C(\mu, M)$ that dependes only on $M$, $\mu$ such that
for all $(x, v)\in U\times\mathbb{R}^n$.
Let $m\in {\rm Lip}(0, T;\mathcal{P}(\overline{\Omega}))$. If we set $f(t, x, v) = L(x, v)+F(x, m(t))$, then the associated Hamiltonian $H$ takes the form
where
The assumptions on $L$ imply that $H_L$ satisfies the following conditions.
1. $H_L\in C^1(U\times \mathbb{R}^n)$ and there exists a constant $M'\geq 0$ such that
2. $D_pH_L$ is differentiable on $U\times\mathbb{R}^n$ and satisfies
where $\mu$ is the constant in (L1) and $C(\mu, M')$ depends only on $\mu$ and $M'$.
For any $t\in [0, T]$, we denote by $e_t:\Gamma\to \overline \Omega$ the evaluation map defined by
For any $\eta\in\mathcal{P}(\Gamma)$, we define
Remark 4.2. We observe that for any $\eta\in\mathcal{P}(\Gamma)$, the following holds true (see [11] for a proof).
(ⅰ) $m^\eta\in C([0, T];\mathcal{P}(\overline{\Omega}))$.
(ⅱ) Let $\eta_i$, $\eta\in\mathcal{P}(\Gamma)$, $i\geq 1$, be such that $\eta_i$ is narrowly convergent to $\eta$. Then $m^{\eta_i}(t)$ is narrowly convergent to $m^\eta(t)$ for all $t\in[0, T]$.
For any fixed $m_0\in\mathcal{P}(\overline{\Omega})$, we denote by ${\mathcal P}_{m_0}(\Gamma)$ the set of all Borel probability measures $\eta$ on $\Gamma$ such that $e_0\sharp \eta = m_0$. For all $\eta \in \mathcal{P}_{m_0}(\Gamma)$, we set
For all $x \in \overline{\Omega}$ and $\eta\in\mathcal{P}_{m_0}(\Gamma)$, we define
It is shown in [11] that, for every $\eta\in \mathcal{P}_{m_0}(\Gamma)$, the set $\Gamma^\eta[x]$ is nonempty and $\Gamma^\eta[\cdot]$ has closed graph. We recall the definition of constrained MFG equilibria for $m_0$, given in [11].
Definition 4.1. Let $m_0\in\mathcal{P}(\overline{\Omega})$. We say that $\eta\in\mathcal{P}_{m_0}(\Gamma)$ is a contrained MFG equilibrium for $m_0$ if
Let $\Gamma'$ be a nonempty subset of $\Gamma$. We denote by $\mathcal{P}_{m_0}(\Gamma')$ the set of all Borel probability measures $\eta$ on $\Gamma'$ such that $e_0\sharp\eta = m_0$. We now introduce special subfamilies of $\mathcal{P}_{m_0}(\Gamma)$ that play a key role in what follows.
Definition 4.2. Let $\Gamma'$ be a nonempty subset of $\Gamma$. We define by $\mathcal{P}_{m_0}^{{\rm Lip}}(\Gamma')$ the set of $\eta\in\mathcal{P}_{m_0}(\Gamma')$ such that $m^\eta(t) = e_t\sharp \eta$ is Lipschitz continuous, i.e.,
Remark 4.3. We note that $\mathcal{P}^{{\rm Lip}}_{m_0}(\Gamma)$ is a nonempty convex set. Indeed, let $j:\overline{\Omega}\rightarrow \Gamma$ be the continuous map defined by
Then,
is a Borel probability measure on $\Gamma$ and $\eta \in\mathcal{P}^{{\rm Lip}}_{m_0}(\Gamma)$.
In order to show that ${\cal P}_{{m_0}}^{{\rm{Lip}}}\left( \Gamma \right)$ is convex, let $\{\eta_i\}_{i = 1, 2}\subset \mathcal{P}_{m_0}^{{\rm Lip}}(\Gamma)$ and let $\lambda_1$, $\lambda_2\geq 0$ be such that $\lambda_1+\lambda_2 = 1$. Since $\eta_i$ are Borel probability measures, $\eta: = \lambda\eta_1+(1-\lambda)\eta_2$ is a Borel probability measure as well. Moreover, for any Borel set $B\in \mathscr{B}(\overline{\Omega})$ we have that
So, $\eta\in\mathcal{P}_{m_0}(\Gamma)$. Since $m^{\eta_1}$, $m^{\eta_2}\in {\rm Lip}(0, T;\mathcal{P}(\overline{\Omega}))$, we have that $m^\eta(t) = \lambda_1m^{\eta_1}(t)+\lambda_2m^{\eta_2}(t)$ belongs to ${\rm Lip}(0, T;\mathcal{P}(\overline{\Omega}))$.
In the next result, we apply Theorem 3.1 to prove a useful property of minimizers of $J_\eta$.
Proposition 4.2. Let $\Omega$ be a bounded open subset of $\mathbb{R}^n$ with $C^2$ boundary and let $m_0\in\mathcal{P}(\overline{\Omega})$. Suppose that (L0), (L1), (D1), and (D2) hold true. Let $\eta\in\mathcal{P}^{{\rm Lip}}_{m_0}(\Gamma)$ and fix $x\in\overline{\Omega}$. Then $\Gamma^\eta[x]\subset C^{1, 1}([0, T];\mathbb{R}^n)$ and
where $L_0 = L_0(\mu, M', M, \kappa, T, ||G||_\infty, ||DG||_\infty)$.
Proof. Let $\eta\in\mathcal{P}_{m_0}^{{\rm Lip}}(\Gamma)$, $x\in\overline{\Omega}$ and $\gamma\in \Gamma^\eta[x]$. Since $m\in {\rm Lip}(0, T;\mathcal{P}(\overline{\Omega}))$, taking $f(t, x, v) = L(x, v)+F(x, m(t))$, one can easly check that all the assumptions of Theorem 3.1 are satisfied by $f$ and $G$. Therefore, we have that $\Gamma^\eta[x]\subset C^{1, 1}([0, T];\mathbb{R}^n)$ and, in this case, (3.21) becomes
where $L_0 = L_0(\mu, M', M, \kappa, T, ||G||_\infty, ||DG||_\infty)$.
We denote by $\Gamma_{L_0}$ the set of $\gamma\in\Gamma$ such that (4.19) holds, i.e.,
Lemma 4.1. Let $m_0\in \mathcal{P}(\overline{\Omega})$. Then, $\mathcal{P}_{m_0}^{{\rm Lip}}(\Gamma_{L_0})$ is a nonempty convex compact subset of $\mathcal{P}_{m_0}(\Gamma)$. Moreover, for every $\eta\in\mathcal{P}_{m_0}(\Gamma_{L_0})$, $m^\eta(t): = e_t\sharp \eta$ is Lipschitz continuous of constant $L_0$, where $L_0$ is as in Proposition 4.2.
Proof. Arguing as in Remark 4.3, we obtain that $\mathcal{P}_{m_0}^{{\rm Lip}}(\Gamma_{L_0})$ is a nonempty convex set. Moreover, since $\Gamma_{L_0}$ is compactly embedded in $\Gamma$, one has that $\mathcal{P}_{m_0}^{{\rm Lip}}(\Gamma_{L_0})$ is compact.
Let $\eta\in\mathcal{P}_{m_0}(\Gamma_{L_0})$ and $m^\eta(t) = e_t\sharp\eta$. For any $t_1, t_2\in[0, T]$, we recall that
Since $\phi$ is 1-Lipschitz continuous, one has that
Since $\eta \in \mathcal{P}_{m_0}(\Gamma_{L_0})$, we deduce that
and so $m^\eta(t)$ is Lipschitz continuous of constant $L_0$.
In the next result, we deduce the existence of more regular equilibria than those constructed in [11].
Theorem 4.1. Let $\Omega$ be a bounded open subset of $\mathbb{R}^n$ with $C^2$ boundary and $m_0\in\mathcal{P}(\overline{\Omega})$. Suppose that (L0), (L1), (D1), and (D2) hold true. Then, there exists at least one constrained MFG equilibrium $\eta \in{\cal P}_{{m_0}}^{{\rm{Lip}}}\left( \Gamma \right)$.
Proof. First of all, we recall that for any $\eta\in{\cal P}_{{m_0}}^{{\rm{Lip}}}\left( \Gamma \right)$, there exists a unique Borel measurable family * of probabilities $\{\eta_x\}_{x\in\overline{\Omega}}$ on $\Gamma$ which disintegrates $\eta$ in the sense that
*We say that $\{\eta_x\}_{x\in \overline{\Omega}}$ is a Borel family (of probability measures) if $x\in \overline{\Omega}\mapsto \eta_x(B)\in \mathbb{R}$ is Borel for any Borel set $B\subset \Gamma$.
(see, e.g., [2, Theorem 5.3.1]). Proceeding as in [11], we introduce the set-valued map
by defining, for any $\eta\in \mathcal{P}_{m_0}(\Gamma)$,
We recall that, by [11, Lemma 3.6], the map $E$ has closed graph.
Now, we consider the restriction $E_0$ of $E$ to ${\cal P}_{{m_0}}^{{\rm{Lip}}}\left( \Gamma \right)$, i.e.,
We will show that the set-valued map $E_0$ has a fixed point, i.e., there exists $\eta\in \mathcal{P}_{m_0}^{{\rm Lip}}(\Gamma_{L_0})$ such that $\eta\in E_0(\eta)$. By [11, Lemma 3.5] we have that for any $\eta\in\mathcal{P}_{m_0}^{{\rm Lip}}(\Gamma_{L_0})$, $E_0(\eta)$ is a nonempty convex set. Moreover, we have that
Indeed, let $\eta\in \mathcal{P}_{m_0}^{{\rm Lip}}(\Gamma_{L_0})$ and $\hat{\eta}\in E_0(\eta)$. Since, by Proposition 4.2 one has that
and by definition of $E_0$ we deduce that
So, $\widehat{\eta}\in\mathcal{P}_{m_0}(\Gamma_{L_0})$. By Lemma 4.1, $\widehat{\eta}\in \mathcal{P}_{m_0}^{{\rm Lip}}(\Gamma_{L_0})$.
Since $E$ has closed graph, by Lemma 4.1 and (4.23) we have that $E_0$ has closed graph as well. Then, the assumptions of Kakutani's Theorem [30] are satisfied and so, there exists $\overline \eta\in \mathcal{P}^{{\rm Lip}}_{m_0}(\Gamma_{L_0})$ such that $\overline \eta\in E_0(\overline \eta)$.
We recall the definition of a mild solution of the constrained MFG problem, given in [11].
Definition 4.3. We say that $(u, m)\in C([0, T]\times \overline{\Omega})\times C([0, T];\mathcal{P}(\overline{\Omega}))$ is a mild solution of the constrained MFG problem in $\overline{\Omega}$ if there exists a constrained MFG equilibrium $\eta\in\mathcal{P}_{m_0}(\Gamma)$ such that
(i) $ m(t) = e_t\sharp \eta$ for all $t\in[0, T]$;
(ii) u is given by
for $(t, x)\in [0, T]\times \overline{\Omega}$.
Theorem 4.2. Let $\Omega$ be a bounded open subset of $\mathbb{R}^n$ with $C^2$ boundary. Suppose that (L0), (L1), (D1) and (D2) hold true. There exists at least one mild solution $(u, m)$ of the constrained MFG problem in $\overline{\Omega}$. Moreover,
(i) $u$ is Lipschitz continuous in $[0, T]\times\overline{\Omega}$;
(ii) $m\in{\rm Lip}(0, T;\mathcal{P}(\overline{\Omega}))$ and ${\rm Lip}(m) = L_0$, where $L_0$ is the constant in (4.19).
The question of the Lipschitz continuity up to the boundary of the value function under state constraints was addressed in [28] and [34], for stationary problems, and in a very large literature that has been published since. We refer to the survey paper [20] for references.
Proof. Let $m_0\in\mathcal{P}(\overline{\Omega})$ and let $\eta\in \mathcal{P}_{m_0}^{\rm Lip}(\Gamma)$ be a constrained MFG equilibrium for $m_0$. Then, by Theorem 4.1 there exists at least one mild solution $(u, m)$ of the constrained MFG problem in $\overline{\Omega}$. Moreover, by Theorem 4.1 one has that $m\in{\rm Lip}(0, T;\mathcal{P}(\overline{\Omega}))$ and ${\rm Lip}(m) = L_0$, where $L_0$ is the constant in (4.19). Finally, by Proposition 4.1 we conclude that $u$ is Lipschitz continuous in $(0, T)\times \overline{\Omega}$.
Remark 4.4. Recall that $F:U\times \mathcal{P}(\overline{\Omega})\rightarrow \mathbb{R}$ is strictly monotone if
for any $m_1, m_2\in {\mathcal P}(\overline \Omega)$, and $\int_{\overline{\Omega}} (F(x, m_1)-F(x, m_2))d(m_1-m_2)(x) = 0$ if and only if $F(x, m_1) = F(x, m_2)$ for all $x\in \overline{\Omega}$.
Suppose that $F$ and $G$ satisfy (4.25). Let $\eta_1$, $\eta_2\in \mathcal{P}_{m_0}^{\rm Lip}(\Gamma)$ be constrained MFG equilibria and let $J_{\eta_1}$ and $J_{\eta_2}$ be the associated functionals, respectively. Then $J_{\eta_1}$ is equal to $J_{\eta_2}$. Consequently, if $(u_1, m_1)$, $(u_2, m_2)$ are mild solutions of the constrained MFG problem in $\overline{\Omega}$, then $u_1 = u_2$ (see [11] for a proof).
5.
Appendix
In this Appendix we prove Lemma 2.1. The only case which needs to be analyzed is when $ x\in\partial\Omega$. We recall that $p\in \partial^p d_\Omega( x)$ if and only if there exists $\epsilon>0$ such that
for some constant $C\geq 0$. Let us show that $\partial^p d_\Omega( x) = D{b_\Omega}( x)[0, 1]$. By the regularity of ${b_\Omega}$, one has that
This shows that $ D{b_\Omega}( x)\in \partial^p d_\Omega( x)$. Moreover, since
we further obtain the inclusion
Next, in order to show the reverse inclusion, let $p\in\partial^p d_\Omega( x)\setminus\{0\}$ and let $ y\in\Omega^c$. Then, we can rewrite (5.1) as
Since $ y\in \Omega^c$, by the regularity of ${b_\Omega}$ one has that
for some constant $C\in\mathbb{R}$. By (5.2) and (5.3) one has that
Hence, passing to the limit for $ y\rightarrow x$, we have that
where $T_{\Omega^c}( x)$ is the contingent cone to $\Omega^c$ at $ x$ (see e.g. [35] for a definition). Therefore, by the regularity of $\partial\Omega$,
where $\lambda\geq 0$ and $v( x)$ is the exterior unit normal vector to $\partial\Omega$ in $ x$. Since $v( x) = D{b_\Omega}( x)$, we have that
Now, we prove that $\lambda \leq 1$. Suppose that $ y\in \Omega$, then, by (5.1) one has that
Hence,
Passing to the limit for $ y\rightarrow x$, we obtain
where $T_{\overline{\Omega}}( x)$ is the contingent cone to $\Omega$ at $ x$. We now claim that $\lambda\leq 1$. If $\lambda >1$, then $\langle D {b_\Omega}( x), w \rangle \geq 0$ for all $w\in T_{\overline{\Omega}}( x)$ but this is impossible since $ D{b_\Omega}( x)$ is the exterior unit normal vector to $\partial\Omega$ in $ x$. Using the regularity of ${b_\Omega}$, simple limit-taking procedures permit us to prove that $\partial d_\Omega( x) = D{b_\Omega}( x)[0, 1]$ when $ x\in\partial \Omega$. This completes the proof of Lemma 2.1.
Acknowledgments
This work was partly supported by the University of Rome Tor Vergata (Consolidate the Foundations 2015) and by the Istituto Nazionale di Alta Matematica "F. Severi" (GNAMPA 2016 Research Projects). The authors acknowledge the MIUR Excellence Department Project awarded to the Department of Mathematics, University of Rome Tor Vergata, CUP E83C18000100006. The second author is grateful to the Universitá Italo Francese (Vinci Project 2015).
Conflict of interest
The authors declare no conflict of interest.













 DownLoad:
DownLoad: