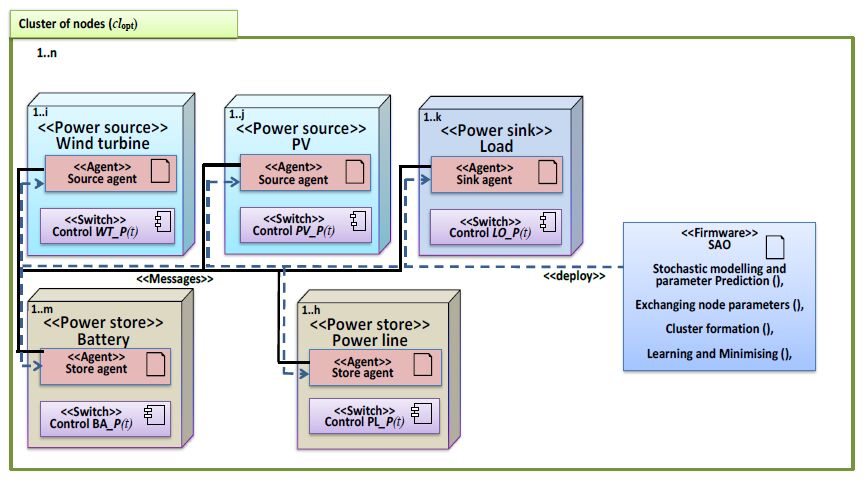
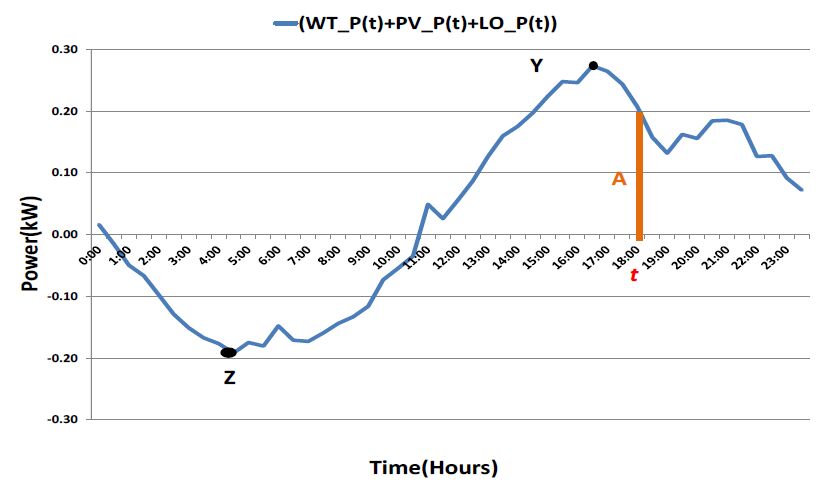
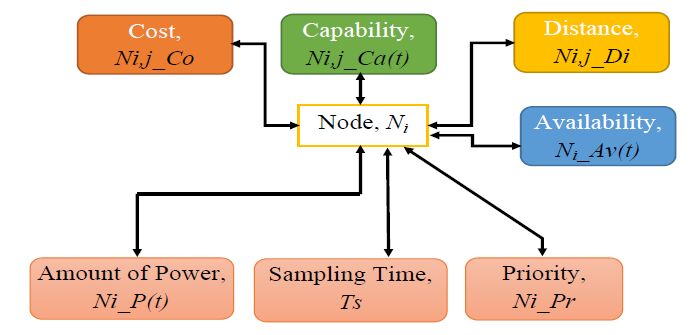
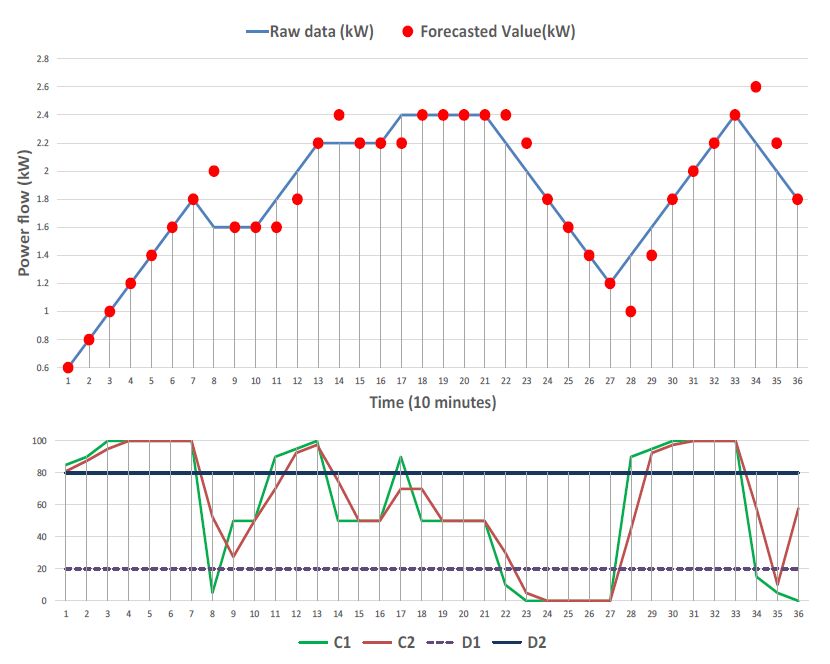
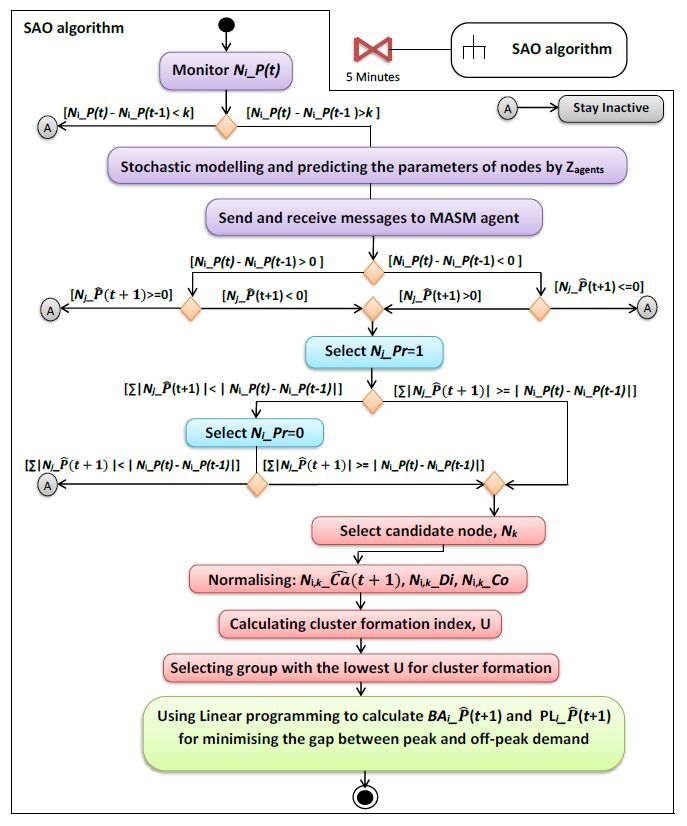
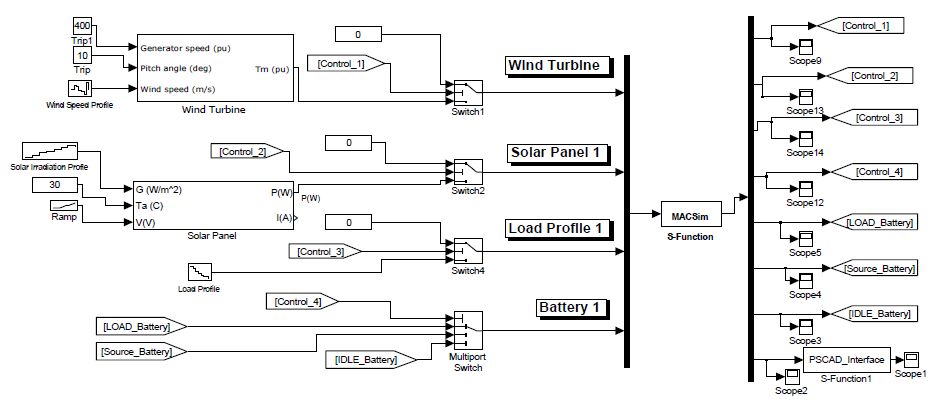
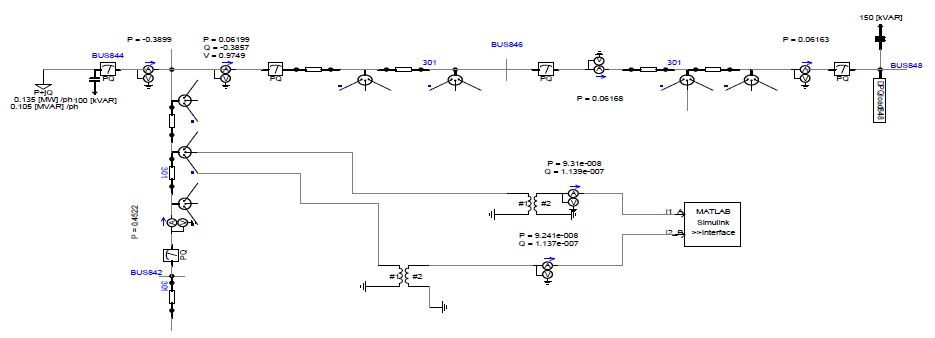
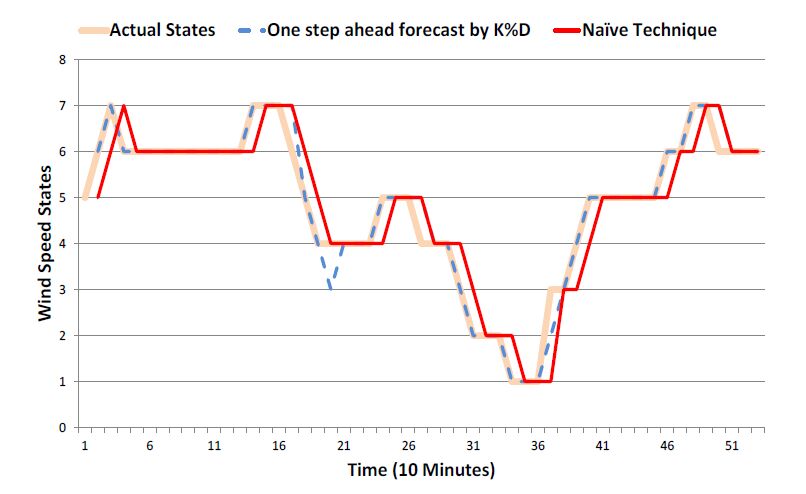
In the current research, a smart grid is considered as a network of distributed interacting nodes represented by renewable energy sources, storage and loads. The source nodes become active or inactive in a stochastic manner due to the intermittent nature of natural resources such as wind and solar irradiance. Prediction and stochastic modelling of electrical energy flow is a critical task in such a network in order to achieve load levelling and/or peak shaving in order to minimise the fluctuation between off-peak and peak energy demand. An effective approach is proposed to model and administer the behaviour of source nodes in this grid through a scheduling strategy control algorithm using the historical data collected from the system. The stochastic model predicts future power consumption/injection to determine the power required for storage components. The stochastic models developed based on the Box-Jenkins method predict the most efficient state of the electrical energy flow between a distribution network and nodes and minimises the peak demand and off-peak consumption of acquiring electrical energy from the main grid. The performance of the models is validated against the autoregressive moving average (ARIMA) and the Markov chain models used in previous work. The results demonstrate that the proposed method outperforms both the ARIMA and the Markov chain model in terms of forecast accuracy. Results are presented, the strengths and limitations of the approach are discussed, and possible future work is described.
1.
Introduction
Plant diseases, such as fungal, viral and bacterial diseases, are a key constraint in yield and quality of cultivated crops worldwide, which often result in considerable economic losses and increased poverty unless appropriate control measures are taken [1,2,3]. It is possible to influence the course of disease development by applying curative chemicals. However, deleterious side effects may arise from overuse of insecticides, such as buildup of toxic residues and loss of beneficial natural enemies of vectors that could render the control ineffective [4]. Therefore plant pathologists and climatologists, in collaboration with other researchers, have developed and implemented economically and environmentally acceptable strategies to manage plant-disease development [5]. Such experiences have led to the development of integrated disease management (IDM) for plant diseases that combines various methods such as chemical, cultural and biological tactics that function effectively to minimize losses and maximize returns [3,6,7]. It has been recognized that one of the main cultural strategies of IDM — control of crop sanitation through replanting healthy plants and roguing infectious plants — has proven to be successful and is now a widely adopted control strategy [8,9,10,11,12]. Diseases such as citrus tristeza disease, cocoa swollen shoot, plum pox and peach mosaic have been successfully controlled by roguing [8,13,14,15,16].
Based on IDM, mathematical models have become an increasingly important tool in the quantitative and qualitative study of epidemic dynamics and disease progress [2,5,7,9,14,17,18,19,20,21]. For example, Madden et al. [22] proposed a number of ordinary differential equation (ODE) models that simulate the spatial and temporal patterns of plant pathogens to understand, compare and summarize the population dynamics of plant diseases in crops. A model of vegetatively propagated plant disease with continuous roguing and replanting strategy established by van den Bosch et al. [23] reads as follows:
where $ S(t) $ and $ I(t) $ represent the numbers of susceptible and infected plants at time $ t $, respectively; $ \sigma $ is the continual replanting rate for the susceptible plants; $ \eta $ is the death or harvest rate; $ \beta $ denotes the transmission rate, which is mediated by insects or other vectors; and $ \omega $ represents the roguing rate for the infected plants. The authors used the above model to determine the effect of disease-control methods on the selection of virus strains. This model is a macro model, with the biological mechanism as follows: the pathogen parasitizes in infected plants; the vector carries the pathogen after contacting the infected plants and then brings the pathogen to the susceptible plants, so the susceptible plants are then infected and transformed into infected plants, which can be cleared. A common assumption for system (1.1) is that control occurs continuously. However, regular pulses provide a more natural description for the control behaviour [24,25,26]. For instance, periodic removal of infected plants was used in 1983 when Fishman et al. [14] analyzed a mathematical model for citrus tristeza disease and determined the effectiveness of the eradication procedure. On the basis of (1.1), Tang et al. [27] considered the cultural control in a periodic way, whose results implied that the infected plants can be completely eradicated if the control period is relatively large.
Previous work considering the cultural control strategy for plant diseases has mainly focused on models with constant roguing rates. However, the roguing rate is not always unchanged [28] but rather depends on a variety of factors such as the number of infected plants. In this case, the roguing rate becomes a function of the number of infections, which leads to a nonlinear roguing rate. The second aspect related to the cultural strategy is that not only is constant replanting feasible but also that proportional replanting makes sense [7]. In addition, when infected plants are rogued, some incidental susceptible plants may be removed accidentally (or deliberately), which we will consider here. Little is known about the dynamics of plant diseases with consideration of the nonlinear management, proportional replanting rate and incidental removal. Hence the first purpose of this study is to extend model (1.1) by implementing periodic removing and replanting at critical times, investigating disease dynamics analytically, seeking the main determinants of epidemic development and evaluating whether current cultural control for plant diseases is effective enough to prevent further spread of the disease.
IDM admits an economically viable threshold under which crop damage can be acceptable [3,29,30]. So the control criterion usually relates to the number of infections passing a threshold value called the economic threshold (ET). The control strategy can only be implemented when the number of infected individuals reaches the ET. This threshold policy satisfies both biological and economical conditions and is thus used to make justified and strategic decisions [27]. The second aim of our study is to further improve the model with a periodic control measure by taking the ET into account in order to maintain the number of infections under the ET, to understand how disease spreads from a theoretical point of view, to determine the impact of control strategies on disease progress and to show the frequency of interventions if the plants exhibit regular and periodic development.
This paper is organised as follows. In Section 2, the impulsive model with periodic control is established. The conditions under which the disease-free periodic solution is locally and globally stable, and the system is persistent, are deduced; the existence conditions of positive periodic solution are obtained by bifurcation theory. Partial rank correlation coefficients are used to assess the impact of parameters on the threshold value that determines the dynamics of the system. In Section 3, we investigate the existence and global stability of one- and two-periodic solutions of the state-dependent impulsive differential model with the ET, where a fold bifurcation occurs. The period of the solution is derived, and the effects of control methods are examined. Finally, some biological conclusions are discussed.
2.
The plant-disease model with periodic control strategy
In this section, we extend model (1.1) by replacing the continuous cultural control measure with a periodic pulse strategy, since the latter is more realistic. Hence the plant-disease model with impulsive removing and replanting strategy at fixed moments is as follows:
where $ \alpha $ denotes density dependence, $ T $ represents the period of deploying control, $ \sigma $ is the constant replanting parameter and $ n\in N $. The parameter $ p $ has different meanings in different ranges. If $ p = 1 $, there is only constant replanting. If $ p > 1 $, then it represents the proportional replanting rate. If $ 0 < p < 1 $, then it represents the proportional removal residual rate, which accounts for the fact that, when the infected plants are rogued, some susceptible plants will be removed accidentally. There are two reasons for this. On the one hand, the susceptible plants near infected plants are at greater risk of infection. Therefore, in order to prevent the spread of disease, when we rogue infected plants, we may choose to remove some nearby susceptible plants at the same time as a precaution. On the other hand, if the infected plants are rogued by mechanical operation, it is likely that some of the nearby susceptible plants will be removed incidentally.
The nonlinear roguing function is chosen to reflect the effect of saturation. If the number of infected plants is small, then the impulse is approximately
in line with standard forms of impulsive control. However, if the number of infected plants is large, then the number of plants that could be removed in practice is limited and will approximate
with the understanding that this quantity is not negative (since $ I(nT^+) $ is large). That is, in a large outbreak, the number of plants removed at each impulse is approximately constant.
Note that, while we are using plant diseases with a vector as our focus, model (2.1) has a much wider range of applications. These could include herbivory or a drosophila colony infesting a fruit tree in an orchard. Our results will thus be generalisable beyond what is usually thought of as plant diseases.
2.1. The existence and stability of the disease-free periodic solution
If $ I(t) = 0, $ then model (2.1) becomes the following subsystem:
System (2.2) exhibits a positive periodic solution $ S^{*}(t) $ that is globally asymptotically stable if $ 0 < p\leq 1 $ or $ p > 1 $ and $ p \exp(-\eta T) < 1 $. See Theorem A.1 in the Appendix. The disease-free periodic solution $ (S^{*}(t), 0) $ of model (2.1), where
is feasible if $ 0 < p\leq 1 $ or if $ p > 1 $ and $ p \exp(-\eta T) < 1. $
Theorem 2.1. The disease-free periodic solution $ (S^{*}(t), 0) $ of $ (2.1) $ is locally asymptotically stable in the first quadrant, provided that one of the following conditions is satisfied:
$(C_{1})$ $ 0 < p\leq 1 $ and $ R_1 < 1; $
$(C_{2})$ $ p > 1, $ $ p \exp(-\eta T) < 1 $ and $ R_1 < 1. $
Here,
Proof. Denote $ U(t) = S(t)+I(t) $. Then, according to the first and second equations of (2.1), we get $ \frac{dU(t)}{dt} = -\eta U(t), $ which yields $ U(t) = U(nT^+)\exp(-\eta (t-nT)) $, $ t\in (nT, (n+1)T] $, $ n\in N. $ It follows from (2.1) that
For $ t\in (nT, (n+1)T], $ we get the analytical solution for the $ S $ component,
Similarly, we have
Denote $ X_n = S(nT^+), \ Y_n = I(nT^+), \ U_n = U(nT^+). $ Then the difference equations that describe the numbers of susceptible and infected plants at an impulse in terms of values at the previous impulse are deduced as follows:
This is a Poincaré map at the impulsive points of model (2.1). Fixed points of system (2.7) correspond to the initial values of periodic solutions of model (2.1). The stability of the disease-free periodic solution of model (2.1) is equivalent to the stability of the boundary steady state of the difference equations (2.7) [31]. There exists a boundary steady state $ \left(\frac{\sigma}{1-p \exp(-\eta T)}, \ 0 \right) $ for system (2.7) that is locally stable if the absolute values of eigenvalues of the following matrix are less than one:
If $ (C_{1}) $ or $ (C_{2}) $ holds, then $ \lambda_{1} = p \exp(-\eta T) < 1 $ and $ \lambda_{2} = (1-\omega)\exp\left(\frac{\beta \sigma (1-\exp(-\eta T))}{\eta (1-p \exp(-\eta T))}-\eta T\right) < 1 $. Therefore, under conditions $ (C_{1}) $ or $ (C_{2}) $, the disease-free periodic solution $ (S^{*}(t), 0) $ of (2.1) is locally asymptotically stable.
Theorem 2.2. If one of the following conditions holds true, then the disease-free periodic solution $ (S^{*}(t), 0) $ of $ (2.1) $ is globally asymptotically stable in the first quadrant:
$(C_{3}) $ $ 0 < p\leq 1 $ and $ R_2^{1} < 1; $
$(C_{4})$ $ p > 1, $ $ p \exp(-\eta T) < 1 $ and $ R_2^{2} < 1. $
Here,
Proof. We first consider the case of $ 0 < p\leq 1. $ It follows from (2.1) that
from which we get
Thus $ U(t) $ is uniformly bounded and, for $ \epsilon_1 > 0 $ small enough, there exists a $ t_{1} > 0 $ such that $ S(t), \ I(t) \leq L_{1} $ with $ t \geq t_1 $ for every solution $ (S(t), \ I(t)) $ of (2.1), where $ L_{1} = \frac{\sigma}{1-\exp(-\eta T)}+\epsilon_1 $.
If $ R_{1} < R_{2}^{1} < 1 $, then, by Theorem 2.1, $ (S^{*}(t), 0) $ is locally asymptotically stable. In order to show the global stability of $ (S^{*}(t), 0), $ we only need to prove its global attractiveness.
It follows from (2.1) that $ d S(t)/dt \leq -\eta S(t), \ S(nT^{+}) = p S(nT)+ \sigma. $ Consider the following system:
which yields $ S(t) \leq Z_1(t) $ and $ Z_1(t)\rightarrow S^{*}(t) $ as $ t \rightarrow \infty $ by Theorem A.1 and the comparison theorem on impulsive differential equations [32]. Hence, for $ \epsilon_2 > 0 $ small enough and large $ t $, we have
Hence there exists a $ t_2 $ such that $ t_2 \geq t_1 $ and (2.11) is true for all $ t \geq t_2. $ From (2.1), we get
for $ t \geq t_2 $. It follows from $ R_{2}^{1} < 1 $ and sufficiently small $ \epsilon_1\ \mbox{and}\ \epsilon_2 $ that
Making use of the comparison theorem on impulsive differential equations again, we get
which gives $ I(nT)\leq I_0 \delta_1^{n} $; hence $ I(nT)\rightarrow 0 $ as $ n\rightarrow \infty. $ Therefore $ I(t)\rightarrow 0 $ as $ t\rightarrow \infty. $
Next, we will prove that if $ \lim\limits_{t\rightarrow \infty}I(t) = 0, $ then $ S(t)\rightarrow S^*(t) $ as $ t\rightarrow \infty. $
The result $ \lim\limits_{t\rightarrow \infty}I(t) = 0 $ shows that, for $ \epsilon_3 > 0 $ small enough, there exists a $ t_3 $ such that $ t_3 \geq t_2 $ and $ 0 < I(t) < \epsilon_3 $ for $ t \geq t_3. $ Thus, for $ t \geq t_3 $,
from which the following equations are obtained:
This system has a positive globally attractive periodic solution $ Z_2^{*}(t) $ for $ t \in (nT, (n+1)T] $, where $ Z_2^*(t) = \frac{\sigma \exp((-\beta\epsilon_3-\eta)(t-n T))}{1- p \exp((-\beta\epsilon_3-\eta)T)} $ with $ Z_2^*(nT^+) = \frac{\sigma}{1- p \exp((-\beta\epsilon_3-\eta)T)}. $ The comparison theorem gives $ Z_2(t)\leq S(t)\leq Z_1(t), $ $ Z_2(t)\rightarrow Z_2^*(t) $ and $ Z_1(t)\rightarrow S^*(t) $ as $ t \rightarrow \infty. $ Therefore there is a $ t_{4} $ for $ \epsilon_4 > 0 $ small enough such that $ t_4 \geq t_3 $ and, for $ t \geq t_{4} $,
Let $ \epsilon_3 \rightarrow 0 $ in (2.17), so that $ Z_2(t)\rightarrow S^*(t) $. Then (2.17) becomes
Hence $ S(t)\rightarrow S^*(t) $ as $ t\rightarrow \infty. $ We have proved the global stability of the disease-free periodic solution $ (S^{*}(t), 0) $ of (2.1) under condition $ (C_{3}) $.
The case of $ p > 1 $ can be proved by the same method as above, so we omit it here. The only point that needs to be illustrated is that, from (2.1), we have
which yields
for $ n \rightarrow \infty, $ since $ p \exp(-\eta T) < 1. $ Hence $ U(t) $ is uniformly bounded. Then $ (S^{*}(t), 0) $ is globally asymptotically stable provided $ (C_{4}) $ is satisfied.
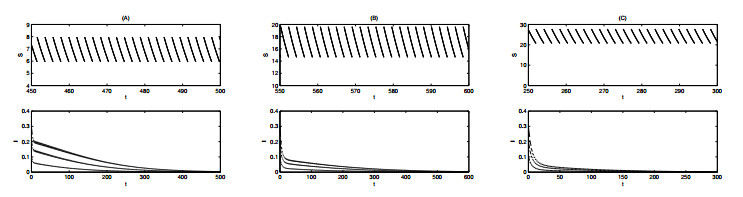
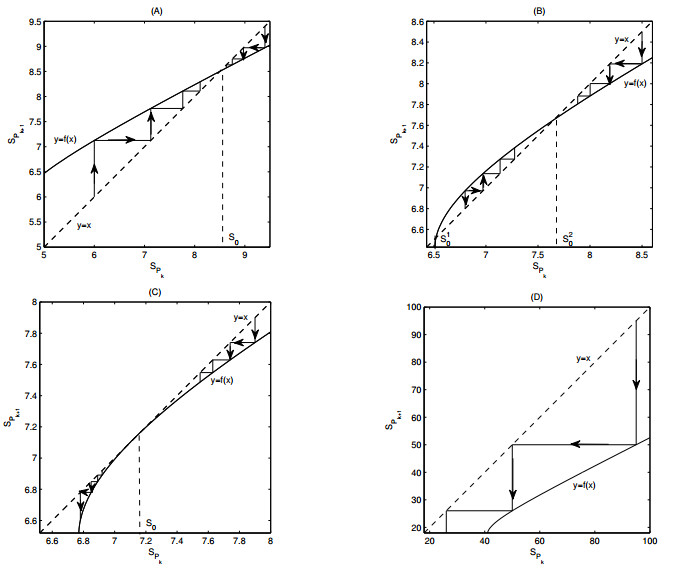
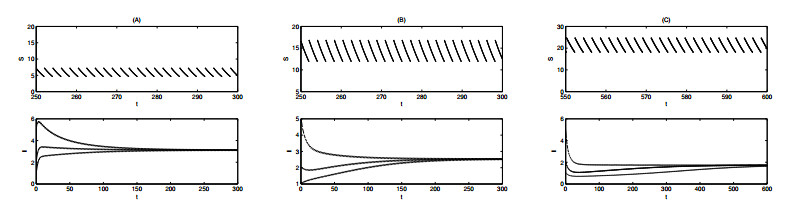
It is interesting to note that the condition $ R_1 < 1 $, which is independent of $ \alpha $, cannot guarantee the global stability of $ (S^{*}(t), 0) $. This shows that the density-dependent factor $ \alpha $ plays a key role in global stability. With the condition $ R_{1} < 1 < R_{2}^{2} $, we can find parameters such that $ p < 1 $ (Figure 1A), $ p = 1 $ (Figure 1B) or $ p > 1 $ (Figure 1C). The disease-free periodic solution is locally asymptotically stable [33,34]. However, using this parameter set, we can see that there are some initial data from which solutions approach a positive periodic solution and finally persist (Figure 1).
2.2. Permanence
The persistence of the system indicates that both susceptible and infected plants can keep surviving. If our goal is to eliminate infected plants, then the persistence suggests control strategies fail to achieve it. Meanwhile, the permanent conditions obtained from analyzing the system can provide scientific support for us to identify the key factors that result in failure and the effectiveness of control strategies, then guide us to establish a good treatment program.
Theorem 2.3. If one of the following conditions holds, then model (2.1) is permanent:
$(C_{5})$ $ 0 < p\leq 1 $ and $ R_1 > 1; $
$(C_{6})$ $ p > 1, $ $ p \exp(-\eta T) < 1 $ and $ R_1 > 1. $
Here, $ R_1 $ is denoted by $ (2.4) $.
Proof. First, suppose $ (C_{5}) $ is satisfied. From the boundedness of (2.1), if $ \epsilon_1 > 0 $ is small enough, there exists a $ t_1 > 0 $ such that $ S(t) \leq L_1, \ I(t) \leq L_1 $ for all $ t \geq t_1, $ where $ L_{1} = \frac{\sigma}{1-\exp(-\eta T)}+\epsilon_1 $. The following system is obtained for all $ t \geq t_1 $:
which gives
Thus, for $ \epsilon_2 > 0 $ sufficiently small, there is a constant $ L_2 = \frac{\sigma \exp(-(\beta L_1+\eta) T)}{1-p \exp(-(\beta L_1+\eta) T)}-\epsilon_2 $ such that $ S(t) \geq L_2 $ for $ t $ large enough. Therefore there exists a $ t_2 $ such that $ t_2 \geq t_1 $ and $ S(t) \geq L_2 $ for all $ t\geq t_2. $ Next, we shall find an $ L_3 > 0 $ such that $ I(t) \geq L_3 $ for $ t $ large enough.
Since $ R_{1} > 1, $ we can choose $ \epsilon_3 $ and $ L_4 $ small enough such that
where $ Z^{*}(t) = \frac{\sigma \exp(-(\beta L_4+\eta) (t-nT))}{1-p \exp(-(\beta L_4+\eta) T)}, \ t \in (nT, (n+1)T]. $ We will prove $ I(t) < L_4 $ cannot hold for all $ t \geq t_2. $ Otherwise, we have
Consider the following system:
which has a positive periodic solution $ Z^{*}(t) $ and, for any solution $ Z(t) $ of (2.21), we have $ |Z(t)-Z^*(t)| \rightarrow 0 $ as $ t \rightarrow \infty, $ where $ Z^*(t) $ is expressed as above and $ Z^*(nT^+) = \frac{\sigma}{1- p \exp((-\beta L_4-\eta)T)}. $ Moreover, there exists a $ t_3 $ such that $ t_3 \geq t_2 $ and $ S(t) \geq Z(t) \geq Z^{*}(t)-\epsilon_3 $ for $ t \geq t_3. $ Thus
for $ t \geq t_3. $ Take $ N^{\ast} \in N $ and $ N^{\ast} T \geq t_3. $ Integrate (2.22) on $ (nT, (n+1)T], \ n \geq N^{\ast}, $ and then
Hence $ I((N^{\ast}+n)T)\geq I(N^{\ast} T) \delta_2^{n}\rightarrow \infty $ as $ n \rightarrow \infty, $ which is a contradiction. Hence there exists a $ t_4 $ such that $ t_4 \geq t_2 $ and $ I(t_4) \geq L_4. $ If $ I(t) \geq L_4 $ for all $ t \geq t_4, $ then let $ L_3 = L_4. $ The proof then follows. Otherwise, take $ t_{5} = \inf_{t > t_4}\{I(t) < L_4\}. $ There are two possible cases to be considered.
Case 1: $ t_{5} = N_1 T, \ N_1 \in N. $ Then $ I(t) \geq L_4 $ for $ t \in [t_4, t_{5}] $ and $ I(t_{5}^+) < L_4. $ Because $ S(t) \geq L_2 $ for $ t \geq t_2 $, the following system is obtained:
Since $ \beta S(t)-\eta \geq \beta L_2-\eta $ for all $ t \geq t_2 $ and if $ \beta L_2-\eta > 0 $, (2.1) will be persistent. The case to be considered is $ \beta L_2-\eta < 0 $. Take $ N_2, \ N_3 \in N $ such that
and
Set $ t_{6} = (N_2+ N_3)T. $ Then there must be a $ t_{7} \in (t_{5}, t_{5}+t_{6}] $ such that $ I(t_{7}) \geq L_4. $ Otherwise, considering (2.21) with $ Z(t_{5}^{+})\leq S(t_{5}^{+}), $ we have
for $ t \in (nT, (n+1)T] $ and $ N_1\leq n\leq N_1+N_2+N_3-1. $ Then
for $ t_{5}+N_2 T \leq t \leq t_{5}+t_{6}. $ By a similar analysis to that of (2.22) and (2.23), we get $ I(t_{5}+t_{6}) \geq I(t_{5}+N_2 T)\delta_2^{N_3}. $ Integrating (2.24) on $ [t_{5}, t_{5}+N_2 T] $ yields $ I(t_{5}+N_2 T) \geq (1-\omega)^{N_2} L_4 \exp((\beta L_2-\eta)N_2 T) $ and $ I(t_{5}+t_{6}) \geq (1-\omega)^{N_2} L_4 \exp((\beta L_2-\eta)N_2 T)\delta_2^{N_3} > L_4, $ which gives a contradiction.
Set $ t_{8} = \inf_{t > t_{5}}\{I(t) > L_4\}. $ Then $ I(t) \leq L_4 $ for $ t \in (t_{5}, t_{8}) $ and $ I(t_{8})\geq L_4. $ For $ t \in (t_{5}, t_{8}), $ let $ t \in (t_{5}+(K_1-1)T, t_{5}+K_1 T], \ K_1 \in N $ and $ K_1 \leq N_2+N_3. $ It follows from (2.24) that
Let $ L_5 = (1-\omega)^{N_2+N_3}L_4 \exp((\beta L_2-\eta)(N_2+N_3)T). $ Thus $ I(t) \geq L_5 $ for $ t \in (t_{5}, t_{8}). $ Since $ I(t_{8}) \geq L_4, $ the same argument can be continued for $ t > t_{8}. $
Case 2: $ t_{5} \neq N_1 T, \ N_1 \in N. $ Then $ I(t) \geq L_4 $ for $ t \in [t_4, t_{5}] $ and $ I(t_{5}) = L_4. $ Suppose $ t_{5} \in (N_4 T, (N_4+1) T), \ N_4 \in N. $ There exist two situations for $ t \in (t_{5}, (N_4+1) T) $ to be considered.
(1) $ I(t) \leq L_4 $ for $ t \in (t_{5}, (N_4+1) T). $ We claim that there must be a $ t_{9} \in [(N_4+1) T, (N_4+1) T+t_{6}] $ such that $ I(t_{9}) > L_4. $ Otherwise, consider (2.21) with $ Z((N_4+1)T^+)\leq S((N_4+1)T^+). $ Then
for $ t \in (N_1T, (N_1+1)T] $ and $ N_4+1 \leq N_1 \leq N_4+N_2+N_3. $ Using a similar analysis as Case 1, we get $ I((N_4+1) T+t_{6}) \geq I((N_4+1) T+N_2 T)\delta_2^{N_3}. $ Integrating (2.24) on $ [t_{5}, (N_4+1) T+N_2 T] $ yields
and
which is a contradiction.
Let $ t_{10} = \inf_{t > t_{5}}\{I(t) > L_4\}. $ Then $ I(t) \leq L_4 $ for $ t \in (t_{5}, t_{10}) $ and $ I(t_{10}) \geq L_4. $ For $ t \in (t_{5}, t_{10}), $ take $ t \in (N_4 T+(K_2-1)T, N_4 T+K_2 T], \ K_2 \in N $ with $ K_2 \leq N_2+N_3+1. $ It follows from (2.24) that
Let $ L_6 = (1-\omega)^{N_2+N_3}L_4 \exp((\beta L_2-\eta)(N_2+N_3+1)T), $ which satisfies $ L_6 < L_5. $ Therefore $ I(t) \geq L_6 $ for $ t \in (t_{5}, t_{10}). $ The same argument can be continued for $ t > t_{10} $ because $ I(t_{10}) \geq L_4. $
(2) There exists a $ t_{11} \in (t_5, (N_4+1) T) $ such that $ I(t_{11}) > L_4. $ Let $ t_{12} = \inf_{t > t_{5}}\{I(t) > L_4\}. $ Then $ I(t) \leq L_4 $ for $ t \in (t_{5}, t_{12}) $ and $ I(t_{12})\geq L_4. $ Integrate (2.24) on $ [t_{5}, t_{12}) $. We have
For $ t > t_{12}, $ the same argument can be continued since $ I(t_{12}) \geq L_4. $ Set $ L_3 = L_6. $ It follows from the above discussion that $ I(t) \geq L_3 $ for all $ t \geq t_4. $
Secondly, the case with $ (C_{6}) $ can be investigated by making use of the same method as the one with $ (C_{5}), $ so here we omit it.
From the preceding three theorems, we see that $ R_1 < 1 $ is only the locally asymptotically stable condition of the periodic solution $ (S^{*}(t), 0) $ of $ (2.1) $, and the key threshold conditions for extinction vs. persistence of the disease are $ R_{2}^{i} < 1 $ ($ i = 1, 2 $) and $ R_{1} > 1 $ respectively. Therefore, $ R_1 $ should not be interpreted as an $ R_0 $-like quantity. Note that the pathogen can persist despite the repeated removal of infected plants. This is because, between roguing events, the infection has a chance to spread to new hosts, thus sustaining it in the long term, in balance with the removal in the form of an impulsive periodic orbit.
Moreover, $ R_{1} < R_{2}^{i} $ holds true if $ p \exp(-\eta T) < 1 $ is valid. What we are interested in next is to examine what will happen under the condition $ R_{1} < 1 < R_{2}^{i} $ ($ i = 1, 2 $). Figure 2 shows that, for $ R_{1} < 1 < R_{2}^{i} $, there are some solutions approaching disease-free periodic solution regardless of the value of $ p $. The parameters chosen here are the same as those in Figure 1, in which there are some solutions that eventually tend to a positive periodic solution, depending on initial values. Hence the dynamics of model (2.1) cannot be determined when $ R_{1} < 1 < R_{2}^{i} $ holds. A problem arising here is to determine the conditions for the existence of a positive periodic solution. Therefore, in the study that follows, we shall examine this issue.
2.3. Existence of the positive periodic solution
Generally speaking, we can take advantage of difference equations of impulsive points (2.7) for the detailed calculation of the initial values of positive periodic solutions that refer to the positive fixed points of (2.7). However, analytically solving the interior equilibria of (2.7), corresponding to its positive fixed points, is difficult. In this subsection, we use bifurcation theory to investigate the existence of a positive periodic solution of model (2.1) near the disease-free periodic solution by setting the impulsive period $ T $ as the bifurcation parameter [35]. We use the following notations in model (2.1):
Using Theorem A.2 (see Appendix), we can deduce the following theorem concerning the existence of a positive periodic solution.
Theorem 2.4. The supercritical branch occurs at the point $ T_{0} $ satisfying $ R_{1}(T_0) = 1 $ and $ p \exp(-\eta T_{0}) < 1 $. Namely, the system will have a positive periodic solution when $ T > T_0 $ and is close to $ T_0, $ provided one of the following conditions of model (2.1) holds:
$ (C_{7}) $ $ 0 < p < 1, $ $ A_1 < 0 $ and $ A_2 > 0; $
$(C_{8}) $ $ 0 < p < 1, $ $ A_1 > 0 $ and $ A_2+A_3 < 0; $
$(C_{9}) $ $ p = 1 $ and $ A_2+A_3 < 0; $
$(C_{10}) $ $ p > 1 $ and $ A_2+A_3 < 0. $
Here, $ A_1 = \eta+\frac{\beta \sigma \exp(-\eta T_{0})\left(p \exp(-\eta T_{0})+p \eta T_{0}-1\right)}{(1-p\exp(-\eta T_{0}))^{2}}, $ $ A_2 = \frac{-2\alpha \omega}{(1-\omega)^{2}}+\frac{2 \beta T_{0}p\left(\frac{1}{1-\omega}-\exp(-\eta T_{0})\right)}{1-p\exp(-\eta T_{0})} $ and $ A_3 = \beta T_{0}\left(1-\exp\left(\frac{\beta \sigma (\exp(-\eta T_{0})-1)}{\eta (1-p \exp(-\eta T_{0}))}\right)\right). $
Proof. See the Appendix.
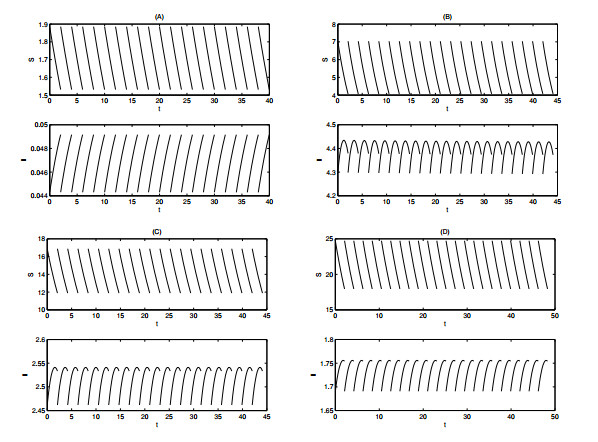
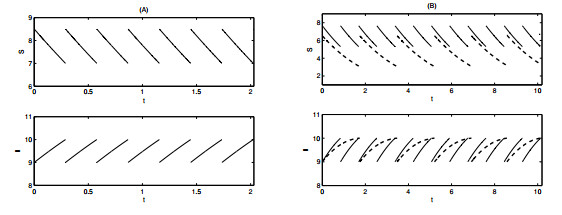
The above theorem reveals that a positive periodic solution exists under some conditions once the disease-free periodic solution loses its local stability. To simulate its existence, appropriate parameters are chosen, in accordance with Theorem 2.4, and Figure 3 is obtained. The periodic solution trajectory in Figure 3A, 3B, 3C and 3D is associated with Conditions $ (C_{7}), $ $ (C_{8}), $ $ (C_{9}) $ and $ (C_{10}), $ respectively. We can see from the four figures that the numbers of both susceptible and infected plants fluctuate periodically with one impulse per period.
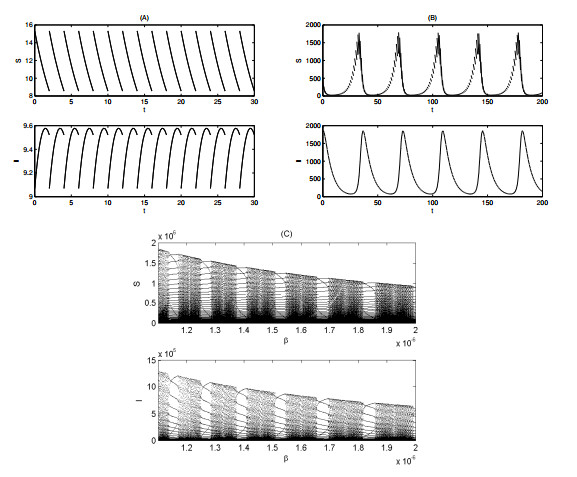
It is essential to mention that the condition $ p \exp(-\eta T) < 1 $ is a sufficient condition for the existence of the disease-free periodic solution and a positive periodic solution. An interesting question arising here is what the dynamic behaviour of model (2.1) would be when $ p \exp(-\eta T) > 1 $. Our numerical simulations show that, aside from a periodic solution with one impulse per period, there exists a periodic solution with period $ \bar{N}T, $ $ \bar{N} \in N $, which indicates that several impulses occur per period, as shown in Figures 4A and 4B. In particular, periodic solutions with a more complex period or chaotic attractors may exist if the transmission rate is relatively small. Figure 4C shows the numbers of both plants at impulsive points corresponding to the initial values of periodic solutions as the transmission rate $ \beta $ varies.
We note that the results in Figures 3 and 4 are highly dependent on initial conditions. Although Theorem 2.4 proves that periodic behaviour is possible and our simulations illustrate this, the results do not easily extend to a greater range of parameter values or initial conditions (results not shown). It follows that the biological significance of these two figures may be limited, so these figures should be considered for illustrative purposes only.
2.4. Sensitivity analysis
Our analysis indicates that $ R_{2}^{i} < 1 $ $ (i = 1, 2) $ are significant threshold conditions on the extinction of plant diseases. To determine the significance of each parameter in predicting the outcome of the disease, we explore the parameter space by performing an uncertainty analysis using Latin Hypercube Sampling (LHS) with 1000 simulations per run. LHS is a statistical sampling method developed by McKay et al. that selects an effective cross-secton of parameter variations within the ranges of values observed empirically [2,36]. Sensitivity analysis is performed by evaluating partial rank correlation coefficients (PRCCs) for various input parameters against output variables (in our case, $ R_{2}^{i} $ $ (i = 1, 2) $), and then the key parameters are determined. In the absence of available data on the distribution functions, we chose a uniform distribution for all input parameters within the minimum and maximum values shown in Table 1 [23] and evaluated PRCCs for all parameters of model (2.1).
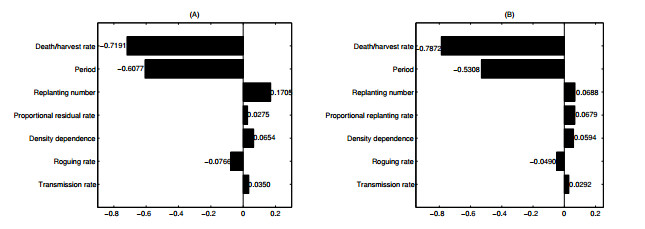
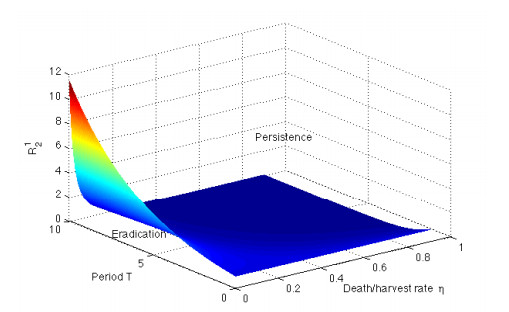
It follows from Figure 5 that the three parameters with the greatest impact on the outcome are the death/harvest rate $ \eta $, the period $ T $ and the replanting rate $ \sigma $. In particular, increasing $ \eta $ or $ T $ decreases $ R_{2}^{i} $ $ (i = 1, 2) $, while increasing $ \sigma $ leads to an increase in $ R_{2}^{i} $. The roguing rate $ \omega $ has a moderate decreasing effect on $ R_{2}^{1} $ for $ 0 < p\leq1 $ (shown in Figure 5A); however, it has only a minor impact on disease spread for $ p > 1 $ (Figure 5B). The proportional replanting rate with $ p > 1 $ has a greater effect in Figure 5B than the reductive rate for $ 0 < p\leq 1 $ in Figure 5A.
Since $ R_2^1 $ depends significantly on $ \eta $ and $ T $, we used the algebraic expression for $ R_2^1 $ to plot a three-dimensional surface (Figure 6), illustrating the dependence on these two parameters. All other parameter values were chosen as the midpoints of their ranges in Table 1. The outcome indicates that high values of $ \eta $ or small values of $ T $ will guarantee $ R_2^1 < 1 $. In particular, if $ \eta $ remains unchanged, then $ R_2^1 > 1 $ unless the period $ T $ is small; that is, if the death/harvesting rate is fixed, then control measures of sufficiently frequent roguing need to be taken to maintain a disease-free state.
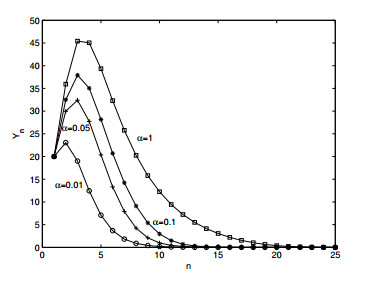
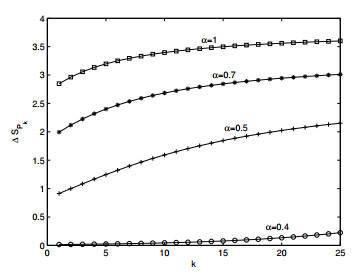
Compared to previous studies on plant diseases [23,27], an important feature of our work here is that the nonlinear roguing rate is included. In view of our sensitivity analysis, we see that the density dependence $ \alpha $ has a moderate impact on the threshold. Using $ (2.7) $, we examine how $ \alpha $ influences the development of the disease, especially the extinction speed of infected plants. See Figure 7. It can be seen that when $ \alpha = 0.01, \ 0.05, \ 0.1 \ \mbox{and}\ 1 $, the infections go to extinction after going through 10, 12, 15 and 22 impulses, respectively. This implies that the nonlinear roguing slows down the extinction speed of infections.
So far, the dynamics of the plant-disease model with periodic cultural control strategy have been investigated. The results show that infected plants can be eradicated provided certain conditions are satisfied. However, complete eradication of infected plants may consume massive resources that are not biologically or economically desirable. An important concept in IDM refers to the economic threshold (ET), at which the control measures should be implemented to prevent an increasing number of infected plants from reaching the economic injury level.
3.
The plant-disease model with economic threshold
In order to measure up to the standard of IDM, we use the ET in crop production. Under this threshold policy, roguing and replanting management needs to be deployed only when the number of infected plants reaches the ET. In such a way, significant economic losses can be avoided. The main purpose of this section is to extend model $ (2.1) $ by taking the ET into consideration for the infected plants, resulting in a state-dependent impulsive model:
3.1. The existence of the periodic solution
We initially focus on the existence of a periodic solution of $ (3.1) $ with one impulsive effect per period denoted by $ \tau. $ In such a case, the solution is called a first-order $ \tau $-periodic solution. Before the main conclusions are presented, the following definition of the Lambert W function needs to be given.
Definition 3.1. [37] The Lambert W function is defined to be multi-valued inverse of the function $ z \rightarrow ze^{z} $ satisfying
It is easy to see that the function $ ze^{z} $ has the positive derivative $ (z+1)e^z $ if $ z > -1. $ The inverse function of $ ze^{z} $ restricted on the interval $ [-1, \infty] $ is defined by $ \mbox{LambertW}(0, z). $ For simplicity, we define $ \mbox{LambertW}(0, z)\equiv \mbox{LambertW}(z) $. Similarly, we define the inverse function of $ ze^{z} $ restricted on the interval $ (-\infty, -1] $ to be $ \mbox{LambertW}(-1, z). $
If the initial number of infected plants is larger than or equal to the ET, then we implement the roguing strategy until the number falls below the ET. After that, the value will no longer exceed the ET, because, once it reaches the ET, the removal strategy will be carried out. Hence, without loss of generality, we can assume that the initial number of infected plants is less than the ET.
It follows from the first and second equations of $ (3.1) $ that any solution $ (S(t), I(t)) $ starting from $ (S_0, I_0) $ does not experience any impulsive effect if $ S_{0} < \frac{\eta}{\beta} $ and $ I_0 < ET. $ Thus, to investigate the existence of the periodic solution, we concentrate on the region $ \Omega = \{(S(t), I(t))\mid S(t) > \frac{\eta}{\beta}, \ I(t) \leq ET\} $.
Theorem 3.1. Let $ d(x) = f_1(x)-f_2(x), $ $ f_1(x) = \frac{\beta}{\eta}\left(\frac{1}{p}-1\right)x-\frac{h}{\eta}-\frac{\beta \sigma}{p \eta}, $ $ f_2(x) = \ln\left(\frac{1}{p}(1-\frac{\sigma}{x})\right), $ $ h = -\eta\ln\left(\frac{1}{1-\frac{\omega}{1+\alpha ET}}\right)-\frac{\beta \omega ET}{1+\alpha ET}, $ $ X^{\ast} = \left(\sigma/ 2+\sqrt{(\sigma/ 2)^{2}+\frac{\eta \sigma}{\beta\left(\frac{1}{p}-1\right)}}\right) $ and $ X_{\ast} = \sigma+\frac{p \eta}{\beta}. $ Then model (3.1) has a unique first-order $ \tau $-periodic solution if one of the following conditions is satisfied:
$(H_{1})$ $ p = 1, $ $ d(X_{\ast}) > 0 $ and $ -\frac{h}{\eta}-\frac{\beta \sigma}{\eta} < 0; $
$(H_{2})$ $ p > 1 $ and $ d(X_{\ast}) > 0; $
$(H_{3})$ $ 0 < p < 1, $ $ X_{\ast} > \frac{\eta}{\beta} $ and $ d(X^{\ast}) = 0; $
$(H_{4})$ $ 0 < p < 1, $ $ X_{\ast} > \frac{\eta}{\beta} $ and $ d(X_{\ast}) < 0. $
Moreover, model (3.1) has two first-order $ \tau $-periodic solutions if the following condition holds:
$(H_{5}) $ $ 0 < p < 1, $ $ X_{\ast} > \frac{\eta}{\beta}, $ $ d(X_{\ast}) > 0 $ and $ d(X^{\ast}) < 0. $
Proof. Let $ (S(t), I(t)) $ be any solution of model (3.1) initiating from $ (S_{0}, I_{0}), $ where $ S_{1} = S(\tau), I_{1} = I(\tau) = ET, S_{1}^{+} = S(\tau^{+}) $ and $ I_{1}^{+} = I(\tau^{+}). $ Without loss of generality, set $ I_{0} = \left(1-\frac{\omega}{1+\alpha ET}\right)ET. $ For $ t \in (0, \tau] $, the solution satisfies the first integral
which yields
that is,
It follows from the properties of the Lambert W function that
If the initial value $ (S_{0}, I_{0}) $ is selected such that
then the solution $ (S(t), I(t)) $ is a $ \tau $-periodic solution. Since $ I_{1}^{+} = I_{0} $ is satisfied, we next show the existence of the horizontal coordinate of initial value $ (S_{0}, I_{0}). $ According to (3.6) and $ S_1 > \frac{\eta}{\beta} $, we have $ S_{0} > \sigma+\frac{p \eta}{\beta}\equiv X_{\ast} $ and
which is equivalent to $ d(S_{0}) = 0. $ Thus the existence of $ \tau $-periodic solutions of model (3.1) is converted into the existence of the positive solutions of $ d(x) = 0 $ with $ x > X_{\ast} $. In view of $ S_1 < S_0 $ and $ S_1 > \frac{\eta}{\beta} $, we have $ 1 < \frac{S_0}{S_1} = p+\frac{\sigma}{S_1} < p+\frac{\beta \sigma}{\eta} $. Hence $ X_{\ast} > \frac{\eta}{\beta} $ should be satisfied. There are several cases to be considered.
(1) $ (H_{1}) $ is true. Then
which shows that $ d(S_{0}) = 0 $ has a unique root satisfying $ S_{0} > X_{\ast} $.
(2) $ (H_{2}) $ is valid. According to
we have $ d'(x) < 0 $ for $ x > X_{\ast}. $ Thus there exists an $ S_{0} $ such that $ S_{0} > X_{\ast} $ and $ d (S_{0}) = 0 $ since $ d (X_{\ast}) > 0 $ and $ d(x) $ is a monotonically decreasing continuous function.
(3) $ (H_{3}) $ holds. It is easy to prove that $ X^{\ast} > X_{\ast} $ if $ X_{\ast} > \frac{\eta}{\beta}. $ Hence $ X^{\ast} $ is the horizontal coordinate we want to obtain.
(4) $ (H_{4}) $ holds. It follows from (3.9), $ X^{\ast} > X_{\ast} $ and $ d' (X^{\ast}) = 0 $ that $ d'(x) < 0 $ for $ x \in (X_{\ast}, X^{\ast}) $; furthermore, $ d'(x) > 0 $ for $ x \in (X^{\ast}, +\infty) $. Then $ 0 > d(X_{\ast}) > d(X^{\ast}) $. It follows that there is an $ S_{0} $ such that $ d(S_{0}) = 0 $ with $ S_{0} > X^{\ast} $ since $ d(X^{\ast}) < 0. $
(5) $ (H_{5}) $ is valid. According to $ d(X_{\ast}) > 0 $, $ d(X^{\ast}) < 0 $ and $ X^{\ast} > X_{\ast} $, we know that there exists an $ S_{0}^{1} $ such that $ d(S_{0}^{1}) = 0 $ with $ X_{\ast} < S_{0}^{1} < X^{\ast} $ because of the continuity of $ d(x). $ Since $ d(x) $ is increasing if $ x > X^{\ast} $ and $ d(X^{\ast}) < 0 $, there is an $ S_{0}^{2} $ such that $ d(S_{0}^{2}) = 0 $ with $ S_{0}^{2} > X^{\ast}. $
Consequently, a unique positive root or two positive roots of $ d(x) = 0 $ with $ x > X_{\ast} $ exist provided one condition of Theorem 3.1 is satisfied, which means that there is a unique periodic solution or two periodic solutions of $ (3.1) $ if conditions $ (H_{i}) $ $ (i = 1, \ldots, 5) $ hold true.
Figure 8 illustrates the existence of the first-order periodic solution. Figure 8A shows the unique periodic solution if $ (H_{4}) $ holds. With $ (H_{1}) $, $ (H_{2}) $ or $ (H_{3}) $, the results are similar to Figure 8A, so we omit them. Figure 8B gives an example of two periodic solutions through the establishment of the assumption $ (H_{5}) $, in which the same parameter set is taken but different initial values are chosen.
3.2. The period of the first-order $ \tau $-periodic solution
Taking the ET into consideration, we refer to the roguing and replanting strategies as "density-dependent control measures". The action to be carried out is to examine and count the number of infected plants so as to determine whether it exceeds the ET or not. In view of Theorem 3.1, plant levels could periodically oscillate with maximum value at the ET, which indicates that the control can be implemented at $ \tau $ intervals, provided the value of $ \tau $ is given. Then the density-dependent control measure can be converted to a periodic control strategy. Such an approach will not only reduce the number of infected plants to a economically viable level but it will also allow us to deploy strategies periodically, which is more convenient and effective than counting the number of infected plants. Based on this, we derive the basic expression of $ \tau $ for the periodic solution.
It follows from $ (2.5) $ and $ (2.6) $ that the periodic solution $ (S(t), I(t)) $ of model (3.1) initiating from $ (S_{0}, I_{0}) $ with $ I_{0} = \left(1-\frac{\omega}{1+\alpha ET}\right)ET $ and $ U_{0} = S_{0}+I_{0} $ reads
and
for $ t \in (0, \tau]. $ Combining the above equations with $ S_{0} = p S(\tau)+\sigma $ yields
which can be solved with respect to $ \tau $ by the properties of the Lambert W function:
In view of $ (3.13) $, the period $ \tau $ of each periodic solution shown in Figure 8 can be easily calculated as follows
3.3. The nonexistence of the order-2 periodic solution
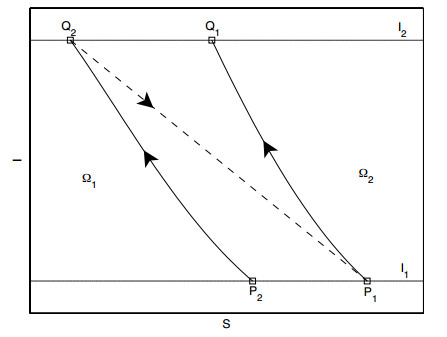
Suppose an order-2 periodic solution of (3.1) exists. Denote
Without loss of generality, take $ P_{1} = (S_{P_{1}}, I^{\ast}) \in l_1 $ as the initial point, as depicted in Figure 9. The solution starting from $ P_{1} $ will reach line $ l_2 $ at the point $ Q_{1} = (S_{Q_{1}}, ET). $ Let the bottom-left side of the phase trajectory $ \widetilde{P_{1}Q_{1}} $ between two lines be the region $ \Omega_{1}, $ and let the top-right side be $ \Omega_{2}. $ An impulsive effect will occur at $ Q_{1} $. If $ Q_{1} $ jumps to the point $ P_{1} $, then a first-order periodic solution $ \widetilde{P_{1}Q_{1}} $ is obtained, while if $ Q_{1} $ jumps to the point $ P_{2} = (S_{P_{2}}, I^{\ast}) \in \Omega_{1}, $ the solution starting from $ P_{2} $ will reach the point $ Q_{2} = (S_{Q_{2}}, ET)\in l_2, $ where $ S_{Q_{2}} < S_{Q_{1}} $ due to the uniqueness of solutions. Then an order-2 periodic solution exists if and only if $ Q_{2} $ jumps to $ P_{1}. $ It follows from $ (3.1) $ that
which give $ S_{Q_{2}^{+}} < S_{P_{2}} < S_{P_{1}} $. Thus it is impossible for $ Q_{2} $ to jump to $ P_{1}, $ and hence an order-2 periodic solution does not exist. We obtain the same result if $ Q_{1} $ jumps to a point of $ l_1 $ in $ \Omega_{2}. $ Similarly, the existence of order-$ n $ periodic solutions with $ n \geq 2 $ can also be ruled out.
3.4. The stability of the periodic solution
Suppose the solution starting from the point $ P_k = (S_{P_k}, I^{\ast})\in l_1 $ reaches the line $ l_2 $ at the point $ Q_k = (S_{Q_k}, ET), $ at which an impulse occurs. Then it jumps to $ P_{k+1} = (S_{P_{k+1}}, I^{\ast})\in l_1 $, where $ I^{\ast}, l_1, l_2 $ are as in (3.14). Using the same method as before, we get a similar equation to (3.7) for the horizontal coordinates of successive impulsive points $ P_{k} $ and $ P_{k+1} $,
where $ -\frac{\beta}{\eta}S_{P_{k}}\exp\left(-\frac{h}{\eta}-\frac{\beta}{\eta}S_{P_{k}}\right) \in [-e^{-1}, 0); $ i.e., $ -\frac{\beta}{\eta}S_{P_{k}}\exp(-\frac{\beta}{\eta}S_{P_{k}}) \geq -\exp(-1+\frac{h}{\eta}), $ $ k = 1, 2, \ldots $ It follows that
with
and $ S_{min} < \frac{\eta}{\beta} < S_{max}. $ Therefore (3.15) is well-defined for $ S_{P_{k}} \geq S_{max} $ due to the fact that $ (S_{P_{k}}, I^{\ast})\in \Omega. $ In fact, the trajectory starting from the point $ (S_{max}, I^{\ast}) $ will reach the point $ (\frac{\eta}{\beta}, ET)\in l_2 $ and be tangent to $ l_2 $, whereupon it will tend to $ (0, 0). $ Hence, if $ S_{max} = X_{\ast} $, then $ d(X_{\ast}) = 0 $; however, the solution starting from $ (X_{\ast}, I^{\ast}) $ is not the periodic solution. In addition, (3.15) refers to the Poincaré map at the impulse points of $ (3.1) $; it is easy to prove that $ f(x) $ with $ x > \frac{\eta}{\beta} $ is a concave function since $ f"(x) < 0 $.
Denote $ g(S) = -\frac{\beta}{\eta}S\exp\left(-\frac{h}{\eta}-\frac{\beta}{\eta}S\right) $. Then
According to (3.7), we get the following result for the periodic solution with initial value $ (S_0, I^{\ast}) $:
3.4.1. The local stability of the periodic solution
It follows from $ S_{0} > X_{\ast} = \sigma+\frac{p \eta}{\beta} $ that $ \lambda_{S_{0}} > 0. $ Using a theorem from Tang & Xiao [38], the local stability of the periodic solution can be determined by $ \lambda_{S_{0}}, $ which means that if $ \lambda_{S_{0}} < 1, $ it is locally asymptotically stable, while if $ \lambda_{S_{0}} > 1, $ it is unstable.
Theorem 3.2. The unique first-order $ \tau $-periodic solution of model (3.1) is unstable if it satisfies $ (H_{1}) $ or $ (H_{2}) $; locally asymptotically stable if it satisfies $ (H_{4}) $; and undergoes a fold bifurcation if it satisfies $ (H_{3}) $. Moreover, if model (3.1) has two first-order $ \tau $-periodic solutions under condition $ (H_{5}) $, then the periodic solution with a smaller horizontal coordinate is unstable and the one with a larger horizontal coordinate is locally asymptotically stable.
Proof. From (3.19), we have
We consider the following five situations:
(1) If $ (H_{1}) $ is valid, then $ \lambda_{S_{0}}-1 = \frac{-\sigma}{S_{0}\left(1-\frac{\beta}{ \eta}(S_{0}-\sigma)\right)} > 0 $. Thus $ \lambda_{S_{0}} > 1 $, which shows that the periodic solution is unstable in this case.
(2) If $ (H_{2}) $ holds, then $ \lambda_{S_{0}} > 1 $ holds true because $ \frac{1}{p}-1 < 0 $. We thus find that the periodic solution is unstable.
(3) If $ (H_{3}) $ is satisfied, then $ \frac{\beta}{\eta}S_{0}(S_{0}-\sigma)(\frac{1}{p}-1)-\sigma = 0 $ if $ S_{0} = X^{\ast}, $ so $ \lambda_{S_{0}} = 1 $. Hence a fold bifurcation occurs here [39].
(4) If $ (H_{4}) $ is satisfied, then, according to the process of the proof of Theorem 3.1, it can be seen that $ S_{0} > X^{\ast} $, from which we have $ \frac{\beta}{\eta}S_{0}(S_{0}-\sigma)(\frac{1}{p}-1)-\sigma > 0 $ and $ \lambda_{S_{0}} < 1 $. It follows that the periodic solution is locally asymptotically stable.
(5) If $ (H_{5}) $ holds, then we get $ X_{\ast} < S_{0}^{1} < X^{\ast} $ and $ S_{0}^{2} > X^{\ast}. $ Thus $ \frac{\beta}{\eta}S_{0}(S_{0}-\sigma)(\frac{1}{p}-1)-\sigma < 0 $ for $ S_{0} = S_{0}^{1}, $ and $ \frac{\beta}{\eta}S_{0}(S_{0}-\sigma)(\frac{1}{p}-1)-\sigma > 0 $ for $ S_{0} = S_{0}^{2}, $ which yields $ \lambda_{S_{0}^{1}} > 1 $ and $ \lambda_{S_{0}^{2}} < 1 $. As a result, the periodic solution with $ S_{0}^{1} $ is unstable and the one with $ S_{0}^{2} $ is locally asymptotically stable.
3.4.2. The global stability of the periodic solution
Previous analysis illustrates that the periodic solution with $ 0 < p < 1 $ under $ (H_{4}) $ or the one with $ S_{0}^{2} $ is locally asymptotically stable. We now turn our attention to global stability.
Claim 3.1.
Proof. See the Appendix.
Theorem 3.3. The first-order $ \tau $-periodic solution of model (3.1) satisfying $ (H_{4}) $ is globally asymptotically stable in $ \Omega_{\ast} = \{(S(t), I(t))\mid S(t) > S_{max}, \ I(t) \leq ET\} $.
Proof. We only need to prove the global attractiveness of the periodic solution. It follows from $ (3.15) $ that
Define functions
If $ S > \frac{\eta}{\beta} $, then
Functions $ g_{1}(S) $ and $ g_{2}(S) $ are well-defined for all $ S \geq S_{max}. $ Both functions are monotonically increasing with respect to $ S, $ so, without loss of generality, we choose $ (S_{max}, I^{\ast}) $ as the first point. Because $ g_{1}(S_{max}) = 1, $ we get
Under condition $ (H_{4}) $, the unique periodic solution exists. Claim 1 and $ (3.23) $ mean that model (3.1) satisfies $ g_{1}(S_{max}) > g_{2}(S_{max}) $. Hence $ g_{1}(S) $ and $ g_{2}(S) $ intersect at $ S_{0} $ with $ S_{0} > X_{\ast} $; that is, $ g_{1}(S_{0}) = g_{2}(S_{0}). $ It follows from $ (3.19) $ that $ f'(S_{P_{k}}) > 0. $ On the basis of above analysis, the following results are obtained:
(1) If $ S_{max} < S_{P_{k}} < S_{0}, $ then $ g_{1}(S_{P_{k}}) > g_{2}(S_{P_{k}}), $ which gives $ f(S_{P_{k}}) > S_{P_{k}}. $ According to the monotonicity of $ f $, we have $ f(S_{P_{k}}) < f(S_{0}) = S_{0}. $ Thus $ S_{P_{k}} < f(S_{P_{k}}) < S_{0} $.
(2) If $ S_{P_{k}} > S_{0}, $ then $ g_{1}(S_{P_{k}}) < g_{2}(S_{P_{k}}), $ which yields $ f(S_{P_{k}}) < S_{P_{k}}. $ Furthermore, $ f(S_{P_{k}}) > f(S_{0}) = S_{0} $. Hence $ S_{0} < f(S_{P_{k}}) < S_{P_{k}}. $
Therefore the periodic solution in this situation is globally attractive and thus is globally asymptotically stable in $ \Omega_{\ast} $. This completes the proof.
We have examined the existence and stability of a first-order $ \tau $-periodic solution under certain conditions. Global stability of the first-order $ \tau $-periodic solution is obtained if condition ($ H_4 $) holds true. It is interesting to investigate global behaviour of model (3.1) under conditions other than ($ H_4 $). By applying the same argument as above, we will address this issue in detail.
Case 1: $ p = 1 $.
(1) $ g_{1}(S_{max}) > g_{2}(S_{max}) $.
It is easy to see from Claim 1 and $ (3.23) $ that $ d(X_{\ast}) < 0 $ and there does not exist any periodic solution. Then $ g_{1}(S_{P_{k}}) > g_{2}(S_{P_{k}}) $ is always valid for $ S_{P_{k}} > S_{max} $, which indicates $ f(S_{P_{k}}) > S_{P_{k}} $; that is, $ S_{P_{k+1}} > S_{P_{k}}. $ Thus the number of the healthy plants will tend to infinity and the number of infected plants can be maintained below the ET.
(2) $ g_{1}(S_{max}) < g_{2}(S_{max}) \mbox{ and } -\frac{h}{\eta}-\frac{\beta \sigma}{\eta} < 0 $.
In this case, $ (H_{1}) $ holds true so that model (3.1) has a unique periodic solution. Then $ g_{1}(S) $ and $ g_{2}(S) $ only intersect at $ S_{0} $. If $ S_{max} < S_{P_{k}} < S_{0}, $ then $ g_{1}(S_{P_{k}}) < g_{2}(S_{P_{k}}) $ and $ S_{P_{k+1}} < S_{P_{k}}, $ which shows the solution will satisfy $ S_{P_{k}} < S_{max} $ after several impulsive effects so both plants will die out. If $ S_{P_{k}} > S_{0}, $ then $ g_{1}(S_{P_{k}}) > g_{2}(S_{P_{k}}) $ and $ S_{P_{k+1}} > S_{P_{k}}, $ so the number of the healthy plants will go to infinity.
(3) $ g_{1}(S_{max}) < g_{2}(S_{max}) \mbox{ and }-\frac{h}{\eta}-\frac{\beta \sigma}{\eta}\geq0 $.
It follows that $ S_{P_{k+1}} < S_{P_{k}}, $ and any solution will eventually approach $ (0, 0). $
Therefore, whether the model has a periodic solution or not, the number of susceptible plants either tends to zero or goes to infinity under the condition $ p = 1 $.
Case 2: $ p > 1 $.
(1) $ g_{1}(S_{max}) > g_{2}(S_{max}) $.
For this case, $ S_{P_{k+1}} > S_{P_{k}}, $ so the number of susceptible plants approaches infinity.
(2) $ g_{1}(S_{max}) < g_{2}(S_{max}) $.
Here $ (H_{2}) $ holds, so model (3.1) has a unique periodic solution. The conclusions of this situation are similar to the results of (2) in Case 1.
Case 3: $ 0 < p < 1 $.
We have examined the case that $ g_{1}(S_{max}) > g_{2}(S_{max}) $. We have another three cases to consider.
(1) $ g_{1}(S_{max}) < g_{2}(S_{max}) $ and $ d(X^{\ast}) = 0 $.
In this case, $ (H_{3}) $ is valid, and there is a unique periodic solution. Hence $ g_{2}(S_{P_{k}}) > g_{1}(S_{P_{k}}) $ is true for $ S_{P_{k}} > S_{max} $ and $ g_{1} $ is tangent to $ g_{2} $ at $ X^{\ast} $. If $ S_{max} < S_{P_{k}} < X^{\ast}, $ then $ S_{P_{k+1}} < S_{P_{k}}, $ so both plants will die out. If $ S_{P_{k}} > X^{\ast}, $ then $ f(S_{P_{k}}) > f(X^{\ast}) = X^{\ast} $, $ X^{\ast} < f(S_{P_{k}}) < S_{P_{k}} $ and the number of healthy plants will approach $ X^{\ast} $. Thus the periodic solution with $ (X^{\ast}, I^{\ast}) $ is semi-stable, and a fold bifurcation occurs at $ X^{\ast} $.
(2) $ g_{1}(S_{max}) < g_{2}(S_{max}) $ and $ d(X^{\ast}) < 0 $.
Here $ (H_{5}) $ is satisfied, and there exist two periodic solutions. Then $ g_{1} $ and $ g_{2} $ intersect at two values, $ S_{0}^{1} $ and $ S_{0}^{2} $. When $ S_{max} < S_{P_{k}} < S_{0}^{1}, $ $ g_{1}(S_{P_{k}}) < g_{2}(S_{P_{k}}) $ and $ S_{P_{k+1}} < S_{P_{k}}; $ when $ S_{0}^{1} < S_{P_{k}} < S_{0}^{2}, $ $ g_{1}(S_{P_{k}}) > g_{2}(S_{P_{k}}) $ and $ S_{0}^{2} > S_{P_{k+1}} > S_{P_{k}} > S_{0}^{1}; $ when $ S_{P_{k}} > S_{0}^{2}, $ $ g_{1}(S_{P_{k}}) < g_{2}(S_{P_{k}}) $ and $ S_{0}^{2} < S_{P_{k+1}} < S_{P_{k}}. $ Hence the periodic solution with $ (S_{0}^{1}, I^{\ast}) $ is unstable, and the one with $ (S_{0}^{2}, I^{\ast}) $ is stable in $ \Omega^{\ast} = \{(S(t), I(t))\mid S(t) > S_{0}^{1}, \ I(t) \leq ET\} $.
(3) $ g_{1}(S_{max}) < g_{2}(S_{max}) $ and $ d(X^{\ast}) > 0 $.
There does not exist any periodic solution, so $ S_{P_{k+1}} < S_{P_{k}}. $ In this case, the susceptible plants tend to extinction and then both plants die out.
The stability of periodic solutions can also be investigated by the method of cobwebbing. We take the case $ 0 < p < 1 $ as an example. It follows from cobweb maps shown in Figures 10B, 10C and 10D that when $ d(X^{\ast}) $ crosses from negative to positive values, the two fixed points (stable and unstable) of the difference equation (3.15) "collide", forming a semi-stable fixed point at $ d(X^{\ast}) = 0 $, and then disappear. This is a fold bifurcation in the discrete-time dynamical system [39]. Note that Figure 10A is a special case generated by the horizontal coordinate of the initial values of the periodic solution satisfying $ S_{0} > X_{\ast} $. In addition, we omit the cobweb map for $ S < S_{0}^{1} $ in Figure 10B, since it is too small to depict clearly; however, we know the susceptible plants tend to extinction.
So far, we have studied the global stability of model (3.1) and obtained that if the system does not have any periodic solution, the susceptible plants either grow and tend to infinity or decrease and die out eventually; conversely, if periodic solutions exist, only the one satisfying $ (H_{4}) $ is globally stable in $ \Omega_{\ast} $, and the one satisfying $ (H_{5}) $ with a larger horizontal coordinate is stable in $ \Omega^{\ast} $.
3.5. Effects of roguing and replanting
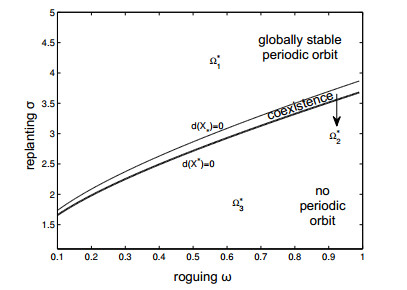
To address the effects of roguing and replanting on the dynamics of model (3.1) with $ 0 < p < 1 $, we let parameters $ \omega $ and $ \sigma $ vary and fix other parameters to build the bifurcation set, as shown in Figure 11. Curves $ d(X_{\ast}) = 0 $ and $ d(X^{\ast}) = 0 $ divide the $ \omega $–$ \sigma $ parameter space into three regions, $ \Omega_{1}^{\ast}, $ $ \Omega_{2}^{\ast} $ and $ \Omega_{3}^{\ast}, $ and the existence of various types of periodic solutions is indicated in different areas. Note that parameter ranges under $ (H_{3}) $, $ (H_{4}) $ and $ (H_{5}) $ correspond to $ d(X^{\ast}) = 0 $, $ \Omega_{1}^{\ast} $ and $ \Omega_{2}^{\ast} $ (or Figures 10C, 10A and 10B), respectively. Therefore, when the replanting number $ \sigma $ and the roguing rate $ \omega $ are selected from $ \Omega_{1}^{\ast} $, the first-order periodic solution is globally asymptotically stable; when they are selected from $ \Omega_{2}^{\ast} $, two first-order periodic solutions coexist, one of which is locally asymptotically stable; if we choose parameters in $ d(X^{\ast}) = 0 $, then there exists a semi-stable first-order periodic solution, and a fold bifurcation occurs; if parameters are selected from $ \Omega_{3}^{\ast}, $ the periodic solution does not exist.
Our goal here is to choose a suitable replanting number and roguing rate such that the first-order periodic solution is globally asymptotically stable, and hence the control action can eventually be managed periodically. For a given roguing rate, the goal can be reached for relatively large replanting numbers. The targets are not realized if the replanting number is relatively small, regardless of the value of the roguing rate. Nevertheless, for a larger replanting number, our objective can be achieved provided the roguing rate is relatively small. Therefore control measures largely affect the dynamic behaviour of model (3.1) in a sense that, on one hand, the number of infected plants can be maintained below the ET; on the other hand, this density-dependent control measure can be converted into a periodic control strategy. From the point view of plant-disease management, this control measure is effective and can be implemented easily.
The stability analysis implies that, even if the number of infected plants can be maintained below the ET, the susceptible plants may approach extinction or infinity. One issue is how quickly the susceptible plants die out or go to infinity. To state this question, according to (3.22), we denote
with $ g(S_{P_{k}}) = -\frac{\beta}{\eta}S_{P_{k}}\exp\left(-\frac{h}{\eta}-\frac{\beta}{\eta}S_{P_{k}}\right) $ and $ S_{P_{k}}\geq S_{max}. $ In light of (3.18), we get
The instability of the periodic solution indicates that $ \frac{d \Delta S_{P_{k}}}{d S_{P_{k}}} > 0 $, which shows that $ \Delta S_{P_{k}} $ is a monotonically increasing function with respect to $ S_{P_{k}} $. Therefore the susceptible plants grow or die out faster and faster as the number of the impulsive effects increases.
It is easy to see from (3.24) that $ \Delta S_{P_{k}} $ is increasing with respect to $ \alpha $, since $ h $ and $ g $ are increasing functions with respect to $ \alpha $ and $ h $ respectively. The simulation in Figure 12 shows that the susceptible plants grow faster and faster as $ \alpha $ increases, which means $ \alpha $ could accelerate the growth speed of susceptible plants. On the contrary, if susceptible plants become extinct, they will die out slower and slower with increasing $ \alpha $, which implies that $ \alpha $ could decelerate the extinction speed.
4.
Discussion
On the basis of the principles of IDM and taking non-continuous implementation of disease control into consideration, we extend the model developed by van den Bosch et al. [23] and establish two plant-disease models using an impulsive cultural strategy with fixed moments and state-dependent controls. Our work is of a general nature and can be applied to a wide range of plant diseases. With respect to the replanting of susceptible plants, the parameter $ p $ is introduced with several biological meanings. In particular, $ p = 1 $ corresponds to only constant replanting being implemented, $ p > 1 $ means proportional replanting is adopted, and $ 0 < p < 1 $ represents the reductive rate and describes the fact that, when infected plants are rogued, some susceptible plants will inevitably be removed. We focus on these three cases to investigate the dynamical behaviour of models (2.1) and (3.1).
Density-dependent roguing can be used to obtain a more accurate evaluation of plant-disease epidemics. This gives rise to the nonlinear impulsive function that makes theoretical analysis more complicated. Thus our study here provides a theoretical framework for analyzing nonlinear impulsive systems, including making use of the difference equations $ (2.7) $ and $ (3.15) $ at impulsive points to discuss the existence and stability of periodic solutions of both models. It is worth noting that the Poincaré map serves an important purpose in completely examining the dynamic behaviour of systems: for the model with periodic impulses $ (2.1) $, we obtained local stability of the disease-free periodic solution; for the model with density-dependent impulses (3.1), the existence and local and global stability of a first-order $ \tau $-periodic solution are obtained.
Our stability analysis for model $ (2.1) $ indicated that if all these control methods are adopted so that $ R_{2}^{i} < 1 $ $ (i = 1, 2) $, suggesting global stability of disease-free periodic solution, then control strategies would be effective enough to eradicate the disease. We conducted a sensitivity analysis to gain a better understanding of the impact of parameters on the threshold when various parameters are changed within the ranges of values observed empirically. The results illustrated that, regardless of the value of $ p $, high harvest rates, large intervention periods and small replanting numbers were required for disease extinction. Furthermore, if the reductive rate or only constant replanting is considered ($ 0 < p \leq 1 $), the roguing strategy with larger removing rate (i.e., $ \omega > \bar{\omega} $) was also effective in terms of reducing $ R_2^1 $ below unity, where
Conversely, if proportional replanting is deployed ($ p > 1 $), small replanting rates can reduce $ R_2^2 $ below unity. These conclusions can be used to guide our periodic inspections of plant diseases.
Periodically exercising control strategies may cost vast resources, especially when the number of infected plants has not reached the ET. Based on IDM, model (2.1) is thus modified by taking the ET into account, and model (3.1) is formulated to control the number of infections below the ET. A special case ($ p = 1, \ \alpha = 0 $ of model (3.1)) was investigated by Tang et al. [27], who proved that there is a unique unstable periodic solution, which is consistent with our result. However, our modelling and conclusions extend those obtained by Tang et al. First, we consider density-dependent roguing, which can better describe reality. Secondly, besides constant replanting ($ p = 1 $), we consider the reductive rate ($ 0 < p < 1 $) and proportional replanting ($ p > 1 $) for susceptible plants when infections are rogued. Thirdly, not only a unique periodic solution but also two periodic solutions may exist. Finally, global stability of the unique periodic solution is deduced under $ 0 < p < 1 $, which is the goal we want to achieve. In addition, using the period obtained, we can not only reduce the number of infected plants to an economically viable level but also implement strategies in a periodic form, which may be convenient to operate. From a biological point of view, it can be concluded that, even though susceptible plants will be incidentally removed in roguing, constant replanting works well and can be easily realized in practice.
Our model has a few limitations, which should be acknowledged. Since infected plants sometimes die easily, equal death rates of both plants may be unreasonable. In our study, we use the same value for reasons of mathematical tractability. The economic threshold for model (3.1) describes a farmer who monitors his field very frequently and, when the density of infected plants passes the ET threshold, goes into the field and rogues. In practice, a grower going into the field to look at diseases in his plants will remove clearly infected plants (or will never do this because even infected plants give some harvest). Growers may not go into the field frequently enough to be able to determine the moment that the ET threshold is passed accurately. Hence our results will be approximations of reality at best. Because individual measures may bring only small benefits, it is possible to improve our models to describe the epidemic of plant diseases by combining several strategies in IDM. The case $ p > 1 $ suggests that new healthy plants would be added to a field in a number relative to the existing number of susceptible plants, which is unlikely to be done in practice, due to issues of space. This could be improved by having a parameter $ K $ representing the maximum number of plants that can be grown and adding new plants proportional to $ K-S-I $. Moreover, herbivores feed on plants, so the infected plants in our models could theoretically be replaced by herbivores and the model studied here could be extended to a plant–herbivore model. This differs from the model of our current research in that we would need to consider the coefficients of energy conversion after herbivores eat plants, as well as the different mortality rates of plants and animals. However, an issue arises in this framework in the case that the disease is transmitted to the animals. Infected plants can be rogued directly, but we cannot easily kill infected animals. We leave these issues for further investigations.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (NSFC 11501446), by the Scientific Research Plan Projects of Education Department of Shaanixi Provincial Government (15JK1765), by the Natural Science Research Fund of Northwest University (14NW17) and by National Government Study Abroad Scholarship of China. RJS? was supported by an NSERC Discovery Grant. For citation purposes, note that the question mark in "Smith?" is part of his name.
Conflict of interest
The authors declare there is no conflict of interest.
Appendix
Theorem A.1. Suppose one of the following conditions is satisfied:
(1) $ 0 < p\leq 1 $
(2) $ p > 1 $ and $ p \exp(-\eta T) < 1. $
Then system (2.2) has a positive periodic solution $ S^{*}(t) $, and, for any solution $ S(t) $ of (2.2), we have $ |S(t)-S^*(t)| \rightarrow 0 $ as $ t \rightarrow \infty, $ where $ S^*(t) = \frac{\sigma \exp(-\eta(t-nT))}{1- p \exp(-\eta T)}, \ t \in (nT, (n+1)T] $.
Proof. Without loss of generality, set $ t\in(nT, (n+1)T], \ n\in N $. It follows from the first equation of (2.2) that $ S(t) = S(nT^+)\exp(-\eta(t-nT)). $ Thus $ S((n+1)T) = S(nT^+)\exp(-\eta T), $ $ S((n+1)T^+) = p S((n+1)T)+\sigma = pS(nT^+)\exp(-\eta T)+\sigma. $ Let $ M_{n+1} = S((n+1)T^+) $. Then
has equilibrium $ M^* = \frac{\sigma}{1-p \exp(-\eta T)} $. Hence, if one of the conditions mentioned above holds, then $ S^*(0^+) = M^* $ and the positive periodic solution of (2.2) is $ S^*(t) = M^* \exp(-\eta(t-nT)), $ $ t \in (nT, (n+1)T], \ n\in N. $ In addition,
Theorem A.2. [35] If $ \mid 1-a_{0}' \mid < 1 $ and $ d_{0}' = 0, $ then we get the following results.
(I) If $ M_1M_2 $ $ \neq 0, $ then we have a bifurcation. Moreover, we have a supercritical branch of a nontrivial periodic solution of (2.27) if $ M_1M_2 < 0 $ and a subcritical branch if $ M_1M_2 $ $ > 0. $
(II) If $ M_1M_2 $ $ = 0, $ then we have an undetermined case, with the following definitions.
Let $ X(t) = (S(t), I(t)) $ be the solution of (2.27), the disease-free periodic solution of (2.27) be $ \delta = (S^{*}(t), 0) $ and $ \Phi $ be the flow associated to the first and the second equations of (2.27), which implies that $ X(t) = \Phi(t, S_{0}, I_{0}), 0 < t \leq T, $ where $ X_{0} = (S_{0}, I_{0}), S_{0} = S(0^{+}), I_{0} = I(0^{+}). $ We assume that the flow $ \Phi $ applies up to time $ T $; that is, $ X(T) = \Phi(T, X_{0}). $
The proof of Theorem 2.4
Proof. Applying Theorem A.2, we make the following calculations.
If $ d_{0}' = 0, $ then $ T_0 $ satisfies the condition
which implies that there exists a $ T_0 $ such that $ R_{1}(T_0) = 1 $. Furthermore,
If $ p\geq 1, $ then $ M_1 > 0 $ holds naturally. It is difficulty to calculate the last item of $ M_2 $; however, it is easy to verify that
If one of the conditions $ (C_7), $ $ (C_8), $ $ (C_{9}) $ or $ (C_{10}) $ is valid, then $ M_1 M_2 < 0 $ holds. Thus, if the parameters satisfy $ (C_7), $ $ (C_8), $ $ (C_{9}) $ or $ (C_{10}), $ then model (2.1) has a supercritical branch at $ T_0. $
The proof of Claim 3.1
Proof.
This completes the proof.









 DownLoad:
DownLoad: