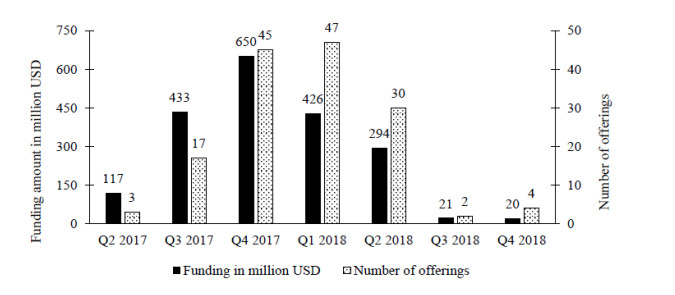
Blockchain-based security token offerings (STOs) provide a new way of crowdfunding and corporate financing. Tokens are immediately transferable and can be traded 24/7 on secondary markets, clearing and settlement is a matter of only a few minutes, tokens can be held personally, i.e. brokers and custody accounts are no longer required and the underlying blockchain ensures transparency of all transactions. This study provides an overview of security tokens and the STO model for corporate financing. Our analysis investigates security tokens from the perspective of a firm looking to raise capital. Building on signaling theory, this paper examines 1) whether companies conducting an STO make use of cheap signals to influence investment behavior and 2) if such use of cheap signals is effective. We analyze a dataset of 151 STOs and identify that cheap signals of human capital and social media are used by projects and have a positive effect on funding success. The type of signals influencing funding success indicate that the market is still immature, as projects have a clear incentive to enlarge the level of asymmetric information between them and potential investors. The anticipated level of punishment for misusing cheap signaling is low, as the mechanism does not represent fraud but "cheating". This is a concern for investor protection.
1.
Introduction
Optimization problems that minimize or maximize objective functions are numerous in real life. Most of them are extraordinarily complex and challenging, which leads to the inability of gradient-based deterministic optimization methods to handle them. Because the objective functions of these problems are hardly guaranteed to be differentiable, these traditional methods easily fall into local optima. Metaheuristic algorithms have flexibility, no gradient mechanism and local optimal avoidance, which make them more popular than deterministic methods. Therefore, metaheuristic algorithms have developed rapidly in the past decades and have made significant achievements in optimization problems in various fields, such as parameter tuning [1,2], feature selection [3,4], scheduling [5,6], system control [7,8] and engineering design [9,10].
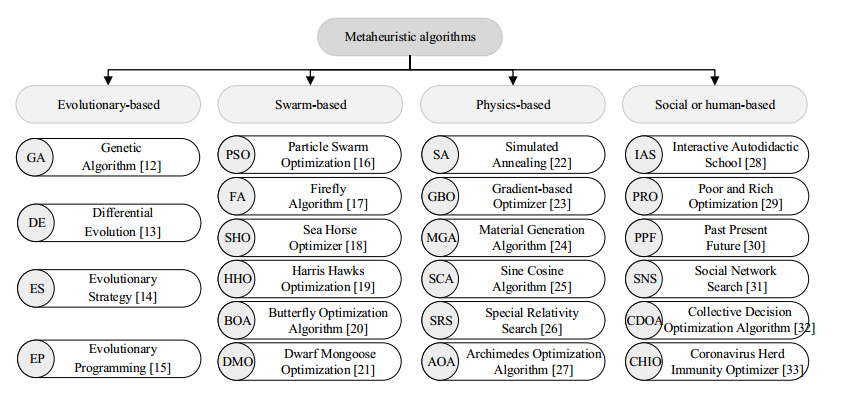
Taking inspiration from nature, metaheuristic algorithms search for optimal solutions through iterative stochastic operations that are within a reasonable time. Scholars have divided these algorithms into four groups: evolution-based, swarm-based, physics-based and social or human-based. Representative metaheuristic algorithms in these four categories are listed in Figure 1. To summarize, most of them have the following characteristics: (1) Their update mechanisms are inspired by some phenomena in nature, such as biological behaviors, physical theorems and chemical phenomena. (2) They have two phases: exploration and exploitation. Exploration is the search for unvisited areas to ensure globally optimal solutions. Exploitation is the intensive search for the most probable region based on accumulated experience to enhance the local search. (3) They are all population-based search schemes, and attention needs to be paid to the interaction between individuals (to promote knowledge sharing and improve the quality of solutions) and the population diversity (to explore the unknown space and overcome local optima). (4) Stochastic strategies and proper parameter definitions in algorithms are essential, and appropriate parameter settings can make algorithms better fits for real problems. In addition, the different update mechanisms and stochastic strategies of these algorithms lead to their different exploration and exploitation capabilities. Hence, the main difference between various algorithms is how to strike a balance between exploration and exploitation [11].
In summary, there are two possible problems with these algorithms: (1) One problem that all algorithms are likely to encounter is how to balance exploitation and exploration. Too much exploration may lead to slow convergence, and too much exploitation may cause falling into local optima. The update mechanisms of some algorithms, such as particle swarm optimization and grey wolf optimizer [34], are based on globally optimal individuals, so these algorithms may converge to a local optimum. (2) The "No Free Lunch (NFL)" [35] theorem logically states that there is no metaheuristic algorithm that is most effective in every situation. For these two reasons, researchers are committed to exploring new algorithms or improving existing ones. This paper is also motivated by these two reasons. For convenience, a list of abbreviations is given in Table 1.
This paper focuses on the Archimedes optimization algorithm (AOA) proposed by Hashim et al. based on physical laws. Inspired by Archimedes' buoyancy principle, AOA generates new solutions by imitating collisions between objects in a liquid. AOA has few parameters, simple interfaces, easy implementation and good optimization effects. As a result, AOA has been extensively applied to practical problems with satisfactory results. Abdelbadie et al. [36] used AOA to clarify the best conditions of a proportional integral regulator, which controls the charge and discharge of superconducting magnetic energy storage systems. Wang et al. [2] employed AOA to tune the main parameters in variational mode decomposition to perform better in diagnostic fault characteristics for both simulated and real situations. Neggaz and Fizazi [37] proposed a wrapper approach based on AOA for feature selection to automatically identify the best facial region features for human gender. Balakrishnan et al. [38] utilized AOA to adjust the parameters in the radial basis function neural network (RBFNN) to construct a merged algorithm, AOA-RBFNN, to achieve higher competence, and it is applied to engineering optimization problems. Annrose [39] applied AOA to improve the classification accuracy of multiple single long short-term memory (LSTM) networks and thus proposed a hybrid depth learning model for bean disease classification.
Like other metaheuristic algorithms, AOA has some drawbacks on some specific issues. All agents in the canonical AOA are handled in the same way, which leads to immature convergence and a tendency to get stuck at local optima, especially when dealing with complex optimization problems. To compensate for these shortcomings, an improved HCAOA is proposed. On the basis of the original AOA, this algorithm combines an orthogonal learning mechanism based on refraction opposition and an Archimedes spiral mechanism based on Levy flight to deal with individuals at different levels. Specifically, the main contributions of this paper are as follows:
● An ameliorative variant of AOA is presented to handle global optimization problems. The idea of hierarchical chains is introduced into AOA and different update strategies are implemented for agents at different levels to enhance optimization capability.
● Orthogonal learning mechanism based on refraction opposition is suggested in AOA, which fully learns information on all dimensions of the optimal individual and effectively avoids AOA falling into local optimum.
● Archimedes spiral integrated Levy flight is introduced into AOA to achieve an extensive range of random disturbances in searching space, thus improving the search ability of AOA.
● Computational Experimental Competition (CEC) 2017 suite and four engineering design problems are employed to evaluate the comprehensive performance of HCAOA.
The outline of the remainder of this article is listed here: Section 2 presents the conventional AOA. Section 3 details the modification and the framework of HCAOA. The feasibility of HCAOA is validated by the CEC 2017 suite in Section 4. The optimization outcomes of HCAOA on engineering design problems are presented in Section 5. Section 6 summarizes the study and presents research ideas for the future.
2.
The conventional AOA
AOA treats objects in a fluid as candidate agents, and each object has its density, volume, acceleration and position. The location of an individual represents a possible solution and is updated by adjusting its density, volume and acceleration. As with other metaheuristic algorithms, the optimization process of AOA contains two parts: exploration and exploitation. In the exploration stage, collisions with random individuals are implemented to diversify populations. During the exploitation phase, there is no collision between objects, and the optimal individual is learned to facilitate local search capability. Its mathematical steps in detail are as follows:
Step 1: Initialize. The initial positions, densities, volumes and accelerations of all individuals are generated randomly by Eqs (1)−(4).
where the subscript i denotes the i-th individual, and the superscript t indicates the t-th iteration. The x1i, den1i, vol1i and acc1i represent the position, density, volume and acceleration of the i-th agent in the first iteration, respectively. The ub and lb are the upper and lower limits of the solution set, respectively. The parameter rand is a D-dimensional random vector generated uniformly in [0,1], and D is the dimension of solutions. Then, all initial individuals are evaluated and the optimal individual is selected. The parameter of the best one is expressed as xbest, denbest, volbest and accbest, correspondingly.
Step 2: Update volumes and densities. The volume and density of the i-th individual in the next generation are updated according to Eqs (5) and (6):
Step 3: Update the transfer operator TFt and density factor dt. The transfer operator determines whether the search behavior changes from exploration to exploitation. The density factor contributes to the search scope from global to local. Their values vary with iteration t using Eqs (7) and (8). The tmax refers to the maximum iteration number.
Step 4: Update accelerations. Different formulas are applied to update accelerations depending on the search phase. When TFt<0.5, the search process is in the exploration stage. There is a collision between the i-th individual and a random one mr, and its acceleration is updated according to Eq (9).
When TFt⩾0.5, it is in the exploitation stage. There is no collision between agents, and the acceleration of the i-th individual is updated by Eq (10).
Then, the updated accelerations are standardized according to Eq (11).
where u is set to 0.9 and l is set to 0.1. The max(acc) and min(acc) are the maximum and minimum of all acc values, respectively.
Step 5: Renew positions. When TFt<0.5, the position of the i-th individual is updated by Eq (12).
where C1 is set to 2 and xrand is the location of a randomly selected individual.
Otherwise, the position of the i-th individual in the exploitation stage is updated by Eq (13).
where C2 is a constant equal to 6. The parameters T and F are calculated by Eqs (14) and (15).
where P=2×rand−C4. The parameters C3 and C4 are set to 2 and 0.05, respectively.
Step 6: Evaluate all individuals. Evaluate all individuals and select the optimal one. Assign xbest, denbest, volbest and accbest. The process of AOA in detail is shown in Figure 2.
3.
The proposed HCAOA
In the canonical AOA, all individuals are treated in the same way. During the exploration period, the positions of individuals are updated by collisions with random individuals. As a result, the knowledge of better individuals is not well learned, slowing down optimization speed. In the exploitation phase, all individuals move towards the optimal one. This causes the aggregation of all individuals to the best one and makes the algorithm get stuck at local optima. Moreover, the whole process of the standard AOA does not fully use the optimal individual, leading to slow convergence speed. Finally, the same boundary treatment for all individuals somewhat reduces population diversity. To address these problems, an improved HCAOA is put forward. On the basis of the original AOA, the algorithm combines an orthogonal learning mechanism based on refraction opposition and an Archimedes spiral mechanism based on Levy flight to deal with individuals at different levels. In addition, a multi-strategy boundary processing mechanism is introduced.
3.1. Orthogonal learning mechanism based on refraction opposition
3.1.1. Refraction opposition-based learning
In metaheuristic algorithms, all individuals move towards the optimal individual, causing the disappearance of population variety and the fall into a local optimum. To overcome this shortcoming, opposition-based learning (OBL) has been proposed [40] and widely used [7]. OBL is a greedy policy that selects a point with better fitness between the initial and the opposite point.
Definition 1 Opposite number. Suppose there exists a number x in [lb,ub], then its opposite number ¯x is obtained by Eq (16).
Definition 2 Opposite spot. Assume X=(x1,x2,⋯xD) is a D-dimensional spatial point, x1, x2, ⋯, xD∈R and xj∈[lbj,ubj](j=1,2,⋯D). Then, its opposite spot is calculated by Eq (17).
In addition, several variants have been derived, such as elite opposition-based learning [41], refraction opposition-based learning (ROBL) [10], quasi opposition-based learning [5] and random opposition-based learning [3]. ROBL is a dynamic oppositional learning strategy based on OBL and the lens imaging principle to help algorithms find better candidate solutions.
The process of obtaining refraction opposition points is shown in Figure 3. There is an object N with height h directly on the coordinate x, x∈[lb,ub]. Place a lens at the midpoint o of lb and ub, and the height h∗ of mirror point N∗ can be obtained based on the lens imaging principle.
The refraction-opposition point is x∗, which is calculated through Eq (18).
Let h/h∗=k, where k is the scaling factor. The refraction-opposition spot x∗ is obtained by Eq (19).
By generalizing to D dimensional space, the refraction-opposition spot is attained by Eq (20).
When k=1, the refraction opposition solution x∗ in Eq (20) is the opposite point in OBL. The opposite point obtained by the OBL strategy is fixed, while the refraction-position point obtained by ROBL dynamically changes when k is set to different values. The reason for using ROBL in this paper is that ROBL provides a variety of solutions due to the randomness of k.
3.1.2. Orthogonal learning
There is a better one when comparing two individuals, but there is no guarantee that this better individual outperforms the other in all dimensions. Each individual has several superior dimensions. Mining better dimensions from each individual is expected to yield a better individual. This requires permutation and combination experiments. However, the number of experiments in traditional permutations grows exponentially as the dimensionality increases, which is unsuitable for optimization algorithms with multiple iterations and individuals in high dimensions. Therefore, orthogonal learning is introduced to find the optimal combination through a few experiments. The orthogonal learning experiment consists of two steps: orthogonal design and factor analysis [42].
Orthogonal design defines the content and number of experiments through predefined orthogonal arrays. Orthogonal arrays provide a series of different combinations that are represented as LM(SQ), where S is layers number, Q is factors number and M is test times. For example, for the experiment with 7 factors and 2 levels, 128(27) trials are required to get an optimal combination when adopting permutation. However, if orthogonal experimental design is employed, the best combination can be found through 8(L8(27)) trials in Eq (21).
Factor analysis assesses the influence of every level of different factors on the outcomes of M trials. For example, the objective function is the spherical function f(x)=∑ix2i. Two individuals are A=[1,3,5,2,3,1,2] and B=[2,1,3,1,2,2,4]. Orthogonal learning is carried out by Eq (21). Table 2 shows the process of obtaining a new individual xnew through factor analysis. The Ai and Bi denote the cumulative fitness value of the i-th factor in the individual A and B, respectively. A smaller cumulative value of an individual on a dimension indicates that dimension value of the individual is the dominant dimension value. All the predominant dimension values are combined to generate a new individual.
3.1.3. The proposed orthogonal learning based on ROBL
In metaheuristic algorithms, the optimal individual plays an essential role. The best one determines the convergence speed. In the exploration phase of AOA, all individuals update their positions through random collisions, which reduces the optimization speed. In the exploitation phase of AOA, all individuals converge to the optimal individual and may fall into a local optimum. Therefore, this paper applies an orthogonal learning mechanism based on refraction opposition to improve convergence speed and the capacity to escape from a local extremum.
This approach employs the ROBL mechanism to generate refraction opposition solutions for the optimal individual. The randomness of k ensures the diversity of refraction opposition solutions, thus reducing the chances of the algorithm immersing a local extremum. In traditional ROBL strategy, the optimal individual is compared with its refraction opposition solution in a greedy way, and the superior individual is selected for the next generation. This does not take full advantage of the information available on all dimensions of the two individuals because one of the two is inevitably superior to the other in some dimensions and inferior to the other in the remaining dimensions. To resolve this issue, orthogonal learning is utilized to fully learn the information of the optimal individual and its refraction opposition individual, combining the dominant dimensions of both to produce a better solution.
3.2. Archimedes spiral mechanism based on Levy flight
An Archimedes spiral describes the trajectory of a point moving away from a stationary point at an invariant velocity and revolving around the fixed point at an unchanging angular velocity. Its polar coordinate r is defined by Eq (22).
where a is the distance from the point of departure to the coordinate origin in polar coordinates, b is the increment of the unit angle of a helix and θ is the rotation angle. Altering a means revolving the spiral and b determines the distance between two adjacent curves. In this paper, we combine Levy flight and Archimedes spiral to discover better solutions in the neighborhood of superior individuals.
The target regions at different stages are different. In the exploration stage, some individuals explore the area around dominant individuals to learn more about them and avoid clueless random search, thus improving optimization speed. Therefore, the update formula in this stage is Eq (23).
During the exploitation phase, the areas near the best individual are focused on searching to enhance optimization ability and avoid local optima. Currently, the locations are updated as in Eq (24).
where l stands for a uniform random number in [−1,1]. Then a in Archimedes spiral corresponds to xti in Eq (23) and xbest in Eq (24), and b in Archimedes spiral corresponds to |xti−xtlevy|×l in Eq (23) and |xbest−xtlevy|×l in Eq (24). The cos(2πl) in Eqs (23) and (24) corresponds to θ in Archimedes spiral. The generated Levy flight solution xtlevy is calculated by Eq (25).
where μ and ν conform to a normal distribution, correspondingly, μ∼N(0,σ2μ), ν∼N(0,σ2ν). σν is 1 and σμ is obtained by Eq (26).
where the value range of β is typically (0,2], and β is taken as 1 in this paper.
Levy flight adopts a random search method combining small steps and long jumps, which can effectively expand the search area. Archimedes spiral mechanism helps to search the neighborhood of excellent individuals, avoiding missing part of the solution space and ensuring mining meticulousness to the maximum extent. In the exploration stage, the integration of the two means allows the proposed algorithm to not only fully learn from the excellent individuals, but also to avoid clueless random mining. In addition, this combination is applied in the exploitation stage to fully explore the neighborhood of the best individual. This can ensure the rigor and accuracy of the search process to enhance local search ability, and improve population diversity to avoid premature convergence phenomena.
3.3. Multi-strategy boundary processing mechanism
In the standard AOA, all individuals are treated with the same boundary processing method at all stages. If the values of new individuals are greater than the upper limits, they are set to the upper limits. Similarly, the values less than the lower bounds are set to the lower bounds. This is the most common boundary processing mechanism in previous algorithms. However, this may affect the diversity of populations to some extent, especially in the exploration phase. There may be multiple individuals who exceed the boundary values in the same dimension and are set to the boundary values. Therefore, this study proposes a multi-strategy boundary processing mechanism that treats individuals differently at different stages. In the exploration phase, the dimension values of individuals outside their range are set to random numbers to increase population diversity. When it comes to the exploitation stage, the traditional boundary treatment is continued. The pseudo-code of the multi-strategy boundary processing mechanism is algorithm 1.
3.4. The frame of HCAOA
All individuals are treated in the same manner in the standard AOA, which does not efficiently learn the information of the optimal and better individuals, thus reducing the convergence speed and possibly leading to a local optimum. Therefore, the HCAOA is proposed in this paper.
All individuals in a population are classified into three classes according to their fitness: the optimal individual, superior individuals and general individuals. The optimal individual is treated through the orthogonal learning mechanism based on refraction opposition, which effectively avoids local optima and improves convergence speed to a certain extent. Superior individuals are processed by Archimedes spiral mechanism based on Levy flight to conduct information mining from better individuals. This avoids clueless random search and improves optimization speed during the exploration period, while ensuring population diversity and reducing the probability of local optimality during the exploitation period. For general individuals, the conventional AOA is applied to effectively utilize its exploration and exploitation capabilities. Among them, the optimal individual is the one with the best fitness in a population, and there is only one. The general individuals make up a% of a population. The rest are superior individuals, and the number is [(1−a%)×popsize−1]. Finally, the multi-strategy boundary processing mechanism is employed to increase population diversity. In accordance with the above analysis, its pseudocode is listed in algorithm 2 in detail. Moreover, the flowchart of HCAOA is depicted in Figure 4.
3.5. Computational complexity
In the worst scenario, the time complexity of HCAOA is calculated based on its pseudocode. Here, N is population size, D is problem dimension and tmax is max iterations.
It takes O(N×D) time to initialize the population. The assessment of the fitness values of all individuals needs O(N×tmax) time. Sorting according to the fitness values takes O(N2×tmax) time. It takes O(D2×tmax) time to implement the orthogonal learning strategy based on refraction opposition for the optimal individual. It takes O((1−a%)×N×D×tmax) time to perform Archimedes spiral mechanism based on Levy flight for superior individuals. It takes O(a%×N×D×tmax) time to perform AOA for general individuals. The multi-strategy boundary processing mechanism needs O(N×D×tmax) time. It takes O(N×tmax) time to carry out greedy selection technique in HCAOA.
On the whole, the total time of HCAOA is O(N×D×tmax+N2×tmax). Thus, in terms of time complexity, HCAOA is more complex than the original AOA.
3.6. Parameters sensitivity analysis
In the new HCAOA, five parameters C1, C2, C3, C4 and a% need to be specified. Among them, C1, C2, C3 and C4 are the parameters in the traditional AOA, and a% is a new parameter that indicates the proportion of general agents in a population. In the proposed HCAOA, the parameter a% is insensitive to these four parameters, so these four parameters are deferred to the values in the original AOA. Multiple tests are executed to judge the parameter a% in this subsection. Sensitivity analysis is performed on four benchmark functions (f1, f10, f11 and f29) picked from various classes of the CEC 2017 test suite. The dimensionality is set to 30. The values of the parameter a% are assigned to {0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9}. The outcomes of different a% are offered in Table 3. It is evident that when parameter a% is set to 80%, HCAOA realizes excellent results.
4.
Experimental results
The optimization capability of HCAOA is examined on the CEC 2017 test suite, and the effects are weighed against nine other classical or new metaheuristics. First, the specific knowledge of the CEC 2017 test suite and parameter settings of different algorithms are presented. Next, the effectiveness of the various strategies in HCAOA are rated. Finally, the proposed HCAOA is evaluated from various perspectives, including qualitative analysis, statistical analysis, stability analysis, convergence analysis and statistical tests.
4.1. Parameter setting and CEC 2017 test suite
The optimization ability of HCAOA is further assessed with the CEC 2017 suite, which is a universal measurement for modern algorithms. There are four types of problems in this suite: unimodal (f1−f3), multimodal (f4−f10), hybrid (f11−f20) and composite cases (f21−f30). As f2 has been removed from this test suite due to its instability, 29 test functions with distinct modalities and complexity are employed to test HCAOA and other competing algorithms. All functions take values in the range [−100,100]. In conclusion, CEC 2017 suite is quite sophisticated and appropriate for studying algorithms' exploration and exploitation abilities.
The proposed HCAOA is compared with AOA, PSO, GWO, SCA, FA, WOA, HHO, BOA and SHO to evaluate the optimization performance of these algorithms from both qualitative and quantitative perspectives. Their parameters are demonstrated in Table 4. It is rational and appropriate to regulate parameters to default values [43]. The dimensions of these testing functions are typed to 30, the population size is 100 and the maximal iteration is 1000. Since the results of these algorithms are randomized, they run separately 30 times to ensure the fairness and objectivity of competitions.
4.2. Impact of strategies
To overcome the shortcomings of the traditional AOA, this paper proposes an improved HCAOA. There are three improvement strategies in HCAOA. The first strategy is to perform the orthogonal learning mechanism based on refraction opposition on the optimal individual. The second is that superior individuals are handled by Archimedes spiral mechanism based on Levy flight. The third strategy is to implement a multi-strategy boundary processing mechanism for all individuals. To evaluate the impact of each strategy, this subsection fuses each of the three strategies into the AOA and constructs three improved versions: AOA-S1, AOA-S2 and AOA-S3. The means and standard deviations (STD) obtained by AOA and its improved versions on CEC 2017 test functions are listed in Table 5. The optimal means on all functions are shown in bold.
Comparing AOA-S1 with AOA, it is clear that AOA-S1 achieves lower means than AOA, except for f18 and f21. The STD values obtained by AOA-S1 are smaller than those obtained by AOA in most cases. These indicate that the first strategy improves the optimization ability of AOA. The optimization results of AOA-S2 are in comparison with those of AOA. AOA-S2 offers lower means on 24 functions and significant improvements on several functions, suggesting that the second strategy enhances the search capability to some extent. AOA-S3 slightly outperforms AOA in terms of averages on 23 functions, and the differences between the two are not great for the other 6 functions. The third strategy is a slight improvement over AOA. The main reason is that the third strategy does not change the exploitation and exploration strategy of AOA, but simply increases population diversity through boundary treatments. Finally, HCAOA with all three strategies applied simultaneously produces more competitive results than the use of any one strategy alone.
4.3. Qualitative analysis results
Five benchmark functions are randomly selected from different categories to present qualitative measures of HCAOA. The qualitative results in Figure 5 include five subplots, namely (1) 2D visualization of benchmark functions, (2) search history, (3) the trajectory in 1st dimension, (4) average fitness of populations and (5) convergence curve.
2D visualization of benchmark functions shows the changes in function values corresponding to the first and second dimensional data. As the dimensions increase, the results become more complex and difficult to plot.
The search history charts illustrate the positions of all individuals from the first to the last generation. The search space is described by chromatic contours, starting with blue (lowest value) and ending with yellow (highest value). Two conclusions can be drawn from these search history graphs. First, the locations of search agents cover almost the entire search space, which indicates that HCAOA has good exploration capability. Second, search agents gather more around the blue line, suggesting that HCAOA achieves good exploitation. In summary, these two points demonstrate that HCAOA has an outstanding collaboration between exploration and exploitation.
The trajectories of the first individual in the first dimension reflect the search behavior. The third column of Figure 5 shows that the trajectories vary greatly in the early phase and tend to flatten out in the late stage. This process highlights a gradual shift from exploration to exploitation of HCAOA as the iterations progress. The trajectories of some graphs have some oscillations, which denotes that HCAOA has the ability to escape from a local extremum. In addition, the more complex the function is, the greater the number of trajectory fluctuations and the longer the oscillation time. These graphs show the global search capability of HCAOA.
The fourth column of Figure 5 displays the average fitness of whole population, reflecting the changes in fitness of entire population during iterations. Overall, the average fitness continues to decrease due to the greedy strategy in HCAOA, which guarantees continuous optimization. It is also found that the average fitness values decrease rapidly in the early period and gradually taper off in the later phase, demonstrating a transition of HCAOA from exploration to exploitation.
Convergence curves represent the behavior of the optimal solution up to now. As described in the fifth column of Figure 5, the convergence curves on all functions are gradually decreasing, indicating that HCAOA is continuously optimizing the results as iterations continue. In addition, convergence curves fall rapidly in the early stage and slowly in the late stage, revealing that HCAOA has a high cooperation between exploration and exploitation.
4.4. Statistical analysis results
This subsection measures the performance of HCAOA and the other nine algorithms by statistical analysis. The results of 30 independent optimizations are summarized and four indictors including mean, standard deviation, best value and worst value are selected for statistical analysis. The statistical grades are shown in Table 6, and optimal values are indicated in bold. Overall, HCAOA scores are best in 97 out of 116 comparisons of four indicators on 29 functions. First, HCAOA gets the best mean values on 26 functions. For f3, AOA and HHO perform better, and HCAOA is third. GWO outperforms HCAOA on f16 and f26, with HCAOA in second place. Second, HCAOA has the 24 best values out of 29 functions for the standard deviation indicator. HCAOA ranks second on f8 and f29, third on f3 and f16, and fourth on f10. Furthermore, from the perspective of best value, HCAOA achieves the optimal value on 21 functions. HCAOA is third on f3 and second on f5, f10, f19, f21, f23, f26 and f27. Finally, HCAOA achieves the best on 26 functions for the worst value metric. For the worst value, HCAOA ranks third on f3 and second on f16 and f29. Even for many functions, the worst results acquired by HCAOA are even more satisfactory than the best value by other algorithms. In summary, HCAOA achieves the best results in terms of mean, standard deviation, best and worst on most benchmarks.
4.5. Stability analysis results
To observe the stability of HCAOA, all algorithms are analyzed through box diagrams on 30 optimization results. The box plots of various algorithms on 8 functions from diverse classifications are exhibited in Figure 6. Medians, lower quartiles, upper quartiles and outliers are presented in box plots. The narrow block indicates that the results obtained by an algorithm are relatively steady. Three conclusions can be drawn from Figure 6. First, HCAOA can get lower boxes than other algorithms in most cases, which means that HCAOA has good optimization effects. Second, the boxplots obtained by HCAOA are always narrowest, which means that HCAOA receives stable optimization results. Finally, there are relatively few outliers in the box charts of HCAOA. In combination, HCAOA produces superior and stable optimization results.
4.6. Convergence analysis results
To validate the convergence efficiency of HCAOA, the same functions are selected from subsection 4.5, and their convergence curves are presented in Figure 7. Their global exploration and local exploitation are more intuitively represented in convergence curves. Figure 7 reveals that HCAOA achieves better results and faster convergence than the other nine algorithms on most functions. In the early stages, GWO converges faster than HCAOA on f1, f4 and f9, WOA has faster convergence on f13 and f15, and the early convergence of HHO on f30 is faster than that of HCAOA. However, as the iterations progress, GWO, HHO and WOA converge slower and enter the local exploitation phase earlier, which may fall into local optima. In contrast, HCAOA has a stronger exploration capability and applies more iterations to search for the global best solution. Therefore, from the final optimization results, it can be concluded that HCAOA maintains fast convergence for a longer time and has better optimization effects. In addition, Figure 7 shows that the curve shapes of HCAOA are very similar to those of AOA. They transfer from global exploration to local exploitation at the same iteration, mainly because they employ the same transfer operator. However, a hierarchical chain, with different processing mechanisms for agents at different levels, allows HCAOA to have faster convergence and better local search capabilities.
4.7. Statistical test results
In the previous subsections, it has been verified that HCAOA has a superior optimization ability compared to other algorithms from the statistical results, convergence analysis results and stability analysis results. To avoid chance, this subsection analyses whether the optimization capability of HCAOA is significantly superior to other algorithms. In the statistical results in subsection 4.3, the mean values of 30 optimization results of different algorithms on 29 functions are compared. It is found that AOA and HHO outperform HCAOA on f3, GWO is superior to HCAOA on f16 and f26, and HCAOA wins over other algorithms on the remaining functions. Statistical tests are conducted based on 30 optimization results, using Wilcoxon rank-sum statistical method to test the null hypothesis of no remarkable distinction between the optimized effects of two algorithms. If p−value>0.05, it implies that the distinction between the optimization effects is not noticeable. In contrast, if p−value⩽0.05, it denotes the divergence is statistically significant, namely H=1.
Table 7 lists Wilcoxon rank-sum test results for HCAOA against other algorithms on CEC 2017. It can be judged that HCAOA wins 251 times, is equal 8 times and loses 2 times in the 261 (29 × 9) comparisons. Among them, the optimization effects of AOA are superior to that of HCAOA on f3, and the optimization effects of GWO on f26 have a marked predominance over that of HCAOA. However, the hypotheses that the results obtained by HHO are significantly better than that obtained by HCAOA on f3 and GWO beats HCAOA on f16 do not hold. In addition, the optimization outcomes of AOA and HCAOA have no apparent distinctions on f14 and f18. On f10, f16, f17, f27 and f29, the differences between the optimization effects obtained by GWO and those obtained by HCAOA are not significant. There is no significant difference between the optimization results of HHO and HCAOA on f3. Finally, the effects of HCAOA are apparently superior to others on the remaining functions. Therefore, from the perspective of statistical tests, the optimization results of HCAOA have a marked predominance over that of other algorithms on most cases.
Finally, Friedman rank test is applied to sort ten algorithms on 29 functions of CEC 2017. The test is a nonparametric approach to compare the comprehensive average performance. From the Friedman test grades in Table 8, HCAOA ranks first, followed by GWO, HHO, SHO, AOA, WOA, SCA, BOA, FA and PSO. The results of Friedman rank test show that HCAOA is effective and stable.
5.
The application of HCAOA to engineering design problems
This section evaluates the ability of HCAOA to solve practical problems through four classical engineering problems. The optimization consequences are compared with those of methods proposed in recent literature. The possible optimal results are deepened in bold.
5.1. Welded beam design
The welded beam design problem aims to minimize the cost by specifying four parameters, including weld thickness (h), length connected to bar (l), bar height (t) and bar thickness (b). The optimization results obtained from HCAOA are compared with those of IGWO [44], AGWO [45], DAQUILA [46], DMO [21], MAOA [47], GJO [48], AVOA [49], MCWOA [50], CQFFA [51], HAO [52] and IHAOAVOA [53]. Based on the results in Table 9, it is clear that HCAOA has the lowest cost.
5.2. Pressure vessel design
The pressure vessel design problem is to determine four parameters including head thickness (Th), shell thickness (Ts), inner radius (R) and cylindrical cross-section length without considering the head (L), so as to reduce the total fee. IGWO [44], AGWO [45], MAOA [47], GJO [48], AVOA [49], SCSO [54], QLGCTSA [55], CQFFA [51] and HAO [52] are applied to solve this problem. The optimal solutions obtained by them are contrasted with those optimized by HCAOA. Table 10 indicates that HCAOA and CQFFA achieve competitive results and outperform the other algorithms.
5.3. Cantilever beam design
The cantilever beam design problem consists of five squares with heights to be determined, and vertical forces act on their free nodes. So the decision variables are the heights of five hollow squares, and the objective is to lessen a cantilever's weight. TQA [56], ECSOA [57], GBO [23], AGWO [45], MFO [58], SHO [18], MGA [24], QLGCTSA [55] and IHAOAVOA [53] are also applied to address the cantilever beam design problem and the best solutions optimized by them are shown in Table 11. It is evident that the HCAOA proposed in this paper provides high-quality optimization results and has the reliable ability to solve practical problems.
5.4. Three-bar truss design
This problem is resolved by designing two cross-sectional areas (A1,A2) to ensure the stress constraints on each of the truss members, with the aim of reducing the overall weight. The optimization results obtained by HCAOA on this problem are compared with those obtained by algorithms such as GJO [48], PRO [29], IDARSOA [59], CSOAOA [60], AVOA [49], SNS [31], MCWOA [50], SRS [26], CQFFA [51] and QLGCTSA [55]. Table 12 indicates that HCAOA obtains the competitive optimization results.
6.
Conclusions
This paper discusses in detail the shortcomings of the canonical AOA. To compensate for these deficiencies, this paper introduces a new idea of hierarchical chains to AOA and proposes an improved HCAOA. This algorithm combines an orthogonal learning mechanism based on refraction opposition and an Archimedes spiral mechanism based on Levy flight to deal with individuals at different levels, effectively avoiding local optimization, preventing clueless random mining and improving optimization speed. Apart from that, a multi-strategy boundary processing mechanism is introduced to maintain the variety of populations.
To validate the effectiveness of HCAOA, multiple experiments based on the CEC 2017 test suite are conducted. The qualitative results demonstrate that HCAOA has outstanding exploration and exploitation abilities and strikes a good collaboration between exploitation and exploration. The quantitative outcomes prove that HCAOA can obtain superior and more stable optimization results than the other nine recent algorithms. In addition, four real-world engineering problems are used to test the ability of HCAOA to solve practical problems. HCAOA achieves competitive optimization results when comparing with the optimal results in the recent literature for the same problems.
In summary, the proposed HCAOA provides outstanding and stable optimization effects, fast convergence and a good ability to jump out from a local extremum. In the future, HCAOA will be extended to complex single-objective optimization problems, for example, imaging segmentation, feature selection, workshop scheduling and parameter optimization. Meanwhile, HCAOA is being developed to solve unconstrained and constrained multi-objective problems. Furthermore, the idea of hierarchical chains can be generalized to other algorithms.
Use of AI tools declaration
The authors declare we have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
The support of the National Natural Science Foundation of China (Grant No. 72131005, 71771066 and 71901014) is greatly appreciated.
Conflict of interest
The authors declare there is no conflict of interest.









 DownLoad:
DownLoad: