1. Introduction
Extensive evidence demonstrates that sleep aids the consolidation of emotionally negative vs.
neutral memory [1,2,3]. In the context of this literature, ‘negative memory’ is defined as memory
performance on tests of previously encoded negative materials, such as narrative passages that
contain descriptions of murder [1] or pictures depicting gory scenes (e.g., a severed hand; [2,4]).
Sleep as opposed to wakefulness leads to greater memory enhancements of such negative materials
compared to neutral counterparts both when this material is learned prior to nocturnal sleep [1,2], as
well as prior to a daytime nap [3]. Such effects may be related to the amount of rapid eye movement
(REM) sleep obtained during the sleep interval [1,3,5], a stage associated with increases in activity of
emotional memory regions (e.g., amygdala, anterior cingulate, hippocampus) as well as changes in
neurochemicals related to emotional processing (e.g., acetylcholine, norepinephrine, cortisol) [6,7,8,9].
Nishida and colleagues [3] found that the amount of REM sleep and corresponding theta
electroencephalography (EEG) rhythms, as well as how quickly participants first entered REM sleep
(i.e., REM sleep latency) during a post-encoding nap was related to memory improvements of
negative pictures, which benefitted from increased recognition rates by those who napped compared
to those who remained awake during the consolidation delay. Moreover, in a study by Wagner, Gais,
and Born [1], participants read and memorized either negative or neutral narrative descriptions at
encoding, and free recall was tested after the first half of a night of sleep, which contains
proportionately more non-rapid eye movement sleep (NREM) than REM sleep, the second half of
nocturnal sleep, which contains more REM than NREM sleep, or comparable periods of wakefulness.
They found that those who slept, and particularly those who obtained the REM-rich sleep late in the
night, recalled more of the negative descriptions than neutral descriptions. Additionally, a follow-up
four years later revealed that both sleep groups had comparable memory for these emotional writings,
likely because the early sleep group was eventually allowed the late-night, REM-rich portion of sleep
after initial testing [10]. Thus, many studies have corroborated the finding that REM is related to
improved emotional memory [1,3,10].
However, sleep’s ability to preserve emotional memories has been shown to operate with a
precision that extends beyond entire pictures or passages. Payne and colleagues [4] presented
participants with scenes that consisted of either a negative or neutral foreground object placed on a
neutral background at encoding. Following a period of nocturnal sleep or daytime wakefulness,
participants were tested on the foreground objects and backgrounds, presented separately and
intermixed with new images. They found that sleep exaggerated an “emotional memory trade-off”
over wakefulness, whereby negative foreground objects were remembered better than neutral ones,
but at the expense of the memory for their corresponding neutral backgrounds, which were not
remembered as well as those originally paired with neutral objects [4]. Critically, sleep had its
greatest effects on the most negative components of the scenes, with memory for the negative objects
improved after sleep not only above that seen after an equivalent period of wakefulness, but also
after just a 30-minute waking delay. Further study has shown that this preferential enhancement of
memory for negative objects following sleep is positively correlated with amounts of REM sleep
achieved during the night [5], corroborating previous research [3], and pointing toward a possible
physiological mechanism for this sleep-dependent memory enhancement [5].
Although this body of literature provides support for sleep’s impact on emotional memory
formation, and suggests possible biological mechanisms active during REM sleep, one problem with
these studies is the lack of information they provide about how sleep affects positive memory, such
as memory for positive images. Yet such a question is important to address because it can inform
research in applied domains, such as the treatment of mood disorders. For example, Major
Depressive Disorder (MDD) results in a bias to remember or ruminate on negative information,
resulting in many MDD studies that focus on negative emotions. However, studies by Heller
et al. [11] and Gruber et al. [12] highlight the importance of positive emotion, finding those with
MDD to experience positive emotions less and have a smaller neural response to positive stimuli
than healthy individuals. Coupled with the fact that MDD is often related to abnormalities in sleep
architecture, including increased REM sleep amount and decreased REM sleep latency [13],
information gleaned from research on sleep’s impact on memory for positive information could play
a role in treatment.
Broadly speaking, positive emotion does aid memory, with research revealing that positive
emotion enhances memory for stimuli such as video clips [14] and pictures [15,16]. This is likely due
to the fact that positive information, like negative information, activates the amygdala [17,18], with
this activation modulating activity in the hippocampus for processing of both positive and negative
information [15]. Further, there is some evidence that memory trade-offs do occur for positive
information when positive images are added to the emotional memory trade-off task [19,20], though
this effect may not be as robust as that for negative images. Previous research has shown the
emotional memory trade-off to occur for positive stimuli only at certain levels of arousal [19,20], or
to disappear at longer delays, after which memory for positive objects remains better than that for
neutral objects, but the backgrounds paired with positive objects are no longer impaired relative to
those paired with neutral objects [19].
As an initial investigation of the specific and neglected influence of sleep on positive memory,
the current study examined the evolution of the emotional memory trade-off for positive information
across periods of nocturnal sleep vs. daytime wakefulness. In order to imitate previous sleep and
emotional memory trade-off studies, which compared negative to neutral scene memory [4,5,21],
positive scenes were compared only to neutral scenes in the current experiment.
If sleep acts on positive and negative information in a similar manner, as some theories of
emotional memory would suggest [17,18], then sleep-based consolidation processes should not only
preferentially enhance memory for positive objects as opposed to neutral objects in the current study,
but should also lead to a corresponding deficit in memory for positive backgrounds compared to
neutral ones, over and above that seen during wakefulness [4,5,21,22]. Alternatively, if the trade-off
effect is truly not as robust for positive information as it is for negative information, sleep may only
selectively preserve memory for positive objects, without a concurrent decrement to their
backgrounds [19,20]. Regardless, given the similarities between the processing of positive and
negative memories [15,17,18], and the neurobiology of REM sleep that makes it ideal for emotional
processing [6,7,8,9], memory for positive (but not neutral) aspects of the stimuli should positively
correlate with markers of REM sleep (i.e., time spent in REM sleep, REM sleep latency), similar to
results of previous trade-off studies that found a positive correlation between REM sleep and
memory for negative scene components [3,5].
2. Methods
2.1. Participants
Participants were Notre Dame students (N = 93) who received either course credit or payment
for participation. Of these participants, 29 constituted the Wake group, 31 the Sleep group, 16 the
AM control group, and 17 the PM control group (see below for details about control groups).
Participants were between the ages of 18 and 32 (M = 19.59 ± 1.82) and were 52% female. In order
to participate, participants had to indicate that they were fluent in English, had normal or corrected
vision, and were not taking any medications that affected the central nervous system, nor had a
history of psychiatric or sleep disorders. This study was approved by the University of Notre Dame
Institutional Review Board. All participants provided written informed consent.
2.2. Materials
Picture stimuli. Trade-off task stimuli consisted of pictures taken from Payne et al. [4] and
Waring and Kensinger [19] who have previously investigated the emotional memory trade-off. The
set included a positive (e.g., chocolate cake) or neutral (e.g., light bulb) object placed on a neutral
background (e.g., kitchen setting or nightstand, respectively; Figure 1). Positive and neutral objects
were selected based on previous ratings of arousal and valence from 23 Notre Dame undergraduates.
Ratings of valence were made using a scale of one (positive) to five (negative) with neutral in the
center. Ratings of arousal were also made using a scale of one (low) to five (high). Selected positive
objects had a mean valence of 1.86 ± 0.21 and a mean arousal of 3.12 ± 0.28. Neutral objects had a
mean valence of 2.90 ± 1.00 and a mean arousal of 1.26 ± 0.09. An independent t-test revealed that
positive objects were rated significantly lower on valence (i.e., more positive) than neutral objects,
t(62) = -25.06, p < 0.001. Further, positive items were significantly more arousing than neutral items
t(62) = 36.13, p < 0.001.
2.3. Design
Subjects participated in two sessions, separated by a 12-hour delay. Those in the Wake group
encoded the scenes at approximately 9am and were tested at 9pm, while those in the Sleep group
encoded the scenes at approximately 9pm and were tested at 9am. After encoding, those in the Wake
group were allowed to leave the lab, while Sleep subjects were wired for sleep-recording
polysomnography (PSG) and spent the night in the laboratory. This allowed the analysis of standard
sleep staging (NREM stages N1-N3, REM). To control for time-of-day confounds, two additional
groups were tested, encoding the material at either 9am (AM control) or 9pm (PM control) and being
tested 20 minutes later [22]. Comparison of the two control groups was used to exclude time-of-day
interpretations.
2.4. Procedure
At the beginning of session one, participants in the Sleep and Wake groups completed a series
of questionnaires assessing demographics, recent sleep habits, mood, anxiety, depression, and
personality characteristics (Table 1). Participants then completed the emotional memory trade-off
encoding task [4,19,22], which required the incidental encoding of 64 scenes displaying 32
high-arousal positive and 32 low-arousal neutral foreground objects (e.g., a cake or light bulb,
respectively) on neutral backgrounds (e.g., a kitchen counter or nightstand, respectively; Figure 1).
Participants studied the scenes for 5 seconds each and then rated the valence and arousal of each
scene. Valence was rated on a scale of one (positive) to seven (negative) with neutral in the center of
the scale. Arousal was also rated on a scale of one (calm) to seven (excited). Pictures were presented
on a Windows system using E-Prime 2.0 software.
Table 1. Baseline Comparison between Sleep and Wake Groups.
| Measure | Sleep | Wake | t-value | p-value |
| All comparisons were non-significant. |
| Negative Affect | 13.58 | 13.39 | 0.17 | 0.86 |
| Positive Affect | 24.61 | 22.71 | 1.05 | 0.30 |
| STAI | 38.61 | 37.68 | 0.44 | 0.66 |
| PSQI | 4.68 | 4.26 | 0.81 | 0.42 |
| BDI | 4.59 | 3.81 | 0.84 | 0.40 |
Following this task, those in the Wake group were allowed to leave the lab, but were asked to
refrain from napping during the day. Alternatively, those in the Sleep group were immediately wired
for PSG recording while watching a non-arousing video. This occurred between 10pm and 11pm. All
subjects were given an 8.5-hour sleep opportunity, with lights-out between 11:15pm and 11:30pm.
Sleep was recorded with Grass polysomnography systems. A montage using EOG
(electrooculography), EMG (electromyography) and EEG leads placed at F3, F4, C3, Cz, C4, O1,
and O2 scalp positions was used, with each electrode referenced to the contralateral mastoid. Sleep
data were scored according to the American Academy of Sleep Medicine [23] standards.
During session two, the Wake and Sleep groups began by completing brief questionnaires to
assess napping, caffeine use, and perceived sleep time during the 12-hr delay. Remember/Know
recognition memory [24,25] was then tested by presenting the 128 old (previously seen) and 64 new
(foils) objects and backgrounds separately and one at a time, and asking participants which were seen
at encoding. Those in the Sleep group began the task approximately 30 minutes after lights-on to
prevent effects of sleep inertia on memory performance. Participants were asked to respond with one
of three responses: Remember indicated that they vividly remembered seeing the image at encoding
along with the context it was presented in, Know indicated that the image seemed familiar to them
but they could not remember the exact context in which it was viewed at encoding, and New
indicated that they did not see the image at encoding. This Remember/Know paradigm allows the
investigation of both vivid memory and familiarity, similar to previous studies [2].
Those in the AM and PM control groups completed all tasks described above, but in a different
order to accommodate the short time delay between encoding and testing. Thus, the control groups
began with the trade-off encoding task and then completed the session-one questionnaires described
above. The questionnaires prevented rehearsal during the 20-minute delay, which was spent in the
lab under supervision of the experimenter. The control groups did not complete the session-two
questionnaires, which were primarily used to inquire of the wake group’s activities during the delay
outside the lab. Following completion of the questionnaires, controls performed the
Remember/Know recognition test following the same instructions given to the Sleep and Wake
groups.
2.5. Data analysis
Because of the independence of Remember and Know responses, direct proportions of
Remember responses were used to indicate recollection (R) while a correction was applied to Know
responses (K/1-R) to prevent underestimation of the familiarity measure [24,25]. Further, hits (i.e.,
correctly identifying a previously seen item as old) were used in conjunction with rates of false
alarms (i.e., incorrectly identifying a new item as old) to yield a corrected memory measure (i.e., hits
— false alarms), even though the rate of false alarms was low (less than 2% for Remember responses,
and less than 13% for Know responses) and was not significantly different between the groups (all
p’s > 0.11).
Further, given that the trade-off effect for negative information appears to be driven by sleep’s
selective preservation of negative objects [4], as well as previous research suggesting that the
trade-off effect may not be as robust for positive information as it is for negative information [19,20],
we conducted two a priori analyses of the data. First, we investigated the full trade-off effect
between the groups with a 2 (Valence: positive, neutral) by 2 (Component: object, background) by 2
(Group: Sleep, Wake) mixed ANOVA for both Remember and Know responses. Second, we used
t-tests to directly compare memory for objects and backgrounds between the groups to investigate
whether sleep selectively benefited the positive components of scenes (i.e. the objects).
3. Results
3.1. Baseline differences
Sleep vs. wake groups. We first investigated whether the Sleep and Wake groups were
comparable on baseline measures of affect, anxiety, sleep quality, and depression measures.
Independent t-tests indicated that the groups did not differ on any baseline measures (Table 1).
Am vs. pm controls. Independent t-tests were also conducted to investigate baseline differences
between the AM and PM control groups on measures of affect, anxiety, sleep quality, and depression.
No significant differences were found on any of the measures (Table 2).
Table 2. Baseline Comparison between AM and PM Control Groups.
| Measure | AM | PM | t-value | p-value |
| All comparisons were non-significant. |
| Negative Affect | 14.75 | 13.29 | 0.72 | 0.48 |
| Positive Affect | 24.81 | 25.94 | -0.43 | 0.67 |
| STAI | 41.37 | 37.41 | 1.31 | 0.20 |
| PSQI | 4.63 | 4.88 | -0.28 | 0.78 |
| BDI | 6.75 | 4.47 | 1.26 | 0.22 |
3.2. Does the emotional memory trade-off occur for positive stimuli?
Given prior evidence suggesting that the full trade-off effect is not always obtained with
positive (as opposed to negative) scenes, we first examined whether the emotional memory trade-off
occurred for positive stimuli generally (i.e., across both the Sleep and Wake groups). An ANOVA on
Remember responses revealed main effects of valence, F(1, 58) = 91.22, p < 0.001, and component,
F(1.58) = 15.63, p < 0.001, which were qualified by a valence by component interaction, F(1, 58) =
180.75, p < 0.001. Although positive objects (M = 0.63 ± 0.22) were remembered better than neutral
objects (M = 0.33 ± 0.20), t(59) = 15.32, p < 0.001, their associated backgrounds (M = 0.41 ± 0.19)
were equally well remembered compared to the backgrounds associated with neutral objects (M =
0.43 ± 0.18), t(59) = -1.37, p > 0.17, a finding inconsistent with the full emotional memory trade-off
effect. A similar analysis on Know responses revealed main effects of valence, F(1, 58) = 17.91,
p = 0.001, and component, F(1, 58) = 7.41, p = 0.009, which were qualified by a valence by
component interaction, F(1, 58) = 46.34, p < 0.001. In this case, not only were positive objects
(M = 0.59 ± 0.28) remembered better than neutral ones (M = 0.37 ± 0.22), t(59) = 6.98, p < 0.001,
but backgrounds associated with positive objects (M = 0.38 ± 0.20) were also remembered worse
than those associated with neutral objects (M = 0.44 ± 0.20), t(59) = -2.69, p < 0.01, consistent with the full emotional memory trade-off effect.
3.3. Positive memory performance across sleep and wake
Upon examining whether the trade-off effect differed across the Sleep and Wake groups, we
obtained a main effect of group on recollection scores, F(1, 58) = 4.43, p = 0.04, with the Sleep group
(M = 0.49, SEM = 0.03) performing better than the Wake group (M = 0.40, SEM = 0.03) overall.
However, there were no interactions between measures of memory and group (all p’s > 0.45).
Specifically, the lack of a three-way interaction among the variables F(1, 58) = 0.046, p > 0.80,
indicates that there were no differences in the trade-off effect across groups, a finding that may be
driven by the absence of a full trade-off effect in the recollection of emotionally positive stimuli.
There was no group main effect, F(1, 58) = 0.27, p > 0.60, and no interactions with group
(all p’s > 0.20) for scores of familiarity.
However, per our a priori hypothesis, we probed the data further by specifically comparing
memory for objects and backgrounds between the Sleep and Wake groups. Here, as predicted, we
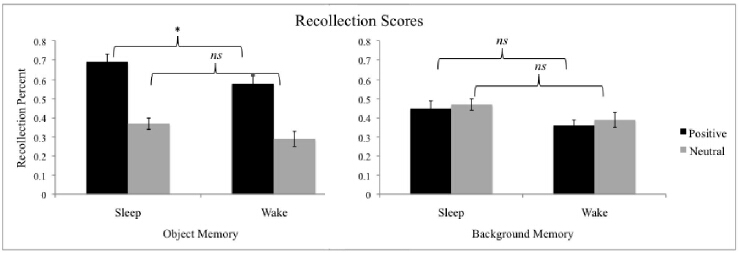
found evidence that the Sleep group recollected positive objects better than the Wake group, t(58) =
2.09, p = 0.04 (Figure 2). Importantly, this was the only significant effect; the Sleep and Wake groups
did not differ on memory for neutral objects, backgrounds paired with neutral objects, or
backgrounds paired with positive objects (see Figure 2 and Table 3). Thus, partially consistent with
prior studies examining memory for emotionally negative information within scenes [4,5], sleep
influenced memory for the emotional, and in this case positive, components of the scenes. For
familiarity, there were no differences between the groups for any of the scene components (Table 4).
Table 3. Component Recollection Results: Sleep vs. Wake
| Sleep | Wake | t-value |
| * = p < 0.05 |
| M | SD | M | SD | |
| Positive Objects | 0.69 | 0.21 | 0.58 | 0.21 | 2.09 * |
| Neutral Objects | 0.37 | 0.18 | 0.29 | 0.21 | 1.77 |
| Positive Backgrounds | 0.45 | 0.21 | 0.36 | 0.17 | 1.82 |
| Neutral Backgrounds | 0.47 | 0.17 | 0.39 | 0.19 | 1.59 |
Table 4. Component Familiarity Results: Sleep vs. Wake.
| Sleep | Wake | t-value |
| M | SD | M | SD | |
| All comparisons were non-significant |
| Positive Objects | 0.58 | 0.31 | 0.61 | 0.25 | -0.34 |
| Neutral Objects | 0.37 | 0.23 | 0.36 | 0.22 | 0.13 |
| Positive Backgrounds | 0.40 | 0.24 | 0.35 | 0.15 | 1.01 |
| Neutral Backgrounds | 0.47 | 0.21 | 0.41 | 0.18 | 1.10 |
3.4. Associations with REM sleep
Pearson’s r correlations were used to investigate the relationship between emotional memory
performance and REM sleep features. Although there was no relationship between recollection of
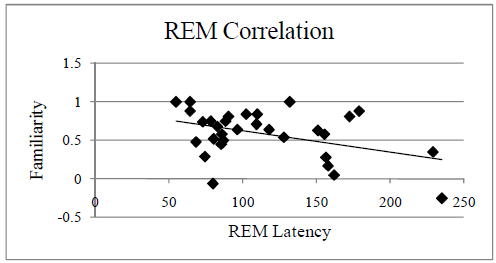
positive objects and total time spent in REM sleep (r = -0.10, p > 0.60), or REM latency (r = 0.10,
p > 0.50), there was a significant correlation between familiarity for positive objects and REM
latency (r = -0.43, p = 0.017; Figure 3). The more quickly participants entered REM sleep, the better
was their memory for positive objects, a finding consistent with our hypothesis of a role for REM
sleep in positive memory formation. There was no relationship between any other memory and sleep
measures.
3.5. Time of day effects
To ensure there were no time-of-day effects on memory performance, a 2 (Control group: AM,
PM) by 2 (Valence: positive, neutral) by 2 (Component: object, background) mixed ANOVA was
performed on the control groups’ Remember responses. Results revealed no significant interactions
with group, and no group main effect, F(1, 31) = 1.32, p > 0.25. Further, there were no differences
between the groups for recollection memory of any of the scene components (Table 5). Similarly, for
Know responses, there were no significant interactions with group, and no group main effect,
F(1, 31) = 0.02, p > 0.90. Finally, there were no differences between the groups for familiarity of any of
the scene components (Table 6).
Table 5. Component Recollection Results: AM vs. PM Controls.
| AM Control | PM Control | t-value |
| M | SD | M | SD | |
| All comparisons were non-significant |
| Positive Objects | 0.83 | 0.17 | 0.85 | 0.15 | -0.38 |
| Neutral Objects | 0.51 | 0.23 | 0.58 | 0.23 | -0.80 |
| Positive Backgrounds | 0.58 | 0.16 | 0.67 | 0.22 | -1.28 |
| Neutral Backgrounds | 0.55 | 0.16 | 0.64 | 0.18 | -1.44 |
Table 6. Component Familiarity Results: AM vs. PM Controls.
| AM Control | PM Control | t-value |
| M | SD | M | SD | |
| All comparisons were non-significant |
| Positive Objects | 0.59 | 0.36 | 0.45 | 0.38 | 1.02 |
| Neutral Objects | 0.39 | 0.24 | 0.43 | 0.26 | -0.42 |
| Positive Backgrounds | 0.33 | 0.14 | 0.35 | 0.26 | -0.26 |
| Neutral Backgrounds | 0.38 | 0.21 | 0.42 | 0.25 | -0.51 |
4. Discussion
The current study investigated the existence of the emotional memory trade-off effect for positive
compared to neutral images after a period of nocturnal sleep and daytime wakefulness. While there
was a general enhancement of memory for positive objects over neutral ones, consistent with the
emotional memory trade-off, the corresponding decrement to backgrounds associated with positive
objects as compared to neutral ones occurred only for memory measures of familiarity, and was not
impacted differently by a period of sleep or wakefulness. Yet, for measures of recollection, we found
that sleep enhanced memory over wakefulness for positive object memory specifically, with no
differences between the groups on memory for any of the neutral components of the studied scenes.
This is the first study to provide preliminary evidence that sleep enhances recollection for specifically
positive components of memories.
4.1. Evidence for the positive memory trade-off
The emotional memory trade-off has been indicated in previous research not only by better
memory for emotional objects as compared neutral objects, but also by a corresponding decrement in
memory for backgrounds associated with emotional objects compared to those associated with neutral
objects [4,19,20]. In the present study, there is some limited evidence for this trade-off effect for
positive scenes, but only for measures of familiarity. The positive memory trade-off for measures of
recollection was not obtained due to the similarity of memory for backgrounds paired with positive and
neutral objects. These findings are inconsistent with previous demonstrations of the emotional
memory trade-off effect for negative scenes, which obtained the trade-off across all measures of
memory specificity [4]. It may be possible that the trade-off effect is less robust for positive
information. Indeed, the few studies that have investigated the emotional memory trade-off for
positive information only obtained the positive memory trade-off at certain levels of arousal [20], or
have found that the decrement in memory for backgrounds placed with positive compared to neutral
objects disappeared over longer delays [19]. Thus, it is possible that consolidation processes impact
memory for the components of positive scenes differently than negative scenes.
Alternatively, the lack of the full trade-off effect for recollection memory in this study may be
because of the instructions given for the Remember/Know test. Specifically, Remember responses
required participants to retrieve contextual details, while for Know responses, such contextual details
were not able to be retrieved. It is possible that the details required for Remember responses prevented
the trade-off effect for recollection because background memory would be necessary for such
responses. Thus, the methods used to test memory may have important consequences for obtaining the
trade-off effect.
4.2. The effect of sleep on memory for positive information
Investigation of the emotional memory trade-off effect between the Sleep and Wake groups
revealed that participants in the Sleep group had better recollection for scene components overall
compared to the Wake group, while familiarity was comparable across both groups. This suggests that
sleep impacted the ability for participants to remember more detailed, vivid memories, as opposed to
information they were simply familiar with. Further, examining memory for object and background
components separately highlighted differences in recollection memory between the groups. Crucially,
although there were no differences in memory for backgrounds between groups, or in memory for
neutral objects, memory for specifically positive objects was enhanced in the Sleep group relative to
the Wake group. Since this memory enhancement was specific to the emotional components, the
current study does offer partial support for an active role of sleep on the consolidation of positive
emotional material. This is in line with previous study of sleep’s impact on negative memory, which
found sleep to have its strongest effect on negative information, enhancing memory for negative
objects above neutral objects compared to a period of wakefulness [4]. Such similarities suggest that
there may be common sleep-dependent processes occurring for positive and negative information.
However, because the results of the present study do not map perfectly onto findings using negative
stimuli, which have found sleep to impact the full trade-off effect for negative information over a
period of wakefulness [4,5], future work will be necessary to fully delineate the nature of any
differences between the sleep dependent processing of positive and negative memories.
It is also important to note that the sample used in the current study was drawn from a university
student population, but that investigating older populations may also yield interesting results for
positive memory formation. The sample for the current study was chosen because it has been the focus
of previous research in this area [4], and thus allowed us to make comparisons to previous findings.
For this reason, the age range we used was an ideal starting point for investigations into the primary
question of this study. However, other positive memory studies have examined older adult populations,
which is important given that older individuals have been suggested to show differences in emotional
memory performance compared to younger adults, even showing a greater preference for positive
compared to negative information [19]. Thus, future work in this area will benefit from investigations
into varying age groups.
4.3. Time of day effects
Although the Sleep and Wake groups performed the encoding and testing sessions at different
times of the day, there is little concern about time-of-day effects on the current results given that there
were no differences found in the performance of the AM and PM control groups. Despite completing
all experimental tasks at drastically different times of the day, these groups showed no differences on
any of the memory measures in the current study. Therefore, the differences between the Sleep and
Wake groups were not due to time-of-day influences, but were a result of the period of sleep or wake
obtained between encoding and testing.
4.4. Associations between positive emotional memory and REM sleep
Measures of REM sleep are commonly associated with emotional memory performance [1,3,5].
This is likely because emotional centers of the brain that support the encoding and retrieval of
emotional memories (e.g., the amygdala; [17]) are intensely activated during REM sleep [6], and
dramatic increases in neurochemicals associated with emotional learning, such as acetylcholine,
norepinephrine, and cortisol, are observed during this stage [6,7,8,9]. While previous studies have found
evidence of this association for negative information [1,3,5], the current study obtained evidence for a
relationship between positive memory performance and REM latency. The faster one achieved the first
stage of REM sleep, the better their familiarity memory of positive objects, thus providing initial
support for a connection between REM sleep and positive memory consolidation. Interestingly, a
similar relationship between REM latency and memory was recently reported, but for negative
pictures [3]. Such a relationship may indicate that quicker entry into REM results in more intense
emotional processing, or may be the result of a greater need for such processing, regardless of memory
valence. Given that the unique neurobiology of this state likely supports processing of emotional
information [6,8,9], achieving such a state more quickly might reflect better and more efficient
processing of the information, which may be adaptive for the individual. Future research will be
needed to determine how this earlier processing benefits emotional memory enhancements.
It should also be noted that while amount of REM sleep has also been associated with memory
performance for negative materials [3,5], REM sleep amount did not correlate with memory for
positive information in the present study. Although the reason for this lack of association is presently
unclear, one possibility is that the REM sleep — emotional memory connection is stronger for
negative than for positive memory. Follow-up investigations are currently underway to test this idea.
5. Conclusions
In summary, the current study investigated sleep’s influence on the neglected emotional memory
trade-off effect for positive information. Recollection memory specifically for the positive
components of images was enhanced by sleep, partially extending previous findings for memory of
negative material. However, while the trade-off effect for negative scenes exists across varying levels
of memory specificity, the trade-off effect for positive scenes was eliminated for the most detailed
memories. Although future research is needed to fully understand what leads to these differences
between memory for positive and negative information after a period of sleep-dependent consolidation,
this work offers a crucial and necessary first step to expand our knowledge of the complex relationship
between sleep, positive emotion, and memory.
Acknowledgements
The authors wish to thank Michelle Wirth and G.A. Radvansky for their advice on the design of
this study, as well as Elizabeth Kensinger and Jill Waring for providing us with the picture stimuli. We
also would like to thank Sara Alger and Tony Cunningham for their help editing the final manuscript.
Conflicts of interest
All authors declare no conflicts of interest in this paper.










 DownLoad:
DownLoad: