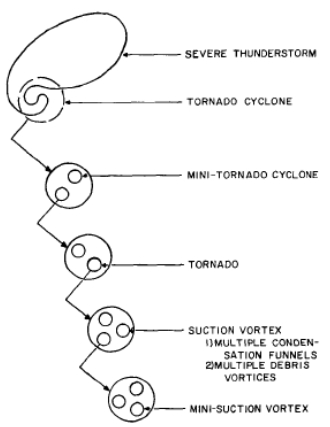
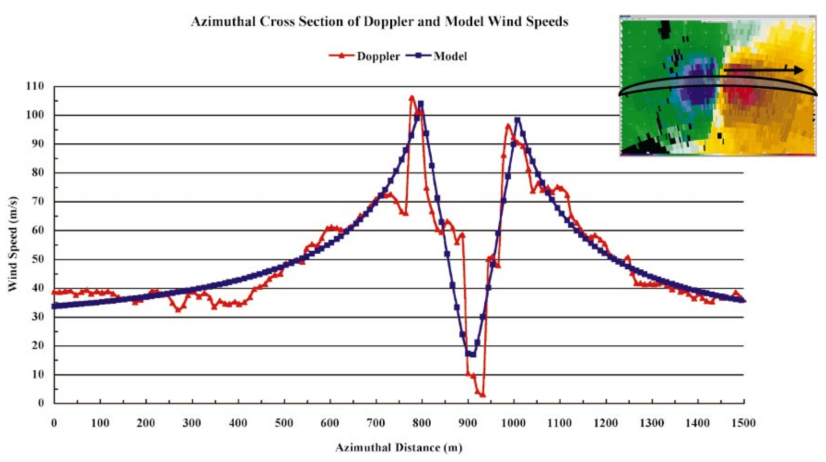
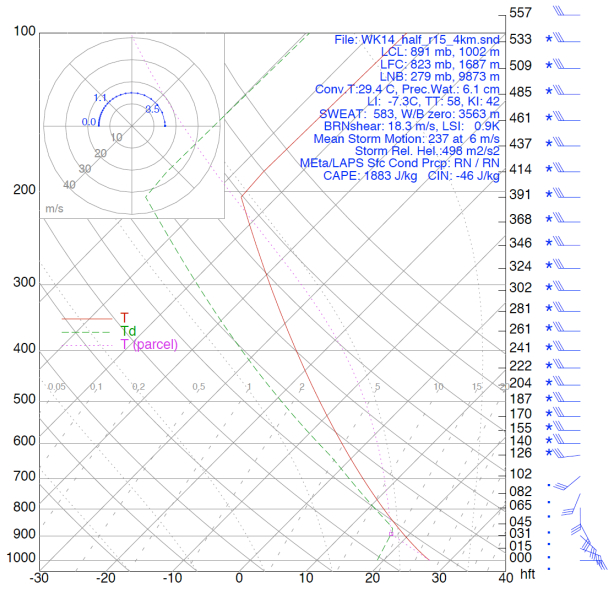
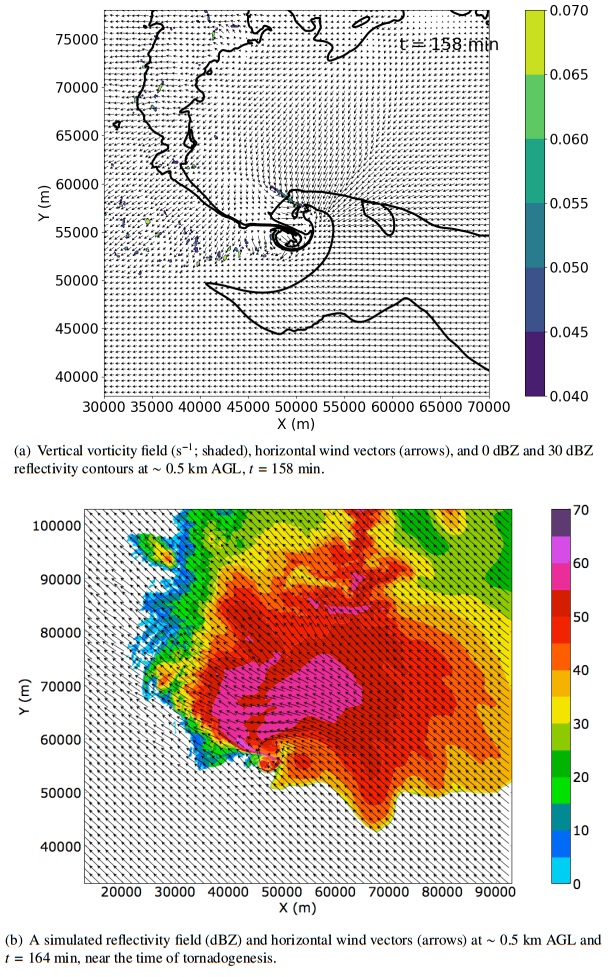
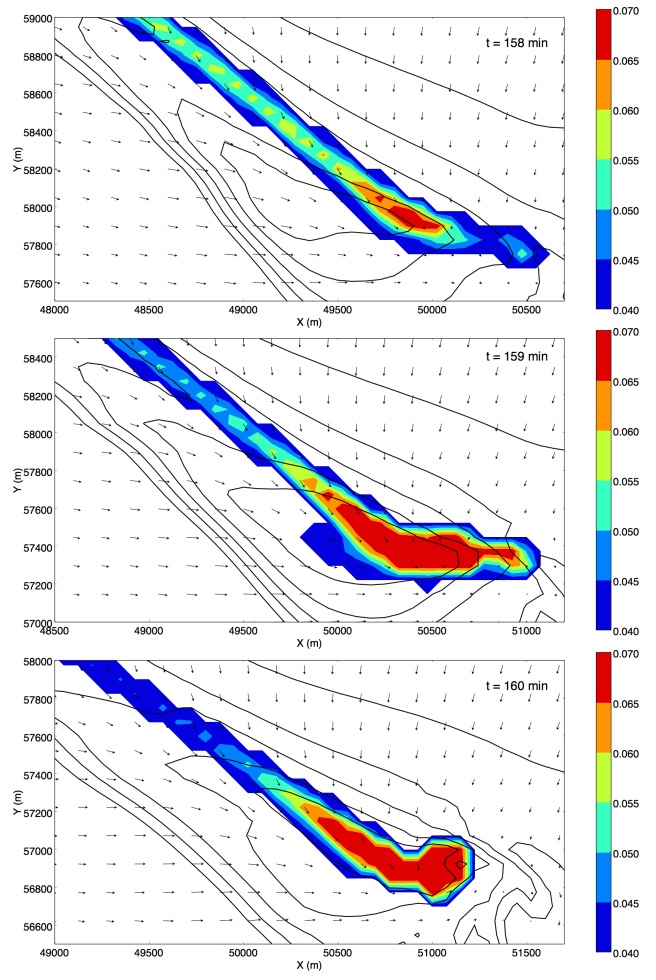
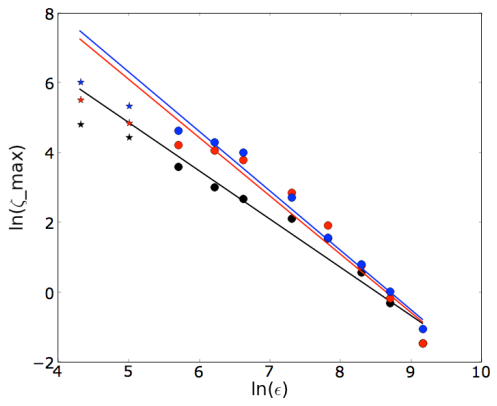
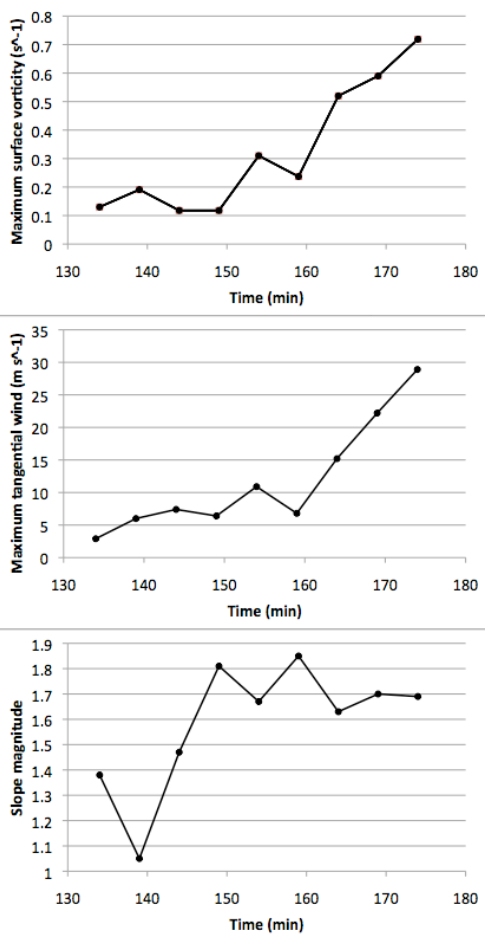
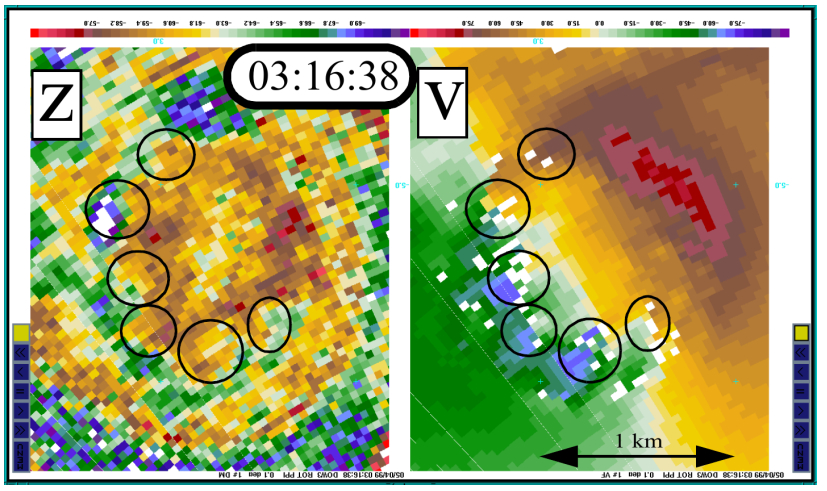
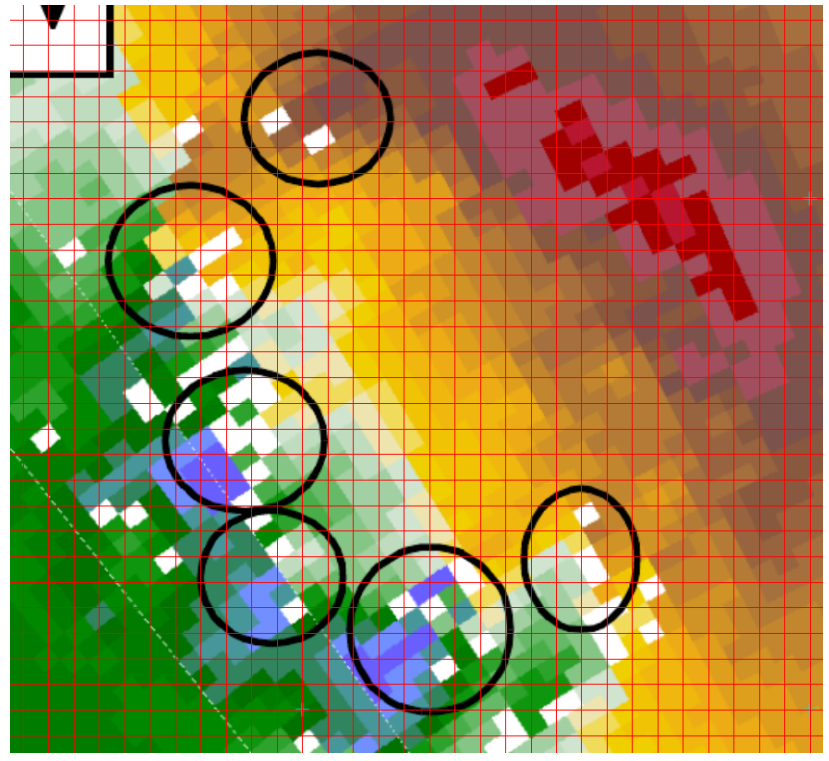
Self-similarity in tornadic and some non-tornadic supercell flows is studied and power laws relating various quantities in such flows are demonstrated. Magnitudes of the exponents in these power laws are related to the intensity of the corresponding flow and thus the severity of the supercell storm. The features studied in this paper include the vertical vorticity and pseudovorticity, both obtained from radar observations and from numerical simulations, the tangential velocity, and the energy spectrum as a function of the wave number. Power laws for the vertical vorticity, pseudovorticity, and tangential velocity obtained from radar observations studied in the literature are summarized. Further support is given to the existence of a power law for vorticity by the analysis of data obtained from a numerical simulation of a tornadic supercell. A possible explanation for an increase in vorticity in a developing tornado is provided, as well as an argument that tornadoes have approximate fractal cross sections and negative temperatures. A power law that relates the increase of the approximate fractal dimension of the cross section of a negative temperature vortex to its energy content is derived, and the possible applicability of the box-counting method to determine this quantity from suitable radar images is demonstrated.
1.
Introduction
Image deblurring or deconvolution is an important topic in image processing due to its wide range of applications in astronomical imaging, robot vision, medical image processing, remote sensing, virtual reality and many others. In the field of image deconvolution, the use of non-linear variational methods have received a great amount of attention in the last few decades. While applying these methods to blurred and noisy images researchers have to face two main difficulties. One difficulty is non-linearity, and the other is related to solve the underlying large matrix system. For this paper, our primary goal is also to deal with these two computational difficulties for a high-order variational model. The total variation (TV) model [1,29,36]
is the most famous non-linear variational model. It has so many desirable properties, but this model transforms smooth functions into piecewise constant functions which generates staircase effects in the deblurred images. That is why the resulting images look blocky. To overcome the problem of staircase effects, one idea is to use mean curvature (MC)-based regularization models [12,19,31,39,40,41],
The MC-based regularization models not only remove the staircase effects but they also preserve the edges in the deblurred images. However, the Euler-Lagrange equations of mean curvature models can be used to solve non-linear fourth-order integro-differential equations. This non-linear high order term comes from the MC functional. Furthermore the discretization of an integro-differential equation results in a large ill-conditioned system that causes numerical algorithms like Krylov subspace methods (e.g. conjugate gradient (CG) method) to slowly converge. The Jacobian matrix of the ill-conditioned system has a block-banded structure with a large bandwidth. The efficient and robust numerical solution is a key issue for MC-based regularization methods due to the ill-conditioned system and high non-linearity.
In this paper, we propose an augmented Lagrangian method for an MC-based image deblurring problem. The augmented Lagrangian methods have already been successfully applied to the optimization problems in image processing and computer vision [9,22,32,37]. In these works, the augmented Lagrangian methods achieve much higher speeds than other numerical methods. The augmented Lagrangian methods have been shown to decompose the original nontrivial minimization problem into a number of subproblems that are easy and fast to solve. Some of them can be solved by fast solvers like the fast Fourier transform (FFT), and others have 'closed-form' solutions. Therefore, the construction of an efficient augmented Lagrangian method for the minimization of a given functional depends on whether one can break down the original functional into simple ones. In our proposed augmented Lagrangian method, we use the cell-centered finite difference scheme along with the midpoint quadrature scheme for discretizing the subproblem for the primary variable u (image) of the associated Lagrangian equations. However, this leads to a large non-linear matrix system. The coefficient matrix of this system is symmetric positive definite (SPD). So the CG method is suitable for the solution of this matrix system. But, the SPD matrix is quite dense which causes the CG method to slowly converge. To overcome the problem of slow convergence due to the CG method, we have introduced a new circulant preconditioned matrix. So, for the solution of the system, instead of applying ordinary CG method, we use a preconditioned CG (PCG) method. By using the proposed new preconditioner fast convergence can be observed in the numerical results.
The contributions of the paper are as follows: (i) we present a preconditioned augmented Lagrangian method for an MC-based image deblurring model; (ii) we introduce a new circulant preconditioned matrix that overcomes the problem of slow convergence due to the CG method inside the augmented Lagrangian scheme and (iii) we present a comparison with existing numerical methods to demonstrate the efficiency of the preconditioned augmented Lagrangian method. The paper includes different sections. The second section explains the image deblurring problem. The third section is about our proposed augmented Lagrangian method for an MC-based image deblurring model. The cell discretization and matrix system are also presented in third section. The fourth section describes the proposed circulant preconditioner, and the fifth section discusses the numerical experiments. We present the conclusions in the last section of the manuscript.
2.
Problem description
We start the paper by presenting a concise description of the image debluring problem. The mathematical relationship of u (original or true image) and z (blurred image) is
The parameter ϵ represents a noise function which can be Gaussian noise, Brownian noise, salt-and-pepper noise etc. In our experiments, we have only considered Gaussian noise. →K represents the blurring operator,
where k(x,y)=k(x−y) is known as translation-invariant kernel. Figure 1 depicts the process of blurring.
If →K=I (identity operator), then Problem (2.1) becomes an image denoising problem. If the blurring operator →K is known then the technique is referred to non-blind deconvolution [14,34,38]. However, if the blurring operator is unknown, then it is called blind deconvolution [6,19,23]. Our research will focus on non-blind deconvolution. →K is a Fredholm-integral operator of the first kind, so it is compact. That is why Problem (2.1) becomes ill-posed [1,35,36]. The image intensity function u lies in a square Ω⊂R2. The position of the pixel in Ω is defined by x=(x,y). Additionally, |x|=√x2+y2 and ‖⋅‖ are the Euclidean norm and L2(Ω) norm respectively. The recovery of u from z makes Problem (2.1) an unstable inverse problem [1,35,36]. The use of the MC regularization functional[12,31,39,41],
makes Problem (2.1) a stable problem. The Problem (2.1) is then to find a u that minimizes the functional
In [41], Zhu and Chan explained the well-posedness of Problem (2.4) for the case of synthetic image denoising. The Euler-Lagrange equations of Problem (2.4) are as follows:
where →K∗is the adjoint operator of →K and n is the outward unit normal. β>0 is added to make the MC functional differentiable at zero. Equation (2.5) is a non-linear fourth order differential equation.
The MC-based regularization models not only remove the staircase effects but they also preserve edges during the recovery of digital images. However, the Euler-Lagrange equations of the MC model can be used to solve the non-linear fourth order integro-differential equation. The MC functional generates a non-linear high-order term. When developing an efficient numerical method, one key issue is determining a proper approximation of the MC functional. In the next section, the non-linearity of MC is treated by introducing three new variables for the associated Lagrangian.
3.
Augmented Lagrangian method
In the given literature [37,40,42,43] one can find lot of work on the augmented Lagrangian method (ALM) for the MC-based image denoising problem but not for the image deblurring problem. In this paper, we have extended the ALM algorithm for application to the image deblurring problem. To develop an ALM for the image deblurring model described by Problem (2.4), we introduce three new variables, i.e., w,→v and →t, and consider the following constrained minimization problem
The associated augmented Lagrangian functional in Problem (3.1) is
where r1,r2 and r3 are the penalization parameters. λ1∈R, →λ2,→λ3∈R3 are Lagrange multipliers and →v,→t∈R3. One of the key issues with ALMs is related to handling the subproblems involving the term →t√|→t|2+β=▽u√|▽u|2+β. This type of term appears due to the mean curvature functional ▽⋅▽u|▽u|. One remedy is to introduce a variable →t=⟨▽u,1⟩ instead of →t=▽u for the curvature term. Accordingly, we will use →v=⟨▽u,1⟩√|⟨▽u,1⟩|2+β. Then, our MC model becomes
Then, the associated augmented Lagrangian functional is
where r1,r2,r3 and r4 are the penalty parameters. λ1,λ3,∈R, →λ2,→λ4∈R3 are Lagrange multipliers and →v,→n,→t∈R3. Here, we have introduced →n to relax the variable →v. R={→n∈L2(Ω):|→n|≤1a.e.n∈Ω} and δR(→n) is a characteristic function on R that can be expressed as
To make the term |→t|−→t⋅→n always non-negative, we need →n∈R. To find the saddle points of the minimization given by Problem (3.3), we need to find the saddle points of the augmented Lagrangian functional given by Eq (3.4). So, we have to fix all variables in Eq (3.4) except one particular variable. Then, we find a critical point of the induced functional to update that particular variable. We repeat the same process for all variables in Eq (3.4). The Lagrangian multipliers will automatically be advanced once all variables are updated. The process will continue until all variables in Eq (3.4) converge to a steady state. The ALM is summarized in the following algorithm.
Now we consider the following subproblems and find their critical points
The standard procedure gives us the following Euler-Lagrange equations for the functionals f1(u) and f4(→v):
respectively, where →v=⟨v1,v2,v3⟩,→t=⟨t1,t2,t3⟩,→n=⟨n1,n2,n3⟩,→λ2=⟨λ21,λ22,λ23⟩ and →λ4=⟨λ41,λ42,λ43⟩. To update the functionals f2(w),f3(t) and f5(→n), we need the following equations:
To update the Lagrangian multipliers, we have the following equations:
3.1. Cell discretization
Since the MC regularizer κ(u)2=(▽⋅▽u|▽u|)2 of the image deblurring problem is not homogeneous in u, we need a spatial kind of discretization especially for the terms that involve derivatives. This is because the role of the spatial mesh size is quite important to the numerical performance of the MC model. So, we partitioned the domain Ω=(0,1)×(0,1) by δx×δy. Additionally,
where the number of equispaced partitions in the direction of x or y is equal to nx and (xi,yj) represents the centers of the cells. Additionally,
where h=1nx; (xi±12,yj) and (xi,yj±12) represent the midpoints of cell edges:
For each i=1,2,...,nx, and j=1,2,...,nx, define
For the function θ(x,y), let θk,l denote θ(xl,ym), where k and l may take values of i−1,i, or i+1 and j−1,j, or j+1 respectively, for integers i,j≥0. For backward and forward discrete functions, we need values at proper discrete points, so we define
Then the central difference discrete functions and discrete gradient are
and
respectively. By applying midpoint quadrature approximation, we have that
3.2. Matrix system
Here, we consider the cell-centered finite-difference (CCFD) method for the MC-based image deblurring problem. The CCFD approximations {Ui,j} to {u(xi,j)} are chosen. So from Eq (3.16) we have that
where g(i,j)=−[d−x(r2t1+λ21)]i,j−[d−y(r2t2+λ22)]i,j. According to the lexicographical ordering of the unknowns, U=[U11U12...Unxnx]t. Then, from Eq (3.27), we have the following matrix system:
Here Kh is a matrix of size n2x×n2x and Bh is a matrix of size 2nx(nx−1)×n2x. The matrices K∗hZ and Gh are of size n2x×1. K∗hKh is symmetric positive semidefinite. The matrix Kh is a block Toeplitz matrix with Toeplitz blocks (BTTB). The structure of the matrix Bh is
where the size of both B1 and B2 is nx(nx−1)×n2x, and
The size of
is (nx−1)×nx and I is an identity matrix. To get the value of u, one has to solve the large matrix system (3.28).
Now given Eqs (3.17) and (3.18), after discretizing, we have that
Then, applying a discrete Fourier transformation followed by a discrete inverse Fourier transformation to Eqs (3.29) and (3.30), one can get v1 and v2, and v3 can be obtained directly from Eq (3.19). To update the variables w,→t,→n and Lagrange multipliers λ1,→λ2,λ3,→λ4, we have to discretize Eqs (3.20)–(3.26) on grid points (i,j). So we need the following equations:
To update the Lagrangian multipliers, we have the following equations:
4.
Preconditioned matrix
To find the value of our main variable u, one has to solve the matrix system given by Eq (3.28). The Hessian matrix K∗hKh+r2B∗hBh of the system given by Eq (3.28) is extremely large for practical application and tends to be quite ill-conditioned when r2 is small. This happens because of the eigenvalues of the blurring operator ˉK are very small and close to zero [36]. K∗hKh is a full matrix, but an FFT can be used to evaluate K∗hKhu in O(nxlognx) operations [36] because the blurring operator ˉK is translation-invariant. The good thing is that the Hessian matrix is SPD.
Theorem 4.1. The inner product ⟨ˉAU,U⟩ is positive for any matrix U≠0, where ˉA=K∗hKh+r2B∗hBh is the Hessian matrix of the system given by Eq (3.28).
Proof. For any matrix U≠0, consider that
This completes the proof.
The CG method is suitable for the solution of the system given by Eq (3.28) owing to the above-mentioned properties. But, the CG method have a quite slow convergence rate due to the system being large and ill-conditioned system. So, we use a PCG method [7,8,10,24,25,26,30]. The preconditioning matrix P must be SPD so that we get an effective solution for our system [2,3,4,11,36]. Here, we introduce our SPD circulant preconditioned matrix P of the Strang-type [27].
where ~Kh is a circulant approximation of Matrix Kh and γ>0. Ih is an identity matrix. While applying the PCG to Eq (3.28), one of the requirements is to take the inverse of the preconditioned matrix P. Since the second term in P is an identity matrix Ih, inversion is not a problem. For the inversion of the first term ~K∗h~Kh, we need to apply FFTs to O(nxlognx) floating-point operations [36].
Now, let ˉA=K∗hKh+r2B∗hBh be the Hessian matrix of the system given by Eq (3.28). Let the eigenvalues of K∗hKh and B∗hBh be λKi and λBi respectively such that λKi→0 and λBi→∞. Then the eigenvalues of P−1ˉA are
One can notice that clearly θi→λBiγ as i→∞. Hence, for λBi≤γ, the spectrum of P−1ˉA is more favorable than the Hessian matrix ˉA. This can also be observed in the numerical examples when we use the PCG algorithm.
5.
Numerical experiments
Here, we present numerical examples for the image deblurring problem. In all experiments, we have used different values of nx, and the resulting matrix system has n2x unknowns. Then the mesh size is h=1/nx. The numerical computations were performed using MATLAB software on an Intel(R) Core(TM) i7-4510U CPU @ 2.00 GHz 2.60 GHz. In all experiments, we have taken the initial guess to be the zero vector. The value of the parameters α and β were set by referencing [5,41]. To observe the optimum value of γ, we have done numerical experiments by using Goldhills image. We found that the value of the peak signal-to-noise ratio (PSNR) does not show much improvement after γ=1. So, one can use optimum value of γ close to one. The results of the experiments are given in Figure 2.
The PSNR is used to measure the quality of the restored images. For numerical calculations, we have used the ke−gen(nx,r,σ) kernel [13,16,17,28]. It is a circular Gaussian filter of size nx×nx with a standard deviation σ and radius r. Figure 3 depicts the ke−gen(120,40,4) kernel.
Example 1.
For this example, we have used three different types of images. These are Goldhills, Kids and Peppers images (see [33]). The Goldhills image is a real image and Peppers image is a nontexture image. The Kids image is a complicated image, because it contains a small scale texture part (shirt) and a large scale cartoon part (face). The different aspects of all images can be seen in Figure 5. Each subfigure has a pixel of 256×256. Here, we have also compared our MC-based ALMs, i.e., ALM and preconditioned ALM (PALM) with the TV-based method (TVM) [1,29,36]. The Hessian matrix of the TV-based model is SPD, so for the numerical calculation we have used the CG method. The parameters of ALM and PALM were established by referencing [42,43]. The parameters for the ALM and PALM were α=8e−9,r1=9.5e−7,r2=1e−6,r3=1e−8,r4=1e−5,β=1 and γ=1. For the TVM algorithm (CG), we have used α=1e−6 and β=1, as according to [36]. For the numerical calculations, the ke−gen(nx,300,10) kernel was used. The stopping criteria for the numerical methods is based on the tolerance tol=1e−7. The Tables 1–3 contain all of the information of this experiment. A performance comparison of the TVM, ALM and PALM is depicted in Figure 7. The relative residues and eigenvalues of the ALM and PALM are depicted in Figures 4 and 6, respectively.
Remarks:
(1) From Figure 5 one can notice that the deblurred images produced via our methods (ALM and PALM) are much better than those produced via the TVM.
(2) From Tables 1–3, one can observe that the PSNR values of the ALM and PALM methods were quite higher than those for the TVM for all images. Although the TVM generates its PSNR value in much less computational time as compared to the ALM and PALM, its PSNR value is quite low. For example, for the Goldhills image with a pixel size of 128×128, the TVM took 37.1002 seconds to generate its 48.5749 PSNR, but the ALM and PALM generated higher PSNR values of 56.3756 and 56.3654 in 40.8027 seconds and 30.5428 seconds respectively. For the Kids image with a pixel size of 256×256, the TVM took 133.0289 seconds to generate a 40.5482 PSNR, but the ALM and PALM generated higher PSNR values of 46.0595 and 46.9837 in 189.2586 seconds and 141.2561 seconds respectively. Similarly, for the Peppers image with a pixel size of 256×256, the TVM took 118.5327 seconds to generate 49.2863 PSNR, but the ALM and PALM generated higher PSNR values of 51.0284 and 51.4522 in 190.3504 seconds and 146.3177 seconds respectively. Similar behavior was observed for other sizes. So, the proposed ALM and PALM tend to generate high-quality deblurred images as compared to the TVM.
Example 2.
Here, we have compared our MC-based ALMs, i.e., the ALM and PALM with the MC-based method proposed by Fairag et al. [18], who developed a One-Level method (OLM) and Two-Level method (TLM) for the MC-based image deblurring problem. For this experiment, we used three different types of images, i.e., the images of Goldhills (real), Cameraman (complicated) and Moon (non-texture). The different aspects of all images can be seen in Figure 8. Each subfigure has apixel size of 256×256.
The parameters for ALM and PALM were α=1e−9,r1=9.5e−7,r2=1e−6,r3=1e−8,r4=1e−5, β=1 and γ=1. For the MC-based algorithms (OLM and TLM) we used α=8e−9 and β=1. The Level-Ⅱ parameter ˜α of the TLM was calculated by referencing the formula presented in [18]. For the numerical calculations, the ke−gen(nx,300,10) kernel was used. The stopping criteria for the numerical methods is based on the tolerance tol=1e−8. Tables 4–6 contain all of the information on this experiment. A performance comparison of the ALM, PALM, OLM and TLM is depicted in Figure 9.
Remarks:
(1) From Figure 8, one can notice that the ALM and PALM methods both generated slightly higher quality results.
(2) From Tables 4–6, it can be observed that the PSNR values of the ALM and PALM were higher than the OLM and TLM for all images. The TLM generated its PSNR in much less time than the OLM and ALM, but not the PALM. For example, for the Goldhills image with a pixel size of 256×256, the OLM, TLM and ALM took 248.5400,128.4097 and 195.2980 seconds, respectively, to deblur the image. But, the PALM only required 126.7891 seconds for deblurring. For the Cameraman image with a pixel size of 128×128, the OLM, TLM and ALM took 24.5327, 19.7541 and 38.4161 seconds, respectively, to deblurred image. But, the PALM only required 18.2997 seconds for deblurring. Similarly, for Moon image with a pixel size of 128×128, the OLM, TLM and ALM took 34.3866, 24.8366 and 25.3032 seconds, respectively, to deblur image. But, the PALM only required 16.4356 seconds for deblurring. Similar behavior was observed for other sizes. So, our PALM consumed much less CPU time than other methods, and it also generated high-quality deblurred images.
6.
Conclusions
An ALM for the primal form of the image deblurring problem with MC regularizational functional has been presented. A new SPD circulant preconditioned matrix has been introduced to overcome the problem of slow convergence due to the CG method inside of the ALM. Numerical experiments were conducted using different kinds of images (synthetic, real, complicated and nontexture) by our proposed PALM with a new preconditioned matrix. We have compared the TV (total variation) based algorithm with our mean curvature based (ALM and PALM) algorithm. The proposed ALMs, i.e., the ALM and PALM were also compared with the latest MC-based techniques i.e., the OLM and TLM. The numerical experiments showed the effectiveness of our proposed PALM method with a new preconditioned matrix. In the future, we will work on developing an ALM for other computationally expensive regularization functionals like the fractional TV regularized tensor [21]. Furthermore, the matrix B∗hBh was also constructed to have a block Toeplitz matrix structure in the system given by Eq (3.28), so, a single term preconditioner like tau preconditioner [15,20] can be used to approximate both the matrices B∗hBh and K∗hKh in order to increase the convergence rate of the CG method inside the ALM.
Acknowledgments
The second and third authors would like to thank King Fahd University of Petroleum and Minerals (KFUPM) for its continuous support. The authors also thank the referees for their very careful reading and valuable comments. This work was funded by KFUPM, Grant No. #SB201012.
Conflict of interest
The authors declare that there is no conflict of interest.










 DownLoad:
DownLoad: