1. Introduction

As a fundamental equation of fluid dynamics, the Navier-Stokes equations have been investigated by many scientists conducting research on numerical schemes for their numerical solutions [7,8,10,17,18,19,22,23]. Analytical solutions of real flow problems including complex geometries are not available, nor likely in the foreseeable future. There are two ways to provide reference data for such problems: One consists in the measurement of quantities of interest in physical experiments and the other is to perform careful numerical studies with highly accurate discretizations. With the prevalence and development of high-performance computers, advanced numerical algorithms are able to be tested for the validation of approaches and codes and for high-order convergence behavior of delicate discretizations. For example, Symmetric Interior Penalty Galerkin (SIPG) and Non-symmetric Interior Penalty Galerkin (NIPG) methods were first introduced originally for elliptic problems by Wheeler [24] and Rivi$\grave{\mbox{e}}$re et al. [16]. Recently, some work based on the SIPG and NIPG methods has been successfully applied to the steady-state and transient Navier-Stokes equations [8,9,15], for which optimal error estimates for the velocity have been derived.

The Navier-Stokes equations are a concise physics model of low Knudsen number (i.e. non-rarefied) fluid dynamics. Phenomena described with the Navier-Stokes equations include boundary layers, shocks, flow separation, turbulence, and vortices, as well as integrated effects such as lift and drag. The physics of Navier-Stokes flows are non-dimensionalized by Mach number $M$ and Reynolds number $Re$,

$M=\frac{\mathbf{u}_{\infty}}{\mathbf{a}},$

(1)

$Re = \frac{\rho \mathbf{u}_{\infty} D}{\mu},$

(2)

where $\rho$ is the density of the fluid, and $\mu$ is the dynamic viscosity. The kinematic viscosity $\nu$ is the ratio of $\mu$ to $\rho$. At low Knudsen numbers, Navier-Stokes surface boundary conditions are effectively no-slip (i.e. zero velocity). Diffusion of momentum from freestream to surface no-slip velocities forms boundary layers decreasing in thickness as Reynolds number increases. Thus, the range of characteristic solution scale increases as the Reynolds number increases. Nonlinear convective terms couped with the strong velocity gradients in the Navier Stokes equations drive fluid flow at even moderate Reynolds numbers to inherently unsteady behavior. Rotational flow is measured in terms of the vorticity $\mathbf{\omega}$, defined as the curl of a velocity vector $\mathbf{v}$,

$w = \nabla {\rm{ \times v}}$

(3)

The related concept of circulation $\Gamma$ is defined as a contour integral of vorticity by

$\Gamma = {\rm{ }}\oint\limits_{\partial S} {{\bf{v}} \cdot {\bf{ds}} = - \int\!\!\!\int\limits_{\bf{S}} {\bf{\omega }} \cdot {\bf{\hat ndS}}}$

(4)

The concept of a vortex is that of vorticity concentrated along a path [3].

Lid driven cavity flows are geometrically simple boundary conditions testing the convective and viscous portions of the Navier Stokes equation in a enclosed unsteady environment. The cavity flow is characterized by a quiescent flow with the driven upper lid providing energy transfer into the cavity through viscous stresses. Boundary layers along the side and lower surfaces develop as the Reynolds number increases, which tends to shift the vorticity center of rotation towards the center. A presence of the sharp corner at the downstream upper corner increasingly generates small scale flow features as the Reynolds number increases. Full cavity flows remain a strong research topic for acoustics and sensor deployment technologies.

For non-streamlined blunt bodies with a cross-flow, an adverse pressure gradient in the aft body tends to promote flow separation and an unsteady flow field. The velocity field develops into an oscillating separation line on the upper and lower surfaces. This manifests as a series of shed vortices forming and then convecting downstream with the mean flow. The von K$\acute{\mbox{a}}$rm$\acute{\mbox{a}}$n vortex street is named after the engineer and fluid dynamicist Theodore K$\acute{\mbox{a}}$rm$\acute{\mbox{a}}$n (1963; 1994). Vortex streets are ubiquitous in nature and are visibly seen in river currents downstream of obstacles, atmospheric phenomena, and the clouds of Jupiter (e.g. The Great Red Spot). Shed vortices are also the primary driver for the the zig-zag motion of bubbles in carbonated drinks. The bubble rising through the drink creates a wake of shed vorticity which impacts the integrated pressures causing side forces and thus side accelerations. The physics of sound generation with an Aeolean's harp operates by alternating vortices creating harmonic surfaces pressure variations leading to radiated acoustic tones. Tones generated by vortex shedding are the so-called Strouhal friction tones. If the diameter of the string, or cylinder immersed in the flow is $D$ and the free stream velocity of the flow is $\mathbf{u}_{\infty}$ then the shedding frequency $f$ of the sound is given by the Strouhal formula

$St=\frac{f D}{\mathbf{u}_{\infty}},$

(5)

where $f={T}^{-1}$, and $St$ is the Strouhal number named after Vincent Strouhal, a Czech physicist who experimented in 1878 with wires experiencing vortex shedding and singing in the wind (Strouhal, 1878; White, 1999). The Strouhal formula provides a experimentally derived shedding frequency for fluid flow. Therefore, we are interested in an investigation of Stouhal numbers of incompressible flow at different Reynolds number.

Let $\Omega$ be a bounded polygonal domain in $\mathbb{R}^2$. The dynamics of an incompressible fluid flow in 2D is described by the Navier-Stokes equations, which include the equations of continuity and momentum, written in dimensionless form [23] as follows:

$\frac{\partial \mathbf{u}}{\partial t}-\nu\Delta \mathbf{u}+(\mathbf{u}\cdot\nabla)\mathbf{u}+\nabla p=\mathbf{f}, \text{in} \Omega\times (0, T)\label{momentum}$

(6)

$\nabla\cdot \mathbf{u}=0, \text{in} \Omega\times (0, T)\label{contin}$

(7)

$\mathbf{u}|_{t=0}=\mathbf{u}_0, \label{initialcond}$

(8)

subject to the boundary conditions on $\partial\Omega:$

$\alpha\mathbf{u}+(1-\alpha)\frac{\partial\mathbf{u}}{\partial\mathbf{n}}=\mathbf{u}_{\infty}.$

Here the parameter $\alpha$ has the limit values of 0 for the free-slip (no stress) condition (Neumann) and 1 for the no-slip condition (Dirichlet); $\mathbf{u}=(u, v)$ is the velocity; $t$ is the time; and $p$ is the pressure. In general, the external force $\mathbf{f}$ is not taken into account in Eq. (6).

Using the divergence free constraint, problem (6)-(8) can be rewritten in the following conservative flux form:

$\frac{\partial \mathbf{u}}{\partial t}-\nu\Delta \mathbf{u}+\nabla\cdot F+\nabla p=\mathbf{f}, \text{in} \Omega\times (0, T)$

(9)

$\nabla\cdot \mathbf{u}=0, \text{in}\Omega\times (0, T)\label{NavierSeqB}$

(10)

$\mathbf{u}|_{t=0}=\mathbf{u}_0, \label{NavierSeqC}$

(11)

with the flux $F$ being defined as

$F(\mathbf{u})=\mathbf{u}\otimes\mathbf{u}=\left[\begin{array}{cc}u^2 uv\\uv v^2\end{array}\right].$

(12)

and $\mathbf{u}\otimes\mathbf{v}=u_iv_j, i, j=1, 2.$ Indeed, it holds

$\mathcal{N}(\mathbf{u})=\left(\begin{array}{c}\frac{\partial (u^2)}{\partial x}+\frac{\partial (uv)}{\partial y}\\ \frac{\partial (uv)}{\partial x}+\frac{\partial (v^2)}{\partial y}\end{array}\right)=\nabla\cdot F(\mathbf{u}).$

A locally conservative DG discretization will be employed for the Navier-Stokes equation (9)-(11). We denote by $\mathcal{E}_h$ a shape-regular triangulation of the domain $\bar{\Omega}$ into triangles, where $h$ is the maximum diameter of elements. Let $\Gamma^I_h$ be the set of all interior edges of $\mathcal{E}_h$ and $\Gamma^B_h$ be the set of all boundary edges. Set $\Gamma_h=\Gamma^I_h\cup \Gamma^B_h.$ For any nonnegative integer $r$ and $s\geq 1$, the classical Sobolev space on a domain $E\subset \mathbb{R}^2$ is

$W^{r, s}(E)=\{v\in L^s(E)| \forall |m|\leq r, \partial^m v\in L^s(E)\}.$

We define the spaces of discontinuous functions

$V=\{\mathbf{v}\in L^2(\Omega)^2: \forall E\in\mathcal{E}_h, \ \mathbf{v}|_E\in (W^{2, 4/3}(E))^2\}, \\ M=\{q\in L^2(\Omega): \forall E\in\mathcal{E}_h, \ q|_{E} \in W^{1, 4/3}(E)\}.$

The jump and average of a function $\phi$ on an edge $e$ are defined by:

$[\phi]=(\phi|_{E_k})|_e-(\phi|_{E_l})|_e, \\ \{\phi\}=\frac{1}{2} \left((\phi|_{E_k})|_e+(\phi|_{E_l})|_e)\right).$

Further, let $\mathbf{v}$ be a piecewise smooth vector-, or matrix-valued function at $\mathbf{x}\in e$ and denote its jump by

$[\mathbf{v}]:=\mathbf{v}^+\cdot\mathbf{n}_{E^{+}}+\mathbf{v}^-\cdot\mathbf{n}_{E^{-}},$

where $e$ is shared by two elements $E^+$ and $E^-$, and an outward unit normal vector $\mathbf{n}_{E^{+}}$ (or $\mathbf{n}_{E^{-}}$) is associated with the edge $e$ of an element $E^{+}$ (or $E^{-}$). The tensor product of two tensors $\mathbf{T}$ and $\mathbf{S}$ is defined as $\mathbf{T}:\mathbf{S}=\sum_{i, j}{T_{ij}S_{ij}}$.

Let $\mathbb{P}_N(E)$ be the set of polynomials on an element $E$ with degree no more than $N.$ Based on the triangulation, we introduce two approximate subspaces $\mathbf{V}_h(\subset V)$ and $M_h(\subset M)$ for integer $N\geq 1$:

$\mathbf{V}_h=\{\mathbf{v}\in L^2(\Omega)^2: \forall E\in\mathcal{E}_h, \ \mathbf{v}_h\in (\mathbb{P}_N(E))^2\}, \\ M_h=\{q\in L^2(\Omega): \forall E\in\mathcal{E}_h, \ q \in \mathbb{P}_{N-1}(E)\},$

The work was motivated by the work of Girault, Rivi$\grave{\mbox{e}}$re and Wheeler on discontinuous finite elements for incompressible flows presented in a series of papers [8,15]. Some projection methods [2,19] have been developed to overcome the incompressibility constraints $\nabla\cdot \mathbf{u}=0$. An implementation of the operator-splitting idea for discontinuous Galerkin elements was developed in [8]. We appreciate the advantages of the discontinuous Galerkin methods, such as local mass conservation, high order of approximation, robustness and stability. In this work, we will make use of the underlying physical nature of incompressible flows in the literature and extend the interior penalty discontinuous Galerkin methods to investigate dynamical behavior of vortex dominated lid-driven and cylinder flows.

The paper is organized as follows. In Section 2, a temporal discretization for the Navier-Stokes equation is presented by operator-splitting techniques, and subsequently, the nonlinearity is linearized. Both pressure and velocity can be solved successively from linear elliptic and Helmholtz-type problems, respectively. In Section 3, a local numerical flux will be given for the nonlinear convection term and an interior penalty discontinuous Galerkin scheme will be used in spacial discretization for those linear equations, and in Section 4, simulations of a lid-driven cavity flow up to $Re=7500$, and a transient flow past a circular cylinder are presented, while a numerical investigation on the Strouhal-Reynolds-number has been done, comparable to the experimental results. Finally, Section 5 concludes with a brief summary.

2. Temporal splitting scheme

We consider here a third-order time-accurate discretization method at each time step by using the previous known velocity vectors. Let $\triangle t$ be the time step, $M=\frac{T}{\triangle t}$, and $t_n=n\triangle t$. The semi-discrete forms of problem (6)-(8) at time $t_{n+1}$ is

$\frac{\gamma_0\mathbf{u}^{n+1}-\alpha_0\mathbf{u}^n-\alpha_1\mathbf{u}^{n-1}-\alpha_2\mathbf{u}^{n-2}}{\triangle t}-\nu\Delta \mathbf{u}^{n+1}+\nabla p^{n+1}\\ =-\beta_0\mathcal{N}(\mathbf{u}^n)-\beta_1\mathcal{N}(\mathbf{u}^{n-1})-\beta_2\mathcal{N}(\mathbf{u}^{n-2})+\mathbf{f}(t_{n+1}),$

(13)

$\nabla\cdot \mathbf{u}^{n+1}=0,$

(14)

which has a timestep constraint based on the CFL condition (see [14]):

$\triangle t \approx O\Big(\frac{\mathcal{L}}{\mathcal{U}N^2}\Big),$

where $\mathcal{L}$ is an integral length scale (e.g. the mesh size) and $\mathcal{U}$ is a characteristic velocity. Because the semi-discrete system (13)-(14) is linearized, thus, a time-splitting scheme can be applied naturally, i.e., the semi-discretization in time (13)-(14) can be decomposed into three stages as follows.

• The first stage

When $\mathbf{u}^n$ and $\mathbf{u}^{n-1}$ ($n\geq 1$) are known, the following linearized third-order formula can be used

$\frac{\gamma_0\tilde{\mathbf{u}}-\alpha_0\mathbf{u}^n-\alpha_1\mathbf{u}^{n-1}-\alpha_2\mathbf{u}^{n-2}}{\triangle t} =-\beta_0\mathcal{N}(\mathbf{u}^n)-\beta_1\mathcal{N}(\mathbf{u}^{n-1})+\mathbf{f}(t_{n+1})$

(15)

with the following coefficients for the subsequent time levels ($n\geq 2$)

$\gamma_0=\frac{11}{6}, \ \alpha_0=3, \ \alpha_1=-\frac{3}{2}, \ \alpha_2=\frac{1}{3}, \ \beta_0=2, \ \beta_1=-1.$

Especially, by using the Euler forward discretization at the first time step ($n=0$), we can get a medium velocity field $\mathbf{u}^1$ by

$\frac{{\mathbf{u}^1}-\mathbf{u}^0}{\triangle t} =-\mathcal{N}(\mathbf{u}^0)+\mathbf{f}(t_{1}),$

and $\mathbf{u}^2$ by

$\frac{\gamma_0\mathbf{u}^2-\alpha_0\mathbf{u}^1-\alpha_1\mathbf{u}^{0}}{\triangle t} =-\beta_0\mathcal{N}(\mathbf{u}^1)-\beta_1\mathcal{N}(\mathbf{u}^{0})+\mathbf{f}(t_{2}),$

which adopts the following coefficients to construct a second-order difference scheme for the time level ($n=2$) in (15)

$\gamma_0=\frac{3}{2}, \ \alpha_0=2, \ \alpha_1=-\frac{1}{2}, \ \alpha_2=0, \ \beta_0=2, \ \beta_1=-1.$

• The second stage

The pressure projection is as follows

$\gamma_0\frac{\tilde{\tilde{\mathbf{u}}}-\tilde{\mathbf{u}}}{\triangle t}=-\nabla p^{n+1}.$

(16)

To seek $p^{n+1}$ such that $\nabla\cdot \tilde{\tilde{\mathbf{u}}}=0$, we solve the system

$-\Delta p^{n+1}=-\frac{\gamma_0}{\triangle t}\nabla\cdot\tilde{\mathbf{u}},$

(17)

with a Neumann boundary condition being implemented on the boundaries as

$\frac{\partial p^{n+1}}{\partial \mathbf{n}}=\mathbf{f}^{n+1}-\beta_0\mathbf{n}\cdot\Big(\frac{\partial \mathbf{u}^n}{\partial t}+\nabla\cdot F(\mathbf{u^n})-\nu\Delta \mathbf{u}^n\Big)\\ -\beta_1\mathbf{n}\cdot\Big(\frac{\partial \mathbf{u}^{n-1}}{\partial t}+\nabla\cdot F(\mathbf{u^{n-1}})-\nu\Delta \mathbf{u}^{n-1}\Big)\\ -\beta_2\mathbf{n}\cdot\Big(\frac{\partial \mathbf{u}^{n-2}}{\partial t}+\nabla\cdot F(\mathbf{u^{n-2}})-\nu\Delta \mathbf{u}^{n-2}\Big):=G_n.$

One can compute the vorticity $\omega^n=\nabla\times \mathbf{u}^n$ at time $t^n=n\cdot\triangle t$. Then we use $p^{n+1}$ to update the intermediate velocity $\tilde{\tilde{\mathbf{u}}}$ by (16).

• The third stage is completed by solving

$\gamma_0\frac{\mathbf{\mathbf{u}}^{n+1}-\tilde{\tilde{\mathbf{u}}}}{\triangle t}=\nu\Delta \mathbf{u}^{n+1},$

which can be written as a Helmholtz equation for the velocity

$-\Delta \mathbf{u}^{n+1}+\frac{\gamma_0}{\nu\triangle t}\mathbf{u}^{n+1}=\frac{\gamma_0}{\nu\triangle t}\tilde{\tilde{\mathbf{u}}}.$

From the three stages given above, we notice that (15) in the semi-discrete systems is presented in a linearized and explicit process, moreover, (17) and (18) are obviously a type of elliptic and Helmholtz problems at each time step as $n\geq 2$. We decouple the incompressibility condition and the nonlinearity, then the pressure and velocity semi-discretizations (17)-(18) will be formulated by the interior penalty discontinuous Galerkin methods in spacial discretizations in the next section.

3. The spatial discretizations

For spacial approximations, assume that piecewise polynomials of order $N$ are employed, then the approximation space can be rewritten as $\mathbf{V}_h=\bigoplus_{k=1}^K\mathbb{P}_N(E_k)^2$. In the approximating polynomial space for the velocity or pressure restricted to each element, a high-order nodal basis can be chosen, consisting of Lagrange interpolating polynomials defined on a reference simplex introduced in [11,12]. We let $\mathbf{u}$ be approximated by $\mathbf{u}_h\in \mathbf{V}_h$ and adopt a suitable approximation for the term $F$, i.e., $F(\mathbf{u})\approx F(\mathbf{u}_h)$, where $F(\mathbf{u}_h)$ also can be represented as the $L^2$-projection of $F(\mathbf{u}_h)$ on each element of $\mathcal{T}_h$. Multiplying the nonlinear term by a test function $\mathbf{v}_h\in \mathbf{V}_h$, integrating over the computational domain, and applying integration by parts, we have

$\int_{\Omega}(\nabla\cdot F)\cdot \mathbf{v}_h d\mathbf{x}=-\sum\limits_{E_k}\int_{E_k}(F\cdot\nabla)\cdot \mathbf{v}_hdx+\sum\limits_{e\in \Gamma_{h}}\int_{e} \mathbf{n}_e\cdot[F\cdot\mathbf{v}_h]ds,$

(19)

where the term $(F\cdot\nabla)\cdot \mathbf{v}_h$ equals to $F_{ij}\frac{\partial {v}_{hi}}{\partial {x}_j}$, for $i, j=1, 2$ and the indexes $i, j$ correspond to the components of the related vectors. On each edge $e\in \partial E_1\cap\partial E_2$ shared by two elements, to ensure the flux Jacobian of purely real eigenvalues, we may define $\lambda_{E_1, e}^+$, $\lambda_{E_2, e}^-$ the largest eigenvalue of the Jacobians $\frac{\partial}{\partial \mathbf{u}}(F\cdot \mathbf{n}_e)\big|_{\bar{\mathbf{u}}_{E_1}}$ and $\frac{\partial}{\partial \mathbf{u}}(F\cdot \mathbf{n}_e)\big|_{\bar{\mathbf{u}}_{E_2}}$, respectively, where $\bar{\mathbf{u}}_{E_1}$ and $\bar{\mathbf{u}}_{E_2}$ are the mean values of $u_h$ on the elements $E_1$ and $E_2$, respectively. The global Lax-Friedrichs flux is generally more dissipative than the local Lax-Friedrichs flux, therefore, we primarily consider the local flux on each edge. Although the Lax-Friedrichs flux is perhaps the simplest numerical flux and often the most efficient flux, it is not the most accurate scheme. A remedy of the problem is to employ high-order finite elements. By replacing the integrand in the surface integral as

$\mathbf{n}_e\cdot[F\cdot\mathbf{v}_h] =\mathbf{n}_e\cdot\{F\}\cdot[\mathbf{v}_h]+ \frac{\lambda_e}{2}[\mathbf{u}_h]\cdot[\mathbf{v}_h],$

with $\lambda_e=\max(\lambda_{E_1, e}^+, \lambda_{E_2, e}^-)$, one can get a DG discretization for the nonlinear term in (19) by the local Lax-Friedrichs flux.

For the pressure correction step (17) and the viscous correction step (18), we use the SIPG method to approximate the correction steps. Choosing the orthonormal Legendre basis and the Legendre-Gauss-Lobatto quadrature points gives a well-conditioned Vandermonde matrix and the resulting interpolation well behaved, which greatly simplifies the formulas. The $C^0$ continuity condition of the basis in the discontinuous Galerkin formulation is not required. Enforcing a weak continuity on the interior edges by a penalty term, we have for (17)

$a(p_h^{n+1}, \phi_h)=L_p(\phi_h), \ \phi\in M_h,$

where

$a(p_h^{n+1}, \phi_h)=\sum_{E_k\in\mathcal{E}_h}\int_{E_k}\nabla p_h^{n+1}\cdot\nabla\phi_h dx-\sum\limits_{e_k\in\Gamma_h}\int_{e_k}\Big\{\frac{\partial p_h^{n+1}} {\partial \mathbf{n}}\Big\}[\phi_h]ds\\ -\sum\limits_{e_k\in\Gamma_h}\int_{e_k}\Big\{\frac{\partial \phi_h}{\partial \mathbf{n}}\Big\}[p_h^{n+1}]ds +\sum\limits_{e_k\in\Gamma_h}\frac{\sigma_e}{|e_k|^{\beta}} \int_{e_k}[p_h^{n+1}][\phi_h]ds, \\ \text{and} L_p(\phi_h)=\sum_{E_k\in\mathcal{E}_h}\int_{E_k}\frac{\gamma_0}{\triangle t} \nabla\cdot\tilde{\mathbf{u}}\phi_h dx+\sum\limits_{e_k\in \partial\Omega}\int_{e_k}\phi_h G_n.$

In general, $\sigma_e$ shall be chosen sufficiently large to guarantee coercivity, more accurately, the threshold values of $\sigma_e$ in ntee coercivity, more accurat are given for $\beta = 1$ in the above formula, which is referred to an SIPG scheme. Especially, as $\beta>1$, the scheme is referred to an over-penalized scheme and the threshold values of $\sigma_e$ are presented in [20,21]. Analogously, the SIPG discretization for (18) is given by

$a(\mathbf{u}_h^{n+1}, \mathbf{v}_h)+\frac{\gamma_0}{\nu\triangle t}(\mathbf{u}_h^{n+1}, \mathbf{v}_h)_{\Omega}=L_\mathbf{u}(\mathbf{v}_h), \forall \mathbf{v}_h\in \mathbf{V}_h,$

where

$a(\mathbf{u}_h^{n+1}, \mathbf{v}_h)=\sum\limits_{E_k\in\mathcal{E}_h} \int_{E_k}\nabla \mathbf{u}_h^{n+1} : \nabla \mathbf{v}_hd\mathbf{x} -\sum\limits_{e_k\in \Gamma_h}\int_{e_k}\{\nabla \mathbf{u}_h^{n+1}\} \mathbf{n}\cdot [\mathbf{v}_h]ds\\ -\sum\limits_{e_k\in \Gamma_h}\int_{e_k}\{\nabla \mathbf{v}_h\}\mathbf{n}\cdot [\mathbf{u}_h^{n+1}]ds +\sum\limits_{e_k\in \Gamma_h}\frac{\sigma_e}{|e_k|^{\beta}}\int_{e_k}[\mathbf{u}_h^{n+1}] \cdot [\mathbf{v}_h]ds,$

and

$L_\mathbf{u}(\mathbf{v}_h)=\Big(\frac{\gamma_0}{\nu\triangle t}\tilde{\tilde{\mathbf{u}}}_h, \mathbf{v}_h\Big)_{\Omega}-\sum\limits_{e_k\in\partial\Omega} \int_{e_k}\Big(\nabla \mathbf{v}_h\cdot \mathbf{n}_e-\frac{\sigma_e}{|e_k|^{\beta}}\mathbf{v}_h\Big)\mathbf{u}_0.$

where $\beta=1.$ As a DG method, these SIPG schemes have some attractive advantages of DG methods including high order $hp\text{-}$approximation, local mass conservation, robustness and accuracy of DG methods for models with discontinuous coefficients and easy implementation on unstructured grids, while the flexibility of $p$-adaptivity (different orders of polynomialsmight be used for different elements) in DG methods has become competitive for modeling a wide range of engineering problems.

4. Numerical results

We present a lid-driven flow problem to verify the efficiency and robustness of the interior penalty discontinuous Galerkin method, and then investigate a flow past a cylinder with walls or without a wall, as well as the relationship between the Strouhal number and the Reynold number. Throughout the section, time steps $\triangle t\leq 1E-03$ are taken.

Example 1. The lid-driven boundary conditions are given by:

$u(x, 1)=1;\ u(1, y)=0;\ u(0, y)=0;\ u(x, 0)=0; \\ v(x, 1)=1;\ v(1, y)=0;\ v(0, y)=0;\ v(x, 0)=0.$

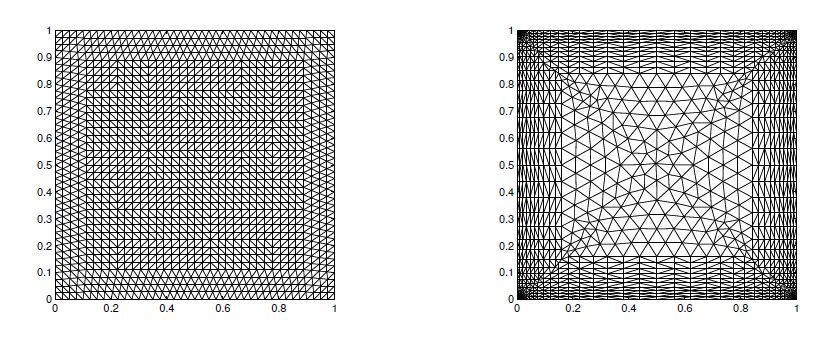
Here the mesh size of the initial coarse grid is 0.2 and then it is uniformly refined three times with piecewise discontinuous elements being applied into the fully discrete SIPG approach.

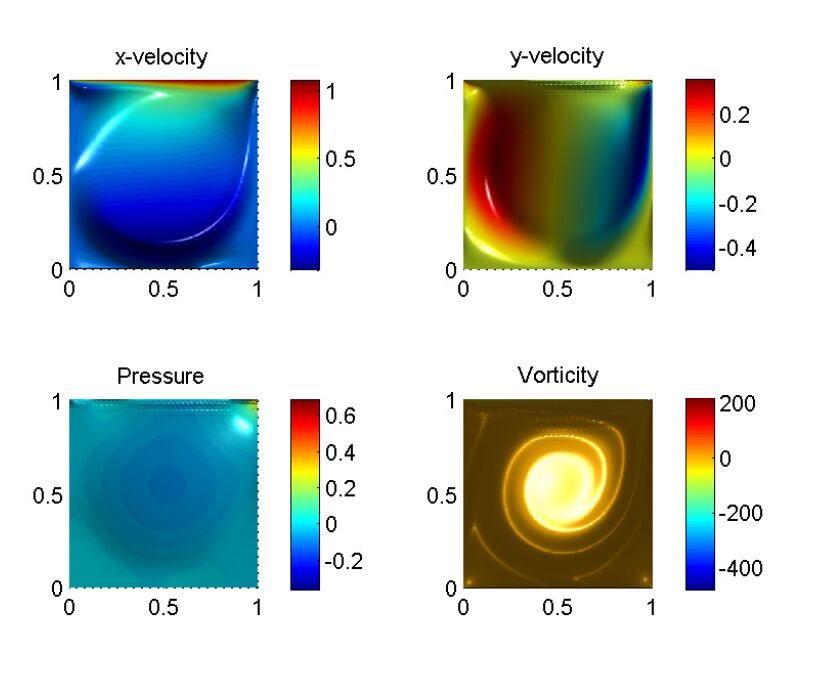
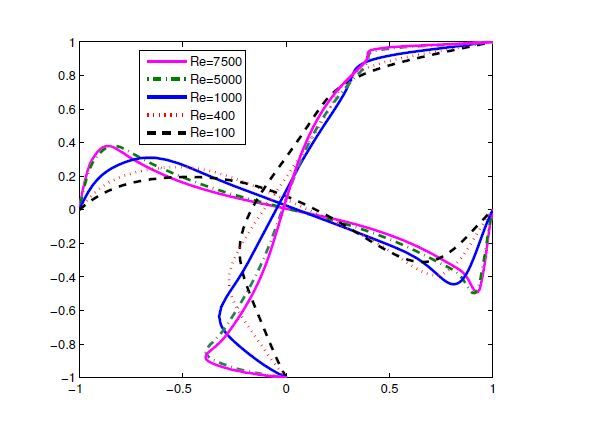
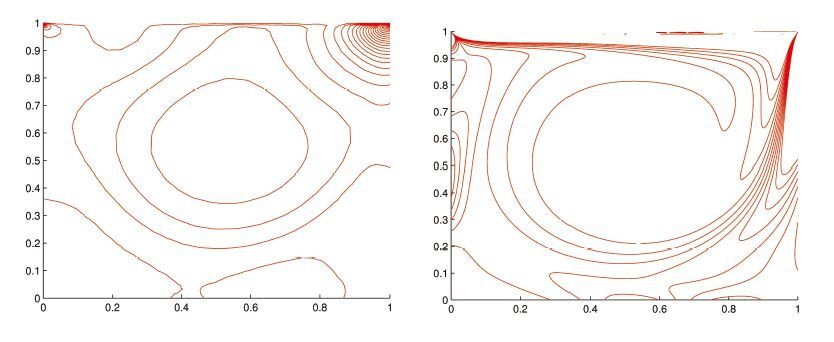
Employing the uniform mesh (see the left profile in Figure1) and approximation polynomials of order 3, we illustrate the velocity vector, pressure and vorticity profiles in Figure2, observing that the main characterization of solutions can be captured by fine meshes well, except a few very small oscillations occurred close to the upper boundary along the lid for computing velocity in $y-$direction and pressure. Oscillations on the upper lid propagates from a velocity singularity that exists at the corners. The boundary condition at the vertex is a jump from zero velocity on the edge to a unit velocity on the upper edge. Nature prevents this singularity with a boundary layer forming along all walls, making the vertex velocity zero. 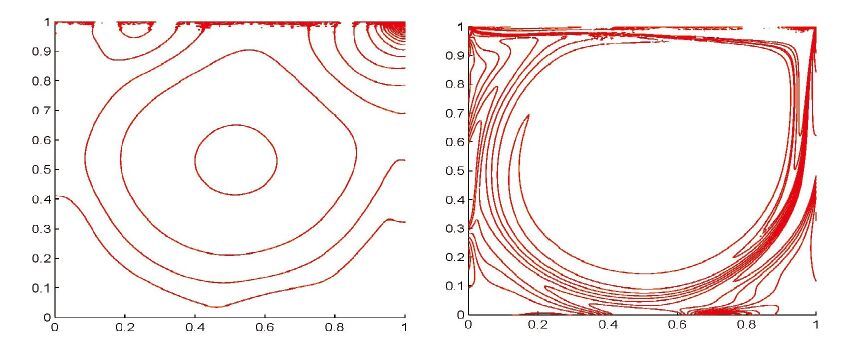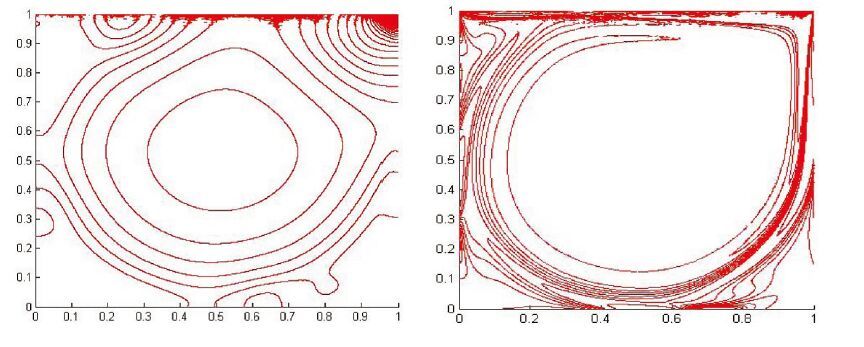It is adaptable to adopt an adaptive meshes for solving those singularity problems. Here, we apply the semi-implicit SIPG method in a locally refined mesh (see the right profile in Figure1) to solve the incompressible flow. In Figure3, the velocity profiles of $(u, v)$ through the geometric center of the cavity are plotted with $Re=100, 400, 1000, 5000, 7500$ taken. From Figures 4-8, with different Reynolds numbers taken up to 7500, the vorticity field exhibits the expected characteristics of a driven cavity flow consisting of a region of vortical flow centrally located. Energy enters the cavity through the viscous boundary later formed by velocity gradients on the upper driven edge. Convection distributes flow properties throughout the domain. Moreover, a video on the dynamical evolution of vorticity isolines ($Re=1000, N=4$) can be browsed through a website (Available from: https://youtu.be/UfGWvnoiW58). These numerical simulations are performed for the Navier-Stokes equations which illustrate the effectiveness of the DG method.

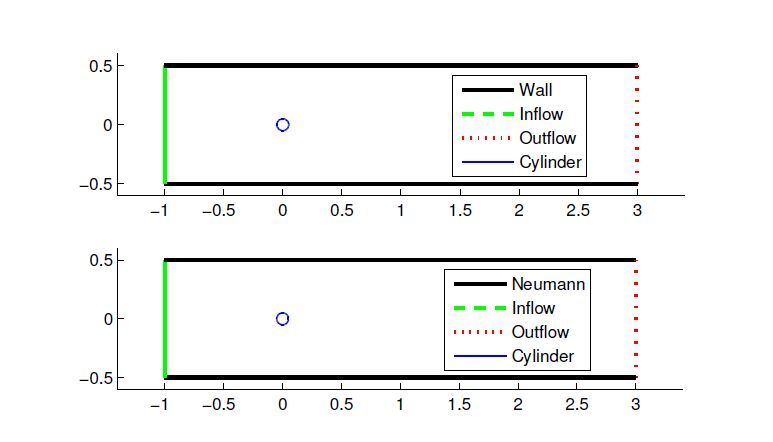
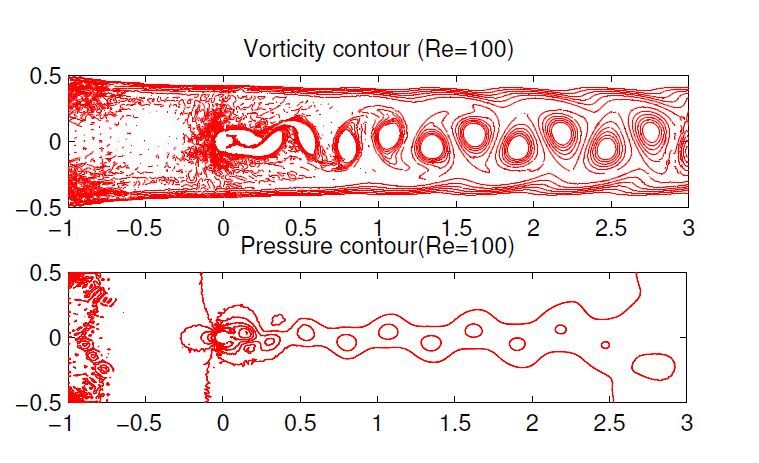
Example 2. We simulate a channel flow past a circular cylinder with a radius $0.05$ at the origin $(0, 0)$ for $Re=100$ by the discontinuous Galerkin method in the domain $(-1, 3)\times(-0.5, 0.5)$. The inflow boundary condition is $(u, v)=(1, 0)$, while the outflow boundary is $\frac{\partial\mathbf{u}}{\partial\mathbf{n}}=0$. To the boundary conditions on the upper and lower sides, we present two different conditions for comparison (see Figure9), which are wall ($u=0, v=0$) and homogeneous Neumann boundary conditions ($u=1, \frac{\partial v}{\partial \bf{n}}=0$), respectively. The homogeneous Neumann boundary condition is a special non-reflecting case, where the boundary flux is zero. For reference, the density of the fluid is given by $\rho=1 \ kg\cdot m^{-3}$ and a locally refined mesh ($\max{h}=0.088$) will be used for the simulations.

Cylinder flow contains the fundamentals of unsteady fluid dynamics in a simplified geometry. The flow properties and unsteadiness are well defined through years of experimental measurements across a wide range of Reynolds numbers [13], making the cylinder an ideal validation testcase for unsteady numerical fluid dynamics simulations.

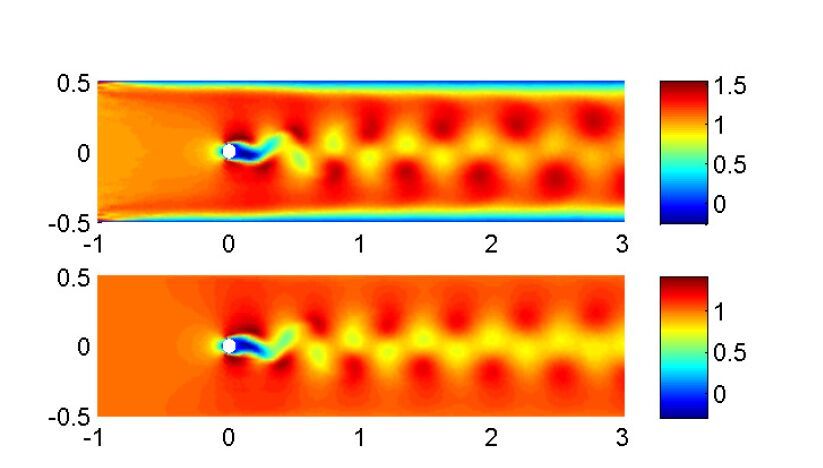
Verification in a numerical domain requires insights from physics for a proper comparison to experimental and theoretical data. In Fig.10, we observe that the boundary layers forms along the upper and lower walls. From continuity of mass, the presence of a boundary layer decreasing the flow velocity near the wall requires an increase in the centerline average flow velocity. The cylinder's wake provides a similar increase in centerline velocities. This implies a non-intuitive reality that drag can increase velocities within constrained domains. This effect is compensated for in wind tunnel test [1] environments topologically similar to Fig.10 with a constant mass flow rate and no-slip walls. Drela [3] develops an analysis for 2D wind tunnels resulting in an effective coefficient of drag of

$C_{d}=\left(1-\frac{1}{2}\frac{c}{H}C_{d}-\frac{\pi}{2}\frac{A}{H^{2}}\right)C_{d_{un}},$

and an effective Reynolds number of

$Re=\left(1+\frac{1}{4}\frac{c}{H}C_{d}+\frac{\pi}{6}\frac{A}{H^{2}}\right)Re_{un},$

where the $un$ subscript represents the uncorrected value, $H$ represents the domain height, $A$ represents the cylinder area and $c$ represents the cylinder radius. Drela's analysis does not specifically include the boundary layer forming on the upper and lower walls. The flow physics associated with wall boundary layer drag differs from cylinder drag in that the wall drag is a distributed effect of monotonically increasing drag with downstream distance rather than a conceptual point source of drag. The wall boundary layer tends to provide a steady acceleration of flow within the interior flow domain (i.e. non-boundary layer portion) leading to an effective buoyancy drag. A secondary feature of the wall boundary layer is that downstream flow features such as vortices are convected at a higher perturbation velocity compared to the initial upstream velocity. For numerical validation of raw experimental data, either the wind tunnel geometry should exactly match the numerical geometry, or the numerical geometry should be corrected using the concepts introduced above to match the actual wind tunnel geometry. Alternatively, the open-air corrected values should be used for validation. The above analysis provides insight into the domain height necessary to reduce volume blockage ($c/H$) and wake buoyancy ($A/H^2$) effects.

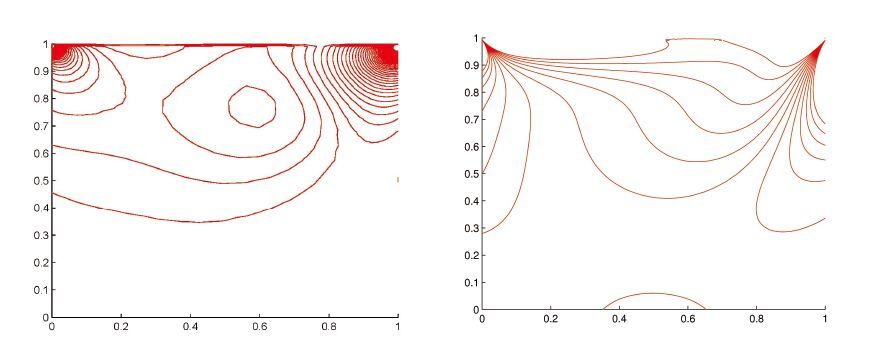
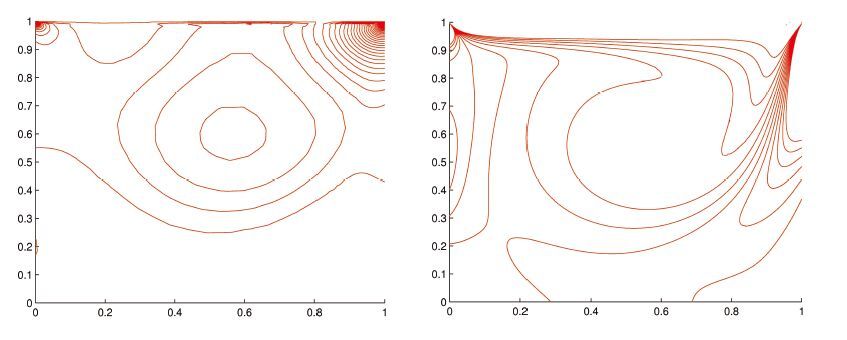
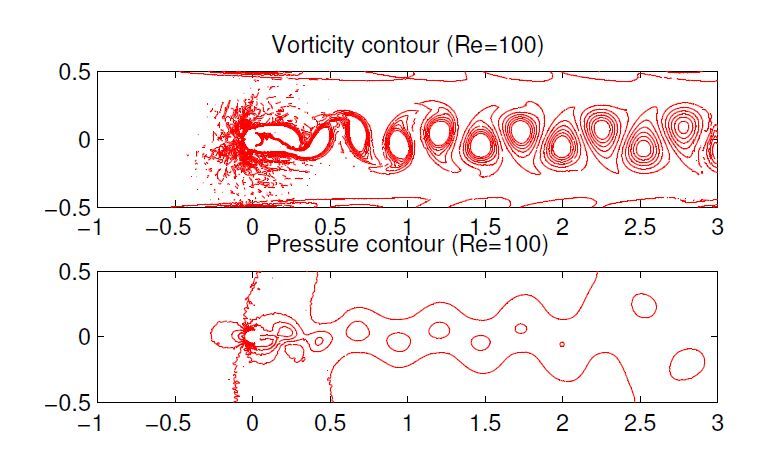
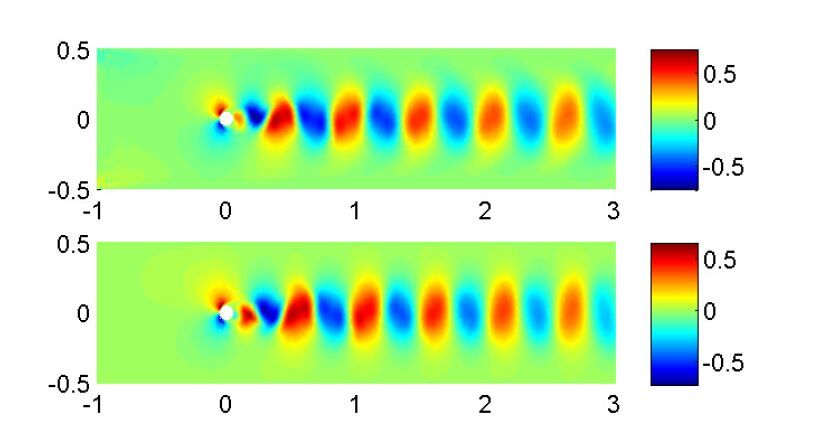
Alternatively, the flow without walls in Figure11 has no interference of the boundary layers along the channel on the up and bottom boundaries, thus the pressure contours expend after flow passing through the cylinder. We also compared the components of the velocity profiles along the x direction in Figure12, and observed that the boundary layers are produced in the top picture rather than in the bottom one. If the effect of the boundary layers disappeared, the velocity in the $x-$direction would reduce dispersively, in other words, the vortex lifespan is less than those produced in the channel with walls. The velocity profiles in the $y-$direction have been given in Figure13.

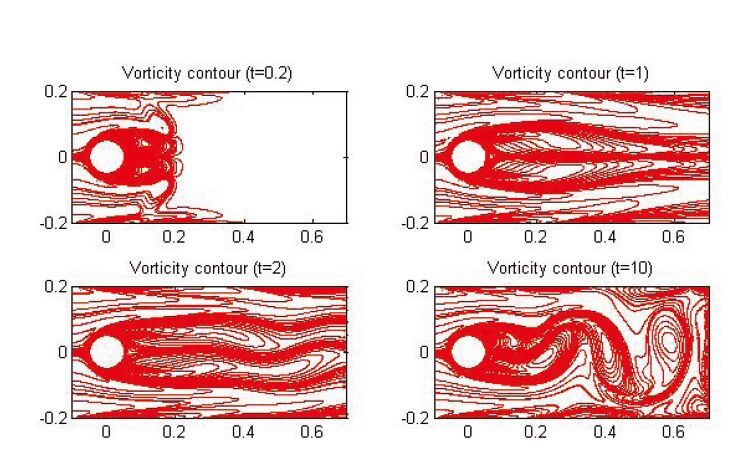
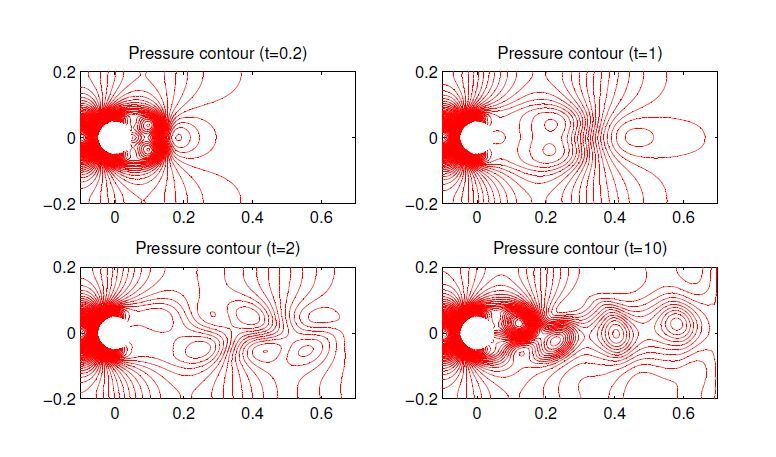
We localize the domain around the cylinder and refine the mesh, then show the vorticity startup behavior in Figure14 as well as the pressure Figure15. Upon startup, two vortices of opposite direction are formed on the upper and lower aft portion of the cylinder. Given a low total simulation time, the flow field resembles the symmetrical low Reynolds number steady flow. As time progresses however, instabilities are magnified and the upper-lower symmetry increases. Given a total time of beyond $t=10$, an autonomous and phased locked set of street vortices are generated. Surface pressures (Figure16 at $Re=80, 140$) generated reflect the process, including a steady startup portion and the eventual vortex shedding frequency. Validation at $Re>41$ requires sufficient time to obtain the unsteady behavior.

To reduce the effect of the boundary layers along the walls, the coefficients of drag and lift as well as the difference of pressure between the leading edge and the trailing edge on the cylinder shall be computed in a larger domain. Then in a domain $\Omega:=[-1, 5]\times [-1, 1]$, higher order DG finite elements have been investigated. Based on the velocity $\mathbf{u}_\infty$ and the diameter of the cylinder $D=0.1$, we will chose different viscosity coefficients $\nu=1e-3, 5e-4, 2.5e-4$ etc. to simulate flow with different Reynolds numbers, that is, the cases $Re=100, 200, 400$, respectively. Our interest is the drag coefficient $C_d$, the lift coefficient $C_l$ on the cylinder and the difference of the pressure between the front and the back of the cylinder

$d_p=p(t; -0.05, 0)-p(t; 0.05, 0).$

We use the definition of $C_d$ and $C_l$ given in [17] as follows:

$C_d=\frac{2}{\rho Du^2_{\max}}\int_{\text{S}}\Big(\rho\nu\frac{\partial \mathbf{u_{t_S}}(t)}{\partial\mathbf{n}}n_y-p(t)n_x\Big)ds, \\ \text{and} C_l=-\frac{2}{\rho Du^2_{\max}}\int_{\text{S}}\Big(\rho\nu\frac{\partial \mathbf{u_{t_S}}(t)}{\partial\mathbf{n}}n_x+p(t)n_y\Big)ds,$

where $\mathbf{n}=(n_x, n_y)^T$ is the normal vector on the cylinder boundary $S$ directing into $\Omega$, $\mathbf{t_S}=(n_y, -n_x)^T$ the tangential vector and $\mathbf{u_{t_S}}$ the tangential velocity along $S$. In the literature, Fey et al. in [6] propose the Strouhal number represented by piecewise linear relationships of the form

$St= ST^{*}+\frac{m}{\sqrt{Re}}$

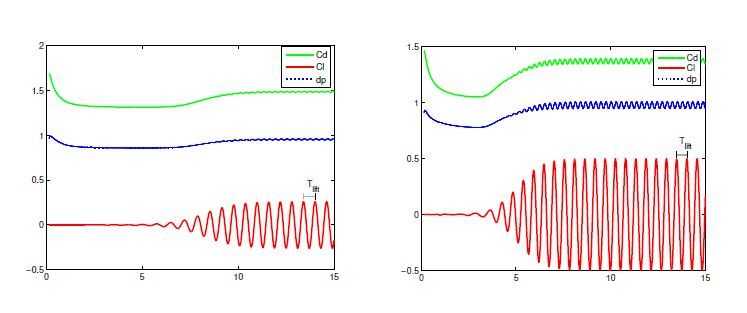
with different values $St^*$ and $m$ in different shedding regimes of the 3D circular cylinder wake. We apply the periodic $T_{lift}$ of the lift coefficients (see Figure16) to express the periodic $T:=\frac{1}{f}$ appearing in the definition of Strouhal number, i.e.,

$St(Re) = \frac{D}{{{T_{lift}}\;\;{{\bf{u}}_\infty }}}\;,$

(20)

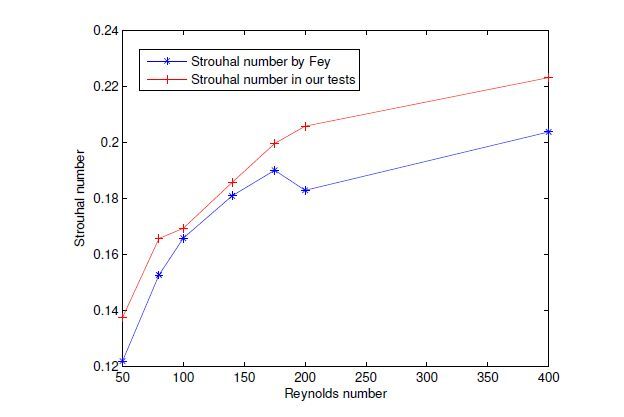
which comes from the classical definition (5). From the evolution of $C_d$, $C_l$ and $d_p$ as in Figure16, we may find a period $T_{lift}$ of the lift coefficients for different values of $Re$ to calculate Strouhal number by (20). In Figure17, a comparison of Strouhal numbers between the experimental estimates in Fey etc. [6] and our estimates from (20) indicates a behavioral match between the unsteady onset at approximately $Re=50$ and the beginning of the transition to turbulence at $Re=180$. Beyond $Re=180$, the onset of turbulence changes the flow physics by drastically increasing the energy spectrum of the shed vorticity. The transition appears as a marked decrease in the Strouhal number prior to $Re=200$. As the present SIPG solver does not include a 3D turbulence model, our estimates follow the laminar results into the actual turbulent region.

5. Conclusion

This paper developed a Symmetric Interior Penalty discontinuous Galerkin numerical solver for the incompressible Navier Stokes equations of fluid flow, with the temporal splitting technique applied in decoupling the diffusion and pressure terms and the local Lax-Friedrichs flux for the DG discretization of the nonlinear convection term. Two testcases are presented: a lid-driven cavity and a cylinder flow. The SIPG method produces stable discretizations of the convective operator for high order discretizations on unstructured meshes of simplices, as a requirement for real-world complex geometries.

Acknowledgments

The authors would like to thank the anonymous referee and editor very much for their valuable comments and suggestions, which greatly help us improve the presentation of this article. The work of the first author was partially supported by the Natural Science Foundation of Gansu Province, China (Grant 145RJZA046), and Special Program for Applied Research on Super Computation of the NSFC-Guangdong Joint Fund (the second phase).

Conflict of Interest

We declare no conflicts of interest in this paper.