1.
Introduction
Starting from the well-known Lighthill-Whitham-Richards (LWR) model [19,20], a variety of macroscopic traffic flow models based on hyperbolic balance laws have been proposed to capture traffic behaviour in different situations. In this paper, we focus on the description of traffic dynamics on road networks. More precisely, we investigate the role of coupling conditions at road junctions. To this aim, we compare the behaviour of the multilane junction model introduced in [14], and the classical LWR model at junctions [11,Chapter 5].
The multilane junction model [14] allows to handle in detail various realistic cases of road junctions, with the major exception of the diverging ones, which requires some additional information on drivers' routing preferences upstream. To avoid cumbersome notation, we recap here the main features of the multilane model in the case of a junction consisting of 2 incoming roads and 1 outgoing road, the number of lanes in each road to be specified later.
Let Mℓ=Mℓ1+Mℓ2 be the number of lanes on the half line x<0, Mℓj being the number of lanes on the j-th incoming road, j=1,2. Similarly, let Mr be the number of lanes on x>0, corresponding to the outgoing road. Each lane has maximal possible density normalized to 1, but each road may have different maximal speed. The detailed model is described in Section 3 below. Clearly, the case of a 1-to-1 junction is included, but not the 1-to-2 junction. This specific situation will be addressed separately in Section 5.
In order to draw a comparison with the LWR model on networks, we sum the vehicle densities on the various lanes, and we compare the total density profile with the solution given by the LWR model with corresponding maximal density. Notice that, in this way, we are led to consider the LWR model at a 2-to-1 junction with maximal density Mℓj on the j-th incoming road and Mr on the outgoing road. This choice is driven by the fundamental principle of conservation of the number of vehicles across the junction. The same approach is used on diverging junctions.
The numerical tests described in Sections 4 and 5 point out similarities and differences between the multilane model and its LWR counterpart. Interestingly, in the case of a 1-to-1 junction, the multilane description captures a different behaviour than those commonly described by the classical LWR approach. Merging junctions display pretty the same dynamics with both approaches, while diverging junctions show a more complex behaviour, acting as FIFO (first-in-first-out) when one outgoing road is fully congested, and as non-FIFO otherwise. Further assessment on the validity of the models necessitate the comparison with suitable real data.
2.
LWR on n-to-m junctions
Macroscopic traffic flow models on networks have been introduced in the mathematical literature since more than two decades [4,15], see also [9,11] for a detailed overview. We recall here the LWR model on n to m junctions, that is on junctions with n incoming roads and m outgoing roads.
A road network is modelled by a finite collection of edges and vertices, representing respectively unidirectional roads and junctions. On each edge I, and thus on each road, traffic flow is described through the Lighthill-Whitham-Richards (LWR) model: the density of vehicles ρ(t,x) satisfies
where fI is assumed to be strictly concave and of class C2, such that f(0)=f(RI)=0, RI being the maximal possible density on road I. In particular, we may choose
where VI is the maximal speed on road I. Note that, with this particular choice of flux, fI attains its unique maximum at θI=RI/2. At network junctions, the conservation of the number of vehicles has to be ensured and, moreover, the usual choice is to maximise the flux through the junction. We introduce therefore the demand and supply functions (see for instance [13]) and express the flux at the junction through an ad hoc minimisation between the two:
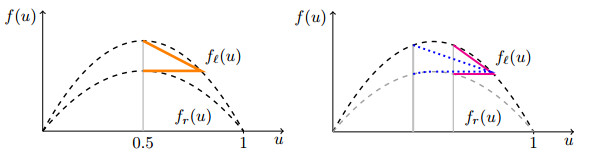
The demand and supply functions introduced above are displayed in Figure 1.
Notice that, as in [13], the flux function fI, as well as the corresponding demand and supply functions, may depend also on time, if traffic regulations are applied.
At each junction, the model includes also of the preferences of the drivers, which are prescribed and known a priori. These preferences describe the distribution of traffic from incoming to outgoing roads and are expressed as elements of a matrix A, called traffic distribution matrix: for a vertex J with n incoming edges I1,…,In and m outgoing edges In+1,…,In+m, the matrix A is given as follows
In other words, each element aj,i of the matrix A gives the percentage of traffic from road Ii going into road Ij at the junction.
In view of the examples considered in this paper, we focus on the cases of one-to-one junctions (modeling speed limit or lane number changes), two-to-one (merging) junctions and one-to-two (diverging) junctions, see Figure 2. In the case of merging junctions, where the number of incoming roads is greater than the number of outgoing roads, it is necessary to introduce a priority parameter for each incoming road to single out a unique solution. In particular, for two-to-one junctions, the two incoming roads are characterised by the priority parameters P and (1−P), with P∈]0,1[.
2.1. 1-to-1 junction
Consider a one-to-one junction and call I1, I2 respectively the incoming and outgoing road. Denote by ρi the density of vehicles in road Ii, i=1,2. Observe that the LWR model (1) on this particular junction is equivalent to a Cauchy problem for a conservation law with discontinuous flux (see, for instance, [16,Chapter 8] for a brief introduction to the topic):
with
H being the Heaviside function. The functions vℓ and vr are strictly decreasing, positive and such that vd(Rd)=0 for d=ℓ,r. One admissible choice is
for a suitable positive constant Vd, leading to the flux function (2).
Concerning the initial datum ρo, it satisfies the following constraints:
Hyperbolic conservation laws with discontinuous flux such as (4) arise in the modelling of several phenomena, such as, for instance, two phase flow in heterogeneous media and traffic flow with rough road conditions. Among the rich literature on the subject, we refer the interested reader to [2,3,7,18,23] and the references therein.
The main issue when dealing with conservation laws with discontinuous flux function is the lack of a unique solution, since the classical theory by Kružkov does not apply. Clearly, Kružkov entropy conditions are valid away from the point(s) of discontinuity of the flux, but they are not enough to provide the uniqueness of solution. With the aim of proving the well-posedness of the problem, various notions of solutions have been introduced in the literature, based of different admissibility conditions. We recall for example the minimal variation criterion introduced by Gimse and Risebro [12] and the Γ-condition described by Diehl [6]. We refer to [3] for a more complete overview.
In the present study, we will focus on the solutions given by the supply-demand flux maximizing criterion classically used in traffic flow modeling (satisfying the entropy criterion of [1]) and by the vanishing viscosity limit [7].
2.2. 2-to-1 junction
In the case of merging junctions, a priority parameter has to be assigned to each incoming road, see [11,Section 5.2.2]. Therefore, in the specific situation of a two-to-one junction, the two incoming roads have priority P and 1−P respectively, with P∈]0,1[. The idea is that, in general, not all vehicles can pass at the junction: denoting by γ the amount of vehicles that can enter the outgoing road in the supply-limited case, Pγ vehicles comes from the first incoming road, and (1−P)γ cars from the second incoming road.
Clearly, since there is only one outgoing road, the traffic distribution matrix A reduces to the two-dimensional vector (1,1).
The initial datum satisfies the following constraints:
Following [13], denoting by ρℓi and ˆγℓi the density and the flux on the incoming roads (i=1,2) and by ρr, ˆγr the density and the flux on the outgoing one, for P∈]0,1[ the fluxes at the junctions are defined as
2.3. 1-to-2 junction
The one-to-two junction is a particular diverging junction, see [11,Section 5.2.1] for more details. (Since there is only one incoming road, there is no need to prescribe a right of way.) In this case, the traffic distribution matrix A is given by:
In [11] a FIFO (first-in-first-out) rule is applied at the junction. In terms of the demand and supply functions (3), the FIFO rule amounts to the following: denoting by ρℓ the density on the incoming road, by ρr1 and ρr2 the densities on the outgoing roads, by γℓ,γr1 and γr2 the fluxes on the incoming and outgoing roads respectively, we have
As a consequence, if one of the outgoing roads is fully congested (i.e. min{Sr1(ρr1), Sr2(ρr2)}=0), the vehicles are stuck at the junction (γℓ=γr1=γr2=0), even if some of them could proceed in the other outgoing road. In order to overcome this problem, non-FIFO models have been developed, see for instance [13]. Non-FIFO model allows some flow through the junction even if one of the outgoing road is fully congested. Using the same notation as before, the non-FIFO rule reads as follows, in terms of the demand and supply functions (3):
In the case of a diverging junction, the initial datum satisfies the following constraints:
3.
A multilane model for n-to-1 junctions (n=1,2)
We recall the main features of the multilane junction model introduced in [14], based on the multilane traffic flow model proposed in [17]. The model provides a description of traffic on road networks with several lanes, allowing for lane changes and overtaking, as well as change in the speed laws and in the number of lanes along the road. In particular, Mℓ⊂N+ represents the set of indexes of the active lanes on ]−∞,0[, with cardinality Mℓ=|Mℓ|≥1; on the other hand, Mr⊂N+ is the set of indexes of the active lanes on ]0,+∞[, with cardinality Mr=|Mr|≥1. We let M≥max{Mℓ,Mr}, its choice depending on the specific situation considered, and we assume, for technical needs, that there are M−Mℓ and M−Mr additional phantom lanes on ]−∞,0[ and ]0,+∞[ respectively. We add moreover a condition (see (19) below), which prevents vehicles from passing from the active to the fictive lanes.
The model reads then as follows: for x∈R and t>0, the vehicle density on lane j, ρj=ρj(t,x), solves the Cauchy problem
with, for j=1,…,M,
H being the Heaviside function. The velocities vd,j, for d=ℓ,r and j=1,…,M, are strictly decreasing positive functions such that vd,j(1)=0. We assume that each map fd,j(u)=uvd,j(u) admits a unique global maximum attained at u=θjd.
We set ρo,j:R→[0,1] for j=1,…,M and
The source terms, which account for the flow rates across lanes, are defined as in [17]:
for d=ℓ,r and j=1,…,M−1, where (a)+=max{a,0} and a−=−min{a,0} and K is a dimensional constant (1/m), which can be assumed equal to 1 after rescaling space and time. To account for separate lanes, such as different roads or fictive lanes, we set
The functions appearing in the source term of (12) are then defined as follows
For the sake of brevity, we introduce the notation ρ=(ρ1,…,ρM), so that the initial data associated to problem (12)–(16)–(17) read ρ(0,x)=ρo(x).
For simplicity, and with slight abuse of notation, we consider ρ=ρ(t,x) for t>0, x∈R. However, as shown in [14], by (16), (17) and (19), there holds ρj(t,x)=0 for all t>0, x∈]−∞,0[ and j∉Mℓ, respectively ρj(t,x)=1 for all t>0, x∈]0,+∞[ and j∉Mr.
In order to compare the multilane model to the LWR model at junctions, we make the following choices. In all the numerical experiments, for the multilane model we choose
with VI>0. Therefore, the maximal speed is the same for all lanes before, respectively after, x=0. This corresponds to the following velocity for the LWR model:
where MI is the cardinality of the active lanes.
Through our numerical integrations, we show that the outcome may be different when not considering the number of lanes involved.
4.
Comparison study
We compare now numerically the solution given by the multilane n-to-1 model with the corresponding LWR solutions. We first describe the numerical schemes used to compute approximate solutions of the considered models. Then we report on some numerical tests, which illustrates the behaviour of solutions in different cases.
4.1. Numerical schemes
We provide in this section the details on the numerical schemes used throughout the paper.
We introduce a uniform mesh in space, of width Δx, and a time step Δt, subject to a suitable CFL condition. For k∈Z set
where xk is the centre of the cell and xk±1/2 its interfaces. Notice that nonnegative integers denote the cells on the positive part of the x-axis. Set λ=Δt/Δx. For the multilane model, we approximate the initial data as follows: for j=1,…,M
recalling that (16) and (17) hold. The approximated initial data for the LWR model is given consequently as the sum of the initial data on various lanes, depending on the configuration under consideration:
● 1-to-1 junction (Section 4.2): the initial data for the LWR model is merely given by the sum, thus
● 2-to-1 junction (Section 4.3): for the merging junction, there are two incoming and one outgoing roads:
● 1-to-2 junction (Section 5): for the diverging junction, there are one incoming and two outgoing roads:
The solution to the multilane model (12)–(16)–(17)–(19) is obtained through a Godunov type scheme, with fractional step to take into account the source terms, see [14,Algorithm 2.1]:
where
with
Dj,d and Sj,d, d=ℓ,r, defined as in (3).
The LWR model is numerically integrated through a Godunov type scheme, which provides the solution to the Cauchy problem (1) that maximises the flux through the junction:
● 1-to-1 junction (Section 4.2):
with F defined as in (23), omitting index j.
In Section 4.2, we apply also a different strategy for the numerical integration of the LWR model: we make use of an upwind scheme, which provides the solution to the Cauchy problem (1) coming from the vanishing viscosity approach. The numerical scheme reads as in (24), where the numerical flux is now chosen as F(x,u,w)=uv(x,w).
● 2-to-1 junction (Section 4.3): we follow [13] so that, exploiting the notation introduced in (9), setting ˆγni=ˆγi(ρnℓ1,−1,ρnℓ2,−1,ρnr,0) for i=ℓ1,ℓ2,r, we have
● 1-to-2 junction (Section 5): as already recalled in Section 2.3, we use two different schemes, satisfying different rules at the junction.
FIFOrule: we follow [11], and exploit the notation already introduced in (10), with γni=γi(ρnℓ,−1,ρnr1,0,ρnr2,0) for i=ℓ,r1,r2.
Non−FIFOrule: we follow [13] and exploit the notation already introduced in (11), with γni=γi(ρnℓ,−1,ρnr1,0,ρnr2,0) for i=ℓ,r1,r2.
For both rules, the scheme amounts to the following:
with the above choices of γni, i=ℓ,r1,r2.
4.2. 1-to-1 junction: From 2 to 3 lanes
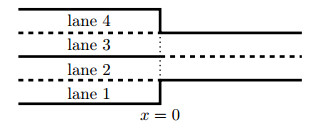
We consider the case of a junction with one incoming road with 2 lanes and one outgoing road with 3 lanes, see Figure 3. For the multilane model, this corresponds to problem (12)–(16)–(19) with Mℓ={1,2}, Mr={1,2,3} and Sℓ,2(u,w)=0. For the LWR model, this is a 1-to-1 junction with maximal density on ]−∞,0[ equal to Mℓ=2, while on ]0,+∞[ it is Mr=3.
Case 1. We choose Vℓ=1.5, Vr=1. The initial datum for the multilane model is
while the initial datum for the LWR model is given by the sum of the above functions, thus
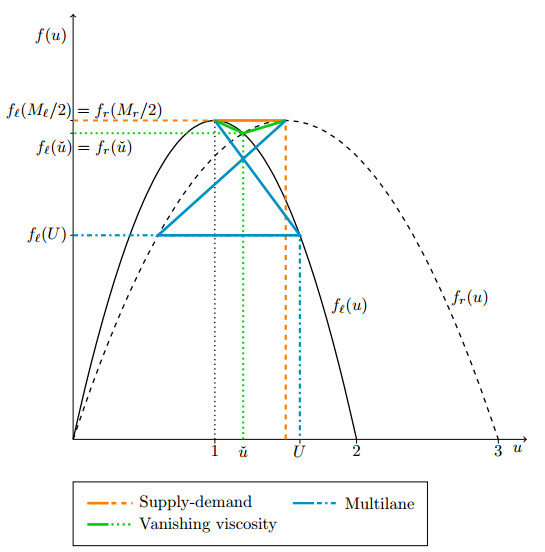
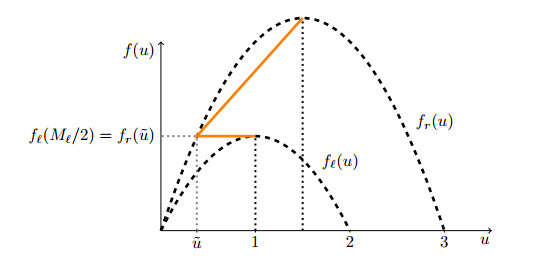
corresponding to the critical densities of the flux functions fℓ and fr respectively, see Figure 4, i.e. the points where the flux functions attain their unique global maximum.
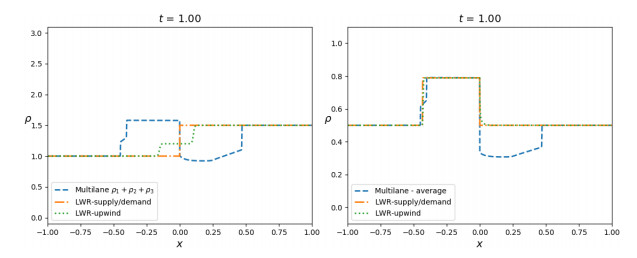
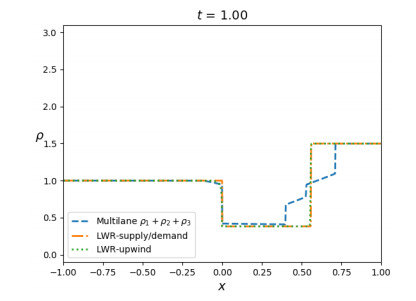
Figure 5, left, displays the solutions of the considered models at time t=1: in particular, it allows to compare the multilane model, namely the sum of the densities on the various lanes, to the LWR model. For the latter, there are many admissible solutions: indeed, depending on the physics of the problem, the solution may be different, see [3] and references therein for a thorough discussion on the choice of the "right" solution and on the physical models behind. In particular, the solutions obtained through the Godunov type scheme and through the upwind scheme are different. The former, obtained via the Godunov type scheme and thus through an ad hoc minimisation between the demand and supply function, is the solution that maximises the flux at x=0, i.e. at the point of discontinuity of the flux: the solution connects fℓ(Ml/2) and fr(Mr/2), see also Figure 4. On the other hand, the intermediate value attained around x=0 by the solution coming from the upwind scheme corresponds to the point ˇu in Figure 4: this point is such that fℓ(ˇu)=fr(ˇu). When higher order effects are taken into account for choosing the "right" solution, the choice of the vanishing viscosity approximation leads to this particular solution.
Concerning the solution of the multilane model, the low value of the sum of the densities right downstream x=0 is due to the fact that, before x=0, the third lane does not exist. Thus, even though vehicles pass from the second to the third lane, the solution in the third lane is given by a shock with positive speed. On the other hand, the queue right upstream x=0 is caused by the congestion of lanes 1 and 2, since after x=0 the maximal speed decreases. Moreover, notice that the solution of the multilane model maximises the flux on each lane at the junction, see also Figure 6, right.
We make a second comparison between the LWR and the multilane model, namely we take the latter in the form of the average of the densities on the various lanes. In this way, the maximal density for the LWR model equals 1 everywhere. The initial datum is therefore given by the average of (25):
which corresponds to the critical density of the flux function on both incoming and outgoing lanes. Figure 5, right, displays the solutions at time t=1. We notice how the solutions resemble each other on the incoming lane: the queue upstream x=0 is well captured by all models. On the other hand, also in this case the behaviour of the multilane model on the outgoing lane strongly differs from the LWR model, for which in this case the supply-demand and the vanishing viscosity solutions coincide.
Recall that, by [14,Lemma 2.3], the multilane model (12)–(16)–(19) preserves the total number of vehicles over time. This property is clearly valid when considering the multilane model in the form of the sum of densities on the various lanes. However, this second type of comparison considering the average of the densities on the various lanes implies that the total number of vehicles is not conserved anymore through the junction: indeed, the total mass is divided by the number of lanes, which is equal to 2 upstream x=0 and 3 downstream.
Case 2. We choose now Vℓ=1 and Vr=1.5 and the same initial data of Case 1. The flux functions for the LWR model are displayed in Figure 7. In this case, the solution obtained with the Godunov type scheme is identical to that obtained through the upwind method, see Figure 8. Notice that the stationary shock at x=0 is slightly smoothed out when using the upwind scheme, due to numerical viscosity. The small slope right before x=0 in the sum of the solutions to the multilane model is caused by the higher flux of vehicles in lane 2 through x=0, since right after x=0 the speed is higher and vehicles can pass also in lane 3.
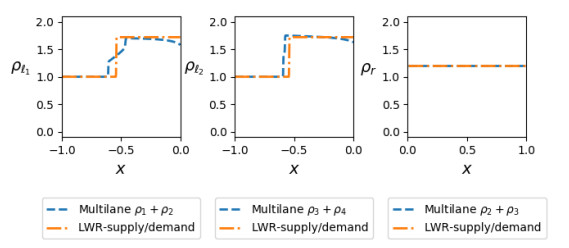
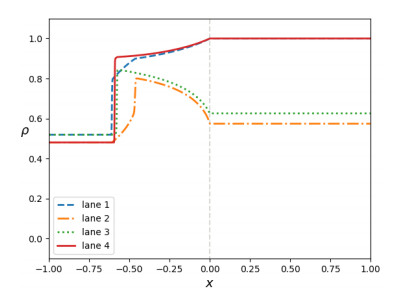
4.3. 2-to-1 junction: From 2+2 to 2 lanes
We consider the case of a junction consisting of two incoming roads with 2 lanes each and one outgoing road with 2 lanes, that is problem (12)–(17)–(19), with Mℓ={1,2,3,4}, Mr={2,3} and initial data
with the additional assumption that there is no flow of vehicles between the second and the third lane on ]−∞,0[, i.e. Sℓ,2(u,w)=0 (we also impose Sr,1(u,w)=Sr,3(u,w)=0). The situation under consideration is depicted in Figure 9. Concerning the LWR model, we denote by ℓ1 and ℓ2 the two incoming roads, and by r the outgoing one. Then, the initial data for problem (1) corresponding to (26) read as follows:
since road ℓ1 is given by lanes 1 and 2 for x∈]−∞,0[, road ℓ2 is given by lanes 3 and 4 for x∈]−∞,0[ and road r is given by lanes 2 and 3 for x∈]0,+∞[. Moreover, we prescribe the priority P=1−P=1/2 on each incoming road. Observe that the maximal density on each road is equal to 2.
Figure 10 displays the solution on each road at time t=1: in each picture we can see both the LWR model and the multilane model, in the form of the sum of the densities on the involved lanes. Notice the asymmetric behaviour of the multilane model: this is due to the asymmetry of the initial data (26) with respect to the lanes that are left after the junction. Indeed, the initial datum in lane 2 has a lower value than in lane 1, while the opposite is true for lane 3 with respect to lane 4. In the former case, this implies that more vehicles have to pass form lane 1 to lane 2 in order to go through the junction, causing the formation of a longer queue, which become visible when summing the two densities, see Figure 10. Figure 11 provides a detail of the multilane model at the same time t=1, allowing a better insight on the queue formation.
5.
A multilane model for a diverge
In this section, we aim to compare the LWR model on a one-to-two (diverging) junction with a multilane model different from the one considered in Section 3. Indeed, we need to account for the drivers' routing preferences upstream, a feature that is not included in the multilane model (12)–(18).
The specific multilane junction is displayed in Figure 12: there are one incoming road with two lanes and two outgoing roads, with one lane each. The core idea is to consider a multi-population model [5,10], where each population is identified by its desired final destination. In the particular case under consideration, we have two populations, which coexist upstream x=0. We assume that, in each lane of the incoming road, a fraction α of the drivers belong to the first population, i.e. wants to go in lane 1 downstream x=0, while the rest is directed towards lane 2. Overtaking is possible only upstream x=0, and, differently from the multilane model considered in Section 3, only vehicles in lane 1 (respectively lane 2) targeting lane 2 (respectively lane 1) change lane. The rate of vehicles changing lane depends on the total density in the target lane: the more the target lane is crowded, the less vehicles are allowed to move into that lane. Moreover, the desire to go in the target lane increases as drivers approach the junction (x=0). Since we focus on the dynamics at the junction, we do not consider the classical overtaking dynamics, which can occur before x=0. This could be added in the source term with minor changes in the overall approach.
Our multilane multi-population model is the following: given the initial data ρo,1 and ρo,2 on R, the initial data on x<0 read
where ρio,j, for i,j∈{1,2}, denotes the amount of drivers in lane j targeting lane i. Setting ρ1=ρ11+ρ21 and ρ2=ρ12+ρ22, the densities ρij, i,j=1,2, satisfy the following system:
where K is a dimensional constant (m/s), which can be assumed equal to 1 after rescaling space and time. In the source terms, the factor |x|−1 represents the increase of the urgency to change lane as the junction approaches.
We observe that a close model which describes traffic on a multilane highway under the hypotheses that traffic is neither perfectly FIFO nor perfectly non-FIFO has been introduced in [22]. Here, we compare the multilane multi-population model (29) to the LWR model for a diverging junction, both in the case of a FIFO rule and of a non-FIFO rule at the junction, see Section 2.3. The incoming roads are paired together, and denoted by the subscript ℓ, while the two distinct outgoing roads are denoted by subscripts r1 and r2 respectively. The initial data for problem (1) is related to the initial data ρo,1,ρo,2 for the multilane multi-population model as follows:
5.1. Numerical scheme
We detail here the numerical scheme exploited for the integration of the multilane multi-population model (29). The scheme is inspired by that presented in [8,21], and the source terms are treated through fractional step.
The space and time mesh are defined as in Section 4.1. The initial data on each lane, ρo,1 and ρo,2, are approximated by ρ01,k and ρ02,k, for k∈Z, as in (22), then distinguished on the negative part of the x-axis according to their target lane: for k≤−1
The solution to the multilane multi-population model (29) is obtained through a Godunov type scheme, with fractional step to account for the source terms. In particular, set ρnj,k=ρ1,nj,k+ρ2,nj,k and introduce the quantity γnj=min{ˆDj(ρj,nj,−1,ρi,nj,−1), Sj(ρnj,0)}, for j=1,2, i=3−j, with Sj as in (3) and ˆDj defined as let θj(w) the point of maximum of the function u↦uvj(u+w), then
Then, for i,j=1,2, we set
with F(u,w)=min{ˆDj(u),Sj(w)}. Concerning the contribution of the source terms, define
so that
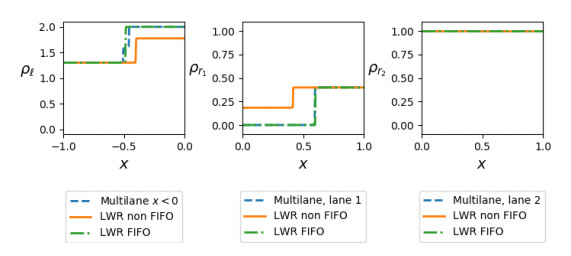
5.2. Example 1: Fully congested outgoing road
The first example we take into account considers a fully congested outgoing road. We choose α=0.4, the maximal speed on the incoming road is Vℓ=1.5 and on both outgoing roads it is Vr=2. The initial data for the multilane multi-population model (29) are
and through (30) we recover the initial data for the corresponding LWR model (1).
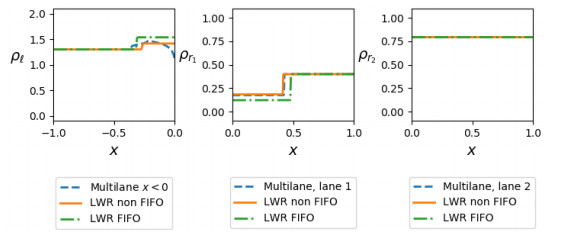
Figure 13 displays the solution on each road at time t=0.5: in each picture we see the LWR model with both FIFO and non-FIFO rule and the multilane multi-population model, in the form of the sum of the densities for x<0. Lane 2 is initially fully congested: no vehicles can enter, and the solution on that lane is clearly the same with all the three models. In this situation, the solution of the multilane multi-population model looks very close to that of the LWR model with FIFO rule. Indeed, non-FIFO rule allows vehicles targeting lane 1 to overcome the junction: they are not queuing waiting for their turn to pass the junction.
5.3. Example 2
In this second example, none of the outgoing lane is fully congested. We keep the same parameters as before, thus α=0.4, Vℓ=1.5, Vr=2. The initial data for the multilane multi-population model (29) are
which differ from (31) only in the density on the second road downstream x=0. Through (30) we recover the initial data for the LWR model (1).
Figure 14 displays the solution on each road at time t=0.5: in each picture we see the LWR model with both FIFO and non-FIFO rule and the multilane multi-population model, in the form of the sum of the densities for x<0. Even though lane 2 is not fully congested downstream x=0, all the three models produce the same solution there. However, on the outgoing road corresponding to lane 1 the solution to the multilane multi-population model (29) is very close to the solution to the LWR model (1) with non-FIFO rule. In the incoming roads, the similarity is reduced, but nevertheless the solution to the LWR model with FIFO rule looks much different than the others, since it reaches a greater value upstream x=0.
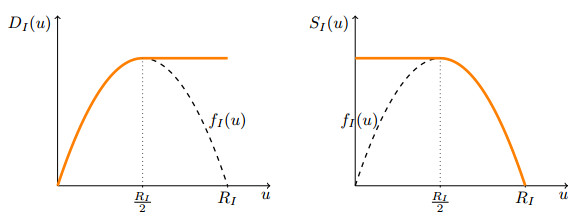









 DownLoad:
DownLoad: