1.
Introduction
We are interested in the quantum Schrödinger-Lohe model
Here $ \psi_i $ $ (i = 1, \, 2, \cdots, N) $ are complex valued functions defined on $ \Bbb{R}^d \times \Bbb{R}^+ $ satisfying $ \| \psi(\cdot, t)\|_{L^2(\Bbb{R}^d)} = 1 $ and $ V = V(x) $ is the real-valued one-body potential. We refer to section 2 for more precise assumptions on $ V $. The standard $ L^2 $ inner product is defined by $ \langle f, g \rangle (t) = \int_{\Bbb{R}^d} f(x, t) \, \bar{g} (x, t) \, dx $ and $ K $ is positive constant representing coupling strength. The Schrödinger-Lohe model (1) was first introduced in [10] as an infinite state generalization of the Lohe matrix model [11].
Quantum synchronization has received much attention from the physics community because of its possible applications in quantum computing and quantum information. The synchronous behaviors of (1) were partially treated in [5,6,7] for some restricted class of initial data and a large coupling strength regime. In particular, dynamical system approach to synchronization of the Schrödinger-Lohe model has been studied in [1,7,8]. Actually, they set
and showed that $ h_{ij} $ satisfies the system of ODEs:
with the initial data $ h_{ij}^0 : = h_{ij}(0) = \int_{\Bbb{R}^d} (\psi_i^0 \bar{\psi}_j^0)(x) \, dx $.
The system (1) admits a unique global solution $ \psi_i $ which was proved in [1,7]. We refer to section 2 for more precise results on the existence and uniqueness of a solution. From now on, we consider the solution of the system (1) with regularity
where $ m> 2+ \frac{d}{2}. $
Let us consider equations
Note that $ \phi_i $ has the same initial data as $ \psi_i $ in (1). Let us denote $ \psi = (\psi_1, \psi_2, \cdots, \psi_N)^t $ and $ \phi = (\phi_1, \phi_2, \cdots, \phi_N)^t $. Our first result is to transform (1) into the decoupled linear Schrödinger equations.
Theorem 1.1. The solution $ \psi_i $ of (1) is given by
Here $ \phi $ is a solution of (4) and $ Y $ is the principal fundamental matrix solution of the ODE system
where
and $ h_{ij} $ are solutions to (3). Note that $ Y(0) $ is an $ N\times N $ identity matrix.
The novelty of this result is that the coupled nonlinear PDEs in (1) are transformed into the decoupled linear Schrödinger equations (4) through the relation (5). The nonlinearity of (1) is hidden from view and appears in the coupled nonlinear ODEs (3). This observation can be used to study asymptotic behavior and the nonlinear stability problem for the Schrödinger Lohe model. We studied in [9] the stability of standing wave solutions for the Schrödinger Lohe model with a harmonic potential $ V = |x|^2 $. We will present another application of Theorem 1.1 in Theorem 1.2.
Taking Theorem 1.1 into account, analysis of the principal fundamental matrix $ Y $ is crucial for understanding the dynamics of the solution to (1). In section 4, we consider the case of $ h_{ij}(t) \to 1 $ exponentially as $ t\to \infty $. Then we have
which is complete synchronization. To state the next Theorem, we define
and
The following result is concerned with the boundedness of $ Y $ for the case of complete synchronization.
Theorem 1.2. Let $ \psi_i $ be the solution of (1) with the initial data satisfying $ \tilde{r}_j(0)>0 $ or $ \mathcal{H}(0)<N $. Then the principal fundamental matrix $ Y $ of
is bounded. Here $ H(t) $ is given by (6).
Remark 1. As an application of Theorem $ 1.2 $, we consider the solution $ \psi_i $ to (1) with $ V = 0 $. Then we have, for the initial data satisfying $ \tilde{r}_j(0)>0 $ or $ \mathcal{H}(0)<N $,
which is derived from the boundedness of $ Y $ and decay estimate $ | \phi_i(x, \, t) | \leq C t^{-d/2} $.
Consider linear differential equation
where $ A(t) $ is $ N \times N $ matrix. In the general case there is no closed form solution $ y $ and an approximation method such as Magnus expansion [3,4,12] has been used. In section 5, we calculate some explicit principal fundamental matrices for special cases.
The rest of this paper is organized as follows. In section 2, we briefly review the basic properties of the Schrödinger Lohe model. In section 3, we prove Theorem 1.1 and present basic properties of the principal fundamental matrix $ Y(t) $. In section 4, Theorem 1.2 is proved. In section 5, we study cases where the principal fundamental matrices can be derived explicitly.
2.
Preliminaries
Let $ V(x) $ be a given smooth real-valued potential function satisfying
Global existence of classical solution to the equation (1) satisfying the condition (7) was proved in [1,7].
Theorem 2.1. Let initial data $ \psi_i^0 \in H^m(\Bbb{R}^d) $ for $ m = 1, \, 2, \cdots $. Then, for any $ T \in (0, \infty) $, the Cauchy problem for (1) has a unique global solution $ \psi_i $ such that
By Sobolev embedding theorem, it is easy to see that for $ m > 2 + \frac{d}{2} $, $ H^m $ solution is a classical solution. We consider initial data $ \psi^0_i \in H^m(\Bbb{R}^d) $ satisfying $ \|\psi_i^0 \|_{L^2(\Bbb{R}^d)} = 1 $. Then the $ L^2 $ norm of $ \psi_i $ is constant along the evolution:
This can be seen as follows. Multiplying (1) by $ \bar{\psi_i} $, taking the imaginary part and integrating by parts, we obtain
which is an ordinary differential equation for $ \|\psi_i \|_{L^2}^2-1 $. Since we have $ \|\psi_i^0 \|_{L^2}^2-1 = 0 $, the uniqueness of solution to ODE says that $ \|\psi_i(t) \|_{L^2}^2 = 1 $.
Considering, for two wave functions $ \psi_i $ and $ \psi_j $ with unit $ L^2 $ norms, that
it is important to study the evolution of $ h_{ij} $ for the behaviors of $ d_{ij} $. The dynamics of $ h_{ij} $ obeys the following ODEs which was proved in [7].
Proposition 1. Let $ \psi_i $ be a solution to (1). Then $ h_{ij} $ satisfies the coupled system of ODEs:
Taking (2) into account, we have
The initial data should be restricted in the following admissible set
We can check that $ (1, \, 1, \, 1)\in \mathcal{A}_3 $ and $ (-1, \, -1, \, -1) \notin \mathcal{A}_3 $.
3.
Proof of Theorem 1.1
In this section, we prove Theorem 1.1 and present basic properties of principal fundamental matrix $ {\mathrm Y} $.
Proof. The system (1) can be rewritten as
where $ N\times N $ matrix $ H $ is given by (6). Note that $ H $ is a matrix of variable $ t $. Let $ Y $ be the principal fundamental matrix solution of the ODE system
Denoting $ \psi(x, t) = Y(t) \phi(x, t) $, we have
Since the principal fundamental matrix $ {\mathrm Y} $ is non-singular and $ Y(0) $ is an identity matrix, we have
This leads to the proof of Theorem 1.1.
Remark 2. We can derive the ODEs (9) in another way. Let us consider
where $ u $ is a vector. Multiplying (1) by $ \bar{u} $ and (10) by $ \bar{\psi}_i $, we have
Then $ \int_{\Bbb{R}^d} ( (11)- \overline{(12)} ) dx $ leads to
Integrating by parts gives us
Denoting $ y_j = \int_{\Bbb{R}^d} \psi_j \bar{u} \, dx $ and considering $ y_i -h_{ii} y_i = 0 $, (13) leads us to
which is (9). Then $ y_i $ is a column vector of $ Y $.
In the remaining part of the section, we present some properties of the principal fundamental matrix $ {\mathrm Y} $. Let us denote the elements of $ {\mathrm Y} $ as $ Y = \big ( y_{ij} \big) $. Then we have
$ \bullet $ By the definition of $ h_{ij} $, we have
Here we used the following fact
which can be derived from the following identity
Integrating by parts, we have $ \frac{d}{dt}\int_{\Bbb{R}^d} \phi_k\bar{\phi}_l\, dx = 0 $. When $ i = j $ in (15), we have
where we considered the conservation of $ L^2 $ norm of $ \psi $. Higher order norm of $ \psi $ can be determined by the similar process. In fact, considering (14), we have $ \nabla \psi_i = \sum_{k = 1}^N y_{ik } \nabla \phi_k $ which implies
where $ \alpha = (\alpha_1, ..., \alpha_d) $ is a multi-index.
$ \bullet $ By Liouville's Theorem, we have
4.
Proof of Theorem 1.2
Here we show a boundedness of principal fundamental matrix $ Y $ for the case of complete synchronization. We first summarize the recent results in [1,8] which show the emergence of the complete synchronization.
Theorem 4.1. [1] Suppose that the initial data satisfy $ {\tilde r}_j^0 > 0 $ for $ j = 1, \cdots, N $. Then, for any solution $ \psi_i $ to (1), we have
Theorem 4.2. [8] Suppose that initial data satisfy $ \mathcal{H}(0) < N $. Then the solution $ h_{ij} $ to (3) converges to $ 1 $ exponentially fast for all i and j.
Next we introduce Theorem 1 in Chapter 2 in [2] which concerns the boundedness of solutions of equations with almost constant coefficients.
Theorem 4.3. Let $ A $ be a constant $ n\times n $ matrix. If all solutions of $ \frac{dy}{dt} = A y $ are bounded as $ t\to \infty $, then the same is true for the solution of
provided that $ \int_0^{\infty} \| B(t)\|\, dt <\infty $. Here $ B(t) $ is $ n \times n $ matrix with elements $ b_{ij} $ and the matrix norm is defined by $ \| B\| = \sum_{i, j = 1}^n |b_{ij}| $.
Now we are ready to prove Theorem 1.2. With the notations
we can rewrite $ \frac{dy}{dt} = H(t) y $ as
Here we denote $ \tilde{y} = (y_1^1, \, y_1^2, \cdots, y_N^1, \, y_N^2)^t $ and $ 2N \times 2N $ matrices
and
with $ 2 \times 2 $ blocks
When the initial data satisfy $ \tilde{r}_j(0)>0 $ or $ \mathcal{H}(0)<N $, Theorem 4.1 or 4.2 tells us that $ r_{ij} $ and $ s_{ij} $ decay exponentially to zero which implies that $ \int_0^{\infty} \| B(t)\|\, dt <\infty $. To show the boundedness of solution to $ \frac{d\tilde{y }}{dt} = \frac{K}{N} A \tilde{y} $, we check that the characteristic polynomial of $ A $ is $ \lambda^2 (\lambda +N)^{2N-2} $. In fact, we have
and $ 2N-2 $ eigenvectors
correspond to eigenvalues $ -N $. Since we have non-positive eigenvalues and two independent eigenvectors corresponding to eigenvalue $ 0 $, all solutions of $ \frac{d\tilde{y} }{dt} = \frac{K}{N} A \tilde{y} $ are bounded for $ t\geq 0 $. Note that if we have only one independent eigenvector corresponding to eigenvalue $ 0 $, then $ t $ factor appears from which boundedness of the solution cannot be induced. Applying Theorem 4.3, we can prove Theorem 1.2.
5.
Explicit solutions
In this section, we study the case where the principal fundamental matrix can be solved explicitly. Consider linear differential equation
If $ A(t) $ commutes with $ \int_0^t A(s) ds $, then the solution to (16) is given by
where $ y_0 $ is the initial value. But in the general case there is no closed form solution, and an approximation method such as Magnus expansion [3,4,12] may have to be used.
For the system (9) we can check, with the notation $ S_j = \sum_{k\neq j}h_{jk} $,
and
Therefore we have the principal fundamental matrix
provided that
From the matrices presented above, we have
where $ A^T $ stands for the transpose of a matrix $ A $. To achieve the relation (17), the equality
has to be justified for all pairs $ (i, j) $.
Recall that the solution $ \phi_j $ to (4) with $ V = 0 $ is given by
Then Theorem 1.1 leads us to
where $ \psi^0 = (\psi_1^0, ..., \psi_N^0)^{t} $. It would be interesting problem to study (4) with some other potentials like $ V = |x|^2 $.
5.1. A two-oscillator system
Here we consider a two-oscillator system. In this case, system (3) can be reduced to a single equation for $ h : = h_{12} $:
with the initial data $ h(0) = h^0 $. Then we have
Hence, all solutions with initial data $ h^0 \not = -1 $ will converge to $ 1 $ exponentially fast as $ t \to \infty $. Considering
we can check that (17) holds if
For $ h^0 \in \Bbb{R} $, we have $ h(t) \in \Bbb{R} $ for which the equality (18) holds. Then we have
We can check $ \mathrm{A} \mathrm{B} = \mathrm{B}\mathrm{A} $ which implies $ e^{\mathrm{A}+\mathrm{B }} = e^{\mathrm{A }} e^{\mathrm{B }} $. Then the principal fundamental matrix reads as
The direct calculation shows
where 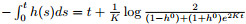 and
and
Therefore we arrive at
Note that 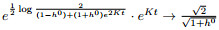 as $ t \to \infty $ for $ h^0 \not = -1 $.
as $ t \to \infty $ for $ h^0 \not = -1 $.
5.2. A three-oscillator system
Here we consider a three-oscillator system. Considering $ h_{ij} = \overline{h_{ji }} $, system (3) becomes the following $ 3\times3 $ system:
Let us consider the case of $ h_{12} = h_{23} = h_{31} $. Actually, if $ h_{12}(0) = h_{23}(0) = h_{31}(0) $ holds initially, the relation is preserved in time, i.e., $ h_{12}(t) = h_{23}(t) = h_{31}(t) $ for $ t>0 $. Then the system (19) reduces to a single equation:
We can check that (17) is satisfied for this case. Actually we have, with the notation of $ h = h_{12} $,
where $ A = (\frac{K}{3})^2 \left( (h+ \bar{h}) \int_0^t (h+ \bar{h})\, ds +2t \right) $, $ B = (\frac{K}{3})^2 \left( - t (h+ \bar{h}) - \int_0^t (h+ \bar{h})\, \right. $ $ \left. ds +t \right) $.
Let us write
where $ G(t) = -\frac{K}{3}\int_0^t (h+\bar{h})(s) ds $. Then the principal fundamental matrix reads as $ e^{G(t) {\mathrm I} } e^{\frac{Kt}{3}{\mathrm D} } $. First of all, we have
Taking into account
where
we have
Let us find more precise form of $ h+ \bar{h} $ in $ G $. With the notation $ h_{12} = f+\mathrm{i} g $, (20) is equivalent to the following two-dimensional system:
Then the solution to the first equation in (21) is given by
where $ f^0 = f(0) $. Considering $ h+ \bar{h} = 2f $, the principal fundamental matrix is given by
where $ G(t) = -\frac{K}{3}\int_0^t 2f(s) ds $.









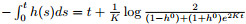 and
and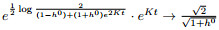 as
as 


 DownLoad:
DownLoad: