1.
Introduction
In the paper, we consider fractional Klein-Gordon-Schrödinger (KGS) equations with the fractional Laplacian
where, f1(|u|2,ϕ)=∂f(|u|2,ϕ)∂|u|2, f2(|u|2,ϕ)=∂f(|u|2,ϕ)∂ϕ,f:R+×R⟼R, u(⋅,t), ϕ(⋅,t) are complex and real valued unknown functions, and the fractional Laplace operator [1,2,3,4] is defined by
Let ϕt=v. Then, the fractional KGS system (1.1)–(1.2) can be expressed as the following form
The fractional KGS system (1.3)–(1.5) has the following mass and energy conserved laws
When α=2, the fractional KGS system (1.1) and (1.2) reduces to the integer KGS system [5,6,7,8,9,10,11,12]. When α≠2, the fractional KGS system [13,14,15,16,17] describes various important physical phenomena. Recently, some attentions have been paid to fractional KGS system with fractional Laplacian, which are fractional version of classical KGS equations and consider long-range interactions. In general, the analytic solution of the fractional KGS system (1.1), (1.2) can not be derived due to nonlocality and nonlinearity. Therefore, numerical method plays an important role in the study of the fractional KGS system (1.1), (1.2). Various numerical methods [13,14,15,16,17] such as the finite difference method, pseudo-spectral method, and symplectic method have been studied the fractional KGS system with f(|u|2,ϕ)=|u|2ϕ, and the stability and convergence of the numerical methods have been discussed.
It is not difficult to find that there are some deficiencies in the numerical schemes of the fractional KGS system. The first deficiencie is that the above finite difference methods are based on fractional center difference scheme, and approximate solutions converge to the exact solution at the rate O(τ2+h2). To the best of the authors'knowledge, there are few research on higher-order scheme for the fractional KGS system. The second deficiencie that the above numerical schemes are only based on one dimension fractional KGS system, and high dimension fractional KGS systems are rarely studied. In addition, there exist few reports on numerical scheme for general fractional KGS system in Eqs (1.1), (1.2) with f(|u|2,ϕ)≠|u|2ϕ.
The main goal of this paper is to construct structure-preserving scheme [18,19,20,21,22] for solving one dimension and two dimension fractional KGS equations with fractional Laplacian operator. Some numerical schemes were proposed to approximate the fractional Laplacian operator. The fractional center difference scheme based on fractional Laplace operator was first developed in [23]. Based on this work, some high-order schemes were constructed, and the results have be applied to some fractional difference equations. In addition, finite element scheme and Fourier spectral scheme of fractional Laplace operator have been studied with some special boundary conditions. In this paper, we use high-order difference scheme for fractional Laplace operator with zero boundary condition. By using some useful lemmas, we prove that the scheme can preserve the mass and energy conservation laws.
All structure-preserving schemes for the nonlinear fractional KGS system (f(|u|2,ϕ)≠|u|2ϕ) face how to efficiently solve a large nonlinear system at each time step. In this paper, we consider structure-preserving scheme for general fractional KGS equations (1.3)–(1.5). The high order central differences are used for the space direction, with the Crank-Nicolson scheme applied to the time direction. However, the numerical scheme is nonlinear scheme, and it takes too much time in the numerical simulation. Recently, scalar auxiliary variable scheme was introduce for gradient flows, and the numerical scheme only requiring solving decoupled linear systems at each time step. As far as we know, there exist few reports on scalar auxiliary variable scheme for fractional KGS system (1.3)–(1.5). In this paper, we show a new scalar auxiliary variable scheme to solve two dimension fractional KGS system (1.3)–(1.5).
In this paper, we first show numerical scheme to solve one dimension fractional KGS system (1.3)–(1.5), and discussed conservation, existence and uniqueness, stability and convergence of the numerical scheme. Second, we show numerical scheme for two dimension fractional KGS system by high order finite difference scheme in span and Crank-Nicolson scheme in time, and discussed conservation of the numerical scheme. Third, we show scalar auxiliary variable scheme to solve two dimension fractional KGS equations. Finally, some numerical examples are given, confirm theoretical results and demonstrate the efficiency of the numerical schemes.
The outline of the paper is as follows. In Section 2, the structure-preserving scheme is proposed for one dimension fractional KGS system, and convergence and stability of the numerical scheme is proved. In Section 3, the high conservative difference scheme is proposed for two dimension fractional KGS system. In Section 4, the numerical experiments are given, and the results verify the efficiency of the conservative difference scheme. Finally, a conclusion and some discussions are given in Section 5.
2.
Structure-preserving scheme for one dimension fractional KGS system
In the section, we show structure-preserving scheme for one dimension fractional KGS system with f(|u|2,ϕ)≠|u|2ϕ, and prove that the scheme can preserve mass and energy conservation laws. Moreover, we show that the arising scheme is uniquely solvable, and approximate solutions converge to the exact solution at the rate O(τ2+h4).
2.1. Some useful lemmas
The fractional KGS system (1.1)–(1.2) contains a fractional Schrödinger equation and a classic Klein-Gordon equation, and we consider boundary condition
Let M,N. Then, choose time-step τ=T/N and mesh size h=(b−a)/M. Denote
Then
Define
Suppose w={wnj; j=0, 1, 2⋯ M, n=0, 1, 2⋯ N} be a discrete function in ˉΩh×ˉΩτ, and
For convenience, we define the finite difference operators
For any grid function u={uj}, v={vj}, define the discrete inner product, L2-norm and Lp-norm as
For 0≤δ≤1, we also define the fractional Sobolev norm ‖u‖Hδ and semi-norm |u|Hδ as
where
Lemma 1. [24] Let f(x)∈C6[xL,xR], 2<j<M−2. Then
When j=1,M−1, then
Lemma 2. [20] Suppose that u∈L1(R) and
Then for a fixed h, we can obtain high order scheme
where
Lemma 3. For any grid functions un∈Z0h, we can obtain
where Im(s),Re(s) mean taking the imaginary part and the real part of a complex number s, respectively.
Lemma 4. [25] (Diserete Sobolev inequality) For every 12≤δ≤1, there exist a constant C=C(δ)>0 independent of h>0 such that
for all u∈l2h.
Lemma 5. [25] (Gagliardo-Nirenberg inequality) For any 14<δ0≤1, there exist a constant Cδ0=C(δ0)>0 independent of h>0 such that
2.2. Conservative difference scheme
Applying Crank-Nicolson scheme in time and higher order difference scheme in space to the fractional KGS system (1.3)–(1.5), we can obtain the following numerical scheme
where
Theorem 1. The scheme (2.1)–(2.5) is conservative in the sense
where
Proof: Multiplying h(Un+1j+Unj)∗ to Eq (2.1) and summing it up for 1≤j≤M−1 can yield
Taking the imaginary part of Eq (2.6) and noting that Lemma 3 yields ‖Un+1‖2=‖Un‖2. When n=0,1,2,⋯, we can obtain Mn=Mn−1⋯=M0.
Multiplying 2h(Un+1j−Unj)∗/τ to Eq (2.1) and summing it up for 1≤j≤M−1 can yield
It follows from Lemma 3 that
Taking the real part of Eq (2.7) and noting that Lemma 3 yields
Multiplying 2h(Vn+1j−Vnj)/τ to Eq (2.2) and summing it up for 1≤j≤M−1 can yield
Multiplying 2h(Φn+1j−Φnj)/τ to Eq (2.3) and summing it up for 1≤j≤M−1 can yield
It follows from literature [24] that
Noting that equation ⟨Φnt,Vnt⟩=⟨Vnt,Φnt⟩, we obtain
Combining Eqs (2.8) and (2.11), we obtain
When n=0,1,2,⋯, we can obtain En=En−1⋯=E0.
In [15], we show the theoretical analysis for f(|u|2,ϕ)=|u|2ϕ+|u|4ϕ. In similar analysis of literature [15], we can obtain the theoretical analysis for f(|u|2,ϕ)=|u|2l⋅ϕm when l,m satisfy certain conditions. For simplicity of notation, we only consider f(|u|2,ϕ)=|u|2ϕ in next theoretical analysis.
Theorem 2. The scheme (2.1)–(2.5) is bounded in the discrete l∞h.
Proof: Using Theorem 1 can obtain ‖Un‖=˜C and
Noting that Young's inequality ab≤14a2+b2, we can obtain
Using Gagliardo-Nirenberg inequality and noting that 14<σ0<α4 can yield
It follows from [22] that there exists a constant 1≤Cα≤(2π)α such that
Substituting Eqs (2.15), (2.16) into Eq (2.12) can yield
Noting that ‖Un‖2Hα2=|Un|2Hα2+‖Un‖2,En=E0, we have
When ε<νCαˆCδ0, there exist a constant C, such that
It follows from Lemma 4 that ‖Un‖l∞h≤C,‖Φn‖l∞h≤C.
2.3. Existence and Unique
Theorem 3. The solution of the numerical scheme (2.1)–(2.5) exists and unique.
Proof: Let Pn=Un−ˆUn,Rn=Vn−ˆVn,Qn=Φn−ˆΦn. Then, it follows from Eqs (2.1)–(2.15) that
Multiplying h(Pn+1j+Pnj)∗ to Eq (2.17) and summing it up for 1<j<M−1 can yield
Taking the imaginary part of Eq (2.20) can obtain
Noting that Theorem 2, then we can obtain
Multiplying (Rn+1j−Rnj)/τ to Eq (2.18) and summing it up for 1<j<M−1 can yield
Multiplying (Qn+1j−Qnj)/τ to Eq (2.19) and summing it up for 1<j<M−1 can yield
It follows from Theorem 2 that the Eq (2.24) can be expressed as the following form
Combining Eq (2.23) can yield
Adding Eqs (2.22) and (2.25) can yield
Let
Then, we can obtain
It follows from Gronwall's inequality that
Noting that ‖Pn+1‖2+‖Qn+1‖2≤Bn, we can obtain ‖Pn+1‖2=0,‖Qn+1‖2=0.
2.4. Convergence and error estimates
Let unj=u(xj,tn), vnj=v(xj,tn), ϕnj=ϕ(xj,tn). Then, we define the local truncation error as
According to Taylor expansion, we obtain the following result.
Theorem 4. |Rnj|≤ˆC(τ2+h4) holds as τ,h→0.
Theorem 5. Suppose that the problem (1.1),(1.2) has a smooth solution, then the solution Un,Φn of difference scheme (2.1)–(2.5) converges to the true solution u,ϕ with order O(τ2+h4) by the‖⋅‖l∞h norm.
Proof: Let enj=Unj−unj,ηnj=Φnj−ϕnj, ξj=Vnj−vnj. Then, we obtain
where
Multiplying h(en+1j+enj)∗ to Eq (2.29) and summing it up for 1<j<M−1 can yield
Taking the imaginary part of Eq (2.32) can yield
Multiplying h(ξn+1j−ξnj)/τ to Eq (2.30) and summing it up for 1<j<M−1 can yield
Multiplying h(ηn+1j−ηnj)/τ to Eq (2.31) and summing it up for 1<j<M−1 can yield
It follows from Cauchy-Schwarz inequality that
Substituting Eqs. (2.36) and (2.37) into Eq (2.35) and noting that Eqs (2.33) and (2.34) yields
Let
Then, we can obtain
It follows from Gronwall's inequality that
Noting that B0=O(τ2+h4), we can obtain
Multiplying h(en+1j−enj)∗/τ to Eq (2.29) and summing it up for 1<j<M−1 can yield
It follows from Eq (2.32) that can obtain
and
Noting that
we can yield
It follows from [15] that can obtain
Thus, Eq (2.40) can be expressed as
Summing up the superscript n to N and then replacing N by n, we get
It follows from Gronwall Inequality that
Noting that Eq (2.38) can yield ‖e‖l∞h≤C(τ2+h4), ‖η‖l∞h≤C(τ2+h4).
2.5. Iterative algorithm
Let U=[U1,U2,⋯,UM−1], V=[V1,V2,⋯,VM−1], Φ=[Φ1,Φ2,⋯,ΦM−1]. Then, we rewrite the numerical scheme (2.1)–(2.5) as the following vector form
where, matrices ˜A, ˜B represent differential matrix of fractional Laplacian operator and classical Laplacian operator, respectively. In order to solve above nonlinear numerical scheme, we will use the following iterative algorithm
3.
Structure-preserving scheme for two dimension fractional KGS system
In this section, we first show Crank-Nicolson scheme in time and high central difference scheme in space, and the obtained scheme preserves mass and energy conservation laws. However, the obtained discrete system is nonlinear system, and it takes too much time in the numerical simulation for two dimension case. Then, we show a equivalent form of two dimension fractional KGS system by introducing some new auxiliary variables. The new system is discretized by the scalar auxiliary variable scheme, and a linear discrete system is obtained, which can preserve energy conservation law.
Now, we consider boundary condition
Let
where M, N be positive integers. Then,
Denote
Then, the grid function can be defined by Unj,k≈u(xj,yk,tn), Φnj,k≈ϕ(xj,yk,tn), where unj,k=u(xj,yk,tn), ϕnj,k=ϕ(xj,yk,tn). For any grid u={uj,k}, ϕ={ϕj,k}, we can define
Lemma 6. [26,27] Suppose that u∈L1(R2) and
Then, for a fixed h=hx=hy, we can obtain high order scheme
where
and g(α)k,l are Fourier expansion coefficients of generation function
which can be calculated as
Lemma 7. Let
where
Then, we obtain
3.1. Crank-Nicolson scheme
Applying Crank-Nicolson scheme in time and higher order difference scheme in space to two dimension fractional KGS system (1.3)–(1.5), we can obtain the following numerical scheme
where
Let
Then, we can obtain
where, ⊗ represents kronecker product of matrices, Dx, Dy are differential matrix of x, y direction, and I is identity matrix.
Lemma 8. [19] Let A∈Rn×n have eigenvalues {λj}nj=1, and let B∈Rm×m have eigenvalues{μj}mj=1. Then the m×n eigenvalues of A⊗B are
Lemma 9. [19] For matrixs A and B, (A⊗B)T=AT⊗BT.
Let Λh=Dx⊗I+I⊗Dy. Then, it follows from Lemmas 8 and 9 that the matrix Λh and A are symmetric positive matrixs. Moreover, there exists fractional symmetric positive difference quotient operator denoted by Λ12h and A12 such that
It follows from Lemmas 8 and 9 that the numerical scheme (3.7)–(3.9) preserves mass and energy conservation laws.
3.2. Scalar auxiliary variable scheme
For f(|u|2,ϕ)=|u|2ϕ, it follows from Eqs (3.2)–(3.6) that we can obtain the following numerical scheme
We can prove that the resulting scheme (3.10)–(3.14) can preserve the mass and energy conservation laws. However, the above numerical scheme is nonlinear scheme. In order to construct linear scheme, we consider also the following finite difference scheme for fractional KGS system (1.3)–(1.5) with f(|u|2,ϕ)=|u|2ϕ
We can also prove that the resulting scheme (3.15)–(3.19) can preserve the mass and energy conservation laws. However, the scheme is only conservation for f(|u|2,ϕ)=|u|2ϕ. For f(|u|2,ϕ)≠|u|2ϕ, we use scalar auxiliary variable scheme to obtain linearly implicit scheme. Let q=√⟨f(|u|2,ϕ),1⟩+C0. Then,
Lemma 10. The fractional KGS system (3.20)–(3.23) has the following energy conserved laws
Applying scalar auxiliary variable scheme in time and higher order difference scheme in space to the fractional KGS system (1.3)–(1.5), we can obtain the following numerical scheme
where ~Uj,kn+12=3Unj,k−Un−1j,k2,~Φj,kn+12=3Φnj,k−Φn−1j,k2.
Theorem 6. The scheme (3.24)–(3.27) is conservative in the sense
where
Proof: Multiplying 2h(Un+1j,k−Unj,k)∗/τ to Eq (3.24) and summing it up for 1≤j,k≤M−1 can yield
Taking the real part of Eq (3.28) yields
Multiplying 2h(Vn+1j−Vnj)/τ to Eq (3.25) and summing it up for 1≤j,k≤M−1 can yield
Multiplying 2h(Φn+1j−Φnj)/τ to Eq (3.26) and summing it up for 1≤j,k≤M−1 can yield
It is easy to check that
Noting that equation ⟨Φnt,Vnt⟩=⟨Vnt,Φnt⟩, we obtain
Multiplying 2hQn+12j,k to Eq (3.27) and summing it up for 1≤j,k≤M−1 can yield
Combining Eqs (3.29), (3.32), (3.33), we obtain
When n=0,1,2,⋯,n, we can obtain En=En−1⋯=E0.
3.3. Iterative algorithm
In above subsection, we construct some structure-preserving schemes to solve two dimension fractional KGS equations. In similar method of one dimension case, we can obtain the iterative algorithms of numerical scheme (3.2)–(3.6) and numerical scheme (3.10)–(3.14). Now, we consider the iterative algorithm of numerical scheme (3.15)–(3.19) and numerical scheme (3.24)–(3.27). Let U=[U11,U12,⋯,UM−1M−1], V=[V11,V12,⋯,VM−1M−1], Φ=[Φ11,Φ12,⋯,ΦM−1M−1]. Then, we rewrite the numerical scheme (3.15)–(3.19) and numerical scheme (3.24)–(3.27) as the following vector form
and
where, matrice B represents differential matrix of two dimension Laplacian operator.
Consider numerical scheme (3.34)–(3.36), if (Un, Φn, Vn), n=0,1,2,⋯ are known, then Φn+1, Vn+1 of numerical scheme (3.34)–(3.36) is solve by the following linear equations
Then, we can obtain Un+1 of numerical scheme (3.34)–(3.36) by solve linear equations
Consider numerical scheme (3.37)–(3.40), the numerical solution Un+1, Φn+1, Vn+1 of numerical scheme (3.37)–(3.40) is solve by the following linear equations
4.
Numerical experiments
In above sections, we study some numerical schemes to solve following one dimension and two dimension fractional KGS systems:
and
Recently, some structure-preserving schemes such as linearly implicit conservative scheme, symplectic scheme and multi-symplectic scheme have been designed and investigated for solving classical and fractional KGS system. However, in these works main system (4.3), (4.4) have been considered. As far as we know, there exist few studies on system (4.1), (4.2). In this paper, we consider not noly structure-preserving scheme of fractional KGS system (4.3), (4.4) but also fractional KGS system (4.1), (4.2). For two dimension case, we show linearly implicit conservative scheme (3.15)–(3.19) and fully implicit conservative scheme (3.10)–(3.14) to solve fractional KGS system (4.3), (4.4), and the fully implicit conservative scheme (3.10)–(3.14) is can obtain numerical result by above iterative algorithm. Moreover, we show also linearly implicit conservative scheme (3.24)–(3.27) and fully implicit conservative scheme (3.2)–(3.6) to solve fractional KGS system (4.1), (4.2). For one dimension case, we only give a fully implicit conservative scheme (2.1)–(2.5), in fact, linearly implicit(3.15)–(3.19) and (3.24)–(3.27) are still applicable to one dimensional case.
In this section, we give some numerical experiments to show the efficiency of the structure-preserving schemes. The first numerical example shows the numerical errors and convergence rates of the structure-preserving scheme, and check conservation property of the schemes. The second numerical example shows the numerical result for the general fractional KGS system. The third numerical example shows the numerical result for two dimension fractional KGS system.
4.1. Experiment A
When α=2, the KGS system (4.3), (4.4) has the following solitary wave solutions [5]
where v is the propagating velocity of the wave and x0 is the initial phase. We consider initial-value (v=0.8,x0=−10)
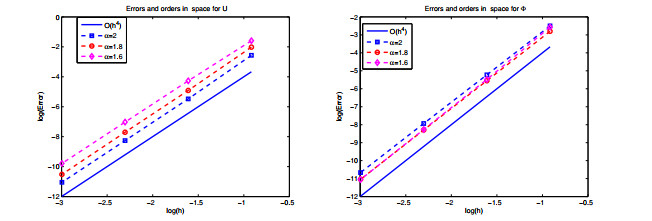
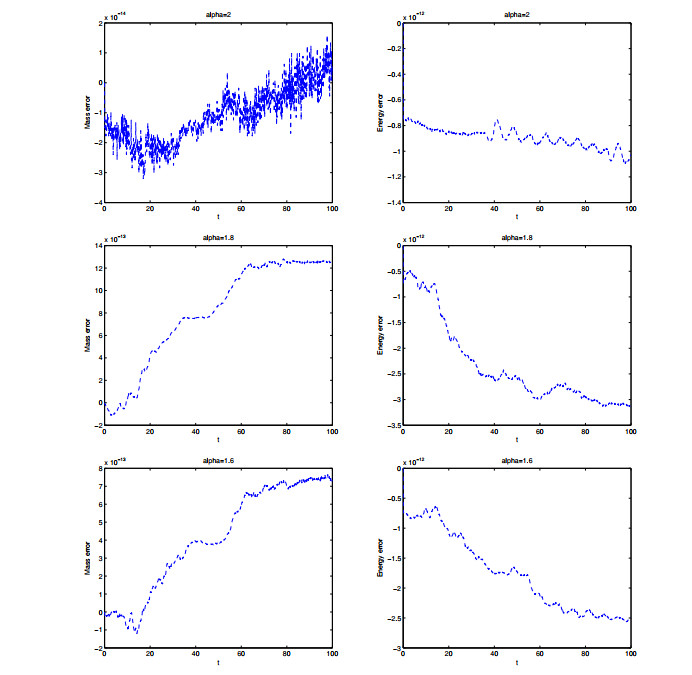
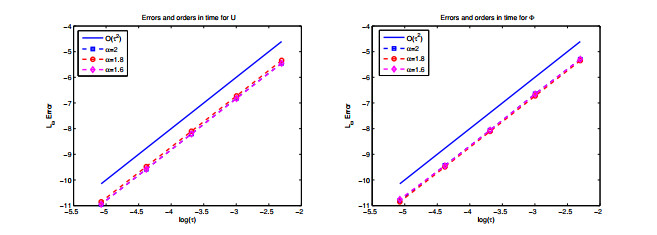
In this example, we text errors, convergence orders and conservation of mass and energy of one dimension KGS system by numerical scheme (2.1)–(2.5). First, we show errors and convergence orders of numerical scheme (2.1)–(2.5) at time t=1. For α≠2, the numerical exact solutions are obtained by a very fine mesh and a small time step. Then, we fix the space mesh h=0.00001 and time step τ=0.00001 to test time convergence orders and space convergence orders by numerical scheme (2.1)–(2.5). The Figures 1–2 show time convergence orders and space convergence orders for different α, and it is found that the scheme is of order 2 in time, order 4 in space. From Figures 1–2, we can draw the observations: the approximate solution converge to the exact solution at the rate O(τ2+h4), and consistent with the theoretical estimates of Theorems 5–6. Second, we examine the conservation of mass and energy with x∈[−20,20],t∈[0,100], τ=0.01,h=0.1. Figure 3 shows relative residuals on the mass and energy errors for different values of α by numerical scheme (2.1)–(2.5). It is found that the numerical scheme preserves mass and energy conservation very well although energy varies with α.
4.2. Experiment B
Consider following one dimension fractional KGS system
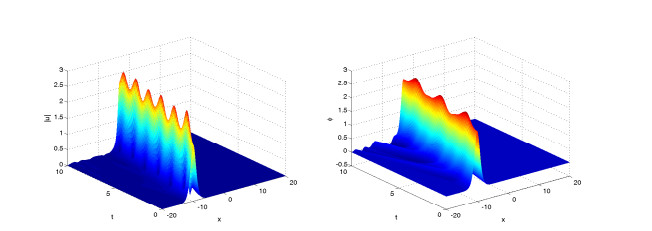
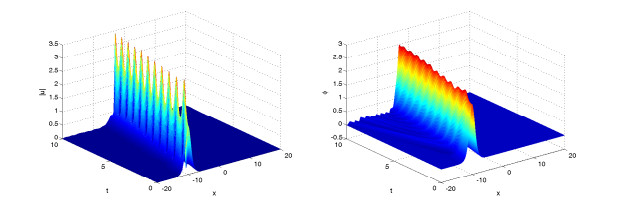
In this example, we simulate solitary wave and collisions of two solitary waves of fractional KGS system (4.5)–(4.8) by numerical scheme (2.1)–(2.5). First, we simulate solitary wave of numerical solutions for different orders α and difference parameter γ by the numerical scheme (2.1)–(2.5).
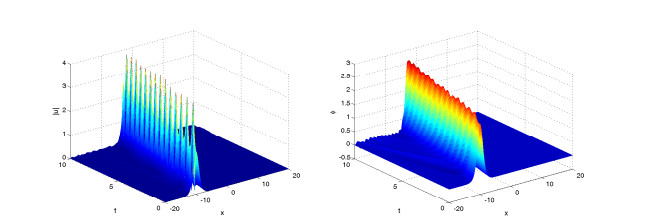
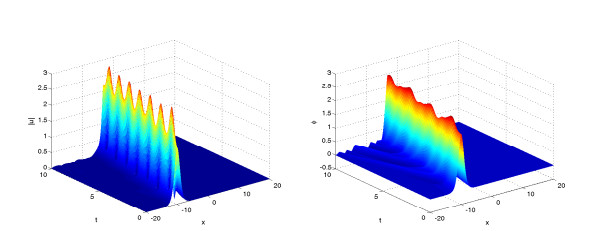
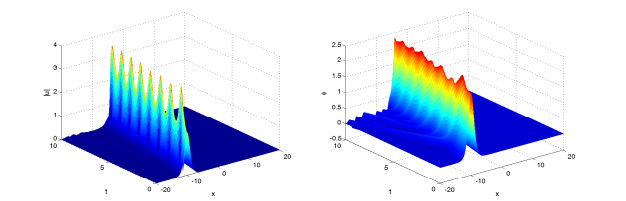
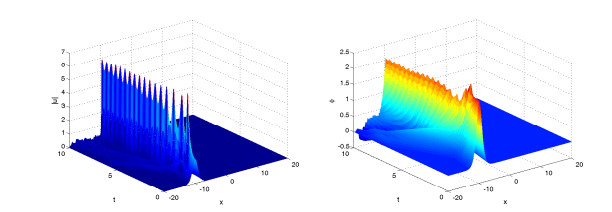
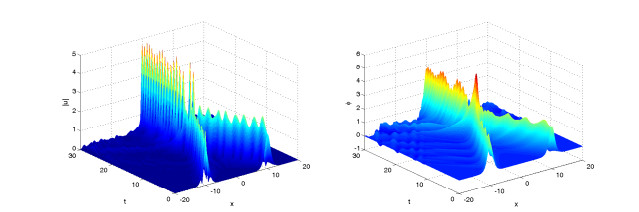
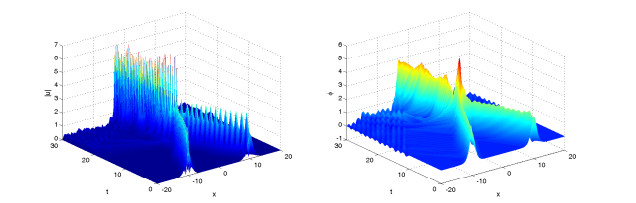
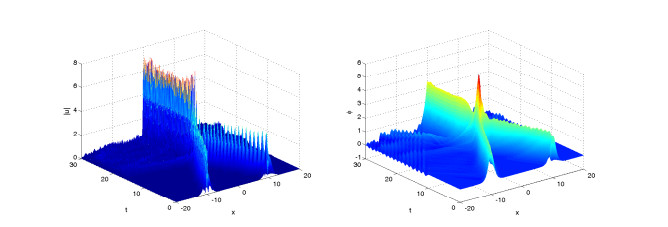
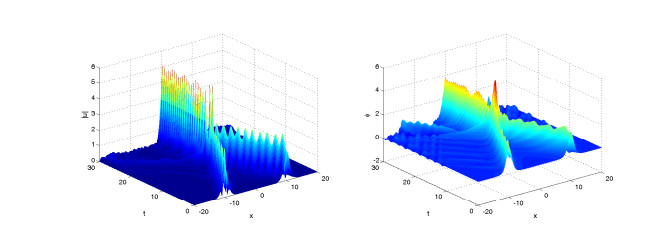
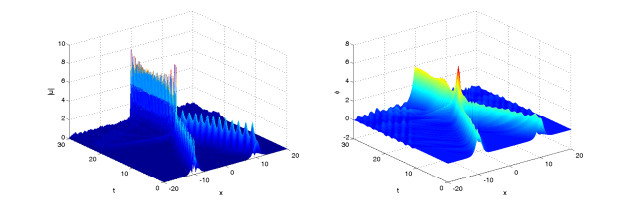
Figures 4–6 display solitary wave of the numerical solutions for difference value of γ=0.8, 1.5, 2 and same value of α=2. It is found that the parameter γ affects the propagation velocity of the solitary wave, and larger γ, the propagation of the soliton got slower.
Figures 7–9 display solitary wave of the numerical solutions for difference value of α=2, 1.8, 1.5 and same value of γ=1. It is found that the parameter α affects also the propagation velocity of the solitary wave, and smaller α, the propagation of the soliton got slower.
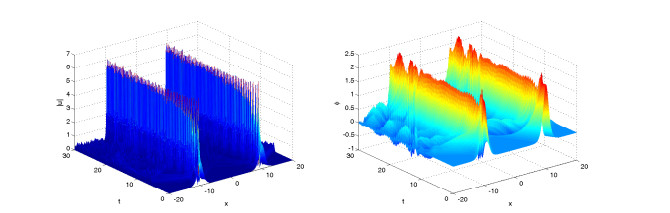
Second, we consider collisions of two solitary waves with x∈[−20,20], t∈[0,30], τ=0.01,h=0.1, and the initial data are chosen as (p1=10,p2=10,v1=0.8,v2=−0.8)
Figures 10–12 display solitary wave of the numerical solutions for difference value of γ=0.8, 1.5, 2 and same value of α=2. Figures 13–15 display solitary wave of the numerical solutions for difference value of α=2, 1.8, 1.5 and same value of γ=1. It is found that the parameters α, γ affect also the propagation velocity of the solitary wave. When smaller α and larger γ, the propagation of the soliton got slower, the soliton changes faster and even a high oscillation appears.
In the two example, we show some numerical results of fractional KGS system (4.5)–(4.8) for solitary wave case and collisions of two solitary waves case. In the process of time evolution, the solitary wave moves towards the boundary gradually, and produces some small waves around the solitary wave. In this paper, we only consider spatial range [−20,20]. If we want to get a better numerical result, we can expand the space a bit, but it will take more calculation time.
4.3. Experiment C
Consider two dimension fractional KGS system
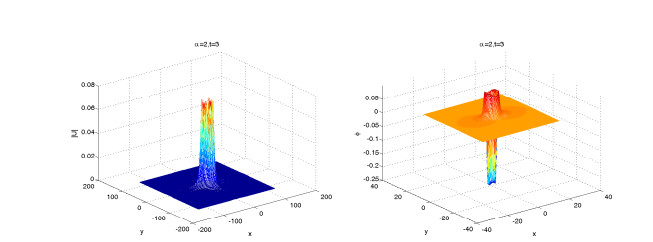
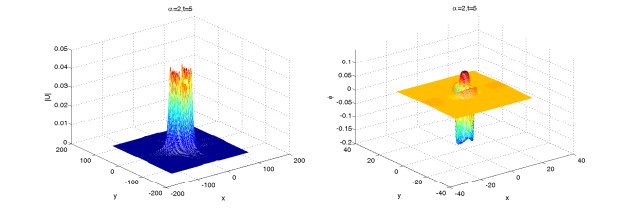
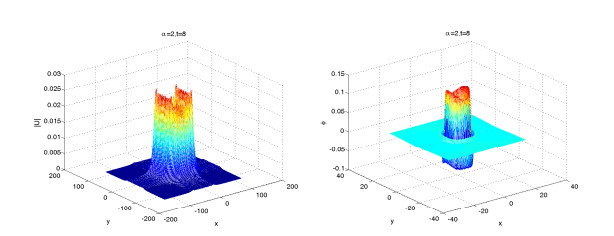
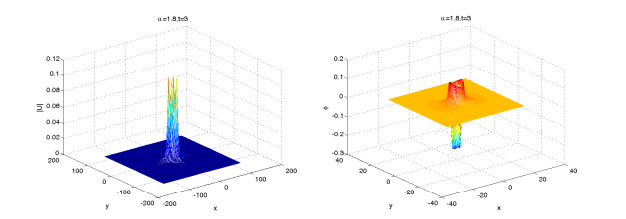
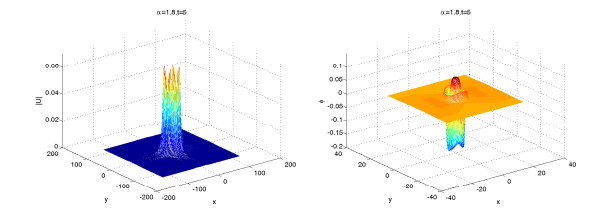
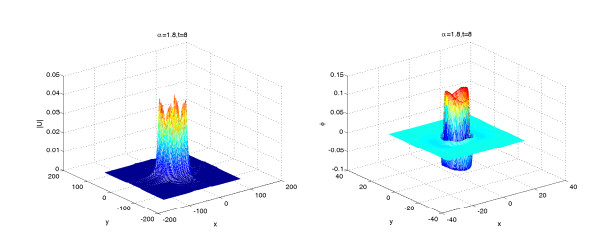
In the example, we simulate solitary wave numerical solutions for different orders α by the scalar auxiliary variable scheme (3.24)–(3.27). Figures 16–18 show the surface plots of the nucleon density |u|2 and meson field ϕ for different time t=3,5,8 and same value of α=2, respectively.
Figures 19–21 show the surface plots of the nucleon density |u|2 and meson field ϕ for different time t=3,5,8 and same value of α=1.8, respectively. From Figures 16–21, we fine that the meson field change periodically, and the order α affects the shape of nucleon field. They also show that α affects the propagation velocity of the solitary wave.
5.
Conclusion
In the paper, we study structure-preserving scheme to solve one dimension and two dimension space fractional KGS equations. First, we use the high central differences scheme in space and Crank-Nicolson scheme in time to discrete one dimension fractional KGS equations, which preserve mass and energy conservation laws of the fractional system. Then, we show that the arising scheme is uniquely solvable and approximate solutions converge to the exact solution at the rate O(τ2+h4). Second, we give the high central differences scheme in space, Crank-Nicolson scheme and scalar auxiliary variable scheme in time for two dimension fractional KGS equations, which preserve one or more analytical properties of the fractional system. Finally, the numerical experiments including some one dimensional and two dimensional fractional KGS systems are given to verify the correctness of theoretical results.
Conflict of interest
The authors declare there is no conflict of interest.
Acknowledgment
This work is supported by National Natural Science Foundation of China (No.12161070).









 DownLoad:
DownLoad: