Ricci solitons of the $\mathbb{H}^{2} \times \mathbb{R}$ Lie group

1.   Introduction

Brucellosis is an infectious bacterial disease often spread via direct contact with infected animals or contaminated animal products ^[1,2]. Brucellosis can transmit to other animals through direct contacts with infected animals or indirect transmission by brucella in the environment. The disease primarily affects cattle, sheep and dogs. In the real world, the infected sheep remain the main source of brucellosis infection, and the basic ewes and other sheep (which includes stock ram and fattening sheep) are often mixed feeding together, therefore there must exist the mixed cross infection between other sheep and basic ewes ^[3]. Brucellosis is prevalent for more than a century in many parts of the world, and it is well controlled in most developed countries. However, more than 500,000 new cases are reported each year around the world ^[4,5,6,7].

Mathematical modeling has the potential to analyze the mechanisms of transmission and the complexity of epidemiological characteristics of infectious diseases ^[8]. In recent years, several mathematical modeling studies have reported on the transmission of brucellosis ^{[3,9,10,11,12,13,14,15,16,17,18,19]}. However, these earlier models have mainly focused on the spread of brucellosis between sheep and human through using the dynamic model. Only Li et al ^[3] proposed a deterministic multi-group model to study the brucellosis transmission among sheep (which the flock of sheep were divided into basic ewes and other sheep). However, they only gave the global stability of disease-free equilibrium and the existence the endemic equilibrium, but the uniqueness and global stability of the endemic equilibrium were not shown when the basic reproduction number is larger than 1. Multi-group model is a class of highly heterogenous models with complex interactions among distinct groups, and the difficulty of global dynamics of multi-group models lies in establishing uniqueness and global stability of endemic equilibrium when basic reproduction number is larger than one ^[20]. In this paper, we want to study the global dynamic behavior of multi-group type model for the transmission of brucellosis among sheep which are absent from previous papers ^[3]. We prove the uniqueness of positive endemic equilibrium through using proof by contradiction, and the global stability of endemic equilibrium by using Lyapunov function. Especially, we give the specific coefficients of global Lyapunov function, and show the calculation method of these specific coefficients. By running numerical simulations for the cases with the basic reproduction number to demonstrate the global stability of the equilibria and the unique endemic equilibrium, respectively. By some sensitivity analysis of the basic reproduction number on parameters, we find that vaccination rate of sheep and seropositive detection rate of recessive infected sheep are very important factor for brucellosis.

This paper is organized as follows. In Section 2, we present the dynamical model. And the mathematical analysis including the uniqueness and global stability of positive endemic equilibrium will be given in Section 3. In Section 4, some numerical simulations are given on the global stability of the equilibria and the unique endemic equilibrium. Section 5 gives a discussion about main results.

2.   The dynamic model

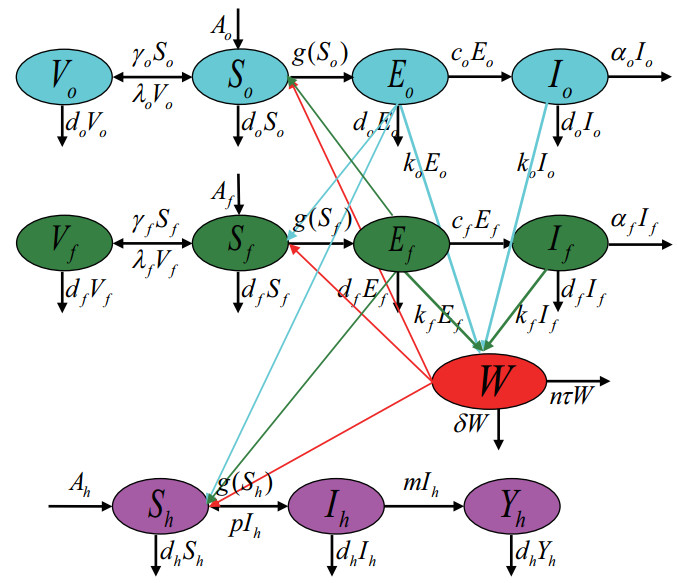
In previous paper ^[3], we proposed a multi-group model with cross infection between sheep and human. In this model, $S_{o}(t), E_{o}(t), I_{o}(t), V_{o}(t)$ and $S_{f}(t), E_{f}(t), I_{f}(t), V_{f}(t)$ represent susceptible, recessive infected, quarantined seropositive infected, vaccinated other sheep and basic ewes, respectively. $W(t)$ denotes the quantity of sheep brucella in the environment. $S_{h}(t), I_{h}(t), Y_{h}(t)$ represent susceptible individuals, acute infections, chronic infections, respectively. There are some assumptions on the dynamical transmission of brucellosis among sheep and from sheep to humans, which are demonstrated in the flowchart (See Figure 1). The following ordinary differential equations can describe a multi-group brucellosis model with Figure 1:

Because the last three equations are independent of the first nine equations, we can only consider the first nine equations. Rewrite system (2.1) for general form into the following model:

Adding the first four equations of (2.2) gives

which implies that $\lim\limits_{t\rightarrow\infty}\sup(S_{i}+E_{i}+I_{i}+V_{i})\leq\frac{A_{i}}{d_{i}}$. It follows from the last equation of (2.2) that $\lim\limits_{t\rightarrow\infty}\sup W\leq \frac{\sum^{2}\limits_{i = 1}\frac{k_{i}A_{i}}{d_{i}}}{\delta}$. Hence, the feasible region

is positively invariant with respect to model (2.2). Model (2.2) always admits the disease-free equilibrium $P_{0} = (S_{i}^{0}, 0, 0, V_{i}^{0}, 0)i = 1, 2$ in $X$, where $S_{i}^{0} = \frac{A_{i}(\lambda_{i}+d_{i})}{d_{i}(d_{i}+\lambda_{i}+\gamma_{i})}, V_{i}^{0} = \frac{A_{i}\gamma_{i}}{d_{i}(d_{i}+\lambda_{i}+\gamma_{i})}$, and $P_{0}$ is the unique equilibrium that lies on the boundary of $X$.

2.1.   The basic reproduction number

According to the definition of $\mathcal{R}_{c}$ in ^[21,22,23] and the calculation of $\mathcal{R}_{o}$ in our previous paper ^[3], we can obtain the basic reproduction number of model (2.2) is

where

3.   Mathematical analysis

In our previous paper ^[3], for the global stability of disease-free equilibrium and the existence of the positive endemic equilibrium of system (2.2), we have following theorems.

Theorem 3.1. If $\mathcal{R}_{0}\leq 1$, the disease-free equilibrium $P_{0}$ of system (2.2) is globally asymptotically stable in the region $X$.

Theorem 3.2. If $\mathcal{R}_{0} > 1$, then system (2.2) admits at least one (componentwise) positive equilibrium, and there is a positive constant $\epsilon$ such that every solution $(S_{i}(t), E_{i}(t), I_{i}(t), W(t))$ of system (2.2) with $(S_{i}(0), E_{i}(0), I_{i}(0), W(0))\in \mathbb{R}_{+}^{n}\times$ $Int$ $\mathbb{R}_{+}^{2n+1}$ satisfies

If $\mathcal{R}_{0} > 1$, then it follows from Theorem 3.2 that system (2.2) is uniformly persistent, together with the uniform boundedness of solutions of (2.2) in the interior of $X$, which implies that (2.2) admits at least one endemic equilibrium in the interior of $X$.

3.1.   The uniqueness of positive endemic equilibrium

Let $P^{*} = (S_{i}^{*}, E_{i}^{*}, I_{i}^{*}, V_{i}^{*}, W^{*}), i = 1, 2$ be a positive equilibrium of system (2.2), we will show its uniqueness in the interior of the feasible region $X$.

Theorem 3.3. System (2.2) only exists a unique positive endemic equilibrium in the region $X$ when $\mathcal{R}_{0} > 1$.

Proof. For the positive equilibrium $P^{*}$ of system (2.2), we have the following equations:

It is easy to obtain that

Hence, the positive equilibrium of system (2.2) is equivalent to the following system

where

Firstly, we prove that $E^{*} = \textbf{e}, \textbf{e} = (e_{1}, e_{2})$ is the only positive solution of system (3.1). Assume that $E^{*} = \textbf{e}$ and $E^{*} = \textbf{k}$ are two positive solutions of system (3.1), both nonzero. If $\textbf{e}\neq \textbf{k}$, then $e_{i}\neq k_{i}$ for some $i$ (i = 1, 2). Assume without loss of generality that $e_{1} > k_{1}$, and moreover that $e_{1}/k_{1}\geq e_{i}/k_{i}$ for all $i$ (i = 1, 2). Since $\textbf{e}$ and $\textbf{k}$ are positive solutions of system (3.1), we substitute them into (3.1). It is easy to obtain

so

But $(e_{i}/e_{1})k_{1}\leq k_{i}$ and $M_{1}(A_{1}-n_{1}e_{1}) < M_{1}(A_{1}-n_{1}k_{1})$; thus from the above equalities we get

This is a contradiction, so there is only one positive solution $E_{i} = \textbf{e}$ of system (3.1). So when $\mathcal{R}_{0} > 1$, system (2.2) only exists a positive equilibrium $P^{*}$.

3.2.   The global stability of positive endemic equilibrium

In this section, we will show the global asymptotic stability of endemic equilibrium $P^{*}$ of system (2.2) in the interior of the feasible region $X$.

Theorem 3.4. Suppose that matrix $[\beta_{ij}]_{1\leq i, j\leq 2}$ is irreducible. Then the endemic equilibrium $P^{*}$ of system (2.2) is globally asymptotically stable in the region $X$ when $\mathcal{R}_{0} > 1$.

Proof. Let $L_{i1} = S_{i}-S_{i}^{*}-S_{i}^{*}\ln \frac{S_{i}}{S_{i}^{*}}+V_{i}-V_{i}^{*}-V_{i}^{*}\ln \frac{V_{i}}{V_{i}^{*}}+E_{i}-E_{i}^{*}-E_{i}^{*}\ln \frac{E_{i}}{E_{i}^{*}}$, $L_{i2} = I_{i}-I_{i}^{*}-I_{i}^{*}\ln \frac{I_{i}}{I_{i}^{*}}$ and $L_{3} = W-W^{*}-W^{*}\ln \frac{W}{W^{*}}$. For $i = 1, 2$, differentiating and using the equilibrium equations give

Using the inequality $1-a\leq-\ln a, a > 0$, one can obtain that

Hence, we have

Similarly, we can obtain

Define the Lyapunov function

It follows that

Considering the following equations

We have

and

Let $a_{i2} = 1$ and take the equation $a_{i2}$ and $a_{i3}$ into the equation $\frac{dL}{dt}$, we can obtain

Due to matrix $[\beta_{ij}]_{1\leq i, j\leq 2}$ is irreducible, hence we can calculate $\upsilon_{1} = \beta_{21}S_{2}^{*}E_{1}^{*}, \upsilon_{2} = \beta_{12}S_{1}^{*}E_{2}^{*}$ such that

The equality $L^{'} = 0$ holds only for $S_{i} = S_{i}^{*}, E_{i} = E_{i}^{*}, I_{i} = I_{i}^{*}, i = 1, 2$ and $W = W^{*}$. Hence, one can obtain that the largest invariant subset where $L^{'} = 0$ is the singleton $P^{*}$ using the same argument as in ^[24]. By LaSalle's Invariance Principle ^[25], $P^{*}$ is globally asymptotically stable in the region $X$ when $\mathcal{R}_{0} > 1$.

Remark 3.1. In this model, the host populations are divided into 2 homogeneous groups. If the host populations have $n$ groups, we can extend our Lyapunov function into the following equation:

Furthermore we can obtain that

Hence, if the matrix $[\beta_{ij}]_{1\leq i, j\leq n}$ is irreducible, and according to the methods and conclusions in ^[24,26,27], there exist constants $\upsilon_{i} > 0, i = 1, 2, ..., n$ such that

4.   Numerical simulations

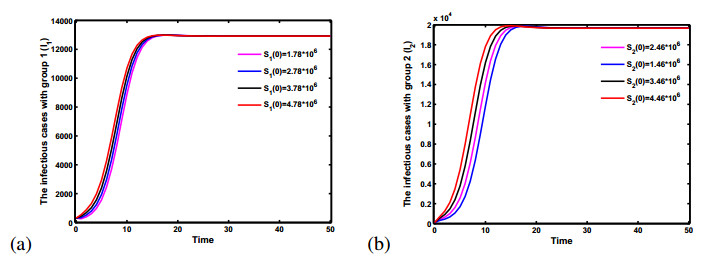
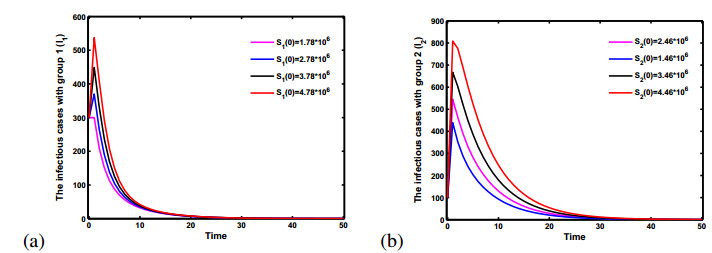
In an epidemic model, the basic reproduction number $\mathcal{R}_{0}$ is calculated and shown to be a threshold for the dynamics of the disease. Taking parameter values $\delta = 3.6, A_{1} = 1976000, d_{1} = 0.6$, $\lambda_{1} = 0.4, A_{2} = 1680000, d_{2} = 0.4$, $\lambda_{2} = 0.4, \alpha_{2} = 12, \alpha_{1} = 12$, $\beta_{1} = 1.0\times10^{-8}, \beta_{11} = 1.8\times10^{-7}$, $\beta_{2} = 1.0\times10^{-8}, \beta_{22} = 2.1\times10^{-7}$, $k_{1} = 15, k_{2} = 15$, $\gamma_{1} = 0.316\times0.82, \gamma_{2} = 0.316\times0.82$, $c_{1} = 0.15, c_{2} = 0.15$, $\beta_{12} = \beta_{21} = 1.35\times10^{-7}$ in paper ^[3], we run numerical simulations with system (2.2) for $\mathcal{R}_{0} > 1$ (see Figure 2) and $\mathcal{R}_{0} < 1$ (see Figure 3) to demonstrate the conclusions in Theorem 3.4 and Theorem 3.1.

4.1.   Uncertainty and sensitivity analysis

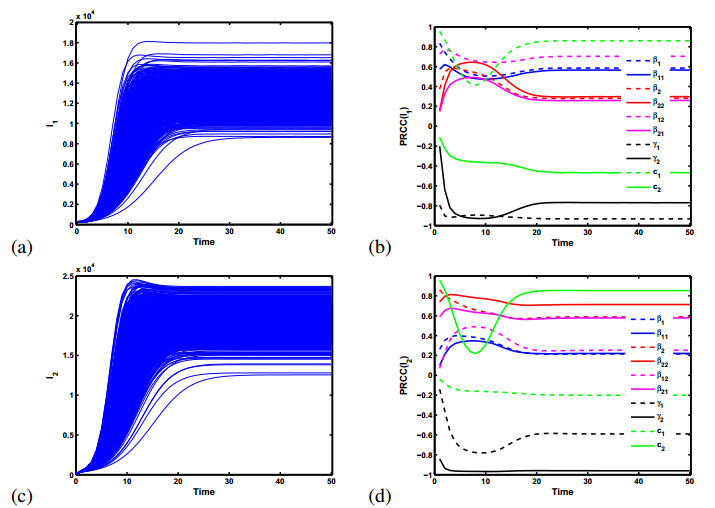
In order to evaluate the influence for infectious individuals over time with the key parameters (such as the efficient vaccination rate $\gamma_{1}, \gamma_{2}$, the seropositive detection rate $c_{1}, c_{2}$, and the transmission rate $\beta_{1}, \beta_{11}, \beta_{2}, \beta_{22}, \beta_{12}, \beta_{21}$). We explored these parameter space by performing an uncertainty analysis using a Latin hypercube sampling (LHS) method and sensitivity analysis using partial rank correlation coefficients (PRCCs) with 1000 samples ^[28]. In the absence of available data on the distribution functions, we chose a normal distribution for all selected input parameters with the same values in paper ^[3], and tested for significant PRCCs for these parameters of system (2.2). PRCC indexes can be calculated for multiple time points and plotted versus time, and this can allow us to assess whether significance of one parameter occur over an entire time interval during the progression of the model dynamics.

Figure 4 show the plots of 1000 runs output and PRCCs plotted for selected parameters with respect to the number of infected individuals in group 1 and 2 for system (2.2). Figure 4 (b) and (d) show that the effects of parameters $\gamma_{1}, \gamma_{2}, c_{1}, c_{2}, \beta_{1}, \beta_{11}$, $\beta_{2}, \beta_{22}, \beta_{12}, \beta_{21}$ change with respect to $I_{1}$ and $I_{2}$ over time. In the early time, these selected parameters with PRCCS have obvious change, and finally they remain constant. In Figure 4 (b), the efficient vaccination rate $\gamma_{1}, \gamma_{2}$ and the seropositive detection rate of group 2 $c_{2}$ are negatively correlated with PRCCs for $I_{1}$, and the other parameters are positively correlated with PRCCs for $I_{1}$. But In Figure 4 (d), the seropositive detection rate of group 2 $c_{2}$ is positively correlated with PRCCs and the seropositive detection rate of group 1 $c_{1}$ is negatively correlated with PRCCs, other parameters have the same correlation with PRCCs for $I_{1}$. From Figure 4, we can see the efficient vaccination rate $\gamma_{1}, \gamma_{2}$ have the strong negatively correlated PRCCs (black solid and dotted lines) for $I_{1}$ and $I_{2}$, and the seropositive detection rate has the strong positively correlated with PRCCs for infected individuals. Hence, one can conclude that the vaccination and the seropositive detection of infected individuals are the effective control measures.

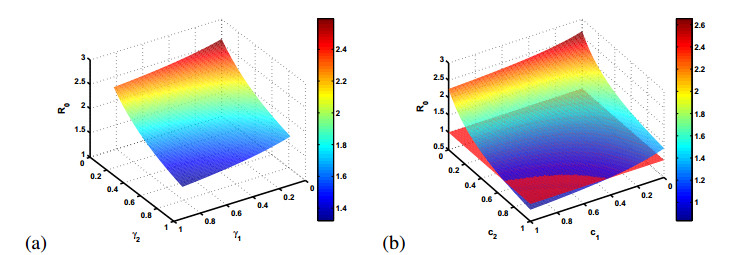
To find better control strategies for brucellosis infection, we perform some sensitivity analysis of the basic reproduction number $\mathcal{R}_{0}$ in terms of the efficient vaccination rate ($\gamma_{1}, \gamma_{2}$) and the seropositive detection rate ($c_{1}, c_{2}$). We show the combined influence of parameters on $\mathcal{R}_{0}$ in Figure 5. Figure 5(a) depicts the influence of sheep efficient vaccination rate $\gamma_{1}, \gamma_{2}$ on $\mathcal{R}_{0}$. Though vaccinating susceptible sheep is an effective measure to decrease $\mathcal{R}_{0}$, $\mathcal{R}_{0}$ cannot become less than one even if the vaccination rate of all sheep is 100$\%$ (which is the efficient vaccination rate $\gamma_{1} = 0.82, \gamma_{2} = 0.82$ in Figure 5(a), under this circumstances $\mathcal{R}_{0} = 1.3207$). Figure 5(b) indicates the influence of seropositive detection rate $c_{1}, c_{2}$ on $\mathcal{R}_{0}$, which shows to increase seropositive detection rate of recessive infected sheep can make $\mathcal{R}_{0}$ less than one, which means under the current control measures, increase seropositive detection rate of recessive infected sheep can control the brucellosis. Hence, we can conclude that combining the strategy of vaccination and detection is more effective than vaccination and detection alone to control brucellosis.

5.   Conclusion and discussion

In this paper, in order to show the uniqueness and global stability of the endemic equilibrium for brucellosis transmission model with common environmental contamination, the multi-group model in paper ^[3] is chosen as our research objectives. Firstly, we show the basic reproduction number $\mathcal{R}_{0}$ of the model (2.2). Then, we obtain the uniqueness of positive endemic equilibrium through using proof by contradiction when $\mathcal{R}_{0} > 1$. Finally, the proof of global asymptotical stability of the endemic equilibrium when $\mathcal{R}_{0} > 1$ is shown by using Lyapunov function. Especially, we give the specific coefficients of global Lyapunov function, and show the calculation method of these specific coefficients. Numerical analysis also show that the global asymptotic behavior of system (2.2) is completely determined by the size of the basic reproduction number $\mathcal{R}_{0}$, that is, the disease free equilibrium is globally asymptotically stable if $\mathcal{R}_{0} < 1$ while an endemic equilibrium exists uniquely and is globally stable if $\mathcal{R}_{0} > 1$. With the uncertainty and sensitivity analysis of infected individuals for selected parameters $\gamma_{1}, \gamma_{2}, c_{1}, c_{2}, \beta_{1}, \beta_{11}, \beta_{2}, \beta_{22}$, $\beta_{12}, \beta_{21}$ using LHS/PRCC method, one can conclude that the efficient vaccination rate $\gamma_{1}, \gamma_{2}$ have the strong negatively correlated PRCCs (black solid and dotted lines in Figure 4), and the seropositive detection rate has the strong positively correlated with PRCCs for infected individuals. By some sensitivity analysis of the basic reproduction number $\mathcal{R}_{0}$ on parameters, we find that vaccination rate of sheep and seropositive detection rate of recessive infected sheep are very important factor for brucellosis.

Acknowledgments

The project is funded by the National Natural Science Foundation of China under Grants (11801398, 11671241, 11601292) and Natural Science Foundation of Shan'Xi Province Grant No. 201801D221024.

Conflict of interest

All authors declare no conflicts of interest in this paper.