Selection of tree species is a key aspect of restoration in megadiverse biomes such as the Atlantic Forest, especially in degraded areas with past intensive land use, which usually present severe limiting conditions. The species must have high survival and growth, not only in the transition between germination and seedling but also between seedling and adult plant until allowing the establishment of a self-sustaining and renewable community. In order to reach this goal, restoration initiatives carried out in the Atlantic Forest have employed high-diversity plantings of tree species from different successional guilds. Notwithstanding, long-term silvicultural knowledge is scarce for the native species from this biome, and the effectiveness of these models is controversial. Our investigation has compared the survival and growth of species and guilds in high-diversity tree species plantings in areas with previous agricultural intensive use. The species and guilds were also compared with respect to seed mass since this parameter is pointed out as an indicator of high survival in early stages. Pioneer and secondary species did not present differences in survival and seed mass, although pioneers exhibited greater growth rate. The late successional (LS) species had lower survival and growth, and higher seed mass. Survival after 8 months and between 8–15 months after seedling planting was inversely correlated with seed mass (r2 = 0.35 and r2 = 0.36, P < 0.001). On the other hand, survival after 8 months was correlated with relative growth rate (RGR) in the same periods of time (r2 = 0.34, P < 0.001). Overall average survival was 41% after 15 months, with the survival of LS species at an average of 12%. Data suggests that the inclusion of LS seedlings could impair the efficacy of restoration during early phases, at least in highly degraded areas. Equally, the inclusion of species with high seed mass should be considered with caution.
1.
Introduction
Staphylococcus aureus is an important prevalent pathogen that can cause a variety of infectious diseases in both humans and animals through different pathways [1],[2]. The multifarious diseases caused by S. aureus include suppurative infections, pneumonia, pericarditis and meningitis in humans [3] and various local or systemic infectious diseases in animals, such as avian arthritis, bovine mastitis and septicemia [4]. Though antibiotics have been widely used for many years, there is still an increasing number of infectious diseases. Especially, multiple drug-resistant strains of S. aureus increase rapidly, such as methicillin-resistant (MRSA) and vancomycin-resistant S. aureus (VRSA) strains [5],[6]. The inefficient treatment of bacterial infections cause substantial economic loss and has been a challenging issue in veterinary medicine. Therefore, it's of great significance to develop new therapies that can supplement or replace the use of antibiotics.
Bacteriophages (phages) are the most abundant and diverse biological entities on the planet, and the number of phages is estimated to be about 1031, approximately10 times of the number of host bacteria [7],[8]. Phages can affect the structure and function of microbial communities, and they play a key role in determining microbial diversity [9]. There are two common types of phages, i.e., lysogenic and lytic phages, and lytic phages can replicate, reproduce and release lysin and have high lytic activity [10]. Recently, phages have been recognized as natural, safe, highly specific and effective alternatives to antibiotics in preventing and treating bacterial infections caused by S. aureus, and they can be used either alone or in combination with other agents [11],[12].
In this study, we performed genome sequencing and biological characterization of S. aureus phage vB_SauS_SA2 isolated from sewage in a livestock market and proposed a new genus Siphoviridae called ‘SA2likevirus’.
2.
Materials and methods
2.1. Bacterial strains and growth conditions
Fifty-three staphylococcal strains were isolated from the skin surface of several animals (pigs, rabbits, and chickens), and they belonged to seven different species, including Staphylococcus aureus, S. saprophyticus, S. gallinarum, S. cohnii, S. sciuri, S. lentus and S. xylosus (Table 1). All strains were cultivated in Luria-Bertani (LB) broth (Biocorp) at 37 °C. Stock cultures were stored in LB broth supplemented with 30% glycerol at −80 °C.
2.2. Phage isolation
Sewage samples (20 mL) were collected from a livestock market in Qingdao, Shandong province, China and filtered through a 0.22 µm membrane for sterilization. Phages were isolated from sewage using the conventional double-layer agar method [13]. Briefly, the filtrate was incubated with S. aureus in LB broth overnight at 37 °C. The culture broth was centrifuged at 12,000 × g for 10 min, and the supernatant was collected and filtered with a 0.22 µm membrane to remove bacterial residues. Then the supernatant was serially diluted in LB broth. Aliquots (100 µL) of these diluted phage suspensions, together with 100 µL of S. aureus culture, were mixed with 5 mL of soft top agar and poured on top of the solidified LB agar plates. The plates were incubated overnight at 37 °C to form plaques. Phage purification was repeated at least three times, and the final purified phages were then collected and stored at 4 °C.
2.3. Transmission electron microscopy (TEM)
The morphology of phage SA2 was examined by transmission electron microscopy (TEM) [14]. The phage suspension was added onto the surface of a copper grid and adsorbed for 15 min. The phages were negatively stained with 2% phosphotungstic acid in darkness for 10 min. The morphology of the phages was examined with a transmission electron microscope (HT7700, Japan) at 80 kV.
2.4. Host range
The host range of phage SA2 on the staphylococcal strains were determined using the efficiency of plating (EOP) [15]. The mixture of phage SA2 and the tested bacterial strains (Table 1) were incubated overnight at 37 °C, and the titers were determined using the double-layer agar method. The efficiency of plating (EOP) values were determined by calculating the ratio of PFUs of each phage-susceptible strain to PFUs obtained with S. aureus F2 strain. The experiment was repeated three times.
2.5. Thermal and pH stability, UV sensitivity
To determine the thermostability of phage SA2, the phage suspensions were incubated at various temperatures (40, 50, 60, 70 and 80 °C), and aliquots (100 µl) were collected after 20, 40, and 60 minutes of incubation, respectively. To evaluate the stability of the phages at different pH levels, the purified phages were incubated in LB broth at different pH levels ranging from 2 to 14 for 1, 2, 3 h, respectively. To observe the ultraviolet (UV) sensitivity of phage SA2, the phage suspensions were continuously exposed for 2 hours at 1.5 cm under an LED UV lamp (power 30 W, light intensity 26.23 µw/cm2). The aliquots were collected each 10 min post exposure. Phage samples were titered using the double-layer agar method [13]. Each experiment was performed in triplicate.
2.6. One-step growth curve
The one-step growth experiment of phage SA2 was carried out as described previously with minor modifications [16]. Briefly, the phages (1.67 × 108 pfu/mL) were mixed with the S. aureus F2 culture (1.01 × 109 cfu/mL) at a MOI of 0.1 and incubated at 37 °C for 5 min. The suspension was centrifuged at 10,000 rpm for 30 s, and the pellets were re-suspended in LB broth, followed by incubation at 37 °C with shaking at 160 rpm. Aliquots (100 µL) were taken every 5 min within the first hour, every 20 minutes within the second hour and every 30 minutes within the third and fourth hours, respectively. The aliquots were then centrifuged at 13,000 g for 3 min, and the titers of phages in the supernatants were immediately determined using the double-layer agar method. The experiments were carried out in triplicates. The burst size was calculated as the ratio of the final count of liberated phage particles to the initial count of phage particles.
2.7.
In vitro bacteriolytic activity
The in vitro bacteriolytic activity of phage SA2 was tested based on the absorbance (OD630) of the culture broth measured at 630 nm using spectrophotometry (ELX800, USA) [17]. The phages (2.8 × 108 pfu/mL) were mixed with the S. aureus F2 culture (5.5 × 108 cfu/mL) at different MOIs of 1, 0.1, 0.01, 0.001, 0.0001, and 0.00001, respectively, followed by incubation at 37 °C for 24 hours. S. aureus culture and LB broth served as a positive control and a negative control, respectively. The absorbance (OD630) of the culture broth was measured at 0.5, 1, 1.5, 2, 2.5, 3, 3.5, 4, 5, 6, 7, 8, 9, 10, 11, 12 and 24 h after the onset of incubation, respectively. The bacteriolytic activity was calculated at the corresponding time points. The experiment was performed in triplicate.
2.8.
Phage genome extraction
Phage genomic DNA was extracted using the phenol-chloroform method [18]. In Brief, the phage suspension was firstly treated with RNase A (5 µg/mL) and DNase I (2 U/mL) at 37 °C for 30 min, followed by incubation at 80 °C for 15 min to deactivate DNase I. Then, purified phages were treated with proteinase K (50 µg/mL) at 56 °C for 1h, in the presence of SDS (0.5%) and EDTA (20 mM). The mixtures were mixed with an equal volume of phenol/chloroform/isoamyl alcohol (25:24:1), followed by centrifugation at 12,000 g for 20 min at 4 °C. The supernatant was mixed with an equal volume of isopropanol and kept at −20 °C overnight. After centrifugation, the pellets were washed three times with cold 75% ethanol. Finally, the pellets were air-dried, dissolved in 50 µl of TE buffer (10 mM Tris-HCl; 1 mM EDTA, pH 8) and stored at −20 °C.
2.9.
Sulfate-polyacrylamide gel electrophoresis (SDS-PAGE)
The structural proteins of phage SA2 were analyzed by SDS-PAGE [19]. Following concentration with PEG 8000/NaCl, the phage particles were mixed with an equal volume of sample buffer (0.05 M Tris-HCl, pH 6.8; 10% glycerol, 2% SDS, 0.1% bromophenol blue, 1.56% DL-Dithiothreitol), and were heated in a boiling water bath for 10 min. After centrifugation (12,000 g, 10 min), the proteins in the supernatant were separated on a 12% SDS-PAGE and protein bands were visualized after staining with Coomassie brilliant blue. Protein bands were excised from the gel, digested by proteases and analyzed by Maldi mass spectrometry (Sangon Biotech, Shanghai).
2.10.
Nature of the phage
To determine whether phage SA2 is lysogenic or lytic, suspicious lysogens were isolated as described with some modifications [20]. Briefly, phage SA2 was mixed with the host strain at MOI of 5 and incubated at 37 °C for 5 min and plated out. Ten colonies were randomly picked out, streaked out 2 times and incubated in LB broth overnight at 37 °C, and then extracted the bacterial genomes for phage gene detection by PCR. The isolates were mixed with phage SA2 and the sensitivity to phage SA2 was tested by the double-layer agar method.
Three primer pairs were designed to amplify 537 bp of the holin (SA2-hol), and 1443 bp of the lysin (SA2-lys) of phage SA2, respectively. The each primer sequences of phage SA2 was: SA2-hol-F 5′-GGGCATATGATGGCAGAATCAAAGAAACAG 3′; SA2-hol-R 5′-CAGCTCGAGTCATTGATTATCTTCCCCTTT 3′; SA2-lys-F 5′-CAGAAAGGGGAAGATAAT 3′; SA2-lys-R 5′-TGTAACGCCAATACCAAT 3′. The PCR amplification reactions were performed in 25 µL, including 1 µL of 30 ng of DNA template, 2 µL of 25 µM of each primer, 12.5 µL of 2 × TS INGKE Master Mix and 9.5 µL ddH2O. The reaction condition was as follows: pre-denaturation at 94 °C for 5 min, followed by 30 cycles of denaturation at 94 °C for 1 min, annealing at 55 °C for 1 min, extension at 72 °C for 2 min, and final extension at 72 °C for 10 min. The PCR amplified products were analyzed by electrophoresis on a 1.0% agarose gel.
2.11.
Genome sequence analysis
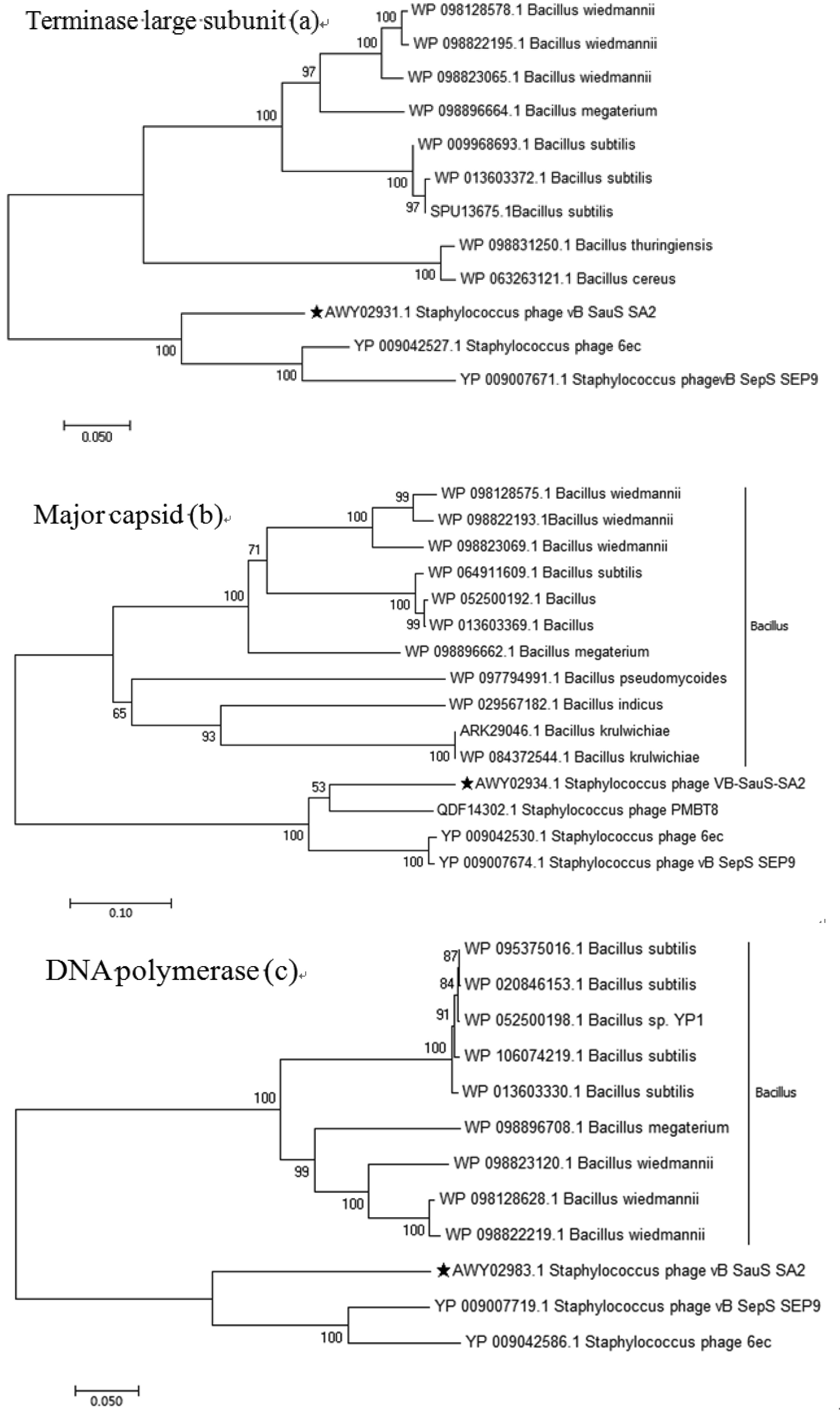
The complete sequence was annotated using the subsystem technology (RAST, http://rast.nmpdr.org) and GeneMark (http://opal.biology.gatech.edu/GeneMark/) [21]. All predicted open reading frames (ORFs) were verified using the online BLASTP (http://www.ncbi.nlm.nih.gov/BLAST). The putative transfer RNA (tRNA)-encoding genes were searched using tRNAscan-SE (http://trna.ucsc.edu/tRNAscan-SE/) [22]. The circular view of the genomic alignment of phage SA2 with other staphylococcal phages was constructed using BLAST Ring Image Generator (BRIG) [23], and the multiple sequences were aligned using Mauve (http://darlinglab.org/mauve/mauve.html) for comparative genomic analysis [24]. The phylogenetic tree of phage SA2 was constructed based on the large terminator subunit, the major capsid, and DNA polymerase using the ClustalW program in MEGA 6 [25].
2.12.
Nucleotide sequence accession number
The complete genome sequence of phage SA2 had been deposited in the GenBank database under the accession number MH356730.
2.13.
Statistical analysis
All data were expressed as mean ± standard deviation (SD) and analyzed using GraphPad Prism 6.0.
3.
Results and discussion
3.1. Morphology of phage SA2
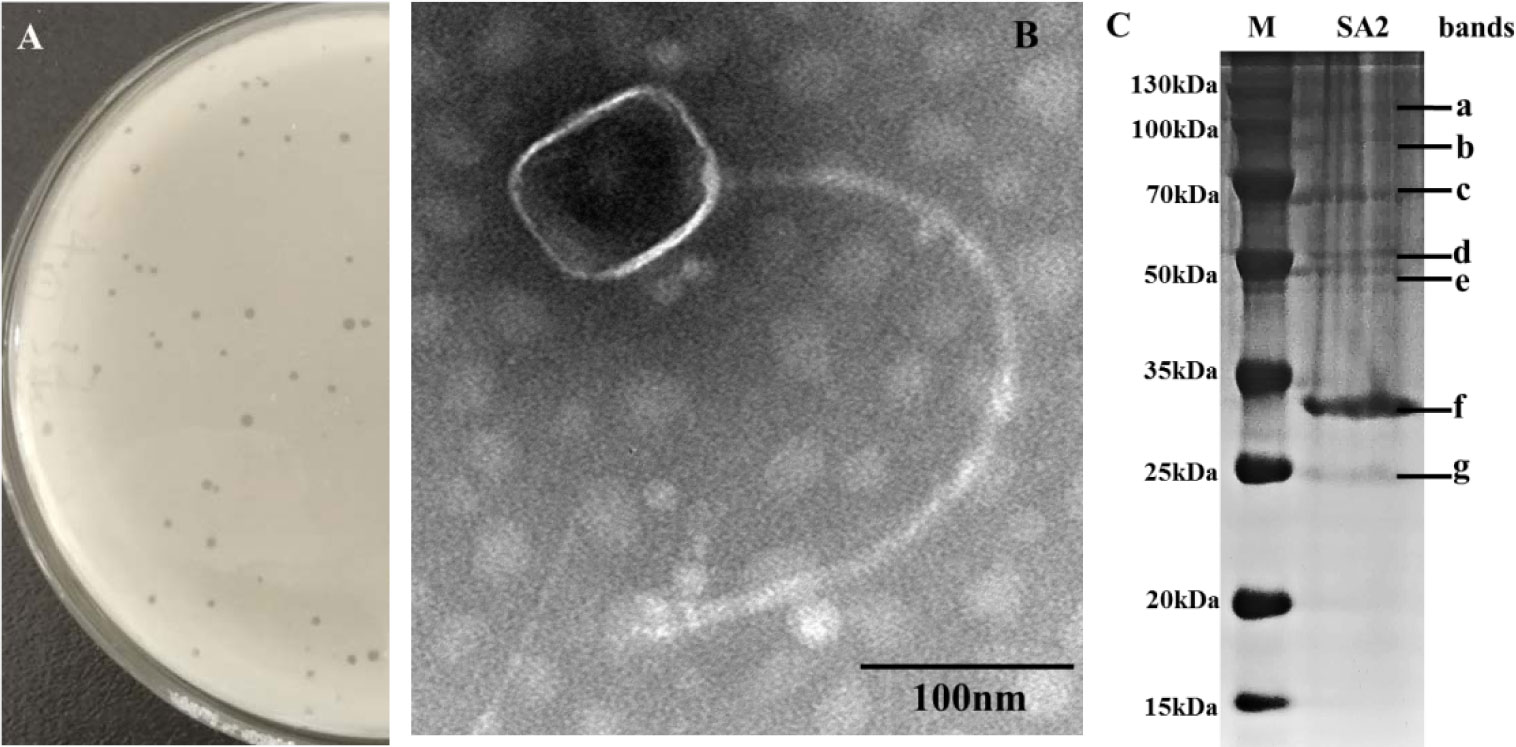
The S. aureus phage SA2 was isolated from sewage using the double-layer agar method with S. aureus F2 strain. The plaques of phage SA2 were clear with a diameter of about 1 mm (Figure 1A). The TEM image showed that phage SA2 had a polyhedral head (75 nm in diameter) and a long curved tail (410 nm in length) (Figure 1B). According to the current classification system developed by the International Committee on Taxonomy of Viruses, phage SA2 was classified as a member of the family Siphoviridae of the order Caudovirales. This phage was designated vB_SauS_SA2, in accordance with the recommendation proposed by Kropinski et al. [26].
3.2. Characterization of phage structural proteins
The structural proteins of phage SA2 were separated by SDS-PAGE, and seven protein bands were visualized on the gel (Figure 1C). The protein band of about 33 kDa (band f in Figure 1C) was identified to be the major capsid protein by mass spectrometry, which is relatively smaller than the capsid protein (42 kDa) of phage SA2. In order to verify the sequenced genome, the gene of the major capsid protein was amplified by polymerase chain reaction using primer (F: 5′-ACAACAGAAGGTGCATCAGC-3′; R: 5′-AACGACAAAAGTCTTCCCAG-3′), and amplification products were sequenced by Shanghai Personal Biotech Co., Ltd. (Personalbio, China), and it revealed that the aligned sequence was consistent with the annotated sequence. Therefore, the smaller size of the separated capsid protein was possibly caused by protein degradation. In addition, the other six protein bands were not detected by mass spectrometry due to their very low concentrations.
3.3. Host range
The host range of phage SA2 was determined by assessing its ability to form plaques on lawns of fifty-three Staphylococcus strains (Table 1). The results showed that phage SA2 lysed 23% (12/53) of test strains. Seven S. aureus strains and five S. saprophyticus strains were sensitive to phage SA2, and no correlation was observed between lytic activity and isolated animal species. Our spot test experiment showed that phage SA2 could lyse 14 test strains and the high sensitivity of the spot test may lead to some false positive results. The difference between EOP results and spot test results has been reported in many literatures [15]. S. aureus phages can lyse a variety of Staphylococcus species, for example, vB_SauM-fRuSau02 can lyse S. saprophyticus, S. intermedius, and other Staphylococcus species [27]. Like S. aureus phage vB_SauM-fRuSau02, SA2 could lyse Staphylococcus species (S. aureus and S. saprophyticus).
3.4. Biological characteristics of SA2
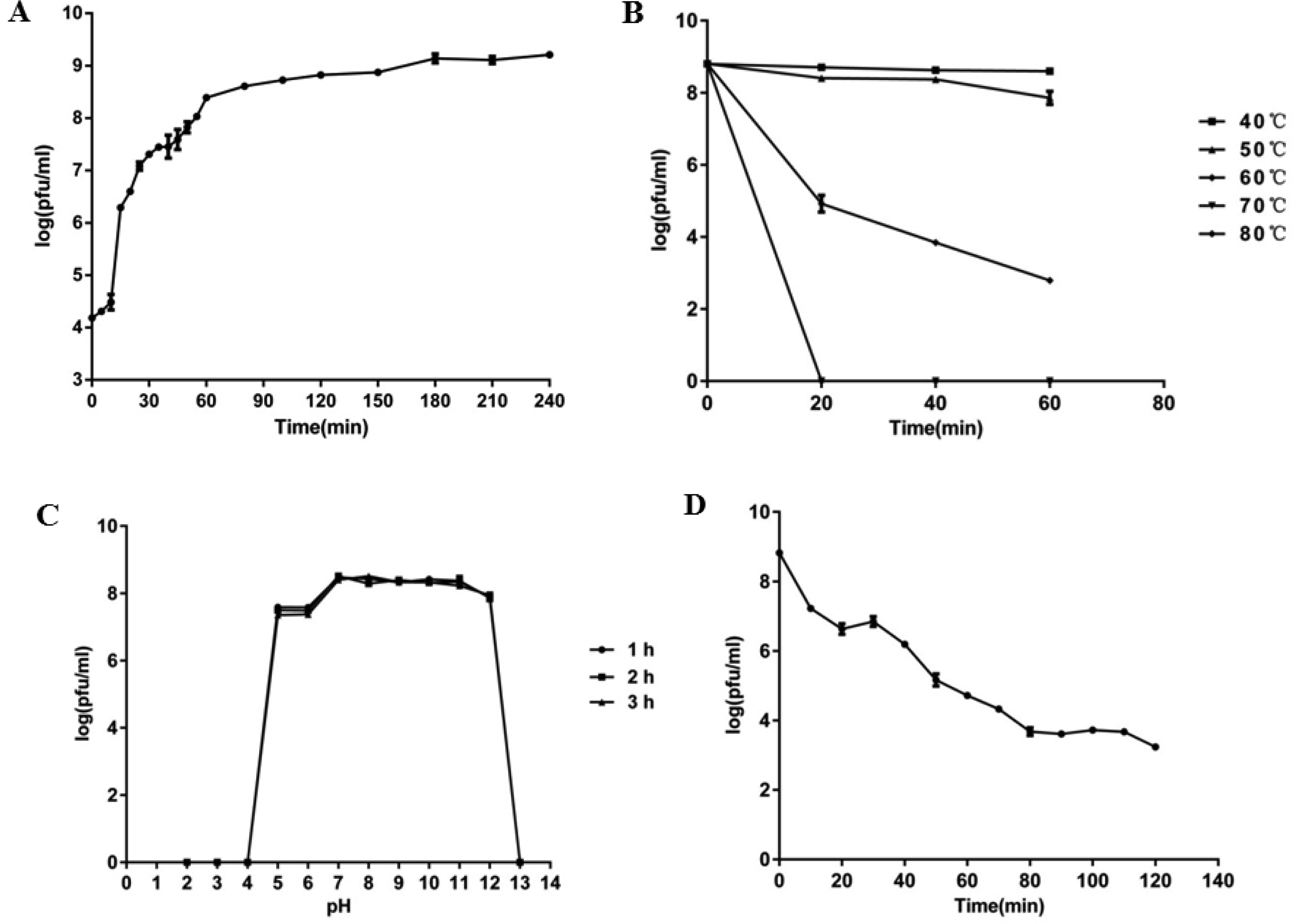
The one-step growth curve showed that the latent period and burst period of phage SA2 were 10 min and 170 min, respectively, and the burst size was about 293 PFUs/infected cell (Figure 2A). The positive linear relationship was found between lysis time and burst size, which is similar to other isogenic λ-phages [28]. Phage SA2 was stable at temperatures ranging from 40 to 50 °C, but the phage titer decreased significantly after heat treatment (60 °C, 20 minutes) and the phages were completely inactivated at 70 °C (Figure 2B). The phage activity was relatively stable over a broad pH range (7–12) after at least 3 h of incubation, but under extreme pH conditions (below pH 5 or above pH 12) the phage titer declined abruptly (Figure 2C). After exposure to ultraviolet light, the phage titer decreased significantly by five orders of magnitude within 2 hours (Figure 2D), showing that UV had a certain lethal effect on the phage SA2.
3.5. In vitro bacteriolytic activity
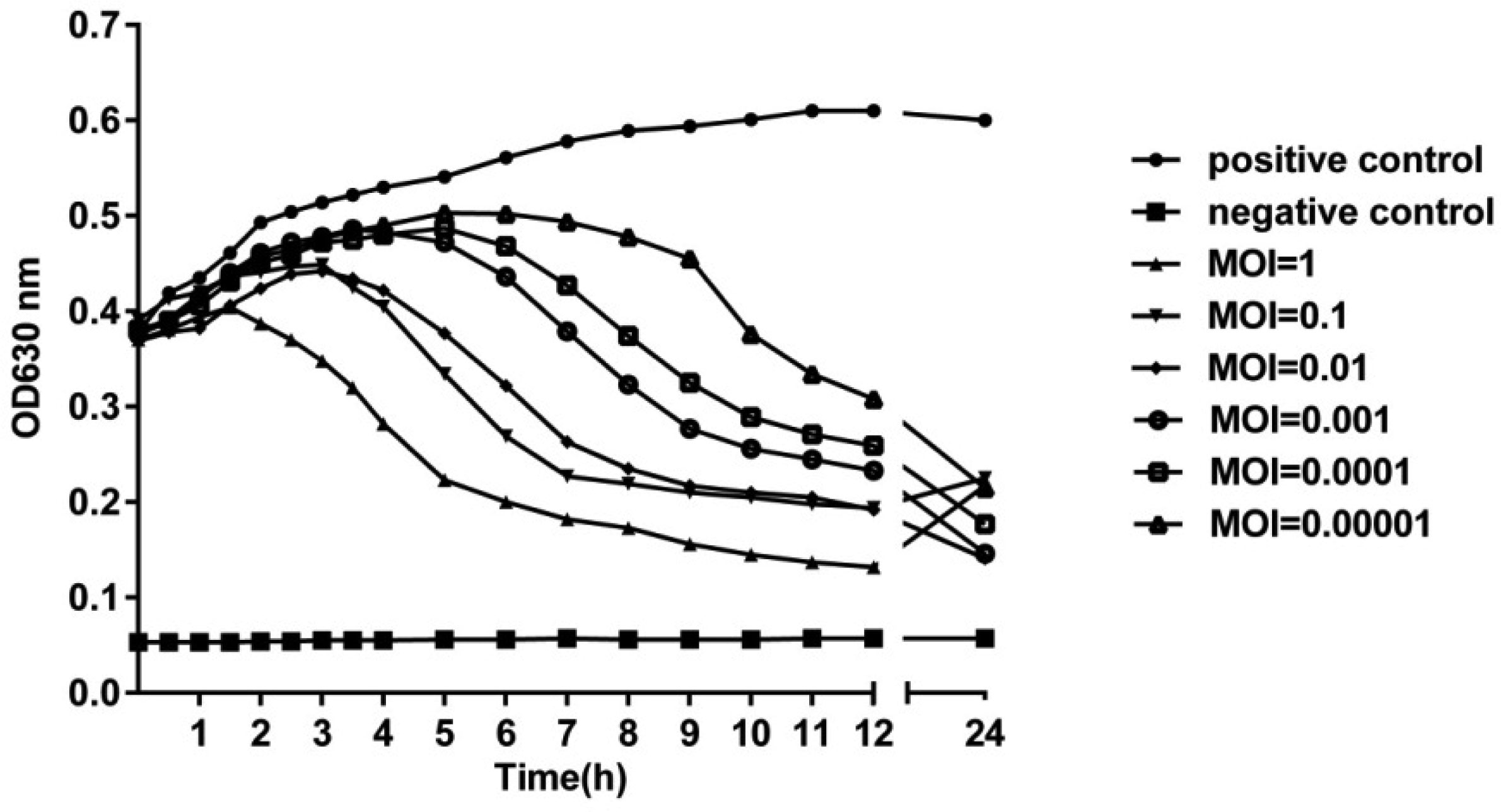
The in vitro bacteriolytic activity of phage SA2 was determined using spectrophotometry, as shown in Figure 3. The absorbance of the positive control increased continuously within 24 hours, while the absorbance of the negative control remained unchanged. In contrast, the absorbance of the culture broth containing phage SA2 and S. aureus at different MOIs increased gradually during the first few hours and then decreased remarkably, indicating that S. aureus was lysed by phage SA2. At 24 h, most of the bacteria were lysed by phage SA2 at all MOIs. The decrease in absorbance during the first few hours (3–7 hours) depended on the MOI values. The higher the MOI value is, the faster the absorbance decreases. For example, the absorbance started to decline as early as about 2 h after the onset of co-incubation at a MOI of 1.
3.6. Characterization of phage SA2 genome
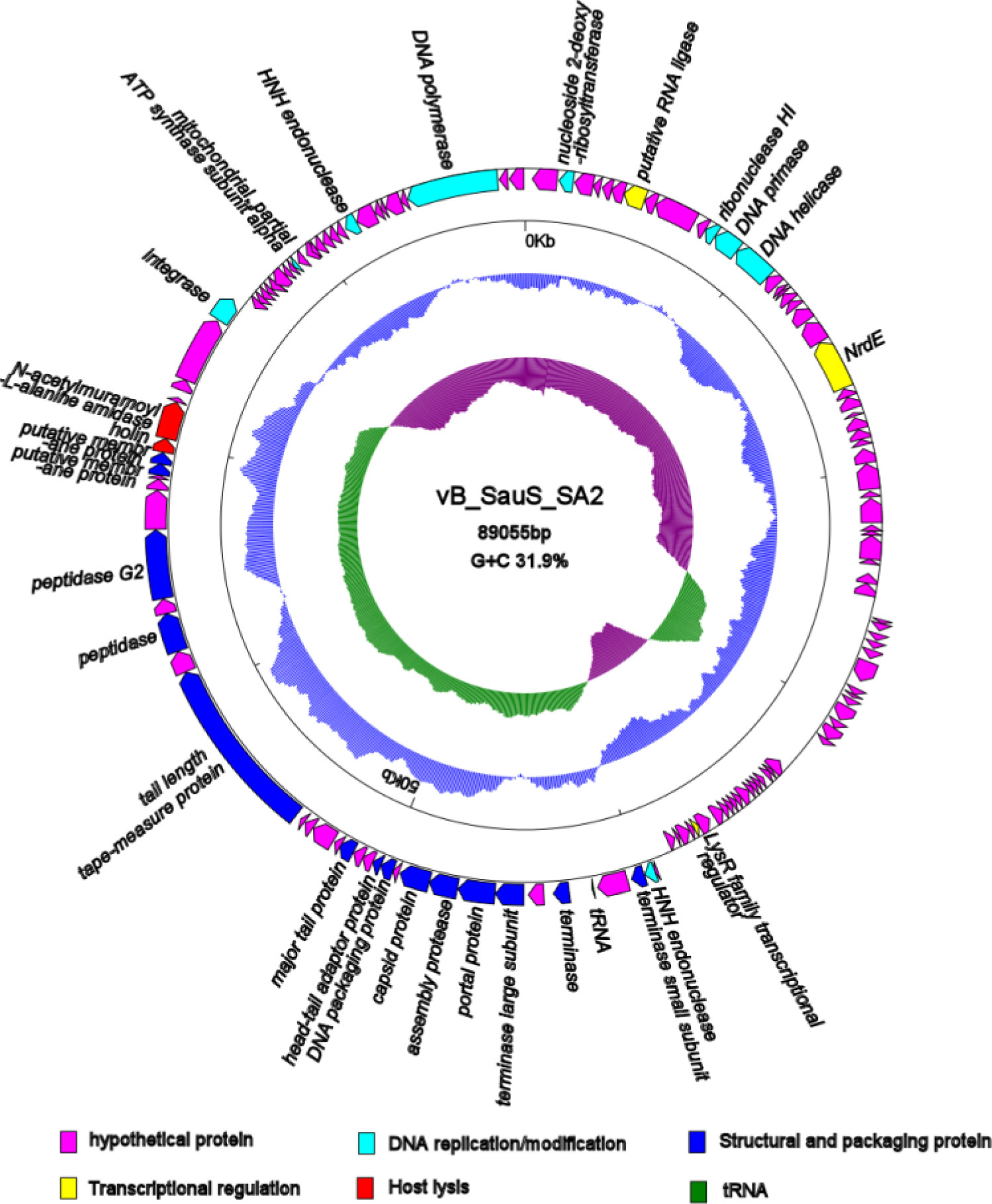
Analysis of the whole genome showed that SA2 was a linear double-stranded DNA molecule of 89,055 bp with an average G + C content of 31.9%. The genome contained 130 predicted open reading frames (ORFs), and the inverted ORFs accounted for 62.3% (81 ORFs) of the total genome. The majority of the ORFs presented an ATG start codon (88.5%), while seven started with TTG, eight with GTG. One tRNA gene (tRNAAsn) was discovered in the genome of phage SA2. No virulence gene was detected. Of the 130 ORFs, 28 had assigned functions, 18 were unique and similar genes were not found in the deposited genomes in the GenBank, while the remaining ORFs were annotated as hypothetical proteins (Table 2). Phage SA2 possessed the same modular genomic architecture as the majority of dsDNA phages [29] (Figure 4), including DNA replication and modification, transcriptional regulation, phage packaging and structural proteins, and proteins involved in host lysis.
DNA replication and modification modules are involved in the coordinated activity of several enzymes. A nucleoside 2-deoxyribosyltransferase was encoded by ORF2 of phage SA2 that showed 78% homology to Staphylococcus phage vB_Sau_S24 (Myoviridae). ORF11 was predicted to encode ribonuclease HI, an enzyme that cleaves the RNA strand of an RNA/DNA hybrid, and it had 42% homology to the genes of Candidatus Rokubacteria bacteria, but without homology to any phage. Other replication proteins of phage SA2 were similar to the proteins of Staphylococcus epidermidis phage. DNA primase (encoded by ORF12) can be used to initiate DNA synthesis [30]. DNA helicase (encoded by ORF13) can utilize ATP hydrolysis to separate the DNA double helix into individual strands [31]. The main function of DNA polymerase (encoded by ORF128) is to fill DNA gaps generated during DNA repair, recombination, and replication. ORF71 and ORF122 were predicted to encode HNH endonucleases that play a variety of roles in the phage lifecycle [32]. These proteins are commonly observed in phages of the Twortlikevirus genus of the family Herelleviridae (formerly the subfamily Spounavirinae of the family Myoviridae), but they are rarely found in staphylococcal Siphoviridae phages [20].
ORF7 was predicted to encode a putative RNA ligase that exhibits 80% high sequence identity to Staphylococcus phage S25-3. ORF21 encoded NrdE, an aerobic Ib ribonucleotide reductase with the basic function of reducing ribonucleotides to deoxyribonucleotides [33]. The LysR family of transcriptional regulators (encoded by ORF65) regulates a diverse set of genes, including those involved in virulence, metabolism, quorum sensing and motor genes [34].
ORF72 and ORF76 encoded the small terminase subunit and large terminase subunit, respectively, which resembled the packaging module of Staphylococcus phage 6ec. Terminase is an enzyme that can insert a single viral genome into the interior of a viral procapsid by a process known as ‘encapsulation or packaging’, and it consists of a small subunit and a large subunit [35]. Typically, the small terminase subunit specifically recognizes viral DNA and recruits the large terminase protein for the initial cleavage. The large terminase subunit has an ATPase activity that provides energy for packaging initiation and termination [36],[37]. Portal protein (encoded by ORF77) shares high amino acid sequence similarity with Staphylococcus phage vB_SepS_SEP9, which can inject DNA into the host cell through a pathway formed by portal protein [38]. Assembly protease (encoded by ORF78) and DNA packaging protein (encoded by ORF81) were also found in phage SA2.
Among the phage structural proteins, ORF82 was predicted to be a head-tail adaptor protein that acted as an adaptor and bound directly to portal proteins during connector assembly [39]. ORF79 and ORF85 were predicted to encode a capsid protein and a major tail protein, respectively. ORF90 was predicted to encode a tail length tape-measure protein (TMP), and TMP was the longest protein product with 2,332 amino acids. TMP determines the length of the tail, and the length of the corresponding gene is proportional to the tail [40], which may explain the large size of the SA2 tail (410 nm). This protein contained peptidoglycan hydrolytic domains (an N-terminal lytic transglycosylase SLT domain and a C-terminal peptidase_M23 domain), which is similar to other staphylococcal Siphoviruses proteins [41]. It is possible that a long tail/TMP may be beneficial in locating phage for optimal infection, ultimately docking the phage (tail tube) on the cell membrane in a more efficient manner [40].
ORF92 was predicted as a peptidase with a prophage endopeptidase tail, which may belong to virion-associated peptidoglycan hydrolase (VAPGHs). VAPGHs are structural components of phage that locally degrade peptidoglycans of the bacterial cell walls during infection [42]. ORF94 was predicted to encode a peptidase G2 with a pectate lyase superfamily protein that could be involved in the degradation of extracellular polymers [20].
The lysis cassette of phage SA2 was comprised of holin and N-acetylmuramoyl-L-alanine amidase. Holin (encoded by ORF100) is a small phage encoding protein that forms large holes on the cell membrane to alter the permeability and performs similar functions as signal peptides [43]. It can be categorized into three subtypes: class I, class II and class III [44]. The holin protein of phage SA2 had two potential class II membrane-spanning domains and shared 62% identity with Staphylococcus phage phiIPLA-RODI (Myoviridae). ORF101 was predicted to encode N-acetylmuramoyl-L-alanine amidase and contained three domains: SH3 peptidoglycan-binding domain, PGRP super-family conserved domain and N-terminal CHAP endopeptidase domain. N-acetylmuramoyl- L -alanine amidase is specifically dedicated to lysis, and holin dedicates to the amidase activation at a precisely defined time [45], which can be attributed to the function of endolysin. Phage likely lyses the host cell to release its progeny through the holin-endolysin lytic system, which is thought to be universal in almost all dsDNA phages [46],[47].
ORF105 was predicted to encode integrase. The results showed that 36 of the 130 ORFs of phage SA2 were homologous to bacterial genome (28%), indicating that these bacteria could contain temperate phages. Our experiments indicated that phage SA2 was able to lysogenize the host bacteria, and ORF100 (holin) (Figure S1A) and ORF101 (lysin) (Figure S1B) of phage SA2 could be detected by PCR in the three isolated colonies, and they were not more sensitive to phage SA2. Interestingly, the integrase gene was also found in the genomic sequence of phage SEP9 (YP_009007700.1), which had 68% homology with SA2, but phage SEP9 was not a lysogenic phage.
3.7.
Phylogenetic and comparative genomic analysis
Genome-wide BLAST analysis revealed that the SA2 genome showed very low similarity with phage genomes deposited in public databases (Table S1). The sequence of phage SA2 was 75% homologous to those of both staphylococcal phage 6ec (KJ804259.1) and staphylococcal phage vB_SepS_SEP9 (KF929199.1), while genome coverage was only 7% and 5%, respectively (Figure S2). Multi-genomic alignment revealed that SA2 had similar regions with homology to the 6ec and SEP9 genomes, but their locations differed (Figure S3). The phylogenetic tree indicated that phage SA2 was related to S. epidermidis bacteriophages 6ec and SEP9, but differed from other staphylococcal phages (Figure 5). The comparative genomic analysis showed that the genome of phage SA2 was 89.5 kb, similar to those of phage SEP9 (92.4 kb), phage 6ec (93.8 kb) and phage PMBT8 (88.1 kb), and the overall G+C content was 31.9%, similar to those of phage SEP9 (29.6%), phage 6ec (29.3%) and phage PMBT8 (31.6%). The phage SEP9 belongs to a ‘Sep9likevirus’ genus, and the phage 6ec has not been assigned to an exact genus yet. So far, most members of the Siphoviridae family of bacteriophages remain unclassified. Since the morphological and genomic of phage SA2 was different from ‘3alikevirus’, ‘77likevirus’, ‘Phietalike-virus’, and ‘Sep9likevirus’ of Staphylococcal Siphoviruses , a new Siphoviridae genus, named ‘SA2likevirus, was proposed based on the unique characteristics of phage SA2.
4.
Conclusions
In this study, we isolated and characterized a novel lysogenic phage SA2 against S. aureus, which belonged to the family Siphoviridae. Phage SA2 showed lytic activity against several S. aureus strains and S. saprophyticus strains. At a MOI of 0.1, phage SA2 showed a short latent period and a long burst period, and the burst size was 293 PFUs/infected cell. Phage SA2 was stable over a wide pH range of 7–12 at 40–50 °C, but it was sensitive to ultraviolet light.
The phage SA2 had a polyhedral head (75 nm in diameter) and a long curved tail (400 nm in length), which was different from that of ‘3alikevirus’, ‘77likevirus’, ‘Phietalike-virus’, and ‘Sep9likevirus’ of Staphylococcal Siphoviruses. The phage SA2 genome showed very low similarity with all phage genomes deposited in public databases. Its linear dsDNA genome was comprised of 130 ORFs, 28 of which had assigned functions, and 18 were unique. One tRNA gene (tRNAAsn) was discovered, and no virulence genes were identified. Holin and N-acetylmuramoyl-L-alanine amidase were predicted, indicating that SA2 may be a newer therapeutic agent against S. aureus infection.
In conclusion, the Siphoviridae phage SA2 isolated in this study had the characteristics of a short latent period, a long burst period, and low genomic homology. It was different from any other known Siphoviridae phages, so we proposed a new Siphoviridae genus named ‘SA2likevirus’. Phage SA2 could lyse S. aureus strains and S. saprophyticus stains, and the unique ability to lyse host cells makes it possible to use phage SA2 as a new tool to explore the mechanisms of pathogenesis and resistance of multiple drug-resistant strains of S. aureus. The findings may provide a valuable reference for further development of phage-based biocontrol agents that are effective against S. aureus.









 DownLoad:
DownLoad: