Resolving environmental, social, and governance challenges: A bibliometric review of ethical supply chain management

1.   Introduction

Population dynamics has always been an important research object of biomathematics. Various groups often have complex interspecific relationships, such as predation, competition, parasitism and mutualism ^[1]. Predation behavior, as a widespread interspecies relationship, has been widely studied. Lotka and Volterra were the first to propose a predator-prey system to describe the widespread interspecies relationship of predation ^[2]. Holling further proposed three functional responses of predators to describe the energy transfer between predators and prey ^[3]. These three functional responses have been applied and perfected by many scientists ^[4]. In 1991, Hastings and Powell proposed a food chain system with chaotic dynamics and studied the dynamics of the model ^[5]. In recent years, many mathematicians have also studied the development and improvement of Hastings-Powell food chain models ^[6,7,8,9].

Fractional calculus is a generalization of traditional calculus, and its order can be composed of integers, fractions or complex numbers^[10]. Fractional calculus can better describe some systems or processes with memory and hereditary properties, and it has been widely used in many fields, such as physics, secure communication, system control, neural networks, and chaos^[11,12]. The method of solving the fractional model has also been widely studied^[13,14]. In ^[15], the Caputo fractional derivative operator is used instead of the integer first derivative to establish an effective numerical method for solving the dynamics of the reaction-diffusion model based on a new implicit finite difference scheme. In ^[16], a numerical approximation for the Caputo-Fabrizio derivative is used to study the dynamic complexity of a predator-prey system with a Holling-type functional response. In ^[17], a new fractional chaotic system described by the Caputo fractional derivative is presented, and how to use the bifurcation diagram of this chaotic system to detect chaotic regions is analyzed. In ^[18], the generalization of Lyapunov's direct method applying Bihari's and Bellman-Gronwall's inequalities to Caputo-type fractional-order nonlinear systems is proposed. In ^[19], the Fourier spectral method is introduced to explore the dynamic richness of two-dimensional and three-dimensional fractional reaction-diffusion equations. In ^[20], the spatial pattern formation of the predator-prey model with different functional responses was studied. ^[21] studied the numerical solution of the space-time fractional reaction-diffusion problem that simulates the dynamic and complex phenomena of abnormal diffusion.

Since most biological mathematical models have long-term memory, fractional differential equations can more accurately and reliably describe the actual dynamic process ^[1,22]. ^[23] proposed fractional predator-prey models and fractional rabies models and studied their equilibrium points, stability and numerical solutions. In ^[24], the authors studied the stability of a fractional-order system by the Lyapunov direct method, which substantially developed techniques to study the stability of fractional-order population models. In ^[9], the authors extended the Hastings-Powell food chain system to fractional order and analyzed its dynamic behavior.

As an important research object of biological mathematics and control theory, population model control has received extensive research and development in recent years ^[25,26,27]. In ^[28], the authors conducted random detection and contacted tracking on the HIV/AIDS epidemic model and used the Adams-type predictor-corrector method to perform fractional optimal control of the model, which significantly reduced the number of AIDS patients and HIV-infected patients. In ^[29], the authors applied the time-delay feedback controller to the fractional-order competitive Internet model to solve the bifurcation control problem of this model. In ^[30], the author considered the influence of additional predators on the Hastings-Powell food chain model and studied the control of chaos in this model.

Biological models are widely studied by scientists, but many classic models study food chain models composed of herbivores and carnivores, and omnivores are rarely considered. In fact, omnivores are widespread in nature and play an important role in the food chain. In this article, the existence of omnivores is fully considered, and a food chain model in which herbivores, omnivores and carnivores coexist is studied. Based on these works, this paper proposes a fractional food chain model with a Holling type-II functional response. The main contributions of this paper are as follows. First, this paper proves the existence and uniqueness of the solution and the nonnegativity and boundedness of the solution. Second, the equilibrium point of the model is calculated, and the local stability of the equilibrium point is proven. Third, a controller is designed to prove the global asymptotic stability of the system by using the Lyapunov method.

This paper is organized as follows. In Section 2, the definitions and lemmas are given, and the food chain model is established. In Section 3, the existence, uniqueness, nonnegativity and boundedness are proven, and the local stability of the equilibrium point of the model is studied. The global stability of the model is studied through the controller. In Section 4, numerical simulations are performed to verify the theoretical results. The conclusion of this article is given in Section 5.

2.   Model description and preliminaries

In this section, some basic knowledge about fractional equations and the theorems and lemmas used in this paper are given, and the fractional food chain system is introduced.

Definition 1. ^[10]. The Caputo fractional derivative of order $\alpha$ of a function $f$, ${\mathbb{R}}^{+}\rightarrow {\mathbb{R}}$, is defined by

where $\Gamma (\cdot)$ is the Gamma function. When $0 < \alpha < 1$,

Definition 2. ^[31]. When the order $a > 0$, for a function $f:(0, \infty)\rightarrow {\mathbb{R}}$, the Riemann-Liouville representation of the fractional integral operator is defined by

where $a > 0$ and $\Gamma (\cdot)$ is the Gamma function.

Lemma 1. (Generalized Gronwall inequality) ^[32]. Assume that $m\geq0$, $\gamma > 0$, and $a(t)$ are nonnegative, locally integrable, and nondecreasing functions defined on $0\leq t\leq T (T\leq\infty)$. In addition, $h(t)$ is a nonnegative, locally integrable function defined in $0\leq t\leq T$ and satisfies

then,

where the Mittag-Leffler function $E_{\gamma}(z) = \sum \limits_{k = 0}^{\infty}\frac{z^{k}}{\Gamma(k\gamma+1)}$.

Lemma 2. ^[10]. Consider the fractional-order system

where $f(t, x(t))$ defined in ${\mathbb{R}}^{+} \times {\mathbb{R}}^{n} \rightarrow {\mathbb{R}}^{n}$ and $\alpha\in(0, 1]$.

The local asymptotic stability of the equilibrium point of this system can be derived from $|arg(\lambda_{i})| > \frac{\alpha\pi}{2}$, where $\lambda_{i}$ are the eigenvalues of the Jacobian matrix at the equilibrium points.

Lemma 3. ^[24]. Consider the system

where $\alpha\in (0, 1]$, $f:[t_{0}, \infty) \times \Omega \rightarrow {\mathbb{R}}^{n}$, and $\Omega \in {\mathbb{R}}^{n}$; if $f(t, x)$ satisfies the local Lipschitz condition about $x$ on $[t_{0}, \infty) \times \Omega$, then there exists a unique solution of (2.2).

Lemma 4. ^[33]. The function $x(t)\in {\mathbb{R}}^{+}$ is continuous and derivable; then, for any $t\geq t_{0}$

There are a variety of complex biological relationships in nature. Predation is the most important biological relationship, and it has received attention from and been studied by many scientists. In ^[5], the author proposed a three-species food chain model. The model consists of one prey $\hat{X}$ and two predators $\hat{Y}$ and $\hat{Z}$. The top predator $\hat{Z}$ feeds on the secondary predator $\hat{Y}$, and the secondary predator $\hat{Y}$ feeds on the prey $\hat{X}$. This is the famous Hastings-Powell model:

where $\hat{R}$ and $\hat{K}$ represent the intrinsic growth rates and environmental carrying capacity, respectively. For $i = 1, 2$, parameters$\hat{A_{i}}$, $\hat{B_{i}}$, $\hat{C_{i}}$ and $\hat{D_{i}}$ are the predation coefficients, half-saturation constant, food conversion coefficients and death rates.

The Hastings-Powell model considers a food chain composed of herbivores, small carnivores and large carnivores but does not consider the existence of omnivores. We consider a food chain consisting of small herbivores $X$, medium omnivores $Y$ and large carnivores $Z$. Among them, omnivores $Y$ prey on herbivores $X$, and carnivores $Z$ prey on omnivores $Y$. They all respond according to Holling II type. This system can be expressed mathematically as

where $X$, $Y$ and $Z$ represent the densities of the prey population, primary predator population and top-predator population, respectively. For $i = 1, 2$, parameters $R_{i}$, $K_{i}$, $A_{i}$, $B_{i}$ and $C_{i}$ are the intrinsic growth rates, environmental carrying capacity, predation coefficients, half-saturation constant and food conversion coefficients, respectively. The parameter $D$ is the death rates for $Z$.

Then, we obtain the following dimensionless version of the food chain model:

the independent variables $x$, $y$ and $z$ are dimensionless population variables; $t$ represents a dimensionless time variable; and $a_{i}$, $b_{i} (i = 1, 2)$ and $d$ are positive.

Research results show that using fractional derivatives to model real-life biological problems is more accurate than classical derivatives^[15]. To better analyze the dynamics between these three populations, we studied the following fractional-order Hastings-Powell System food chain model:

where $\alpha\in(0, 1)$ is the fractional order.

3.   Main results

3.1.   Properties of the solution

Theorem 1. The fractional-order Hastings-Powell System food chain model (2.6) has a unique solution.

Proof: We will study the existence and uniqueness of the system (2.6) in $[0, T]\times\Omega$, where $\Omega = \{(x, y, z)\in {\mathbb{R}}^{3} : 0\leq x, y, z\leq H\}$. Let $S = (x, y, z)$, $\bar{S} = (\bar{x}, \bar{y}, \bar{z})$, $F(S) = (F_{1}(S), F_{2}(S), F_{3}(S))$ and

For any $S, \bar{S} \in\Omega$, it follows from (3.1) that

where $L = max\{r_{1}+\frac{r_{1}M}{K_{1}}+M, r_{2}+\frac{r_{2}M}{K_{2}}+2M+b_{1}M^{2}, d+M+b_{2}M^{2}\}$, Based on Lemma 3, $F(S)$ satisfies the Lipschitz condition with respect to $S$ in $\Omega$. According to the Banach fixed point theorem in ^[34], system (2.6) has a unique solution in $\Omega$.

Theorem 2. Set $A = \{{x, y, z)\in \mathbb{R}}^{3} : 0 < x+y+z < \frac{K_{1}(r_{1}+v)^{2}}{4r_{1}v}+ \frac{K_{2}(r_{2}+v)^{2}}{4r_{2}v} \}$ as a positively invariant set of system (2.6), and the solutions are bounded.

Proof: let $g(t)\triangleq g(x(t), y(t), z(t)) = x(t)+y(t)+z(t)$,

let

According to the positive knowledge of all parameters and the nonnegativity of the solutions,

we obtain

Since $E_{\alpha}(-vt^{\alpha})\geq0$, when $g(0)\leq\frac{u}{v}$, $\lim\limits_{t \to \infty} \sup g(t)\leq\frac{u}{v}$. According to the nonnegativity of the system (2.6), $g(t)\geq 0 (\forall t \geq 0)$; hence, $A = \{{x, y, z)\in \mathbb{R}}^{3} : 0 < x+y+z < \frac{K_{1}(r_{1}+v)^{2}}{4r_{1}v}+ \frac{K_{2}(r_{2}+v)^{2}}{4r_{2}v} \}$ is a positively invariant set of system (2.6), and the solutions are bounded.

3.2.   Equilibria and their stability

Let

Then, the equilibrium points are $E_{0} = (0, 0, 0)$, $E_{1} = (K_{1}, 0, 0)$, $E_{2} = (0, K_{2}, 0)$ and $E_{*} = (x_{*}, y_{*}, z_{*})$, where

For system (2.6), the Jacobian matrix at the equilibrium point $(x', y', z')$ is

where $e_{1} = a_{2}-b_{2}d$, $e_{2} = \frac{b_{2}d}{e_{1}}+1$, $e_{3} = 1+b_{1}x'$, $e_{4} = \frac{2r_{1}x'}{K_{1}}+\frac{a_{1}d}{e_{1}e_{3}^{2}}$, $e_{5} = \frac{a_{1}x'}{e_{3}}$.

Theorem 3.3. For system (2.6), the equilibrium points $E_{0}$ and $E_{1}$ are saddle points.

Proof: The Jacobian matrices evaluated at $E_{0}$ and $E_{1}$ are

According to Lemma 2, when the eigenvalues are all real numbers and all negative, the equilibrium points are locally asymptotically stable.

The eigenvalues of $J(E_{0})$ are $\lambda_{01} = r_{1}$, $\lambda_{02} = r_{2}$ and $\lambda_{03} = -d$. The eigenvalues of $J(E_{1})$ are $\lambda_{11} = -r_{1}$, $\lambda_{12} = r_{2}+\frac{a_{1}K_{1}}{b_{1}K_{1}+1}$ and $\lambda_{13} = -d$.

Then, we have $\lambda_{01}, \lambda_{02} > 0$, $\lambda_{03}, \lambda_{11} < 0,$ and $\lambda_{13} < 0$, so the equilibrium points $E_{0}$ and $E_{1}$ are saddle points.

Theorem 4. For system (2.6), if $r_{1} < a_{1}K_{2}$ and $\frac{a_{2}K_{2}}{(b_{2}K_{2}+1)} < d$, then the equilibrium point $E_{2} = (0, K_{2}, 0)$ is locally asymptotically stable.

Proof: The Jacobian matrix evaluated at $E_{2}$ is

The eigenvalues of $J(E_{2})$ are $\lambda_{1} = r_{1}-a_{1}K_{2}$, $\lambda_{2} = -r_{2}$ and $\lambda_{3} = \frac{a_{2}K_{2}}{b_{2}K_{2}+1}-d$.

Therefore, if $r_{1} < a_{1}K_{2}$ and $\frac{a_{2}K_{2}}{(b_{2}K_{2}+1)} < d$, the equilibrium point $E_{2}$ is locally asymptotically stable.

The characteristic equation of equilibrium points $E_{*} = (x_{*}, y_{*}, z_{*})$ is given as

where

$A = 2f_{4}-2r_{1}-e_{5}+f_{2}z_{*}+f_{1}de_{3}^{2}+f_{5}-\frac{f_{2}b_{2}dz_{*}}{e_{1}e_{2}}$,

$B = (B_{1}+B_{2})$,

$B_{1} = e_{4}e_{5}+e_{5}r_{1}+r_{1}^{2}-2r_{1}f_{4}-f_{2}r_{1}z_{*}-2e_{5}f_{4}+\frac{e_{1}^{2}dz_{*}}{a_{2}} - f_{6}e_{5}-f_{6}r_{1}-2r_{1}f_{5}$,

$B_{2} = 2e_{3}^{2}f_{1}f_{5}+2f_{2}f_{4}z_{*}+a_{1}f_{3}e_{3}^{2}z_{*} +\frac{4dr_{2}f_{4}}{e_{1}k_{1}}+r_{1}f_{7}-f_{1}f_{7}de_{3}-2f_{4}f_{7}$,

$C = \frac{dz_{*}(a_{1}dK_{1}e_{3}^{2}-e_{1}K_{1}r_{1}+2e_{1}r_{1}x_{*})}{f_{1}K_{1}}$,

where $f_{1} = \frac{a_{1}}{e_{1}}$, $f_{2} = \frac{a_{2}}{e_{2}}$, $f_{3} = \frac{f_{2}d}{e_{1}}$, $f_{4} = \frac{r_{1}x_{*}}{K_{1}}$, $f_{5} = \frac{r_{2}d}{e_{1}K_{2}}$, $f_{6} = \frac{a_{1}de_{3}^{2}}{e_{1}}$, $f_{7} = \frac{b_{2}f_{3}z_{*}}{e_{2}}$.

For Eq. (3.2), define the discriminant as

With reference to the results of ^[35] and ^[36], we obtain the following fractional Routh-Hurwitz conditions:

$1.$ If $D(P) > 0$, $A > 0$, $C > 0$, and $AB-C > 0$, $E_{*}$ is locally asymptotically stable.

$2.$ If $D(P) < 0$ and $A\geq0$, $B\geq0$, and $C > 0$, when $\alpha < \frac{2}{3}$, $E_{*}$ is locally asymptotically stable.

$3.$ If $D(P) < 0$, $A > 0$, $B > 0$, and $AB = C$, then for all $\alpha \in (0, 1)$, $E_{*}$ is locally asymptotically stable.

Theorem 5. If $D(P) < 0$, $C > 0$ and $AB\neq C$, then $\alpha_{*}\in(0, 1)$ exists; when $\alpha\in(0, \alpha_{*})$, $E_{*}$ is locally asymptotically stable; when $\alpha\in(\alpha_{*}, 1)$, $E_{*}$ is unstable. The system diverges at the critical value $E_{*}$.

Proof: If $D(P) < 0$, then the eigenvalues of Eq. (3.2) have one real root $\lambda_{1} = a$ and two complex conjugate roots $\lambda_{2, 3} = b\pm ci$. Then, Eq. (3.2) can be written as

where $A = -a-2b$, $B = b^{2}+c^{2}+2ab$, $C = -a(b^{2}+c^{2})$, $c > 0$, $a, b, c \in\mathbb{R}$.

From $C > 0$, then $a < 0$, and then $|arg(\lambda_{1})| = \pi > \frac{\alpha\pi}{2}$.

From $AB\neq C$, then $-a^{2}b+b(b^{2}+c^{2})\neq -2ab^{2}$ $\Longrightarrow$ $-2b[(a+b)^{2}+c^{2}]\neq0$ $\Longrightarrow$ $b\neq0$ and $(a+b)^{2}+c^{2}\neq0$.

Thus, we can obtain $|arg(\lambda_{2, 3})| = |arctan(\frac{c}{b})| = arctan|\frac{c}{b}|\in(0, \frac{\pi}{2})$.

Then, $\alpha_{*}\in(0, 1)$ exists; when $\alpha\in(0, \alpha_{*})$, $\frac{\alpha\pi}{2} < arctan|\frac{c}{b}|$, according to Lemma 2, $E_{*}$ is locally asymptotically stable, and when $\alpha\in(\alpha_{*}, 1)$, $\frac{\alpha\pi}{2} > arctan|\frac{c}{b}|$, $E_{*}$ is unstable.

3.3.   Global asymptotic stability

To study the asymptotic stability of system (2.6), three controllers will be added. The controller is proposed as follows: $\mu_{1} = m_{1}x(x-x_{*})$, $\mu_{2} = m_{2}y(y-y_{*})$, and $\mu_{3} = m_{3}z(z-z_{*})$. where $m_{1}$, $m_{2}$ and $m_{3}$ represent negative feedback gains, which are defined as real numbers. Clearly, if $m_{i} = 0 (i = 1, 2, 3)$ or $x = x_{*} (y = y_{*}, z = z_{*})$, then $\mu_{i} = 0 (i = 1, 2, 3)$, so it will not change the equilibrium point of system (2.6).

Controllers added into system (2.6) as follows

One gives a Lyapunov function as:

then,

Consider $E_{*}$ to be the equilibrium point:

According to Lemma 4, we can obtain

When $m_{1}\geq\frac{a_{1}b_{1}(2y_{*}+x_{*})}{2(1+b_{1}x_{*})}-\frac{r_{1}}{K_{1}}$, $m_{2}\geq\frac{a_{2}b_{2}(2z_{*}+y_{*})}{2(1+b_{2}y_{*})}+\frac{a_{1}b_{1}x_{*}}{2(1+b_{1}x_{*})}-\frac{r_{2}}{K_{2}}$, and $m_{3}\geq\frac{a_{2}b_{2}y_{*}}{2(1+b_{2}y_{*})}$, it follows that $D^{\alpha}V\leq0$. We can show that the equilibrium point $E_{*}$ is uniformly asymptotically stable.

4.   Numerical examples

In this section, we use the Adams-Bashforth-Molton predictor-corrector algorithm numerical simulation. This method is described in detail in ^[37] and ^[38].

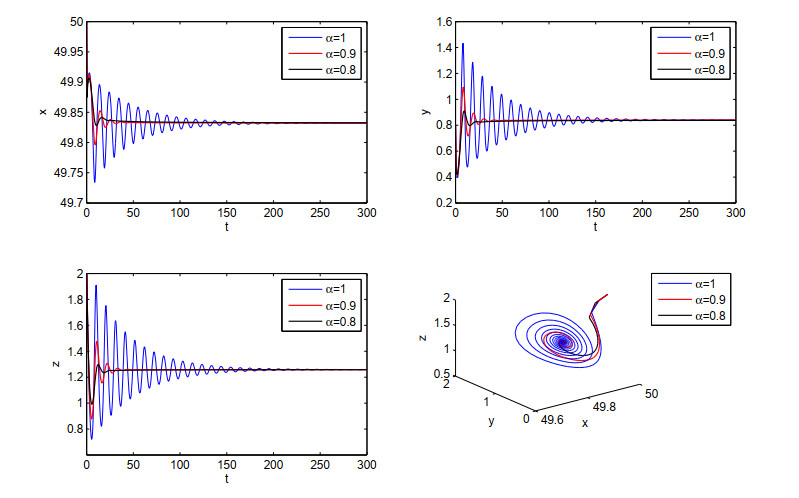
Example 1. In system (2.6), let $r_{1} = 1$, $r_{2} = 0.6$, $K_{1} = 50$, $K_{2} = 10$, $a_{1} = 1$, $a_{2} = 0.6$, $b_{1} = 5$, $b_{2} = 0.01$ and $d = 0.5$. System (2.6) has a positive equilibrium point $E_{*} = (49.8479, 0.8403, 1.2597)$. According to Theorem 3.5, when $\alpha = 1$, $\alpha = 0.9$, $\alpha = 0.8$, and $E_{*}$ is locally asymptotically stable, it can be seen from Figure 1 that the order $\alpha$ will affect the speed at which the system converges to the equilibrium point. The relevant results are shown in Figure 1.

Example 2. In system (2.6), let $r_{1} = 1$, $r_{2} = 0.6$, $K_{1} = 50$, $K_{2} = 30$, $a_{1} = 1$, $a_{2} = 0.6$, $b_{1} = 5$, $b_{2} = 0.2$ and $d = 0.2$. System (2.6) has a positive equilibrium point $E_{*} = (49.9382, 0.3571, 1.4158)$. It follows from Theorem 3.5 that system (2.6) has a bifurcation at $\alpha_{*}$. When $\alpha = 0.95$ and $\alpha = 0.8$, $E_{*}$ is locally asymptotically stable, and when $\alpha = 0.98$, $E_{*}$ is unstable. The relevant results are shown in Figure 2.

Example 3. To verify the sensitivity of the system (2.6) to initial conditions and other parameters, according to the method in ^[39], apply the positive Euler format to transform the differential model into the following discrete form:

where $\delta$ is the time step size. We use the parameters of Example 1 to study Lyapunov exponents. Figure 3 shows that system (2.6) is in a stable state and is less sensitive to initial conditions.

5.   Conclusions

This paper studies a new fractional-order food chain model with a Holling type-II functional response. First, the existence, uniqueness, nonnegativity and boundedness of the solution of the model are discussed. Second, the local stability of each equilibrium point is discussed. Third, controllers $\mu_{1} = m_{1}x(x-x_{*})$, $\mu_{2} = m_{2}y(y-y_{*})$ and $\mu_{3} = m_{3}z(z-z_{*})$ are proposed and added to the system. Using the Lyapunov method, sufficient conditions for the positive equilibrium point to reach the global uniformly asymptotically stable state are obtained. Finally, we use numerical simulations to verify the theoretical results.

Acknowledgments

This work was supported by the Shandong University of Science and Technology Research Fund (2018 TDJH101).

Conflict of interest

The author declares no conflicts of interest in this paper.