Analytical insight into fractional Fornberg-Whitham equations using novel transform methods

Safyan Mukhtar; Wedad Albalawi; Faisal Haroon; Samir A. El-Tantawy; Safyan Mukhtar; Wedad Albalawi; Faisal Haroon; Samir A. El-Tantawy

doi:10.3934/math.2025375

AIMS Mathematics

2025, Volume 10, Issue 4: 8165-8190. doi: 10.3934/math.2025375

Previous Article Next Article

Research article Special Issues

Analytical insight into fractional Fornberg-Whitham equations using novel transform methods

1.
Department of Basic Sciences, General Administration of Preparatory Year, King Faisal University, P.O. Box 400, Al Ahsa 31982, Saudi Arabia; fharoon@kfu.edu.sa
2.
Department of Mathematics and Statistics, College of Science, King Faisal University, P.O. Box 400, Al Ahsa 31982, Saudi Arabia
3.
Department of Mathematical Sciences, College of Science, Princess Nourah bint Abdulrahman University, P.O. Box 84428, Riyadh 11671, Saudi Arabia; wsalbalawi@pnu.edu.sa
4.
Department of Physics, Faculty of Science, Port Said University, Port Said 42521, Egypt; samireltantawy@yahoo.com, tantawy@sci.psu.edu.eg
5.
Department of Physics, Faculty of Science, Al-Baha University, Al-Baha 1988, Saudi Arabia

Received: 10 February 2025 Revised: 27 March 2025 Accepted: 29 March 2025 Published: 09 April 2025
MSC : 34G20, 35A20, 35A22, 35R11

This work addressed one of the most essential evolutionary equations that was widely used in describing various nonlinear wave propagation and dispersive phenomena in various scientific and engineering applications, which was called the nonlinear fractional Fornberg-Whitham (FFW). Due to the importance of this equation, we examined it by employing two highly effective techniques: the residual power series method (RPSM) and the new iterative approach (NIM), both distinguished by their efficacy in solving more complicated nonlinear fractional evolutionary equations. Moreover, we integrated the Elzaki transform with both approaches to create Elzaki RPSM (ERPSM) and Elzaki NIM (ENIM) to ease the calculations. The ERPSM effectively combined the power series approach with residual error analysis to generate highly accurate series solutions, while ENIM provided alternative frameworks for handling nonlinearities and achieving rapid convergence. Comparative studies of the obtained solutions highlighted these methods' efficiency, accuracy, and reliability in solving fractional-order differential equations. The results underscored the potential of these analytical techniques for modeling and solving complex fractional wave equations, contributing to the advancement of mathematical physics and computational fluid dynamics.

Keywords:

Citation: Safyan Mukhtar, Wedad Albalawi, Faisal Haroon, Samir A. El-Tantawy. Analytical insight into fractional Fornberg-Whitham equations using novel transform methods[J]. AIMS Mathematics, 2025, 10(4): 8165-8190. doi: 10.3934/math.2025375

Related Papers:

[1]	Yinwan Cheng, Chao Yang, Bing Yao, Yaqin Luo . Neighbor full sum distinguishing total coloring of Halin graphs. AIMS Mathematics, 2022, 7(4): 6959-6970. doi: 10.3934/math.2022386
[2]	Baolin Ma, Chao Yang . Distinguishing colorings of graphs and their subgraphs. AIMS Mathematics, 2023, 8(11): 26561-26573. doi: 10.3934/math.20231357
[3]	Ningge Huang, Lily Chen . AVD edge-colorings of cubic Halin graphs. AIMS Mathematics, 2023, 8(11): 27820-27839. doi: 10.3934/math.20231423
[4]	Huifen Ge, Shumin Zhang, Chengfu Ye, Rongxia Hao . The generalized 4-connectivity of folded Petersen cube networks. AIMS Mathematics, 2022, 7(8): 14718-14737. doi: 10.3934/math.2022809
[5]	Kai An Sim, Kok Bin Wong . On the cooling number of the generalized Petersen graphs. AIMS Mathematics, 2024, 9(12): 36351-36370. doi: 10.3934/math.20241724
[6]	Fugang Chao, Donghan Zhang . Neighbor sum distinguishing total choice number of IC-planar graphs with restrictive conditions. AIMS Mathematics, 2023, 8(6): 13637-13646. doi: 10.3934/math.2023692
[7]	Bana Al Subaiei, Ahlam AlMulhim, Abolape Deborah Akwu . Vertex-edge perfect Roman domination number. AIMS Mathematics, 2023, 8(9): 21472-21483. doi: 10.3934/math.20231094
[8]	Yanyi Li, Lily Chen . Injective edge coloring of generalized Petersen graphs. AIMS Mathematics, 2021, 6(8): 7929-7943. doi: 10.3934/math.2021460
[9]	Ali Raza, Mobeen Munir, Tasawar Abbas, Sayed M Eldin, Ilyas Khan . Spectrum of prism graph and relation with network related quantities. AIMS Mathematics, 2023, 8(2): 2634-2647. doi: 10.3934/math.2023137
[10]	Bao-Hua Xing, Nurten Urlu Ozalan, Jia-Bao Liu . The degree sequence on tensor and cartesian products of graphs and their omega index. AIMS Mathematics, 2023, 8(7): 16618-16632. doi: 10.3934/math.2023850

Abstract

1. Preliminaries

Let $G$ be a simple, non-trivial connected graph with vertex set $V(G)$ . For any two distinct vertices $u$ and $v$ in $G$ , $u$ - $v$ geodesic is a shortest walk between $u$ and $v$ without repetition of vertices. Two vertices are said to be adjacent if there is an edge between them, and they are also called neighbors of each other. The collection of all the neighbors of a vertex $v$ in $G$ is called the (open) neighborhood of $v$ , denoted by $N(v)$ .

A vertex $v$ of $G$ distinguishes a pair $(x, y)$ of distinct vertices of $G$ , if the number of edges in $v$ - $x$ geodesic is different from the number of edge in $v$ - $y$ geodesic. If $(x, y)$ is a pair of neighbors in $G$ , then $v$ is said to be adjacently distinguish the pair $(x, y)$ . Equivalently, a vertex $v$ adjacently distinguishes a pair $(x, y)$ of two neighbors if the difference between the number of edges in $v$ - $x$ geodesic and the number of edges in $v$ - $y$ geodesic is one.

A set $D \subseteq V(G)$ is a distinguishing set (metric generator) for $G$ if the members of $D$ distinguish every pair of distinct vertices in $G$ . The cardinality of a smallest distinguishing set for $G$ is called the metric dimension of $G$ , denoted by $dim(G)$ ^[7,23]. The concept of distinguishing set was introduced, very firstly, by Blumenthal ^[5] in the general context of metric spaces. It was later rediscovered and studied, in the context of graphs, by Slater with the name locating set/reference set ^[23]. Independently, Harary and Melter studied distinguishing set as resolving set (metric generator) ^[7,20]. Applications of this notion to the navigation of robots in networks are discussed in ^[13,21], and applications to pharmaceutical chemistry in ^[10,11]. For more details about the theory and applications of this notion, we refer the readers to the papers cited in ^{[3,5,8,9,12,13,14,15,19,22]} and the references therein.

A set $A \subseteq V(G)$ is a neighbor-distinguishing set (local metric generator) for $G$ if the members of $A$ adjacently distinguish every pair of neighboring (adjacent) vertices in $G$ . The cardinality of a smallest neighbor-distinguishing set for $G$ is called the adjacency (local) metric dimension of $G$ , and we denote it by $dim_a(G)$ .

The problem of distinguishing every two neighbors with the aid of distance (the number of edges in a geodesic) in a connected graph was introduced and studied by Okamoto et al. in 2010 ^[16]. Then, up till now, this notion endlessly received remarkable interest of many researchers working with distance in graphs. In 2015 and 2018, every two neighbors in the corona product of graphs are distinguished ^[6,18], while this problem for strong product and lexicographic product of graphs was solved in 2016 ^[4] and in 2018 ^[2,6], respectively. Using the neighbor-distinguishing problem of primary subgraphs, this problem was solved for the super graphs of these subgraphs in 2015 ^[17]. In 2018, Salman et al. proposed linear programming formulation for this problem and distinguished neighbors in two families of convex polytopes ^[19]. Recently, in 2019, split graphs of complete and complete bipartite graphs have been considered in the context of this problem ^[1]. Due to this noteworthy attention of researchers to this problem, we extend this study towards a very renowned family of generalized Petersen graphs in this article. Next, we state two results, proved by Okamoto et al. ^[16], and Salman et al. ^[19], respectively, which will be used in the sequel.

Theorem 1. ^[16] Let $G$ be a non-trivial connected graph of order $n$ . Then $dim_a(G)$ $= n-1$ if and only if $G$ is a complete graph, and $dim_a(G) = 1$ if and only if $G$ is a bipartite graph.

Proposition 2. ^[19] A subset $A$ of vertices in a connected graph $G$ is a neighbor-distinguishing set for $G$ if and only if for every $u\in V(G)$ and for each $v\in N(u)$ , the pair $(u, v)$ adjacently distinguished by some element of $A$ .

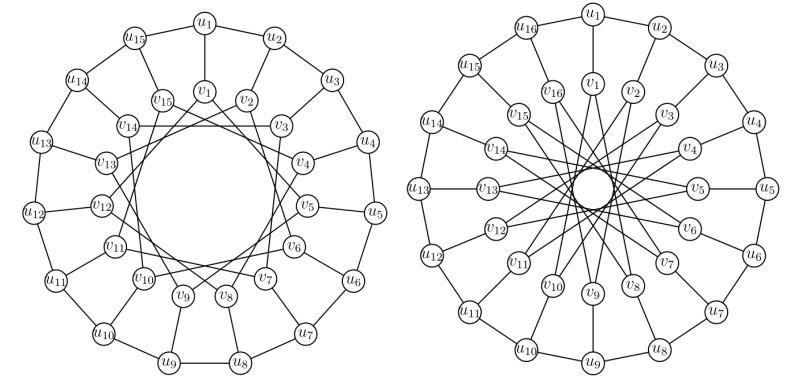
Watkins, in $1969$ ^[24], generalized the eminent Petersen graph, and proposed the notation $P(n, m)$ to this generalized family, where $n \geq 3$ and $1 \leq m \leq \lfloor \frac{n-1}{2} \rfloor$ . $P(n, m)$ is a cubic graph having the set

$V(P(n, m)) = \{ u_{1} , u_{2} , \dots, u_{n} , v_{1} , v_{2} , \dots, v_{n} \}$

as the vertex set, and the set

$E(P(n, m)) = \bigcup\limits_{i = 1}^{n}\left\{u_ix, v_iy\; ;\; x\in N(u_i), \; y \in N(v_i)\right\}$

as the edge set, where $N(u_i) = \{u_{i+1}, u_{i-1}, v_i \}$ and $N(v_i) = \{u_i, v_{i+m}, v_{i-m} \}$ for each $1 \leq i \leq n$ , and the indices greater than $n$ or less than $1$ will be taken modulo $n$ . Vertices $u_i$ and $v_i$ $(1 \leq i \leq n)$ are called the outer vertices and inner vertices, respectively, in $P(n, m)$ . Figure 1 depicts graphs to two different families of generalized Petersen graphs.

Figure 1. Generalized Petersen graphs

$P(15, 4)$ and

$P(16, 7)$ .

DownLoad: Full-Size Img PowerPoint

The rest of the paper is divided into two sections: one is on the family of generalized Petersen graphs $P(n, 4)$ ; and the second is on the family of generalized Petersen graphs $P(2n, n-1)$ . These families have been considered in the context of metric dimension problem by Naz et al. ^[15] and Ahmad et al. ^[3], respectively. Here, we solve the neighbor-distinguishing problem for these families.

2. Family of generalized Petersen graphs $P(n, 4)$

In the next result, we show that only two vertices of $P(n, 4)$ perform the neighbor-distinguishing.

Theorem 3. For $n\geq 9$ , let $G$ be a generalized Petersen graph $P(n, 4)$ , then a neighbor-distinguishing set for $G$ is a $2$ -element subset of $V(G)$ .

Proof. For $n = 9$ , it is an easy exercise to see that the set $A = \{v_1, v_2 \}$ is a neighbor-distinguishing set for $G$ . For $n\geq 10$ , let $A$ be a $2$ -element subset of $V(G)$ . Then, according to Proposition 2, we would perform neighbor-distinguishing for each pair $(x, y)$ , where $x \in V(G)$ and $y \in N(x)$ . Note that, if $x \in A$ , then $(x, y)$ is adjacently distinguished, because the number of edges in $y-x$ geodesic is $1$ , while the number of edges in $x-x$ geodesic is $0$ . Now, we discuss the following eight cases:

Case 1: ( $n = 8k$ with $k\geq 2$ )

Let $A = \{v_1 = a_1, v_3 = a_2\}$ , then

● the number of edges in $u_1-a_2$ geodesic is 3,

● the number of edges in $u_2-a_2$ geodesic is 2,

● the number of edges in $v_1-a_2$ geodesic is 4,

● the number of edges in $v_2-a_2$ geodesic is 3.

Further, and provide the lists of number of edges in $x-a_1$ and $x-a_2$ geodesics for all $x \in V(G)-A$ .

Table 1. List of the number of edges in geodesics from the outer vertices to

$a \in A$ in

$P(n, 4)$ .

Geodesic	The number of edges in the geodesic
$u_i-a$	$i \equiv 0$ (mod 4)	$i \equiv 1$ (mod 4)	$i \equiv 2$ (mod 4)	$i \equiv 3$ (mod 4)
$n = 8k$ with $k\geq 2$ , and $A = \{v_1 = a_1, v_3 = a_2\}$
$u_i- a_1$ , $1\leq i \leq 4k+1$	$\frac{i+8}{4}$	$\frac{i+3}{4}$	$\frac{i+6}{4}$	$\frac{i+9}{4}$
$u_i- a_1$ , $4k+2\leq i \leq n$	$\frac{n-i+8}{4}$	$\frac{n-i+5}{4}$	$\frac{n-i+10}{4}$	$\frac{n-i+11}{4}$
$u_i- a_2$ , $3\leq i \leq 4k+3$	$\frac{i+4}{4}$	$\frac{i+7}{4}$	$\frac{i+6}{4}$	$\frac{i+1}{4}$
$u_i- a_2$ , $4k+4\leq i \leq n$	$\frac{n-i+12}{4}$	$\frac{n-i+13}{4}$	$\frac{n-i+10}{4}$	$\frac{n-i+7}{4}$
$n = 8k+1$ with $k\geq 2$ , and $A = \{v_1 = a_1, v_4 = a_2\}$
$u_i- a_1$ , $1\leq i \leq 4k+1$	$\frac{i+8}{4}$	$\frac{i+3}{4}$	$\frac{i+6}{4}$	$\frac{i+9}{4}$
$u_i- a_1$ , $4k+2\leq i \leq n$	$\frac{n-i+11}{4}$	$\frac{n-i+8}{4}$	$\frac{n-i+5}{4}$	$\frac{n-i+10}{4}$
$u_i- a_2$ , $4\leq i \leq 5k+1$	$\frac{i}{4}$	$\frac{i+3}{4}$	$\frac{i+6}{4}$	$\frac{i+5}{4}$
$u_i- a_2$ , $5k+2\leq i \leq n$	$\frac{n-i+11}{4}$	$\frac{n-i+8}{4}$	$\frac{n-i+13}{4}$	$\frac{n-i+14}{4}$
$n = 8k+2$ with $k\geq 1$ , and $A = \{v_1 = a_1, v_2 = a_2\}$
$u_i- a_1$ , $1\leq i \leq 4k+2$	$\frac{i+8}{4}$	$\frac{i+3}{4}$	$\frac{i+6}{4}$	$\frac{i+9}{4}$
$u_i- a_1$ , $4k+3\leq i \leq n$	$\frac{n-i+10}{4}$	$\frac{n-i+11}{4}$	$\frac{n-i+8}{4}$	$\frac{n-i+5}{4}$
$u_i- a_2$ , $2\leq i \leq 4k+3$	$\frac{i+8}{4}$	$\frac{i+7}{4}$	$\frac{i+2}{4}$	$\frac{i+5}{4}$
$u_i- a_2$ , $4k+4\leq i \leq n$	$\frac{n-i+6}{4}$	$\frac{n-i+11}{4}$	$\frac{n-i+12}{4}$	$\frac{n-i+9}{4}$
$n = 8k+3$ with $k\geq 1$ , and $A = \{v_1 = a_1, v_3 = a_2\}$
$u_i- a_1$ , $1\leq i \leq 4k+2$	$\frac{i+8}{4}$	$\frac{i+3}{4}$	$\frac{i+6}{4}$	$\frac{i+9}{4}$
$u_i- a_1$ , $4k+3\leq i \leq n$	$\frac{n-i+5}{4}$	$\frac{n-i+10}{4}$	$\frac{n-i+11}{4}$	$\frac{n-i+8}{4}$
$u_i- a_2$ , $3\leq i \leq 5k$	$\frac{i+4}{4}$	$\frac{i+7}{4}$	$\frac{i+6}{4}$	$\frac{i+1}{4}$
$u_i- a_2$ , $5k+1\leq i \leq n$	$\frac{n-i+13}{4}$	$\frac{n-i+10}{4}$	$\frac{n-i+7}{4}$	$\frac{n-i+12}{4}$
$n = 8k+4$ with $k\geq 1$ , and $A = \{v_1 = a_1, v_4 = a_2\}$
$u_i- a_1$ , $1\leq i \leq 4k+3$	$\frac{i+8}{4}$	$\frac{i+3}{4}$	$\frac{i+6}{4}$	$\frac{i+9}{4}$
$u_i- a_1$ , $4k+4\leq i \leq n$	$\frac{n-i+8}{4}$	$\frac{n-i+5}{4}$	$\frac{n-i+10}{4}$	$\frac{n-i+11}{4}$
$u_i- a_2$ , $3\leq i \leq 5k+2$	$\frac{i}{4}$	$\frac{i+3}{4}$	$\frac{i+6}{4}$	$\frac{i+5}{4}$
$u_i- a_2$ , $5k+3\leq i \leq n$	$\frac{n-i+8}{4}$	$\frac{n-i+13}{4}$	$\frac{n-i+14}{4}$	$\frac{n-i+11}{4}$
$n = 8k+5$ with $k\geq 1$ , and $A = \{v_1 = a_1, v_2 = a_2\}$
$u_i- a_1$ , $1\leq i \leq 5k+1$	$\frac{i+8}{4}$	$\frac{i+3}{4}$	$\frac{i+6}{4}$	$\frac{i+9}{4}$
$u_i- a_1$ , $5k+2\leq i \leq n$	$\frac{n-i+11}{4}$	$\frac{n-i+8}{4}$	$\frac{n-i+5}{4}$	$\frac{n-i+10}{4}$
$u_i- a_2$ , $2\leq i \leq 5k+2$	$\frac{i+8}{4}$	$\frac{i+7}{4}$	$\frac{i+2}{4}$	$\frac{i+5}{4}$
$u_i- a_2$ , $5k+3\leq i \leq n$	$\frac{n-i+11}{4}$	$\frac{n-i+12}{4}$	$\frac{n-i+9}{4}$	$\frac{n-i+6}{4}$
$n = 8k+6$ with $k\geq 1$ , and $A = \{v_1 = a_1, v_2 = a_2\}$
$u_i- a_1$ , $1\leq i \leq 4k+2$	$\frac{i+8}{4}$	$\frac{i+3}{4}$	$\frac{i+6}{4}$	$\frac{i+9}{4}$
$u_i- a_1$ , $4k+6\leq i \leq n$	$\frac{n-i+10}{4}$	$\frac{n-i+11}{4}$	$\frac{n-i+8}{4}$	$\frac{n-i+5}{4}$
$u_i- a_2$ , $1\leq i \leq 4k+3$	$\frac{i+8}{4}$	$\frac{i+7}{4}$	$\frac{i+2}{4}$	$\frac{i+5}{4}$
$u_i- a_2$ , $4k+7\leq i \leq n$	$\frac{n-i+6}{4}$	$\frac{n-i+11}{4}$	$\frac{n-i+12}{4}$	$\frac{n-i+9}{4}$
$n = 8k+7$ with $k\geq 1$ , and $A = \{v_1 = a_1, v_3 = a_2\}$
$u_i- a_1$ , $1\leq i \leq 4k+3$	$\frac{i+8}{4}$	$\frac{i+3}{4}$	$\frac{i+6}{4}$	$\frac{i+9}{4}$
$u_i- a_1$ , $4k+6\leq i \leq n$	$\frac{n-i+5}{4}$	$\frac{n-i+10}{4}$	$\frac{n-i+11}{4}$	$\frac{n-i+8}{4}$
$u_i- a_2$ , $2\leq i \leq 5k+1$	$\frac{i+4}{4}$	$\frac{i+7}{4}$	$\frac{i+6}{4}$	$\frac{i+1}{4}$
$u_i- a_2$ , $5k+4\leq i \leq n$	$\frac{n-i+13}{4}$	$\frac{n-i+10}{4}$	$\frac{n-i+7}{4}$	$\frac{n-i+12}{4}$

| Show Table

DownLoad: CSV

Table 2. List of the number of edges in geodesics from the inner vertices to

$a \in A$ in

$P(n, 4)$ .

Geodesic	The number of edges in the geodesic.
$v_i-a$	$i \equiv 0$ (mod 4)	$i \equiv 1$ (mod 4)	$i \equiv 2$ (mod 4)	$i \equiv 3$ (mod 4)
$n = 8k$ with $k\geq 2$ , and $A = \{v_1 = a_1, v_3 = a_2\}$
$v_i - a_1$ , $1\leq i \leq 4k+1$	$\frac{i+12}{4}$	$\frac{i-1}{4}$	$\frac{i+10}{4}$	$\frac{i+13}{4}$
$v_i - a_1$ , $4k+2\leq i \leq n$	$\frac{n-i+12}{4}$	$\frac{n-i+1}{4}$	$\frac{n-i+14}{4}$	$\frac{n-i+15}{4}$
$v_i - a_2$ , $3\leq i \leq 4k+3$	$\frac{i+8}{4}$	$\frac{i+11}{4}$	$\frac{i+10}{4}$	$\frac{i-3}{4}$
$v_i- a_2$ , $4k+4\leq i \leq n$	$\frac{n-i+16}{4}$	$\frac{n-i+17}{4}$	$\frac{n-i+14}{4}$	$\frac{n-i+3}{4}$
$n = 8k+1$ with $k\geq 2$ , and $A = \{v_1 = a_1, v_4 = a_2\}$
$v_i- a_1$ , $1\leq i \leq 3k+1$	$\frac{i+12}{4}$	$\frac{i-1}{4}$	$\frac{i+10}{4}$	$\frac{i+13}{4}$
$v_i- a_1$ , $3k+10\leq i \leq n$	$\frac{n-i+15}{4}$	$\frac{n-i+12}{4}$	$\frac{n-i+1}{4}$	$\frac{n-i+14}{4}$
$v_i- a_2$ , $4\leq i \leq 4k$	$\frac{i-4}{4}$	$\frac{i+7}{4}$	$\frac{i+10}{4}$	$\frac{i+9}{4}$
$v_i- a_2$ , $4k+6\leq i \leq n$	$\frac{n-i+15}{4}$	$\frac{n-i+4}{4}$	$\frac{n-i+17}{4}$	$\frac{n-i+18}{4}$
$n = 8k+2$ with $k\geq 1$ , and $A = \{v_1 = a_1, v_2 = a_2\}$
$v_i- a_1$ , $1\leq i \leq 3k+2$	$\frac{i+12}{4}$	$\frac{i-1}{4}$	$\frac{i+10}{4}$	$\frac{i+13}{4}$
$v_i- a_1$ , $3k+10\leq i \leq n$	$\frac{n-i+14}{4}$	$\frac{n-i+15}{4}$	$\frac{n-i+12}{4}$	$\frac{n-i+1}{4}$
$v_i- a_2$ , $2\leq i \leq 3k+3$	$\frac{i+12}{4}$	$\frac{i+11}{4}$	$\frac{i-2}{4}$	$\frac{i+9}{4}$
$v_i- a_2$ , $3k+11\leq i \leq n$	$\frac{n-i+2}{4}$	$\frac{n-i+15}{4}$	$\frac{n-i+16}{4}$	$\frac{n-i+13}{4}$
$n = 8k+3$ with $k\geq 1$ , and $A = \{v_1 = a_1, v_3 = a_2\}$
$v_i- a_1$ , $1\leq i \leq 3k+3$	$\frac{i+12}{4}$	$\frac{i-1}{4}$	$\frac{i+10}{4}$	$\frac{i+13}{4}$
$v_i- a_1$ , $3k+10\leq i \leq n$	$\frac{n-i+1}{4}$	$\frac{n-i+14}{4}$	$\frac{n-i+15}{4}$	$\frac{n-i+12}{4}$
$v_i- a_2$ , $3\leq i \leq 4k+1$	$\frac{i+8}{4}$	$\frac{i+11}{4}$	$\frac{i+10}{4}$	$\frac{i-3}{4}$
$v_i- a_2$ , $4k+8\leq i \leq n$	$\frac{n-i+17}{4}$	$\frac{n-i+14}{4}$	$\frac{n-i+3}{4}$	$\frac{n-i+16}{4}$
$n = 8k+4$ with $k\geq 1$ , and $A = \{v_1 = a_1, v_4 = a_2\}$
$v_i- a_1$ , $1\leq i \leq 4k+3$	$\frac{i+12}{4}$	$\frac{i-1}{4}$	$\frac{i+10}{4}$	$\frac{i+13}{4}$
$v_i- a_1$ , $4k+4\leq i \leq n$	$\frac{n-i+12}{4}$	$\frac{n-i+1}{4}$	$\frac{n-i+14}{4}$	$\frac{n-i+15}{4}$
$v_i- a_2$ , $3\leq i \leq 5k+2$	$\frac{i-4}{4}$	$\frac{i+7}{4}$	$\frac{i+10}{4}$	$\frac{i+9}{4}$
$v_i- a_2$ , $5k+3\leq i \leq n$	$\frac{n-i+4}{4}$	$\frac{n-i+17}{4}$	$\frac{n-i+18}{4}$	$\frac{n-i+15}{4}$
$n = 8k+5$ with $k\geq 1$ , and $A = \{v_1 = a_1, v_2 = a_2\}$
$v_i- a_1$ , $1\leq i \leq 4k+1$	$\frac{i+12}{4}$	$\frac{i-1}{4}$	$\frac{i+10}{4}$	$\frac{i+13}{4}$
$v_i- a_1$ , $4k+6\leq i \leq n$	$\frac{n-i+15}{4}$	$\frac{n-i+12}{4}$	$\frac{n-i+1}{4}$	$\frac{n-i+14}{4}$
$v_i- a_2$ , $2\leq i \leq 4k+2$	$\frac{i+12}{4}$	$\frac{i+11}{4}$	$\frac{i-2}{4}$	$\frac{i+9}{4}$
$v_i- a_2$ , $4k+7\leq i \leq n$	$\frac{n-i+15}{4}$	$\frac{n-i+16}{4}$	$\frac{n-i+13}{4}$	$\frac{n-i+2}{4}$
$n = 8k+6$ with $k\geq 1$ , and $A = \{v_1 = a_1, v_2 = a_2\}$
$v_i- a_1$ , $1\leq i \leq 3k+2$	$\frac{i+12}{4}$	$\frac{i-1}{4}$	$\frac{i+10}{4}$	$\frac{i+13}{4}$
$v_i- a_1$ , $3k+14\leq i \leq n$	$\frac{n-i+14}{4}$	$\frac{n-i+15}{4}$	$\frac{n-i+12}{4}$	$\frac{n-i+1}{4}$
$v_i- a_2$ , $1\leq i \leq 3k+3$	$\frac{i+12}{4}$	$\frac{i+11}{4}$	$\frac{i-2}{4}$	$\frac{i+9}{4}$
$v_i- a_2$ , $3k+15\leq i \leq n$	$\frac{n-i+2}{4}$	$\frac{n-i+15}{4}$	$\frac{n-i+16}{4}$	$\frac{n-i+13}{4}$
$n = 8k+7$ with $k\geq 1$ , and $A = \{v_1 = a_1, v_3 = a_2\}$
$v_i- a_1$ , $1\leq i \leq 3k+3$	$\frac{i+12}{4}$	$\frac{i-1}{4}$	$\frac{i+10}{4}$	$\frac{i+13}{4}$
$v_i- a_1$ , $3k+14\leq i \leq n$	$\frac{n-i+1}{4}$	$\frac{n-i+14}{4}$	$\frac{n-i+15}{4}$	$\frac{n-i+12}{4}$
$v_i- a_2$ , $2\leq i \leq 4k+1$	$\frac{i+8}{4}$	$\frac{i+11}{4}$	$\frac{i+10}{4}$	$\frac{i-3}{4}$
$v_i- a_2$ , $4k+12\leq i \leq n$	$\frac{n-i+17}{4}$	$\frac{n-i+14}{4}$	$\frac{n-i+3}{4}$	$\frac{n-i+16}{4}$

| Show Table

DownLoad: CSV

Case 2: ( $n = 8k+1$ with $k\geq 2$ )

Let $A = \{v_1 = a_1, v_4 = a_2\}$ , then

● the number of edges in $u_1-a_2$ geodesic is 3,

● the number of edges in $u_2-a_2$ geodesic is 3,

● the number of edges in $u_3-a_2$ geodesic is 2.

Further, – provide the lists of number of edges in $x-a_1$ and $x-a_2$ geodesics for all $x \in V(G)-A$ .

Table 3.

$\lambda_i$ is the number of edges in a

$v_i-a_1$ geodesic, and

$\lambda_j$ is the number of edges in a

$v_j-a_2$ geodesic.

$i$	$3k+2 \equiv 2 (mod \ 4)$	$3k+3 \equiv 3 (mod \ 4)$	$3k+4 \equiv 0 (mod \ 4)$	$3k+5 \equiv 1 (mod \ 4)$	$3k+6 \equiv 2 (mod \ 4)$	$3k+7 \equiv 3 (mod \ 4)$	$3k+8 \equiv 0 (mod \ 4)$	$3k+9 \equiv 1 (mod \ 4)$
$\lambda_i$	$\frac{5k}{4}$	$\frac{3k+16}{4}$	$\frac{3k+16}{4}$	$\frac{3k+4}{4}$	$\frac{5k-4}{4}$	$\frac{5k+8}{4}$	$\frac{5k+8}{4}$	$\frac{3k+8}{4}$
$j$	$1$	$2$	$3$	$4k+1 \equiv 1 (mod \ 4)$	$4k+2 \equiv 2 (mod \ 4)$	$4k+3 \equiv 3 (mod \ 4)$	$4k+4 \equiv 0 (mod \ 4)$	$4k+5 \equiv 1 (mod \ 4)$
$\lambda_j$	$4$	$4$	$3$	$k+1$	$k+3$	$k+3$	$k$	$k$

| Show Table

DownLoad: CSV

Case 3: ( $n = 8k+2$ with $k\geq 1$ )

Let $A = \{v_1 = a_1, v_2 = a_2\}$ , then

● the number of edges in $u_2-a_2$ geodesic is 2.

Further, , and provide the lists of number of edges in $x-a_1$ and $x-a_2$ geodesics for all $x \in V(G)-A$ .

Table 4.

$\lambda_i$ is the number of edges in a

$v_i-a_1$ geodesic, and

$\lambda_j$ is the number of edges in a

$v_j-a_2$ geodesic.

$i$	$3k+3 \equiv 3 (mod \ 4)$	$3k+4 \equiv 0 (mod \ 4)$	$3k+5 \equiv 1 (mod \ 4)$	$3k+6 \equiv 2 (mod \ 4)$	$3k+7 \equiv 3 (mod \ 4)$	$3k+8 \equiv 0 (mod \ 4)$	$3k+9 \equiv 1 (mod \ 4)$	$-$	$-$
$\lambda_i$	$\frac{5k}{4}$	$\frac{3k+16}{4}$	$\frac{3k+4}{4}$	$\frac{3k+16}{4}$	$\frac{5k-4}{4}$	$\frac{5k+8}{4}$	$\frac{3k+8}{4}$	$-$	$-$
$j$	$1$	$2$	$3k+4 \equiv 0 (mod \ 4)$	$3k+5 \equiv 1 (mod \ 4)$	$3k+6 \equiv 2 (mod \ 4)$	$3k+7 \equiv 3 (mod \ 4)$	$3k+8 \equiv 0 (mod \ 4)$	$3k+9 \equiv 1 (mod \ 4)$	$3k+10 \equiv 2 (mod \ 4)$
$\lambda_j$	$3$	$0$	$\frac{5k}{4}$	$\frac{3k+16}{4}$	$\frac{3k+4}{4}$	$\frac{5k+8}{4}$	$\frac{5k-4}{4}$	$\frac{5k+8}{4}$	$\frac{3k+8}{4}$

| Show Table

DownLoad: CSV

Case 4: ( $n = 8k+3$ with $k\geq 1$ )

Let $A = \{v_1 = a_1, v_3 = a_2\}$ , then

● the number of edges in $u_1-a_2$ geodesic is 3,

● the number of edges in $u_2-a_2$ geodesic is 2.

Further, , and provide the lists of number of edges in $x-a_1$ and $x-a_2$ geodesics for all $x \in V(G)-A$ .

Table 5.

$\lambda_i$ is the number of edges in a

$v_i-a_1$ geodesic, and

$\lambda_j$ is the number of edges in a

$v_j-a_2$ geodesic.

$i$	$3k+4 \equiv 0 (mod \ 4)$	$3k+5 \equiv 1 (mod \ 4)$	$3k+6 \equiv 2 (mod \ 4)$	$3k+7 \equiv 3 (mod \ 4)$	$3k+8 \equiv 0 (mod \ 4)$	$3k+9 \equiv 1 (mod \ 4)$	$-$	$-$
$\lambda_i$	$\frac{5k}{4}$	$\frac{3k+4}{4}$	$\frac{3k+16}{4}$	$\frac{5k+8}{4}$	$\frac{5k-4}{4}$	$\frac{3k+8}{4}$	$-$	$-$
$j$	$1$	$2$	$4k+2 \equiv 2 (mod \ 4)$	$4k+3 \equiv 3 (mod \ 4)$	$4k+4 \equiv 0 (mod \ 4)$	$4k+5 \equiv 1 (mod \ 4)$	$4k+6 \equiv 2 (mod \ 4)$	$4k+7\equiv 3 (mod \ 4)$
$\lambda_j$	$4$	$3$	$k+1$	$k$	$k+3$	$k+3$	$k$	$k+1$

| Show Table

DownLoad: CSV

Case 5: ( $n = 8k+4$ with $k\geq 1$ )

Let $A = \{v_1 = a_1, v_4 = a_2\}$ , then

● the number of edges in $v_1-a_2$ geodesic is 4,

● the number of edges in $v_2-a_2$ geodesic is 4,

● the number of edges in $u_1-a_2$ geodesic is 3,

● the number of edges in $u_2-a_2$ geodesic is 3.

Moreover, and provide the lists of number of edges in $x-a_1$ and $x-a_2$ geodesics for all $x \in V(G)-A$ .

Case 6: ( $n = 8k+5$ with $k\geq 1$ )

Let $A = \{v_1 = a_1, v_2 = a_2\}$ , then

● the number of edges in $u_1-a_2$ geodesic is 2,

● the number of edges in $v_1-a_2$ geodesic is 3.

Further, , and provide the lists of number of edges in $x-a_1$ and $x-a_2$ geodesics for all $x \in V(G)-A$ .

Table 6.

$\lambda_i$ is the number of edges in a

$v_i-a_1$ geodesic, and

$\lambda_j$ is the number of edges in a

$v_j-a_2$ geodesic.

$i$	$4k+2 \equiv 2 (mod \ 4)$	$4k+3 \equiv 3 (mod \ 4)$	$4k+4 \equiv 0 (mod \ 4)$	$4k+5 \equiv 1 (mod \ 4)$
$\lambda_i$	$k+1$	$k+4$	$k+4$	$k+1$
$j$	$4k+3 \equiv 3 (mod \ 4)$	$4k+4 \equiv 0 (mod \ 4)$	$4k+5 \equiv 1 (mod \ 4)$	$4k+6 \equiv 2 (mod \ 4)$
$\lambda_j$	$k+1$	$k+4$	$k+4$	$k+1$

| Show Table

DownLoad: CSV

Case 7: ( $n = 8k+6$ with $k\geq 1$ )

Let $A = \{v_1 = a_1, v_2 = a_2\}$ , then

● the number of edges in $v_{3k+3}-a_1$ geodesic is $\frac{5k+4}{4} \equiv 3 (mod \ 4)$ ,

● the number of edges in $v_{3k+4}-a_2$ geodesic is $\frac{5k+4}{4} \equiv 0 (mod \ 4)$ ,

● the number of edges in $u_{4k+3}-a_1$ geodesic is $k+2$ ,

● the number of edges in $u_{4k+4}-a_1$ geodesic is $k+3$ ,

● the number of edges in $u_{4k+5}-a_1$ geodesic is $k+2$ ,

● the number of edges in $u_{4k+4}-a_2$ geodesic is $k+2$ ,

● the number of edges in $u_{4k+5}-a_2$ geodesic is $k+3$ ,

● the number of edges in $u_{4k+6}-a_2$ geodesic is $k+2$ .

Further, , and provide the lists of number of edges in $x-a_1$ and $x-a_2$ geodesics for all $x \in V(G)-A$ .

Table 7.

$\lambda_i$ is the number of edges in a

$v_i-a_1$ geodesic, and

$\lambda_j$ is the number of edges in a

$v_j-a_2$ geodesic.

$i$	$3k+4 \equiv 0 (mod \ 4)$	$3k+5 \equiv 1 (mod \ 4)$	$3k+6 \equiv 2 (mod \ 4)$	$3k+7 \equiv 3 (mod \ 4)$	$3k+8 \equiv 0 (mod \ 4)$	$3k+9 \equiv 1 (mod \ 4)$	$3k+10 \equiv 2 (mod \ 4)$	$3k+11 \equiv 3 (mod \ 4)$	$3k+12 \equiv 0 (mod \ 4)$	$3k+13 \equiv 1 (mod \ 4)$
$\lambda_i$	$\frac{3k+16}{4}$	$\frac{3k+4}{4}$	$\frac{3k+16}{4}$	$\frac{5k}{4}$	$\frac{3k+20}{4}$	$\frac{3k+8}{4}$	$\frac{5k+6}{4}$	$\frac{5k-4}{4}$	$\frac{5k+8}{4}$	$\frac{3k+12}{4}$
$j$	$3k+5 \equiv 1 (mod \ 4)$	$3k+6 \equiv 2 (mod \ 4)$	$3k+7 \equiv 3 (mod \ 4)$	$3k+8 \equiv 0 (mod \ 4)$	$3k+9 \equiv 1 (mod \ 4)$	$3k+10 \equiv 2 (mod \ 4)$	$3k+11 \equiv 3 (mod \ 4)$	$3k+12 \equiv 0 (mod \ 4)$	$3k+13 \equiv 1 (mod \ 4)$	$3k+14 \equiv 2 (mod \ 4)$
$\lambda_j$	$\frac{3k+16}{4}$	$\frac{3k+4}{4}$	$\frac{3k+16}{4}$	$\frac{5k}{4}$	$\frac{3k+20}{4}$	$\frac{3k+8}{4}$	$\frac{5k+8}{4}$	$\frac{5k-4}{4}$	$\frac{5k+8}{4}$	$\frac{3k+12}{4}$

| Show Table

DownLoad: CSV

Case 8: ( $n = 8k+7$ with $k\geq 1$ )

Let $A = \{v_1 = a_1, v_3 = a_2\}$ , then

● the number of edges in $v_{1}-a_2$ geodesic is $4$ ,

● the number of edges in $u_{4k+4}-a_1$ geodesic is $k+2$ ,

● the number of edges in $u_{4k+5}-a_1$ geodesic is $k+2$ ,

● the number of edges in $u_{1}-a_2$ geodesic is $3$ ,

● the number of edges in $u_{5k+2}-a_2$ geodesic is $\frac{3k+12}{4} \equiv 2 (mod \ 4)$ ,

● the number of edges in $u_{5k+3}-a_2$ geodesic is $\frac{5k+4}{4} \equiv 3 (mod \ 4)$ .

Moreover, , and provide the lists of number of edges in $x-a_1$ and $x-a_2$ geodesics for all $x \in V(G)-A$ .

Table 8.

$\lambda_i$ is the number of edges in a

$v_i-a_1$ geodesic, and

$\lambda_j$ is the number of edges in a

$v_j-a_2$ geodesic.

$i$	$3k+4 \equiv 0 (mod \ 4)$	$3k+5 \equiv 1 (mod \ 4)$	$3k+6 \equiv 2 (mod \ 4)$	$3k+7 \equiv 3 (mod \ 4)$	$3k+8 \equiv 0 (mod \ 4)$	$3k+9 \equiv 1 (mod \ 4)$	$3k+10 \equiv 2 (mod \ 4)$	$3k+11 \equiv 3 (mod \ 4)$	$3k+12 \equiv 0 (mod \ 4)$	$3k+13 \equiv 1 (mod \ 4)$
$\lambda_i$	$\frac{5k+4}{4}$	$\frac{3k+4}{4}$	$\frac{3k+16}{4}$	$\frac{3k+20}{4}$	$\frac{5k}{4}$	$\frac{3k+8}{4}$	$\frac{3k+8}{4}$	$\frac{5k+12}{4}$	$\frac{5k+8}{4}$	$\frac{5k-4}{4}$
$j$	$4k+2 \equiv 2 (mod \ 4)$	$4k+3 \equiv 3 (mod \ 4)$	$4k+4 \equiv 0 (mod \ 4)$	$4k+5 \equiv 1 (mod \ 4)$	$4k+6 \equiv 2 (mod \ 4)$	$4k+7 \equiv 3 (mod \ 4)$	$4k+8 \equiv 0 (mod \ 4)$	$4k+9 \equiv 1 (mod \ 4)$	$4k+10 \equiv 2 (mod \ 4)$	$4k+11 \equiv 3 (mod \ 4)$
$\lambda_j$	$k+2$	$k$	$k+3$	$k+4$	$k+1$	$k+1$	$k+4$	$k+3$	$k$	$k+2$

| Show Table

DownLoad: CSV

In all of these eight cases, for $y \in N(x)$ , if we denote

● the number of edges in $x-a_1$ geodesic by $\alpha_1$ ,

● the number of edges in $y-a_1$ geodesic by $\beta_1$ ,

● the number of edges in $x-a_2$ geodesic by $\alpha_2$ ,

● the number of edges in $y-a_2$ geodesic by $\beta_2$ ,

then it can be seen that

$\rm{either}\; \; |\alpha_1-\beta_1| = 1\; \; \rm{whenever}\; \; \alpha_2 = \beta_2, \; \; \rm{or}\; \; |\alpha_2 - \beta_2| = 1\; \; \rm{whenever}\; \; \alpha_1 = \beta_1,$

which implies that either $a_1 \in A$ or $a_2 \in A$ adjacently distinguishes the pair $(x, y)$ . Hence, $A$ is a neighbor-distinguishing set for $G$ .

Theorem 4. For $n\geq 9$ , if $G$ is a generalized Petersen graph $P(n, 4)$ , then $dim_a(G) = 2$ .

Proof. Since $dim_a(G) = 1$ if and only if $G$ is a bipartite graph, by Theorem 1. So $dim_a(G)\geq 2$ , because $G$ is not a bipartite graph. Hence, we get the required result, by Theorem 3.

3. Family of generalized Petersen graphs $P(2n, n-1)$

The results of this section provide the solution of the problem of neighbor-distinguishing in the generalized Petersen graphs $P(2n, n-1)$ .

Theorem 5. For all $n\geq 3$ , if $G$ is a generalized Petersen graph $P(2n, n-1)$ , then the set $A = \{u_1, v_{n-1} \}$ is a neighbor-distinguishing set for $G$ .

Proof. According to Proposition 2, we have to perform neighbor-distinguishing for each pair $(x, y)$ , where $x \in V(G)$ and $y \in N(x)$ . When $x \in A$ , then the pair $(x, y)$ adjacently distinguished by $x$ , because the number of edges in $y-x$ geodesic is $1$ while the number of edges in $x-x$ geodesic is $0$ . Further, provides the list of number of edges in $x-u_1$ and $x-v_{n-1}$ geodesics for all $x \in V(G)-A$ .

Table 9. List of the number of edges in

$x-a$ geodesics for

$x \in V(G)-A$ and

$a \in A$ .

Geodesic	The number of edges in the geodesics
When $n = 2k+1$ , $k\geq 1$
For $i$ /geodesics	$u_i- u_1$	$u_i- v_{n-1}$	$v_i- u_1$ $i$ is odd	$v_i- u_1$ $i$ is even	$v_i- v_{n-1}$ $i$ is odd	$v_i- v_{n-1}$ $i$ is even
$1 \leq i \leq k-1$	$i-1$	$i+2$	$i$	$i$	$i+3$	$i+1$
$k \leq i \leq k+1$	$i-1$	$2k-i+1$	$i$	$i$	$2k-i+2$	$2k-i$
$i = k+2$	$\frac{n+1}{2}$	$k-1$	$\frac{n+1}{2}$	$\frac{n+1}{2}$	$2k-i+2$	$2k-i$
$k+3 \leq i \leq 2k$	$2k-i+4$	$2k-i+1$	$2k-i+3$	$2k-i+3$	$2k-i+2$	$2k-i$
$i = 2k+1$	$i-2k+2$	$i-2k+1$	$i-2k+1$	$i-2k+1$	$i-2k+2$	$i-2k+2$
$i = 2k+2$	$4$	$i-n+2$	$3$	$3$	$i-2k$	$i-2k$
$2k+3 \leq i \leq 3k$	$i-2k$	$i-2k+1$	$i-2k-1$	$i-2k-1$	$i-2k+2$	$i-2k$
$i = 3k+1$	$i-2k$	$i-n+1$	$i-n$	$i-n$	$k+2$	$k$
$i = 3k+2$	$\frac{n+1}{2}$	$k$	$i-n$	$i-n$	$k+1$	$k-1$
$3k+3 \leq i \leq 4k$	$2n-i+1$	$4k-i+2$	$2n-i+2$	$2n-i+2$	$4k-i+3$	$4k-i+1$
$i = 2n-1$	$2$	$3$	$3$	$3$	$4$	$4$
$i = 2n$	$1$	$2$	$2$	$2$	$1$	$1$
When $n = 2k$ , $k\geq 2$
$1 \leq i \leq k-2$	$i-1$	$i+2$	$i$	$i$	$i+3$	$i+1$
$i = k-1$	$i-1$	$n-i$	$i$	$i$	$k$	$k$
$k \leq i \leq k+1$	$i-1$	$n-i$	$i$	$i$	$2k-i-1$	$2k-i+1$
$i = k+2$	$i-1$	$n-i$	$\frac{n}{2}$	$\frac{n}{2}$	$n-i-1$	$n-i+1$
$k+3 \leq i \leq 2k-1$	$2k-i+3$	$2k-i$	$2k-i+2$	$2k-i+2$	$2k-i-1$	$2k-i+1$
$i = 2k$	$3$	$2$	$2$	$2$	$3$	$3$
$i = 2k+1$	$4$	$3$	$3$	$3$	$2$	$2$
$2k+2 \leq i \leq 3k-2$	$i-2k+1$	$i-2k+2$	$i-2k$	$i-2k$	$i-2k+1$	$i-2k+3$
$i = 3k-1$	$i-2k+1$	$i-2k+2$	$i-2k$	$i-2k$	$k$	$k$
$3k \leq i \leq 3k+1$	$2n-i+1$	$4k-i$	$i-2k$	$i-2k$	$4k-i+1$	$4k-i-1$
$i = 3k+2$	$k-1$	$k-2$	$\frac{n}{2}$	$\frac{n}{2}$	$4k-i+1$	$4k-i-1$
$3k+3 \leq i \leq 4k-2$	$2n-i+1$	$4k-i$	$2n-i+2$	$2n-i+2$	$4k-i+1$	$4k-i-1$
$i = 2n-1$	$2$	$3$	$3$	$3$	$4$	$4$
$i = 2n$	$1$	$2$	$2$	$2$	$1$	$1$

| Show Table

DownLoad: CSV

Now, for any $y\in N(x)$ , if we denote

● the number of edges in $x-u_1$ geodesic by $\alpha_1$ ,

● the number of edges in $y-u_1$ geodesic by $\beta_1$ ,

● the number of edges in $x-v_{n-1}$ geodesic by $\alpha_2$ ,

● the number of edges in $y-v_{n-1}$ geodesic by $\beta_2$ ,

then it can be seen that

$\rm{either}\; \; |\alpha_1-\beta_1| = 1\; \; \rm{whenever}\; \; \alpha_2 = \beta_2, \; \; \rm{or}\; \; |\alpha_2 - \beta_2| = 1\; \; \rm{whenever}\; \; \alpha_1 = \beta_1,$

which implies that either $u_1 \in A$ or $v_{n-1} \in A$ adjacently distinguishes the pair $(x, y)$ . Hence, $A$ is a neighbor-distinguishing set for $G$ .

Theorem 6. For $n\geq 3$ , if $G$ is a generalized Petersen graph $P(2n, n-1)$ , then $dim_a(G) = 2$ .

Proof. Since $dim_a(G) = 1$ if and only if $G$ is a bipartite graph, by Theorem 1. So $dim_a(G)\geq 2$ , because $G$ is not a bipartite graph. Hence, we get the required result, by Theorem 5.

4. Conclusions

Distinguishing every two vertices in a graph is an eminent problem in graph theory. Many graph theorists have been shown remarkable interest to solve this problem with the aid of distance (the number of edges in a geodesic) from last four decades. Using the technique of finding geodesics between vertices, we solved the problem of distinguishing every two neighbors in generalized Petersen graphs $P(n, 4)$ and $P(2n, n-1)$ . We investigated that, in both the families of generalized Petersen graphs, only two vertices are adequate to distinguish every two neighbors.

Acknowledgments

The authors are grateful to the editor and anonymous referees for their comments and suggestions to improve the quality of this article. This research is supported by Balochistan University of Engineering and Technology Khuzdar, Khuzdar 89100, Pakistan.

Conflict of interest

The authors declare that they have no conflict of interest.

References

[1]	A. Akgul, A novel method for a fractional derivative with non-local and non-singular kernel, Chaos, Soliton. Fract., 114 (2018), 478–482. https://doi.org/10.1016/j.chaos.2018.07.032 doi: 10.1016/j.chaos.2018.07.032
[2]	E. K. Akgul, Solutions of the linear and non-linear differential equations within the generalized fractional derivatives, Chaos, 29 (2019), 023108. https://doi.org/10.1063/1.5084035 doi: 10.1063/1.5084035
[3]	S. A. El-Wakil, E. M. Abulwafa, M. A. Zahran, A. A. Mahmoud, Time-fractional KdV equation: formulation and solution using variational methods, Nonlinear Dyn., 65 (2011), 55–63. https://doi.org/10.1007/s11071-010-9873-5 doi: 10.1007/s11071-010-9873-5
[4]	S. A. El-Wakil, E. M. Abulwafa, E. K. El-shewy, A. A. Mahmoud, Time-fractional KdV equation for electron-acoustic waves in plasma of cold electron and two different temperature isothermal ions, Astrophys Space Sci., 333 (2011), 269–276. https://doi.org/10.1007/s10509-011-0629-6 doi: 10.1007/s10509-011-0629-6
[5]	S. A. El-Wakil, E. M. Abulwafa, E. K. El-shewy, A. A. Mahmoud, Ion-acoustic waves in unmagnetized collisionless weakly relativistic plasma of warm-ion and isothermal-electron using time-fractional KdV equation, Adv. Space Res., 49 (2012), 1721–1727. https://doi.org/10.1016/j.asr.2012.02.018 doi: 10.1016/j.asr.2012.02.018
[6]	A. Atangana, Fractal-fractional differentiation and integration: connecting fractal calculus and fractional calculus to predict complex system, Chaos, Soliton. Fract., 102 (2017), 396–406. https://doi.org/10.1016/j.chaos.2017.04.027 doi: 10.1016/j.chaos.2017.04.027
[7]	M. Caputo, Linear models of dissipation whose Q is almost frequency independent-II, Geophys. J. Int., 13 (1967), 529–539. https://doi.org/10.1111/j.1365-246X.1967.tb02303.x doi: 10.1111/j.1365-246X.1967.tb02303.x
[8]	M. Caputo, M. Fabrizio, A new definition of fractional derivative without singular kernel, Progr. Fract. Differ. Appl., 1 (2015), 73–85.
[9]	A. A. Kilbas, H. M. Srivastava, J. J. Trujillo, Theory and applications of fractional differential equations, Vol. 204, Elsevier, 2006.
[10]	K. M. Owolabi, A. Atangana, Chaotic behaviour in system of noninteger-order ordinary differential equations, Chaos, Soliton. Fract., 115 (2018), 362–370. https://doi.org/10.1016/j.chaos.2018.07.034 doi: 10.1016/j.chaos.2018.07.034
[11]	G. B. Whitham, Variational methods and applications to water waves, Proc. R. Soc. London Ser. A, 299 (1967), 6–25. https://doi.org/10.1098/rspa.1967.0119 doi: 10.1098/rspa.1967.0119
[12]	B. Fornberg, G. B. Whitham, A numerical and theoretical study of certain non-linear wave phenomena, Philos. Trans. R. Soc. London, Ser. A, 289 (1978), 373–404. https://doi.org/10.1098/rsta.1978.0064 doi: 10.1098/rsta.1978.0064
[13]	F. Abidi, K. Omrani, The homotopy analysis method for solving the Fornberg–Whitham equation and comparison with Adomian's decomposition method, Comput. Math. Appl., 59 (2010), 2743–2750. https://doi.org/10.1016/j.camwa.2010.01.042 doi: 10.1016/j.camwa.2010.01.042
[14]	A. Chen, J. Li, X. Deng, W. Huang, Travelling wave solutions of the Fornberg–Whitham equation, Appl. Math. Comput., 215 (2009), 3068–3075. https://doi.org/10.1016/j.amc.2009.09.057 doi: 10.1016/j.amc.2009.09.057
[15]	J. Yin, L. Tian, X. Fan, Classifcation of travelling waves in the Fornberg–Whitham equation, J. Math. Anal. Appl., 368 (2010), 133–143. https://doi.org/10.1016/j.jmaa.2010.03.037 doi: 10.1016/j.jmaa.2010.03.037
[16]	J. Zhou, L. Tian, A type of bounded traveling wave solutions for the Fornberg–Whitham equation, J. Math. Anal. Appl., 346 (2008), 255–261. https://doi.org/10.1016/j.jmaa.2008.05.055 doi: 10.1016/j.jmaa.2008.05.055
[17]	J. Lu, An analytical approach to the Fornberg–Whitham type equations by using the variational iteration method, Comput. Math. Appl., 61 (2011), 2010–2013. https://doi.org/10.1016/j.camwa.2010.08.052 doi: 10.1016/j.camwa.2010.08.052
[18]	M. G. Sakar, F. Erdogan, The homotopy analysis method for solving the time-fractional Fornberg–Whitham equation and comparison with Adomian's decomposition method, Appl. Math. Model., 37 (2013), 8876–8885. https://doi.org/10.1016/j.apm.2013.03.074 doi: 10.1016/j.apm.2013.03.074
[19]	T. Mathanaranjan, D. Vijayakumar, Laplace decomposition method for time-fractional Fornberg-Whitham type equations, J. Appl. Math. Phys., 9 (2021), 260–271. https://doi.org/10.4236/jamp.2021.92019 doi: 10.4236/jamp.2021.92019
[20]	P. P. Sartanpara, R. Meher, S. K. Meher, The generalized time-fractional Fornberg–Whitham equation: an analytic approach, Partial Differ. Equ. Appl. Math., 5 (2022), 100350. https://doi.org/10.1016/j.padiff.2022.100350 doi: 10.1016/j.padiff.2022.100350
[21]	A. El-Ajou, O. A. Arqub, S. Momani, Approximate analytical solution of the non-linear fractional KdV-Burgers equation: a new iterative algorithm, J. Comput. Phys., 293 (2015), 81–95. https://doi.org/10.1016/j.jcp.2014.08.004 doi: 10.1016/j.jcp.2014.08.004
[22]	T. Eriqat, A. El-Ajou, M. N. Oqielat, Z. Al-Zhour, S. Momani, A new attractive analytic approach for solutions of linear and non-linear neutral fractional pantograph equations, Chaos, Soliton. Fract., 138 (2020), 109957. https://doi.org/10.1016/j.chaos.2020.109957 doi: 10.1016/j.chaos.2020.109957
[23]	A. El-Ajou, Z. Al-Zhour, A vector series solution for a class of hyperbolic system of Caputo time-fractional partial differential equations with variable coefficients, Front. Phys., 9 (2021), 525250. https://doi.org/10.3389/fphy.2021.525250 doi: 10.3389/fphy.2021.525250
[24]	A. El-Ajou, Adapting the Laplace transform to create solitary solutions for the non-linear time-fractional dispersive PDEs via a new approach, Eur. Phys. J. Plus, 136 (2021), 229. https://doi.org/10.1140/epjp/s13360-020-01061-9 doi: 10.1140/epjp/s13360-020-01061-9
[25]	Y. Zhou, L. Peng, On the time-fractional Navier-Stokes equations, Comput. Math. Appl., 73 (2017), 874–891. https://doi.org/10.1016/j.camwa.2016.03.026 doi: 10.1016/j.camwa.2016.03.026
[26]	M. N. Oqielat, A. El-Ajou, Z. Al-Zhour, T. Eriqat, M. Al-Smadi, A new approach to solving fuzzy quadratic Riccati differential equations, Int. J. Fuzzy Log. Intell. Syst., 22 (2022), 23–47. https://doi.org/10.5391/IJFIS.2022.22.1.23 doi: 10.5391/IJFIS.2022.22.1.23
[27]	A. M. Malik, O. H. Mohammed, Two efficient methods for solving fractional Lane-Emden equations with conformable fractional derivative, J. Egypt. Math. Soc., 28 (2020), 1–11. https://doi.org/10.1186/s42787-020-00099-z doi: 10.1186/s42787-020-00099-z
[28]	T. Eriqat, M. N. Oqielat, Z. Al-Zhour, A. El-Ajou, A. S. Bataineh, Revisited Fisher's equation and logistic system model: a new fractional approach and some modifications, Int. J. Dynam. Control, 11 (2023), 555–563. https://doi.org/10.1007/s40435-022-01020-5 doi: 10.1007/s40435-022-01020-5
[29]	M. N. Oqielat, T. Eriqat, Z. Al-Zhour, O. Ogilat, A. El-Ajou, I. Hashim, Construction of fractional series solutions to non-linear fractional reaction-diffusion for bacteria growth model via Laplace residual power series method, Int. J. Dynam. Control, 11 (2023), 520–527. https://doi.org/10.1007/s40435-022-01001-8 doi: 10.1007/s40435-022-01001-8
[30]	V. Daftardar-Gejji, H. Jafari, An iterative method for solving non-linear functional equations, J. Math. Anal. Appl., 316 (2006), 753–763. https://doi.org/10.1016/j.jmaa.2005.05.009 doi: 10.1016/j.jmaa.2005.05.009
[31]	M. A. Awuya, D. Subasi, Aboodh transform iterative method for solving fractional partial differential equation with Mittag-Leffler kernel, Symmetry, 13 (2021), 2055. https://doi.org/10.3390/sym13112055 doi: 10.3390/sym13112055
[32]	H. Jafari, M. Nazari, D. Baleanu, C. M. Khalique, A new approach for solving a system of fractional partial differential equations, Comput. Math. Appl., 66 (2013), 838–843. https://doi.org/10.1016/j.camwa.2012.11.014 doi: 10.1016/j.camwa.2012.11.014
[33]	M. M. Khalil, S. Ur Rehman, A. H. Ali, R. Nawaz, B. Batiha, New modifications of natural transform iterative method and q-homotopy analysis method applied to fractional order KDV-Burger and Sawada–Kotera equations, Partial Differ. Equ. Appl. Math., 12 (2024) 100950. https://doi.org/10.1016/j.padiff.2024.100950
[34]	L. Zada, R. Nawaz, S. Ahsan, K. S. Nisar, D. Baleanu, New iterative approach for the solutions of fractional order inhomogeneous partial differential equations, AIMS Math., 6 (2021), 1348–1365. https://doi.org/10.3934/math.2021084 doi: 10.3934/math.2021084
[35]	A. W. Alrowaily, M. Khalid, A. Kabir, A. H. Salas, C. G. L. Tiofack, S. M. E. Ismaeel, et al., On the Laplace new iterative method for modeling fractional positron-acoustic cnoidal waves in electron-positron-ion plasmas with Kaniadakis distributed electrons, Braz. J. Phys., 55 (2025), 106. https://doi.org/10.1007/s13538-025-01735-8 doi: 10.1007/s13538-025-01735-8
[36]	A. H. Almuqrin, C. G. L. Tiofack, A. Mohamadou, A. Alim, S. M. E. Ismaeel, W. Alhejaili, et al., On the "Tantawy Technique" and other methods for analyzing the family of fractional Burgers' equations: applications to plasma physics, J. Low Freq. Noise, Vib. Active Control, 2025. https://doi.org/10.1177/14613484251314580
[37]	H. A. Alyousef, R. Shah, C. G. L. Tiofack, A. H. Salas, W. Alhejaili, S. M. E. Ismaeel, et al., Novel approximations to the third- and fifth-order fractional KdV-type equations and modeling nonlinear structures in plasmas and fluids, Braz. J. Phys., 55 (2025), 20. https://doi.org/10.1007/s13538-024-01660-2 doi: 10.1007/s13538-024-01660-2
[38]	M. Almheidat, H. Yasmin, M. Al Huwayz, R. Shah, S. A. El-Tantawy, A novel investigation into time-fractional multi-dimensional Navier–Stokes equations within Aboodh transform, Open Phys., 22 (2024), 20240081. https://doi.org/10.1515/phys-2024-0081 doi: 10.1515/phys-2024-0081
[39]	A. H. Ganie, S. Noor, M. Al Huwayz, A. Shafee, S. A. El-Tantawy, Numerical simulations for fractional Hirota–Satsuma coupled Korteweg–de Vries systems, Open Phys., 22 (2024), 20240008.
[40]	S. Noor, W. Albalawi, R. Shah, M. M. Al-Sawalha, S. M. E. Ismaeel, S. A. El-Tantawy, On the approximations to fractional nonlinear damped Burger's-type equations that arise in fluids and plasmas using Aboodh residual power series and Aboodh transform iteration methods, Front. Phys., 12 (2024), 1374481. https://doi.org/10.3389/fphy.2024.1374481 doi: 10.3389/fphy.2024.1374481
[41]	S. A. El-Tantawy, R. T. Matoog, R. Shah, A. W. Alrowaily, S. M. E. Ismaeel, On the shock wave approximation to fractional generalized Burger–Fisher equations using the residual power series transform method, Phys. Fluids, 36 (2024), 023105. https://doi.org/10.1063/5.0187127 doi: 10.1063/5.0187127
[42]	G. Adomian, Solving frontier problems of physics: the decomposition method, Vol. 60, Springer Science and Business Media, 2013.
[43]	J. H. He, Homotopy perturbation technique, Comput. Methods Appl. Mech. Eng., 178 (1999), 257–262. https://doi.org/10.1016/S0045-7825(99)00018-3 doi: 10.1016/S0045-7825(99)00018-3
[44]	J. H. He, Approximate analytical solution for seepage flow with fractional derivatives in porous media, Comput. Methods Appl. Mech. Eng., 167 (1998), 57–68. https://doi.org/10.1016/S0045-7825(98)00108-X doi: 10.1016/S0045-7825(98)00108-X
[45]	V. Daftardar-Gejji, S. Bhalekar, Solving fractional diffusion-wave equations using a new iterative method, Fract. Calc. Appl. Anal., 11 (2008), 193–202.
[46]	D. Baleanu, K. Diethelm, E. Scalas, J. J. Trujillo, Fractional calculus: models and numerical methods, Vol. 3, World Scientific, 2012.
[47]	J. Zhang, X. Chen, L. Li, C. Zhou, Elzaki transform residual power series method for the fractional population diffusion equations, Eng. Lett., 29 (2021).
[48]	E. Keshavarz, Y. Ordokhani, M. Razzaghi, Bernoulli wavelet operational matrix of fractional order integration and its applications in solving the fractional order differential equations, Appl. Math. Model., 38 (2014), 6038–6051. https://doi.org/10.1016/j.apm.2014.04.064 doi: 10.1016/j.apm.2014.04.064
[49]	P. Rahimkhani, Y. Ordokhani, E. Babolian, Numerical solution of fractional pantograph differential equations by using generalized fractional-order Bernoulli wavelet, J. Comput. Appl. Math., 309 (2017), 493–510. https://doi.org/10.1016/j.cam.2016.06.005 doi: 10.1016/j.cam.2016.06.005
[50]	A. El-Ajou, O. A. Arqub, S. Momani, Approximate analytical solution of the non-linear fractional KdV-Burgers equation: a new iterative algorithm, J. Comput. Phys., 293 (2015), 81–95. https://doi.org/10.1016/j.jcp.2014.08.004 doi: 10.1016/j.jcp.2014.08.004
[51]	T. M. Elzaki, The new integral transform Elzaki transform, Global J. Pure Appl. Math., 7 (2011), 57–64.
[52]	M. Suleman, T. M. Elzaki, Q. Wu, N. Anjum, J. U. Rahman, New application of Elzaki projected differential transform method, J. Comput. Theor. Nanosci., 14 (2017), 631–639. https://doi.org/10.1166/jctn.2017.6253 doi: 10.1166/jctn.2017.6253
[53]	A. K. H. Sedeeg, A coupling Elzaki transform and homotopy perturbation method for solving non-linear fractional heat-like equations, Am. J. Math. Comput. Model., 1 (2016), 15–20.
[54]	S. Bhalekar, V. Daftardar-Gejji, New iterative method: application to partial differential equations, Appl. Math. Comput., 203 (2008), 778–783. https://doi.org/10.1016/j.amc.2008.05.071 doi: 10.1016/j.amc.2008.05.071
[55]	B. He, Q. Meng, S. Li, Explicit peakon and solitary wave solutions for the modified Fornberg-Whitham equation, Appl. Math. Comput., 217 (2010), 1976–1982. https://doi.org/10.1016/j.amc.2010.06.055 doi: 10.1016/j.amc.2010.06.055
[56]	A. H. Almuqrin, C. G. L. Tiofack, D. V. Douanla, A. Mohamadou, W. Alhejaili, S. M. E. Ismaeel, et al., On the "Tantawy Technique" and other methods for analyzing Fractional Fokker Plank-type Equations, J. Low Freq. Noise, Vib. Active Control, 2025. https://doi.org/10.1177/14613484251319893
[57]	S. A. El-Tantawy, A. S. Al-Johani, A. H. Almuqrin, A. Khan, L. S. El-Sherif, Novel approximations to the fourth-order fractional Cahn–Hillard equations: application to the Tantawy Technique and other two techniques with Yang transform, J. Low Freq. Noise, Vib. Active Control, 2025. https://doi.org/10.1177/14613484251322240
[58]	S. A. El-Tantawy, S. I. H. Bacha, M. Khalid, W. Alhejaili, Application of the Tantawy technique for modeling fractional ion-acoustic waves in electronegative plasmas having Cairns distributed-electrons, Part (I): fractional KdV solitary waves, Braz. J. Phys., 55 (2025), 123.

This article has been cited by:

莉周, Vertex Reducible Edge (Total) Coloring of Two Classes of Generalized Petersen Graph, 2023, 13, 2160-7583, 1851, 10.12677/PM.2023.136188

Reader Comments

Your name:*

Email:*
© 2025 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)