Dedicated to E. N. Dancer on the occasion of his 75th birthday, with profound respect for his mathematical contributions and our very best wishes for his personal files.
1.
Introduction
This paper studies the one-dimensional boundary value problem
where λ∈R is a parameter, and a:[0,1]→[0,∞), a≠0, is a piece-wise continuous function. This problem is said to be non-degenerate if
as, in such a case, large positive constants provide us with supersolutions of (1.1) and hence, by the maximum principle, all the solutions (λ,u) with u≠0 are bounded. Instead, when [α,β]⊂a−1(0) for some α,β∈[0,1] with α<β, problem (1.1) is said to be degenerate. In these problems, large positive constants fail to be supersolutions, making the analysis of (1.1) substantially harder since large solutions may, and actually do, appear. Degenerate problems have attracted a great deal of attention during the past few decades since the publication of the papers by Brézis and Oswald [2], Ouyang [3] and Fraile et al. [4]. In particular, they have shown to be crucial in developing the theory of metasolutions (see the monograph of López-Gómez [5], as well as the list of references therein). When a−1(0) is a tiny set with empty interior, (1.1) behaves much like a non-degenerate problem (see, e.g., Daners and López-Gómez [6]).
By adopting the point of view of global bifurcation theory, we see a solution of (1.1) as a pair (λ,u) consisting of a value of λ and a piece-wise C2 function satisfying the boundary value problem (1.1). Observe that (λ,0) is a solution for all λ∈R; it will be referred to as the trivial solution. The nonlinearity of the differential equation has been chosen to be odd, so that the solutions of (1.1) arise by pairs: (λ,u) and (λ,−u). This considerably simplifies the description of the solution set of (1.1), without reducing the novelty of the findings of this paper.
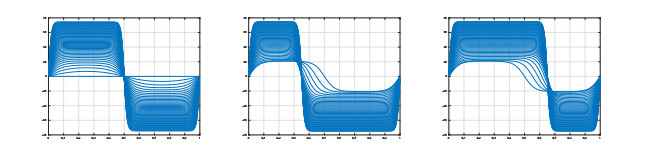
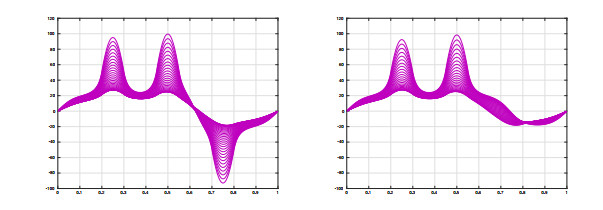
According to the Cauchy–Lipschitz theorem for second order differential equations, for every solution (λ,u) of (1.1) with u≠0 and any z∈[0,1] such that u(z)=0, necessarily u′(z)≠0. Therefore, the zeroes of nontrivial solutions, also called nodes in this paper, must be simple. Consequently, u changes sign at any interior node. As a byproduct, the solutions of (1.1) have, at most, finitely many interior nodes, possibly none, as they might be either positive or negative in (0,1). In this paper, by a nodal solution we mean a solution with n≥1 interior nodes; otherwise, the solution is either positive, or negative. Figure 1 shows some plots of positive, negative and nodal solutions of (1.1) for constant a, whose construction will be described next.
In the simplest case when a(x) is constant, e.g., a≡1, by the symmetries of the differential equation, the one-node solutions satisfying u′(0)>0 can be constructed by simply gluing together the positive solution in (0,12) with the negative solution in (12,1). Analogously, the two-node solutions satisfying u′(0)>0 can be constructed by gluing the positive solutions in (0,13) and (23,1) with the negative one in (13,23), and a similar argument can be applied to construct all nodal solutions of (1.1). Indeed, the solutions with n−1 interior nodes, n≥2, are determined by the positive or negative solutions on appropriate subintervals of the form (a,b), with b−a=1n. Such sign-definite solutions exist if, and only if, λ>(πb−a)2=(nπ)2 (see, e.g., [7,Theorem 2.1]). When a(x) is constant, this is a very classical result that can be easily established through a shooting argument involving the phase portrait and the symmetries of the differential equation. In the same case, the uniqueness of the nodal solution with u′(0)>0, if it exists, is a direct consequence of the strong maximum principle (see, e.g., Cubillos [8], if necessary). We summarize all these elements in the following well-known result.
Theorem 1.1. Suppose a≡1. Then,
(a) problem (1.1) has a positive solution if, and only if, λ>λ1=:π2. Moreover, it is symmetric about x=12;
(b) for every integer n≥2, problem (1.1) has a solution with n−1 (interior) nodes in (0,1), if, and only if, λ>λn=:(nπ)2. Moreover, in such case, its nodes must be equidistant;
(c) for every integer n≥1 and λ>(nπ)2, there exists a unique solution of (1.1) with n−1 interior nodes such that u′(0)>0.
Figure 2 shows the global bifurcation diagram of (1.1) in the special case when a≡1. For any solution (λ,u), we are plotting the value of the parameter λ, in abscissas, versus the value maxu if u′(0)>0, or minu if u′(0)<0, in ordinates. Thus, each point on every plotted curve represents a different solution of (1.1).
According to Figure 2, (λ,0) is the unique solution of (1.1) if λ≤λ1, (1.1) has a positive solution and a negative solution for each λ∈(λ1,λ2], a positive solution, a negative solution, a one-node solution with u′(0)>0 and another one with u′(0)<0 if λ∈(λ2,λ3], and so on… Thus, whenever λ increases and crosses a value of λn, the number of solutions of (1.1) increases by two.
Moreover, the set of nontrivial solutions of (1.1) is made up of a sequence of components, C±n, n≥1, bifurcating from (λ,0) at λ=λn, and consisting of solutions with n−1 interior nodes: C+n denotes the set of solutions (λ,u) with n−1 nodes such that u′(0)>0, while C−n consists of the solutions with u′(0)<0. By the analyticity of the underlying time maps with respect to λ, along any of these curves, u can be parameterized as an analytic curve with respect to λ, i.e., C±n are analytic curves for all integer n≥1.
When, instead of being a positive constant, a(x) is assumed to be a general continuous function satisfying (1.2), or a positive piece-wise continuous function, the phase portrait techniques used to derive Theorem 1.1 fail and other techniques, like the topological degree, must be invoked to get the corresponding existence results. In this case, the global results by Rabinowitz [9,10,11] establish that, essentially, the same results are true as soon as (1.2) holds, except for the arc connectedness of the components C±n. In the setting of [9], C±n were only shown to be closed and connected subsets, maximal for the inclusion, of the solution set of (1.1), because they were constructed by means of the Leray–Schauder degree. Nevertheless, also in this general case, as a consequence of the strong maximum principle, the positive solution is unique if it exists and, as a byproduct of the implicit function theorem, C+1 is also a real analytic curve (see, e.g., [4], [5], and [6]). Furthermore, by a recent result of López-Gómez and Sampedro [12], for every n≥2, each of the components C±n consists of a discrete set of analytic arcs of curve plus a discrete set of branching points, because of the analyticity of the nonlinearity of (1.1). In particular, all these components are arc connected according to the structure theorem of analytic manifolds (see [12] for further details). The reader is sent to Rabinowitz [9,10,11], López-Gómez [13,Chapter 6], and Dancer [14,15] for an overview of the most relevant results in the context of the classical theory.
Although the global bifurcation diagram under condition (1.2) is reminiscent of the one plotted in Figure 2, no uniqueness result of one-node solutions is known for (1.1) under condition (1.2); the uniqueness results of López-Gómez and Rabinowitz [16,17] are only valid in the context of degenerate problems. As a matter of fact, the component C±2 might bend backwards providing us with some interval of λ's where (1.1) admit several one-node solutions, or it might even exhibit some secondary, or tertiary, bifurcations, and the existence of some further components of solutions with one interior node cannot be excluded, as those isolas might be provoked by the spatial heterogeneities of a(x). Since the simplest problem of the uniqueness of the one-node solutions under condition (1.2) has remained open since [9,10,11] were published almost fifty years ago, answering this question, either in the affirmative or in the negative, is extremely challenging. This is the main goal of this work.
Now, we will introduce the class of weight functions a(x) considered in this paper. First, for any given integer κ≥2, we choose κ subintervals of [0,1] of the form (αj,βj), j∈{1,...,κ}, such that
● 0<α1<β1<α2<β2<⋯<ακ<βκ<1,
● 0<h=βj−αj for all j∈{1,...,κ}, i.e., these κ intervals have the same length, h>0,
● αi+βj=1 if i+j=κ+1, i.e., (αi,βi) is the symmetric of (ακ+1−i,βκ+1−i), with respect to 0.5, for all i∈{1,...,κ},
● h<α1=1−βκ.
Then, for each of these choices, we consider the weight functions
for every ε∈[0,1], which are symmetric about 12 and piece-wise constant. We are considering symmetric weight functions as it is well documented that breaking the symmetry of the problem simply provokes that branches with bifurcation points split into two or more separated components, whose mathematical treatment is more intricate (see, e.g., [18]). In some sense, the symmetries do reorganize the global bifurcation diagrams in a more friendly way.
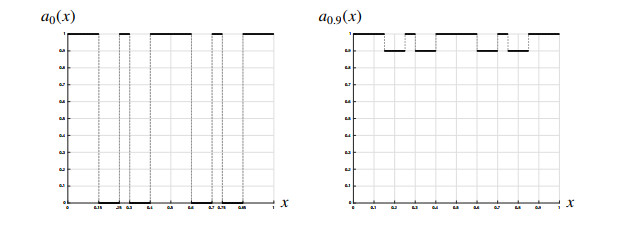
Figure 3 plots two choices of aε(x) for κ=4. The first one for ε=0, the second one for ε=0.9. Naturally, for the choice ε=0, problem (1.1) is degenerate with
Thus, h=0.1 and
When κ=2n for some integer n≥1, we have that βn<12<αn+1 and, hence, aε(x)=1 for all x∈(βn,αn+1). When, κ=2n+1 for some integer n≥1, necessarily, by the symmetry of aε, one has that αn+1<12<βn+1 and hence, aε(x)=ε for all x∈[αn+1,βn+1].
The weight functions aε(x) defined in (1.3) can be chosen as close as we wish to the constant 1 in [0,1] by taking ε sufficiently close to 1. Although establishing the precise meaning of "sufficiently close" might be hard, most of us will agree that ε=0.9999 is really close to 1. Therefore, for problem (1.1) with a(x)=a0.9999(x) one expects, in agreement with Theorem 1.1, a unique one-node solution for some interval of values of λ, regardless the value of κ and αj, βj, j∈{1,...,κ}. However, for the special choice (1.4) with ε=0.9999, our numerical experiments presented in Section 6 reveal that (1.1) possesses, for some ranges of λ, at least 14 solutions with one interior node: 7 with u′(0)>0, and another 7 with u′(0)<0. Among the first ones, one is symmetric about 12, and the remaining 6 are asymmetric, and 3 among the asymmetric ones are reflection about 12 of the remaining 3. Even more astonishingly, our numerical experiments suggest that this multiplicity result holds for really huge intervals of λ's! More precisely, in this paper we are constructing some examples with κ∈{2,3,4}, for which
such that (1.1) possesses 6, 10 and 14 one-node solutions, respectively, for large intervals of values of λ. Based on our numerical experiments, we conjecture that, whenever a(x) satisfies (1.3), there exists ε0>0 such that, for every ε∈(ε0,1), the problem (1.1) possesses (at least) 4κ−2 one-node solutions for large intervals of λ's. Nevertheless, it is not clear how these branches of solution disappear as ε↑1 to recover the uniqueness that occurs for ε=1 (see the discussion at the end of Section 4). This is a rather unexpected effect on the global structure of the set of one-node solutions of (1.1), and it is due to the presence of spatial heterogeneities in the weight function a(x). It is striking that one can construct situations with a(x) arbitrarily closed to 1 in the L∞-norm for which the problem (1.1) can have an arbitrarily large number of one-node solutions. As a byproduct, the associated global bifurcating diagrams of one-node solutions of (1.1) in the general case when a(x) is not constant have nothing to do with the classical paradigm plotted in Figure 2 (see the global bifurcations diagrams in Sections 4, 5 and 6). More precisely, besides C±2, they might contain up to 2κ−2 unbounded isolas consisting of asymmetric solutions, and C±2 might have one, or more, secondary bifurcations.
Throughout this paper, for every p,q∈[0,1] with p<q, and any V∈L∞(p,q), we will denote by τn[−D2+V;(p,q)], n≥1, the sequence of (real) eigenvalues of the linear eigenvalue problem
ordered so that τn<τn+1 for all n≥1. It is well known that each of these eigenvalues is algebraically simple. Moreover, the eigenfunctions associated with τn[−D2+V;(p,q)] have n−1 interior nodes in (p,q). Thus, for every n≥1, τn[−D2+V;(p,q)] is the unique eigenvalue to which an eigenfunction with n−1 interior nodes is associated. For notational simplicity, we will denote
When a(x) is given by (1.3) with ε=0, (1.1) becomes a degenerate problem where a−1(0) has κ≥2 components having the same length h. Assume that h<12: in such a case, thanks to [7,Theorem 2.1], (1.1) has a positive, or negative, solution, if and only if
Moreover, the solution is unique if it exists. Similarly, by [16,Corollary 3.6], (1.1) has a solution with one interior node if and only if
(note that λ2<σ1, because h<12). Furthermore, thanks to [1,Corollary 4.1], there exists η>0 such that, for every λ∈[σ1−η,σ1), (1.1) possesses, at least, 4κ−2 solutions with one interior node.
In this paper, re-elaborating on some of the technical devices of [1], we will show (see Theorem 3.1) that there exists ε0>0 such that, for every ε∈(0,ε0], the problem (1.1) with a(x) given by (1.3) possesses at least 2κ−2 one-node solutions for every λ>σ1 and at least 4κ−2 for each λ∈(σ1,σ2). This result is the first existing multiplicity result of nodal solutions for problem (1.1) in the classical case. Although some ideas are borrowed from [1], our result has a completely different nature, since it deals with the non-degenerate case at a different range of λ's.
Moreover, rather unexpectedly, the numerical results of this paper reveal that, in most of the circumstances, this local multiplicity result is maintained for values of ε very close to 1 and for large intervals of λ. The singular perturbation problem of determining the precise behavior of the global bifurcation diagrams of the one node solutions of (1.1) as ε↑1 remains open in this paper. Our numerical experiments reveal that this problem is extremely intricate.
A crucial aspect of our study is ascertaining the precise evolution of the interior nodes of the one-node solutions of (1.1) as the parameters λ and ε change. Actually, by the uniqueness of the positive solutions of (1.1) on any subinterval of [0,1], the node, z, of a one-node solution, u, determines it univocally. Thus, z can be identified with u for all practical purposes. By the symmetries of (1.1), when a≡1 it turns out that z=12 for all λ>λ2. However, when ε<1, besides the two symmetric nodal solutions with z=12, there arise one-node solutions with their respective nodes placed on each of the intervals (αj,βj), j∈{1,...,κ}.
To conclude this section, we discuss the linearized stability of any one-node solution (ˉλ,ˉu) of (1.1), which is given by the sign of τ1[−D2+3a(x)ˉu2−ˉλ;(0,1)]. Since
it becomes apparent that
and hence, by the monotonicity of the τn's with respect to the potential V (see [20], if necessary), we find that
Therefore, (ˉλ,ˉu) is linearly stable if
while it is linearly unstable if
Moreover, in the latter case, its unstable manifold is one-dimensional.
This paper is organized as follows. Section 2 borrows from López-Gómez and Rabinowitz [1,16,17] the main concepts and technical devices used in this work. Section 3 establishes the main new analytical result, Theorem 3.1. The rest of the paper discusses a series of numerical experiments to strongly suggest how the local theorems of Sections 2 and 3 are indeed global, in the sense that they still hold true for ε very close to 1 and very large intervals of λ.
2.
Preliminaries. A multiplicity result for ε=0
Throughout the rest of this paper, we assume that a=aε has been chosen to satisfy (1.3) with ε∈[0,1]. This problem has been analyzed for the case ε=0, in López-Gómez and Rabinowitz [1,16], and López-Gómez, Molina-Meyer and Rabinowitz [7], where, in order to study the solutions of (1.1) with one interior node satisfying u′(0)>0, the following C1-map was introduced
where v(x;z,λ,ε) is the unique positive solution of
and w(x;z,λ,ε) is the unique negative solution of
provided these solutions exist. Naturally, should they exist, the function
provides us with a 1-node solution of (1.1) if, and only if, φ(z,λ,ε)=0. Thus, through this scheme one can identity the 1-node solution u with the position of its node z. In particular, the problem of analyzing the 1-node solutions of (1.1) is equivalent to the problem of analyzing φ−1(0).
When ε>0, the problems (2.2) and (2.3) are non-degenerate and, hence, v and w are well defined if and only if
respectively. When ε=0 the situation is more subtle because
Thus, the problem is degenerate in the sense that a(x) vanishes somewhere in (0,1). In such a case, according to [7,Theorem 2.1], whether or not v and w do actually exist depends on the precise location of z. Precisely,
Similarly,
In particular, this shows that, for every ε∈[0,1], the condition
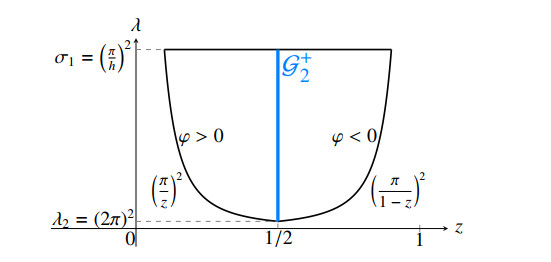
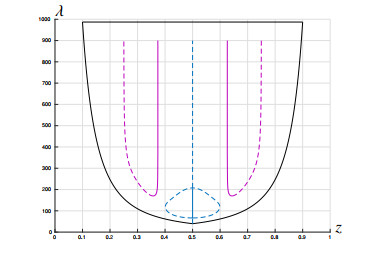
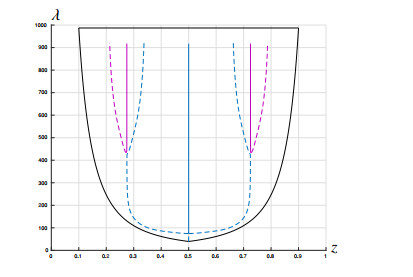
is necessary for the existence of a 1-node solution of (1.1). Note that (z,λ)=(12,λ2) is the crossing point of the curves λ=(πz)2 and λ=(π1−z)2 in the (z,λ)-plane. Thus, (2.5) implies that, necessarily, λ>λ2. Moreover, in the degenerate case ε=0, since κ≥2, another necessary condition for the existence of v and w is λ<σ1. Thus, when ε=0, if v and w exist, necessarily (z,λ)∈R, where R denotes the set of pairs (z,λ)∈(0,1)×(λ2,σ1) satisfying (2.5) that has been depicted in Figure 4. Furthermore, based on the theorem of Crandall and Rabinowitz [19],
Therefore, for every ε∈[0,1],
which explains why (1.1) does have a 1-node solution in this case if, and only if, λ∈(λ2,σ1), when ε=0, and if and only if λ>λ2, when ε>0. This methodology goes back to López-Gómez and Rabinowitz [16], where it was developed to characterize the existence of 1-node solutions for the degenerate problem when ε=0.
For the special choice (1.3) with ε∈[0,1], as a(x) is symmetric about x=12, it is apparent that
and hence φ(12,λ,ε)=0 for all λ∈(λ2,σ1) if ε=0, and for all λ>λ2 if ε>0. In particular, (1.1) has a unique 1-node solution with u′(0)>0 and z=12.
Let F denote the map (λ,u)↦(z,λ), where u is a solution of (1.1) with the single interior node z. Since F is continuous, it maps connected subsets in R×C1[0,1] to connected subsets in R2. In particular, the component of solutions C+2 (respectively, C−2) bifurcating from (λ2,0) is transformed into a connected subset denoted by G+2 (respectively, G−2) bifurcating from (12,λ2). Points of the form (z,σ1) may not lie in the range of this map if ε=0, although they lie in its closure. Figure 4 shows the region R and the component G+2 in a (real) case where z=12 for all (λ,u)∈C+2 and ε=0.
Although, according to (2.4), on the top boundary of R at level λ=σ1 the solution v(x;z,σ1,0) is not defined if z≥β1, we can extend the definition of v(x;z,σ1,0) to cover the case z≥β1 by setting
Indeed, since v(x;z,λ,0) is increasing with respect to λ for every x∈(0,z), the limit (2.6) is well-defined. Moreover, with the ingredients of the proofs of [7,Theorem 2.3], [1,Theorem 2.2] and [1,Theorem 2.6], the next properties hold.
Suppose z∈(0,β1). Then, v(x;z,σ1,0) is the unique positive solution of (2.2) at λ=σ1 and ε=0.
Suppose z=β1. Then, v(z;z,σ1,0)=0, v(x;z,σ1,0)=+∞ for all x∈[α1,β1), and v(x;z,σ1,0)=ℓ1(x) for all x∈[0,α1), where ℓ1 is the unique positive solution of the singular problem
Observe that, although for this particular problem the uniqueness of ℓ1 can be inferred from the phase-portrait techniques of López-Gómez and Rabinowitz [1], it is a direct consequence from the multidimensional uniqueness theorems of López-Gómez and Maire [21] and López-Gómez, Maire and Véron [22].
Suppose z∈(β1,β2). Then, v(x;z,σ1,0)=ℓ1(x) for all x∈[0,α1), v(x;z,σ1,0)=+∞ for every x∈[α1,β1], and v(x;z,σ1,0)=m1(x) for each x∈(β1,z], where m1(x) is the unique positive solution of the singular problem
Suppose z=β2. Then, v(x;z,σ1,0)=ℓ1(x) if x∈[0,α1), v(x;z,σ1,0)=+∞ if x∈[α1,β1], v(x;z,σ1,0)=ℓ2(x) if x∈(β1,α2), where ℓ2(x) is the unique positive solution of the singular problem
v(x;z,σ1,0)=+∞ for all x∈[α2,β2), and v(z;z,σ1,0)=0.
More generally, suppose κ≥3, i∈{2,...,κ−1}, and z∈(βi,βi+1). Then,
where, for every j∈{2,...,κ}, ℓj is the unique positive solution of
and, for every i∈{2,...,κ}, mi(x) denotes the unique positive solution of
Now, suppose that z=βκ. Then,
Finally, for every z∈(βκ,1],
Similarly, for every z∈(ακ,1), w(x;z,σ1,0) is the unique negative solution of (2.3) at λ=σ1 and ε=0. Moreover, when z=ακ, we have that w(z;z,σ1,0)=0, w(x;z,σ1,0)=−∞ for all x∈(ακ,βκ], and w(x;z,σ1,0)=n1(x) for all x∈(βκ,1], where n1 denotes the unique negative solution of the singular problem
And so on... Naturally, the following definition is consistent
and it turns out that φ(z,σ1,0)=limλ↑σ1φ(z,λ,0). Moreover, the next result holds; it is [1,Proposition 4.1].
Theorem 2.1. Suppose that a=aε is given by (1.3) with ε=0. Then, for every j∈{1,...,κ−1} and z∈[βj,αj+1], we have that
Moreover, for every j∈{1,...,κ}, there exists ζj∈(αj,βj) such that
When κ≥3, by using the symmetry of aε and a phase portrait analysis, it can be shown that, in (2.7), ζj=αj+βj2 for every j∈{2,...,κ−1}. As a consequence of the previous theorem, since φ(z,λ,0) varies continuously with respect to λ for λ∈(λ2,σ1], it is apparent that the next multiplicity result holds; it is Corollary 4.1 of López-Gómez and Rabinowitz [1].
Theorem 2.2. Suppose that a=aε is given by (1.3) with ε=0. Then, there exists η>0 such that, for each λ∈[σ1−η,σ1), the problem (1.1) possesses, at least, 2κ−1 solutions, (λ,uj), 1≤j≤2κ−1, having one interior node and such that u′(0)>0.
By the symmetry of the problem, under the assumptions of Theorem 2.2, (1.1) has another 2κ−1 solutions, (λ,Uj), with U′j(0)<0, 1≤j≤2κ−1. Actually, Uj=−uj, 1≤j≤2κ−1. Therefore, altogether (1.1) posseses, at least, 4κ−2 solutions having one interior node for this range of λ's.
3.
A multiplicity result for λ>σ1 and sufficiently small ε>0
Naturally, as soon as ε>0, the problem (1.1) with a=aε given by (1.3) is non-degenerate, because aε(x)>0 for all x∈[0,1]. Thus, the functions v(x;z,λ,ε) and w(x;z,λ,ε) are well defined for every λ>λ2 and ε∈(0,1] if (2.11) holds. Moreover, by uniqueness, they vary continuously with respect to λ>λ2, ε>0 and z∈(0,1). In particular, much like in the degenerate case when ε=0 and λ∈(λ2,σ1], we can define φ(x;z,λ,ε) through (2.1) for these values of λ, ε and z. By analyzing the behavior of v(x;z,λ,ε) and w(x;z,λ,ε) as ε↓0, we are able to obtain the result holds. It is the first existing multiplicity result for 1-node solutions in the classical non-degenerate setting. Although it resembles Theorem 2.2, in the sense that for some range of λ's the number of obtained solutions is the same, it is relevant to keep in mind that the nature of this result is completely different, since it deals with the case λ>σ1 and the non-degenerate case ε>0.
Theorem 3.1. Suppose that a=aε satisfies (1.3). Then:
(a) for every λ>σ1, there exists ε0=ε0(λ)>0 such that, for each ε∈(0,ε0], the problem (1.1) possesses, at least, 2κ−2 solutions with one interior node;
(b) for every λ∈(σ1,σ2), there exists ε1=ε1(λ)>0 such that, for each ε∈(0,ε1], the problem (1.1) has, at least, 4κ−2 solutions with one interior node.
Remark 3.2. If ε>0 in κ−1 intervals (αj,βj), while ε=0 in the remaining one, then, thanks to Theorem 2.3 of López-Gómez and Rabinowitz [16], problem (1.1) admits exactly two nodal solutions for each λ∈[σ1,σ2). Thus, increasing ε in one single well has dramatic consequences, as, due to Theorem 3.1, (1.1) admits 4κ−2 solutions with one interior node, regardless the value of κ≥2.
In the rest of this section we will provide a proof of Theorem 3.1. We will first show that, for every λ>σ1 and sufficiently small ε>0, the function φ(z,λ,ε) defined by (2.1), with λ>σ1, possesses κ−1 zeroes. Then, we will prove that for each λ∈(σ1,σ2) φ(z,λ,ε) possesses κ additional zeros. We will derive these properties from a sharp asymptotic analysis of v(x;z,λ,ε) and w(x;z,λ,ε) as ε↓0.
The limiting behavior of these two functions depends on the precise location of z in (0,1). The next preliminary result shows that, whenever z≥βj, j≥1, the function v(⋅;z,λ,ε) blows up in (αi,βi) for all i∈{1,...,j} as ε↓0. It extends some previous findings of [24] in a different context.
Note that the map ε↦v(⋅;z,λ,ε) is decreasing, because, due to [23,Theorem 7.10], the smaller ε, the bigger the solution of (2.2). Consequently, its point-wise limit as ε↓0 is well defined.
Lemma 3.3. Suppose that λ>σ1 and z≥βj for some j≥1. Then, for every (sufficiently small) η>0 and i∈{1,...,j}, the solution v of (2.2) satisfies
Proof. Let i≥1 be an integer such that i≤j and set V:=√εv. Then, in the interval (αi,βi), V solves the differential equation −V″=λV−V3. Thus, since V(αi)>0 and V(βi)≥0, V provides us with a positive supersolution of the homogeneous boundary value problem
Since λ>σ1, this problem admits a unique positive solution, denoted by V0. By [23,Th. 7.10], it follows that V0≤V=√εv. Finally, (3.1) is a direct consequence of the estimate v≥V0√ε by letting ε↓0.
With some additional effort, and using the specific structure of the weight aε given by (1.3), we are able to obtain the following result.
Proposition 3.4. Suppose that λ>σ1 and z>βj for some j≥1. Then, for every i∈{1,...,j},
Proof. Thanks to Lemma 3.3, it suffices to prove
For convenience, we set vε:=v(⋅;z,λ,ε), and divide the proof into several steps.
Step 1: proof of (3.3) for α1. Since a≡1 in [0,α1], it is easily seen that, for every x∈(0,α1) and ε∈(0,1],
Based on [5,Th. 3.4], the unique positive solution, ℓ1, of the singular problem
satisfies ℓ1=limM↑∞LM, where LM is the unique positive solution of
The uniqueness of ℓ1, as well as of the remaining large positive solutions of this paper, is a direct consequence of the theory of López-Gómez and Maire [21] and López-Gómez, Maire and Véron [22]. Then, thanks to [23,Th. 7.10], it is easily seen that, for sufficiently large M>0, vε≤LM≤ℓ1 in [0,α1). Hence, v0:=limε↓0vε≤ℓ1 (observe that this point-wise limit is well defined by the monotonicity of vε with respect to ε). Moreover, with slightly more effort, a standard phase portrait analysis also shows that v′ε(0)<ℓ′1(0) if ε∈(0,1], as otherwise vε would not be defined in the whole interval [0,α1]. Thus, by (3.5),
for all ε∈(0,1]. In order to prove that limε↓0vε(α1)=+∞, we can argue by contradiction assuming that there exists a constant C>0 such that vε(α1)≤C for all ε∈(0,1]. Then, by (3.5), there also exists a positive constant ˜C such that |v′ε(α1)|≤˜C for all ε∈(0,1], and, setting Vε:=√εvε, it is apparent that
Since −V″ε=λVε−V3ε in [α1,β1], it follows from (3.6) that Vε→0 in [α1,β1] as ε↓0, which contradicts Vε≥V0>0, where V0 is the unique positive solution of (3.2). Therefore, vε(α1)↑+∞ as ε↓0. Note that, since Lvε(α1)=vε in [0,α1], we can infer from [5,Th. 3.4] that
Step 2: proof of (3.3) for β1. Since aε≡ε in [α1,β1], owing to (3.5), it becomes apparent that, for every ε∈(0,1],
Thus, by Step 1, we find that
To show that limε↓0vε(β1)=+∞, we will argue by contradiction assuming that {vε(β1)}ε∈(0,1], is bounded from above. We first show that, for ε∼0, vε is decreasing in a left neighborhood of β1. This will imply, together with (3.7), that
Indeed, in the contrary case, by Lemma 3.3 and our contradiction hypothesis, for every ε∼0 there would exist yε<β1, yε∼β1, such that where vε(yε)<vε(β1) and yε is a local minimum point. Thus,
which implies 0≥λ−εv2ε(yε). Thus, letting ε↓0, we find that λ≤0, which contradicts λ>σ1 and concludes the proof of (3.8).
Let η>0 be such that β1+η<min{z,α2}. By the monotonicity of vε with respect to ε, either {vε}ε∈(0,1] is bounded in [β1,β1+η], or
Suppose the first option occurs. Then, it follows from the differential equation that v″ε also is bounded in [β1,β1+η] uniformly in ε∈(0,1]. Thus, since
and ∫xβ1v″ε(s)ds is bounded, we can infer from (3.8) that limε↓0v′ε(x)=−∞ uniformly in x∈[β1,β1+η]. Consequently, for every integer n≥1, there exists ε0=ε0(n)>0 such that v′ε≤−n in [β1,β1+η] if ε<ε0. Hence,
for all ε<ε0. Therefore, since vε(β1) is bounded and n can be is arbitrarily large, we find that vε(β1+η)<0 for sufficiently small ε>0, which is impossible, because vε is positive everywhere. This contradiction shows that (3.9) holds.
For every ε∈(0,1], let xε∈[β1,β1+η] be such that vε(xε)=‖vε‖C[β1,β1+η]. Since vε(β1) is bounded, (3.12) implies that xε∈(β1,β1+η] for sufficiently small ε>0. Suppose that xε∈(β1,β1+η). Then, v′ε(xε)=0 and v″ε(xε)≤0. Thus,
which implies vε(xε)≤√λ and contradicts (3.9). Therefore, xε=β1+η for sufficiently small ε>0. So, according to (3.9), we find that limε↓0vε(β1+η)=+∞, which contradicts the estimate vε≤ℓ2, where ℓ2 denotes the unique positive solution of the singular problem
This contradiction shows that limε↓0vε(β1)=+∞.
Step 3: proof of (3.3) in the remaining cases. Now, we suppose that z>β2 and set v0(α2):=limε↓0vε(α2). This limit (which is either a positive real number, or +∞) exists by the monotonicity of vε with respect to ε∈(0,1]. Moreover, by [23,Th. 7.10], vε≤ℓ2 in [β1,α2]. Thus, by a standard compactness argument, the point-wise limit v0:=limε↓0vε in [β1,α2] provides us with the unique positive solution of the singular problem
Actually, vε→v0 in C1[β1+δ,α2−δ] as ε↓0 for all δ>0, δ∼0. Thus, since for every x∈(β1,α2) and ε>0, we have that
it becomes apparent that the right hand side of (3.10) remains bounded as ε↓0. Therefore, by adapting the argument of proof of Step 1, it readily follows that v0(α2)=+∞. As a byproduct, v0=ℓ2 in (β1,α2). Furthermore, since
the proof of Step 2 can be as well adapted to conclude that
This procedure can be repeated for the other αi's and βi's, and ends the proof.
Remark 3.5. From the proof of Proposition 3.4, it is apparent that, as soon as z>βj for some j≥2, limε↓0vε=ℓj in [βj−1,αj], where ℓj is the unique positive solution of
Naturally, the negative solution wε(x):=w(x;z,λ,ε) satisfies similar properties as vε when ε↓0. Thus, to obtain the proof of Theorem 3.1 from Proposition 3.4 and Remark 3.5, one can argue as follows.
Proof of Theorem 3.1. (a) Suppose that z∈(βj−1,αj) for some j∈{2,…,κ}. Then, based on the generalized Keller–Osserman condition of [27], the a priori bounds of Keller [25] and Osserman [26], and the point-wise monotonicity of vε(x):=v(x;z,λ,ε) as ε↓0, it becomes apparent that, in the interval [βj−1,z], vε approximates, as ε↓0, the unique positive solution of
denoted by pz. Similarly, in [z,αj], wε approaches, as ε↓0, the unique negative solution of
denoted by nz. Since a careful phase portrait analysis reveals that
by continuous dependence, it becomes apparent that, for sufficiently small ε>0,
Therefore, for every j∈{2,…,κ}, φ(z(ε),λ,ε)=0 for some z(ε)∈(βj−1,αj), which provides us with at least 2(κ−1) different solutions of (1.1) with one interior node.
(b) When λ∈(σ1,σ2), to construct the remaining 2κ solutions with one node, we work in (αi,βi) for any given i∈{1,...,κ}. Once λ has been fixed, we define
Since σ1<λ<σ2, the following relations hold
Thus, for every z∈(z−,i(λ),z+,i(λ)), we have that
Consequently, by [5,Th. 4.1], the functions vε:=v(⋅;z,λ,ε) and wε:=w(⋅;z,λ,ε) are well defined in (αi,z] and [z,βi), respectively, for all ε∈[0,1], as well as
We start by considering ε=0. As z<αi+βi2 for z∼z−i(λ),
Thus, [28,Th. 2.4] gives
With some additional effort, one can prove that limz↓z−i(λ)w′0(z)=−∞, because w0(z)=0. On the other hand, the inequality in (3.24) guarantees that v0 converges to some finite profile in (αi,z] as z↓z−i(λ); thus limz↓z−i(λ)v′0(z) is finite. Hence, we can conclude that φ(z,λ,0)>0 provided z>z−i(λ) is sufficiently close to z−i(λ). By continuity, φ(z,λ,ε)>0 for sufficiently small ε>0.
Similarly, one can prove that φ(z,λ,ε)<0 for sufficiently small ε>0 provided z<z+i(λ) is sufficiently close to z+i(λ). Therefore, φ admits κ zeroes which are different from the ones obtained in part (a), since they lie in (αi,βi), i∈{1,…,κ}. Equivalently, (1.1) admits, at least, 2κ solutions with one node for sufficiently small ε>0, besides the 2κ−2 solutions constructed in Part (a).
4.
An example with κ=2
In this section, we provide some numerical results related to the case (1.3) with κ=2,
and ε∈[0,1). Then,
Figure 5 shows the global bifurcation diagram of 1-node solutions, (λ,u), with u′(0)>0, for ε=0. As remarked above, once the sign of the derivative at x=0 has been chosen, every solution (λ,u) is uniquely identified, apart from the value of λ of course, by the position of its interior zero z. Thus, in all the bifurcation diagrams of this paper, we represent the values of z in abscissas versus the values of λ in ordinates.
In agreement with Theorem 2.2, (1.1) has three 1-node solutions with u′(0)>0 for each λ<σ1 sufficiently close to σ1. One of them satisfies z=0.5 and is odd about 0.5. Numerically, we see that the other 1-node solutions satisfy z∼0.35 and z∼0.65, respectively, if λ∼σ1. Observe that those values are the midpoints of the vanishing intervals of a0(x), [0.3,0.4] and [0.6,0.7], respectively. These branches bifurcate from the branch of 1-node solutions with z=0.5 at λb∼104.8215.
We now describe the stability of the solutions, which determines their local attractive or repelling character. As noticed in Section 1, we already know that the linear stability of any 1-node solution is determined by the sign of the lowest eigenvalue of its linearized equation and that, if a 1-node solution is unstable, then its unstable manifold is one-dimensional. According to [19], the branch of nodal solutions with z=0.5 bifurcates from (λ,u)=(λ,0) at λ=λ2. Thanks to the exchange stability principle [29], it consists of unstable solutions until λ reaches λb. At such a point, the solutions with z=0.5 become stable for any further value of λ. Once again, by the exchange stability principle, the curves that bifurcate from the branch of solutions with z=0.5 consist of unstable solutions until λ reaches σ1 where they become metasolutions, much like v and w introduced in (2.2) and (2.3), respectively, as λ↑σ1. In Figure 5, as in the remaining bifurcation diagrams of this paper, the dashed curves represent unstable solutions, while the continuous ones consist of stable solutions.
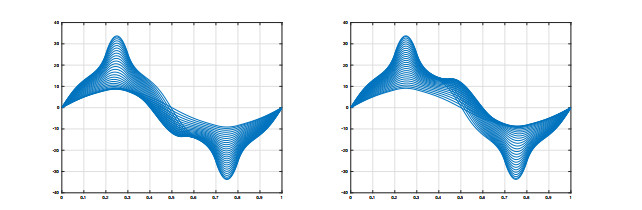
Figure 6 shows a series of solutions along each of these curves for a series of increasing values of λ. In the first picture we have plotted the nodal solutions with z=0.5. It is apparent that, as λ increases, they become much larger in
than in the complement of a−10(0). Actually, as already discussed in Section 2, these solutions blow up, as λ↑σ1, to +∞ in [0.3,0.4], and to −∞ in [0.6,0.7], while they stabilize to the appropriate large solutions in the complement of a−10(0), in agreement with [1,Theorem 2.2]. In particular, in the interval [0.4,0.6] they converge, as λ↑σ1, to the unique 1-node solution of the singular problem
The central plot of Figure 5 shows a series of solutions on the left bifurcated branch of Figure 4. The node of these solutions approaches 0.35, the middle point of the interval [0.3,0.4], as λ↑σ1. These solutions blow-up to −∞ in [0.6,0.7] as λ↑σ1, while in the complement they stabilize to certain large solutions, confirming what is established by [1,Theorem 2.2]. In particular, in the interval [0,0.6] they converge, as λ↑σ1, to the unique large solution with one interior node at 0.35 of the singular problem
In the right picture of Figure 6 we have plotted a series of solutions on the right bifurcated branch of Figure 5. By the internal symmetries of (1.1) for the choice (1.3), with (4.1), they are reflections about 0.5 of the ones plotted in the central picture. Thus, their nodes stabilize to 0.65, and they blow-up to +∞ in [0.3,0.4] as λ↑σ1.
As expected from Theorem 3.1(a), for sufficiently small ε>0, some of the previous nodal solutions are defined for all values of λ>σ1. Surprisingly, our numerical computations show that this is true also for ε close to 1. For example, Figure 7 shows the corresponding global bifurcation diagram for ε=0.9999.
Essentially, the solutions behave in the same way as in the special case when ε=0, except for the relevant fact that they are defined for all values of λ>σ1 for which we performed the computations. Figure 8 shows a series of plots of the nodal solutions along each of the three branches of Figure 7.
As before, the left picture superimposes the plots of a series of solutions along the central branch, with z=0.5, the central picture plots a series of solutions on the left secondary branch, whose nodes approach 0.35 as λ increases, and the third one superimposes the plots of a series of solutions on the right secondary branch, whose nodes approach 0.65 as λ grows. The reader should compare the huge qualitative differences between the growth of the solutions plotted in Figures 6 and 8. Although the nodes behave in a rather similar way, approaching either 0.5, or the midpoints of [0.3,0.4] or [0.6,0.7], the solutions are much flatter in the present situation, where a0.9999 is very close to the constant 1.
Therefore, although Theorem 3.1 only guarantees, for sufficiently small ε>0, the existence of one solution for every λ>σ1 and of three if λ∈(σ1,σ2), this local result might actually have a global character in the sense that, according to our numerical experiments, there are very large ranges of λ and ε for which (1.1) still has three nodal solutions with one interior node.
And, what is even more striking, is that, according to our numerical simulations, the same structure is maintained at least up to ε=0.99999999, though in such a case the bifurcation point from the central branch grew up to λb=435.0634. This causes a great perplexity to us, as problem (1.1) with a≡1 has a unique solution with one interior node at z=0.5, whereas the nodes of the solutions along the secondary branches for ε=0.99999999 still approach 0.35 and 0.65 as λ increases for really huge intervals of λ. The extremely challenging problem of ascertaining how these nodal solutions disappear as ε↑1, and only one solution remains for ε=1, is left open in this paper.
We can think of two possibilities. The first one is that the secondary branches actually form a loop bifurcating from the central branch at an another (huge) value of λ, and that such a loop shrinks to a single point up to disappear as ε↑1, analogously to what happens in Figure 14. This global structure of the bifurcation diagram could be established, for example, if one is able to adapt to this situation the arguments provided by Dancer and López-Gómez in [30,Theorem 3.1]. The second possibility is that the bifurcation point λb(ε) converges to ∞ as ε↑1. Actually, analyzing this singular perturbation problem is a serious challenge which needs to be tackled if one wishes to understand how local heterogeneities can have global effects even at large parameter scales. The challenge arises also from the numerical point of view, as, for sufficiently large λ, we are working close to the computational limits of the computer.
5.
An example with κ=3.
In this section we present the results of our numerical computation related to a weight aε as in (1.3) with κ=3 and
In particular, (4.2) still holds true. Figure 9 shows the global bifurcation diagram of 1-node solutions that we have computed for ε=0. In agreement with Theorem 2.2, problem (1.1) has 5 nodal solutions (λ,u) with u′(0)>0 for λ<σ1 sufficiently close to σ1. Nevertheless, our computations show that there is some intermediate range of values of λ where the problem has up to seven solutions with u′(0)>0.
By simply having a glance at Figure 9, it is easily realized that the set of nodal solutions of (1.1) with u′(0)>0 consists of three components. Namely, the central one G+2, plus two additional components: one on the left of G+2, say H+2,ℓ, and another one on its right, H+2,r, which are isolated with respect to the trivial solution (λ,u)=(λ,0).
Moreover, observe that G+2 contains a closed loop of unstable solutions. It surrounds the solutions with z=0.5 and bifurcates from such a curve at λb,1=66.4542 and λb,2=207.4892. The two lateral folding type components have their turning points at
Thus, for every λ∈(λt,λb,2) problem (1.1) has, at least, 14 solutions, (λ,u): 7 among them satisfy u′(0)>0, and their opposite, with u′(0)<0. The solutions with z=0.5 are unstable for λ∈(λ2,λb,1), stable for λ∈(λb,1,λb,2) and unstable for λ∈(λ2,b,σ1), in agreement with the exchange stability principle, [29].
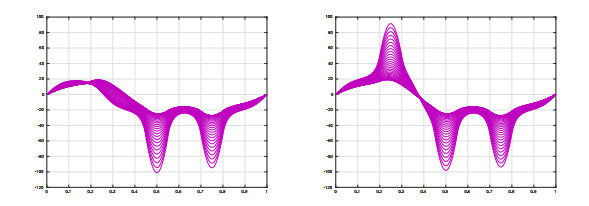
Figure 10 shows the plots of a series of 1-node solutions with z=0.5 along G+2. The solutions on the first picture were computed for λ close to λ2=(2π)2, while the solutions on the second picture where computed for a range of λ's closer to σ1. These solutions blow up to +∞ in [0.2,0.3], and to −∞ in [0.7,0.8], as λ↑σ1, whereas they stabilize on the complement of these two intervals to the appropriate large solutions, either positive, negative, or nodal.
Figure 11 shows the plots of a series of solutions with one interior node along the closed loop of G+2. Although the nodes of these solutions perturb from z=0.5 at the bifurcation values λb,1, λb,2, and separate away from 0.5 a substantial amount, reaching approximatively 0.4 in the first picture and 0.6 in the second one, observe that they do not reach the remaining two intervals of a−10(0).
Figure 12 shows the plots of a series of solutions on each of the two half-branches of the component H+2,ℓ for a series of values of λ up to 400. The solutions on the first picture, where z∼0.25, are unstable, while those on the second picture are stable and satisfy z∼0.375 (see Figure 9). Note that 0.375 is the midpoint of [0.3,0.45], in agreement with Theorems 2.1 and 2.2. Moreover, our numerical simulations show that also when the node z lies in [0.2,0.3], it converges to the midpoint of such interval. This actually goes beyond the scope of Theorems 2.1 and 2.2. The solutions of the first picture must blow-up to −∞ in [0.45,0.55]∪[0.7,0.8] as λ↑σ1, while in the complement of these two intervals they stabilize to the appropriate large solutions. The solutions on the second picture, instead, must blow-up to +∞ in [0.2,0.3] and to −∞ in [0.45,0.55]∪[0.7,0.8], while they stabilize on [0,1]∖a−10(0) to the appropriate large solutions, either positive, negative, or nodal, as λ↑σ1.
Finally, Figure 13 shows the plots of a series of nodal solutions on the component H+2,r for the same range of values of λ used in Figure 12. The profiles are similar to those computed along H+2,ℓ, except for the fact that now the nodes approach the values 0.625 and 0.75, respectively, as λ↑σ1. In particular, these solutions blow up to +∞ in [0.2,0.3]∪[0.45,0.55] as λ↑σ1. Moreover, the stable solutions, those with z∼0.625, also blow up to −∞ in [0,7,0.8] as λ↑σ1.
This precise point-wise behavior of the nodal solutions as λ↑σ1 agrees with the results of Theorems 2.1 and 2.2. Actually, such an information has been crucial to construct the global bifurcation diagram plotted in Figure 9, as it will become apparent in a few moments. To compute the component G+2 (or, equivalently, C+2), we numerically solved the bifurcation problem from u=0 at λ=λ2 and then continued the bifurcated curve, detecting and marking the two bifurcation points along it. We stopped when we reached a value of λ sufficiently close to σ1. Once computed the whole branch in this way, we went back to the secondary bifurcation points to complete the computation of the closed loop.
As far as the global folding type components are concerned, as they do not bifurcate from u=0 but from certain metasolutions at λ=σ1, their existence must be inferred from Theorem 2.2. Indeed, thanks to Theorem 2.2, (1.1) has five solutions for λ<σ1, λ∼σ1, and, thanks to [1,7,16], their sharp point-wise behavior as λ↑σ1 is well known (see Figures 10, 12 and 13). The knowledge of such limiting behavior has been crucial to compute the components H+2,ℓ and H+2,r, as described in Section 7.
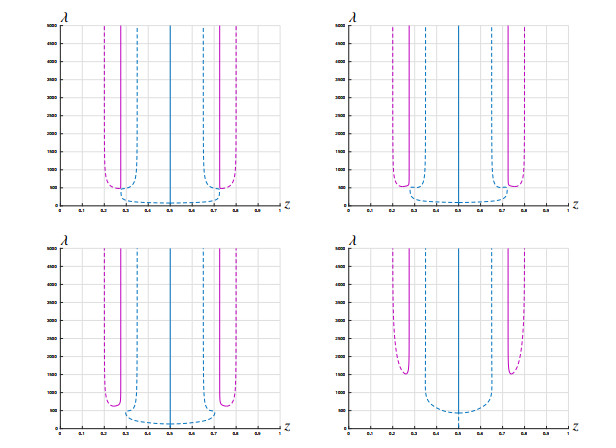
Once we completed this analysis, we considered the non-degenerate problem (1.1) with the choice (5.1) and ε∈(0,1). Figure 14 shows the corresponding global bifurcation diagrams for ε=0.1, ε=0.7, ε=0.8 and ε=0.9999, respectively.
In the global bifurcation diagram for ε=0.1, the loop of solutions on G+2 bifurcates from the solution with z=0.5 at λb,1=69.5268 and λb,2=193.3319, while the turning points of the components H+2,ℓ and H+2,r occur at λt=173.5823. In the global bifurcation diagram for ε=0.7, these values changed to λb,1=110.7253, λb,2=160.4316, and λt=214.8051. According to our numerical experiments, the closed loop bifurcating from the nodal solutions with z=0.5, is persistent for all values of ε until some critical value εc∈(0.77,0.78) where it shrinks to a single point before disappearing for all further values of ε for which we have computed the global bifurcation diagram. Once the closed loop disappears, all the solutions of the central branch are unstable. In the case ε=0.8, λt=230.2345. Finally, λt=1.1068×103 when ε=0.9999. Thus, it is apparent that, although λt increases as the secondary bifurcation parameter ε approaches 1, the increasing rate is not as high as one might expect. Anyway, observe that the structure of the bifurcation diagrams is maintained for all the larger values of ε for which we have computed them, going much beyond the local perturbation result given by Theorem 3.1.
6.
An example with κ=4
In this section we will discuss the model (1.1) for the choice (1.3) with κ=4, ε∈[0,1) and (1.5). According to Theorems 2.2 and 3.1 the associated problems admit, at least, 14 solutions with one interior node, for λ in a left neighborhood of σ1 when ε=0 and for λ∈(σ1,σ2) and ε>0 sufficiently small, respectively. Moreover, for λ≥σ2 and ε>0 sufficiently small, Theorem 3.1 guarantees the existence of, at least, 6 solutions with one interior node.
In Figure 15 we have plotted the global bifurcation diagram that we have computed for ε=0. In agreement with the result of Theorem 2.2, for the present choice of a(x), problem (1.1) possesses, at least, seven solutions (λ,u) with one interior node and u′(0)>0. By the symmetry of the problem, the pairs (λ,−u) provide us with other seven (different) solutions.
As in the case analyzed in Section 5, the solution set consists of three components. namely, the component, G+2 (or, equivalently, C+2), bifurcating from u=0 at λ=λ2, plus two additional supercritical folds, H+2,ℓ and H+2,r. The component G+2 consists of the \lq"symmetric" solutions with z=0.5 plus a secondary curve of solutions bifurcating supercritically from the primary curve at λb=74.8175 and filled in by linearly unstable solutions, in full agreement with the exchange stability principle, [29]. As the turning points of the components H+2,ℓ and H+2,r occur at λt=433.9062>λb, problem (1.1) has --- limited to solutions with one interior node and u′(0)>0 ---, at least, one solution (λ,u) for each λ∈(λ2,λb], three solutions for each λ∈(λb,λt), five at λ=λt and seven for each λ∈(λt,σ1). The nodes of these solutions, as well as their point-wise behaviors as λ↑σ1, obey the general patterns described in Section 2. Therefore, the solution blows up to ±∞ as λ↑σ1 in every component of a−10(0), except the one containing the node z. Precisely, if u′(0)>0 and the component of a−10(0) completely lies on the left of z, the solution blows up to +∞, while it approximates −∞ if the component completely lies on the right of z.
As suggested by Theorem 3.1, the structure of the global bifurcation diagram plotted in Figure 16 is maintained for ε>0, ε∼0, at least for λ∈(σ1,σ2). Nevertheless, our numerical experiments show that the same global structure persists for all further values of ε∈(0,1) for which we have computed it, and the full multiplicity result given by Theorem 3.1(b) also holds for λ≥σ2. Figure 16 shows a series of global bifurcation diagrams computed for ε=0.1, ε=0.5, and , confirming that our multiplicity results, of a local nature, are actually valid, at least, for all .
Table 1 provides us with the values of , and in each of the global bifurcation diagrams plotted in Figure 15.
As in all cases analyzed in the previous sections, the analysis of the fine behavior of the global bifurcation diagram as remains an open problem in this paper.
To conclude, we remark that, in general, the number of components of the solution set of (1.1) can vary with the distribution of the intervals where , as well as with the value of the parameter . In particular, some of our numerical simulations (not presented here) suggest that there are examples where, besides the components , and , the model exhibits some additional \lq"isola"\, also containing nodal solutions. A complete description of these more sophisticated aspects will appear elsewhere.
7.
On the numerical experiments
In most of previous works devoted to numerical continuation of reaction-diffusion problems, a pseudo-spectral method combining a trigonometric spectral method with collocation at equidistant points has been usually used to discretize (1.1), especially to compute the small solutions bifurcating from (see, e.g., Gómez-Reñasco and López-Gómez [31], López-Gómez, Eilbeck, Duncan and Molina-Meyer [32], López-Gómez and Molina-Meyer [33], López-Gómez, Molina-Meyer and Tellini [34], López-Gómez, Molina-Meyer and Rabinowitz [7], and Fencl and López-Gómez [35]).
This method gives high accuracy at a rather reasonable computational cost (see, e.g., Canuto, Hussaini, Quarteroni and Zang [36]). In particular, the pseudo-spectral method is very efficient and versatile for choosing the shooting direction from the trivial solution in order to compute small classical solutions, as it provides us with the true values for the first bifurcation points from the trivial solution, where is the number of internal mesh points (see Eilbeck [37]).
However, in this paper, we have preferred to use a centered finite difference scheme with equidistant points in order to discretize (1.1), because it is more adequate for solutions with large gradients, like ours (cf. the right plot of Figure 9). This method runs much faster when computing global solution branches in the bifurcation diagrams than the pseudo-spectral method but gives only rough approximations of the true bifurcation values from the trivial solution. To compensate for this inconvenient, the finite difference method requires a substantially higher number of internal mesh points in comparison to the pseudo-spectral method. Indeed, the -th eigenvalue () of the tridiagonal Toeplitz matrix corresponding to the discretization of the operator is given by
(see, e.g., [38,Section 2]), and it converges to the exact value as . For our computations, we chose , so that
For general Galerkin approximations, the local convergence of the solution paths at regular, turning and simple bifurcation points was proven by Brezzi, Rappaz and Raviart in [39,40,41], and by López-Gómez, Molina-Meyer and Villareal [42] and López-Gómez, Eilbeck, Duncan and Molina-Meyer in [32] for codimension two singularities in the context of systems. Such results rely on the approximate implicit function theorem (see, e.g., López-Gómez, [43,Theorem 3.2]). In all these situations, the local structure of the solution sets for the continuous and the discrete models are equivalent provided that a sufficiently fine discretization is performed.
The global continuation solvers used to compute the solution curves of this paper, as well as the dimensions of the unstable manifolds of the solutions filling them, have been built from the theory of Allgower and Georg [44], Crouzeix and Rappaz [45], Eilbeck [37], Keller [46], López-Gómez [43] and López-Gómez, Eilbeck, Duncan and Molina-Meyer [32].
In order to compute the component (or, equivalently, ), we started from a value of bigger than, but close to the bifurcation point and used the initial iterate , since, there, it provides us with a first order approximation of the shape of the solutions bifurcating from , and our correction algorithm based on Newton's method easily converged to a solution of problem (1.1). Then, by performing a global continuation with the Keller-Yang algorithm [47], and detecting whether secondary bifurcation points were present, we were able to obtain the global structure of .
As for the other components, namely the global supercritical folds, Theorem 2.1 allows us to know the shape of the solutions, in particular the position of their nodes for , , and we used this information to construct adequate predictions to compute globally these components. For instance, when we computed the component containing the nodal solutions with one interior node close to in Figure 9, we chose as the initial iterate, , for the underlying Newton method used to compute a first nodal solution on the curve, some bounded, not necessarily continuous function which is positive in and negative in or, at least, whose node is close enough to . In addition, this initial iterate must be large enough, otherwise the Newton method converges to the trivial solution . An a posteriori analysis seems to indicate that is adequate provided its discrete norm is greater than the discrete norm of the solution we are trying to calculate. Once located this first point on the component, our path-following code provided us with the entire component using the Keller and Yang algorithm [47] to transform the supercritical turning points of these folds, which are singular points for the original system, into regular points for an augmented system, as explained by López-Gómez in [43,p. 206].
The complexity of the computed bifurcation diagrams, due to the existence of interior and boundary layers for the nodal solutions, required an extremely careful control of all the continuation steps in our codes for values of close to when , as well as for all when . This explains why the existing commercial packages, such as AUTO-07P, are of no utility when dealing with differential equations in the presence of spatial heterogeneities. Actually, Doedel and Oldeman already emphasized on page 185 of the AUTO-07P manual available at https://depts.washington.edu/bdecon/workshop2012/auto-tutorial/documentation that
"given the non-adaptive spatial discretization, the computational procedure here is not appropriate for PDEs with solutions that rapidly vary in space, and care must be taken to recognize spurious solutions and bifurcations."
Indeed, this is one of the main problems that we found in our numerical experiments, because, for the special choice (1.3) with , the nodal solutions grew to , or , in some of the intervals as , and, actually, the fact that (1.1) has a unique nodal solution with for , while it can admit an arbitrarily large number of nodal solutions with for really close to , is an amazing (new) phenomenology that could not have been established numerically without the analytical results established in [1].
We now detail the computational parameters used in this paper to obtain the bifurcation diagrams. As a stopping criterion for the Newton method, we considered an iteration to be satisfactory when the norm of our augmented system, evaluated at such an iteration, was smaller than . In order to determine bifurcation points, a bisection method with the same tolerance has been implemented, in order to find points where the determinant of the Jacobian of the augmented system vanishes.
Since at some point, solutions became very large in some intervals and, hence, computational times started to increase considerably, an adaptive step in the Keller–Yang algorithm has been implemented. An initial step size equal to has been chosen, allowing then the algorithm to vary the step size between and , depending on the precision required. Close to turning points or when a new branch was initiated, high precision or, equivalently, a very small step size was required, while far from these points a lower precision was acceptable.
An empirical method consisting in detecting the rate of change of the slope of the bifurcation curves with respect to has provided acceptable results at a very low computational cost. In particular, we used the quantity to measure such changes and a threshold value of to decide whether to shorten or to increase the step length. We remark that, in order to avoid computational problems, determining when the bifurcation diagrams become very narrow, for instance at the turning points, is extremely important, as pointed out in [34,48].
Acknowledgments
This work has been supported by the Ministry of Science, Technology and Universities of Spain, under Research Grant PGC2018-097104-B-I00, and by the IMI of Complutense University of Madrid.
Conflict of interest
The authors declare there is no conflicts of interest.









 DownLoad:
DownLoad: