Approximate controllability of evolution hemivariational inequalities under nonlocal conditions

1.   Introduction

Waste issue is a global concern and is on the rise due to the growth of urban areas and population, with predictions showing a potential increase of 70% by 2050 if no measures are taken to address it ^[1]. To effectively manage waste, various techniques are utilized including source reduction and waste minimization ^[2], recycling ^[3], waste-to-energy ^[4], landfill management ^[5] and education and awareness ^[6]. With the increasing complexity of waste composition and the absence of a standardized waste classification system make waste identification challenging, resulting in disparities in waste generation and management practices across different regions ^[7,8]. Comprehending household solid waste management practices is essential for the progress of integrated solid waste management ^[9]. Identifying waste plays a pivotal role in the waste management process as it enables facilities to manage, recycle and diminish waste suitably while ensuring compliance with regulations and monitoring their advancement over time.

Various studies and approaches that utilize deep learning models for efficient waste sorting and management which can contribute to a more sustainable environment has been done. Models such as RWNet ^[10], Garbage Classification Net ^[11], Faster Region-Based Convolutional Neural Network ^[12] and ConvoWaste ^[13] were proposed and evaluated for their high accuracy and precision rates in waste classification. These studies also highlight the importance of accurate waste disposal in fighting climate change and reducing greenhouse gas emissions. However, the model used may necessitate particular hardware or may have limitations confined to a paper. Some studies also incorporate IoT ^[14] and waste grid segmentation mechanisms ^[15] to classify and segregate waste items in real time.

By integrating machine learning models with mobile devices, waste management efforts can be made more precise, efficient and effective. One of the research uses an app that utilizes optimized deep learning techniques to instantly classify waste into trash, recycling and compost with an accuracy of 0.881 on the test set ^[16]. While it shows the potentiality the benchmarking with other state of art model is still needed and is limited in classifying waste into three types. In response, we introduce MWaste a mobile app that utilizes computer vision and deep learning techniques to classify waste materials into trash, plastic, paper, metal, glass or cardboard types. The app provides users with suggestions on how to manage waste in a more straightforward and fun way.

The app is tested on various neural network architectures and real-world images, achieving highest precision of 92% on the test set. This app can function with or without an internet connection and rewards users by mapping the carbon footprint of the waste they managed. The app's potential to facilitate efficient waste processing and minimize greenhouse gas emissions that arise from improper waste disposal can help combat climate change. Additionally, the app can furnish valuable data for tracking the waste managed and preserved carbon footprints. The rest of this paper is structured as follows: Methods section explains the MWaste system architecture. The Training section covers the training process and the Evaluation section explains experimental evaluations. Lastly, the Conclusion section summarizes research findings.

2.   Methods

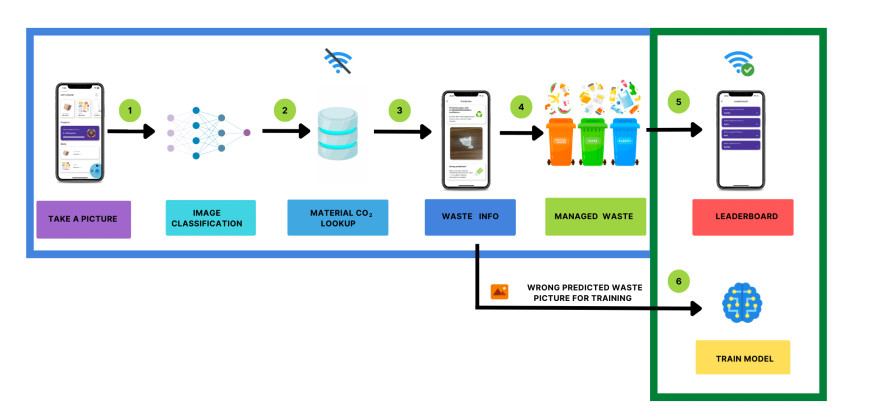
Classifying waste using machine learning is a challenging task since determining the recyclability or compostability of waste based on images is difficult due to the properties of the material being hard to detect from images. Besides, waste can take on various shapes and forms which requires machine learning techniques to handle such variability and the recyclability of waste depends on the local recycling center's capabilities which the app must consider. Taking those considerations into account, the app is designed in such a way that feedbacks are collected from users and can operate smoothly with or without an internet connection. The waste image is obtained from the gallery or camera and is passed through the waste classification model which is trained to categorize the waste. The classification model is the result of training a specific CNN model on a dataset of labeled images. Several state of the art convolutional neural network methods are tested in this research which included Inception V3 ^[17], MobileNet V2 ^[18], Inception Resnet V2 ^[19], Resnet 50 ^[20], Mobile Net ^[21] and Xception ^[22]. The model is then converted into TensorFlow Lite model as they are highly optimized, efficient and versatile making them ideal for running real-time predictions on mobile. The workflow of MWaste app is shown in Figure 1.

Figure 1.  Workflow of MWaste.

DownLoad: Full-Size Img PowerPoint

Once identified, the model calculates the carbon emissions associated with the material and provides waste management recommendations. For misclassification, users can submit the waste image for further analysis. Managing waste earns reward points and the amount of carbon footprint saved is also tracked. An internet connection is required to submit wrongly predicted waste images and sync accumulated points.

3.   Training

This section describes the training procedure and parameter settings used in this research.

3.1.   Dataset

For this research publicly available trashnet dataset ^[23] is utilized, consisting of 2527 images across six classes. Glass, paper, cardboard, plastic, metal and trash. These images were captured using Apple iPhone 7 Plus, Apple iPhone 5S and Apple iPhone SE with the objects placed on a white posterboard in sunlight or room lighting. The distribution of data based on their label counts is shown in Figure 2. The dataset consists of 501 images of glasses, 410 images of metals, 403 images of cardboard, 482 images of plastic and 137 images of trash. The annotations for the dataset were performed by experts.

Figure 2.  Datasets comprising the count of items in each class.

DownLoad: Full-Size Img PowerPoint

To accommodate the variations in orientations of recycled material and expand the dataset size several data augmentation techniques were employed. These included random rotation, brightness adjustment, translation, scaling and shearing. Furthermore, mean subtraction and normalization were applied to the images. Example of sample images from the dataset are shown in Figure 3. For robustness 70% of the images were used for training, 13% for testing and 17% for validation.

Figure 3.  Sample images of each class from the dataset.

DownLoad: Full-Size Img PowerPoint

3.2.   Procedure

The gathered dataset is processed through different models while keeping all parameters constant. Subsequently, the outcomes are attentively analyzed. Categorical cross-entropy is employed to gauge the loss as it is suitable for multiclass problems ^[24]. Meanwhile, accuracy serves as a metric and Adam is the optimizer of choice given that it applies momentum and adaptive gradient for computing adaptive learning rates for each parameter ^[25].

Global average pooling is added to create one feature map per category in the final convolutional layer for the classification task ^[26]. Three dense layers are then employed to learn complex functions and improve the accuracy of classification. To avoid overfitting, dropout is added as a regularization technique ^[27]. Softmax is used as an activation function to convert the output values into probabilities ^[28].

4.   Evaluation

In this section, different evaluation metrics are discussed and the results are compared based on them.

4.1.   Evaluation metrics

The evaluation measures can be used to explain the performance of various models. The study employs the Accuracy Score and F1 Score as evaluation metrics.

4.1.1.   Accuracy score

Classification accuracy is defined as the percentage of accurate predictions out of the total number of samples analyzed. To calculate accuracy in classification, the number of correct predictions is divided by the total number of predictions and the resulting fraction is expressed as a percentage by multiplying it by 100 ^[29]. The formula for the accuracy score is as follows (Eq 1).

4.1.2.   F1 score

When attempting to compare two models with contrasting levels of accuracy and recall such as one with poor precision but strong recall, it can be challenging. Improving accuracy may have an adverse effect on recall and vice versa which can result in confusion ^[30]. Hence, the F1-score is utilized as a means of comparing the two sets and serves as a valuable metric for evaluating both recall and precision simultaneously.

The F1-score is employed when dealing with imbalanced class data situations ^[31]. As most real-world classification problems involve uneven case distributions, the F1-score is a more suitable metric for evaluating the model compared to accuracy (Eq 2).

4.2.   Model evaluation

Models are evaluated with same settings and their outputs are measured using evaluation metrics: accuracy score, and f1-score. After comparing the models as shown in Table 1, it can be seen that InceptionResNetV2 and Xception have higher accuracy but the loss is higher for InceptionResNetV2 and InceptionV3 models. Figure 6 illustrates the classification result of a waste material from the given training set. Accuracy and loss of each model during training along with each iterations is shown in Figure 4.

Table 1.  Evaluation of the accuracy and F1 score of various deep learning techniques applied to specific datasets.

Methods	MobileNet	Inception V3	Inception ResNet V2	ResNet 50	MobileNet V2	Xception
Cardboard	0.94	0.95	0.97	0.91	0.97	0.96
Glass	0.85	0.86	0.90	0.86	0.78	0.91
Metal	0.86	0.88	0.91	0.83	0.86	0.95
Paper	0.91	0.92	0.96	0.86	0.93	0.94
Plastic	0.89	0.88	0.91	0.86	0.83	0.90
Trash	0.52	0.68	0.68	0.41	0.32	0.67
Accuracy	0.87	0.89	0.92	0.84	0.86	0.92

---

 | Show Table

DownLoad: CSV

Figure 4.  Comparison of loss and accuracy of models at different epoches and iterations.

DownLoad: Full-Size Img PowerPoint

Models are trained with same settings i.e. using NVIDIA Tesla T4 GPU in Colab and there execution time is noted. The results are shown in Table 2.

Table 2.  Parameters and the amount of time taken to complete the training (in seconds) of different models.

Methods	MobileNet	Inception V3	Inception ResNet V2	ResNet 50	MobileNet V2	Xception
Parameters	5855942	25478438	5855942	27263366	5855942	24537134
Time (in seconds)	1031.14	1172.39	999.01	1230	999.10	1794.85

---

 | Show Table

DownLoad: CSV

Based on the above table we can observe that MobileNet, MobileNetV2 and InceptionResNetV2 have same parameters. Among these models InceptionV3 and MobileNetV2 demonstrate shorter training times. However, Xception stands out with a longer training time despite its high parameters. Figure 5 displays the confusion matrix for each model using the given dataset. This matrix indicates the performance, strengths and weaknesses of each model and can also assist in identifying problematic class predictions.

Figure 5.  Confusion matrix of different models.

DownLoad: Full-Size Img PowerPoint

Figure 6.  Classification outputs of waste in MWaste app.

DownLoad: Full-Size Img PowerPoint

5.   Conclusions and future work

This study presents a mobile application that utilizes deep learning techniques to classify waste in real-time. The performance and cost effectiveness of several state of the art waste classification models are evaluated and the most optimal model is selected. In our case, we found Inception ResNetV2. Afterwards, the model undergoes a minimization process and is integrated into the application, enabling waste categorization into six distinct groups. Plastic, paper, metal, glass, cardboard and trash. The app incorporates gamification strategies such as a leaderboard based on waste management points to motivate users to dispose of waste properly and is made available to public^*.

^*https://github.com/sumn2u/deep-waste-app

The team plans to improve the accuracy of the classification system, form partnerships with local recycling companies and expand the dataset to raise awareness of environmental impacts and reduce incorrect waste disposal.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

My heartfelt appreciation goes out to Gary Thung and Mindy Yang for sharing the TrashNet dataset on Github for public use. This dataset has proven to be an invaluable asset for my research or project on waste management and classification and I am deeply thankful for their hard work in gathering and disseminating this information to a larger audience.

Conflict of interest

The author declares no conflict of interest in this paper.