1.
Introduction
The concept of "identity" has garnered significant attention since the mid-20th century, with a notable increase in related publications [7]. As Engeström highlighted, identity is not a static entity but a continuous, never fully complete process [18]. It is dynamic and shaped by an individual's experiences and interactions with others [66]. Identity research has grown across multiple disciplines, including sociology, psychology, and education [34,60]. This shift reflects a broader movement in educational research, which now views identity development as a central part of learning rather than solely focusing on knowledge acquisition [53].
Identity research has gained prominence in mathematics education to understand a student's engagement with mathematics [35]. However, the philosophical diversity surrounding the concept of identity makes it challenging to establish a consistent measure of mathematical identity. Mathematical identity is complex and shaped by various contextual, relational, and affective factors [37,45].
Mathematical identity is "one's beliefs, attitudes, feelings, and dispositions about mathematics and the resulting motivation and approach to learning and using mathematics" [46]. This identity is influenced by various factors, including mathematical beliefs, attitudes, motivation, and achievement, all of which shape a student's identity as a mathematics learner. Developing a positive mathematical identity is widely seen as a critical outcome of successful mathematics education programs, where students who hold such identities are more likely to engage in problem-solving and value mathematics as a discipline [50].
Globally, research on mathematical identity has established connections between variables such as attitudes towards mathematics, motivation, beliefs, and achievement [11]. However, mathematical identity encompasses more than these variables, involving deeper affective dimensions related to students' self-concept and long-term mathematics engagement [38,13]. Despite significant global research, much of this work has been conducted in Western contexts [25,29]. Studies examining how beliefs, attitudes, and motivation contribute to mathematical identity in non-Western contexts, particularly in Turkey, remain scarce.
Moreover, existing research often emphasizes demographic factors such as gender and socioeconomic status. At the same time, the role of family education level and the influence of mathematical beliefs and attitudes are less frequently explored. This gap in the literature is significant, as understanding how socio-demographic factors influence mathematical identity is critical to address educational inequalities and to improve student outcomes in diverse contexts in countries such as Turkey. Therefore, there is an urgent need for more comprehensive research in this area, which can inform educational policies and interventions to foster positive mathematical identities, especially in underrepresented and non-Western regions.
1.1. Aim of the study
The present study aims to address this gap by examining the predictors of mathematical identity among Turkish elementary school students. Specifically, it explores how gender, socioeconomic status, family education level, mathematics achievement, mathematical beliefs, attitudes towards mathematics, and motivation contribute to the formation of mathematical identity. By focusing on sociodemographic influences, this study seeks to provide insights that can inform educational practices and policies to foster positive mathematical identities in diverse student populations. The research questions are as follows:
1. What is the level of a student's mathematical identity, mathematical beliefs, attitudes towards mathematics, and motivation for mathematics?
2. How do gender, socioeconomic status, family education level, mathematics achievement, mathematical beliefs, attitudes towards mathematics, and mathematics motivation predict mathematical identity?
2.
Literature review
Theoretical frameworks play a pivotal role in understanding how mathematical identity develops and is shaped by external factors [8]. Wenger's theory of identity as a socially constructed and dynamic process provides a foundation to understand how a student's mathematical identity is influenced by their interactions within the educational system [66]. Wenger argues that identity is formed through participation in communities of practice, where individuals negotiate meaning and construct their identities through shared experiences. This framework is particularly relevant in examining how students from different socioeconomic backgrounds develop their mathematical identities in diverse classroom settings.
Martin et al. expanded on this by defining mathematical identity as the intersection of a student's beliefs, attitudes, and dispositions towards mathematics [46]. According to Martin, students' mathematical identities are influenced not only by their intrinsic motivation and self-concept, but also by external factors such as family education level and societal expectations. This study applies Martin's framework to explore how Turkish students' mathematical identities are shaped by sociodemographic characteristics such as gender, family education level, and socio-economic status.
The gap in the literature lies in the limited research that explores mathematical identity in non-Western contexts, particularly in Turkey. While global studies have established the importance of mathematical beliefs and the motivation in shaping identity [11,13], there remains a lack of understanding of how sociodemographic factors intersect with these variables in culturally diverse settings. This study addresses this gap by applying these theoretical frameworks to investigate how such factors influence Turkish students' mathematical identities, thereby contributing to the broader understanding of identity development in mathematics education.
2.1. Identity
Several challenges arise with the concept of identity [39] being used in different senses in scientific research, and the need for coherent definitions and a theoretical incoherence about identity in the field is notable [13]. One of the challenges is to operationalize identity in a traceable, observable, and measurable way. Sfard and Prusak observed that identity is often treated as a self-evident, experiential idea, thus avoiding the difficult task of defining and operationalizing identity [60]. Furthermore, identity is shaped by a complex interaction of factors [64]. Under the difficulty of conceptualizing identity, we can make mathematical identity more understandable by revealing the interactions between the variables of attitudes towards mathematics, motivation, beliefs, and mathematics achievement, which we consider essential among the factors affecting mathematical identity, and we know that there are relationships between them.
2.2. Mathematical identity
What it means to be mathematical in any setting determines one's identity, which is defined both individually and collectively [4]. Mathematical identity is an individual and social construct consisting of a person's mathematics-related experiences, beliefs, attitudes, perceptions, and other factors that influence mathematical identity [55]. This identity can impact one's mathematical achievement and development [13]. Moreover, identity is a decisive and often overlooked factor in mathematics learning [23]. Despite these reasons, research focusing on identity in mathematics education has been relatively limited until recently [5,9,10,12,21,22,51]. The health, richness, and quality of a student's mathematical identity significantly impacts their future opportunities [24,25,28] and society [25]. Indeed, mathematical identity is conceived as a useful analytical lens for educational research [20]. Similar to personal identity, mathematical identity is multiple, fluid, unstable, (re)constructive, multi-contextual, relational, and affective. It changes over time and is constantly being constructed. Moreover, different contexts, situations, social relations, and audiences can influence mathematical identity [45]. Based on the complex interactions between the factors that affect mathematical identity, we expect to better understand the students' mathematical identities and, thus, the relationships between students and mathematics.
2.3. Belief in mathematics
Mathematical beliefs are a factor that can affect a student's reaction when learning mathematics, when responding to mathematical problems, and when determining how they choose an approach to solve the problem [44]. Beliefs constitute one of the basic structures that support the effective development of mathematics and include a student's value judgment about their mathematics learning [15]. In mathematics, belief can take many different forms. It is linked to skills related to performing mathematics [16] and influences a student's attitude and way of working in mathematics. In addition, mathematical identity definitions include a student's belief about whether they can perform mathematics and whether they belong to mathematics [28]. Researchers have begun to define mathematical identity as a socio-motivational construct that refers to one's dispositions and ingrained beliefs about one's ability to effectively participate and perform in mathematical contexts as a learner and user of mathematics [60]. As such, mathematical identity is fundamental to a student's belief about themself as a potential mathematician [61]. If identity is not fixed [17] and is dynamic [41], then it may change over time. Considering that beliefs about mathematics are a natural component of identity [42], mathematical beliefs can serve as a precursor to mathematical identity development.
2.4. Mathematics attitude
Attitude differs from belief in that it is less cognitive than belief. Philipp stated that beliefs are either psychologically held propositions of understanding or propositions about the world [50]. Conversely, attitudes are related to behavior, feelings, or ways of thinking that indicate a person's disposition or opinion. Lin and Huang defined an attitude towards mathematics as either positive, negative or neutral feelings and dispositions towards mathematics [43]. Numerous studies have been published on students' attitudes towards mathematics, which are of a great interest to educators and are always translated into liking and disliking the subject [6,14]. Students with a positive attitude towards mathematics tend to enjoy the subject, understand its value, and trust it; therefore, they will likely prioritize their mathematics studies [40,49]. Research shows that mathematics identity is developed through engagement in mathematical practices [12,26]. Similarly, the relationship between mathematics identity and attitude is essential [29]. However, identity goes beyond attitudes regarding the disposition towards mathematics. In this context, the attitude towards mathematics is one of the leading factors in developing mathematical identity.
2.5. Mathematics motivation
Motivation is a student's energy and drive to learn, is defined as engagement, is challenging, and requires a productive work behavior [46]. Many factors influence a student's achievement in mathematics, in which motivation is at the center. Research has repeatedly shown that non-cognitive factors such as student motivation, emotions, and learning environment characteristics have a tangible impact on a student's academic performance [54,56].
Schunk et al. argued that motivation plays a crucial role in predicting students' attitudes, strategy use, beliefs, and achievement in academic situations [58]. These concepts are known to be important in the construction of mathematical identity. Moreover, motivation is shown as one of the dimensions of mathematical identity [2]. However, motivation factors should also be considered in identity studies. Thus, mathematics motivation will help to conceptualize mathematical identity development.
3.
Method
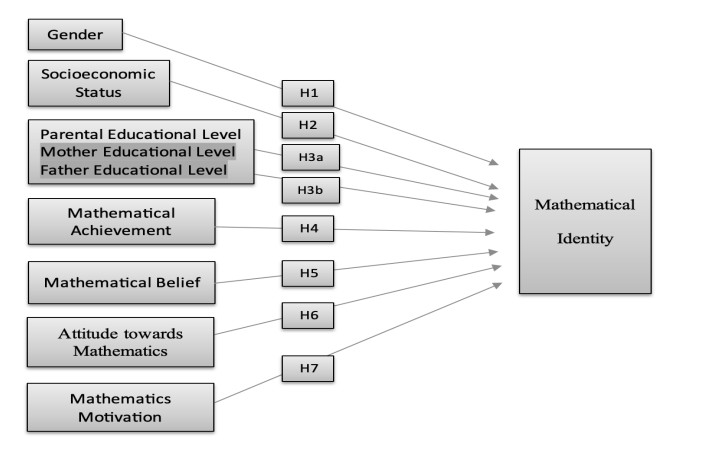
This study examined the predictors of Turkish students' mathematical identities. It adopted the survey research design. The model discussed the change between variables, and the direction and degree of this change were revealed [36]. The study employed a survey research design and involved a sample of 520 elementary school students from public schools in the southern region of Turkey, thus representing a diverse cross-section of the student population regarding gender, socioeconomic status, and family education levels. Stratified random sampling was used to ensure that the sample was representative of the broader population. The sample size of 520 was determined based on Cohen's power analysis guidelines, thereby aiming for a medium effect size with a statistical power of 0.80 and a significance level of 0.05 [3]. This sample size provided a sufficient power to detect significant relationships between the study variables. Stratified random sampling was employed to categorize the participants into specific strata, such as gender, socioeconomic status, and educational background. Then, each stratum was randomly sampled to ensure a proportional representation. This method allowed for a more nuanced analysis of the subgroup differences and contributed to the generalizability of the findings within the sampled region. Data were collected between October 1, 2023, and November 30, 2023, during the 2023-2024 academic year. The instruments, including a self-description form and a demographic questionnaire, were administered during regular class hours. The students were instructed to complete the surveys in their classrooms under the supervision of their teachers, thus ensuring a controlled environment that minimized distractions and external influences. This approach ensured consistent data collection procedures across all the participants. The hypotheses examined in the study and the model tested are presented in Figure 1.
H1. Gender is a positive predictor of mathematical identity.
H2. The socioeconomic level is a positive predictor of mathematical identity.
H3a. A mother's education level is a positive predictor of mathematical identity.
H3b. The father's education level is a positive predictor of mathematical identity.
H4. Mathematics achievement is a positive predictor of mathematical identity.
H5. Mathematical belief is a positive predictor of mathematical identity.
H6. Attitude towards mathematics is a positive predictor of mathematical identity.
H7. Mathematical motivation is a positive predictor of mathematical identity.
3.1. Participants
A total of 520 middle school students, 221 female (42.5%) and 299 male (57.5%), participated in the study. Of the students, 109 (21%) were in the 5th grade, 79 (15.2%) were in the 6th grade, 100 (19.2%) were in the 7th grade, and 232 (44.6%) were in the 8th-grade students. A total of 47 students (9%) described their families as poor, 327 (62.9%) described their families as average, and 146 (28.1%) described their families as well-off. The educational level of the students' mothers is as follows: 60 (11.5%) are illiterate, 135 (26%) are primary school graduates, 63 (12.1%) are secondary school graduates, 127 (24.4%) are high school graduates, and 135 (26%) are university graduates. The education level of the students' fathers is as follows: 16 (3.1%) are illiterate, 102 (19.6%) are primary school graduates, 96 (18.5%) are middle school graduates, 137 (26.3%) are high school graduates, and 169 (32.5%) are university graduates.
3.2. Instruments
Data were collected using a personal information form and four scales. Ethical procedures were fulfilled before data collection. Permission for the study was obtained with the approval of the Necmettin Erbakan University Social and Human Sciences Ethics Committee. Then, the personal information form and scales were combined into a single form and delivered to the teachers online, and the teachers shared the relevant form with the students. Voluntary participation was required for the study, and a consent form was presented to all the participants. All data were collected at the beginning of the 2023-2024 academic year.
3.2.1. Personal information form
The researchers developed this form for this study. The students were asked about their gender, family education level, grade level, socioeconomic status, and math grade.
3.2.2. Mathematical identity scale
The "Measuring Mathematical Identity in Lower Secondary School" scale was developed in the study by Kaspersen and Ytterhaug [37]. The scale has a single-factor structure. The items are evaluated on a 4-point scale (Never/rarely (1), Sometimes (2), Often (3), Always/almost always (4)). In the scale consisting of 20 items, the 9th item was reverse coded. Cronbach's alpha coefficient was found to be.85. An increase in the score obtained from the scale is interpreted as a strong identification with mathematical identity. The scale was adapted to Turkish for this study. In this study, Cronbach's alpha coefficient of the scale was calculated as.86. The factor loadings of the scale ranged between.565 and.709. The AVE (Average Variance Extracted) value is.51, and the CR (Composite Reliability) value is.87. The factor loadings for all items of the scale are provided in the appendix (see Appendix 1).
3.2.3. Mathematical belief scale
In the study, the "Mathematical Belief Scale" developed by Tarmizi and Tarmizi [62] was used to measure the middle school students' mathematical beliefs. Each item was scored on a 6-point Likert-type scale ranging from 1 (strongly disagree) to 6 (strongly agree). The students' responses were summed, and their beliefs about their mathematical competence were calculated. High scores indicate high and positive beliefs. Cronbach's alpha coefficient of the students' beliefs about their mathematical competence was 0.89. The scale was adapted to Turkish for this study. In this study, the Cronbach's alpha coefficient of the scale is.93. The factor loadings of the scale varied between.679 and.820. The AVE value of the scale is.52, and the CR value is.92. The factor loadings for all items of the scale are provided in the appendix (see Appendix 1).
3.2.4. Attitude scale towards mathematics for secondary school students
The "Attitude Towards Mathematics Scale for Secondary School Students" developed by Yáñez-Marquina and Villardón-Gallego [67] was adapted into Turkish by Şen [59]. The original form of the scale consists of 19 items. In line with the analysis, 1 item was removed from the scale, and 18 items were included in the Turkish adaptation. Each item was scored on a 10-point Likert-type scale ranging from 1 (strongly disagree) to 10 (strongly agree). As a result of the study, the factor structure of the adapted scale was found to form a 3-factor model (self-identity, perceived usefulness of mathematics, interest) consistent with the original structure. The confirmatory factor analysis results showed that the scale met the desired fit indices in the literature. According to the reliability study, the Cronbach's alpha coefficient of the scale was calculated as 0.91. The factor loadings for all items of the scale are provided in the appendix (see Appendix 1).
3.2.5. Mathematical motivation scale
The "Mathematics Motivation Scale" was adapted from the "Motivated Strategies for Learning Questionnaire" developed by Pintrich et al. [52]. The scale consists of six factors, and the internal consistency coefficient ranged from.85 to.94. The 27-item scale has a Cronbach's alpha coefficient of.91. Each item was scored on a 5-point Likert-type scale ranging from 1 (strongly disagree) to 5 (strongly agree). In this study, the Cronbach's alpha coefficient of the scale was calculated as.94, and factor loadings ranged from.684 to.800. The AVE value of the scale is.51, and the CR value is.94. The facgtor loadings for all items of the scale are provided in the appendix (see Appendix 1).
3.3. Data analysis
Descriptive statistical analyses and structural equation modeling were used to analyze the data. Descriptive analyses were conducted in SPSS, version 26.0, and the mathematics achievement scores were converted into standard Z scores. The following goodness-of-fit criteria were used in the structural equation model analysis: χ2/df (<5; Chi-square divided by degrees of freedom), RMSEA (<0.08; Root Mean Square Error of Approximation), SRMR (<0.08; Standardized Root Mean Square Residual), NFI (≥ 0.90; Normed Fit Index), GFI (≥ 0.90; Goodness-of-Fit Index), CFI (≥ 0.90; Comparative Fit Index), and TLI (≥ 0.90; Tucker-Lewis Index) [3,33,54].
4.
Results
Descriptive analyses were conducted to answer the study's first research question. The findings are presented in Table 1.
Instruments such as the Mathematics Belief Scale consisted of multiple items (17 items), and the total score was obtained by summing the responses across all the items. This resulted in a score range of 17 to 102, with higher scores reflecting stronger mathematical beliefs. The 'M/k' column in Table 1 represents the mean score for each scale, where M refers to the total score and k refers to the number of items. For instance, the Mathematics Belief Scale's average score was calculated by dividing the total score by the number of items (17). This ensures a comparability between the scales with a different number of items.
According to Table 1, the scores obtained from the scales of mathematics identity (M = 2.55, SD = .44), mathematics belief (M = 4.00, SD = .84), attitude towards mathematics (M = 5.98, SD = 1.20) and mathematics motivation (M = 3.74, SD = .93) are at an average level. Mathematics achievement scores ranged between 5.00 and 100.00 (M = 79.98, SD = .80).
Table 2 presents the variance-covariance values of the variables tested in the study. Accordingly, the highest variance value belongs to attitude towards math (var = 6.95), and the lowest variance value belongs to the socioeconomic level (var = .33). In addition, the highest covariance value is between math achievement and math motivation (cov = 7.72), followed by maternal education level and mathematics motivation (cov = 7.50).
Table 2 shows the correlations between the Turkish students' mathematics achievement, beliefs, attitudes, motivation, and demographic factors. The data indicate a significant and high correlation between the parents' educational levels (mother and father) (r = 0.73, p < 0.01), thus suggesting that the parents' education levels are generally aligned. Significant positive relationships were found between mathematics achievement (Z score) and belief (r = 0.36, p < 0.01), as well as motivation (r = 0.36, p < 0.01), thus indicating that the students' achievements are related to their beliefs and motivation. Among identity-related factors, the highest correlation was found between identity and belief (r = 0.59, p < 0.01), thus suggesting that students with stronger beliefs tend to develop a stronger mathematical identity. These findings provide a deeper understanding of the key determinants of mathematical identity, thus enhancing the discussion.
4.1. Additional regression and interaction effects
We conducted multiple regression analyses and tested for interaction effects to further examine the relationships between variables. Specifically, we explored how gender interacts with mathematical beliefs and how the socioeconomic status interacts with motivation to predict the mathematical identity. The interaction between gender and mathematical beliefs was not statistically significant (β = 0.08, p > .05), thus indicating that gender did not significantly moderate the relationship between beliefs and mathematical identity. However, the interaction between socioeconomic status and motivation was marginally significant (β = 0.14, p < .10), thus suggesting a weak moderating effect.
In terms of the main effects, mathematical beliefs emerged as the strongest predictor of mathematical identity (β = 0.30, p < .001), followed by mathematical motivation (β = 0.46, p < .001) and attitude towards mathematics (β = 0.16, p < .05). These results align with previous studies that indicated the pivotal role of beliefs and motivation in shaping a student's mathematical identity [11,13].
A variance-covariance matrix is included in Table 3 to capture the variability and relationships between the variables. This approach was used instead of a correlation matrix to align with the requirements of structural equation modeling (SEM), as the variance-covariance matrix provides a more detailed representation of the underlying data structure and helps to ensure the stability of the SEM estimates. A correlation matrix was not provided due to concerns about multicollinearity and the need for the covariance matrix in the SEM analysis.
4.2. Model fit indices and additional analysis
The structural equation model proposed in this study was tested using model fit indices. The goodness-of-fit values obtained were as follows: χ2 (df = 4) = 4.48, RMSEA = 0.03, SRMR = 0.01, NFI = 0.94, CFI = 0.95, and TLI = 0.94. The SEM analysis was conducted using SPSS-Amos, version 26, which allowed for the estimation of the model parameters and fit indices. This software was chosen for its ability to handle complex models and to provide robust estimations of model fit. Specifically, RMSEA values below 0.05 indicate a close fit, and CFI/TLI values above 0.90 are generally acceptable [3]. According to established thresholds, the model fit indices (χ2/df = 4.48, RMSEA = 0.03, SRMR = 0.01, NFI = 0.94, GFI = 0.91, CFI = 0.95, TLI = 0.94) indicate an acceptable to good model fit [33]. Specifically, RMSEA values below 0.05 indicate close fit, and CFI/TLI values above 0.90 are generally acceptable [3]. These values suggest that the proposed model provides a reasonable fit to the observed data, thereby capturing the relationships between the variables without overfitting. The acceptance and rejection of the hypotheses tested in this context are presented in Table 4.
According to the results of the analysis, H1 (β = .01, p > .05, t = .38), H2 (β = .04, p > .05, t = .91), H3a (β = -.09, p > .05, t = -1.45), and H4 (β = .08, p > .05, t = .66) were rejected. However, hypotheses H3b (β = .93, p < .05, t = 2.25), H5 (β = .30, p < .001, t = 12.90), H6 (β = .16, p < .05, t = .38), and H7 (β = .46, p < .001, t = 7.40) were accepted.
In conclusion, mathematical beliefs had the strongest positive predictive relationship with mathematical identity, followed by mathematical motivation and attitude towards mathematics.
Mathematical beliefs emerged as the strongest predictor of mathematical identity (β = 0.30, p < .001), consistent with findings from Cribbs et al. [11]. Mathematical motivation was the second strongest predictor (β = 0.46, p < .001), thus highlighting its significant role in identity development. Attitudes towards mathematics also had a significant, though smaller, effect (β = 0.16, p < .05). Additional analyses showed a weak interaction effect between socioeconomic status and motivation (β = 0.14, p < .10). The model fit indices (RMSEA = 0.03, CFI = 0.95) indicate a good fit with the data.
5.
Discussion
This study examined the predictors of the mathematical identity of middle school students in a Turkish sample. It tested whether the student's gender, socioeconomic level, and mother and father education level were significant predictors of mathematical identity. Hypotheses H1, H2, and H3a were rejected, and hypothesis H3b was accepted.
Some of the results contradicted previous literature. Previous research showed a link between gender and mathematics identities. The findings revealed a statistically significant but very low correlation between these two variables [9,61]. However, previous research has found a significant relationship between socioeconomic status and math identities [21,51]. In the context of gender and socioeconomic status, while the results suggest no significant impact of these variables on mathematical identity, previous research has indicated potential cultural differences in how these factors interact with educational outcomes [22]. Specifically, Turkey's educational policies and practices, such as coeducational schooling and national STEM initiatives, may influence how gender and socioeconomic factors can affect a student's mathematical identity. Future studies could explore these dynamics in more depth to understand the cultural nuances that may lead to divergent results in different educational contexts.
In addition to the conclusion that students with parents with higher levels of education generally develop a stronger mathematics identity [10,22,51], some studies found no significant relationship between mathematics identity and the parental education level [9,21]. Therefore, why might gender, socioeconomic status, and parental education differ in predicting mathematical identity in the Turkish sample?
First, Turkey has serious initiatives to include all students in mathematics education. The Ministry of National Education, in cooperation with TÜBİTAK and universities, launched the "Mathematics Mobilization" to facilitate the learning of mathematics by adapting it to daily life skills and to ensure that students love this subject from an early age [63]. According to the Ministry of National Education (MoNE) [48] statistics, the enrollment rate by gender in public and private secondary schools in the 2022–2023 academic year was 98.38% for boys and 98.36% for girls. Considering that coeducation is practiced in Turkey and that the gap in schooling rates between girls and boys has significantly closed in recent years, no difference is expected in terms of the development of mathematical identity in the classes where girls and boys have started the "Mathematics Mobilization." However, the enrollment rate by gender indicates that families support boys and girls with the exact expectations. Gender expectations, inequalities in opportunity, and family dynamics may affect a student's mathematical identity [22]. All of these factors may have led to the formation of mathematical identity scores in all groups without any difference.
Recent studies in Turkey reported that students were concerned about their future and were willing to choose professions with high income levels [68]. Employment opportunities are primarily in math-related fields such as STEM [19]. Therefore, mathematical identity development is a tool for students in families with a low socioeconomic status who are concerned about their future. In this context, it can be more supported because mathematics is one of the most essential introductory courses in primary education. By encouraging students to think abstractly and logically, it facilitates their academic performance in other subjects [65]. Thus, there is an increased potential to have high-paying professions. However, a study showed that several indicators of socioeconomic status, such as parental social capital, parental involvement, and region of residence (urban, suburban, town, or rural), did not significantly affect math identity [21]. Socioeconomic status may be related to a student's math identity, but this relationship is complex and further study is needed [22].
Within the scope of the study, the analysis of whether the maternal and paternal education level is a significant predictor of mathematical identity showed that the maternal education level of the students was not a significant predictor of their mathematical identity. In contrast, the result was the opposite in the variable of paternal education level. Previous studies [9,10,21,22,51] needed to differentiate between maternal and paternal education levels. The results obtained in these studies could be more consistent. Mathematics is seen as abstract and difficult to understand. To support the student's mathematical identity development, it is necessary to maximize their mathematical beliefs, attitudes, and motivation [5]. The level of maternal and paternal education plays a vital role in a child's mathematical identity development. For example, parents with higher levels of education often contribute more to their children's education. They can influence the children's self-belief and academic motivation, which may affect the children's mathematical identity development [32]. The data collected in the Turkish sample showed that the level of the father's education was higher than the level of the mother's education. In this context, the maternal education level was not a significant predictor of mathematical identity. However, it was a significant and relatively important predictor, which can be seen as an expected situation.
In the study, it was observed that mathematics achievement was not related to mathematical identity. This result does not align differently with previous studies [1,27]. However, the sample of this study was conducted at the middle school level, which is disadvantaged in terms of mathematics experience compared to high school and higher grade levels. Research showed that mathematics identity is developed by participating in mathematical practices [9,26]. On the other hand, it is known that as the mathematics identity is strengthened, a student's mathematics achievement in future grades also increases [5]. In this context, the reason for the rejection of hypothesis H4 can be explained. Similar to the findings by Saha et al. [57], this study identified motivation, teaching methods, and external factors as significant predictors of a student's mathematical performance. Both students and teachers emphasize the importance of clear concepts and consistent practice as pivotal elements in overcoming mathematical challenges.
In addition, mathematical beliefs, attitudes towards mathematics, and mathematics motivation variables were found to be related to mathematical identity. These findings have important theoretical implications for the tested model. These factors may be necessary to understand the effects on mathematical identity because they can influence a student's mathematical beliefs, attitudes, and motivation [5]. When students see themselves as suitable to learn mathematics and enjoy what they do in mathematics classes, it allows them to overcome negativity and develop good relationships with mathematics [47]. Therefore, it is essential to consider these factors to strengthen a student's mathematical identity and increase their mathematics achievement. The analysis of whether mathematical beliefs, attitudes, and motivation are significant predictors of mathematical identity shows that a student's mathematical beliefs, attitudes, and motivation are significant and relatively essential predictors of their mathematical identity. Students with positive mathematical beliefs, motivation, and attitudes tend to develop a stronger mathematical identity. This finding may contribute to extend the results of previous studies [5,9,21,51]. It is essential to understand the factors that affect a student's mathematical identity development and to develop strategies to ensure the student's mathematical identity development.
6.
Limitations and recommendations
Although the study utilized stratified random sampling to ensure representativeness, it was limited to a specific geographic region, which may affect the generalizability of the results to other student populations. Future research could benefit from employing similar methods in more diverse regions to enhance the external validity.
Nevertheless, the fact that mathematical identity has been addressed for the first time in a Turkish sample provides insight into the literature in the cultural context. In addition, participation in the study was completely voluntary. Therefore, the students who participated in the study were already open to developing their mathematical identities. Thus, the selected sample may not provide a fully representative result.
In the last two decades, there has been a significant increase in studies focusing on identity in mathematics education. Methodologically, most studies on student identity have relied on qualitative instruments. Very few [4,37] have utilized quantitative measures. Although most studies have relied on interviews, some have shifted attention to how student identities are enacted and co-constructed in the learning activity [30,31]. Therefore, it may be essential to conduct quantitative research in future studies.
Finally, the model to determine the predictors of mathematical identity in this study was limited by the variables included. Not all constructs outlined in the scales were included in the analysis. However, there may be other predictors to conceptualize mathematical identity. The predictors to be identified may vary according to the culture of the sample. Contrary to the literature, this study conducted in the Turkish sample showed that gender, socioeconomic status, maternal education level, and mathematics achievement did not significantly affect mathematical identity. Therefore, causality studies with the same mathematical variables and modeling studies with different variables can be conducted in future studies.
Additionally, the reliance on self-reported data poses potential limitations, as the student's perceptions may not fully reflect their true mathematical identities. Furthermore, the study's quantitative approach may not capture the deeper, qualitative aspects of identity development, which could be better explored through either longitudinal or mixed-methods research designs. These limitations suggest that future studies should incorporate both quantitative and qualitative approaches to offer a more comprehensive understanding of mathematical identity.
7.
Conclusions
The study examined the predictors of students' mathematical identity in a Turkish sample. The findings showed that gender, socioeconomic status, and maternal education level, which have been repeated in the literature for some time, did not predict mathematical identity. However, mathematical belief, attitude towards mathematics, and motivation positively predicted mathematical identity, whereas achievements in mathematics did not predict mathematical identity. The study's findings generally emphasize the importance of mathematical beliefs, attitudes towards mathematics, and motivation for mathematics. These findings can form an essential part of the theoretical framework of mathematical identity. In this context, with the concept of identity having different meanings in scientific research, the need for consistent definitions of identity in mathematics education can be eliminated alongside theoretical inconsistencies. This study provides critical insights into the factors that influence mathematical identity among Turkish students. However, the practical implications of these findings suggest that educators should focus on strengthening a student's mathematical beliefs, attitudes, and motivation through targeted interventions. Educational programs that integrate real-world applications of mathematics, coupled with socioemotional support, could enhance a student's positive mathematical identity and overall academic success. Teachers can help students build resilience and a long-lasting engagement with the subject by fostering a growth mindset towards mathematics.
Conflict of interest
The author declares no conflict of interest in any part of this article.
Ethics declaration
This study was approved by the ethics committee of the Necmettin Erbakan University (2023-375).









 DownLoad:
DownLoad:


