Stochastic model of economic cycles and its econometric application

1.   Introduction

The integration of wireless sensor networks (WSNs) within the framework of the Internet of Things (IoT) has marked a significant milestone in the current technological society. These networks, composed of autonomous nodes collecting data from the environment, play a crucial role in building intelligent and connected systems. The importance of WSNs in the IoT lies in their ability to provide real-time information, enabling more agile and efficient decision-making in various applications, from environmental monitoring to supply chain management.

However, this technological advancement is not without challenges, and the security of WSNs emerges as an unavoidable priority. In particular, the propagation of malware in these networks poses a serious threat that can compromise the integrity and confidentiality of collected data. The importance of ensuring the security of WSNs, especially concerning malware propagation, becomes an essential element to preserve the reliability of IoT systems as a whole. This aspect takes on special relevance in critical environments such as health and infrastructure, where the reliability of information is crucial.

In this context, the development of mathematical models to simulate the propagation of malware on WSNs emerges as an essential tool. These models not only allow a better understanding of propagation patterns but also facilitate the evaluation of security strategies and the implementation of preventive measures. In this regard, several mathematical and computational models have been proposed, and some of them will be reviewed in Section 3. The importance of addressing malware propagation through mathematical approaches lies in the ability to anticipate potential threats and mitigate associated risks, thereby strengthening the resilience of WSNs. In this work, we will explore these crucial aspects and propose innovative approaches to address emerging challenges in the landscape of WSNs within the context of the IoT.

The main goal of this work is to propose a new model to study the propagation of malware on WSNs with the aim to address some of the deficiencies found in the global models proposed to date. Specifically, the main contributions of this paper are the following:

● Get a more realistic description of malware propagation on WSNs by considering: 1) New compartments of devices: susceptible, patched susceptible, latent non-infectious, latent infectious, compromised non-infectious, compromised infectious, damaged, ad deactivated; and 2) a novel way to determine the incidence term based on a new definition of the time unit that takes into account the average routings performed by different nodes.

● The basic reproductive number is explicitly computed and some control strategies are presented from its analytical study.

The rest of the paper is organized as follows: In Section 2, the fundamentals of WSNs are introduced. The state of the art related to the design of mathematical models for malware propagation is presented in Section 3. Section 4 is devoted to the mathematical description of WSNs. The specifications of the novel model proposed in this work are shown in Section 5. The explicit and detailed description of the new model is presented in Section 6, and, finally, the conclusions and future work are shown in Section 7.

2.   WSNs: definition and main characteristics

2.1.   The fundamentals of WSNs

A WSN is a network composed of several sensor devices or nodes (also called "smart sensors") deployed massively in a specific region with monitoring, wireless communication, and computing capabilities. The main goal of a WSN is to collect and transmit environmental data.

Functionally, nodes are low-power devices equipped with one or more sensors (mechanical, thermal, biological, chemical, optical, magnetic, etc.), a processor, a memory, a power source, and other components necessary for their proper functioning. Since these nodes have limited memory and they are usually deployed in hard-to-reach locations (which also complicates their maintenance), they must have radio connectivity to transmit collected data to a base station. In this sense, it is important to note that one of the most significant limitations of WSNs is energy management in the sensor devices. Therefore, one of their main objectives is energy conservation by optimizing communication and monitoring processes.

Due to their small size, low cost, and ease of deployment, WSNs have several applications in various fields: tracking and surveillance of military targets, environmental monitoring to predict natural disasters, patient monitoring (e-Health), infrastructures monitoring (Industry 4.0), agricultural crop monitoring (Smart Agriculture), etc. ^[1,2,3].

The process of transmitting data between the node that "collected" it and the base is governed by algorithms that continuously select the most efficient route, considering node limitations such as memory, battery, etc. WSNs can be classified as "single-hop networks" (in contrast to "multi-hop networks"), meaning that information is transmitted from node to node until it reaches its final destination.

The devices deployed in a WSN can be of different types depending on their functions and capabilities. The most numerous class is composed of "motes" or sensor nodes whose mission is to monitor the environment and transmit that information (in addition to routing data packets from other sensor nodes). Additionally, there are gateway nodes or collector nodes whose goal is to receive all information sent by sensor nodes and allow interconnection between the WSN and a TCP/IP (Transmission Control Protocol/Internet Protocol) network. For this purpose, assistance from a base station (data collector based on a common computer or embedded system) is required.

2.2.   Security of WSNs

The security of WSNs is essential as many of their uses and applications are related to very sensitive phenomena or situations (monitoring combat zones, disaster management, monitoring critical infrastructure, etc.). Protecting WSNs is challenging since each node is a potential target for a logical or physical attack. Among logical attacks, some are aimed at monitoring communications by intercepting and modifying data, impersonating the identity of legitimate nodes to inject false information into the network, etc. Privacy concerns are significant in WSNs given the large volume of data generated and transmitted, which could be easily accessed remotely. Physical attacks aim to directly access nodes to reprogram their operation, manually introduce malicious nodes, intentionally damage deployed nodes, etc. ^[4,5].

The main security requirements when deploying and operating a WSN would be the following:

● Confidentiality: Data monitored by a given sensor should not leak to an unauthorized neighbor node. The key distribution process is fundamental to ensuring the security of the transmission channel.

● Authentication: The user must be sure that the data used in any decision-making process comes from a reliable source.

● Integrity: It should not be possible to modify the data collected and transmitted by the sensor devices by, for example, injecting manipulated data from a "malicious" node.

● Timeliness: It is necessary to ensure that the information is up-to-date at all times, especially when implementing key exchange protocols.

● Availability: It is a basic point to ensure availability, within the energy consumption margins, of the largest number of nodes for the longest possible monitoring period.

● Temporal synchronization: To save energy, each sensor must be able to deactivate its transmission/reception capability during certain periods of time.

Cyberattacks on WSNs can be of different types: denial service attacks, sybil attacks, traffic analysis attacks, etc., and in the great majority, malicious code plays an important role. The methodology that can be carried out to try to prevent and counteract these attacks is mainly based on the development of three fundamental types of actions: 1) implementation of defensive measures ^[6,7,8], 2) use of cryptographic protocols ^[9,10,11], and 3) implementation of key management infrastructures ^[12,13,14].

3.   State of the Art: A comprehensive review of malware propagation models in WSNs

Malware stands out as a basic tool in the development of cyberattacks on various systems and/or computer networks. Traditionally, its malicious activity has been focused on devices with sufficient computational resources (processing, communication, etc.), such as computers, smartphones, etc., connected to different types of networks. More recently, its use has extended to devices with much more limited processing capabilities, such as wearable devices or, more specifically, sensor devices deploying the WSNs ^[15].

In the realm of WSNs malware activity primarily revolves around the "reprogramming" of the infected node (for example, considering host specifications regarding memory, processing and communication capabilities, or energy consumption). This alteration affects its functionalities related to monitoring and/or transmission (modification of collected environmental data, disruption of connections with adjacent nodes, compromise of data packet integrity, etc.) or may even cause permanent damage. Moreover, the propagation process depends not only on the characteristics of the sensor devices but also on the routing protocols implemented in the WSN ^[16]. As a consequence the study of the dissemination of different specimens of malware in WSNs is an area of interest that the scientific community has begun to explore in recent years by proposing and analyzing mathematical propagation models.

In the vast majority of works that appeared in scientific literature and proposed mathematical models to simulate malware propagation in WSNs, ordinary differential equations are commonly used to describe the dynamics. These are continuous and global models, and usually follow the same framework as models developed to study the spread of biological agents (classical Mathematical Epidemiology), with minor specific modifications as including new compartments, consideration of some characteristics specific to WSNs, etc. These studies are inherently theoretical with the challenge lying in theoretical demonstrations of the stability of the system, and their practical application and efficiency are not thoroughly analyzed. To a lesser extent, individual-based models have emerged, attempting to address some deficiencies in global models, which are accentuated in the context of malware propagation.

In the following we will review models proposed in recent years. The great majority of these models are of a global nature (both deterministic and stochastic), with very few proposals based in the individual-based modeling paradigm.

As global models, noteworthy examples include a review in ^[17] that examines SI (Susceptible-Infectious) compartmental models based on the Kermack-McKendrick paradigm adapted for studying malware propagation in WSNs. This study determines that models proposed to date inadequately consider energy and memory management, the use of authentication schemes, and sensor mobility, among other factors. In ^[18], a global SEIRS (Susceptible-Exposed-Infectious-Recovered-Susceptible) model is proposed and analyzed, considering nodes that collect correlated information in a certain common monitoring area. Spatial correlation is considered to analyze the dynamics of the computer virus in event-controlled WSNs. A Susceptible-Unexposed-Infected-Isolated-Removed epidemic model is presented in ^[19] where the qualitative study is shown. In ^[20], a global SIR (Susceptible-Infectious-Recovered) mathematical model is presented for cluster-based WSNs (differentiating nodes that are grouped in clusters from those that are not). Additionally, an attack/defense game is established between malware and implemented defensive elements, obtaining infection and recovery rates associated with the mixed Nash equilibrium strategy. Other works using game theory (and cellular automata in the description of the dynamics) to study malware propagation in a WSN through SIS (Susceptible-Infectious-Susceptible) and SIRD (Susceptible-Infectious-Recovered-Damaged) compartmental models can be found in ^[21] and ^[22], respectively. In ^[23], a global SIRS-L (Susceptible-Infectious-Recovered-Susceptible-Low energy devices) model is proposed and qualitatively analyzed where sensor nodes can recharge energy, and a new compartment, $L$, is considered for devices with low energy levels. A very similar work by the same authors that analyze a SISL model can be found in ^[24]. This compartment, representing nodes with low energy load, is also considered in ^[25], where a SILRD type (Susceptible-Infectious-Node with low energy level-Recovered-Dead) model is proposed and analyzed, such that the energy depletion due to malware action is considered. In ^[26], a SIR model with a nonlinear incidence term and a sigmoid recovery rate is proposed and studied from a qualitative perspective, determining the most efficient control strategies. A similar study on a SEIR model is presented in ^[27], where the Pontryagin maximum principle is used to determine the optimal control strategy. In ^[28], a qualitative analysis is conducted on an SIRS model considering two types of recovered nodes: those with total immunity and those who have recovered from infection but can be reinfected. In ^[29], a purely theoretical study proposes a SEIRS-V model (spreading a computer worm in a WSN) that includes the immunized compartment ($V$) and explicitly calculates its solution using the homotopy perturbation method. In ^[30], an SEIQRV (Susceptible-Exposed-Infectious-Quarantined-Recovered-Vaccinated) compartmental model is proposed, considering the compartment of quarantined nodes ($Q$). A qualitative study of solutions is given, examining the effect of node density and transmission radius on malware spread. In ^[31], a susceptible-unexposed-infected-isolation-removed model is proposed and its dynamics are described by means of a system of ordinary differential equations whose qualitative analysis is also presented. In ^[32], a probabilistic model is proposed on complex networks where the dynamics are defined by a system of stochastic ordinary differential equations; in addition to susceptible nodes, two types of infected nodes (with high battery level and low battery level) and "secured" nodes are also considered. In this work a theoretical study of the stability in probability is performed. In ^[33], a qualitative study is carried out, proposing a SCIRS (Susceptible-Carrier-Infectious-Recovered-Susceptible) compartmental model that introduces the compartment of "carrier" nodes, similar to ^[34]. In ^[35], the authors propose a hybrid model based on cellular automata and differential equations to simulate the spatiotemporal spread of malware on a WSN. The continuous model is qualitatively studied by analyzing the stability of the equilibrium points obtained. In ^[36], a theoretical study is conducted on an SIQPD (Susceptible-Infectious-Quarantined-Patched-Damaged) model considering that sensor nodes can move. This model is an improvement of those proposed by several of the same authors in ^[37,38]. In ^[39], an SIS model is constructed, considering specific characteristics of the network such as limited energy use and node density in the definition of epidemiological coefficients. In ^[40], a stochastic SIRD model is designed (the dynamics are described by means of Markov chains) where both the spatial distribution of nodes and their differences in vulnerability to malware are considered. Another stochastic SIS model has been recently proposed in ^[41], where a simple derivation of the exact Markov chain for random propagation of the malicious code is presented.

The mathematical description of the spread of malware using fractional epidemiological models has been also proposed: In ^[42], a SEIVR (Susceptible-Exposed-Infectious-Vaccinated-Recovered) model on scale-free networks was introduced and analyzed, and in ^[43] the qualitative analysis of a SEIR model was presented and the optimal control strategy was also discussed. In ^[44], another fractional-order compartmental epidemic model was presented and analyzed: The population of devices is divided into susceptible, exposed, infected, recovered and vaccinated, and bot theoretical and numerical aspects are studied. Moreover, the optimal control problem for a fractional malware propagation model is studied in ^[45] in the case of underwater WSNs, and these control strategies are improved using machine learning techniques such as deep neural networks and random forest. Furthermore, propagation models based on differential equations have also been proposed to study the behavior of malware and develop the corresponding antivirus software ^[46]. Some characteristics of the life cycle of nodes are taken into account in ^[47] such that several compartments are considered: susceptible, susceptible and sleeping, infectious, infectious and sleeping, recovered, recovered and sleeping, and dead. The authors use a system of differential equations to represent the transition between these states in such a way that states a decision-making problem between the system and the specimen of malicious code as an optimal control problem. In ^[48], a model for malware propagation in underground and above-ground WSNs was introduced and analyzed. In this compartmental model, the devices are divided into susceptible, exposed, infectious, recovered, and low energy and each of this compartments is subdivided into underground and above-ground devices. Moreover, three basic features are captured in this model: the cross-infection, the infection time and low energy, and three hybrid control schemes are considered: the recovery scheme, quarantine, and pulse charging. A detailed study of the conditions for optimal control is done from a classic point of view and deep learning techniques are used.

Following this review of the scientific literature, it can be observed that the majority of works focus on the theoretical analysis of the proposed mathematical model, often overlooking the characteristics of malware propagation on WSNs that are only tangentially considered within the mathematical description. While some models take into account some of these factors (see, for example, ^[48]), it is not the norm. Consequently, it seems opportune to design new families of models with the aim to provide the most possible detailed description of this phenomenon: considering new compartments of devices, incorporating characteristics of the data routing process in WSNs into the incidence term, etc.

On the other hand, in the field of individual models, in ^[49], the authors propose an individual-based, discrete, and stochastic SEIRS-F (Susceptible-Exposed-Infectious-Recovered-Susceptible-Failed) model aiming to analyze malware propagation on a WSN and to study the reliability of its components in this situation. In ^[50], an SITPS (Susceptible-Infected-Traced-Patched-Susceptible) compartmental model is studied, considering, in addition to the classic compartments of susceptible and infected nodes, the compartments of "tracked" ($T$) and "repaired" ($P$). This is a stochastic individual-based model (based on Markov chains), where the authors analyze the optimal epidemic control strategies. In ^[51], the authors propose a stochastic SI individual-based model to compute the probability associated to an industrial IoT device to be compromised by an Advanced Persistent Threat (APT). In ^[52,53], two works based on similar theoretical techniques are presented to analyze a propagation model of false data malware (false data injection attack).

4.   Mathematical description of WSNs

4.1.   Node specifications

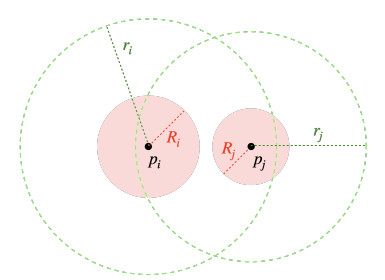
In this work, we will consider $N$ deployed nodes: $n_1, n_2, \ldots, n_N$, such that $p_i = \left(x_i, y_i\right)\in\mathbb{R}^2$ stands for the cartesian coordinates of the position of the $i$-th node $n_i$, with $1 \leq i \leq N$. Additionally, we will assume that $R_i$ denotes the monitoring radius such that $B\left(p_i, R_i\right) = \lbrace \left(x, y\right)\in \mathbb{R}^2\colon \left(x-x_i\right)^2+\left(y-y_i\right)^2 \leq R_i \rbrace$ is the monitoring area of the $i$-th sensor node, and $r_i$ is the transmission radius with $B\left(p_i, r_i\right) = \lbrace \left(x, y\right)\in \mathbb{R}^2\colon \left(x-x_i\right)^2+\left(y-y_i\right)^2 \leq r_i \rbrace$ being the transmission area (see Figure 1), so that any node $n_j$ such that $p_j \in B\left(p_i, r_i\right)$ will be able to receive data transmitted by node $n_i$.

4.2.   Node deployment

Node deployment in the monitoring region $\mathcal{R} \subset \mathbb{R}^2$ can be done either in a predetermined manner (placing nodes in predefined locations) or in a non-predetermined manner (placing these devices in locations distributed more or less randomly). When constructing the model, the monitoring region $\mathcal{R}$ can be considered as a continuum (see Figure 2(a)) or it can be "discretized" into equal cells (square shape) and distributed homogeneously (see Figure 2(b)).

Once the nodes are deployed, the directed network defining the topology of contacts, $\mathcal{G} = \left(\mathcal{V}_\mathcal{G}, \mathcal{E}_\mathcal{G}\right)$, is created and it is denoted as local connectivity (nodal) network. Here, the vertices of the network represent the sensor nodes: $\mathcal{V}_\mathcal{G} = \lbrace n_1, n_2, \ldots, n_N\rbrace$, and there exists an edge between node $n_i$ and $n_j$, $e_{ij} = \left(n_i, n_j\right)\in \mathcal{E}_\mathcal{G}$, whenever node $n_j$ is located within the transmission area of node $n_i$: $p_j \in B\left(n_i, r_i\right)$.

If all transmission radii are equal, $r_i = r_j$ for $1 \leq i < j\leq N$, the local connectivity network is defined by an undirected graph since $e_{ij} = e_{ji}\in\mathcal{E}_\mathcal{G}$. This is the situation we will work with.

Example 1. Figure 3 illustrates the local connectivity network defined by the deployment of $N = 100$ nodes - all equipped with the same transmission radius - shown in Figure 2.

5.   Specifications of the proposed model

5.1.   Node life cycle

Certain characteristics inherent to the sensor nodes constituting a WSN must be taken into account when designing epidemiological models. Among these, the most important is the management of energy consumption. In this way, during the period when the node is not performing monitoring or communication (reception and transmission) tasks, it remains "dormant" or "asleep, " maintaining energy consumption at the minimum possible level. On the other hand, when it is carrying out the aforementioned tasks, the node is in an "active" state, consuming only the energy necessary for the proper development of these activities.

Although sensor devices are designed to have low energy consumption, if they only have one power source, it will eventually be depleted over time, and the node will cease its operation, becoming "inactive." Some nodes may additionally be equipped with a secondary energy supply source that provides them with energy obtained from the environment, which will impact the lifespan of the device.

Consequently, the activity of a sensor node consists of:

1) Monitoring the environment at regular time intervals.

2) Sending the data obtained from monitoring to the sink node.

3) Routing the data packets received (collected and emitted by other sensor nodes) toward the sink node.

It can be assumed that activities 1) and 2) are performed sequentially with little time lapse between them and at predefined time intervals. Activity 3) is carried out whenever the node receives a data packet "in transit" to the sink node (see Figure 4).

As it is assumed that routing protocols should optimize the distance traveled, both self-transmissions (sending the collected data) and transmissions due to routing received data packets from other nodes, should be directed toward the nearest neighboring nodes to the sink node.

5.2.   Specifications of the propagation and infection processes

When designing any mathematical model to simulate the spread of a particular agent in a specific environment, it is crucial to clearly define the main characteristics of propagation and infection processes. These specifications will determine the variables and coefficients involved in the model, as well as the design of equations governing the dynamics of the phenomenon. Considerations should include both the environment of the spread (a WSN, in this case), the properties of the agent being propagated (malware in our case), and the actors that can host this malicious code (the sensor nodes of the network).

5.2.1.   Propagation process

Regarding the propagation process, the following assumptions will be made:

1) At the onset of the outbreak, there will be a single infectious node capable of spreading the malware throughout the network (obviously, it will not be isolated).

2) The malicious code will propagate from one sensor node to another, utilizing legitimate communications established between them as a result of their activities (data transmission and data routing). This minimizes the chance of detection by potential security measures implemented in the WSN. It is noteworthy that, in this case, a "proper contact" can be defined as any transmission initiated by an infectious node, and whose recipient is a susceptible node, not vice versa. That is, a transmission initiated by a susceptible node toward an infectious node (even if the infectious node sends a data reception confirmation back to the susceptible node) will not be considered as a proper contact. It is assumed that the presence of malicious code embedded in these confirmation transmissions would be easily detected.

3) Direct spread will always occur toward nodes within the transmission range of the infectious node. If, for example, $n_i$ is an infectious node and $n_j \notin B\left(n_i, r_i\right)$, then the probability of the malware being directly transmitted (not through intermediary nodes belonging to any path connecting them) from $n_i$ to $n_j$ is zero. However, during each time unit, the code initially transmitted from $n_i$ could reach nodes that are not within its transmission range, thanks to routing.

4) Spread to nodes within the transmission range (neighbor nodes) could be of two types, depending on the specifications of the malicious code:

(ⅰ) Unrestricted spread: The malware specimen lacks the ability to know the state of neighboring nodes (due to technical or other issues) and, consequently, attempts to spread indiscriminately.

(ⅱ) "Intelligent" spread: The malware specimen has the ability to fully or partially know the characteristics of neighboring nodes and can, consequently, decide to spread only to those sensor nodes of interest.

5.2.2.   Infection process

Regarding the infection process, the following scheme will be followed:

1) When the malware specimen reaches a node, it has to "bypass" the security measures implemented in it so that if a intrusion attempt is detected, it is blocked, and the malware does not infect the sensor node (keeping it in the "susceptible" state).

2) If security measures cannot detect the intrusion, then the malware infects the node, which becomes a "latent" state. The malware evaluates the utility of the host for its purpose. If the malicious code determines that the infected node is not of interest, it tries to spread to a neighboring node. During this period (where the malicious code attempts to infect another device), the host node will be in the "infectious-latent" state and will return to the susceptible state after the malware has successfully spread. If, on the other hand, the specimen of malware determines that the infected node is useful, it decides on the type of attack to perform: carrying out malicious activity without physical harm to the node (for example: malicious manipulation of collected data or data in transit), or physically damaging the node. In the first case, the node is to be in the "compromised" state, while in the second case, the node is in the "damaged" state.

3) During the malicious activity, the malware may have the ability to spread (in which case the node is in the "compromised-infectious" state) or simply limit itself to carrying out malicious activity in the node itself (state "compromised").

4) The security measures implemented in the network and in the node could detect the presence of malware, and in this case, they would evaluate if it is possible to eliminate the malicious code. If possible, the node would be "free" of malware, and its state would transition to "patched-susceptible." Otherwise, (when countermeasures could not eliminate the malware), the node would be disconnected from the network, transitioning its state to "deactivated."

5) Finally, if the malware activity in the infectious or compromised node is not detected, it will continue its operation until it ends. At this point, the node will return to the susceptible state. The duration of this period (infectious or compromise period) will be variable obviously, the greater the activity and the longer the period in which this malicious activity is carried out, the greater the probability of being detected).

5.3.   The state set

As is previously discussed, the characteristics of the propagation and infection processes of the malware specimen, as well as the particularities of both the nodes and the WSN as a whole, define what is called the state set $\mathcal{X}$. This is a finite set whose elements are all the possible states in which each node, at each step of time, can be found (susceptible, exposed, infected, compromised, immunized, etc.). Thus, in general, $\mathcal{X} = \lbrace x_1, x_2, \ldots, x_m \rbrace$.

In the case of designing global models, we can work with two types of variables depending on whether we consider the discretized monitoring region or the continuum monitoring region. Thus, in the first case, many variables will be defined as there are states and the number of tessellations in the region $\mathcal{R}$:

where $s_k(t)\in\mathcal{X}$ is the state of the $k$-th sensor node at time $t$. In the second case, that is, if we consider the region $\mathcal{R}$ as a continuum, the variables will be defined as follows:

Note that if we work with the discretized region, it is obviously possible to define "global" variables:

In this work, it is assumed that the node population remains constant not only globally but also in each of the possible cells into which $\mathcal{R}$ is divided so that:

Taking into account all these considerations, the possible states in which any node may be are the following:

● Susceptible, $S$: The node is "free" of malware and either has never been infected before, or having been infected, such intrusion was not detected.

● Patched susceptible, $S_P$: The node is "free" of malware, having been infected at some previous time when security measures successfully detected and eliminated the malicious code.

● Latent (non-infectious), $L$: This is an infected node in which the malware is determining what activity to perform based on the characteristics of the node.

● Latent infectious, $L_I$: The node will not be attacked by the malware but is being used as a transmission vector for its spread through the network (it is infectious).

● Compromised (non-infectious), $A$: A node that is infected and is being attacked without physical damage.

● Compromised infectious, $A_I$: An infected node that is being attacked without physical damage and, at the same time, is serving as a transmission vector for the spread of malware to neighboring nodes.

● Damaged, $D$: This is an infected node that has been attacked by malware, causing physical damage that prevents its operation.

● Deactivated, $Q$: An infected node in which the malware has been successfully detected but could not be eliminated, so it has been disconnected from the rest of the network.

Consequently, the state set is:

In Figure 5, the flow diagram representing all the transitions between states is shown.

5.4.   Temporal unit

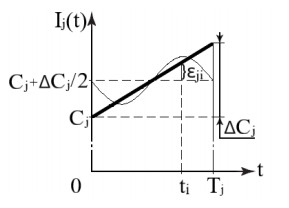
The correct definition of the temporal unit is a key factor in the model development as all epidemiological coefficients (and equations) depend on it. In our case, as is mentioned earlier, the milestones that determine the propagation process are the legitimate transmissions made by nodes, both of the data collected by themselves during the monitoring process and the data packets they receive from other nodes and have to route to reach the sink node. Therefore, we believe that the notion of a temporal unit should strongly depend on the number of such transmissions, specifically the number of own transmissions emitted by a sensor node. In this sense, given a number of monitorings (and subsequent transmissions) $c$, we define the temporal unit as the period of time during which $c$ own transmissions of a sensor node occur (see Figure 6).

5.5.   Additional considerations

In the novel global model that is proposed in the following section, some additional assumptions will be made, derived from what has already been previously established, and the nature of global models:

● Transmissions carried out by each node (whether own or associated with the routing process) will be directed toward all nodes in its neighborhood.

● The number (average) of own transmissions of each node per unit of time will be $K_0 = \langle k \rangle \cdot c$, where $\langle k \rangle$ is the average degree of the network.

● The number of routings performed by an arbitrary node per unit of time depends proportionally on the betweenness centrality of nodes and the average length of the shortest paths between nodes.

● The path taken by a data packet during a unit of time has an average length $l$, which will be reduced by one unit after each monitoring. Consequently, during the period of time that lasts one unit of time, the data collected in the $i$-th ($1 \leq i \leq c$) monitoring carried out during that unit will travel a path of length $l-(i-1)$ (see Figure 7).

6.   The global model on the continuous monitoring region

6.1.   Transition from susceptible to Latent

The mathematical determination of the incidence term is one of the most important (and decisive) tasks in designing a mathematical model to simulate the propagation of malware on a WSN. Considering the previous description of the propagation process, infection can occur when there exist an effective contact (communication between sensor nodes) between an infectious node (either in a latent state, $L_I$, or attacked, $A_I$) and a susceptible node (whether it is an "original" susceptible or a patched susceptible). In this way, we have:

where

where $k\left(N\right)$ stands for the average appropriate contacts of each node with the rest of the sensor nodes per unit of time, and $0 < q_A\leq q_L \leq 1, 0 < \hat{q}_A\leq \hat{q}_L \leq 1$ are the probabilities that a suitable contact leads to infection when receiving a transmission from a node in infectious latent state $L_I$ or from a node in infectious attacked state $A_I$, respectively. Additionally, it is assumed that $\hat{q}_A \leq q_A$ and $\hat{q}_L \leq q_L$.

Taking into account the above, we have:

where $K_0 = \langle k \rangle \cdot c$ is the average self-transmissions of the node, and $K_1\left(N\right)$ is the (average) number of routings each node manages in each unit of time. Specifically, in this work, we assume:

where $l-\left(\delta-1\right) < L\leq l-\delta$ and $L$ is the average length of the shortest paths between any pair of nodes in the WSN. Note that $C_B(n_i)$ is the betweenness centrality associated to the $i$-th sensor node.

In summary, we will have:

6.2.   Transition from Latent to infected

Considering the above, once the malicious code reaches a sensor node, it proceeds to evaluate it to decide what activity to develop: not attack the node and use it as a transmission vector or attack the sensor node with a higher or lower level of "aggressiveness". We can assume that during each unit of time, there is a fraction of nodes, $0 \leq \gamma_L \leq 1$, that are not attacked, another fraction of nodes, $0 \leq \gamma_D \leq 1$, are attacked and damaged, and another fraction of nodes, $0 \leq \gamma_A \leq 1$, which are attacked and used to carry out malicious activity without disabling them. Within these latter nodes, a fraction defined by $0 \leq \nu \leq 1$ will not be used as transmission vectors (infectious nodes). There will also be a fraction $0 \leq \omega \leq 1$ of latent nodes that are detected as infected by security countermeasures, of which another fraction $0 \leq \rho \leq 1$ will be possible to eliminate the malicious code specimen. Finally, it will be assumed that there will be a small fraction (per unit of time), $0\leq \eta \leq 1$, of latent nodes that cannot be classified. Therefore, we will have $\gamma_L+\gamma_D+\gamma_A+\eta+\omega+\rho = 1$. Additionally, we can make the following assumptions about the numerical value of these epidemiological coefficients:

● There will be fewer attacked and/or damaged nodes than non-attacked nodes: $\gamma_D+\gamma_A \leq \gamma_L$. Also, there will be many fewer damaged nodes than attacked nodes: $\gamma_D \ll \gamma_A$.

● The fraction of latent nodes detected by security countermeasures will be very small not only in comparison with these epidemiological coefficients: $\omega, \rho \ll \eta, \gamma_D, \gamma_A$, but also in relation to the detection and elimination rates that affect attacked and infectious nodes.

● The fraction of nodes in which a decision cannot be made will be very low: $\eta \ll \gamma_L, \gamma_D, \gamma_A$.

As a consequence, we are assuming that: $0 \leq \omega, \rho \ll \eta \ll \gamma_D \ll \gamma_A \leq \gamma_L$.

6.3.   Transitions from infected to susceptible and/or disabled

It is assumed that security countermeasures are constantly monitoring the WSN to detect (and eliminate, if possible) malware. Roughly speaking its detection will consist in searching for suspicious or unusual activities of the nodes. Remember that in infected nodes, the activities carried out by the malware (during monitoring and legitimate transmission periods -to try to go unnoticed-) are the following:

● Development of malicious activity in a node without permanently damaging it.

● Irreversibly damaging a node.

● Attempt to spread to other nodes.

Depending on the state of the node, different activities will be carried out, and it is reasonable to assume that the more activities are performed, the more probability of detection there will be. In this sense, the minimum detection probability (per unit of time) can be assigned to latent state $L$ nodes, as mentioned earlier, $0 \leq \omega \leq 1$. From here, we will assume the following: $\omega_{L_I} = c \omega, \omega_A = 2 c \omega, \omega_{A_I} = 3 c \omega$, where $\omega_{L_I}, \omega_{A}$, and $\omega_{A_I}$ are the detection probabilities for latent infectious, attacked, and infectious attacked nodes, respectively.

On the other hand, the rate of elimination of malicious code will be assumed to be the same regardless of the state of the considered node: $0 \leq \rho \leq 1$. Finally, infected nodes where the malware has not been detected and has completed its malicious activity will become, again, susceptible in a fraction that will depend on the state of the node: $0 \leq \epsilon \leq 1$ for attacked nodes and $0 \leq \zeta \leq 1$ for latent infectious nodes. In Figure 8 the transition diagram of the described model is illustrated.

6.4.   The system of ordinary differential equations governing the model dynamics

As indicated in Subsection 5.3, the variables used in this model are the following:

Then, taking into account the specifications of the model given above, the system of ordinary differential equations that governs its dynamics is:

where $N = \sum_{i = 1}^8X_i(t)$ for all $t$. Also, the following initial conditions will be considered:

Note that the feasible region of this system is $\Gamma = \lbrace (X_1, \ldots, X_8) \in (\mathbb{R}^{+})^8 \text{ such that } X_1 + \ldots + X_8 \leq N \rbrace$, so only solutions living in this region will be of interest.

Proposition 2. The system determined by equations (6.6)-(6.13) always has an infection-free equilibrium point $P_{0}^\ast = (X_{1, 0}^\ast, \ldots, X_{8, 0}^\ast)$ defined by the following coordinates:

Proof. The equilibrium points are solutions of the system

namely:

From Eqs (6.20)–(6.22), it follows that:

so the system (6.17)–(6.25) is reduced to the equation $N = X_1 + X_2 + X_7 + X_8$. This immediately yields that if $X_{1, 0}^\ast = N_{1, 0}^\ast$, $X_{2, 0}^\ast = N_{2, 0}^\ast$, and $X_{7, 0}^\ast = N_{7, 0}^\ast$, then $X_{8, 0}^\ast = N - N_{1, 0}^\ast - N_{2, 0}^\ast - N_{7, 0}^\ast$, and the statement is proven. □

Proposition 3. If $\gamma_D = 0$, then the system determined by Eqs (6.6)–(6.13) has an endemic equilibrium point $P_{e}^\ast = (X_{1, e}^\ast, \ldots, X_{8, e}^\ast)$ such that:

1) If $\omega = 0$, it is given by:

2) If $\rho = 1$, it is given by:

where:

Proof. Considering Eq (6.23) and assuming that $X_3 \neq 0$, we have $\gamma_D = 0$, so the system can be written as follows:

From Eqs (6.35) and (6.36), it follows that:

and from Eq (6.38), it is deduced that either $\omega = 0$ or $\rho = 1$. Thus:

1) In the first case, when $\omega = 0$, then $X_2 = 0$, and the system becomes:

The first equation is a tautology, so only the last equation remains and the result stated in the proposition is obtained.

2) In the second case, if $\rho = 1$ (with $\omega \neq 0$), then

and the system becomes:

The first equation is a tautology, and from the remaining equation, through a simple calculation, the result of the proposition is obtained. □

It can be assumed that $a_1\alpha_L+a_2 \alpha_A \neq 0$ and $a_1 \hat\alpha_L+a_2\hat\alpha_A\neq 0$ since $\alpha_L$ and $\alpha_A$ cannot be zero at the same time (for there to be incidence). Additionally, it can also be supposed that $\gamma_L \neq 0$ and $\gamma_A \neq 0$ because otherwise there would be no transition between latent and infective-latents and attacked nodes, respectively.

Note that the endemic equilibrium point exists when several very special conditions are satisfied, namely:

1) $\gamma_D = 0$, meaning that the malicious code specimen is not capable of permanently damaging sensor nodes and rendering them disabled.

2) Either

2.1) $\omega = 0$, meaning that security countermeasures are not capable of detecting the presence of the malicious code specimen.

2.2) or $\rho = 1$, meaning that security countermeasures are capable of eliminating the malware specimen from all nodes where it has been detected.

Meeting these conditions would simplify the model significantly by eliminating three transitions between compartments. Consequently, this case can be considered as marginal.

6.5.   Calculation and analysis of the basic reproductive number

Theorem 4. The basic reproductive number associated with the previously described epidemiological model for malware propagation is given by:

Proof. We will apply the next-generation method (see, for example, ^[54,55]) to compute in an explicit way its basic reproductive number. Thus, considering only the variables corresponding to compartments of infected nodes, the system (6.6)–(6.13) can be written as follows:

with $\mathcal{V}_i = \mathcal{V}_i^–\mathcal{V}_i^+$, where:

such that $\mathcal{F}_i$ represents the appearance of new nodes in compartment $X_i$ from infection, $\mathcal{V}_i^+$ indicates the number of nodes entering in state $X_i$ due to system dynamics, and $\mathcal{V}_i^-$ stands for the number of nodes disappearing from compartment $X_i$ due to model dynamics.

A simple computation shows that:

and

so that

Consequently we have:

and the basic reproductive number will be the spectral radius of the matrix $\left(\mathcal{F} \mathcal{V}^{-1}\right)_{P_0^\ast}$, i.e.:

thus finishing the proof. □

The most relevant epidemiological coefficients of the model are those that appear in the explicit expression of the basic reproductive number since this is a crucial threshold parameter that determines the behavior of the temporal evolution of infectious nodes. Considering the meaning of the concept of the basic reproductive number, the lower the numerical value of this coefficient, the easier it is to control the epidemic outbreak. Consequently, the fundamental goal is to try to reduce the value of $\mathcal{R}_0$ below $1$, since it is reasonable to establish the main prophylactic strategies as those aimed at reducing the value of $\mathcal{R}_0$. Note that, in our case, the basic reproductive number can be written as follows:

which means that $\mathcal{R}_0$ will decrease when:

1) The denominator $\omega+\gamma_L+\gamma_A+\gamma_D$ increases.

2) $N_{1, 0}^\ast$ and/or $N_{2, 0}^\ast$ decrease.

3) $\frac{\gamma_L}{\zeta+c\omega}$ and/or $\frac{\gamma_A\left(1-\nu\right)}{\epsilon+3c\omega}$ decrease.

4) $q_L, q_A, \hat q_L, \hat q_A$ decrease.

5) $\frac{k\left(N\right)}{N}$ decreases.

These are purely mathematical conditions, and some of them may not have "physical" or epidemiological significance or be impractical in practice. Analyzing them in some detail, we can draw the following conclusions:

1) The denominator $\omega+\gamma_L+\gamma_A+\gamma_D$ roughly represents the rate of abandonment from the compartment of nodes in the latent state $L$. From a practical standpoint, it makes sense to increase $\omega\left(1-\rho\right)$, which is the fraction of latent nodes that are detected and become deactivated, thus preventing them from becoming infectious in the future. However, it does not make much sense to increase $\omega \rho$ or $\gamma_A \nu$, and, certainly, it makes no sense to increase $\gamma_L$ or $\gamma_A \left(1-\nu\right)$ since it would be increasing the compartment of susceptibles in the first case (potential future infectives) or the compartments of infectives, $L_I$ and $A_I$, in the second case.

2) Obviously, if we reduce the number of nodes susceptible to infection, the infectious outbreak will be contained. This could be achieved either by immunizing them (a process not considered in the current model) or by isolating them from the network (which would negatively impact its operation).

3) In principle, it would not be possible to decrease the rates $\gamma_L$ or $\gamma_A$ since they correspond to characteristics of the malicious code specimen, and it is assumed that we would not have access to them. The same would apply to increasing the rates $\nu, \zeta$, and $\epsilon$. However, it would be possible to influence the detection rate $\omega$ of latent nodes, although it would only be practically useful, as discussed in point (1), to increase $\omega\left(1-\rho\right)$.

4) The contagion probabilities $q_L, q_A, \hat q_L$, and $\hat q_A$ decrease if we enhance the effectiveness of security measures implemented in the nodes.

5) Decreasing $k\left(N\right)$ implies reducing the number of contacts (direct transmissions and routing transmissions) of the nodes. This is not possible without affecting the proper functioning of the WSN.

6.6.   Numerical simulations

We will illustrate the proposed model with some simulations considering different contact topologies: complete network, homogeneous grid network, random network, scale-free network, and small-world network.

In Table 1, the values of the epidemiological coefficients considered in all simulations are presented. These are purely illustrative numerical values.

It will be assumed that at the initial time, we have the following compartment configuration:

which means that all nodes at $t = 0$ are susceptible except for a single node in the latent and infectious state. In addition, as mentioned earlier, simulations will be performed on WSNs whose network topology is defined by five complex networks of different typologies. For the sake of simplicity, we assume $N = 100$ and consider the following contact topologies (note that for $N > 100$, the simulations obtained are similar if the same epidemiological coefficients, global structural indices, and initial conditions are considered):

● Complete network, $\mathcal{G}_1$.

● Homogeneous grid network, $\mathcal{G}_2$:

● Random network (ER type with connection probability $p = 0.5$), $\mathcal{G}_3$:

● Scale-free network with the number of reconnected nodes $n = 3$, $\mathcal{G}_4$:

● Small-world network (WS model with reconnection probability $p = 0.1$), $\mathcal{G}_5$:

In Table 3, some of the main structural coefficients associated with these networks are shown.

In addition to the previously mentioned values of the coefficients, we will suppose that for each step of time, there will be $c = 3$ monitorings/direct transmissions from each node, and the length of the path traveled in the WSN by a data packet in each time unit is $l = \max\lbrace L_1, L_2, L_3, L_4, L_5 \rbrace = 7$. Additionally, in Table 3 the values of the respective contact rates $k(N)$ in the cases under consideration are shown:

If the system of differential equations governing the dynamics of the model is numerically solved using the above data (we will use MATHEMATICA software for this simulations), the solutions shown in Figures 13–17 are obtained. Note that in all cases, the system evolves toward an infection-free equilibrium state. Also, it can be observed that in two cases (those using the complete network and the random network), there is an initial increase in the number of infected nodes before declining, while in simulations where the WSN has a homogenous grid, scale-free, or small-world topological structure, the infectious outbreak disappears immediately without any impact on the network. This fact could have been foreseen simply by considering the data in Table 3, where it can be observed that given that all simulations have been obtained from the same values of epidemiological coefficients, it is precisely the impact of the network topology on the computation of $k(N)$ that strongly determines the epidemic evolution.

In Figure 18, the evolution of the latent compartment in WSNs with contact topologies defined by ER random networks with different connection probabilities $p$ is shown. The corresponding values are presented in Table 4.

It can be observed that as the connection probability used in the random network construction algorithm decreases, the prevalence (number of infected nodes) becomes more "flattened" until a certain threshold value of $p$ - when $\mathcal{R}_0$ is less than $1$- where the number of nodes in the latent state decreases from the initial time.

Finally, it should be noted that the definition given for incidence severely undervalues network topologies defined from homogenous grid, scale-free, and small-world networks, even considering the same numerical values for the malware's epidemiological coefficients. Obviously, the effect of propagation cannot be the same as in a complete or random network (constructed using a high probability in the ER algorithm), but, in my opinion, it shouldn't be so slight, especially when empirical evidence shows that contagion probabilities, $q_L$ and $q_A$, should be multiplied by $10^3$ to achieve similar behaviors.

7.   Conclusions and future work

In this work, following a review of the state of the art regarding mathematical models for simulating malware propagation in WSNs, a novel way of defining incidence has been proposed, which takes into account the average number of routings per unit of time. Based on this, a new propagation model has been designed. Through a detailed analysis of the phenomenon, this model considers more compartments than those employed in other existing models.

Taking into account all these compartments ($8$ in total), the study of stability becomes overly complex, although it is possible to explicitly obtain the expression for the basic reproductive number. Subsequently, an analysis of the basic reproductive number can be performed to determine key containment measures.

The proposed model is of a global nature, where the studied variables represent the size or density of the considered epidemiological compartments (for example, the number of infected devices at each step of time). Consequently, it does not take into account the specific characteristics of each of the devices within the WSN (both those related to the processes of propagation and infection, as well as the specific contact topologies). This is a potential limitation of the model that could be addressed by studying the development of individual-based models, which is left as future work. On the other hand, although certain specific aspects and characteristics of WSNs and malware propagation have been considered in this work, further exploration is needed in the ad hoc design of epidemiological coefficients for models simulating malware propagation. Furthermore, as future work, the simplification of the proposed model by using fewer compartments is suggested, thereby enabling an in-depth qualitative analysis.

Use of AI tools declaration

The author declares he has used Artificial Intelligence (AI) tools in the revision (and improvement) of the English of this article. Moreover, AI tools have not been used for other purposes.

Acknowledgments

This research was funded by "Fundación Memoria de D. Manuel Solórzano Barruso" (Universidad de Salamanca, Spain) under grant number FS/2-2022.

Conflict of interest

The authors declare there is no conflict of interest.