Hybrid optimized artificial neural network using Latin hypercube sampling and Bayesian optimization for detection, classification and location of faults in transmission lines

1.   Introduction

Traffic signs give drivers instructions and information that are indispensable in protecting human life and property. Therefore, automatic traffic sign recognition is an important computer vision task ^[1,2,3]. In recent years, driver assistance systems (DAS) ^[4,5,6,7] have developed rapidly. Traffic sign recognition is an integrated function of DAS. Normally, professional equipment is mounted on the top of a vehicle to capture traffic sign images. Under real-world conditions, these images are distorted due to various natural and human factors including vehicle speed, weather, destroyed signs, angles, etc. Hence, we apply data augmentation to simulate all kinds of situations. These enhancement techniques refer to rotations, crop, scale, lighting variations and weather conditions changes, which may eventually decrease the traffic sign recognition network performance.

As for the field of traffic sign recognition, it is a famous problem of computer vision tasks. A lot of literature ^[8,9,10] has studied the topic of traffic sign detection, and some reviews are available in ^[11,12]. In ^[13], an algorithm based on Gaussian kernel support vector machines (SVMs) ^[14] is utilized for traffic sign classification. From experimental results, the proposed algorithm is robust under various conditions including translation, rotation and scale. Ayoub ^[15] presented a random forest classifier and gave satisfactory results on the Swedish Traffic Signs Dataset. Lu ^[16] proposed a graph embedding approach that preserved the sparse representation property by using L2, 1-norm. Experiments demonstrate that the proposed approach outperformed previous traffic sign recognition approaches.

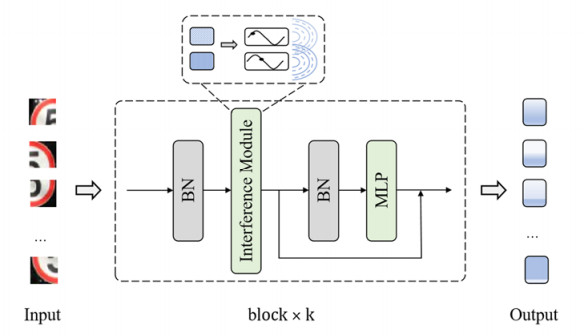
In this paper, we introduce the interference module inspired by ^[17], which dynamically aggregates information by improving the representation way of information according to different semantic contents of an image. In quantum mechanics, a wave function containing both amplitude and phase ^[18] represents an entity. We describe each entity that is generated by the convolutional filters as a wave to realize the information aggregation procedure dynamically. The amplitude is the real-value feature representing the content of each entity, while the phase term is represented as a complex value. These wave-like entities intervene with each other and close phases tend to enhance each other. The whole framework is constructed by stacking the interference module and channel-mixing multi-layer perceptrons (MLPs). Figure 1 summarizes the architecture. We further conduct ablation experiments and analyze the performance of the proposed model. The final experimental results demonstrate the visible priority of the existing architectures (shown in Table 2).

Figure 1.  The structure chart of our proposed model. k is the number of the block. BN refers to batch normalization.

DownLoad: Full-Size Img PowerPoint

The contributions of our work are as follows: we propose a novel method (WiNet) for traffic sign recognition. A new convolution structure is introduced for learning multi-scale features and it is successfully combined with a wave function. Additionally, our model achieves the most performance compared with several concurrent works based on ResMLP ^[19], ResNet50, PVT ^[20] and ViT ^[21]. We also test the robustness of all models on datasets with a sufficient number of synthetic samples. Furthermore, we analyze the effects of type of representation on the overall wave interference network that dynamically aggregates information by improving the representation of them according to different semantic contents of an image.

The rest of the paper is organized as follows: Section 2 reviews related methods applied to traffic sign recognition. Section 3 introduces the formulation and architecture of the proposed model. We present experiments and implementation details in Section 4, and further analyze the effectiveness of different modules and activation functions in Section 5. Finally, we draw conclusions in Section 6.

2.   Related work

In recent decades, many methods have been proposed for traffic sign recognition. We briefly review related literature ^[22,23]. It can be divided into traditional methods, methods based convolutional neural networks (CNNs) and methods with attention mechanisms.

Traditional methods for traffic sign recognition: Before CNNs, traffic sign recognition depended on hand-crafted features. In ^[15], the comparison of different combinations of four features was conducted, including the histogram of oriented gradients (HOG), Gabor, local binary pattern (LBP) and local self-similarity (LSS). The authors tested the proposed method on the Swedish Traffic Signs Data set. Machine learning methods have also been utilized to solve related problems, such as random forests, logistic regression ^[24] and SVM ^[25].

CNN for traffic sign recognition: With the rapid development of memory and computation, CNN-based architectures have been the mainstream in the computer vision field. Many works have used CNNs for traffic sign classification. The committee of the CNN-based approach ^[26] obtains a high recognition rate of 99.15%, which is above the human recognition rate of 98.98%. In the GTSRB competition in 2011, multi-scale CNNs ^[27] made full use of local and global features and established a new record of an error rate of 1.03%. ^[28] proposes a novel deep network for traffic sign classification that achieves outstanding performance on GTSRB. The author utilized spatial transformer layers ^[29] and a modified version of the inception module ^[30] to build the model. The well-designed inception module allows the network to classify intraclass samples precisely. The spatial transformer layer improves the robustness of the network to deformations such as translation, rotation and scaling of input images.

Attention mechanism for traffic sign recognition: The attention mechanism can adapt to select important information from the input feature. For the outstanding performance, attention mechanism and variants have been applied to a variety of tasks. These improvements include channel attention ^[31], spatial attention ^[32] and global attention ^[33]. This paper ^[34] proposed an attention-based convolutional pooling neural network (ACPNN). Convolutional pooling replaces max pooling. The ACPNN was validated on the German Traffic Sign Recognition Benchmark (GTSRB). Experiments showed it was robust against external noises and increased recognition accuracy. Based on the ice environment traffic sign recognition benchmark (ITSRB), the author proposed an attention network based on high-resolution traffic sign classification (PFANet) ^[35] and reached 93.57% accuracy. At the same time, its performance on the GTSRB was as good as the newest and most effective networks.

3.   Methods

In this section, we describe our proposed network for traffic-sign recognition in detail. First, we describe the interference module. Then, we describe the whole structure of our proposed network. At last, we describe our data augmentation techniques.

3.1.   Interference module

Figure 2.  The structure of the interference module. In the representing and aggregating structure, a $3\times 3$ depthwise convolution is used to aggregate information.

DownLoad: Full-Size Img PowerPoint

In recent years, many neural network modules based on CNN have been proposed such as ^[36,37]. In the interference module, the extraction structure of features based on convolution adopts residual-like connections within a single residual block ^[38]. After the input is normalized, it is split into two subsets which have the same spatial size and number of channels, denoted by ${X}_{1}$ and ${X}_{2}$, respectively. Each ${X}_{i}$ corresponds to a $3\times 3$ convolution, denoted by ${K}_{i}\left(\right)$, where $\mathrm{i}\in \{1, \mathrm{ }2\}$. ${\mathrm{X}}_{2}$ is added with the output of ${K}_{1}\left(\right)$ and then fed into ${K}_{2}\left(\right)$. At last, a $1\times 1$ convolution makes sure the channel number is the same as that of the following module. The output result can be calculated using the following formula:

We name the output ${\mathrm{E}}_{\mathrm{i}}$. The final output ${\mathrm{E}}_{\mathrm{i}}$ can capture feature information from a larger receptive field. Different channels often contain the complete content of different objects in deep neural networks ^[39]. By using a $1\times 1$ convolution, different channels are assigned to corresponding weights. It is worth noting that the feature extraction structure not only achieves adaptability in the spatial dimension ^[36] but also adaptability in the channel ^[36] dimension.

The output ${\mathrm{E}}_{\mathrm{i}}$ is the feature map extracted by the convolutional filters. To describe the feature map concretely, we refer to each feature as an entity. Next, each entity will be converted into a wave. After all, waves have aggregated each other, the new feature map will be generated and fed into the next stage.

An entity is represented as a wave ${B}_{j}$ with both amplitude and phase information. A wave can be formulated by

where ${B}_{j}$ returns the j-th wave, $i$ is the imaginary unit and ${i}^{2} = -1$. The |.| denotes the absolute value operation. $\otimes$ means element-wise multiplication. The amplitude $\left|{\mathrm{A}}_{\mathrm{j}}\right|$ represents the information of each entity. A periodic function of the ${e}^{i{\theta }_{j}}$ makes its values distribute over a fixed range. ${\theta }_{j}$ is the phase and points out the current location of an entity in a period.

In Eq (2), a wave is represented a complex-value. To embed it in the module, we expand it with Euler's formula. It can be written as

To get the above equation, we are required to design the form of information expression about both amplitude and phase. The amplitude $\left|{\mathrm{A}}_{\mathrm{j}}\right|$ is a real-value feature in the formula. In fact, the absolute operation in the formula is not implemented. A feature map ${x}_{j} = {R}^{N\times \mathrm{C}}$ is taken as the input, and we use a plain channel_FC operation ^[17] to estimate the amplitude. Specifically, a Tanh activation is adopted to gain the nonlinearity ability. Compared with Relu activation, we found Tanh activation achieves significantly better performance. As can be seen from Figure 3, a wave with a phase has a direction. The value range of Tanh activation is -1–1. Positive and negative numbers can be used to represent different directions. So Tanh activation can help models achieve better performance. Comparisons of Tanh activation with Relu activation are shown in Table 6.

Figure 3.  The superposition of two waves with different phases. The dashed lines describe waves with different initial phases. The solid lines describe the superposition results of two waves.

DownLoad: Full-Size Img PowerPoint

In the above paragraphs, we presented the relevant mathematical expressions. Next, we introduce a concrete evaluation expression about the phase and the result of two waves superimposed.

where the learnable parameter ${W}^{c}$ is the weight. The phase plays an important role in the whole module. It points out the current location of an entity in a period. We take the simplest method to estimate the phase whose parameters are represented with the output value from Tanh activation.

To dynamically adjust the relationship between different entities with fixed parameters, we take the token_FC operation ^[17] to aggregate information. The token-FC is formulated as:

where the learnable parameter ${W}^{t}$ is the weight. A feature map ${x}_{k}\in {R}^{N\times C}$ is taken as the input. Here, j means the j-th entity. Finally, the real-value output ${O}_{j}$ can be written as:

where the learnable parameter W^t and ${W}^{i}$ are the weights. As can be seen from Figure 3, when two waves have a similar phase, the output ${O}_{j}$ tends to be enhanced. The same semantic content of the input feature map can be extracted in Figure 7 of Section 4.

In the channel dimension, the $1\times 1$ convolution is conducive to fusing information among different channels. To enhance the information fusion ability in the spatial dimension, we use MLPs to exchange information among different entities. Before MLPs, we also apply batch normalization. We adopt residual learning to fusion information from MLPs. As Table 6 illustrates, MLPs significantly improve the performance compared with the network structure not containing MLPs.

3.2.   Wave interference network

In terms of the network architecture, our model is a simple hierarchical structure with 4 stages. Each stage will decrease the output spatial resolution, i.e., $\mathrm{H}/2\times \mathrm{W}/2$, $\mathrm{H}/4\times \mathrm{W}/4$, $\mathrm{H}/8\times \mathrm{W}/8$ and $\mathrm{H}/16\times \mathrm{W}/16$. Here, H and W represent the height and width of the input image. The number of output channels is increasing with the decrease of resolution. The detailed configuration can be seen in Table 1.

Table 1.  The detailed setting of WiNet.

Stage	Output size	Blocks
1	$\mathrm{H}/2\times \mathrm{W}/2\times 64$	2
2	$\mathrm{H}/4\times \mathrm{W}/4\times 128$	3
3	$\mathrm{H}/8\times \mathrm{W}/8\times 256$	4
4	$\mathrm{H}/16\times \mathrm{W}/16\times 512$	2

---

 | Show Table

DownLoad: CSV

At the beginning of each stage, we downsample the input and control the downsampling rate by using the stride number. In the first stage, we use a $6\times 6$ convolution with stride 2 to embed an input image with the shape $\mathrm{H}\times \mathrm{W}\times 3$. In the following three stages, there is a $3\times 3$ convolution with stride 2 to downsample the input data. Note that all other layers in a stage keep the same output size. We use a global average pooling operation for the feature map from the last stage and then adopt a linear classifier to predict the logits.

3.3.   Datasets and data augmentation

In general, it is very difficult to estimate which model gives better performance. Many authors evaluate their models on different datasets. To enrich the set of traffic signs, some authors sample images from multiple datasets to perform the evaluation ^[40,41,42]. On the other hand, lots of authors use their own private datasets ^[43,44] instead of public datasets ^[45,46]. In order to be fair, we adopt the ratio of the training set and test set in the CTSRD database that ensures different models are implemented at the same benchmark. We carried out several data augmentation techniques to extend the training set for addressing the challenges from various realistic scenarios.

To demonstrate the generalization of our model, we train our model on another well-known benchmark. The German Traffic Sign Recognition Benchmark (GTSRB) ^[47] consists of more than 50,000 images in which the classes of traffic signs are more than 40, but we consider only images with a size of at least 30 pixels. All images are resized to $64\times 64$ resolution. The remaining images are ignored on account of the low human visual identification rate. Many models ^{[48,49,50,51]} have obtained good results on this dataset, so the comparison between different models is more convincing.

Data augmentation has shown its validity in deep networks. It effectively expands the size of the training set, which is an important factor to consider when training models. A sufficient amount of training data contributes to modulating millions of learnable parameters during the training phase. In real-world situations, traffic signs may be distorted in shape because of human factors. Traffic sign images may contain various appearance distortions such as brightness and contrast. In order to simulate various physical changes in real-world scenarios, we apply image processing techniques to each image randomly and expand the original training dataset as large as five times. Every image is only augmented by one of the available methods in processing, which makes sure that each augmentation operation has the same probability of being implemented. Some samples of original and sample results from these techniques are presented in Figure 4. There are many imaging processing libraries. We apply Albumentations, except for rain, to complete all options. To recapitulate briefly, we perform four classes of augmentations in the data preprocessing stage:

Figure 4.  Several synthetic examples of traffic-sign instances.

DownLoad: Full-Size Img PowerPoint

● Random weather. We apply data augmentation to achieve weather effects such as sunny, foggy, rainy and snowy. Synthetic samples keep the size and aspect ratio of input images.

● Random blur. We apply data augmentation to blurred original images. Methods of data augmentation include Blur, MotionBlur, GaussianBlur and MedianBlur in Albumentations.

● Random affine. Geometric transformations for data augmentation are common and effective methods. PiecewiseAffine, Affine and RandomResizedCrop in Albumentations are selected to generate synthetic samples.

● Gause noise. Gauss Noise in Albumentations generates a matrix of random values. Moreno-Barea ^[52] found adding noise to images can make models more robust on nine datasets from the UCI repository ^[53].

4.   Experiments

In this section, we conduct a few analytical experiments to explore our proposed model. To make the comparison fair, we carried out all experiments under the same settings. We report our results on CTSRD, which achieves significant improvements compared with other state-of-the-art models. In addition, we verify the effectiveness of Tanh activation and MLPs. Result visualizations further show the effectiveness of our model.

4.1.   Implementation details

We implemented our experiments on a PC with an Intel i5-11400H, an NVIDIA GeForce RTX 3050 GPU, and 16 GB RAM. All models are carried out with TensorFlow. During training, we ensure all models use the same parameters for fairness. We train all models using Adam with the same initial learning rate of 10−4. Due to the limitation of the video card, the mini-batch size is set to 64. After considering the resolution of input images, the image is resized to 64 pixels in both width and height. To fuse spatial dimension information, we set the window size to 3 empirically in the interference module. All models are trained for 60 epochs on the original dataset. We train again all models for 30 epochs when using data augmentation and greatly increasing the size of the original dataset.

Table 2 presents the comparison of WiNet with other models, including ResMLP, ResNet50, PVT and ViT. WiNet achieves the best accuracy, which outperforms ResMLP, ResNet50, PVT and ViT by 5.8%, 2.4%, 23.5% and 11%, respectively. This clearly demonstrates that our model has a strong ability to extract features. In comparison to ResNet50 with fewer parameters, our WiNet not only has larger throughputs but also performs better. In particular, WiNet achieves 100% accuracy when images using data augmentation were added to the training set.

Table 2.  Comparisons with some other models on CTSRD.

Model	Params	Throughput (image/s)	Original dataset	Original dataset including synthetic examples
			Top-1 Accuracy (%)	Top-1 Accuracy (%)
ResMLP	14.52 M	13	94.0	97.2
ResNet50	23.7 M	19	97.4	99.7
PVT	12.3 M	13	76.3	89.5
ViT	85.8 M	11	88.8	95.7
ours	26.1 M	14	99.8	100

---

 | Show Table

DownLoad: CSV

We give quality histograms in Figure 5, while corresponding statistics (median, mean and standard deviation of all models) are provided in Table 3. It can be seen that the distribution of predicted probability for our model is closer to 1 than for other models trained on CTSRD simultaneously. Statistics further verify the results that WiNet has a higher median value, mean value and a smaller discrete degree.

Figure 5.  Quality histogram about the predicted probability of all models on CTSRD.

DownLoad: Full-Size Img PowerPoint

Table 3.  Quality histogram statistics of all models on CTSRD.

Model	Median	Mean	Std. Dev.
ResMLP	0.99	0.96	0.109
ResNet50	1.00	0.99	0.047
PVT	0.95	0.85	0.184
ViT	0.99	0.94	0.121
ours	1.00	0.99	0.034

---

 | Show Table

DownLoad: CSV

In order to further analyze the model's performance, we utilize data augmentation including weather, Gauss, blur and affine on the testing set, and then make predictions. Data augmentation has made the distribution of the testing set different from the training set, so it can be used to test the model's robustness. Table 4 lists the predicted results of the model on the testing set. In the above case, our model shows good performance. We use models, which are trained on the training set with synthetic samples, to predict this testing set. As can be seen from Table 5, the performance of WiNet surpasses ResNet50 and has a sharp boost with +2.71, +3.52, +2.21 and +2.76 points for weather, Gauss, blur and affine, respectively. It indicates that our model's effectiveness can be fully exploited on a larger dataset.

Table 4.  Results of testing robustness on CTSRD.

Model	Weather	Gauss	Blur	Affine
ResMLP	44.08%	53.01%	51.86%	54.71%
ResNet50	70.26%	65.05%	64.09%	65.75%
PVT	35.66%	32.25%	32.80%	37.46%
ViT	48.14%	47.34%	47.09%	48.35%
ours	73.37%	61.48%	60.48%	62.64%

---

 | Show Table

DownLoad: CSV

Table 5.  Results of the model on testing set and training set with synthetic samples.

Model	Weather	Gauss	Blur	Affie
ResNet50	91.22%	91.57%	90.97%	91.27%
ours	93.93%	95.09%	93.18%	94.03%

---

 | Show Table

DownLoad: CSV

Except for considering the accuracy of our model, it is crucial to test the generalization of our model by training on different datasets. We divided the dataset from GTSRB into training and validating datasets according to the original proportion. We trained the model with 30 epochs, batch size 64, learning rate 0.0001 and Adam optimizer. The solid curves show the accuracy change, while the dashed curves show the loss change. Here, we can see from Figure 6 that the highest accuracies of both training (21,792 images) and validating datasets (6893 images) are 1.00. The overall trends of accuracies for both training and validating datasets are increasing with epochs. After around 16 epochs, only slight fluctuations can be observed. We observed similar but opposite trends in the loss-changing curves. The losses of both training and testing datasets are very small. In these curves, we can see our proposed model has the advantages of minor loss and high accuracy. This result indicates that our model keeps a good generalization ability rather than only fitting CTSRD.

Figure 6.  Loss and accuracy curves of the training and validating processes. The blue and red line on the chart above represents the training and validating processes, respectively. The annotation indicates the best result and corresponding epoch in the training and validating processes.

DownLoad: Full-Size Img PowerPoint

4.2.   Ablation studies and visualization

In this section, we ablate some design components to explore their effectiveness. For a more intuitive feeling, we draw some feature maps with heatmaps in the aggregating process.

To evaluate the performance of design components, we take WiNet with Tanh activation and MLPs as the baseline model. WiNet-Relu is built by replacing Tanh activation with Relu activation on the baseline model. WiNet-noMLP is equal to the baseline model removing MLPs. Ablation results are reported in Table 6. It is obvious that two components play an important part in learning effective parameters. Tanh activation improves the accuracy of WiNet by about 1.2% compared with WiNet-Relu. Without MLPs, the model's performance is down by at least 0.4% (99.8% vs 99.4%).

Table 6.  Ablation study with different fusions.

Model	WiNet-Relu	WiNet-noMLP	WiNet
Top-1 Accuracy	98.5%	99.4%	99.8%

---

 | Show Table

DownLoad: CSV

Diagrams are an important tool to help people intuitively understand the world. In Section 3.1 (Figure 3 and Eq (6)), we analyze the superposition of two waves with different phases. In order to have a better understanding of the effects of the representation type, we take the visualized feature maps of a traffic sign as an example. From Figure 7, we can clearly see that the visualized feature maps of the first stage with the similar contents are aggregated together. Similar parts in the picture have a closer phase reformulated. Similar parts gradually stick out in the aggregating process, so we get a strong stereo effect from the picture. As the number of network layers deepens, the model extracts more abstract features.

Figure 7.  The visualized feature maps of a traffic sign.

DownLoad: Full-Size Img PowerPoint

5.   Conclusions

We propose a novel deep learning architecture for traffic sign recognition, whose mechanism for aggregating information is different from the existing transformer, CNN architectures or MLP architectures. In the proposed approach, we combine a new CNN-based module with a wave function successfully. Firstly, we get multi-scale feature representations by the CNN-based module. Then, we utilize channel-FC operations to estimate the amplitude and phase information. Amplitude and phase are key parameters to dynamically modulate relationship entities with similar contents. Extensive experimental evaluations are performed according to different strategies to explore the superiority of the proposed architecture or understand how that works. We will explore further how to use the information representation in different fields or directly use the information representation to preprocess raw data. We also hope our work can encourage people to get new ideas from physical phenomenon.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work is jointly supported by the National Natural Science Foundation of China under Grant 61976055, the special fund for education and scientific research of Fujian Provincial Department of Finance under Grant GY-Z21001 and Scientific Research Foundation of Fujian University of Technology under Grant GY-Z22071.

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.