Dialogic teaching practices and student performance in mathematics in Asian countries

1.   Introduction

It is well known that the spectral method has high-order accuracy for smooth problems. The spectral method together with the difference method and the finite element method has become an important method for the numerical solution of partial differential equations (PDEs), and has been successfully applied to solve many practical problems. In recent years, with regard to the differential equations of time evolution, the high-order discrete scheme in time has received widespread attention and has become one of the hot spots in the field of numerical computing. The discontinuous Galerkin method in time is constantly developing, and a better higher-order discrete scheme in time is established ^[1,2,3]. The explicit, implicit and implicit-explicit Runge-Kutta methods have also made great progress: a local discontinuous Galerkin method with implicit-explicit time-marching is used to solve the multi-dimensional convection-diffusion problems and time-dependent incompressible fluid flow in ^[4,5,6]. In ^[7,8,9], the spectral method in time and the time multi-interval spectral method are also proposed. The single interval and multi-interval Legendre spectral methods in time are established for the parabolic equations, in which the $L^2$-optimal error estimate in space is obtained in ^[10].

The Maxwell equation is a set of important PDEs that describes electromagnetic field phenomena, and some effective numerical methods have been established for the Maxwell equation by scholars ^[11,12,13]. The finite-difference time-domain method (also called Yee's scheme) for the Maxwell equation is proposed in ^[14]. In ^[15,16], an energy-conserved splitting spectral method for solving the Maxwell equation is given. For the 2-D Maxwell equation, a Legendre-Galerkin method in space and the energy-conserved splitting spectral method in time is constructed ^[17]. In previous work, the different method is used in the time direction. For the 1-D Maxwell equation of inhomogeneous media with discontinuous solutions, the multidomain Legendre-Galerkin and the multidomain Legendre-tau method are established in ^[18,19], and the optimal error estimates of the semi-discrete schemes are given.

Consider the following 1-D Maxwell equation ^[20]

where $I_x = (-1, 1)$, $I_t = (0, T]$, and $\Omega = I_x\times I_t$. $E_z$ and $H_y$ stand for the electric field and the magnetic field, respectively. The positive constants $\epsilon$ and $\mu$ stand for the electric permeability and the magnetic permeability, respectively.

In ^[21,22], an $h$-$p$ version of the Petrov-Galerkin time stepping method is used to solve the nonlinear initial value problems by transforming the second-order problem into a first-order system. For the linear second-order wave equation, it is often transformed into the first-order system similar to equation (1.1) by using the substitution $v = \frac{ \partial u}{ \partial t}, \; w = \frac{ \partial u}{ \partial x}$ ^[23]. It is interesting to note that some methods use the derivative as the main unknown function, and $u$ is expressed as the integral of $w$.

In this paper, a Legendre-tau space-time (LT-ST) spectral method is developed to solve the 1-D Maxwell equation $(1.1)$ and a time multi-interval Legendre-tau spectral method is considered. The scheme is based on the Legendre-tau method, which uses polynomials of different degrees are used to approximate the electric field $E_z$ and magnetic field $H_y$, respectively, so that they can be decoupled in computation. After decoupling, it is an equation only about $E_z$, which can be solved by the method in ^[10]. The method is also applied to the numerical solutions of the 1-D nonlinear Maxwell equation.

The paper is organized as follows. In Section 2, a Legendre-tau space-time spectral method for $(1.1)$ is presented, and stability analysis and error estimate are given. In Section 3, a time multi-interval Legendre-tau spectral method is developed, and its error estimate is also obtained. Some numerical results are given in Section 4. Finally, the method is applied to the numerical solution of the 1-D nonlinear Maxwell equation in Section 5.

2.   Legendre-tau space-time spectral method

In this section, a Legendre-tau space-time spectral method is presented for the problem $(1.1)$. Moreover, the stability and the error estimate of this method are given.

2.1.   Preliminaries

Let $(\cdot, \cdot)_Q$ and $\|\cdot\|_Q$ be the inner product and the norm of $L^2(Q)$, where Q stands for $\Omega$, $I_x$ and $I_t$, respectively. For a nonnegative integer $m$, let $\|\cdot\|_{m, I}$ and $|\cdot|_{m, I}$ be the norm and the semi-norm of the classical Sobolev space $H^m(I)$, where $I$ stands for $I_x$ or $I_t$, respectively. Define

For a pair of positive integers $N$ and $M$, define $L = (N, M)$. Let $\mathbb P_{N}(I_x)$ be the space of polynomials of degree at most $N$ on $I_x$. Define the polynomial space

and the approximation space in space

Let $\mathbb P_{M}(I_t)$ be the space of polynomials of degree at most $M$ on $I_t$, we define the approximation space in time

Let $x^C_j$ and $\omega_{j}^{C}(0\leq j\leq N)$ be the Chebyshev-Gauss-Lobatto (CGL) points and the corresponding weights on $I_x$. We define the CGL interpolation operator $I_N^C v \in V_N$:

Similarly, let $x^L_j$ and $\omega_{j}^{L}(0\leq j\leq N)$ be the Legendre-Gauss-Lobatto (LGL) points and the corresponding weights on $I_x$. $I_N^L v \in V_N$ denotes the LGL interpolation operator, and

We denote by $P_{N}: L^{2}(I_x) \rightarrow V_N$ the $L^2(I_x)$-Legendre projection operator and define $P_{N}^1:H^{1}(I_{x}) \rightarrow V_{N}$ by

It is easy to see that

Let $C$ be a generic positive constant independent of $N$, and the following approximation results can be found in ^[10,24].

Lemma 2.1. If $u\in H^r(I_x)$, then

Let $t^C_j$ and $\omega_{j}^{C}(0\leq j\leq M)$ be the CGL points and the corresponding weights on $I_t$, and let $t^L_j$ and $\omega_{j}^{L}(0\leq j\leq M)$ be the LGL points and the corresponding weights on $I_t$. We denote by $P_M:L^{2}(I_t)\rightarrow V_{M}$ the $L^{2}(I_t)$-Legendre projection operator and define $P^1_{M}:H^1(I_t)\rightarrow V_{M}$ as

It is easy to find that

The following approximation result can be found in ^[10].

Lemma 2.2. If $u\in H^{\sigma}(I_t)$ and $\sigma \geq 1$, then

where $C$ is a positive constant independent of $M$.

The problem $(1.1)$ is expressed in a weak form: Find $E_{z} \in H_0^{1}(I_x)\otimes H^{1}(I_t)$ and $H_{y} \in L^2(I_x)\otimes H^{1}(I_t)$ such that

The LT-ST scheme to the problem $(1.1)$ is: Find $E_{zL} \in V_N^{0}\otimes V_{M}$ and $H_{yL} \in V_{N-1}\otimes V_{M}$ such that

2.2.   Stability analysis

In the following section, the stability analysis of (2.10) is considered. Suppose that there are perturbations $\tilde f_i(i = 1, 2)$ on the right-hand side. For simplicity, the original notations $E_{zL}$ and $H_{yL}$ are used to represent the solutions to the perturbation problem, which satisfies the following perturbation equation:

Theorem 2.1. Let $E_{zL}$ and $H_{yL}$ are the solutions to (2.11). Suppose that $\tilde f_i(i = 1, 2)$ are perturbations on the right-hand side, such that

Proof. Taking $v = \tilde{E}_{zL}: = t^{-1}E_{zL}\in V_{N}^{0}\otimes V_{M-1}$ and $w = \tilde{H}_{yL}: = t^{-1}H_{yL}\in V_{N-1}\otimes V_{M-1}$ in (2.11), we get

which leads to

By integration by parts,

and using the Cauchy-Schwarz inequality

where $\tilde{E}_{zL}(T)$ = $\tilde{E}_{zL}(x, T)$ and $\tilde{H}_{yL}(T)$ = $\tilde{H}_{yL}(x, T)$. Substituting (2.15)-(2.16) into (2.14),

and noting that $\|E_{zL}\|_\Omega\leq T\|\tilde E_{zL}\|_\Omega, \; \; \|H_{yL}\|_\Omega\leq T\|\tilde H_{yL}\|_\Omega$, we get the result of (2.12).

2.3.   Error estimate

In the following section, the error estimate of (2.10) is given. In order to deal with the error of the initial value, the following auxiliary problem is considered ^[25]

Firstly, the estimate between the two solutions to (2.10) and (2.18) is considered. We define

By (2.5) and (2.8), we have

and

Let $e_z = E_{zL}-E_{a}$ and $e_y = H_{yL}-H_{a}$. By (2.10) and (2.20), the following error equation is obtained

Due to (2.18), we have $\epsilon \partial_t E = \partial_x H$, $\mu \partial_t H = \partial_x E$, and

Similar to the proof of Theorem 2.1, we obtain the following error estimate.

Theorem 2.2. Let $E_a$ and $H_a$ be the projections (2.19) of $E$ and $H$ (2.18), respectively. Let $E_{zL}$ and $H_{yL}$ be the solutions to (2.10), respectively. Assuming that $\sigma\geq1$, $r\geq2$, $E, H\in C([0, T]; H^r(I_x))\cap L^2(I_x; H^\sigma(I_t))$, and then there exists a positive constant $C$ such that

Proof. By (2.12) and (2.21), we have

According to Lemma 2.1 and 2.2, it follows that

Substituting (2.24)-(2.25) into (2.23), the error estimate (2.22) is obtained.

Next, the error estimate between the solutions to (2.10) and (1.1) is considered.

Theorem 2.3. Let $E_z$, $H_y$, $E_{zL}$, and $H_{yL}$ be the solutions to (1.1) and (2.10), respectively. Assume that $\sigma\geq1$, $r\geq2$, $E, H\in C([0, T]; H^r(I_x))\cap L^2(I_x; H^\sigma(I_t))$, and then there exists a positive constant $C$ such that

Proof. Firstly, the error between the solutions to (2.18) and (1.1) is estimated. Let $e_z = E-E_{z}$ and $e_y = H-H_{y}$. By (1.1) and (2.18), we get the following error equation

Then, we consider the inner product on $I_x$

which leads to

Next, integrating over $t$

and taking $t = T$, we have

According to Lemma 2.1, it follows that

Substituting (2.32) into (2.30)-(2.31), we obtain

On the other hand, by Lemmas 2.1-2.2, we have

From (2.22) and (2.33)-(2.34), the error estimate (2.26) is obtained.

3.   Time multi-interval Legendre-tau spectral method

In this section, a time multi-interval Legendre-tau spectral scheme is developed and its error estimate is obtained.

3.1.   Preliminaries

Let $K$ be a positive integer and a partition of the computational interval $I_t$ is given as

where

Let ${\cal M} = (M_1, \cdots, M_K)$ and $L = (N, {\cal M})$. We define the space of approximate functions in time as

where ${\mathbb P}_{M_k}(I_k)$ denotes the space of polynomials of degree at most $M_k$ on $I_k$. We define the space of the test functions in time as

where ${\cal M}-1 = (M_1-1, \cdots, M_K-1)$.

Let $\hat{I} = (-1, 1)$ be a reference interval, $\hat{t}_j^{k}$ and $\hat{\omega}_{j}^{k}(0\leq j\leq M_k)$ be the LGL points and the corresponding weights on $\hat{I}$. We denote by $\{\hat{t}^{k}_j\}$ and $\{\hat{\omega}_{j}^{k}\}$ be the LGL points and the corresponding weights on $I_k$. Next, we define

where $\tau_k = a_k-a_{k-1}$.

Letting $v^k\equiv v|_{I_k}$, for any $u, v\in C(\bar{I})$ and $\omega_j^k = \frac{1}{2}\tau_k\hat{\omega}_{j}^{k}$, we define

Similarly, we denote $\hat{t}_j^{k, C}$ and $\hat{\omega}_j^{k, C}$ be the CGL points and the corresponding weights on $\hat{I}$. Let $\{\hat{t}^{k, C}_j\}$ and $\{\hat{\omega}_{j}^{k, C}\}$ be the CGL points and the corresponding weights on $I_k$.

We define LGL interpolation operator $I_{\cal M}^L:C(\bar{I})\rightarrow W_{\cal M}$ by

Similarly, for the CGL interpolation operator $I_{\cal M}^L:C(\bar{I})\rightarrow W_{\cal M}$, which satisfies

Define the following relation

Let $\hat P_{M_k -1}: L^{2}(\hat I) \rightarrow \mathbb P_{M_k -1}$ the $L^2$-Legendre projection operator by $P_{{\cal M}-1}: L^{2}(I_t) \rightarrow W_{{\cal M} -1}$ such that

Let $\hat P_{1, M_k}: H^{1}(\hat I) \rightarrow \mathbb P_{M_k}$ be the Legendre projection operator, which satisfies

and $P_{1, {\cal M}}$ be generated by $P_{1, M_k}:H^1(I_k)\to {\mathbb P}_{M_k}(I_k)$ such that

The following approximation results can be found in ^[10].

Lemma 3.1. If $v\in H^{\sigma}(I_t)$ and $\sigma\geq1$, then

where $C$ is a generic positive constant independent of $\tau_k$, $M_k$.

The time multi-interval Legendre-tau spectral method for the problem (1.1) is : Find $E_{zN}^{k} \in V_N^{0}\otimes W_M$ and $H_{yN}^{k}\in {V}_{N-1}\otimes W_M$ such that

We set

Let $\Omega_k = I_x\times \hat{I}_k$, and (3.5) can be written as: For $1\leq k \leq K$, find $E_{zL}^{k} \in V_N^{0}\otimes {\mathbb P}_{M_k}(\hat{I}_k)$ and $H_{yL}^{k}\in {V}_{N-1}\otimes {\mathbb P}_{M_k}(\hat{I}_k)$ such that

where $E_{zL}^{0}(x, \tau_0) = I_N^L E_{z0}(x), \; \; H_{yL}^{0}(x, \tau_0) = P_{N-1} I_N^L H_{y0}(x)$ when $k = 1$.

3.2.   Error estimate

In the following, we present the error estimate. In order to deal with the error of the initial value, we consider the following auxiliary problems on $\Omega_k, \; \; 1\le k\le K$,

Similar to the process of the single-interval, we define $E_{a}^{k} = P_{N}^{1}P^1_{M_k}E^{k}$, $H_{a}^{k} = P_{N-1}P^1_{M_k}H^{k}$, and denote

Let $e_z^k = E_{ zL }^k-E^{k}_{a}$ and $e_y^k = H_{ yL }^k-H^{k}_{a}$, the following error equation is obtained

For each subinterval in the multi-interval, using Theorem 2.2 and Lemma 3.1, the error estimate between the solution to (3.6) and the projection of the solution to (3.7) is obtained

Let $\mathbf{e}_z^k = E^k-E^k_{z}$ and $\mathbf{e}_y^k = H^k-H^k_{y}$, the results are similar to (2.30)-(2.31) for the multi-interval case,

Using the triangle inequality, we get

which leads to

By the Cauchy-Schwarz inequality, $\sum_{m = 1}^{k-1}\tau_m = a_{k-1}$, and (3.9), we derive

According to (2.7) and Lemma 2.1, it follows that

As (2.32), we have

Substituting the above estimation results into (3.10)-(3.11), we obtain

By (2.7), Lemma 2.1 and 2, we get

If $\tau_k\equiv \tau, M_k\equiv M$ for simplicity, and combining (3.9) and (3.15)-(3.16), we get the following error estimate.

Theorem 3.1. Let $E_z$ and $H_y$ be solutions to (1.1), respectively. Let $E_{zL}^K$ and $H_{yL}^K$ be solutions to (3.5), respectively. Let $E^k$ and $H^k$ be solutions to (3.7), respectively. Assuming that $\sigma\geq1$, $r\geq2$, $E_z, H_y\in C([0, T]; H^r(I_x))\cap L^2(I_x; H^\sigma(I_t))$, $E^k, H^k\in C([0, \tau_k]; H^r(I_x))\cap L^2(I_x; H^\sigma(\hat{I}^k))$, and then there exists a positive constant $C$ such that

4.   Numerical examples

In this section, some numerical results are presented. We define

Example 4.1. The LT-ST spectral method for the 1-D Maxwell equation

Consider the problem (1.1) with ${I}_x = (0, 1)$, ${I}_t = (0, 1)$, ${\Omega} = {I}_x\times {I}_t$, $\epsilon = 1$, and $\mu = 1$. The solution is as

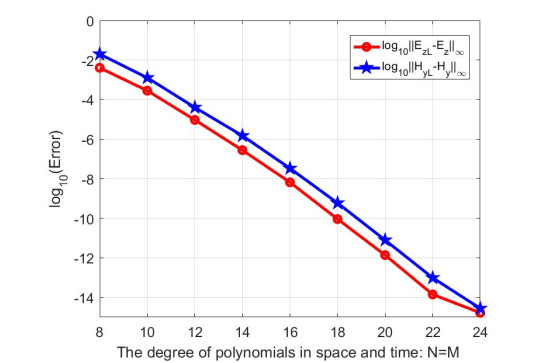
In Figure 1, the values of $\rm log_{10}$ $\mathbb{E}_{\infty}(E_z)$ and $\rm log_{10}$ $\mathbb{E}_{\infty}(H_y)$ is obtained when $t = 1$. It can be seen from Figure 1 that the LT-ST method has spectral accuracy both in the time and space, which is consistent with the results of theoretical analysis.

To check the high accuracy, we compare the numerical errors of our scheme (2.10) with the Legendre-tau spectral method in space and the leapfrog-Crank-Nicolson method in time (LT-LFCN) ^[19]. For convenience of notation, let $(N, \tau)$ be the degree of the polynomial in the space approximation and the time step for the LT-LFCN method.

The $L^{\infty}$-error of the LT-LFCN scheme and our method (2.10) at $t = 1$ are listed in Table 1. It can be seen from Table 1 that on the same PC machine, the proposed method takes shorter time than the LT-LFCN method.

Example 4.2. The time multi-interval Legendre-tau spectral method for the 1-D Maxwell equation

Further, the method (3.6) is used to solve Example 1 of $N = M_k = 24$ and $0\leq t\leq 5$, and the numerical results are shown in Table 2.

5.   Application to the 1-D nonlinear Maxwell equation

In this section, the proposed method is applied to the numerical solution of the 1-D nonlinear Maxwell equation. The approximating of the nonlinear term is calculated by interpolation at the CGL point, and implemented with the help of Fast Legendre transformation.

5.1.   Scheme

Now, we apply the LT-ST method to solve the 1-D nonlinear Maxwell equation as ^[26]

where the nonlinear function $J(E_z) = \sigma(|E_z|)E_z$ with $\sigma(s)$ is a real valued function representing the electric conductivity.

The problem (5.1) can be written in a weak form: Find $E_{z} \in H_0^{1}(I_x)\otimes H^{1}(I_t)$ and $H_{y} \in L^2(I_x)\otimes H^{1}(I_t)$ such that

Combining the interpolation operator both in space and time, a 2-D interpolation is defined as $I_{(N, M)}^L$. The LT-ST method to the problem $(5.1)$ is: Find $E_{zL} \in V_N^{0}\otimes V_{M}$ and $H_{yL} \in V_{N-1}\otimes V_{M}$ such that

We briefly describe the implementation of scheme $(5.3)$. For simplicity, taking $\Omega = [-1, 1]\times [-1, 1]$. Let $L_k$ be the Legendre polynomial of degree $k$, and the basis functions in space are

where $\phi_k(x) = L_k(x)-L_{k-2}(x)$.

The basis functions in time are

where $\phi_k(t) = L_k(t)-L_{k-2}(t)$.

The approximate solutions and the test functions are expressed as

The interpolation polynomial of the nonlinear term can be expressed as $I_{(N, M)}^CJ(E_{zL}) = \Psi(t)\hat{J}\Phi^T(x)$. The following algebraic equation is obtained from $(5.3)$

where $\hat{E}$ and $\hat{H}$ are matrices composed of coefficients of approximate solutions $E_{zL}$ and $H_{yL}$, respectively. For simplicity, (5.4) can be rewritten in matrix form as

A simple implicit-explicit iteration method is used to solve (5.5). In order to separate the initial conditions from the coefficient matrix, $\hat{E}$, $\hat{H}$, $M_t$ is divided into the following forms as

where $\hat{E_i}$ and $\hat{H_i}$ are the first rows of the coefficient matrix $\hat{E}$ and $\hat{H}$ respectively, corresponding to the initial value, $M^t_i$ is the first column of $M^t$. By the properties of the basis function and the orthogonality of Legendre polynomials show that both $K^t$ and $D$ are diagonal matrices, and the elements on the diagonal of $K^t$ are 2 except that the first element is zero. Thus, (5.5) can be expressed as

Let

In computations. We use the following simple explicit-implicit iteration scheme for (5.7),

when $k = 0$, using the initial information of $E_{zL}$ in (5.3), and taking $E^{[0]}_{zL}(t)\equiv E_{zL}(0)$ as the initial guess of the iteration. The iterative scheme (5.9) is a linear equation of $\hat{E}_0^{[k+1]}$, which can be solved by the method in ^[10].

Combining the interpolation operator in space and the multi-interval interpolation operator in time in Section 3, a 2-D interpolation is defined as $I_{(N, \cal{M})}^L$. The time multi-interval Legendre-tau spectral method for (5.1) is: Find $E_{zN}^{k} \in V_N^{0}\otimes W_{\cal M}$ and $H_{yN}^{k}\in {V}_{N-1}\otimes W_{\cal M}$ such that

In computation, the interval is shifted to $\hat{I}_k = (0, \tau_k)$. Let $\Omega_k = I_x\times \hat{I}_k$, and then (5.10) can be written as: Find $E_{zL}^{k} \in V_N^{0}\otimes {\mathbb P}_{M_k}(\hat{I}_k)$ and $H_{yL}^{k}\in {V}_{N-1}\otimes {\mathbb P}_{M_k}(\hat{I}_k), \; 1\leq k \leq K$, such that

where $E_{zL}^{0}(x, \tau_0) = I_N^L E_{z0}(x)$ and $H_{yL}^{0}(x, \tau_0) = P_{N-1} I_N^L H_{y0}(x)$ when $k = 1$.

5.2.   Numerical examples

Example 5.1. The LT-ST method for the 1-D nonlinear Maxwell equation

Consider the problem (5.1), and set the right-hand function of the first equation to $f(x, t)$. According to ^[26], the nonlinear term is given as

where ${I}_x = (0, 1)$, ${I}_t = (0, 1)$, ${\Omega} = {I}_x\times {I}_t$, and $\epsilon = \mu = 1$. The solution is

and the right-hand side of the first equation is

The scheme (5.3) is used to solve Example 5.1, and the values of $\rm log_{10}$ $\mathbb{E}_{\infty}(E_z)$ and $\rm log_{10}$ $\mathbb{E}_{\infty}(H_y)$ are obtained when $t = 1$. It can be seen from Figure 2 that the method has high accuracy both in time and space.

ItNum represents the number of iterations. Further, the method (5.11) is used to solve Example 5.1 in the case of $N = M_k = 24$ and $0\leq t\leq 5$, the numerical results are shown in Table 3.

Example 5.2. Comparison of the LT-ST method of 1-D nonlinear Maxwell equation and related computation results

Consider the same problem as in Example 5.1, but the nonlinear is given as ^[26]

Taking the same solution (5.12), the right-hand function of the first equation is

The Scheme (5.3) is applied to Example 5.1, and the values of $\rm log_{10}$ $\mathbb{E}_{\infty}(E_z)$ and $\rm log_{10}$ $\mathbb{E}_{\infty}(H_y)$ is obtained when $t = 1$. Computational results are given in Figure 3 to show that the LT-ST method has high accuracy both in time and space.

In order to compare the accuracy with the LT-LFCN method, we use it and the LT-ST method to computate Example 5.2, respectively. The LT-LFCN method is as follows:

Let $\tau$ be the time step, $t_k = k\tau\, \, (k = 0, 1, \cdot\cdot\cdot, n_T; T = n_T \tau).$ Denote $u^k(x): = u(x, k\tau)$, and we define

The LT-LFCN scheme to the problem $(5.1)$ is: For $1\leq k\leq n_T-1$, find $E^k_{zN}\in V^0_N$ and $H^k_{yN}\in V_{N-1}$ such that

The $L^{\infty}$-error of the LT-LFCN method (5.15) and the proposed method (5.3) at $t = 1$ are shown in Table 4. The results in Table 4 demonstrate that on the same PC machine, the proposed method provides more accurate results using less time than the LT-LFCN method.

The scheme (5.11) is also used to solve Example 5.2 for long-time computation. Numerical results are given in Table 5 with $N = M_k = 24$ and $0\leq t\leq 5$ to show the effectiveness of the LT-ST method.

6.   Conclusions

In this paper, the LT-ST method is investigated for the 1-D Maxwell equation and the time multi-interval Legendre-tau spectral method is considered. Error estimates for the method of single and multidomain are given, respectively. Numerical results are consistent with the theoretical analysis. Compared with the LT-LFCN method, the proposed method has advantages in accuracy and computation time. Moreover, the space-time spectral method is developed for the numerical solutions of the 1-D nonlinear Maxwell equation. In the future, the multidomain spectral method in space will be developed to solve the case of inhomogeneous media.

Acknowledgments

The research was supported by the National Natural Science Foundation of China (Grants No. 11971016).

Conflict of interest

The authors declare no conflict of interest.